Доказать тождество с помощью диаграмм эйлера венна: Диаграммы Эйлера-Венна онлайн

Операции над множествами — Студопедия

Поделись с друзьями

Над множествами можно выполнять действия (операции), напоминающие сложение и умножение чисел. Но не тождественные им.

Объединением (суммой0 множеств А и В называется множество, обозначаемое через АÈВ, содержащее те и только те элементы, которые принадлежат множеству А или В.

Краткая запись: АÈВ = {x | xÎ A или хÎ В}.

Соответствующая диаграмма Эйлера – Венна:

	АÈВ- заштрихованная область

Пример: А = {2, 5, 7, 9}, В = {3, 5, 8, 9, 12}.

АÈВ = {2, 5, 7, 9}È{3, 5, 8, 9, 12}= {2, 5, 7, 9, 3, 8, 12}.

Соответствующая диаграмма:

Пересечением (произведением) множеств А и В называется множество, обозначаемое через АÇВ и состоящее из тех и только из тех элементов, которые принадлежат множеству А и множеству В.

Краткая запись: АÇВ = {x | xÎA и хÎВ}.

Соответствующая диаграмма Эйлера- Венна:

АÇВ – заштрихованная область

Пример: АÇВ= {2, 5, 7, 9}Ç{3, 5, 8, 9, 12}= {5,9}.

Диаграмма:

Разностью множеств А и В называется множество, обозначаемое через А\В и состоящее из тех и только из тех элементов, которые принадлежат А и не принадлежат В.

Краткая запись: А\В = {x| xÎ A и xÏB}.

Соответствующая диаграмма Эйлера- Венна:

		А\В- заштрихованная область

Пример: А\В = {2, 5, 7, 9}\{3, 5, 8, 9, 12}= {2, 7}.

Диаграмма:

Если АÇВ = Æ, то А\В= А и В\А = В.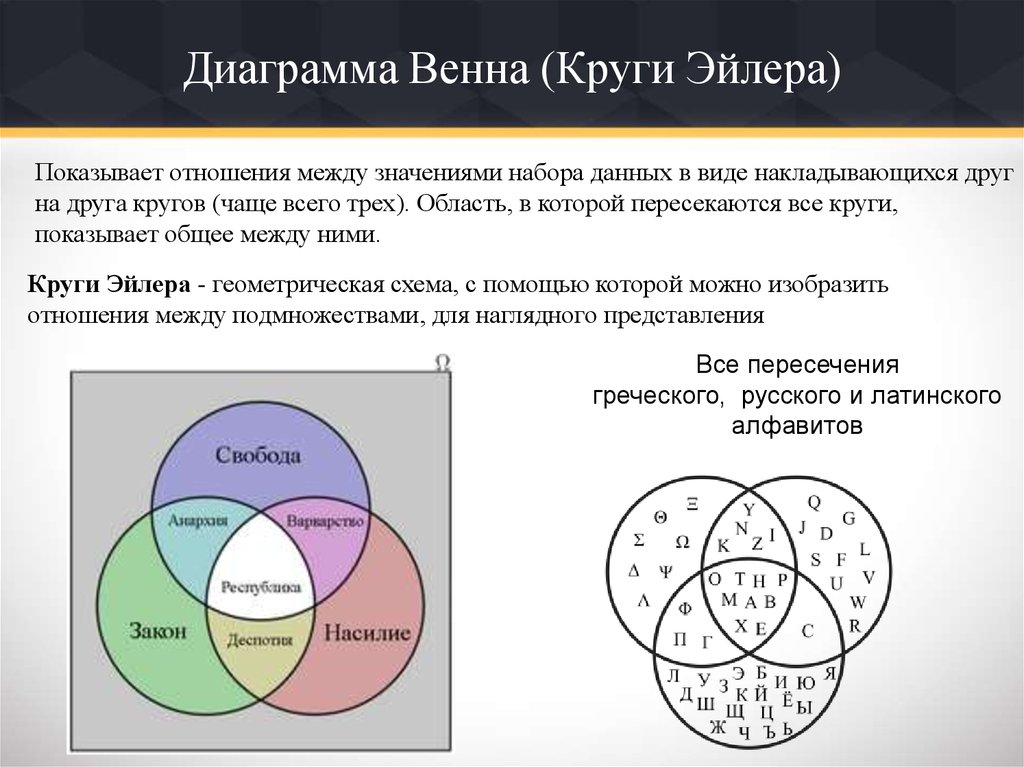

Если А Í В, то А\В = Æ.

Если U – универсальное множество и АÍ U, то разность U\A называется дополнением множества А до множества U и обозначается .

Краткая запись: = {x| xÎU и xÏA}.

Соответствующая диаграмма Эйлера- Венна:

Симметрической разностью множеств А и В называется множество, обозначаемое АDВ и состоящее из тех и только из тех элементов, которые принадлежат А\В или В\А.

Краткая запись: ADB= {x| xÎA\B или xÎB\A}.

Соответствующая диаграмма Эйлера- Венна:

Пример: АDВ = {2, 5, 7, 9}D{3, 5, 8, 9, 12}= {2, 7, 3, 8, 12}.

Диаграмма:

Пример: Найти множество: (АÇВ)D(С\Q), где:

Расставим порядок действий и выполним их по порядку:

4. Алгебра множеств.

Непосредственной проверкой можно доказать справедливость следующих соотношений:

1. Коммутативность

2. Ассоциативность

3. Дистрибутивность

4. Закон поглощения

5. Закон де Моргана

Приведенные выше соотношения называются тождествами алгебры множеств.

Заметим, что если в равенстве заменить È на Ç, U на Æ и наоборот, то получим справедливое равенство.

Этот закон называется принципом двойственности.

Докажем, например, справедливость равенства аналитически и с помощью диаграмм Эйлера – Венна.

Пусть х Є АU В, что означает хÎU и хÏАÈВ. Отсюда следует, что хÏА и хÏВ, но тогда

Построим диаграммы для обеих частей равенства и сравним их.

Диаграмма для левой части :

Диаграмма для правой части:

Сравнивая диаграммы, убеждаемся в справедливости равенства.

Пользуясь тождествами можно производить преобразования над множественными выражениями и доказывать тождества.

Пример1: доказать тождество

Рассмотрим два способа: с помощью диаграмм и тождеств.

1 способ

Левая часть тождества

— результат

Правая часть тождества

— результат

2 способ

Преобразуем левую часть тождества :

Тем самым доказали верность тождества.

Пример2: Доказать тождество: Составить двойственное и тоже доказать.

Доказательство справедливости равенства и двойственного равенства с помощью диаграмм предлагаем выполнить самостоятельно.

Приведем доказательство справедливости данного равенства путем преобразований (доказательство для двойственного проведите самостоятельно):

Пример3: Доказать тождество:

Преобразуем правую часть тождества:

Тождество доказано.

5. Теорема о количестве подмножеств конечного множества.

Рассмотрим множество А = {1, 2, 3 }, где |A| = 3, и множество В = {5, 6, 7, 8}, где |B| = 4.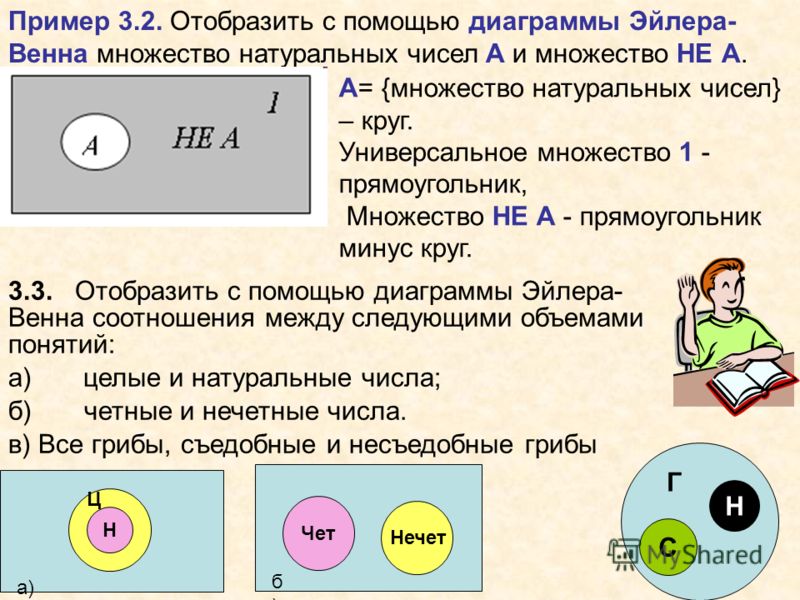

Составим всевозможные подмножества множества А:

А, Æ, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}.

Всего получили 8 подмножеств.

Составим всевозможные подмножества множества В:

В, Æ, {5}, {6}, {7}, {8}, {5,6}, {5,7}, {5,8}, {6,7}, {6,8}, {7,8}, {5,6,7}, {5,7,8}, {6,7,8}, {5,6,8}.

Получили 16 подмножеств.

Используя результаты рассмотренных примеров, можно предположить справедливость следующего равенства: n = 2

m, где n – количество подмножеств данного конечного множества, m – мощность множества.

Справедливость предположения подтверждает теорема, которую мы примем без доказательства.

Теорема: Если для конечного множества А его мощность равна т, то количество всех подмножеств данного множества, обозначаемое Р(А), равно 2^т.

Пример: Вычислить количество подмножеств множества М – делителей числа 20.

Составим множество М и найдем его мощность :

М = {1,2,4,5,10,20}. Мощность |M| = 6, тогда количество подмножеств равно Р(М) = 2⁶ = 64.

6. Формула включений и исключений.

Проиллюстрируем теперь применение операций над множест­вами для решения задач о нахождении числа элементов мно­жеств, заданных несколькими условиями. Ниже мы будем рас­сматривать только конечные множества.

Пример: В классе 30 учащихся, 16 из них занимаются му­зыкой, 17 увлекаются теннисом, а 10 занимаются и музыкой, и теннисом. Есть ли в классе ученики, равнодушные и к музыке, и к теннису, и если есть, то сколько их?

Решение: Если сложить число учащихся, интересующихся музыкой, с числом учащихся, занимающихся теннисом, т. е. 16+17=33, то учащиеся, интересующиеся и музыкой, и тенни­сом, окажутся учтенными дважды. Поэтому, чтобы определить число учащихся, интересующихся музыкой или теннисом, нужно из суммы 16+17 вычесть число учащихся, учтенных дважды, т. е. тех, кто интересуется и музыкой, и теннисом. По условию их 10. Таким образом, число интересующихся теннисом или музы­кой равно: 16+17—10=23 ученика. А так как в классе всего 30 учащихся, то 30—23 ==7 учащихся равнодушны и к музыке, и к теннису.

Задача решена по следующему алгоритму: пусть имеется два конечных множества А и В. Тогда:

п(АÈ В) = п(А) + п(В )- п(АÇ В) (1)

В нашем случае А — множество учащихся, интересующихся му­зыкой, и n(A) = 16, В—множество учащихся, интересующихся теннисом, и n(B) = 17, n(AÇB) =10, и тогда по полученной формуле n(AUВ)=16+17-10=23.

Усложним задачу: пусть к тем, кто интересуется в классе му­зыкой — множеству А, и к тем, кто увлекается теннисом — мно­жеству В, добавляются еще и те, кто интересуется театром— множество С. Сколько учеников увлекается или музыкой, или теннисом, или театром, т. е. чему равно число n{AÈ B È C)?

Если множества А, В и С пересекаются лишь попарно, т. е. АÇВÇС=Æ, то подсчет можно вести, как и прежде: снача­ла сложить п(А)+п(В)+п(С), а затем вычесть число тех эле­ментов, которые подсчитаны дважды, т. е. вычесть число n{AÇ B}+n(AÇ C)+n(BÇ C). Если же множество АÇВÇС¹Æ,, то его элементы оказались неучтенными: сначала их трижды учли, когда складывали п(А}+п (В)+п(С), а затем трижды отнимали их, вычитая

n{AÇ B}+n(AÇ C)+n(BÇ C).

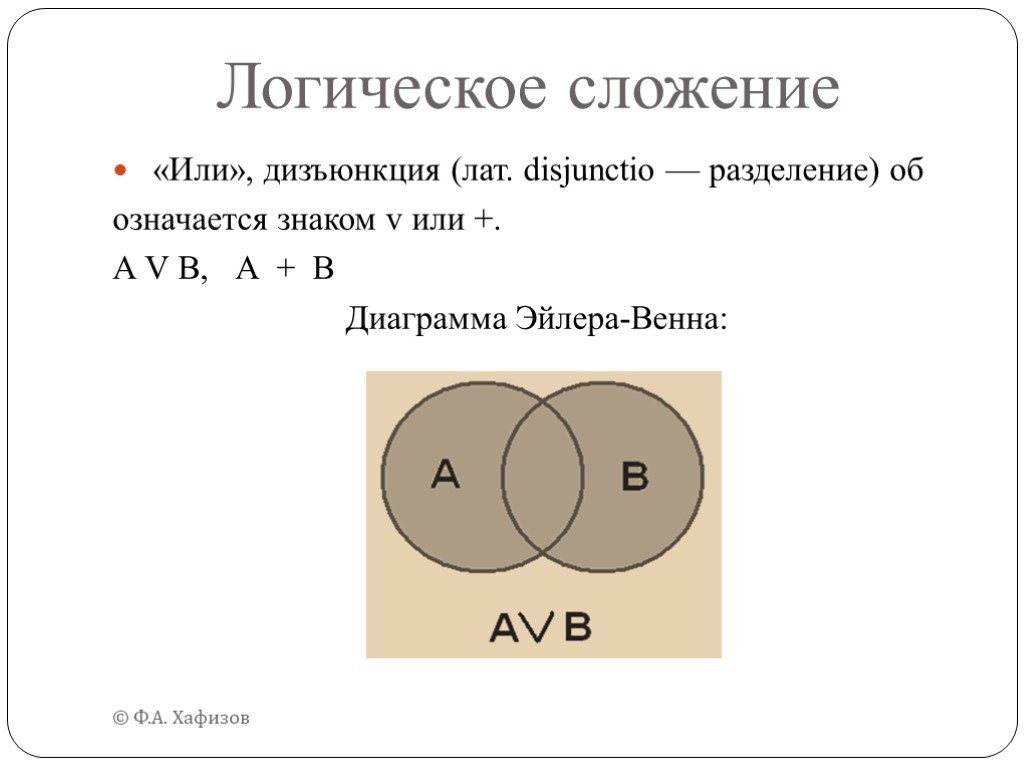
Таким об­разом, число

п(А)+п(В)+п(С )- (n{AÇ B}+n(AÇ C)+n(BÇ C))

меньше истинного результата ровно на число элементов в пере­сечении множеств АÇВÇС, которое и следует добавить для по­лучения верного результата:

п(А)+п(В)+п(С )- (n{AÇ B}+n(AÇ C)+n(BÇ C))+п(АÇ ВÇ С) (2)

Аналогичная формула может быть получена для любого числа множеств.

В формулах (1) и (2) подсчитывается, сколько раз каждый элемент включается и исключается, поэтому их называют фор­мулами включений и исключений.

Рассмотрим несколько примеров применения полученных формул.

Пример1: На вступительном экзамене по математике были предложены три задачи: по алгебре, планиметрии и стереометрии. Из 1000 абитуриентов задачу по алгебре решили 800, по планиметрии — 700, а по стереометрии — 600 абитуриентов. При этом задачи по алгебре и планиметрии решили 600 абитуриен­тов, по алгебре и стереометрии — 500, по планиметрии и стерео­метрии — 400. Все три задачи решили 300 абитуриентов.

Суще­ствуют ли абитуриенты, не решившие ни одной задачи, и если да, то сколько их?

Решение. Пусть U — множество всех абитуриентов, А —. множество абитуриентов, решивших задачу по алгебре, В — множество абитуриентов, решивших задачу по планиметрии, С — множество абитуриентов, решивших задачу по стереометрии. По условию n(U) =1000, n(A) = 800, n(В)=700, n(С)=600, n(AÇB)= 600, n(AÇC) = 500, n(BÇC) = 400, n(AÇBÇC) =300. В множество AÇBÇC включены все абитуриенты, решившие хо­тя бы одну задачу. По формуле (2) имеем:

n(А U В U С) == 800 + 700 + 600 — 600 — 500 — 400 + 300 =900.

Отсюда следует, что не все поступающие решили хотя бы одну задачу. Ни одной задачи не решили

n(U) — n(AUBUC)=1000 — 900==100 (абитуриентов).

Пример2: Социологи опросили 45 учащихся девятых клас­сов, среди которых 25 юношей. При этом выяснилось: 30 человек имеют за полугодие оценки 4 и 5, из них 16 юношей, спортом занимаются 28 учеников, среди них 18 юношей, и 17 учеников, успевающих только на хорошо и отлично, 15 юношей учатся на хорошо и отлично и занимаются спортом. Первый математик класса взглянул на результаты и заявил, что там есть ошибки. Как это ему удалось выяснить?

Решение: Обозначим через А множество юношей, В — множество успевающих на 4 и 5, С — множество спортсменов. По условию задачи n(A)=25, n(В)=30, n(С)=28, n(AÇB)=16, n(AÇC)=18, n(BÇC)=17, n(AÇBÇC)=15. Найдем общее чис­ло учащихся, которые или являются юношами, или занимаются спортом, или успевают на 4 и 5. По формуле (2) получаем:

n (A UBUC)=25+30+28- 16- 18- 17+15=47. Этого быть не может, так как обследовалось всего 45 учеников! Следовательно, в данных сведениях есть ошибки.

На рисунке это решение проиллюстрировано с помощью диаграммы Эйлера — Венна.

В пересечении множеств А, В и С за­пишем число 15, так как по условию n(AÇBÇC)=15. В мно­жестве AÇB\С запишем число 16—15=1, в множестве BÇC\А — число 18-15=3, в множестве BÇC\А—число 17-15=2, в множестве A\(BÈC)— число 25-(1+15+3)=6, в множестве В\(А ÈC) — число 30-(1 + 15+2)= 12, в множест­ве С\(АÈВ)— число 28-(3+15+2)=8. Чтобы найти n(АÈВÈС), достаточно сложить записанные числа, поскольку они соответствуют множествам, не пересекающимся между со­бой. Получим число 47 > 45, что невозможно по условию задачи.

Задачи для самостоятельного решения

1. Опишите множество М точек на плоскости: a) {M| OM = R}; б) {M| OM£ R}; в) {M| AM = MB}.

2. Даны множества : Построить множество ((АDВ)È(В\С)) . Найти количество подмножеств построенного множества. Показать соответствующую диаграмму Эйлера – Венна.

3. Доказать с помощью диаграмм Эйлера – Венна справедливость закона поглощения.

4. Доказать тождества с помощью диаграмм и путем преобразований:

5. В отделе института работают несколько человек. Каждый из них знает хотя бы один иностранный язык, причем: 6 знают немецкий, 6 – английский, 7 – французский, 4 – английский и немецкий, 3 – немецкий и французский, 2 – французский и английский, 1 – все три языка. Сколько всего человек работает в отделе? Сколько из них знают только английский?

6. Из 35 учащихся класса 20 посещают математический кружок, 11 – физический, 10 – не посещают кружки. Сколько учеников посещают математический и физический кружки одновременно, сколько – только математический?

Контрольные вопросы

1. Объясните понятие множества. Приведите примеры множеств. Как обозначаются множества и их элементы?

2. Какие существуют способы задания множеств?

3. С помощью характеристического свойства задайте конечное, бесконечное несчетное, бесконечное счетное и пустое множества.

4. Как обозначается принадлежность элемента множеству и не принадлежность?

5. Какие существуют отношения между двумя множествами?

6. Перечислите операции над множествами с приведением соответствующих диаграмм Эйлера – Венна.

7. Перечислите тождества алгебры множеств.

8. Сформулируйте теорему о количестве подмножеств конечного множества.

9. Запишите формулы количества элементов в объединении двух и трех множеств.

---

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:  

---



Дискретная математика

Вариант 8.

Задание №1.

Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграмм Эйлера-Венна.

Решение:

Что и требовалось доказать.

Проверим с помощью диаграмм Эйлера-Венна:

Результаты совпали.

Задание №2.

С помощью таблицы истинности установите эквивалентны ли данные формулы:

Решение:

0	0	1	1	0	0	1	1
0	1	1	0	0	0	1	1
1	0	0	1	0	1	1	1
1	1	0	0	1	1	0	1

Итак, данные формулы неэквивалентны, поскольку в выделенных столбцах значения не совпали.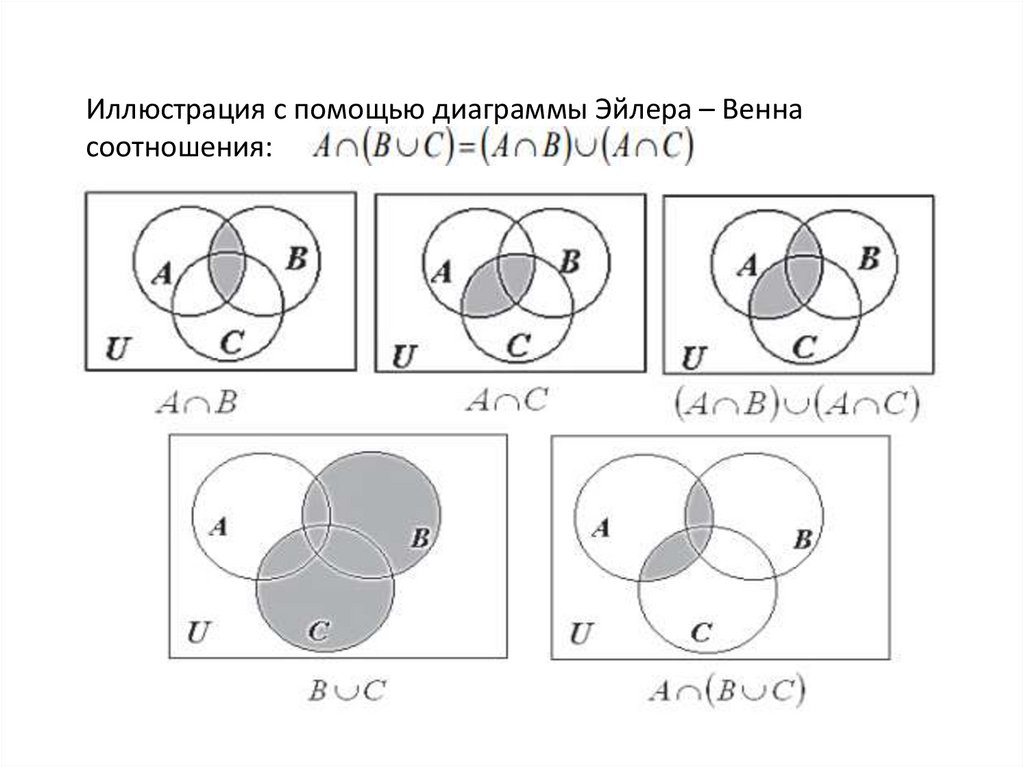

Задание № 3.

Проверьте, является ли данное отношение отношением эквивалентности.

Отношение «число x больше или равно числа y».

Решение:

Отношение является отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Проверим выполнимость рефлексивности (отношение рефлексивно на множестве М, если ).

.

Тогда рефлексивность выполняется.

Проверим выполнимость симметричности (отношение симметрично на множестве М, если ).

Если , то не для всех пар будет выполняться условие , следовательно, рефлексивность не выполняется.

Таким образом, отношение «число x больше или равно числа y» не является отношением эквивалентности.

Задание № 4 .

Нарисовать на плоскости граф G=[V, E] (единственный с точностью до изоморфизма), имеющий заданную матрицу úçdijúçсвоей матрицей смежности. Найти матрицу инцидентности úçrijúçграфа G.

Решение:

Матрица симметрична, тогда граф не является ориентированным. Искомый граф имеет 4 вершины и 4 ребра. Построим его:

Перенумеруем ребра:

Составим матрицу инцидентности:

Задание № 5.

Нарисовать на плоскости орграф G=[N, A] (единственный с точностью до изоморфизма), имеющий заданную матрицу úçdijúçсвоей матрицей смежности. Найти матрицу инцидентности úçcijúçграфа G.

Решение:

Матрица симметрична. Искомый граф имеет 4 вершины, 4 пары обычных ребер, каждая из которых направлена в противоположном направлении, а также 4 петли. Построим его:

Матрица инцидентности:

< Предыдущая		Следующая >

дискретная математика — «Если A, то B» в диаграммах Венна (или Эйлера)

спросил 7 лет, 7 месяцев назад

Изменено 7 лет, 7 месяцев назад

Просмотрено 3к раз

$\begingroup$

Как представить на диаграмме «Если А, то В»? Я думал, что это будет простое подмножество вроде $A ⊂ B$. c \cup B$.

С другой стороны, ваша интерпретация тоже не неверна, а просто о другом. Утверждение «Если $A$, то $B$» говорит о том, что каждое условие, при котором истинно $A$, также является условием, при котором истинно $B$. Следовательно, множество условий, при которых истинно $A$, является подмножеством множества условий, при которых истинно $B$.

Итак, ваша диаграмма соответствует самому утверждению (в каком случае оно истинно), а другая диаграмма соответствует истинностному значению утверждения (заштрихованная область — когда оно истинно). 9c\cup B$, как они говорили.

$\endgroup$

$\begingroup$

Это довольно просто — внешняя форма B и A полностью включены

$\endgroup$

4

2.3: Диаграммы Венна и диаграммы Эйлера

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4871

• Pamini Thangarajah
• Mount Royal University

При работе с множествами и их операциями часто полезно использовать диаграммы Венна:

Пример \(\PageIndex{1}\): \((A \cap B) \cap C\)

Рассмотрим \((A \cap B) \cap C\):

Пример \(\PageIndex{2}\): \((A \cap B) \cup C\)

Рассмотрим \((A \cap B) \cup C\):

Сейчас рассмотрим \((A \cup C) \cap (B \cup C)\):

Пример \(\PageIndex{3}\):

Рассмотрим \(A\) ^c \(\cup B\):

Пример \(\PageIndex{4}\):

Рассмотрим \(A\) ^c \(\cap (B \cup C)\):

Другое использование Диаграммы Венна иллюстрируют следующий результат:

Определение: Термин

Пусть \( n(A)=\) число элементов множества \(A. \). Тогда для любых двух конечных множеств \(A\) и \(B,\) \(n(A \cup B)= n(A)+n(B)-n(A \cap B).\)

 

Пример \(\PageIndex{5}\):

Был проведен опрос 150 студентов первого курса университета. 40 из них специализировались на математике, 30 из них специализировались на английском языке, 20 специализировались на естественных науках, 7 имели двойную специализацию по математике и английскому языку, и ни у кого не было двойной (тройной) специальности по естествознанию. У скольких студентов были специальности, отличные от математики, английского языка или естественных наук?

Давайте для начала воспользуемся диаграммой Венна, хорошо?

Итак, мы знаем, что \(n = 150\), и мы можем подсчитать, сколько студентов мы учитываем в настоящее время:

\[s = \Sigma \{23 + 33 + 20 + 7\} = 83\]

Используя это, мы можем определить, сколько студентов мы еще не посчитали:

\[150 — 83 = 67.\]

Итак, 67 студентов имели специальности, не входящие в наши три категории.

Пример \(\PageIndex{6}\):

Предположим, группу студентов в кампусе колледжа попросили сравнить несколько анимационных фильмов будущего, и они получили следующую информацию.

• 37 нравится «Красавица и Чудовище»
• 26 нравится «Босс-молокосос»
• 25 Нравится «Король Лев»
• 16 лайков «Красавица и чудовище» и «Босс-молокосос»
• 12 лайков «Красавица и чудовище» и «Король Лев»
• 10 лайков «Босс Бэби» и «Король Лев»
• 4 нравятся все три фильма
• 5 не нравится ни один из этих фильмов.

1. Скольким студентам понравился только «Король Лев»?
2. Скольким студентам понравились только два фильма?
3. Сколько студентов было опрошено?

Давайте воспользуемся диаграммой Венна, чтобы разобраться:

Здесь мы знаем общее количество голосов, полученных за каждый фильм, но некоторые люди могли проголосовать дважды! Итак, используя данные, сначала заполним пересекающиеся участки:

Теперь мы можем использовать данные для заполнения остальных, прежде чем отвечать на вопросы.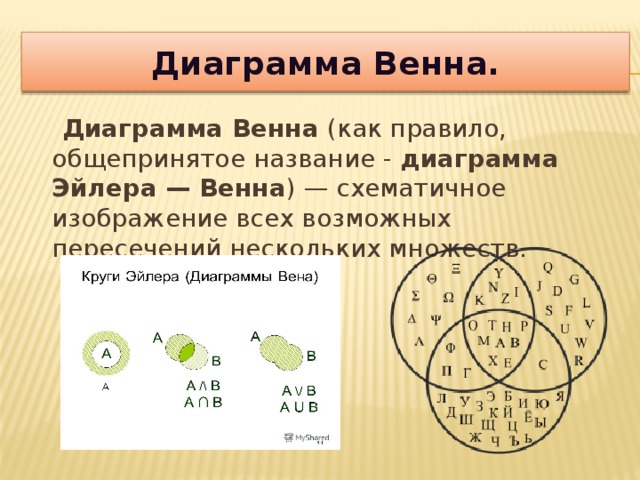 Не забудьте включить в \(U\) тех, кто не попадает ни в одну другую категорию:

Теперь, когда у нас есть четкая картина, мы можем начать отвечать на вопросы:

1. Сколько студентов понравился только «Король Лев»?

Итак, наш ответ: «Семи студентам понравился только «Король Лев».

2. Скольким студентам понравились только два фильма?

Наш ответ: \(8 + 6 + 12 = 26\) (сумма трех выделенных разделов), поэтому «26 студентам понравились только два фильма».

3. Каково было общее количество опрошенных студентов?

Начнем со сложения значений каждого раздела:

\(n = \Sigma \{7, 4, 13, 6, 12, 8, 4, 5\} = 59\)

Итак, наш ответ: «Было опрошено 59 студентов».

Резюме

Пусть \( n(A)=|A|=\) количество элементов в множестве \(A.\) Тогда для любых двух множеств \(A\) и \(B,\) \( n(A \чашка B)=n(A)+n(B)-n(A \cap B).\)

Диаграмма Эйлера

Диаграмма Эйлера показывает соответствующие отношения между наборами, а диаграмма Венна показывает все возможности.