№ 11.5 Алгебра 9 класс Мордкович. Докажите, что функция не является ни четной, ни нечетной. – Рамблер/класс
№ 11.5 Алгебра 9 класс Мордкович. Докажите, что функция не является ни четной, ни нечетной. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Поможете мне, друзяки?
Докажите, что функция у = х2 + х не является ни четной,
ответы
Ну вот, смотри:
Функция ни четная, ни нечетная.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
10 класс
11 класс
Химия
похожие вопросы 5
Домашняя контрольная работа № 3 Вариант 2 10. При каких значениях р уравнение… Мордкович 8 класс алгебра
10. При каких значениях р уравнение -х 2 + 6х — 2 = р:
а) не имеет корней;
б) имеет один корень; (Подробнее…)
ГДЗМордкович А.Г.Алгебра8 класс
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.
..)ГДЗ11 классКолмогоров А.Н.Алгебра
Васильевых. 50 вариантов ответов по русскому языку. Вариант 31 ч.2 Задание 9 ОГЭ Русский язык 9 класс Однородные обособленные приложения
Среди предложений 27-32:
(27) Нет-нет да и набирала Анюта, когда была дома одна и было грустно, Митрошин номер, и (Подробнее…)
ГДЗРусский языкОГЭ9 классВасильевых И.П.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые).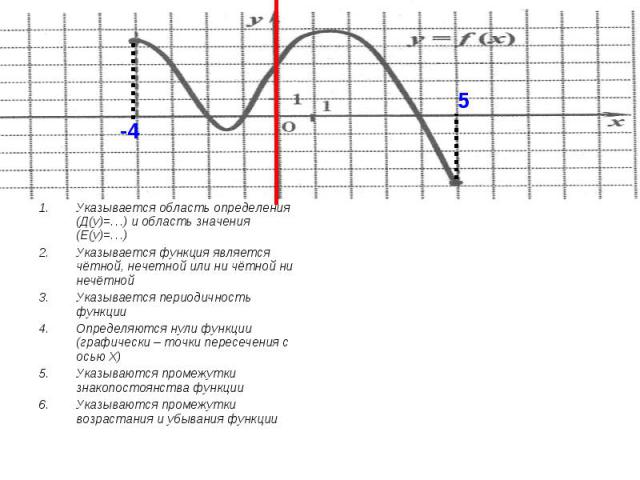
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
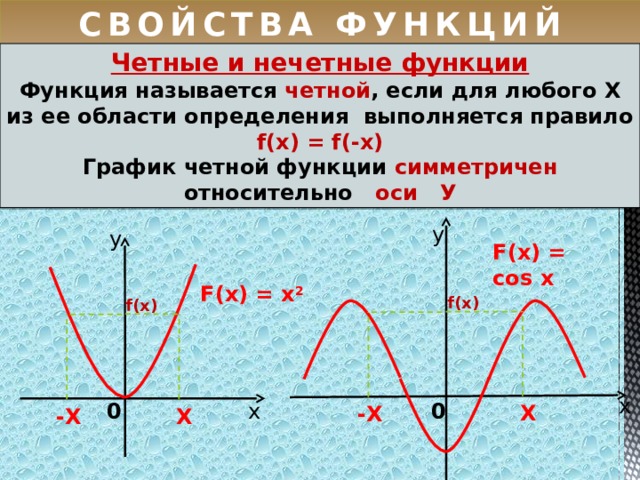
Четные и нечетные функции
Из истории функции:
Термин «функция» ввел в математику Готфрид Лейбниц (1646-1716).Он употреблял его в очень узком смысле, связывая только с геометрическими образами.
Лишь И.Бернулли дал определение функции, свободное от геометрического языка: «Функцией переменной величины называется количество, образованное каким угодно способом преобразования этой переменной величины и постоянных».
Леонард Эйлер (1707-1783 гг.), вводя в своём учебнике понятие функции, говорил лишь, что «когда некоторые количества зависят от других таким образом, что при изменении последних и сами они подвергаются изменению, то первые называются функциями вторых».
В развитие понятия функции внесли свой вклад французский математик
Ж.
-Б. Фурье
(1768-1830 гг.), русский ученый Н.И. Лобачевский
(1792-1856 гг.), немецкий математик Дирихле
( 1805-1859 гг.) и др. ученые, и общепризнанным
стало следующее определение: « Переменная
величина у называется функцией переменной
величины х, если каждому значению величины
х соответствует единственное определенное
значение величины у»
Функция f (x) называется четной, если для любого х D выполняются условия:
1) -х D, то есть область определения D(f) функции f симметрична относительно начала координат.
2) f (–x) = f (x), то есть в симметричных точках х и –х функция f принимает одинаковые значения.
График
четной функции на всей области определения
симметричен относительно оси OY. Четные
функции обладают «хорошими» алгебраическими
свойствами: сумма, разность, и произведение
двух четных функций тоже являются четными
функциями.
Примерами
четных функций могут служить y =
cos x, y = |x|, y = x2 + |x|, f(x)=x2k ,xR
Функция f (x) называется нечетной, если
для любого х D выполняются условия:
1)-х D
2) f (–x) = –f (x).
Иными
словами функция называется нечетной,
если ее график на всей области определения
симметричен относительно начала координат.
Примерами нечетных функций являются
y = sin x, y = x3.
Свойства
четности и нечетности для функций
не являются отрицаниями друг друга,
как для четности и нечетности
натуральных чисел.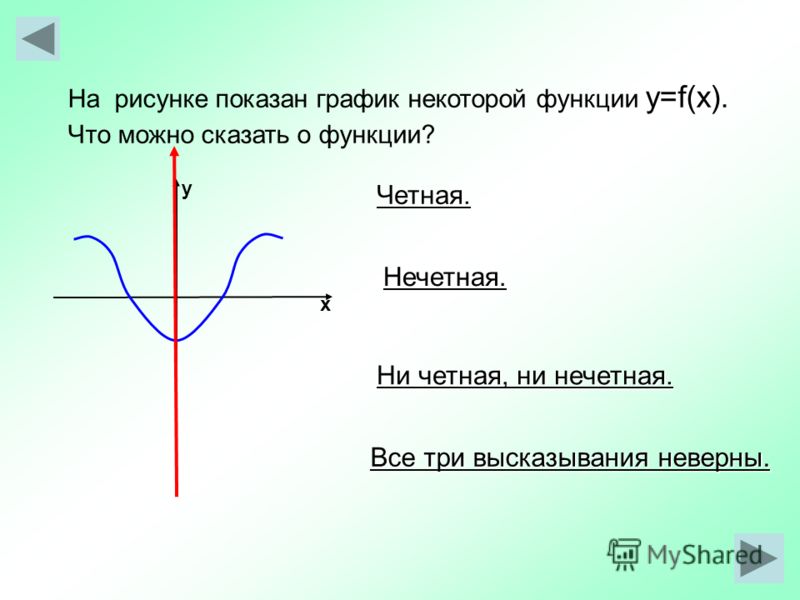
Равенства f(-x)=
f(x) и f(-x)= -f(x) не противоречат друг другу.
Они могут выполняться одновременно —
правда, только в случае, когда f(x)= f(-x)=0.
Поэтому функция может быть одновременно
и четной, и нечетной. Простейшим примером
такой функции является функция у=0. Функции,
которые одновременно четные и нечетные
– это функции, имеющие в качестве области
определения произвольное множество чисел,
но принимаемые на ней только нулевое
значение.
Чтобы
исследовать функцию
на четность или нечетность
нужно:
- Проверить симметрична ли область определения функции относительно начала координат
- Проверить равенства f(-x)= f(x)
Примеры:
1)f(x)=
f(-x)= .
2)g(x)=
f(-x)= = f(x).
При решении задач, где требуется выяснить, является ли заданная функция четной или нечетной, нужно быть очень внимательным и не судить только по-внешнему виду главного равенства.
Например:
f(x)=log(x+) , D(f)=R
f(-x)=log(-x+)
Значит f(-x)= -f(x), y= f(x)- нечетная функция.
Ссылка на то, что выражения f(x) и f(-x) «разные», поэтому f(x) f(-x), ничего не доказывает. Условие четности заключается в истинности высказывания: « Для любого x D(f) выполнено числовое равенство f(-x)= -f(x)»
А утверждение о том, что условие четности не выполняется, заключается в истинности высказывания, являющегося отрицанием предыдущего: «Существует x
Область определения функции
y = x3 + 1 охватывает всю числовую ось
и поэтому симметрична относительно начала
координат, однако f (–1) ≠ f(1). Значит, функция
y = x3 + 1 не является ни четной, ни
нечетной. Представляют интерес следующие утверждения:
- 1.Сумма (разность) четных функций четна, а нечетных – нечетна.
- 2.Произведение или частное двух нечетных функций четно.
- 3.Произведение или дробь двух четных функций четно.
- 4.Произведение или дробь четной и нечетной функции нечетно.
- 5.Композиция двух четных функций четна.
- 6.Композиция двух нечетных функций нечетна.
- 7.Композиция любой функций с четной четна (но не наоборот)
- 8.Функция, обратная четной, четна, а нечетной – нечетна.
- 9.Производная четной функции нечетна, а нечетной – четна.
То
же верно про производную третьего
пятого и вообще любого нечетного
порядка.
Производная четного
Докажем утверждения под номером 7 и 9.
№7.
Дано:
y= f(x) и y= g(x)-четная функция.
Доказать:
y=f (g(x))- четная функция.
Доказательство:
Так как g(x)-четная функция, то g(-x)=g(x) , следовательно f(g(-x))= f(g(x)), что и требовалось доказать
№9
Дано:
f (x)-четная функция.
Доказать:
f /(x)-нечетная функция/
Доказательство:
f /(-x)=(f(-x))/(-x)/=f/ (x)(-1)=-f /(x)
Что и требовалось доказать.
Как
правило, функция, взятая «наугад», не
будет ни четной, ни нечетной.
Возникает
вопрос: зачем вводить понятия четности
и нечетности, если «большинство» функций
таковыми не являются?
Ответ
на этот вопрос мы нашли в статье А.Землякова
«Четные и нечетные функции», где он приводит
два примера: физический и математический.
Физический
пример использования
чётных и нечётных
функци.
Если физическая система обладает какой-нибудь симметрией, то и связанные с нею функции часто имеют те или иные свойства симметрии. В простейших случаях возникают как раз четные или нечетные функции.
рисунок
6
Пример:
На горизонтальный стержень – ось Ох – надета однородная пружина, концы которой закреплены в симметричных точках x=-d и x=d, а к середине пружины – в точке x=0 – прикреплена шайба, свободно (без трения) перемещающаяся вдоль стержня.
а) Пусть
шайба отведена в точку с координатой
x.
Обозначим через F(x) величину силы, действующей
на шайбу со стороны пружины (точнее говоря,
проекцию этой силы на ось Ох), а через
U(x)-потенциальную энергию шайбы в этом
положении. Очевидно, пружине безразлично,
вправо или влево отводится шайба: абсолютная
величина силы и потенциальная энергия
при смещениях x и –x одинаковы, то есть
и U(x) =U(-x)
Учитывая, что сила в положениях x и –x направлена в противоположные стороны (рис б, в), можем записать F(-x)=-F(x).
Таким образом, из одних лишь соображений симметрии мы получаем следующее:
1)Функция F(x), выражающая зависимость силы F от смещения x, нечетная;
2)Функция
U(x),выражающая зависимость потенциальной
энергии от смещения, четная.
Математический
пример.
Очевидно,
степенная функция f(х)= хn, где
nN, при этом четном n будет четной, а
при нечетном n – нечетной.
Произвольный
многочлен p(x), вообще говоря, не будет
ни четной, ни нечетной функцией. Однако
его можно представить в виде суммы двух
многочленов
p+(x) и p—(x), являющихся соответственно четной и нечетной функциями.
Например:
p(x)= х7+2х6-х5-3х4-13х2+х+17= p+(x) + p—(x),где
p+(x)= 2х6-3х4-13х2+17 — сумма одночленов из p(x), содержащих х в четной степени, а
p—(x)= х7-х5+х — сумма одночленов из p(x), содержащих х в нечетной степени.
Оказывается, что не только многочлен, но и любую функцию с симметричной областью определения можно представить в виде суммы четной и нечетной функции!
Теорема:
Если функция f удовлетворяет условию симметрии (С), то ее можно представить в виде суммы двух функций — четной f+(х) и нечетной f —(х):
f(х) = f+(х)+ f —(х) (1)
области
определения которых те же, что
у функций f: D(f+)= D (f —)= D (f), причем такое
представление единственно.
Доказательство.
Допустим, что функция f(х) уже представлена в виде (1) и функции f — и f+ удовлетворяют соотношениям
f+(-х)+ = f+(х),
f —(-х) =-f —(х) (2)
Подставив в формулу (1) вместо х значение –х, из формул (2) получим
f(-х)= f+(х) – f —(х) (3)
Складывая равенства (1) и (3), получаем
f(х)+ f(-х)= 2 f+(х), откуда
f+(х)= (4а)
Аналогично, вычитая (3) из (1), находим
f —(х)= (4б)
Таким
образом, если функция f представима
в виде (1), то функции f+ и f — однозначно отыскиваются по функции f
с помощью формул (4).
Следовательно, если
представление (1) существует, то оно единственно.
А теперь — небольшой трюк: для произвольной функции f определим функции
f+ и f — соотношениями (4).
исчисление — четное нечетное или ни одно
спросил
Изменено 8 лет, 10 месяцев назад
Просмотрено 17 тысяч раз
$\begingroup$
Если функции f(x) и g(x) четные, то является ли f + g четным? Если функции f(x) и g(x) нечетные, то является ли нечетным f + g? Что, если f(x) четно, а g(x) нечетно?
Теперь интуитивно я понимаю, что для первого ответ будет ЧЕТНЫЙ
Для второго будет НЕЧЕТНЫЙ
А для последнего будет Ни то, ни другое.
Но я не знаю, как это обосновать… Просто интуитивно пришло мне в голову: Может ли кто-нибудь показать мне путь через алгебру, чтобы доказать мое утверждение.
- исчисление
- алгебра-предварительное исчисление
- функции
$\endgroup$
2 93.$ Тогда $f$ четно, а $g$ нечетно, но $$(f+g)(-1)=0\neq2=(f+g)(1)$$ и $$(f+g )(-1)=0\neq-2=-(f+g)(1),$$, поэтому $f+g$ не четно и не нечетно. Остальные три случая я оставляю вам.
$\endgroup$
3
$\begingroup$
Пусть $f(x)$ и $g(x)$ — четные функции. Тогда у нас есть $$ (f+g)(-x) = f(-x) + g(-x) = f(x)+g(x) = (f+g)(x) $$
Пусть $f( x)$ и $g(x)$ — нечетные функции. Тогда у нас есть $$ (f+g)(-x) = f(-x)+g(-x) = -f(x) -g(x) = -(f+g)(x) $$
Пусть $f(x)$ — четная функция, а $g(x)$ — нечетная функция.