Докажите что середины сторон любого четырехугольника являются вершинами: Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.

ГДЗ по геометрии 8 класс Атанасян. Гл.VII №567. Докажите, что середины сторон .. – Рамблер/класс

ГДЗ по геометрии 8 класс Атанасян. Гл.VII №567. Докажите, что середины сторон .. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Хотелось бы разобраться с заданием Гл. VII №567.
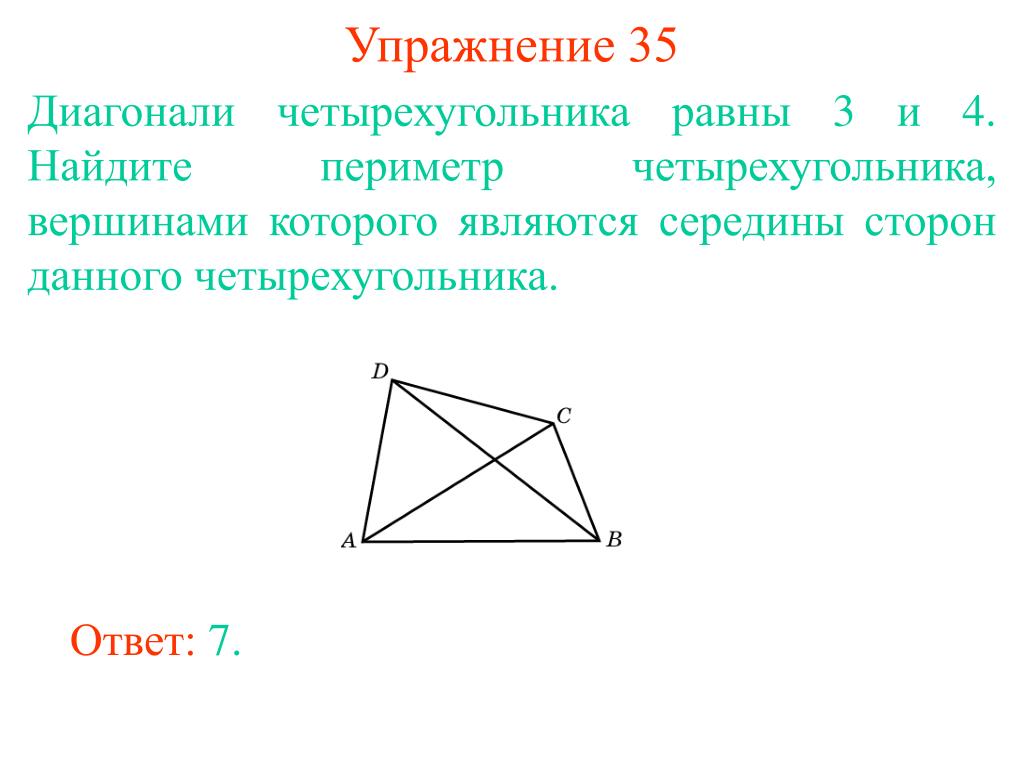
Докажите, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма

ответы

Я думаю, что решение задачи Гл.VII №567 — вот это:

Пусть точки М, N, Р, Q — середины сторон четы-
рехугольника ABCD. Тогда MN и PQ — средние линии
треугольников АВС и ADC.
Поэтому MN||AC,

Значит, что MN||PQ и MN = PQ. Следовательно,
четырехугольник MNPQ — параллелограмм.
 
 
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Экскурсии

Мякишев Г.Я.

Психология

Химия

похожие вопросы 5

ГДЗ по геометрии 8 класс Атанасян. Гл.V №441. Докажите, что прямые,….

Не понимаю, как решить задачу Гл.V №441.

Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.
  (Подробнее…)

11 класс8 классГеометрияАтанасян Л.С.

Постройте отрезок № 1166 ГДЗ Геометрия 9 класс Атанасян Л.С.

Постройте отрезок А1В1 который получается из данного отрезка АВ поворотом вокруг данного центра О: а) на 120° по часовой стрелке; б) на (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Выручайте № 1175 ГДЗ Геометрия 9 класс Атанасян Л.С.

Даны прямая а и точки М и N, лежащие по одну сторону от неё. Докажите, что на прямой а существует единственная точка X, такая, что (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

ГДЗ Русский язык 11 класс Греков В. Ф. §50 Вопрос 285 Спишите, ставя глаголы в нужной личной форме настоящего времени

Как отвечать?
Спишите, ставя глаголы в нужной личной форме настояще-
го времени. Укажите спряжение каждого глагола. (Подробнее…)

ГДЗРусский языкГреков В.Ф.11 классШкола

Найдите № 1212 ГДЗ Геометрия 9 класс Атанасян Л.С.

Найдите объём правильной четырёхугольной пирамиды, если сторона её основания равна т, а плоский угол (т. е. угол грани) при вершине (Подробнее…)

ГДЗГеометрия9 классАтанасян Л.С.

Средняя линия выпуклого четырехугольника: свойства, определение

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Что такое средняя линия четырехугольника

В данной публикации мы рассмотрим определение и основные свойства средних линий выпуклого четырехугольника касательно точки их пересечения, соотношения с диагоналями и т.д.

Примечание: далее мы будем рассматривать только выпуклую фигуру.

• Определение средней линии четырехугольника
• Свойства средней линии четырехугольника
  • Свойство 1
  • Свойство 2
  • Свойство 3
  • Свойство 4
  • Свойство 5
  • Свойство 6

Определение средней линии четырехугольника

Отрезок, соединяющий середины противоположных сторон четырехугольника (т. е. не пересекающий их), называется его средней линией.

• EF – средняя линия, соединяющая середины AB и CD; AE=EB, CF=FD.
• GH – средняя линия, сеодиняющая середины BC и AD; BG=GC, AH=HD.

Свойства средней линии четырехугольника

Свойство 1

Средние линии четырехугольника пересекаются и в точке пересечения делятся пополам.

• EF и GH (средние линии) пересекаются в точке O;
• EO=OF, GO=OH.

Примечание: Точка O является центроидом (или барицентром) четырехугольника.

Свойство 2

Точка пересечения средних линий четырехугольника является серединой отрезка, соединяющего середины его диагоналей.

• K – середина диагонали AC;
• L – середина диагонали BD;
• KL проходит через точку O, соединяя K и L.

Свойство 3

Середины сторон четырехугольника являются вершинами параллелограмма, который называется параллелограммом Вариньона.

Центром образованного таким образом параллелограмма и точкой пересечения его диагоналей является середина средних линий исходного четырехугольника, т.е. точка их пересечения – O.

Примечание: Площадь параллелограмма равняется половине площади четырехугольника.

Свойство 4

Если углы между диагоналями четырехугольника и его средней линией равны, значит диагонали имеют одинаковую длину.

• EF – средняя линия;
• AC и BD – диагонали;
• ∠ELC = ∠BMF = α, следовательно AC=BD. 

Свойство 5

Средняя линия четырехугольника меньше или равна полусумме непересекающих ее сторон (при условии, что данные стороны параллельны).

EF – средняя линия, не пересекающаяся со сторонами AD и BC.

Иначе говоря, средняя линия четырехугольника равняется половине суммы не пересекающих ее сторон тогда и только тогда, когда данный четырехугольник является трапецией. В этом случае рассматриваемые стороны являются основаниями фигуры.

Свойство 6

Для вектора средней линии произвольного четырехугольника выполняется следующее равенство:

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Назначение 3

Назначение 3

Чтение за неделю 3

B&B, Глава 4.

Эта глава содержит основные свойства параллельного линии и трансверсали. Он также вводит координаты и наклон линии.

Чтение

Хейлброн будет объявлено позже.

Упражнения 5 (до 13 октября, среда)

E5.1. Четырехугольники со средней точкой

Дан четырехугольник ABCD, середины сторон равны вершины четырехугольника, который мы называем четырехугольником с серединой из ABCD. Докажите, что четырехугольник ABCD с серединой является параллелограмм.

Е5.2. Построение параллелей

Проведите линию AB и точку C не на этой линии. Построить с помощью линейки и компаса линию, проходящую через С, которая параллельна к линии АВ.

Упражнения 6 (до пятницы 15.10)

Е5.1. Диагонали параллограмма

Дайте определение параллелограмма. Докажите, что четырехугольник является параллелограммом тогда и только тогда если диагонали делят друг друга пополам. (Другими словами, диагонали пересекаются в точке M которая является серединой каждой диагонали.)

E5.2 A Построение параллелограмма

Даны 3 точки A, B, C, не лежащие на одной прямой. Используйте E5.1, чтобы построить точку D так, чтобы ABCD был параллограммом.

Задание 3 (60 баллов, сдать пн 18.10)

В этих доказательствах вы можете использовать теоремы в главах 1, 2, 3 B&B. Также при проблемах с Глава 4 B&B вы можете использовать теоремы, которые предшествуют в книге что вы пытаетесь доказать. Вы также можете использовать то, что вы сами доказать в домашнем задании до тех пор, пока вы соблюдаете логическую последовательность и не заканчивайте круговыми рассуждениями.

3.1 Четырехугольники со средней точкой (10 баллов)

(a) Для четырехугольника ABCD докажите, что четырехугольник с серединой ABCD является параллелограммом. (Да, это повтор предыдущего упражнения.)

(b) Если ABCD — воздушный змей, какой многоугольник является средней точкой четырехугольник? Докажите свое утверждение.

( Примечание : В задача такого рода, вы должны дать лучшее или самое сильное возможное ответьте, прописано ли это каждый раз. Например, это верно, что многоугольник является параллелограммом, но это не является удовлетворительным ответ.)

3.2 Параллелограммы (15 точек)

Докажите следующие задачи на B&B, стр. 113-114. Важно: Используйте определение параллелограмма в начале Упражнений по п. 113. Не используйте другие эквивалентные определения.

Для инструментов вы можно использовать все, что доказано в B&B через p. 122.

1. Докажите 2 и обратное 5.
2. Докажите 3 и обратное 7.
3. Докажи 6.

3.3 Ромб (10 баллов)

(a) Ромб определяется как четырехугольник с четырьмя равными сторонами. Докажите, что ромб является параллелограммом.

(b) Докажите, что параллелограмм с перпендикулярными диагоналями является ромб.

3.4 Специальный треугольник (10 баллов)

Пусть ABC — равнобедренный треугольник (AB = AC = x), и пусть D — точка на отрезке AB так, что CD = CB = y .

а) Чему равны длины BD и AD относительно x и y?

(б) Если треугольник DAC также является равнобедренным (т. е. DA=DC), найдите отношение x/y.

3.5 Специальные четырехугольники со средней точкой (15 баллов — или больше за необычайно хорошие ответы)

(a) Рассмотрим это утверждение: Если четырехугольник с серединой четырехугольника ABCD — прямоугольник, то ABCD — воздушный змей.

Докажите, если это правда. Если неверно, приведите контрпример и, если сможете, объясните, для каких четырехугольников середина четырехугольника является прямоугольником.

(b) Рассмотрим это утверждение: если четырехугольник ABCD в средней точке является ромбом, то ABCD является прямоугольником.

Докажите, если это правда. Если неверно, приведите контрпример и, если можете, объясните, для каких четырехугольников середина четырехугольника является ромбом.

Вернуться на домашнюю страницу Math 444.

Теорема Вариньона (HSG.

CO.C.11)

Щелкните или коснитесь, чтобы создать 4 вершины четырехугольника на холсте справа. Затем я сделаю фокус-покус и нарисую несколько линий, чтобы создать новая фигура.

Нажмите кнопку C выше, чтобы очистить холст, а затем нарисуйте еще 4 точки. Попробуйте сделать действительно дурацкий четырехугольник. Что происходит каждый раз? Что ты заметил?

То, что вы должны увидеть, если я все сделал правильно (и если вы действительно сделали четырехугольник), это еще один четырехугольник — зеленый, вершины которого середины указанного четырехугольника. Круто то, что какой бы дурацкий четырехугольник ты ни построил, мой зеленый четырехугольник всегда будет параллелограммом, у которого противоположные стороны параллельны и конгруэнтны.

---

Давайте докажем это

Теорема о средней линии треугольника сэкономит нам много времени. Слева я нарисовал случайный четырехугольник, \(\маленький\mathtt{ABCD}\). Когда я рисую диагонали \(\small\mathtt{\overline{AC}}\) и \(\small\mathtt{\overline{BD}}\), я формирую четыре больших треугольники: \(\small\Delta\)\(\small\mathtt{ABD}\), \(\small\Delta\)\(\small\mathtt{CBD}\), \(\small\Delta\) \(\small\mathtt{ABC}\) и \(\small\Delta \)\(\маленький\mathtt{ADC}\).

Это делает сторону \(\small\mathtt{\overline{PQ}}\) средней частью \(\small\Delta\)\(\small\mathtt{ABD}\), стороной \(\small\mathtt{ \overline{RS}}\) а средний сегмент \(\small\Delta\)\(\small\mathtt{CBD}\), сторона \(\small\mathtt{\overline{QR}}\) средний сегмент \(\small\Delta\)\ (\маленький\mathtt{ABC}\) и сторона \(\small\mathtt{\overline{PS}}\) средний сегмент \(\small\Delta\)\(\small\mathtt{ADC}\), потому что средний сегмент — это сегмент, соединяющий середины двух сторон треугольника.

Итак, поскольку мы знаем, что (\(\small\mathtt{\overline{PQ}}\) и \(\small\mathtt{\overline{RS}}\)) являются средними отрезками, теорема о среднем отрезке треугольника говорит нам, что каждая из них параллельна диагонали \(\small\mathtt{\overline{BD}}\). Это означает, что они параллельны друг другу. Треугольник Теорема о среднем отрезке также говорит нам, что \(\small\mathtt{\overline{PQ}}\) и \(\small\mathtt{\overline{RS}}\) составляют половину длины \(\small \mathtt{\overline{BD}}\). И если они оба составляют половину длины чего-то, они должны быть конгруэнтны. Итак, \(\small\mathtt{\overline{PQ}}\) и \(\small \mathtt{\overline{RS}}\) конгруэнтны и параллельны.

Те же рассуждения, которые мы использовали в предыдущем абзаце, можно применить к сторонам \(\small\mathtt{\overline{PS}}\) и \(\small\mathtt{\overline{QR}}\) вместе с диагональю \(\small\mathtt{\overline{AC}}\), демонстрируя, что \(\small\mathtt{\overline{PS}}\) и \(\small\mathtt{\overline{QR}} \) являются параллельны и конгруэнтны и доказывают, что четырехугольник \(\small\mathtt{PQRS}\) является параллелограммом.

Удлинители

Прелесть этой стратегии доказательства в том, что она работает даже на «странных» четырехугольниках, где четырехугольник, образованный середины пересекает две стороны исходного четырехугольника. Кроме того, эта стратегия может помочь вам также показать, что результирующий параллелограмм всегда имеет половину площади исходного четырехугольника, хотя это становится немного сложнее со «странными» четырехугольниками.

No related posts.