Натуральная степень. Степень с натуральным показателем. Степень с натуральным
Степень с натуральным показателем
Степенью с натуральным показателем называется выражение вида:
an
где a – действительное число;
n – натуральное число.
В выражении an
an
a называют основание степени,
основание степени –> an
n называют показателем степени:
an <– показатель степени
Важно:
Обратите внимание, когда мы говорим о степени с натуральным показателем, то именно показатель является натуральным числом.
Основание же степени может быть любым действительным числом.
Степень числа a с натуральным показателем n равна числу a, n раз умноженному на себя:
an = a * a * a * … (n раз)
Пример степени с натуральным показателем
Пример степени с натуральным показателем:
24 = 2 * 2 * 2 * 2 = 16
Отрицательное число в степени с натуральным показателем
Основанием степени с натуральным показателем может быть любое действительное число, а не только целое положительное.
Пример отрицательного числа в степени с натуральным показателем:
(-2)4 =
-2 * (-2) * (-2) * (-2) = 16
Простая дробь в степени с натуральным показателем
Простая дробь является действительным числом.
Пример возведения простой дроби в натуральную степень:
(2/5)3 = 2/5 * 2/5 * 2/5 = 8/125
Отрицательная простая дробь в степени с натуральным показателем
Пример возведения отрицательной простой дроби в натуральную степень:
(-2/5)3 = -2/5 * (-2/5) * (-2/5) = -8/125
Десятичная дробь в степени с натуральным показателем
Десятичная дробь является действительным числом.
Пример возведения десятичной дроби в натуральную степень:
(2,5)3 = 2,5 * 2,5 * 2,5 = 15,625
Отрицательная десятичная дробь в степени с натуральным показателем
Пример возведения отрицательной десятичной дроби в натуральную степень:
(-2,5)3 = -2,5 * (-2,5) * (-2,5) = -15,625
Пример возведения отрицательной десятичной дроби в натуральную степень (здесь показатель степени четный):
(-2,5)2 = -2,5 * (-2,5) = 6,25
Четный и нечетный показатель степени
Обратите внимание на возведение в степень отрицательных чисел:
1.
2. А если отрицательное число возводят в нечетную степень, то результат будет отрицательным
Простые примеры возведения отрицательного числа в четную и нечетную степень:
(-2)2 = -2 * (-2) = 4
четная степень, результат положительный
(-2)3 = -2 * (-2) * (-2) = -8
нечетная степень, результат отрицательный
Отрицательная степень
Со школы всем нам известно правило о возведении в степень: любое число с показателем N равно результату перемножения данного числа на самого себя N-ное количество раз. Иными словами, 7 в степени 3 — это 7, умноженное на себя три раза, то есть 343. Еще одно правило — возведение любой величины в степень 0 дает единицу, а возведение отрицательной величины представляет собой результат обычного возведения в степень, если она четная, и такой же результат со знаком «минус», если она нечетная.
Правила же дают и ответ, как возводить число в отрицательную степень. Для этого нужно возвести обычным способом нужную величину на модуль показателя, а потом единицу поделить на результат.
Из этих правил становится понятно, что выполнение реальных задач с оперированием большими величинами потребует наличия технических средств. Вручную получится перемножить на самого себя максимум диапазон чисел до двадцати-тридцати, и то не более трех-четырех раз. Это не говоря уж о том, чтобы потом еще и единицу разделить на результат. Поэтому тем, у кого нет под рукой специального инженерного калькулятора, мы расскажем, как возвести число в отрицательную степень в Excel.
Решение задач в Excel
Для разрешения задач с возведением в степень Excel позволяет пользоваться одним из двух вариантов.
Первое — это использование формулы со стандартным знаком «крышечка». Введите в ячейки рабочего листа следующие данные:
Таким же образом можно возвести нужную величину в любую степень — отрицательную, дробную.
-C2.
Второй вариант — использование готовой функции «Степень», принимающей два обязательных аргумента — число и показатель. Чтобы приступить к ее использованию, достаточно в любой свободной ячейке поставить знак «равно» (=), указывающий на начало формулы, и ввести вышеприведенные слова. Осталось выбрать две ячейки, которые будут участвовать в операции (или указать конкретные числа вручную), и нажать на клавишу Enter. Посмотрим на нескольких простых примерах.
Формула | Результат | ||||
СТЕПЕНЬ(B2;C2) | |||||
СТЕПЕНЬ(B3;C3) |
|
Как видим, нет ничего сложного в том, как возводить число в отрицательную степень и в обычную с помощью Excel.
Ведь для решения данной задачи можно пользоваться как привычным всем символом «крышечка», так и удобной для запоминания встроенной функцией программы. Это несомненный плюс!
Перейдем к более сложным примерам. Вспомним правило о том, как возводить число в отрицательную степень дробного характера, и увидим, что эта задача очень просто решается в Excel.
Дробные показатели
Если кратко, то алгоритм вычисления числа с дробным показателем следующий.
- Преобразовать дробный показатель в правильную или неправильную дробь.
- Возвести наше число в числитель полученной преобразованной дроби.
- Из полученного в предыдущем пункте числа вычислить корень, с условием, что показателем корня будет знаменатель дроби, полученной на первом этапе.
Согласитесь, что даже при оперировании малыми числами и правильными дробями подобные вычисления могут занять немало времени. Хорошо, что табличному процессору Excel без разницы, какое число и в какую степень возводить.
C$3».
Число / Степень | |||||
Обратите внимание, что положительные числа (даже нецелые) без проблем вычисляются при любых показателях.
Числом, возведенным в степень, называют такое число, которое несколько раз умножено само на себя.
Степень числа с отрицательным значением (a — n) можно определить на подобии того, как определяется степень того же числа с положительным показателем (a n) . Однако, оно также требует дополнительного определения. Определяется такая формула как:
a — n = (1 / a n)
Свойства отрицательных значений степеней чисел аналогичны степеням с положительным показателем. Представленное уравнение a m / a n = a m-n может быть справедливым как
«Нигде, как в математике, ясность и точность вывода не позволяет человеку отвертеться от ответа разговорами вокруг вопроса
».
А. Д. Александров
при n больше m , так и при m больше n . Рассмотрим на примере: 7 2 -7 5 =7 2-5 =7 -3 .
Для начала необходимо определить то число, которое выступает определением степени. b=a(-n) . В этом примере -n является показателем степени, b — искомое числовое значение, a — основание степени в виде натурального числового значения. Затем определить модуль, то есть абсолютное значение отрицательного числа, которое выступает в роли показателя степени. Вычислить степень данного числа относительного абсолютного числа, как показателя. Значение степени находится делением единицы на полученное число.
Рис. 1
Рассмотри степень числа с отрицательным дробным показателем. Представим, что число а это любое положительное число, числа n и m — натуральные числа. Согласно определению a , которое возведено в степень — равняется единице, разделенной на это же число с положительной степенью (рис 1).
Когда степенью числа является дробь, то в таких случаях используются исключительно числа с положительными показателями.
Стоит помнить , что ноль никогда не может быть показателем степени числа (правило деления на ноль).
Распространению такого понятия как число стали такие манипуляции, как расчеты измерения, а также развитие математики, как науки. Ввод отрицательных значений было обусловлено развитием алгебры, которая давала общие решения арифметических задач, независимо от их конкретного смысла и исходных числовых данных. В индии еще в VI-XI веках отрицательные значения чисел систематически употребляли во время решения задач и растолковывались таким же образом, что и сегодня. В европейской науке отрицательные числа начали обширно употребляться благодаря Р. Декарту, который дал геометрическое толкование отрицательным числам, как направлениям отрезков. Именно Декарт предложил обозначение числа возведенного в степень отображать как двухэтажную формулу a n .
Возведение в отрицательную степень — один из основных элементов математики, который часто встречается при решении алгебраических задач. Ниже приведена подробная инструкция.
Как возводить в отрицательную степень — теория
Когда мы число в обычную степень, мы умножаем его значение несколько раз. Например, 3 3 = 3×3×3 = 27. С отрицательной дробью все наоборот. Общий вид по формуле будет иметь следующий вид: a -n = 1/a n . Таким образом, чтобы возвести число в отрицательную степень, нужно единицу поделить на данное число, но уже в положительной степени.
Как возводить в отрицательную степень — примеры на обычных числах
Держа вышеприведенное правило на уме, решим несколько примеров.
4 -2 = 1/4 2 = 1/16
Ответ: 4 -2 = 1/16
4 -2 = 1/-4 2 = 1/16.
Ответ -4 -2 = 1/16.
Но почему ответ в первом и втором примерах одинаковый? Дело в том, что при возведении отрицательного числа в четную степень (2, 4, 6 и т.д.), знак становится положительным.
Если бы степень была четной, то минус сохранился:
4 -3 = 1/(-4) 3 = 1/(-64)
Как возводить в отрицательную степень — числа от 0 до 1
Вспомним, что при возведении числа в промежутке от 0 до 1 в положительную степень, значение уменьшается с возрастанием степени. Так например, 0,5 2 = 0,25. 0,25
Пример 3: Вычислить 0,5 -2
Решение: 0,5 -2 = 1/1/2 -2 = 1/1/4 = 1×4/1 = 4.
Ответ: 0,5 -2 = 4
Разбор (последовательность действий):
- Переводим десятичную дробь 0,5 в дробную 1/2. Так легче.
Возводим 1/2 в отрицательную степень. 1/(2) -2 . Делим 1 на 1/(2) 2 , получаем 1/(1/2) 2 => 1/1/4 = 4
Пример 4: Вычислить 0,5 -3
Решение: 0,5 -3 = (1/2) -3 = 1/(1/2) 3 = 1/(1/8) = 8
Пример 5: Вычислить -0,5 -3
Решение: -0,5 -3 = (-1/2) -3 = 1/(-1/2) 3 = 1/(-1/8) = -8
Ответ: -0,5 -3 = -8
Исходя из 4-го и 5-ого примеров, сделаем несколько выводов:
- Для положительного числа в промежутке от 0 до 1 (пример 4), возводимого в отрицательную степень, четность или нечетность степени не важна, значение выражения будет положительным.
При этом, чем больше степень, тем больше значение. - Для отрицательного числа в промежутке от 0 до 1 (пример 5), возводимого в отрицательную степень, четность или нечетность степени неважна, значение выражения будет отрицательным. При этом, чем больше степень, тем меньше значение.
При этом, чем больше степень, тем больше значение.Как возводить в отрицательную степень — степень в виде дробного числа
Выражения данного типа имеют следующий вид: a -m/n , где a — обычное число, m — числитель степени, n — знаменатель степени.
Рассмотрим пример:
Вычислить: 8 -1/3
Решение (последовательность действий):
- Вспоминаем правило возведения числа в отрицательную степень. Получим: 8 -1/3 = 1/(8) 1/3 .
- Заметьте, в знаменателе число 8 в дробной степени. Общий вид вычисления дробной степени таков: a m/n = n √8 m .
- Таким образом, 1/(8) 1/3 = 1/(3 √8 1). Получаем кубический корень из восьми, который равен 2. Исходя отсюда, 1/(8) 1/3 = 1/(1/2) = 2.
- Ответ: 8 -1/3 = 2
Как использовать отрицательные фракции в уравнениях
Как использовать отрицательные фракции в уравнениях
Jana Russick
29 августов дробь — это дробь со знаком минус перед ней.
Давайте покажем вам, как применять отрицательные дроби к уравнениям.
Что такое отрицательная дробь?
Вычитание дробей и применение отрицательной дроби к уравнению работают одинаково:
Когда вы вычитаете число, вы отнимаете его значение от другого числа. Иногда это может привести к тому, что конечное число будет меньше 0. Это показано в числовой строке ниже:
Изображение предоставлено: Desmos
Сложение двух чисел объединяет их значения. В приведенной выше числовой строке вы складываете значение положительной 1 и отрицательной , что равносильно вычитанию 1 .
При вычитании отрицательной дроби знак минус отменяется знаком вычитания. Вот почему исходная дробь превращается в положительное число:
То же самое происходит, когда вы умножаете дроби, обе из которых являются отрицательными числами:
Если вы посмотрите на переднюю часть дробей в этих скобках, обе они имеют отрицательные знаки. Когда вы умножаете две отрицательные дроби (или любые два отрицательных числа), результатом будет положительное число.
Примеры отрицательных дробей
Давайте решим эти математические задачи с отрицательными дробями, которые включают неправильные дроби и наименьший общий знаменатель:
Приведенные выше дроби являются неправильными дробями, потому что у каждой из них верхнее число (числитель) больше нижнего числа (знаменателя). Они также имеют разные знаменатели, поэтому нам нужно найти наименьший общий знаменатель, который является наименьшим членом, на который делятся 7 и 14 :
28 , это будет наименьший общий знаменатель. Теперь давайте перемножим числители и знаменатели, чтобы получить знаменатели числа 9.0053 28 .
Теперь, когда это эквивалентные дроби (у них один и тот же знаменатель), мы можем перейти к этой отрицательной дроби:
Мы можем упростить эту отрицательную дробь, разделив оба значения на 14, так как 14 входит в оба 14 поровну. и 28:
Когда вы будете использовать отрицательные дроби?
Вычитание дроби — это то же самое, что добавление отрицательной дроби.
А умножение двух отрицательных дробей всегда дает положительный ответ. Знание того, как использовать отрицательные дроби, поможет вам лучше понять, как комбинировать дробные значения, и может быть полезно в вашей повседневной деятельности, такой как приготовление пищи.
Дополнительная помощь с домашним заданием по математике
- Лучшие стратегии умножения десятичных дробей
- Как решать дроби с показателями
- Пошаговое руководство по делению дробей на целые числа
Упрощение выражения с помощью дробной черты | Преалгебра |
Результаты обучения
- Определите отрицательные дроби, которые эквивалентны при условии, что их отрицательный знак находится в другом месте
- Упростите выражения, содержащие дроби, используя порядок операций
Куда ставится знак минус в дроби? Обычно перед дробью ставится знак «минус», но иногда встречаются дроби с отрицательным числителем или знаменателем.
Помните, что дроби обозначают деление. Дробь
−13-\frac{1}{3}−31
может быть результатом деления отрицательного числа
−13\frac{-1}{3}3−1
на положительный, или деления
1−3\frac{1}{-3}−31
положительного на отрицательное. Когда числитель и знаменатель имеют разные знаки, частное отрицательно. Если и числитель и знаменатель отрицательны, тогда сама дробь положительна, потому что мы делим отрицательное на отрицательное.
−1−3 = 13отрицательныйотрицательный = положительный \ гидроразрыв {-1} {-3} = \ гидроразрыва {1} {3} \ гидроразрыва {\ текст {отрицательный}} {\ текст {отрицательный}} = \ текст {положительный }−3−1=31negativenegative=positive
Размещение отрицательного знака в дроби
Для любых положительных чисел
a и ba\text{ и }ba и b
,
−ab=a−b=−ab\frac{-a}{b}=\frac{a}{-b} =-\frac{a}{b}b−a=−ba=−ba
Пример
Какие из следующих дробей эквивалентны
7−8?\frac{7}{-8}?−87?
−7−8,−78,78,−78\frac{-7}{-8},\frac{-7}{8},\frac{7}{8},-\frac{7} {8}−8−7,8−7,87,−87
Решение:
Частное положительного и отрицательного отрицательно, поэтому
7−8\frac{7}{ -8}−87
отрицательно.
Из перечисленных дробей
−78and−78\frac{-7}{8}\text{and}-\frac{7}{8}8−7and−87
также отрицательны.
попробуй
#146162
Полосы дробей действуют как символы группировки. Выражения над и под разделительной чертой следует рассматривать так, как если бы они были заключены в круглые скобки. Например,
4+85−3\frac{4+8}{5 — 3}5−34+8
означает
(4+8)÷(5−3)\left(4+8). \right)\div \left(5 — 3\right)(4+8)÷(5−3)
. Порядок операций говорит нам сначала упростить числитель и знаменатель — как если бы были скобки — прежде чем делить.
Мы добавим дроби к нашему набору группирующих символов из раздела «Использование языка алгебры», чтобы получить здесь более полный набор.
Группировка символов
Упростите выражение с помощью дробной черты
- Упростите числитель.
- Упростите знаменатель.
- Упростите дробь.
Пример
Упростить:
4+85−3\frac{4+8}{5 — 3}5−34+8
Показать решение
Решение:
4+85−3\frac{4+8}{5 — 3}5−34+8 | |
| Упростите выражение в числителе. | 125−3\frac{12}{5 — 3}5−312 |
| Упростите выражение в знаменателе. | 122\фрак{12}{2}212 |
| Упростите дробь. | 666 |
Попробуйте
#146163
В следующем видеоролике представлен еще один пример упрощения различных выражений, содержащих дробную черту. 9{2}+2}22+24−2(3)
4−64+2\frac{4 — 6}{4+2}4+24−6
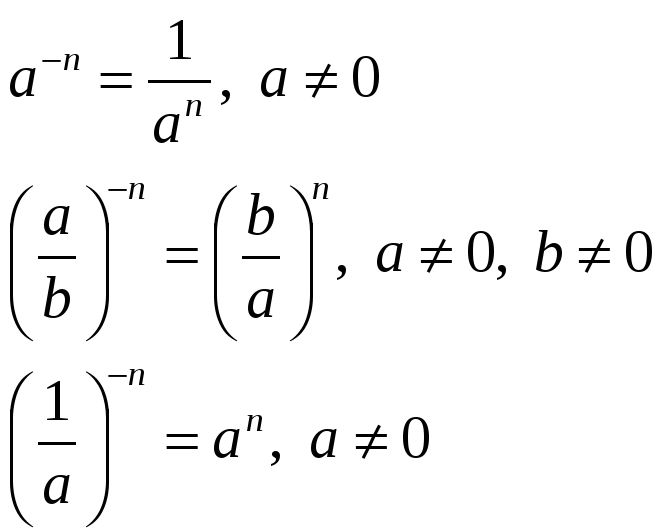
−26\frac{-2}{6}6−2
−13-\frac{1}{3}−31
Попробуйте
#146164
9{2}}{64 — 16}64−16(4)21648\фрак{16}{48}4816
13\frac{1}{3}31
Попробуйте
#146165
Пример
Упростить:
4(−3)+6(−2)−3(2)−2\frac{4\left(-3\right)+6\left(-2\right)}{-3\left (2\справа)-2}−3(2)−24(−3)+6(−2)
Показать решение
Решение:
4(−3)+6(−2)−3(2)−2\frac{4\left(-3\right)+6\left(-2\right) }{-3\влево(2\вправо)-2}−3(2)−24(−3)+6(−2) | |
| Умножить. | −12+(−12)−6−2\frac{-12+\left(-12\right)}{-6 — 2}−6−2−12+(−12) |
Упрощение. |