Сложение и вычитание дробей – правила (5 класс, математика)
4.1
Средняя оценка: 4.1
Всего получено оценок: 93.
4.1
Средняя оценка: 4.1
Всего получено оценок: 93.
Сложение и вычитание дробей процесс не сложный, но специфический. Поэтому, чтобы в курсе математики 5 класса не возникло проблем с той темой, стоит подробнее разобраться во всех ее аспектах.
Дробь
Что такое дробь? Дробь – это деление, недовведенное до конца. То есть, чтобы получить дробь ${7\over{15}}$ нужно взять число, поделить его на 15 частей и из них оставить только 7 .
Именно дроби лежат в основе многих процессов. Без них невозможно было бы посчитать процент по кредиту, определить, какая часть тепла проходит через окно, даже посчитать, сколько кусочков пиццы причитается каждому из друзей, не получилось бы без дробей.
Но иногда приходится дроби складывать и вычитать согласно сочетательному свойству деления:
а:в+с:в=(а+с):в
В большинстве различных формул стоит знак «+».
Виды дробей
Перед тем, как преступить к рассмотрению сложения и вычитания дробей, нужно обратить внимание на тот факт, что дроби бывают разные, и в зависимости от вида дробей будет немного меняться и сам процесс сложения.
Виды дробей:
- Правильные и неправильные. Неправильные дроби могут превращаться в смешанные, т.е. дроби, у которых есть целая и дробная часть. Правильными дробями называются дроби, у которых числитель меньше знаменателя.
- Обыкновенные и десятичные. В зависимости от знаменателя выделяют десятичные и обыкновенные дроби. Десятичные дроби имеют знаменатель кратный 10, при этом такая дробь должна быть записана в строку, иначе она считается обыкновенной.
Отдельной строкой идут смешанные числа, то есть неправильные дроби, в которых выделили целую часть.
Сложение и вычитание дробей
Правило сложения и вычитания дробей:
- Сравнение знаменателей. Обратите внимание, что сочетательного свойство, благодаря которому возможны операции над дробями, работает только если у дробей одинаковые числители.
- Если знаменатели различны, то необходимо привести дроби к одинаковому знаменателю. Для этого выписываются оба знаменателя, для них находится наибольшее общее кратное НОК, которое и будет являться знаменателем дроби-результата. Числитель и знаменатель домножаются на одно и то же число так, чтобы дроби приобрели одинаковые знаменатели. Если знаменатели дробей одинаковы, то этот пункт можно пропустить.
- После этого дроби подводят под один знаменатель. Под чертой остается тот самый НОК, который мы нашли, а в числителе записывается сумма или разность, где в качестве первого слагаемого или уменьшаемого выступает числитель первой дроби, а в качестве второго слагаемого или вычитаемого выступает числитель второй дроби.
- Выполняется действие в числителе.
- При необходимости выделяется целая часть дроби.
Десятичные дроби складываются по тому же принципу, что и обычные числа. К числам дописываются разряды так, чтобы получились числа с одинаковым количеством знаков после запятой. Приведем небольшой пример:
3,65-2,6=3,65-2,60=1,05
Что мы узнали?
Мы поговорили о том, что такое дробь. Обговорили порядок действий при сложении и вычитании дробей. Обсудили, как выполнить необходимое условие сложение и привести дроби к одному знаменателю. Выделили виды дробей и поговорили о каждом из них.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.Пока никого нет. Будьте первым!
Оценка статьи
4.1
Средняя оценка: 4.1
Всего получено оценок: 93.
А какая ваша оценка?
Формулы для решения задач на дроби для 5 класса
В 5 классе на уроках математики ученики знакомятся с дробями и процентами.
В 6 классе эта тема повторяется, но изучается более глубоко. А встречаться дроби и проценты продолжат вплоть до задач внешнего тестирования (ЗНО) для 11 класса.
Обыкновенная дробь — это пара чисел, записанных через черту.
Число под чертой (знаменатель), показывает, на сколько частей разделили целое.
Число над чертой (числитель) показывает, сколько этих частей выбрано.
То есть дробь $\frac{3}{8}$ (три восьмых) означает, что целое было разделено на 8 частей, а взято из них три.
Существуют три класса задач на дроби: нахождение дроби от числа, нахождение числа по его дроби и выражение отношения чисел в виде дроби.
Как найти дробь от числа
В задачах на дробь от числа известно само число и дробь, которая от него взята. А найти требуется, какую величину составит эта дробь. Рассмотрим такую задачу
Пример 1.1.
В самолёте 120 пассажиров. $\frac{2}{5}$ (две пятых) из них летят в самолёте в первый раз. Сколько пассажиров летит в первый раз?
Это задача на нахождение дроби от числа.
Есть число: 120.
Есть дробь: $\frac{2}{5}$
Нужно найти, чему равны две пятых от 120.
Решаются задачи на нахождение дроби от числа так.
Решение
Задаём себе два вопроса:
1. Чему равна $\frac{1}{5}$ (одна пятая) от 120?
Для этого 120 делим на 5, получаем 24.
Результат 24, корый мы получили, нужно умножить на 2.
Получаем 48.
Значит, $\frac{2}{5}$ от 120 составляет 48.
Ответ: 48 пассажиров летят впервые.
Попробуем решить ещё одну задачу на нахождение дроби от числа.
Пример 1.2.
В городе живут 1 500 000 человек. Из них $\frac{3}{25}$ — школьники. Сколько в городе школьников?
Решение
1. Чему равна $\frac{1}{25}$ от 1 500 000?
1 500 000:25 = 60 000
2. Чему равны $\frac{2}{25}$ от 1 500 000?
60 000*3 = 180 000
Ответ: 180 000 школьников.
Когда вы набрались опыта решать такие задачи по вопросам, эти два вопроса можно свести в одно действие и использовать правило:
Чтобы найти дробь от числа, нужно это число умножить на дробь
Или, что то же самое:
Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби и умножить на её числитель
Пример 1.
В автосалон завезли 14 автомобилей. За месяц продали 2/7 этого количества. Сколько автомобилей продали?
Решение
Умножим 14 на $\frac{2}{7}$:
$14\cdot \frac{2}{7} = \frac{14\cdot 2}{7} = 2\cdot 2 = 4$
Ответ: 4 автомобиля.
Теперь рассмотрим задачи второго типа:
Как найти число по дроби
В задачах этого типа исходное число неизвестно. Зато известна величина некоторой части от этого числа и какую дробь составляет эта часть от исходного числа. Для удобства рассмотрим, как бы выглядели эти же три задачи, если бы в них требовалось найти число по дроби.
Пример 2.1.
В самолёте сидят пассажиры (сколько их неизвестно!). Известно, что 48 пассажиров или $\frac{2}{5}$ (две пятых) от их количества летят впервые. Нужно найти: сколько всего пассажирова в самолёте?
Решение
Эти 48 пассажиров, которые летят впервые, составляют две пятых ($\frac{2}{5}$) от общего количества пассажиров в салоне.
Мы можем найти одну пятую?
Да, нужно 48 разделить на 2.
48:2 = 24.
Мы узнали, что одна пятая часть от всех пассажиров — это 24 человека. Сколько всего пассажиров? В пять раз больше, то есть 24х5 = 120.
Ответ: 120 пассажиров всегов самолёте
Понятно? Давайте разберём ещё одну задачу.
Пример 2.2.
Три двадцать пятых ($\frac{3}{25}$) населения города составляют школьники. Школьников в городе 180 000. Каково общее население города?
Решение
Опять само число (то есть население города) на неизвестно, зато известно, чему равны $\frac{3}{25}$ от него.Значит, можно сначала найти, чему равна $\frac{1}{25}$ от населения города. Разделим 180 000 на 3:
180 000:3 = 60 000
Зная одну двадцать пятую, можно найти и целое, умножив 60 000 на 25.
60 000х25 = 1 500 000
Ответ: в городе 1 500 000 жителей
Когда будете уверенно решать задачи на нахождение числа по его дроби по вопросам, можно будет заменить эти вопросы одним действием и использовать правило:
Чтобы найти число по его дроби, известную величину нужно разделить на эту дробь
Или, что то же самое:
Чтобы найти число по его дроби, известную величину нужно разделить на числитель дроби и умножить на её знаменатель
Пример 2.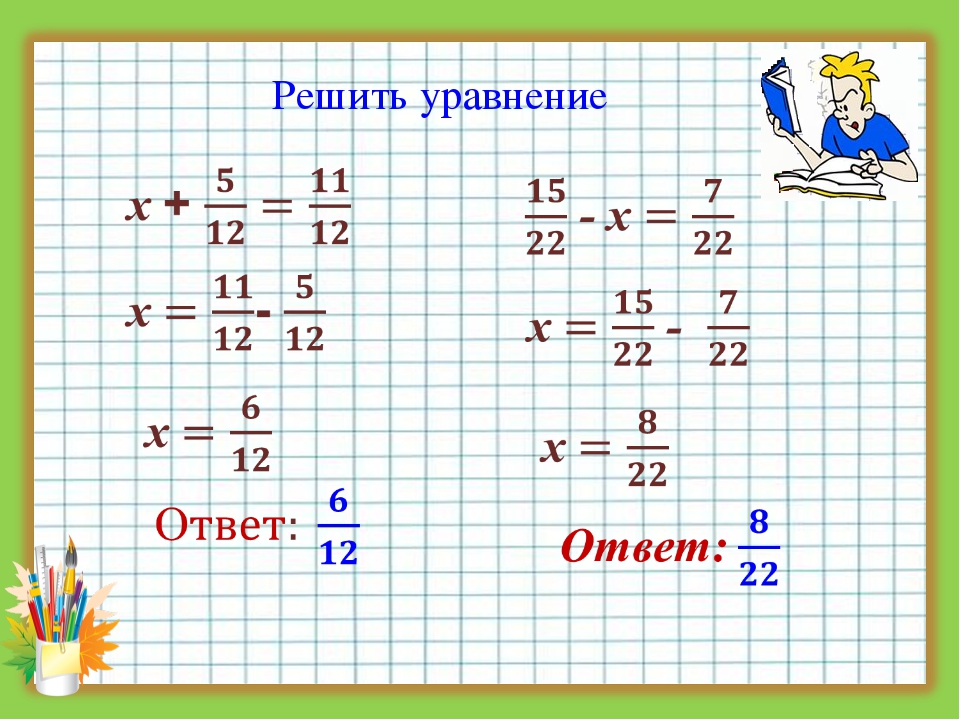
3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4, что составляет 2/7 всех автомобилей. Сколько автомобилей завезли в салон?
Решение
Разделим 4 на $\frac{2}{7}$:
$4: \frac{2}{7} = \frac{4\cdot 7}{2} = 2\cdot 7 = 14$
Ответ:
14 автомобилей завезли в салон.И перейдём теперь к третьему типу задач на дроби, которые изучаются в математике 5 класса:
Как найти отношение двух чисел и выразить его в виде дроби
В задачах на нахождение отношения оба числа известны, а нужно найти, какую дробь второе число составляет от первого. Решаются они проще всего
Пример 3.1.
В самолёте 120 пассажиров. Из них 48 человек летят в первый раз. Какая часть пассажиров летит в первый раз?
Решение
Чтобы найти, какую дробь 48 составляет от общего количества пассажиров (120), нужно 48 разлелить на 120 и затем скоратить, что возможно.
Доля летящих впервые пассажиров составляет $\frac{48}{120}$.
И числитель, и знаменатель делятся на 2, значит, можно сократить на 2.
$\frac{48}{120}=\frac{24}{60}$
Сократим ещё раз на 2:
И ещё раз:
$\frac{12}{30} = \frac{6}{15}$
Теперь можно сократить на 3:
$\frac{6}{15} = \frac{2}{5}$
Больше сокращать не на что — это и можно записать как окончательный ответ задачи.
Ответ: $\frac{2}{5}$ пассажиров летят впервые.
Так что правило для решения задач на нахождение отношения чисел самое простое:
Чтобы найти, в виде какой дроби выражается отноешние двух чисел, нужно сначала записать дробь, в которой числитель и знаменатель — эти числа, а затем сократить её.
Обратите внимание, что дробь $\frac{A}{B}$ обозначает, какую долю величина А составляет от величины В и правильно записывайте величины в числитель и знаменатель.
Разберём ещё два примера.
Пример 3.2.
В городе с населением 1 500 000 жителей живут 180 000 школьников.
Какую часть населения города составляют школьники?
Решение
Нужно найти, какую часть 180 000 составляет от 1 500 000?
Записываем дробь и сокращаем:
$\frac{180000}{1500000}=\frac{18}{150}=\frac{9}{75}=\frac{3}{25}$
Ответ: школьники составляют $\frac{3}{25}$ от общего населения города
Пример 3.3.
Из завезённых в автосалон автомобилей за месяц продали удалось продать всего 4. Какую часть от всех автомобилей это составляет, если всегов автомалон завезли 14 машин?
Решение
Точно так же, берём дробь $\frac{4}{14}$ и сокращаем:
$\frac{4}{14}=\frac{2}{7}$
Ответ: продали $\frac{2}{7}$ от общего количества автомобилей.
Вот как решаются задачи на дроби. Вы найдёте справочники по формулам математики 5, 6 и других классов в разделе «Математика в школе».
Игры с дробями для пятиклассников онлайн
Часто задаваемые вопросы:Q1: Как мы можем умножать дроби?
Ответ: Чтобы умножить дроби, мы умножаем числители обеих дробей, чтобы получить новый числитель, и умножаем знаменатели обеих дробей, чтобы получить новый знаменатель.
Затем мы можем упростить полученную дробь, если это возможно. Например, 4/5 х 2/3 = (4 х 2) / (5 х 3) = 8/15.
Q2: Как складывать правильные дроби?
Ответ: Чтобы сложить правильные дроби, если знаменатели совпадают, сложите числители, сохраняя знаменатель одинаковым. Чтобы сложить дроби с разными знаменателями, нам сначала нужно преобразовать обе дроби в дроби с общим знаменателем, а затем сложить их так же, как мы складываем одинаковые дроби.
Q3: Как вы учите детей складывать и вычитать дроби?
Ответ: Чтобы складывать или вычитать дроби с одинаковыми знаменателями, дети должны складывать или вычитать числители, сохраняя знаменатель одинаковым. Чтобы сложить или вычесть дроби с разными знаменателями, нам сначала нужно преобразовать обе дроби в дроби с общим знаменателем, а затем сложить или вычесть их так же, как мы делали это раньше в случае одинаковых знаменателей.
В4. Как упростить дроби в математике?
Ответ: Мы можем упростить дроби, разделив числитель и знаменатель на их наибольший общий делитель.
Например, чтобы упростить 12/18, мы сначала находим наибольший общий делитель 12 и 18, который равен 6. Теперь разделим и числитель, и знаменатель на 6, чтобы получить упрощенную форму 12/18, которая равна 2/3.
В5: В каком классе изучают сложение и вычитание дробей?
Ответ: Сложение и вычитание дробей с одинаковыми знаменателями преподается в 4 классе. Но сложение и вычитание дробей с разными знаменателями преподается в 5 классе, где нам сначала нужно преобразовать обе дроби в дроби с общим знаменателем, а затем сложить или вычесть их так же, как мы делаем с дробями с теми же знаменателями.
Q6: Как вы решаете текстовые задачи на деление дробей?
Ответ: Первый шаг — понять задачу со словом, чтобы определить числа или дроби, которые необходимо разделить. Затем разделите полученные числа или дроби, чтобы получить ответ.
В7. Как умножить дробь на целое число?
Ответ: Чтобы умножить дробь на целое число, нужно умножить числитель дроби на целое число, а знаменатель оставить прежним.
Это дает нам продукт, и мы можем упростить продукт, если это необходимо.
Дроби вводятся в 3 классе. Это сложная тема для детей этого возраста, поскольку они привыкли только к основным математическим понятиям, таким как счет. Поэтому рекомендуется использовать много математических игр, манипуляций и занятий. Если вы прямо объясните части дроби 3-класснику, это определенно вызовет путаницу. Вместо этого, в реальных жизненных ситуациях, таких как раздача пирожных друзьям или покупка половины/четверти фунта овощей или заправка топливного бака автомобиля на четверть/половину/полностью и т. д.
SplashLearn предлагает программу обучения, основанную на деятельности, для достижения четко определенных наборов навыков обучения. Такие действия, как определение дробей и моделирование дробей , дают детям прочную основу для изучения темы.
Математические игры для дробей:
В 5 классе дети переходят от основных понятий дроби к сложению, вычитанию, умножению и делению дробей.
Использование математических игр — эффективный способ для относительно сложных тем, подобных этим. Некоторые из математических игр, обсуждаемых ниже, могут улучшить понимание математических операций над дробями.
Сложение с использованием дробных кругов: Количество игроков 2-4
Дробные круги, разрезанные на разные дроби, смешиваются между собой. Каждый ребенок случайным образом берет один дробный круг из лота по мере того, как подходит его/ее очередь. Тот, кто завершает все первым, выигрывает игру.
Игра в кости с дробным сложением: Количество игроков 2-4
Каждый ребенок может бросить кубик со знакомыми дробями, такими как , , , на сторонах. Дроби, брошенные каждым ребенком, каждый раз складываются, и тот, кто первым достигает целого, выигрывает игру. Его можно сделать более интересным, добавив отрицательные дроби, чтобы дети также применяли свойства вычитания.
Построение дробных полос для умножения: Количество игроков 1
Имея квадратную сетку, скажем, размером 10 на 10, построение дробных полос для представления дробей, заданных путем выбора и перетаскивания требуемых массивов, может быть учебным занятием.
Далее детей нужно заставить построить дробь произведения аналогичным образом.
Математические манипуляторы для обучения дробям
Дроби вводятся в 3-м классе с использованием таких манипуляторов, как дробные круги, дробные диаграммы и дробная стенка.
Полоски дробей: Визуальные модели, такие как полоски дробей, очень помогают в объяснении таких понятий, как сложение, вычитание, умножение и деление дробей.
Сложение:
Вычитание:
Умножение:
9000 9
Подразделение:
Методика обучения дробным играм для 5-х классов
Сложение и вычитание разнородных дробей :
Дети уже в 4 классе знакомы со сложением и вычитанием дробей с одинаковыми знаменателями.
В 5 классе дети узнают, как складывать дроби с разными знаменателями.
Рассмотрим пример сложения дробей ½ и ¼.
Это может быть представлено полосами дробей, как показано на рисунке.
Поскольку знаменатели не совпадают, нельзя просто сложить числители, чтобы сложить две дроби.
Здесь первым шагом является оценка первой дроби, если бы целое было разделено на 4.
Если разделить целое на четыре равные части, то первая дробь будет иметь вид:
То есть заштрихованы две части из четырех. Это эквивалентно затенению одной части из двух.
Таким образом, эквивалентно .
Итак, сложение можно представить как:
Алгебраически сложение можно выполнить как + .
Дети уже умеют находить равные дроби, умножая числитель и знаменатель на одно и то же число. Итак, первое правило сложения разных дробей — писать слагаемые с одинаковым знаменателем, используя равнозначные дроби. Тогда дроби подобны и могут быть сложены путем сложения числителей.
Например, добавьте .
Умножьте числитель и знаменатель первой дроби на 3, а знаменатель второй дроби — на 4. Итак, добавьте:
+ .
Вычитание дробей можно выполнять по тому же правилу.
Например, — .
Дети также используют понятие сложения и вычитания разных дробей в текстовых задачах.
Например, Зинат закончила свой проект с Тиной, а Тина сделала его. Вместе какая часть проекта завершена?
Чтобы найти готовую деталь, нужно сложить две дроби.
. Итак, проект завершен.
Дети также оценивают правильность результатов, сопоставляя размер дополнений.
Например, рассмотрим дроби и . Если сумма этих двух чисел будет записана как путем сложения числителей и знаменателей по отдельности, ребенок 5-го класса может указать, что она неверна, поскольку она меньше половины, тогда как одно из слагаемых равно половине.
Сложение и вычитание смешанных дробей:
Сложение смешанных дробей с разными знаменателями можно смоделировать с помощью дробной полосы, числовой прямой или дробной черты.
Рассмотрим дополнение .
Как складывать дроби в числовой строке, показанной ниже.
Алгебраически это можно сделать двумя способами. Целые части и дробные части и дробные части могут быть добавлены отдельно. То есть
Другой способ состоит в том, чтобы преобразовать смешанное число в неправильную дробь. Затем сгенерируйте эквивалентные дроби так, чтобы слагаемые имели одинаковый знаменатель. Теперь сложите две одинаковые дроби.
Здесь смешанная дробь может быть записана как . Сложение можно выполнить, как показано ниже:
Добавление различных рабочих листов со смешанными дробями в SplashLearn имеет достаточно проблем, чтобы тщательно попрактиковаться в теме. Некоторые задачи требуют точного ответа, в то время как другие требуют, чтобы ребенок округлил ответ до ближайшей половины. Это также дает практику для концепции округления.
Следующая концепция заключается в вычитании смешанных дробей. Более простой способ — разделить целую и дробную части и вычесть.
Просто ребенку нужно быть особенно осторожным с вычитанием с перегруппировкой.
Например, ребенок может ошибиться в , если разделит целую и дробную части и вычитает.
Это можно сделать следующим образом:
Теперь вычтите.
=
Вычитание, в отличие от задач калькулятора смешанных дробей, в SplashLearn не просто просит детей ввести окончательные ответы, но готовит детей к каждому шагу вычислений, подобных приведенному выше. Также, как и в случае сложения, детей просят округлить сложные дроби до 0, 1 или ½.
Словесные задачи играют роль моста между теорией и применением темы в математике. Решая словесные задачи на вычитание в отличие от смешанных чисел, дети закрепляют базовые знания и применяют их в реальных жизненных ситуациях.
Дробь в виде деления числителя на знаменатель:
Предположим, что 25 фунтов сахара поровну распределены между 6 людьми. Чтобы найти количество сахара, полученное каждым человеком, нужно 25 разделить на 6.
То есть 25 ÷ 6 или . Таким образом, дробь — это еще один способ представления деления. Записывается как деление числителя на знаменатель.
Записав в виде смешанной дроби, каждый человек получит фунты сахара.
Умножение двух дробей:
Умножение всегда представляет собой повторяющееся сложение. То есть умножение дроби на 3 равносильно сложению дроби 3 раза. В 4 классе дроби дети научились умножать дробь на целое число с помощью наглядных моделей, а также методом прямого умножения.
Когда дробь умножается на целое число c, это, по сути, число a, сложенное вместе c раз и разделенное на число c. Представьте, что три бутерброда делят четверо детей. Таким образом, каждый получит по бутерброду. Обратите внимание, что продукт — это, по сути, часть бутерброда, которую получил каждый ребенок, умноженная на количество детей. Таким образом, это произведение в сумме дает общее количество бутербродов, то есть 3.
В 5 классе дети учатся умножать дроби с помощью дробных полосок изначально.
Позже они понимают, что при умножении дробей числители умножаются вместе, как и знаменатель.
То есть . Дети применяют это свойство для прямого умножения дробей.
То есть .
Умножение смешанных дробей:
Рассмотрим умножение двух дробей, хотя бы одна из которых является смешанной дробью. Сначала преобразуйте смешанную дробь в неправильную дробь. Затем умножьте числители и знаменатели отдельно.
Например, чтобы умножить и , сначала перепишите как неправильную дробь, следуя математическому порядку операций.
Теперь умножьте две дроби.
Неправильную дробь можно записать как смешанную дробь как .
Процедура умножения смешанных дробей аналогична.
Теперь уменьшите общие делители двух дробей, которые необходимо умножить.
SplashLearn предоставляет хорошо оформленный рабочий лист по теме умножения смешанных дробей. Там вы можете практиковать навыки и опыт вычислений.
Сложные задачи, такие как нахождение площади прямоугольного бассейна дробных размеров, дают практическое применение вычислений, изученных по этой теме. Кроме того, дети также решают задачи с более сложными дробями, такими как смешанные дроби, используя аналогичную технику.
Интерпретация умножения как масштабирования
Когда нужно умножить две дроби, и если мы сравним размер одного из факторов с размером произведения, мы можем фактически предсказать размер произведения в зависимости от размера второго фактор.
Например, рассмотрим дроби и . Второй множитель больше 1. Таким образом, произведение будет числом, большим, чем первый множитель. То есть умножение на дробь, большую 1, расширит вторую дробь.
Аналогичным образом рассмотрим произведение и . Второй фактор. Таким образом, умножение на сократит значение первого множителя . То есть умножение на дробь меньше 1 приведет к сжатию второй дроби.
SplashLearn предлагает широкий спектр практических задач по этой теме с оценкой возможных значений факторов, а также продукта.
Деление единичных дробей на целые числа:
Рассмотрим задачу на деление, . Переведя это на слова, каков будет размер каждой части, если разделить на 4 равные части?
Это можно представить с помощью дробных полос, как показано на рисунке:
Алгебраически деление на число эквивалентно записи дроби с числом в качестве знаменателя и делимым в качестве числителя. То есть деление эквивалентно умножению на обратное.
Деление на 4 аналогично умножению на .
Рабочие листы для деления дробей на деление единичной дроби на целое число
Словесные задачи, связанные с темой, можно решить либо с помощью дробных полос, как показано выше, либо путем решения уравнений с дробями, которые представляют задачу.
Например, если торт в четверть фунта, то есть фунт, поровну распределен между 5 людьми, то найдите вес торта, который получит каждый человек.
Уравнение, представляющее проблему, .
Решение уравнения, .
То есть каждый человек получит фунтов торта.
Деление целого числа на дробную часть:
Теперь, как разделить целое число на дробную часть?
Яблоки нужно раздать детям по половинке яблока. Если яблок шесть, скольким детям можно их раздать?
Это можно перевести как сколько половинок в целом 6?
Используя символ деления, можно записать это как .
Алгебраически деление 6 на то же, что и умножение 6 на .
Дети могут практиковать визуальные модели, а также алгебраическое деление для деления целого числа на единичную дробь в
Дети применяют знания по теме для решения текстовых задач, например, сколько одной четвертой может быть подается из 3-х пицц?
То же, что и
Общие базовые государственные стандарты по математике для пятого класса: обзор
Перейти к:
Операции и алгебраическое мышление | Числа и операции с основанием десять | Число и операции-дроби | Измерения и данные | Геометрия
Операции и алгебраическое мышление
Запись и интерпретация числовых выражений.
5.OA.A.1
Используйте круглые и фигурные скобки в числовых выражениях и вычисляйте выражения с этими символами.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.OA.A.2
Напишите простые выражения, которые записывают вычисления с числами, и интерпретируйте числовые выражения без их вычисления.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Анализ шаблонов и взаимосвязей.
5.OA.B.3
Сгенерируйте два числовых шаблона, используя два заданных правила. Определите очевидные отношения между соответствующими терминами. Сформируйте упорядоченные пары, состоящие из соответствующих терминов из двух шаблонов, и отобразите упорядоченные пары на координатной плоскости.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
Числа и операции с основанием 10
Понимание системы стоимостных значений.
5.НБТ.А.
1
Знайте, что в многозначном числе цифра на одном месте представляет в 10 раз больше, чем она представляет на своем правом месте, и 1/10 того, что она представляет на своем левом месте.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
5.NBT.A.2
Объясните закономерности в количестве нулей произведения при умножении числа на степень 10 и объясните закономерности в расположении десятичной точки когда десятичная дробь умножается или делится на степень 10. Используйте целые числа в степени для обозначения степеней 10.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NBT.A.3
Читать, писать и сравнивать десятичные дроби с тысячными.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Выполнение операций с многозначными целыми числами и с десятичными до сотых.
5.NBT.B.5
Свободно умножайте многозначные целые числа по стандартному алгоритму.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
5.NBT.B.6
Нахождение целых чисел в частных с до четырехзначными делимыми и двузначными делителями, используя стратегии, основанные на разрядном значении , свойства операций и/или связь между умножением и делением. Проиллюстрируйте и объясните расчет, используя уравнения, прямоугольные массивы и/или модели площадей.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NBT.B.7
Сложение, вычитание, умножение и деление десятичных долей до сотых с использованием конкретных моделей или рисунков и стратегий, основанных на разрядности, свойствах операций и/или отношений между сложением и вычитанием; свяжите стратегию с письменным методом и объясните используемую аргументацию.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
Числа и дроби
Используйте эквивалентные дроби в качестве стратегии для сложения и вычитания дробей.
5.NF.A.1
Сложение и вычитание дробей с разными знаменателями (включая смешанные числа) путем замены данных дробей эквивалентными дробями таким образом, чтобы получить эквивалентную сумму или разность дробей с одинаковыми знаменателями.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NF.A.2
Решайте словесные задачи на сложение и вычитание дробей, относящихся к одному и тому же целому, включая случаи разных знаменателей, например, с помощью визуальные дробные модели или уравнения для представления проблемы. Используйте эталонные дроби и числовой смысл дробей для мысленной оценки и оценки обоснованности ответов.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
Применение и расширение предыдущего понимания умножения и деления для умножения и деления дробей.
5.NF.B.3
Интерпретировать дробь как деление числителя на знаменатель (a/b = a ÷ b). Решайте текстовые задачи на деление целых чисел, чтобы получить ответы в виде дробей или смешанных чисел, например, используя визуальные модели дробей или уравнения для представления задачи.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NF.B.4
Применить и расширить прежнее понимание умножения, чтобы умножить дробь или целое число на дробь.
См. соответствующие рабочие листы, рабочие тетради, игры, упражнения, планы уроков
5.NF.B.5
Интерпретировать умножение как масштабирование (изменение размера) по:
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
5 .NF.B.6
Решайте реальные задачи, связанные с умножением дробей и смешанных чисел, например, используя визуальные модели дробей или уравнения для представления задачи.
См. соответствующие рабочие листы, рабочие тетради, игры, планы уроков
5.NF.B.7
Примените и расширьте прежнее понимание деления, чтобы разделить единичные дроби на целые числа и целые числа на единичные дроби.
См. соответствующие рабочие листы, рабочие тетради
Измерения и данные
Преобразование одинаковых единиц измерения в заданной системе измерения.
5.MD.A.1
Преобразование между стандартными единицами измерения разного размера в заданной системе измерений (например, преобразование 5 см в 0,05 м) и использование этих преобразований при решении многоэтапных задач реального мира.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
Представление и интерпретация данных.
5.MD.B.2
Постройте линейный график для отображения набора данных измерений в долях единицы (1/2, 1/4, 1/8). Используйте операции над дробями для этого класса, чтобы решить задачи, связанные с информацией, представленной в линейных графиках.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
Геометрические измерения: понимание концепции объема и соотнесение объема с умножением и сложением.
5.MD.C.3
Распознавать объем как атрибут объемных фигур и понимать принципы измерения объема.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
5.
MD.C.4
Измерение объемов путем подсчета кубических единиц, используя кубические сантиметры, кубические дюймы, кубические футы и импровизированные единицы измерения.
См. соответствующие рабочие листы, рабочие тетради, планы уроков
5.MD.C.5
Свяжите объем с операциями умножения и сложения и решите реальные и математические задачи, связанные с объемом.
См. соответствующие рабочие листы, рабочие тетради, упражнения, планы уроков
Геометрия
Графические точки на координатной плоскости для решения реальных и математических задач.
5.G.A.1
Используйте пару перпендикулярных числовых линий, называемых осями, для определения системы координат, где пересечение линий (начало координат) расположено так, чтобы совпадать с 0 на каждой линии и заданной точкой в плоскость находится с помощью упорядоченной пары чисел, называемой ее координатами. Поймите, что первое число указывает, как далеко нужно пройти от начала координат в направлении одной оси, а второе число указывает, как далеко нужно пройти в направлении второй оси, при условии, что имена двух осей и координаты соответствуют (например, ось x и координата x, ось y и координата y).