Дроби 5 класс примеры: Сложение и вычитание обыкновенных дробей

примеры с дробями для тренировок

Тренажёр для 5 класса: примеры с дробями для тренировок

1 2 3 4 5 6 7 8 9 0 . C

Ответить

<table> <tr> <td> <p>7</p> <p>2</p> </td> <td> + </td> <td> <p>2</p> <p>3</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>1</p> <p>3</p> </td> <td> + </td> <td> <p>10</p> <p>9</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>4</p> <p>1</p> </td> <td> + </td> <td> <p>3</p> <p>10</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>7</p> <p>4</p> </td> <td> + </td> <td> <p>4</p> <p>5</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>9</p> <p>3</p> </td> <td> + </td> <td> <p>10</p> <p>3</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>8</p> <p>5</p> </td> <td> + </td> <td> <p>6</p> <p>10</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>4</p> <p>2</p> </td> <td> + </td> <td> <p>8</p> <p>9</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>8</p> <p>3</p> </td> <td> + </td> <td> <p>7</p> <p>3</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>8</p> <p>1</p> </td> <td> + </td> <td> <p>10</p> <p>3</p> </td> <td> = </td> </tr> </table>

<table> <tr> <td> <p>2</p> <p>3</p> </td> <td> + </td> <td> <p>7</p> <p>5</p> </td> <td> = </td> </tr> </table>

Попробуй другие онлайн тренажеры с дробями

Сложение и вычитание дробей 5 класс

Обыкновенные дроби 5 класс примеры для тренировки

Умножение дробей.

Тренажер 5 класс

Что такое часть от целого?

Тема «дроби» в 5 классе в математике одна из самых сложных для восприятия школьниками. А упражнения с дробями в 5 класс вызывают страх и неприязнь. Без тренировки по этим темам никак!
Также эта тема очень большая, поскольку охватывает сразу несколько разделов. При изучении дробей в математике очень важно не упустить момент если ребенок что-то хоть немного недопонял или сомневается или не уверен.Главное сразу приступить к тренировкам и решению заданий и примеров на тему ДРОБИ для 5 класса. Чем раньше — тем лучше.

В данном случае главное объяснить где применяется «дробная часть числа», а также наглядность примеров дробей для 5 класса по математике. Само слово «Дробь» уже подразумевает дробление, деление, часть от чего-то. В школьной программе 5 класса к примерам по математике для тренировки с дробями приступают только после изучения всех операций над целыми числами. Вначале дети тренируются на примерах с простыми дробями для 5 класса по математике . Затем, приступают к примерам сложнее на умножение дробей. Их также легко можно отработать на тренажёре умножения дробей

Но объяснить ребенку что такое обыкновенные дроби и решать задания, и познакомиться с примерами решения дробей лучше гораздо раньше.

Это сформирует пространственное представление и логическое мышление. Наш тренажер сложения дробей в этом, конечно, поможет. А в 5 классе изучение дробей со сверстниками не составит труда! Но если надо решить уже имеющуюся дробь, ту придет на помощь калькулятор решающий дроби. Вы также можете распечатать примеры на дроби для 5 класса с ответами для тренировки
Как бы ребенок не решал упражнения с дробями для 5 класса для тренировки подойдет любой способ. Хоть решать решать обыкновенные дроби используя онлайн тренажер, хоть распечатать и решать на листке бумаги примеры с простыми дробями для 5 класса для тренировки на нашем сайте. Главное много практики, много упражнений с дробями и много тренировок. В 5 классе главное отточить навыки.

Как рассказать про часть, чтобы ребенок понял?

Дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы. Правильные дроби – это дроби, в которых числитель меньше знаменателя Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя

Дробь — число не целое, оно обозначает количество долей целого

Обыкновенная дробь состоит из двух частей: числитель и знаменатель

Дроби бывают правильные и неправильные. У правильных дробей числитель меньше знаменателя. У неправильных дробей наоборот, числитель больше знаменателя, а значит любую неправильную дробь можно перевести в смешанную, выделив у нее целую часть и отняв ее из числителя

Познакомься с другими тренажерами курса

Меры измерения

Мер величин много и в них легко запутаться. Изучайте меры длины, времени и массы на тренажере

Скорей заниматься

Римские цифры

Множество примеров различной сложности помогут ребенку быстро запомнить римские цифры

Скорей заниматься

Задачи на объем, площадь, периметр

Решение задач на применение формул объем, площадь, периметр

Скорей заниматься

Умножение обыкновенных дробей / Обыкновенные дроби / Справочник по математике 5-9 класс

1. Главная
2. Справочники
3. Справочник по математике 5-9 класс
4. Обыкновенные дроби
5. Умножение обыкновенных дробей

Чтобы умножить обыкновенную дробь на натуральное число, нужно ее числитель умножить на это число, а знаменатель оставить без изменения.

Примеры:

Обратите внимание, если в ответе получается неправильная дробь, то из нее выделяют целую часть.

Если мы умножаем на натуральное число, которое можно сократить с числом, стоящим в знаменателе, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).

Пример:

Произведением двух дробей является дробь, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей.

Пример:

Если мы перемножаем дроби, у которых можно сократить числитель первой и знаменатель второй дроби и (или) знаменатель первой и числитель второй дроби, то сначала выполняют сокращение, а затем умножение (такой ход действий облегчает вычисления).

Примеры:

Умножение смешанных чисел

Чтобы выполнить умножение смешанных чисел, нужно записать эти числа в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

Примеры:

Для обыкновенных дробей, как и для натуральных чисел, выполняются свойства умножения (переместительное свойство умножения, сочетательное свойство умножения, распределительные свойства умножения относительно сложения и относительно вычитания). Также при умножении дроби на ноль (или нуля на дробь) получаем ноль, и при умножении дроби на единицу (или единицы на дробь) получим равную ей дробь.

Примеры:

Чтобы умножить смешанное число на натуральное число, можно представить смешанное число в виде неправильной дроби, а затем воспользоваться правилом умножения дроби на натуральное число или можно умножить целую часть на натуральное число, далее умножить дробную часть на натуральное число и полученные произведения сложить.

Пример:

Нахождение дроби от числа

Чтобы найти дробь от числа, нужно умножить число на эту дробь.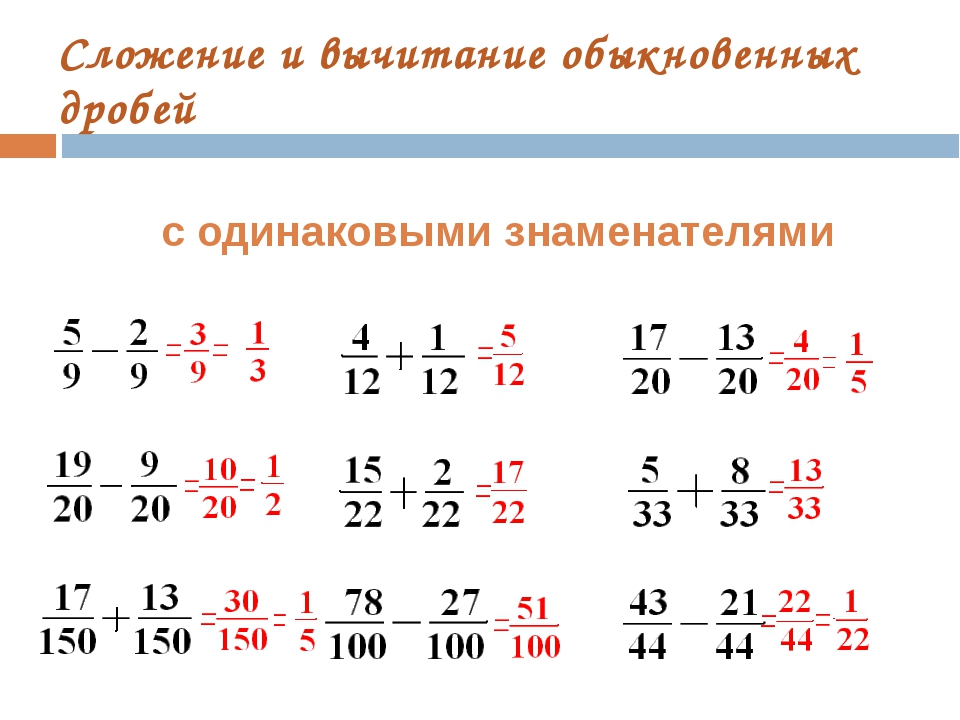

Примеры:

а) Найти от числа 20.

Решение:

б) Найти 0,6 от числа 9.

Решение:

9·0,6 = 5,4.

в) Найти 30 % от числа 500.

Решение:

1) 30% = 30 : 100 = 0,30 = 0,3

2) 500·0,3 = 150.

Взаимно обратные числа

Два числа, произведение которых равно 1, называют взаимно обратными.

Примеры:

1) , значит, числа — взаимно обратные;

2)

Чтобы определить число обратное смешанному числу, нужно представить это смешанное число в виде неправильной дроби.

Пример:

, значит, числу обратно число .

Запомните:

• Числом, обратным 1, является само число 1.
• Для числа 0 обратного числа не существует.
• Обратным числу является число .
• Если — натуральное число, то обратным ему является число .

Советуем посмотреть:

Доли. Обыкновенные дроби

Сравнение дробей

Делители и кратные

Признаки делимости на 10, на 5 и на 2

Четные и нечетные числа

Признаки делимости на 9 и на 3

Простые и составные числа

Разложение на простые множители

Наибольший общий делитель

Наименьшее общее кратное

Деление и дроби

Сложение и вычитание дробей с одинаковыми знаменателями

Смешанное число

Сложение и вычитание смешанных чисел

Основное свойство дроби

Решето Эратосфена

Приведение дробей к общему знаменателю

Сравнение, сложение и вычитание дробей с разными знаменателями

Деление обыкновенных дробей

Обыкновенные дроби

Правило встречается в следующих упражнениях:

5 класс

Задание 567, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1348, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1751, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

6 класс

Номер 402, Мерзляк, Полонский, Якир, Учебник

Номер 407, Мерзляк, Полонский, Якир, Учебник

Номер 629, Мерзляк, Полонский, Якир, Учебник

Задание 547, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 767, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 947, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1159, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1173, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1364, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

Задание 1376, Виленкин, Жохов, Чесноков, Шварцбург, Учебник

7 класс

Номер 380, Мерзляк, Полонский, Якир, Учебник

Номер 429, Мерзляк, Полонский, Якир, Учебник

Номер 470, Мерзляк, Полонский, Якир, Учебник

Номер 536, Мерзляк, Полонский, Якир, Учебник

Номер 565, Мерзляк, Полонский, Якир, Учебник

Номер 570, Мерзляк, Полонский, Якир, Учебник

Номер 1027, Мерзляк, Полонский, Якир, Учебник

Номер 1040, Мерзляк, Полонский, Якир, Учебник

Номер 1052, Мерзляк, Полонский, Якир, Учебник

Номер 1118, Мерзляк, Полонский, Якир, Учебник

8 класс

Номер 13, Мерзляк, Полонский, Якир, Учебник

Номер 65, Мерзляк, Полонский, Якир, Учебник

Номер 260, Мерзляк, Полонский, Якир, Учебник

Номер 272, Мерзляк, Полонский, Якир, Учебник

Номер 281, Мерзляк, Полонский, Якир, Учебник

Номер 315, Мерзляк, Полонский, Якир, Учебник

Номер 355, Мерзляк, Полонский, Якир, Учебник

Номер 397, Мерзляк, Полонский, Якир, Учебник

Номер 398, Мерзляк, Полонский, Якир, Учебник

Номер 402, Мерзляк, Полонский, Якир, Учебник

---

Что такое дробь? — Определение, факты и примеры

Что такое дробь?

Фракции представляют собой части целого или набора объектов. Дробь состоит из двух частей. Число в верхней части строки называется числителем. Он сообщает, сколько равных частей целого или набора взято. Число под чертой называется знаменателем. Он показывает общее количество равных частей, на которые делится целое, или общее количество одинаковых объектов в коллекции.

Родственные игры

Доля целого

Когда целое делится на равные части, количество частей, которое мы берем, составляет дробь.

Если торт разделить на восемь равных частей и один кусок торта положить на тарелку, то говорят, что на каждой тарелке есть $\frac{1}{8}$ торта. Читается как «одна восьмая» или «1 на 8».

Связанные рабочие листы

Доля набора объектов

Всего 5 детей.

3 из 5 — девочки. Итак, доля девушек составляет три пятых ( $\frac{3}{5}$ ).

2 из 5 мальчиков. Итак, доля мальчиков составляет две пятых ( $\frac{2}{5}$ ).

Равные и неравные части

Чтобы определить дробь, нужно разделить целое на равные части.

Представление дроби

Дробь может быть представлена ​​тремя способами: в виде дроби, процента или десятичной дроби. Рассмотрим каждую из трех форм представления.

Дробное представление,

Первой и наиболее распространенной формой представления дроби является $\frac{a}{b}$. Здесь а — числитель, а b — знаменатель. И числитель, и знаменатель разделены горизонтальной чертой.

Пример: Дробь $\frac{3}{4}$ можно понять следующим образом.

Числитель: 3

Знаменатель: 4

Дробь представляет собой три части, когда целое делится на четыре равные части.

Десятичное представление

В этом формате дробь представляется в виде десятичного числа.

Пример: Дробь $\frac{3}{4}$ можно представить в виде десятичной дроби, разделив числитель (3) на знаменатель (4). $\frac{3}{4}$ = 0,75.

Таким образом, в десятичном представлении $\frac{3}{4}$ записывается как 0,75.

Процентное представление

В этом представлении дробь умножается на 100, чтобы преобразовать ее в проценты.

Пример: Если мы хотим представить в процентах, мы должны умножить $\frac{3}{4}$ на 100.

 $\frac{3}{4}$ x 100 = 0,75 x 100 = 75. Таким образом, мы можем представить $\frac{3}{4}$ как 75%.

Дроби в числовой строке

Дроби могут быть представлены в числовой строке, как показано ниже.

Типы дробей

Основными частями дроби являются числитель и знаменатель . На их основе можно определить различные типы фракций. Давайте рассмотрим некоторые распространенные типы дробей.

Смешанные дроби в неправильные дроби

Смешанные дроби можно преобразовать в неправильные дроби, умножив целое число на знаменатель и прибавив его к числителю. Он становится новым числителем, а знаменатель остается неизменным.

Пример: 8$\frac{2}{3}$ = $\frac{(8 \times 3) + 2}{3}$ = $\frac{26}{3}$

Заключение

Самый простой способ научить детей этой теме — помочь им визуализировать дроби. Это можно сделать с помощью вырезок из бумаги или интерактивных онлайн-игр, подобных тем, которые доступны на SplashLearn. Посетите веб-сайт SplashLearn, чтобы найти интересные способы изучения различных математических концепций.

Решенные примеры с дробями

1. Преобразовать смешанное число 4$\frac{3}{5}$ в неправильную дробь.

Решение: 4$\frac{3}{5}$ = $\frac{(4 ✕ 5) + 3}{5}$  = $\frac{20 + 3}{5}$  = $\ frac{23}{5}$ 

2. Эквивалентны ли дроби $\frac{14}{20}$ и $\frac{7}{10}$?

Решение:  

Простейшая форма $\frac{14}{20}$ = $\frac{7}{10}$

Простейшая форма $\frac{7}{10}$ = $\ frac{7}{10}$

Поскольку простейшей формой обеих дробей является $\frac{7}{10}$, мы можем сказать, что эти две дроби эквивалентны.

3. Из следующих дробей отделить правильную и неправильную дробь

$\frac{9}{2}$, $\frac{4}{11}$, $\frac{16}{16} $, $\frac{2}{3}$, $\frac{7}{9}$, $\frac{5}{6}$

Решение:

Правильная дробь: $\frac{4 }{11}$, $\frac{2}{3}$, $\frac{7}{9}$, $\frac{5}{6}$

Неправильная дробь: $\frac{9}{ 2}$, $\frac{16}{16}$

4. Преобразовать $\frac{2}{5}$ в процентах.

Решение:

$\frac{2}{5} \times 100%$  = 40%

Практические задачи на дроби

1

Какая из следующих дробей является неправильной?

$\frac{3}{10}$

$\frac{7}{16}$

$\frac{18}{11}$

$\frac{12}{17}$

Правильный ответ: $\frac{18}{11}$
$\frac{18}{11}$ — неправильная дробь, так как числитель (18) больше знаменателя (11).

2

Что из следующего является десятичным представлением дроби $\frac{3}{8}$?

0,5

0,75

0,80

0,375

Правильный ответ: 0,375
Деление числителя (3) на знаменатель (8) дает десятичное число 0 .375.

3

При каком значении x следующие две дроби будут эквивалентны?

$\frac{3}{7}$ и $\frac{x}{21}$

2

9

6

8

Правильный ответ: 9
$\frac{(3 ✕ y )}{(7 ✕ y)}$ = $\frac{x}{21}$
Теперь найдем 7 x y = 21. Мы знаем, что y = 3. Таким образом, числитель должен быть 3 x 3 = 9.

4

Какой тип дроби $\frac{2}{5}$?

Правильная дробь

Единичная дробь

Неправильная дробь

Смешанная дробь

Правильный ответ: Правильная дробь
Поскольку числитель меньше знаменателя, данная дробь является правильной дробью.

Часто задаваемые вопросы о дробях

Как проще всего определить, можно ли преобразовать число в смешанную дробь?

Самый простой способ определить это — сравнить числитель со знаменателем. Если числитель больше знаменателя, дробь неправильная и может быть преобразована в смешанную дробь.

Есть ли реальные примеры использования дробей?

Дроби очень распространены в повседневной жизни. Когда мы покупаем продукты или печем торт, отмечаем вечеринку или подсчитываем бюджет в начале месяца, дроби используются.

Что такое правильная дробь?

Правильные дроби — это дроби, у которых числитель меньше знаменателя. Десятичное значение правильной дроби всегда меньше 1.

Где используются равные дроби?

Эквивалентные дроби помогают в ряде случаев, когда расчеты включают дробные числа. Например, сложение и вычитание дробей становятся очень простыми, когда используются свойства эквивалентности дробей.

Что такое дробь? Определение, части, примеры

Дробь показывает часть целого. Это целое может быть регионом или коллекцией. Слово «фракция» происходит от латинского слова «fractio», что означает «ломать». Египтяне, будучи первой цивилизацией, изучавшей дроби, использовали дроби для решения своих математических задач, которые включали в себя деление продуктов питания, припасов и отсутствие валюты в слитках.

В Древнем Риме дроби записывались только словами, обозначающими часть целого. В Индии дроби сначала записывались с одним числом над другим (числитель и знаменатель), но без черты. Только арабы добавили линию, которая используется для разделения числителя и знаменателя.

1.	Что такое дроби?
2.	Части дроби
3.	Типы фракций
4.	Дроби в числовой строке
5.	Часто задаваемые вопросы о дробях

Что такое дроби?

В математике дроби представлены числовым значением, которое определяет часть целого. Дробь может быть частью или частью любого количества из целого, где целым может быть любое число, определенное значение или вещь. Давайте разберемся с этой концепцией на примере. На следующем рисунке показана пицца, разделенная на 8 равных частей. Теперь, если мы хотим выразить одну выбранную часть пиццы, мы можем выразить ее как 1/8, что показывает, что из 8 равных частей мы имеем в виду 1 часть.

Означает одну из восьми равных частей. Его также можно прочитать как:

• Одна восьмая или
• 1 на 8

Если мы выберем 2 части пиццы, это будет выражено как 2/8. Точно так же, если мы имеем в виду 6 частей этой пиццы, мы запишем это как 6/8 как дробь.

Части дроби

Все дроби состоят из числителя и знаменателя и разделены горизонтальной чертой, известной как дробная черта.

• Знаменатель указывает количество частей, на которые было разделено целое. Он помещается в нижнюю часть дроби под дробной чертой.
• Числитель указывает, сколько разделов дроби представлено или выбрано. Он ставится в верхней части дроби над дробной чертой.

Типы фракций

На основании числителя и знаменателя, которые являются частями дроби, существуют различные типы дробей, перечисленные ниже:

Правильная дробь

Правильные дроби — это дроби, в которых числитель меньше знаменателя. Например, 5/7, 3/8, 2/5 и т. д. — правильные дроби.

Неправильная дробь

Неправильная дробь — это дробь, в которой числитель больше или равен знаменателю. Оно всегда такое же или больше, чем целое. Например , 4/3, 5/2, 8/5 и так далее.

Дробная единица

Дроби, в которых числитель равен 1, называются единичными дробями. Например , 1/4, 1/7, 1/9 и так далее.

Смешанная дробь

Смешанная дробь представляет собой смесь целого числа и правильной дроби. Например, \(5\frac{1}{3}\), где 5 – целое число, а 1/3 – правильная дробь, или \(2\frac{2}{5}\), \( 7\frac{9}{11}\) и так далее.

Эквивалентная дробь

Эквивалентная дробь — это дроби, представляющие одно и то же значение после их упрощения. Чтобы получить эквивалентные дроби любой заданной дроби:

• Мы можем умножить и числитель, и знаменатель данной дроби на одно и то же число.
• Мы можем разделить и числитель, и знаменатель данной дроби на одно и то же число.

Пример: Найдите две дроби, равные 5/7.

Решение:

Эквивалентная дробь 1: Умножим числитель и знаменатель на одно и то же число 2. Это означает, что 5/7= (5 × 2)/(7 × 2) = 10/14

Эквивалентная дробь 2: Умножим числитель и знаменатель на одно и то же число 3. Это означает, что 5/7 = (5 × 3)/(7 × 3) = 15/21

Следовательно, 10/14, 15/21 и 5/7 — эквивалентные дроби.

Подобные и разные дроби

Подобные дроби — это дроби, имеющие одинаковые знаменатели. Например, 5/15, 3/15, 17/15 и 31/15 похожи на дроби.

В отличие от дробей, дроби имеют разные знаменатели. Например, 2/7, 9/11, 3/13 и 39/46 — разные дроби.

Дробь в числовой строке

Представление дробей на числовой прямой демонстрирует интервалы между двумя целыми числами, что также показывает нам фундаментальный принцип построения дробных чисел. Дроби на числовой прямой можно представить, составив равные части целого, то есть от 0 до 1. Знаменатель дроби будет представлять количество равных частей, на которые числовая линия будет разделена и отмечена. Например, если нам нужно представить 1/8 на числовой прямой, нам нужно отметить 0 и 1 на двух концах и разделить числовую прямую на 8 равных частей. Тогда первый интервал можно обозначить как 1/8. Точно так же следующий интервал можно пометить как 2/8, следующий — как 3/8 и так далее. Следует отметить, что последний интервал представляет 8/8, что означает 1. Обратите внимание на следующую числовую строку, которая представляет эти дроби в числовой строке.

☛Статьи по теме

• Умножение дробей
• Деление дробей
• Сложение и вычитание дробей

Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в прямом эфире один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

 

Примеры дробей

1. Пример 1: Запишите две эквивалентные дроби для 5/15

   Решение:

   Давайте запишем эквивалентные дроби для 5/15, используя умножение и деление.

   а.) Умножим числитель и знаменатель на одно и то же число 2. Это означает, что (5 × 2)/(15 × 2) = 10/30

   б.) Разделим числитель и знаменатель с тем же номером 5. Это означает, что (5 ÷ 5)/(15 ÷ 5) = 1/3

   Следовательно, 10/30 и 1/3 эквивалентны 5/15. Другими словами, 10/30, 1/3 и 5/15 являются эквивалентными дробями.

2. Пример 2: В классе 48 учеников, 1/4 из них смотрят мультфильмы. Сколько школьников не смотрят мультфильмы?

   Решение:

   Общее количество учеников = 48, доля учеников, которые смотрят мультфильмы = 1/4

   Количество учеников, которые смотрят мультфильмы = 1/4 × 48 = 12

   Таким образом, количество школьников, не смотрящих мультики = 48 — 12 = 36

   Следовательно, число школьников, не смотрящих мультики, равно 36.

3. Пример 3: Укажите истинное или ложное значение.

   а.) Правильные дроби – это дроби, у которых числитель меньше знаменателя.

   б.) 9/2 — правильная дробь.

   в.) 3/4 и 2/4 подобны дробям.

   Решение:

   а.) Правильные дроби — это дроби, у которых числитель меньше знаменателя.

   b.) Неверно, 9/2 — неправильная дробь, потому что числитель больше знаменателя.

   в.) Верно, что 3/4 и 2/4 подобны дробям, потому что у них одинаковые знаменатели.

перейти к слайдуперейти к слайдуперейти к слайду

Хотите построить прочную основу в математике?

Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.

Забронировать бесплатный пробный урок

Практические вопросы по дробям

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о дробях

Что такое дроби в математике?

Дроби в математике представляют числовое значение, выражающее часть целого. Целое может быть любым числом, определенным значением или вещью. Фракции представлены в виде p/q. Например, ¼, ½, ¾ и так далее.

Какие существуют типы дробей?

Дроби классифицируются по следующим основаниям:

• На основании числителя и знаменателя дроби делятся на правильные дроби, неправильные дроби, смешанные дроби.
• На основании групп они подразделяются на похожие дроби, непохожие дроби и эквивалентные дроби.

Сколько частей в дроби?

Дробь состоит из двух частей: числителя и знаменателя.

• Числитель: Числитель представляет собой число, расположенное над дробной чертой. Например, в 6/7 числитель 6.
• Знаменатель: Знаменатель указывает число, расположенное под дробной чертой. Например, в 6/7 7 является знаменателем.

Что такое 0,125 в виде дроби?

0,125, поскольку дробь может быть записана как 1/8. Мы можем преобразовать десятичную дробь в дробь следующим образом. 0,125 = 125/1000 = 5/40 = 1/8

Как связаны дроби и десятичные числа?

Дроби и десятичные дроби — это разные способы представления чисел. Дроби записывают в виде p/q, где q≠0, например, 3/5; а в десятичных числах целая часть числа и дробная часть связаны с запятой, например, 3,56. Дробь можно преобразовать в десятичную, если разделить данный числитель на знаменатель. Точно так же, чтобы преобразовать десятичную дробь в дробь, мы записываем данную десятичную дробь в качестве числителя, а под ней ставим дробную черту. Затем мы помещаем 1 прямо под десятичной точкой, за которой следует необходимое количество нулей. Затем эту дробь можно упростить. Например, если нам нужно преобразовать 0,5 в дробь, мы помещаем 10 в знаменатель и удаляем десятичную точку, что дает 5/10. После сокращения дроби получаем (5 ÷ 5) / (10 ÷ 5) = 1/2.

Как упростить дроби?

Чтобы упростить дробь, мы сначала запишем множители для числителя и знаменателя. Затем определите наибольший общий множитель между ними и разделите числитель и знаменатель на наибольший общий множитель (GCF). Приведенная дробь, которую мы получаем, является простейшей формой данной дроби. Например, чтобы упростить 36/45, мы найдем НОД 36 и 45. НОД 36 и 45 = 9. Теперь разделим числитель и знаменатель на 9., то есть (36 ÷ 9)/(45 ÷ 9) = 4/5

Как умножать дроби?

Чтобы умножить любые две дроби, мы сначала умножаем числители, затем умножаем знаменатели. Затем упростите полученную дробь. Например, 3/5 × 15/18 = 45/90 = 1/2.

Как делить дроби?

Чтобы разделить одну дробь на другую, мы сначала записываем обратную величину второй дроби, а затем умножаем дроби. Другими словами, мы умножаем первую дробь на обратную величину второй дроби. Написав обратную величину второй дроби, умножаем дроби обычным способом. Мы умножаем числители, а затем умножаем знаменатели. Затем упростите полученную дробь, если требуется. Например, 5/6 ÷ 1/5 = 5/6 × 5/1 = 25/6 = \(4\frac{1}{6}\)

Как называются дроби с одинаковым знаменателем?

Дроби с одинаковым знаменателем называются подобными дробями. Например, 4/7, 3/7, 5/7 похожи на дроби, потому что у них один и тот же знаменатель.

Как определить, какая дробь больше?

Чтобы определить большую дробь, сначала нужно проверить, подобны ли данные дроби дробям. Для этого нам нужно сравнить знаменатели.

• При одинаковых знаменателях больше дробь с большим числителем. Например, чтобы сравнить 3/4 и 2/4, мы можем легко проверить числители и сказать, что 3/4 > 2/4
.
• В случае разных знаменателей мы переводим данные дроби в подобные дроби, записывая для них общий знаменатель, а затем сравниваем числители. Например, чтобы сравнить 2/3 и 4/5, мы найдем наименьшее общее кратное (НОК) знаменателей. Как только знаменатели станут одинаковыми, мы сможем легко сравнивать дроби. НОК чисел 3 и 5 равно 15. Теперь переведем их так, чтобы знаменатели стали одинаковыми. Умножим первую дробь 2/3 на 5/5, то есть 2/3 × 5/5 = 10/15. Теперь умножим вторую дробь 4/5 на 3/3, то есть 4/5 × 3/3 = 12/15. Сравните дроби: 10/15 и 12/15. Поскольку знаменатели одинаковы, мы сравним числители и увидим, что 12 > 10 . Дробь с большим числителем является большей дробью, то есть 10/15 < 12/15. Следовательно, 2/3 < 4/5.

Все ли дроби меньше 1?

Нет, все дроби не меньше 1.

• Правильные дроби больше 0, но меньше 1. (Числитель меньше знаменателя).
• Неправильные дроби всегда равны 1 или больше 1. (Числитель больше или равен знаменателю)

Как складывать дроби с разными знаменателями?

Чтобы сложить дроби с разными знаменателями, нам нужно выполнить следующие шаги. Сложим дроби 4/5 + 6/7

• Шаг 1: Поскольку знаменатели в данных дробях разные, мы найдем НОК 5 и 7, чтобы сделать их одинаковыми. НОК 5 и 7 = 35,
• Шаг 2: После этого шага мы умножим 4/5 на 7/7, то есть (4/5) × (7/7) = 28/35, а 6/7 на 5/5, ( 6/7) × (5/5) = 30/35. Этот шаг преобразует их в похожие дроби с одинаковыми знаменателями.
• Шаг 3: Теперь знаменатели совпадают, поэтому мы можем сложить числители и сохранить общий знаменатель. Новые дроби с общими знаменателями — 28/35 и 30/35. Итак, 28/35 + 30/35 = (28 + 30)/35 = 58/35 = \(1\frac{23}{35}\).

Как умножать дроби на целые числа?

Чтобы умножить дроби на целые числа, мы записываем целое число в виде дроби, помещая 1 в знаменатель, а затем следуем обычной процедуре умножения дробей. Например, давайте умножим 5/8 × 3. Здесь 3 — целое число, и мы запишем его как 3/1. Теперь умножим 5/8 × 3/1 = 15/8 = \(1\frac{7}{8}\)

Что такое сравнение дробей?

Сравнение дробей означает нахождение большей и меньшей дроби между любыми двумя или более дробями. Например, давайте сравним 3/16 и 7/16. Сначала рассмотрим знаменатели данных дробей: 3/16 и 7/16. Поскольку знаменатели одинаковы, мы можем сравнить числители. Мы видим, что 3 < 7. Дробь с большим числителем является большей дробью. Следовательно, 3/16 < 7/16. В случае, если дроби имеют разные знаменатели, мы преобразуем их в подобные дроби, найдя НОК знаменателей и записав соответствующие эквивалентные дроби.