Обзор и применение » Spajić® DOO
ЛУЧШЕЕ РЕШЕНИЕ ДЛЯ АВТОМОБИЛЬНОЙ И АВИАЦИОННОЙ ПРОМЫШЛЕННОСТИ
Мы предлагаем широкий ассортимент абразивов из рубленой проволоки, разных материалов, разных диаметров предназначенных для удовлетворения потребностей всех наших клиентов.
Наша рубленая проволока (дробь) имеет возможность повторного использования со сроком службы примерно мин. 4200 циклов, независимо от размера зерна и твердости.
Дробь, полученная путем рубки проволоки, имеет высокую степень однородности по форме и твердости, что напрямую влияет на качество обработки поверхности обрабатываемого материала.
Принимая во внимание большое количество возможных повторных работ, дробь, полученная из проволоки, длится дольше, так что существует очевидная экономия при заказе и покупке другого количества других абразивов.
Учитывая большое количество возможных повторных использований, абразивные материалы из рубленой проволоки служат дольше, что позволяет экономить на повторном заказе и покупке другого количества абразива.

Тот факт, что частицы проволоки не ломаются, приводит к увеличению длительности рабочей смеси, используемой для обработки.
ФОРМЫ ЗЕРНА
ЦИЛИНДРИЧЕСКАЯ ФОРМА
характеризуется острыми краями, образующимися при резке проволоки. Цилиндрическая форма дроби является очень эффективной формой операции очистки, но она не подходит для операций микро-ковки.
ОБКАТАННАЯ ДРОБЬ — ПЕРВИЧНАЯ ОБКАТКА (CCW)
острые края удаляются в процессе, называемом «обкатка». Обкатанная дробь из проволоки используется для операций очистки, увеличения шероховатости поверхностей, удаление литейного песка, острых кромок, коррозии и покрытий, а также для микро-ковки в автомобильной и аэрокосмической промышленности.
ДВОЙНАЯ ОБКАТКА ДРОБИ (CCW)
имеет двойную обкатку для формирования более сферической формы.
СФЕРИЧЕСКИ ЗАКРУГЛЕННАЯ ДРОБЬ (SCCW)
является наиболее обкатанной, чтобы придать гладкую, сферическую форму. Эта форма дроби используется в самых требовательных операциях дробеструйной обработки и микро-ковки.
Эта форма дроби используется в самых требовательных операциях дробеструйной обработки и микро-ковки.
ПРЕИМУЩЕСТВА ПРОВОЛОЧНОЙ ДРОБИ
МЕНЬШИЕ ЗАГРЯЗНЕНИЯ ОБРАБАТЫВАЕМЫХ ПОВЕРХНОСТЕЙ
Рубленая проволока (дробь) на своей поверхности не имеет слоя оксида железа и не оставляет остатков оксида железа на обрабатываемых деталях – обрабатываемые поверхности становятся чище и светлее, чем при дробеструйной/дробеметной обработке литой дробью. Литые абразивы оставляют загрязнения и отложения на поверхностях деталей, которые подвергаются струйной или дробеструйной обработке. Литые абразивы, которые ломаются и / или деформируются, могут оставлять небольшие частицы, отпечатанные на поверхности, которая обрабатывается. Рубленая проволока (дробь) не раскалывается на крошечные части и не оставляет следов, отпечатанных на обрабатываемой поверхности. В связи с вышеизложенным, от рубленой проволоки (дроби) остается в 10-20 раз меньше отложений на обрабатываемых поверхностях.
ВЫСОКАЯ ДОЛГОВЕЧНОСТЬ
Благодаря своей микроструктуре, полученной путем холодного волочения без внутренних повреждений (трещины, кавитация, пористость), срок службы рубленой дроби из проволоки, как известно, выше по сравнению с литой дробью. Микроструктура рубленой проволочной дроби — это перлит, который является наилучшим сочетанием твердости и долговечности. Микроструктура литой дроби — бейнит (быстро деформируется) или мартенсин (приводит к разрушению частиц). Минимальный срок службы (долговечность) рубленой проволочной дроби Spajic® составляет 4200 циклов, независимо от размера частиц и твердости. В дополнение к самому сроку службы очень важна модель износа процесса, особенно в процессах микро-ковки (наклепа, упрочнение). Литая дробь изнашивается таким образом, что первоначальная форма значительно деформируется или частицы распадаются на более мелкие кусочки. Рубленая проволочная дробь изнашивается за счет уменьшения размера зерна, а форма становится долее круглой.
ВЫСОКАЯ ПРОИЗВОДИТЕЛЬНОСТЬ УСТОЙЧИВОСТИ
Проволочная дробь обладает высокой прочностью, благодаря своей стабильности с точки зрения размера зерна, стабильности с точки зрения формы, твердости и плотности. Литая дробь имеет меньшую долговечность из-за очень быстрого изменения формы (деформация, разрушение на мелкие куски).
ВРЕМЯ ПРОЦЕССА / РАСХОД ДРОБИ
Рубленая проволочная дробь значительно сокращает время дробеструйной обработки. Литая дробь из-за повышенного износа увеличивают общий процесс. Потребление рубленой дроби уменьшается, т.е. на 33-67% меньше, чем литой дроби (данные основаны на базе нескольких клиентах). Меньшее время обработки, а также более низкое потребление рубленой дроби от проволоки снижает эксплуатационные расходы и расходы на техническое обслуживание.
МИКРОСТРУКТУРА / РАЗМЕР ЗЕРНА
Микроструктура рубленой проволочной дроби — это перлит, который является наилучшим сочетанием твердости и долговечности. Микроструктура литой дроби — бейнит (быстро деформируется) или мартенсит (приводит к разрушению частиц). Размер зерна рубленой дроби из проволоки является однородным (все зерна имеют одинаковые размеры). Размер зерна литой дроби неравномерен (зерна разных размеров).
Микроструктура литой дроби — бейнит (быстро деформируется) или мартенсит (приводит к разрушению частиц). Размер зерна рубленой дроби из проволоки является однородным (все зерна имеют одинаковые размеры). Размер зерна литой дроби неравномерен (зерна разных размеров).
ИЗМЕНЕНИЕ РАЗМЕРА ЗЕРНА
Рубленая проволочная дробь изготавливается из проволоки одного и того же диаметра, и все частицы практически идентичны, размер частиц не изменяется. Литая дробь производится из частиц разных размеров.
ВЫСОКАЯ УСТОЙЧИВОСТЬ К РАЗРУШЕНИЮ
Дробь из проволоки имеет тенденцию изнашиваться и становиться меньше по размеру, а не разрушаться с образованием частиц с острыми краями, которые могут вызвать повреждение поверхности детали.
УМЕНЬШЕННАЯ ПЫЛЬ (СНИЖЕНИЕ ПЫЛЕОБРАЗОВАНИЯ)
Дробь из проволоки является существенно более прочной и устойчивой к разрушению, в результате чего уменьшается образование пыли от самой дроби. Литая стальная дробь приводит к появлению большого количества пыли, которая образуется от самих частиц.
УВЕЛИЧЕН СРОК СЛУЖБЫ ДЕТАЛЕЙ
Детали, при дробеметной обработке рубленой дробью, показывают более длительный срок службы по сравнению на детали, обрабатываемые литой дробью. В лаборатории были проведены испытания на усталость, чтобы определить, какой вид дроби влияет на срок службы деталей. Детали, обработанные дробью из проволоки, показали более продолжительный и более стабильный срок службы деталей, чем детали, обработанные литыми абразивами.
ЗНАЧИТЕЛЬНОЕ СОКРАЩЕНИЕ РАСХОДОВ
Высокий срок службы проволочной дроби SPAJIC® приводит к снижению затрат на потребление, экономии на замене фильтрующих элементов, экономии затрат на обслуживание оборудования.
Двухэтажная дробь. Специфика работы с многоэтажными дробями
) и знаменатель на знаменатель (получим знаменатель произведения).
Формула умножения дробей:
Например:
Перед тем, как приступить к умножению числителей и знаменателей, необходимо проверить на возможность сокращения дроби .
Деление обыкновенной дроби на дробь.
Деление дробей с участием натурального числа.
Это не так страшно, как кажется. Как и в случае со сложением , переводим целое число в дробь с единицей в знаменателе. Например:
Умножение смешанных дробей.
Правила умножения дробей (смешанных):
- преобразовываем смешанные дроби в неправильные;
- перемножаем числители и знаменатели дробей;
- сокращаем дробь;
- если получили неправильную дробь, то преобразовываем неправильную дробь в смешанную.
Обратите внимание! Чтобы умножить смешанную дробь на другую смешанную дробь, нужно, для начала, привести их к виду неправильных дробей, а далее умножить по правилу умножения обыкновенных дробей.
Второй способ умножения дроби на натуральное число.
Бывает более удобно использовать второй способ умножения обыкновенной дроби на число.
Обратите внимание! Для умножения дроби на натуральное число необходимо знаменатель дроби разделить на это число, а числитель оставить без изменения.
Из, приведенного выше, примера понятно, что этот вариант удобней для использования, когда знаменатель дроби делится без остатка на натуральное число.
Многоэтажные дроби.
В старших классах зачастую встречаются трехэтажные (или больше) дроби. Пример:
Чтобы привести такую дробь к привычному виду, используют деление через 2 точки:
Обратите внимание! В делении дробей очень важен порядок деления. Будьте внимательны, здесь легко запутаться.
Обратите внимание, например:
При делении единицы на любую дробь, результатом будет таже самая дробь, только перевернутая:
Практические советы при умножении и делении дробей:
1. Самым важным в работе с дробными выражениями является аккуратность и внимательность. Все вычисления делайте внимательно и аккуратно, сосредоточенно и чётко. Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
Лучше запишите несколько лишних строчек в черновике, чем запутаться в расчетах в уме.
2. В заданиях с разными видами дробей — переходите к виду обыкновенных дробей.
3. Все дроби сокращаем до тех пор, пока сокращать уже будет невозможно.
4. Многоэтажные дробные выражения приводим в вид обыкновенных, пользуясь делением через 2 точки.
5. Единицу на дробь делим в уме, просто переворачивая дробь.
краткое содержание других презентаций
«Применение формул сокращенного умножения» — . Разложение многочленов на множители. 1 способ. Применение формул сокращённого умножения: Формулы сокращённого умножения были известны еще 4000 лет назад. Доказательство неравенства. Вместо «произведение a и b» говорилось «прямоугольник, содержащийся между а и в», вместо а? — «квадрат на отрезке а». (x – 2)? + (x + 2)? = 2(x – 3)(x? + 3x + 9) (x-2+x+2)((x-2)? — (x-2)(x+2) + (x+2)? = 2(x?-27) 2x(x? – 4x + 4 – x? + 4 + x? + 4x +4) = 2x? – 54 2x(x? + 12) = 2x? – 54 2x? + 24x – 2x? = — 54 24x = — 54 x = — 2,25.
«Сложение и вычитание алгебраических дробей» — Алгебраические дроби. 2. Найти наименьший общий знаменатель для дробей. Изучение новой темы. 4а?b. Цели: 4. Сложение и вычитание алгебраических дробей с разными знаменателями (уроки 11 — 13). Примеры:
«Дроби 8 класс» — 8 класс. 2. X + Y · Z = + · . + Z? = + ()?. + + = + + . 1. 3. X · (Y + Z) = · (+). + +. X = ; Y = ; Z = . Построение рациональных выражений. Многоэтажные дроби. /+++==. Дроби. МОУ «Медновская СОШ» Антонюк Ф.Г. Многоэтажная дробь.
«Рациональные числа 8 класс» — Алгебра.8 класс Рациональные числа. Задания для закрепления учебного материала. flash-карточки (http://school-collection.edu.ru) Учитель математики Муниципального общеобразовательного учреждения «Средняя общеобразовательная школа №19» г. Кандалакша Чернявская Татьяна Борисовна. Проверь себя.
«Урок алгебры в 8 классе» — Работа над ошибками: 4 раза. ? 3. Учитель Жарова Л. В. Отработка вычислительных навыков. Тема: «Определение степени с целым отрицательным показателем».
«Статистика» — На фотографиях первоклассники. Краснощёков Сергей – рост 140 см. Вывод: учащиеся начальной школы имеют средний рост 131 см. Мода: 139см. Сколько тетрадей в портфеле несу? Собрать сведения о составе контингента учащихся Будаговской средней школы. Маматкулов Гена – рост 105 см. Мальчиков больше только на одного. Эпиграф. Юноши и девушки старших классов имеют средний арифметический рост 171 см.
Теперь, когда мы научились складывать и умножать отдельные дроби, можно рассматривать более сложные конструкции. Например, что, если в одной задаче встречается и сложение, и вычитание, и умножение дробей?
В первую очередь, надо перевести все дроби в неправильные. Затем последовательно выполняем требуемые действия — в том же порядке, как и для обычных чисел. А именно:
- Сначала выполняется возведение в степень — избавьтесь от всех выражений, содержащих показатели;
- Затем — деление и умножение;
- Последним шагом выполняется сложение и вычитание.

Разумеется, если в выражении присутствуют скобки, порядок действий изменяется — все, что стоит внутри скобок, надо считать в первую очередь. И помните о неправильных дробях: выделять целую часть надо лишь тогда, когда все остальные действия уже выполнены.
Переведем все дроби из первого выражения в неправильные, а затем выполним действия:
Теперь найдем значение второго выражения. Тут дробей с целой частью нет, но есть скобки, поэтому сначала выполняем сложение, и лишь затем — деление. Заметим, что 14 = 7 · 2 . Тогда:
Наконец, считаем третий пример. Здесь есть скобки и степень — их лучше считать отдельно. Учитывая, что 9 = 3 · 3 , имеем:
Обратите внимание на последний пример. Чтобы возвести дробь в степень, надо отдельно возвести в эту степень числитель, и отдельно — знаменатель.
Можно решать по-другому. Если вспомнить определение степени, задача сведется к обычному умножению дробей:
Многоэтажные дроби
До сих пор мы рассматривали лишь «чистые» дроби, когда числитель и знаменатель представляют собой обыкновенные числа. Это вполне соответствует определению числовой дроби, данному в самом первом уроке.
Это вполне соответствует определению числовой дроби, данному в самом первом уроке.
Но что, если в числителе или знаменателе разместить более сложный объект? Например, другую числовую дробь? Такие конструкции возникают довольно часто, особенно при работе с длинными выражениями. Вот пара примеров:
Правило работы с многоэтажными дробями всего одно: от них надо немедленно избавляться. Удалить «лишние» этажи довольно просто, если вспомнить, что дробная черта означает стандартную операцию деления. Поэтому любую дробь можно переписать следующим образом:
Пользуясь этим фактом и соблюдая порядок действий, мы легко сведем любую многоэтажную дробь к обычной. Взгляните на примеры:
Задача. Переведите многоэтажные дроби в обычные:
В каждом случае перепишем основную дробь, заменив разделительную черту знаком деления. Также вспомним, что любое целое число представимо в виде дроби со знаменателем 1. Т.е. 12 = 12/1; 3 = 3/1. Получаем:
В последнем примере перед окончательным умножением дроби были сокращены.
Специфика работы с многоэтажными дробями
В многоэтажных дробях есть одна тонкость, которую всегда надо помнить, иначе можно получить неверный ответ, даже если все вычисления были правильными. Взгляните:
- В числителе стоит отдельное число 7, а в знаменателе — дробь 12/5;
- В числителе стоит дробь 7/12, а в знаменателе — отдельное число 5.
Итак, для одной записи получили две совершенно разных интерпретации. Если подсчитать, ответы тоже будут разными:
Чтобы запись всегда читалась однозначно, используйте простое правило: разделяющая черта основной дроби должна быть длиннее, чем черта вложенной. Желательно — в несколько раз.
Если следовать этому правилу, то приведенные выше дроби надо записать так:
Да, возможно, это некрасиво и занимает слишком много места. Зато вы будете считать правильно. Напоследок — пара примеров, где действительно возникают многоэтажные дроби:
Задача. Найдите значения выражений:
Итак, работаем с первым примером. Переведем все дроби в неправильные, а затем выполним операции сложения и деления:
Переведем все дроби в неправильные, а затем выполним операции сложения и деления:
Аналогично поступим со вторым примером. Переведем все дроби в неправильные и выполним требуемые операции. Чтобы не утомлять читателя, я опущу некоторые очевидные выкладки. Имеем:
Благодаря тому, что в числителе и знаменателе основных дробей стоят суммы, правило записи многоэтажных дробей соблюдается автоматически. Кроме того, в последнем примере мы намеренно оставили число 46/1 в форме дроби, чтобы выполнить деление.
Также отмечу, что в обоих примерах дробная черта фактически заменяет скобки: первым делом мы находили сумму, и лишь затем — частное.
Кто-то скажет, что переход к неправильным дробям во втором примере был явно избыточным. Возможно, так оно и есть. Но этим мы страхуем себя от ошибок, ведь в следующий раз пример может оказаться намного сложнее. Выбирайте сами, что важнее: скорость или надежность.
Тема «Действия с алгебраическими дробями» вызывает у учащихся 7-8 классов определённые
трудности, так как требует хороших знаний материала, изученного ранее: «Действия с обыкновенными дробями», «Преобразование многочленов»,
«Формулы сокращённого умножения».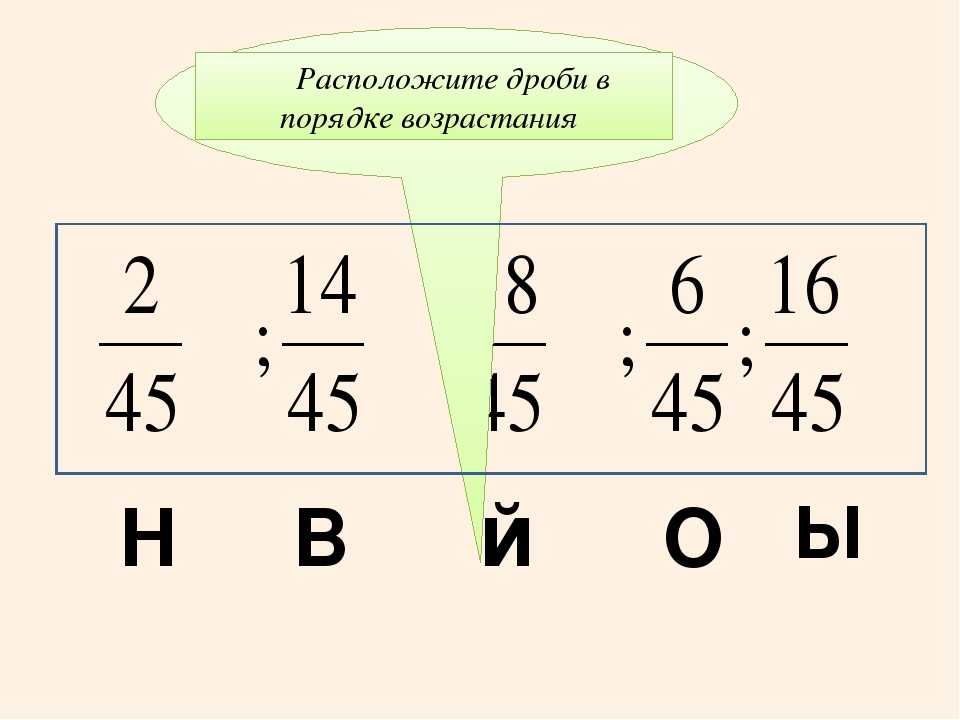 Если предшествующие знания по каким-то причинам сформированы
недостаточно прочно, то под наплывом нового материала они как бы растворяются и, как следствие, являются тормозом для дальнейшего успешного обучения.
Если предшествующие знания по каким-то причинам сформированы
недостаточно прочно, то под наплывом нового материала они как бы растворяются и, как следствие, являются тормозом для дальнейшего успешного обучения.
Успешно реализовывать задачу закрепления «старых» и
формирования «новых» знаний позволяет визуализация учебного материала. Если учебная информация
сопровождается определёнными рисунками, соответствующими формулами, зрительными подсказками,
то её смысл становится видимым, понятным и, как следствие, лучше запоминается.
Именно поэтому мы обратились к новым учебнику и задачнику для 7-го класса, выпущенных
Санкт-Петербургским Институтом Продуктивного обучения Российской Академии Образования .
Эти пособия отличается от других особым структурированием
учебной информации небольшими порциями, которые можно охватить «одним взглядом»; теоретический материал сопровождается
здесь умело подобранными иллюстрациями, необходимыми комментариями, замечаниями, выделением ключевых понятий.
Разнообразие заданий, таких как, «Алгоритмы и автоматы», серии,
тесты, тренажеры, «Посмотрите и …», «Выберите ответ» и другие, предоставляет ученику определённую
свободу выбора, а не загоняют его в жесткие рамки: «реши или найди ответ». Эти задания дают богатейший
материал для индивидуальной работы со слабыми и сильными учащимися. Большое количество нестандартных упражнений,
которые учат мыслить, творить, придумывать, находить выход из затруднительных ситуаций,
предвидеть результат (исследовательские работы, комбинаторные задачи), – позволяет ученикам активизировать
свою мыслительную деятельность, а учителю работать творчески.
В восьмом классе мурманского лицея № 1
по материалам данных учебника и задачника был проведён открытый урок «Многоэтажные дроби». Эта тема выбрана не случайно. В действующих учебниках она отражена мало (например, в учебнике под ред. С.А. Теляковского рассмотрен только один такой пример, решенный с помощью основного свойства дроби). Иногда «многоэтажность» заменяется традиционным действием деления, что приводит к громоздким и не всегда оправданным вычислениям. Однако на вступительных экзаменах в вузы часто встречаются задания, связанные с преобразованием многоэтажных дробей.
Однако на вступительных экзаменах в вузы часто встречаются задания, связанные с преобразованием многоэтажных дробей.
На уроке мы попытались реализовать идею составления алгоритма преобразования многоэтажной дроби самими учащимися.
Целью данного урока являлось:
1) создать алгоритм работы с многоэтажными дробями;
2) научиться использовать его при преобразовании выражений;
3) убедиться в том, что алгоритмы позволяют рационально выполнять математические операции, и что каждый сам может их создавать.
На уроке каждому лицеисту был выдан комплект специальных материалов, в которых учащиеся работали карандашом. В случае если задание было выполнено неверно,
ученик мог исправить свои записи с помощью ластика и тут же записать правильное решение.
Это позволило учащимся чувствовать себя раскованно, не бояться делать ошибки, не ждать ответов других учеников.
Знакомство с многоэтажными дробями началось в процессе выполнения упражнения,
в котором необходимо было построить новые рациональные выражения с помощью заданных выражений (). Лицеисты заполнили пропуски в двух
первых примерах, остальные задания было предложено выполнить дома. После того,
как учащиеся выполнили второй пример (), состоялось обсуждение его структурных особенностей. Заметили, что первое слагаемое
образовалось в результате деления дроби на дробь, что привело к необычному выражению – четырёхэтажной дроби.
Лицеисты заполнили пропуски в двух
первых примерах, остальные задания было предложено выполнить дома. После того,
как учащиеся выполнили второй пример (), состоялось обсуждение его структурных особенностей. Заметили, что первое слагаемое
образовалось в результате деления дроби на дробь, что привело к необычному выражению – четырёхэтажной дроби.
Затем перешли к общим схемам строения многоэтажных дробей ().
Ещё раз обратили внимание на то, что под буквами подразумеваются рациональные выражения, что при делении дроби
на дробь первая дробь является делимым, а вторая – делителем. В соответствующей многоэтажной дроби делимое
становится числителем, а делитель – знаменателем. В результате получается четырёхэтажная дробь (схема А, ).
Символ деления здесь заменяется
чертой, которую называют основной чертой дроби. Обратили внимание на значение и правило оформления основной черты дроби.
Далее обсудили схему В (),
выяснили, сколько этажей имеет данная дробь, что записано в числителе,
что в знаменателе, где расположена основная черта дроби. Схему С (), лицеисты
рассмотрели самостоятельно.
Схему С (), лицеисты
рассмотрели самостоятельно.
В примерах теста (), необходимо было найти выражения многоэтажными дробями. Выполнить задания теста, то есть для каждого выражения найти верный ответ, записанный в верхней строке, учащимся было предложено дома.
Алгоритм деления дроби на дробь
был рассмотрен на предыдущих уроках (а также алгоритмы умножения и сложения дробей).
Поэтому лицеисты уже знали, что стрелками обозначено действие умножение.
Поставив стрелки в первой записи, они без труда, видя окончательный результат,
расставили стрелки и во втором выражении.
После этого мы снова вернулись
к рисунку 2 и схеме В (), лицеистам был задан вопрос: «А всегда ли
надо (пусть даже мысленно) целое заменять дробью со знаменателем 1 ,
нельзя ли и здесь создать мини-алгоритм?» После обсуждения пришли к
правилу преобразования трёхэтажной дроби. В схеме С (), учащимся
было предложено самим попробовать восстановить стрелку у первого выражения. Лицеисты быстро справились с этим заданием.
Лицеисты быстро справились с этим заданием.
Затем перешли к практическим примерам 1 и 2 (), где необходимо было
заполнить пропуски, используя выработанный алгоритм (). Это задание не вызвало особых затруднений у учащихся.
Далее рассмотрели более сложные примеры: в числителе
или в знаменателе присутствует несколько множителей (). Сначала разобрали случай, когда в числителях верхней и нижней дробей встречаются общие множители.
Применив алгоритм работы с многоэтажными дробями, заметили, что общий множитель сокращается, если он присутствует в числителях обеих дробей. Случай, когда общий
множитель есть в знаменателях обеих дробей, учащиеся разобрали самостоятельно и сами сделали соответствующий вывод.
Выполнив преобразование многоэтажной дроби по алгоритму, лицеисты убедились, что в подобных случаях сокращать нельзя. В примере 3 (). необходимо было сначала сократить дробь,
а затем применить алгоритм преобразования многоэтажной дроби.
Учащиеся с большой заинтересованностью зачеркивали общие множители, рисовали стрелки и заполняли пропуски.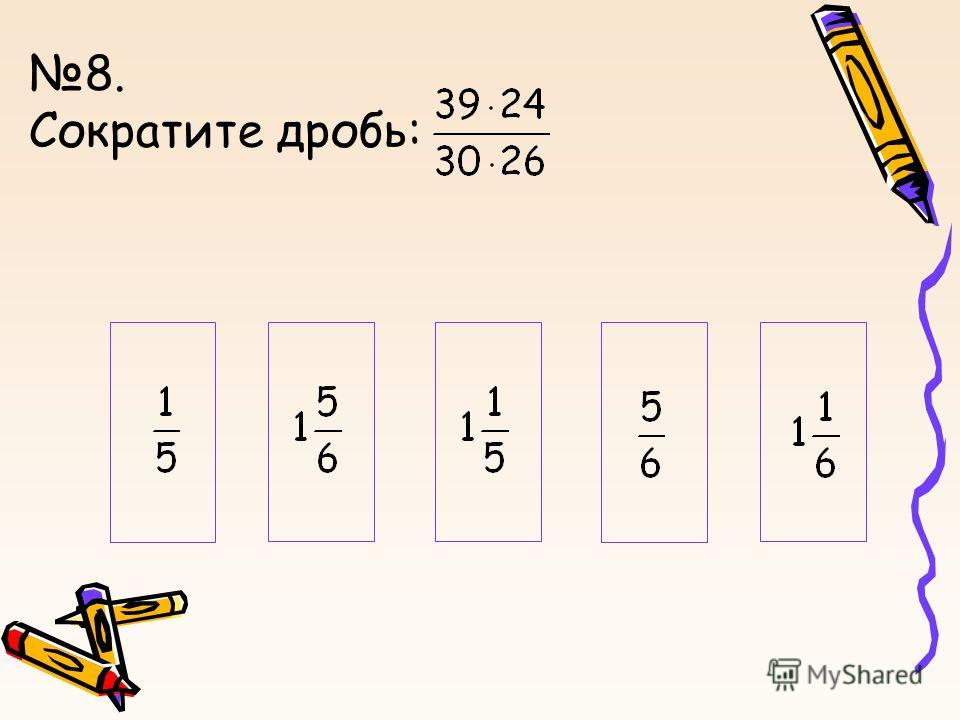
В четвертом задании лицеисты сразу же заметили общие
множители в числителях обеих дробей и формулу сокращённого умножения в знаменателе нижней дроби.
Разложив на множители и сократив знаменатели, а также числители, учащиеся довольно быстро получили верный результат. Задания 5, 6, 7 () лицеистам предлагалось выполнить дома.
Затем перешли к тождественным преобразованиям многоэтажных алгебраических дробей
. В примере 1 () предлагалось заполнить пропуски
в числителях дробей и затем записать окончательный результат. Многие учащиеся при сложении целого и дроби
применяли соответствующий алгоритм (ставили стрелки от m к 1 ). Данный пример не вызвал особых затруднений у лицеистов.
Задание «Посмотрите и найдите» № 2 () поначалу
испугало учащихся («значение такого сложного выражения надо найти устно?!»), но, после того, как преобразовали знаменатель первой многоэтажной дроби и увидели, что она равна 1 ,
вторую дробь сократили довольно быстро и верно. Результат вычислений записали в рамочку внизу примера.
Выполнение примера № 3 () заняло немного больше времени,
так как не все сразу заметили противоположные выражения, при сокращении которых получается –1 .
Упражнение 4 () начали выполнять после того, как прочитали комментарий. Лицеисты самостоятельно заполняли пропуски
в вычислениях, пользуясь алгоритмом. Затем все сверили свои результаты с решением этого примера, оформленным на обороте классной доски (). Те из учащихся, кто выполнил задание 4 быстрее других,
начали выполнять первые примеры упражнения 5 (), которое было задано на дом.
Для того чтобы выяснить, как усвоен алгоритм преобразования многоэтажной дроби в конце урока была проведена игра. Каждый ученик
получил листок с шуточными заданиями «Шторм на море» () и «Полицейские и воры» (). Учащиеся самостоятельно преобразовывали «многоэтажную дробь»:
сокращали (зачёркивали) общие множители, ставили стрелки и записывали получившийся результат в пустую рамочку. После выполнения всеми этого упражнения,
сверили получившиеся результаты с ответами, оформленными на обороте классной доски.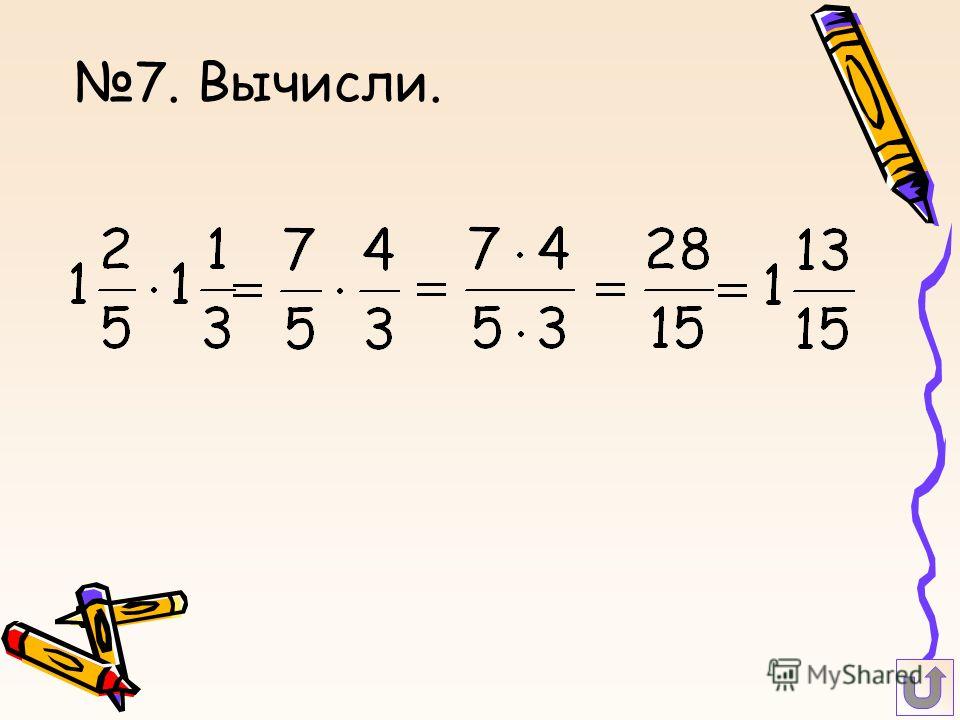 Одни учащиеся рисовали маяк, корабль, штурвал и якорь,
другие записывали только начальные буквы этих слов (). (На рисунках внизу: Ш – шериф,
П – полицейский, М – мошенница, К – карманник).
Все лицеисты без ошибок справились с этим необычным и интересным для них заданием.
Одни учащиеся рисовали маяк, корабль, штурвал и якорь,
другие записывали только начальные буквы этих слов (). (На рисунках внизу: Ш – шериф,
П – полицейский, М – мошенница, К – карманник).
Все лицеисты без ошибок справились с этим необычным и интересным для них заданием.
Работать с визуальными учебными материалами учащимся очень нравится,
так как на этих уроках они творят сами, не созерцают со стороны работу учителя и более сильных учащихся,
а принимают активное участие в решении той или иной учебной задачи и видят результаты своей работы тут же.
Подобные уроки проходят у детей эмоционально,
они чувствуют себя первооткрывателями, радуются своим успехам, стремятся выполнить как можно больше
разнообразных заданий, попробовать свои силы при решении довольно сложных упражнений.
Так как на таких уроках мало пишется, но много думается, то польза от них колоссальная.
Распечатать комплект визуальных дидактических материалов по теме данной статьи.
Предлагаемые комплекты дидактических материалов на экране отражаются не совсем точно,
но распечатываются рисунки прекрасно!
Литература
- Башмаков М.
 И. Многочлены и алгебраические дроби. Учебник алгебры для 7 кл.
Выпуск 1. Конструктор книги Резник Н. А. – СПб.: Изд-во ЦПО «Информатизация образования», 2000.
И. Многочлены и алгебраические дроби. Учебник алгебры для 7 кл.
Выпуск 1. Конструктор книги Резник Н. А. – СПб.: Изд-во ЦПО «Информатизация образования», 2000. - Башмаков М.И., Резник Н.А. Задачник по алгебре для 7 класса общеобразовательной школы. – СПб.: Изд-во ЦПО «Информатизация образования», 2001.
- Резник Н.А. Визуальные уроки. Компл. дидакт. матер. к шк. урокам. — СПб.: Свет, 1996.
Уважаемые коллеги!
Мы с благодарностью примем
ваши замечания и предложения.
Наталья Резник ([email protected]),
Наталия Ежова ([email protected])
Умножение и деление дробей.
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Эта операция гораздо приятнее сложения-вычитания ! Потому что проще. Напоминаю: чтобы умножить дробь на дробь, нужно перемножить числители (это будет числитель результата) и знаменатели (это будет знаменатель). То есть:
То есть:
Например:
Всё предельно просто . И, пожалуйста, не ищите общий знаменатель! Не надо его здесь…
Чтобы разделить дробь на дробь, нужно перевернуть вторую (это важно!) дробь и их перемножить, т.е.:
Например:
Если попалось умножение или деление с целыми числами и дробями — ничего страшного. Как и при сложении, делаем из целого числа дробь с единицей в знаменателе — и вперёд! Например:
В старших классах часто приходится иметь дело с трехэтажными (а то и четырехэтажными!) дробями. Например:
Как эту дробь привести к приличному виду? Да очень просто! Использовать деление через две точки:
Но не забывайте о порядке деления! В отличие от умножения, здесь это очень важно! Конечно, 4:2, или 2:4 мы не спутаем. А вот в трёхэтажной дроби легко ошибиться. Обратите внимание, например:
В первом случае (выражение слева):
Во втором (выражение справа):
Чувствуете разницу? 4 и 1/9!
А чем задается порядок деления? Или скобками, или (как здесь) длиной горизонтальных черточек. Развивайте глазомер. А если нет ни скобок, ни черточек, типа:
Развивайте глазомер. А если нет ни скобок, ни черточек, типа:
то делим-умножаем по порядочку, слева направо !
И еще очень простой и важный приём. В действиях со степенями он вам ох как пригодится! Поделим единицу на любую дробь, например, на 13/15:
Дробь перевернулась! И так бывает всегда. При делении 1 на любую дробь, в результате получаем ту же дробь, только перевернутую.
Вот и все действия с дробями. Вещь достаточно простая, но ошибок даёт более, чем достаточно. Примите к сведению практические советы, и их (ошибок) будет меньше!
Практические советы:
1. Самое главное при работе с дробными выражениями — аккуратность и внимательность! Это не общие слова, не благие пожелания! Это суровая необходимость! Все вычисления на ЕГЭ делайте как полноценное задание, сосредоточенно и чётко. Лучше написать две лишние строчки в черновике, чем накосячить при расчёте в уме.
2. В примерах с разными видами дробей — переходим к обыкновенным дробям.
3. Все дроби сокращаем до упора.
4. Многоэтажные дробные выражения сводим к обыкновенным, используя деление через две точки (следим за порядком деления!).
5. Единицу на дробь делим в уме, просто переворачивая дробь.
Вот вам задания, которые нужно обязательно прорешать. Ответы даны после всех заданий. Используйте материалы этой темы и практические советы. Прикиньте, сколько примеров вы смогли решить правильно. С первого раза! Без калькулятора! И сделайте верные выводы…
Помните – правильный ответ, полученный со второго (тем более – третьего) раза – не считается! Такова суровая жизнь.
Итак, решаем в режиме экзамена ! Это уже подготовка к ЕГЭ, между прочим. Решаем пример, проверяем, решаем следующий. Решили все — проверили снова с первого по последний. И только потом смотрим ответы.
Вычислить:
Порешали?
Ищем ответы, которые совпадают с вашими. Я специально их в беспорядке записал, подальше от соблазна, так сказать.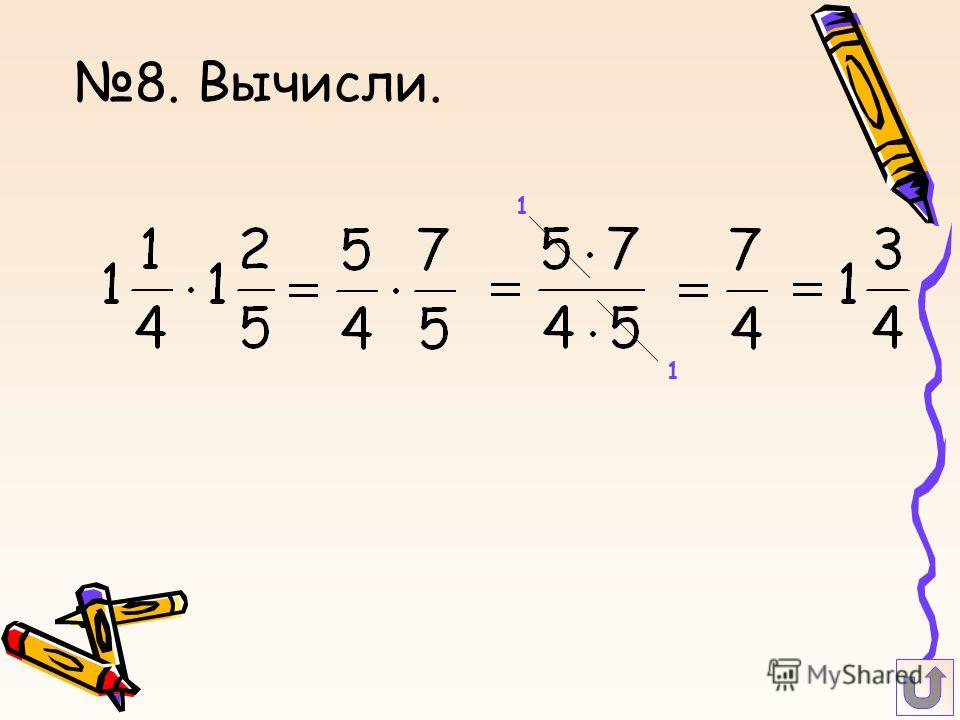 .. Вот они, ответы, через точку с запятой записаны.
.. Вот они, ответы, через точку с запятой записаны.
0; 17/22; 3/4; 2/5; 1; 25.
А теперь делаем выводы. Если всё получилось — рад за вас! Элементарные вычисления с дробями — не ваша проблема! Можно заняться более серьёзными вещами. Если нет…
Значит, у вас одна из двух проблем. Или обе сразу.) Нехватка знаний и (или) невнимательность. Но… Это решаемые проблемы.
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
в Северном русском народном хоре проводят мастер-классы по хореографии — Двина 29
Это продолжение серии интерактивных программ в рамках социально-культурного проекта министерства культуры Архангельской области «Культурный саквояж».
Хотя проект «Дроби, дроби бей!» рассчитан на людей старшего возраста, на мастер-класс в Архангельске собрались участники самодеятельных творческих коллективов и любители народного танца всех возрастов.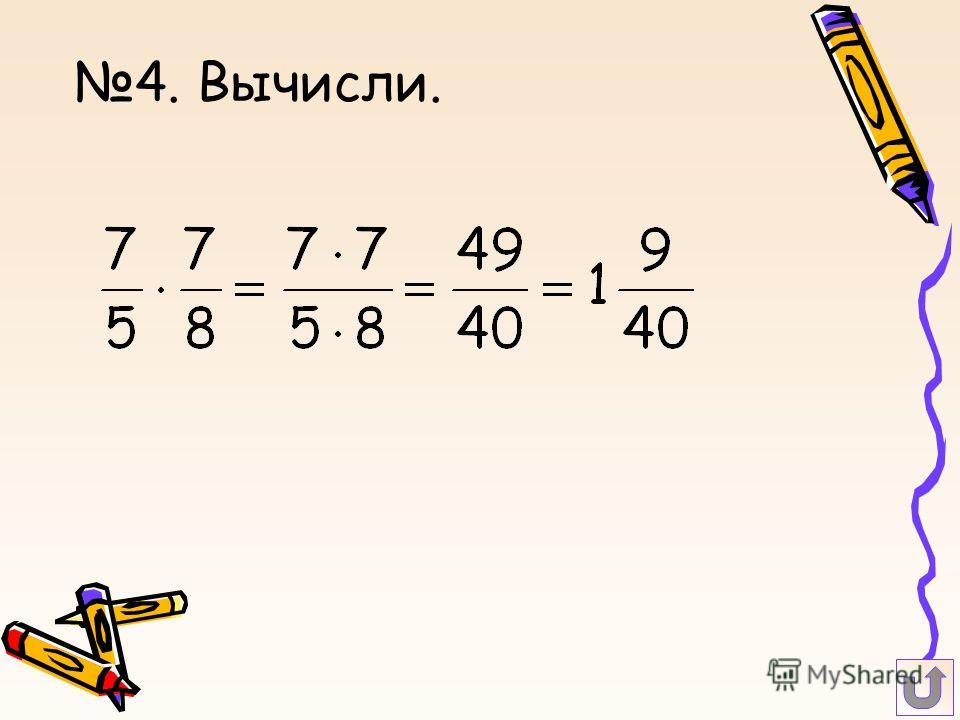
На занятии они постигали азы всего лишь одного из многочисленных элементов русской народной хореографии – дроби. Секретами профессионального мастерства делился главный балетмейстер Государственного академического Северного русского народного хора Александр Селиванов.
Оказалось, что правильно бить дроби – совсем не просто. В танце даже шагать надо по-особенному. Северная красавица идет – словно лебедь плывет, не шелохнется. При этом на девице может быть не один, а несколько сарафанов. Вес такого наряда достигает нескольких килограммов.
– Как бы красиво ни была одета девушка, она должна уметь правильно ходить, чтобы обратить на себя внимание в хороводе: красиво, ровно, с достоинством, держа корпус и стать. Чтобы этого добиться, нужно вес тела перенести на полупальцы и с этим ощущением полета нести себя вперед, – пояснил Александр Селиванов.
Искусство выбивания дроби состоит всего из трех основных движений: шаг, удар и перескок. Из этих простых элементов создается бесконечное многообразие русского народного танца. Комбинации шагов, ударов, двойных ударов рождают неповторимый индивидуальный рисунок танца, у каждого исполнителя свой.
Комбинации шагов, ударов, двойных ударов рождают неповторимый индивидуальный рисунок танца, у каждого исполнителя свой.
– Сложность танца не в количестве движений, а в их вариациях. Идут танцоры по кругу, и вдруг один сделал в какой-то момент вместо шага удар – дробь становится неповторимой. Это творчество танцора, его живая импровизация. Так постепенно он находит для себя какое-то решение, а затем пять-восемь решений соединяет в комбинацию, и эта комбинация становится индивидуальной, ее невозможно повторить, – рассказал Александр Селиванов. – Рисунки северных хороводов повторяют узоры народных росписей. В танце при помощи хороводных движений, шагов, может быть, даже каких-то дробных комбинаций мы рисуем эти узоры.
Народный танец – основа основ
Участники мастер-класса изучали дроби с большим интересом. Многие пришли уже подготовленными, несколько лет занимаясь в творческих коллективах. Русская песня неотделима от танца. Петь и плясать, водить хороводы наши предки умели с детства, нам же приходится учиться с азов, как азбуку постигать искусство северной кадрили.
Галина Семушина десять лет пела в «Радеюшке» и уже шесть лет занимается в хоре ветеранов «Поморочка»: «Мне очень интересно научиться правильно плясать кадриль. Я бесконечно люблю наши северные танцы. Они дают такой заряд настроения, хорошей энергии. Хватает на всю неделю до следующего занятия».
Участницы хореографического коллектива «Каблучок» филиала «Космос» при МУК «Луч» раньше бывали только на концертах Северного хора, на мастер-класс пришли впервые.
– Очень хотелось бы продолжения, закрепить. Мы серьезно относимся к изучению народного танца. Занимаемся для души, чтобы осуществить все то, что не могли осилить, когда работали, – рассказала участница коллектива Светлана Поспелова.
Воспитанники коллектива «Золотая стрекоза» ДК АО «Быт» в полном составе приехали на мастер-класс из Новодвинска. Народный танец – не их профиль, девочки занимаются эстрадным и современным танцем, но педагоги посчитали, что окунуться в атмосферу народной хореографии будет полезным.
– Для нас на мастер-классе многое было открытием.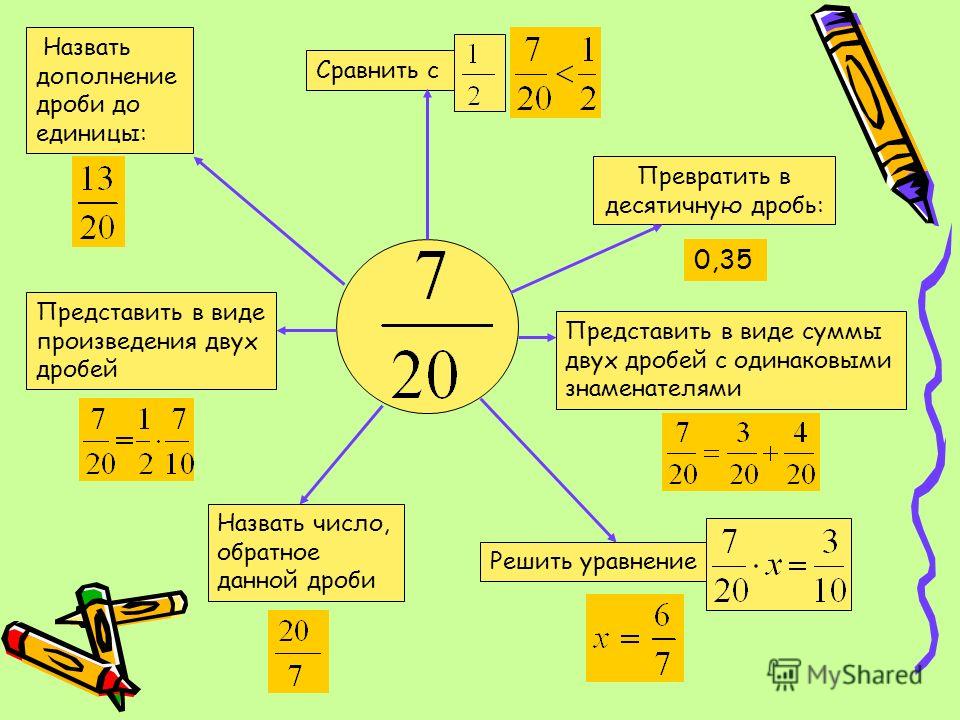 Мы детей окунули в ту атмосферу, которой они никогда не касались, и они были под большим впечатлением. Конечно, они видят народный танец. И они под большим впечатлением! Мы живем в России, и надо знать свою традицию, ведь вся современная хореография вышла из народного танца. Это наши истоки, – считает заместитель директора по творческой работе Дворца культуры Галина Маркова.
Мы детей окунули в ту атмосферу, которой они никогда не касались, и они были под большим впечатлением. Конечно, они видят народный танец. И они под большим впечатлением! Мы живем в России, и надо знать свою традицию, ведь вся современная хореография вышла из народного танца. Это наши истоки, – считает заместитель директора по творческой работе Дворца культуры Галина Маркова.
По мнению главного балетмейстера Северного русского народного хора Александра Селиванова, участницы мастер-класса с программой справились на отлично.
– Вначале было тяжело, но все получилось. Главное – понять структуру, очередность ударов. Если человек слышит музыку, понимает ритм, и если музыка играется с азартом, в этот ритм невозможно не попасть. Я сегодня это наблюдал. Народный танец незаменим. Во все периоды были разные пути хореографического развития: модерн и постмодерн, контемпорари, в хип-хопе множество разных направлений, но народный танец всегда шел по своему пути. Человек, который любит русскую культуру, попробует то или иное направление и все равно вернется к народному танцу. Ему это будет необходимо. Ну а танцевать для себя никогда не поздно.
Ему это будет необходимо. Ну а танцевать для себя никогда не поздно.
О проекте «Культурный саквояж»
В рамках проекта министерства культуры Архангельской области «Культурный саквояж» люди старше 60 лет могут посетить мероприятия учреждений культуры Архангельской области по льготной цене. В рамках проекта в Северном русском народном хоре разработано и уже реализуется четыре концертных программы «Порато баско» о народном костюме, «Споемте, друзья» об особенностях народного вокала, музыкальные инструменты и «Дроби, дроби бей!» об основах народного танца.
Надежда Лебедева
ИА DVINA29
25 марта 2022 в 07:45Главное за неделю
Острые эффекты экструдированных фракций гороха на гликемический ответ, инсулин, аппетит и прием пищи у здоровых молодых людей, результаты двойного слепого рандомизированного перекрестного исследования
Рандомизированное контролируемое исследование
. 2021 сен;46(9):1126-1132.
2021 сен;46(9):1126-1132.
doi: 10.1139/apnm-2020-0571. Epub 2021 4 марта.
Эли Джей Джонстон 1 , Ребекка С Моллард 1 , Дайанна Дандено 1 , Дилан С. Маккей 2 , Нэнси Эймс 3 , Джулианна Карран 4 , Даниэль Р Бушар 5 , Питер Дж. Джонс 6
Принадлежности
- 1 Департамент наук о пищевых продуктах и питании человека, Университет Манитобы, МБ, Канада.
- 2 Департамент общественных наук о здоровье, Университет Манитобы, МБ, Канада.

- 3 Министерство сельского хозяйства и продовольствия Канады, Правительство Канады.
- 4 Pulse Canada, 920-220 Portage Ave., Winnipeg, MB R3C 0A5, Канада.
- 5 Факультет кинезиологии, Университет Нью-Брансуика, Нью-Брансуик, Канада.
- 6 Основы питания для здоровья (NFH), Vaudreuil-Dorion, QC, Канада.
- PMID: 33661714
- DOI: 10.1139/апнм-2020-0571
Рандомизированное контролируемое исследование
Alie J Johnston et al. Appl Physiol Nutr Metab.
2021 Сентябрь
Appl Physiol Nutr Metab.
2021 Сентябрь
. 2021 сен;46(9):1126-1132.
doi: 10.1139/apnm-2020-0571. Epub 2021 4 марта.
Авторы
Али Дж. Джонстон 1 , Ребекка С Моллард 1 , Дайанна Дандено 1 , Дилан С. Маккей 2 , Нэнси Эймс 3 , Джулианна Карран 4 , Даниэль Р Бушар 5 , Питер Дж. Джонс 6
Принадлежности
- 1 Департамент наук о пищевых продуктах и питании человека, Университет Манитобы, МБ, Канада.

- 2 Департамент общественных наук о здоровье, Университет Манитобы, МБ, Канада.
- 3 Министерство сельского хозяйства и продовольствия Канады, Правительство Канады.
- 4 Pulse Canada, 920-220 Portage Ave., Winnipeg, MB R3C 0A5, Канада.
- 5 Факультет кинезиологии, Университет Нью-Брансуика, Нью-Брансуик, Канада.
- 6 Основы питания для здоровья (NFH), Vaudreuil-Dorion, QC, Канада.
- PMID: 33661714
- DOI:
10.
 1139/апнм-2020-0571
1139/апнм-2020-0571
Абстрактный
Преимущества потребления бобовых в гликемическом контроле хорошо известны; однако исследования, изучающие влияние фракций бобовых, включенных в экструдированные продукты, ограничены. В рандомизированном перекрестном исследовании с повторными измерениями взрослые ( n = 26) потребляли каши, приготовленные из овсяной муки (контроль), овсяной муки и горохового крахмала (крахмал), овсяной муки и горохового белка (белок), овсяной муки, гороха. крахмал и гороховый белок (крахмал+белок), овсяная мука, гороховое волокно и гороховый белок (волокно+белок) и гороховое волокно, гороховый крахмал и гороховый белок (волокно+крахмал+белок). Концентрации глюкозы в крови (BG) и инсулина, а также площадь прироста аппетита под кривой (iAUC) рассчитывали до (0-120 мин) и после (120-200 мин) приема пищи ad libitum для измерения потребления пищи. Перед едой общее среднее значение BG и iAUC были ниже после каш с белком, крахмалом+белком, белком+клетчаткой и волокном+крахмалом+белком по сравнению с крахмалом и контролем. Что касается общих средних концентраций инсулина перед едой, то сочетание клетчатки и белка приводило к более низкому ответу по сравнению с контролем, крахмалом и белком и зерновыми с белком. Клетчатка+крахмал+белок также приводили к снижению инсулина по сравнению с белковыми злаками. IAUC инсулина перед едой была ниже после приема клетчатки + белка по сравнению с контролем и белковыми злаками. Включение белка желтого гороха и клетчатки в овсяные хлопья для завтрака снижает постпрандиальную гликемию; однако этот эффект зависит от типа фракции. ClinicalTrials.gov: NCT02366572. Новинка: Включение бобовых белков и клетчатки в сухие завтраки на основе овсяной муки снижает постпрандиальную реакцию глюкозы. Гликемические преимущества целых бобовых, по крайней мере, в некоторой степени сохраняются в некоторых фракциях бобовых.
Что касается общих средних концентраций инсулина перед едой, то сочетание клетчатки и белка приводило к более низкому ответу по сравнению с контролем, крахмалом и белком и зерновыми с белком. Клетчатка+крахмал+белок также приводили к снижению инсулина по сравнению с белковыми злаками. IAUC инсулина перед едой была ниже после приема клетчатки + белка по сравнению с контролем и белковыми злаками. Включение белка желтого гороха и клетчатки в овсяные хлопья для завтрака снижает постпрандиальную гликемию; однако этот эффект зависит от типа фракции. ClinicalTrials.gov: NCT02366572. Новинка: Включение бобовых белков и клетчатки в сухие завтраки на основе овсяной муки снижает постпрандиальную реакцию глюкозы. Гликемические преимущества целых бобовых, по крайней мере, в некоторой степени сохраняются в некоторых фракциях бобовых.
Ключевые слова: амидон; аппетит; аппетит; глюкоза крови; волокно; волокна; гликемия; гликемия; инсулин; инсулин; бобовые; горох; поис; постпрандиальный; белок; белки; импульсы; крахмал.
Похожие статьи
Острые эффекты экструдированных бобовых закусок на гликемический ответ, инсулин, аппетит и потребление пищи у здоровых молодых людей в двойном слепом рандомизированном перекрестном исследовании.
Джонстон А.Дж., Моллард Р.К., Дандено Д., Маккей Д.С., Эймс Н., Карран Дж., Бушар Д.Р., Джонс П.Дж. Джонстон А.Дж. и соавт. Appl Physiol Nutr Metab. 2021 июль; 46 (7): 704-710. doi: 10.1139/apnm-2020-0572. Epub 2020 21 декабря. Appl Physiol Nutr Metab. 2021. PMID: 33347383 Клиническое испытание.
Острое воздействие горохового белка и клетчатки шелухи по отдельности и в сочетании на уровень глюкозы в крови, аппетит и потребление пищи у здоровых молодых мужчин — рандомизированное перекрестное исследование.

Моллард Р.С., Луховой Б.Л., Смит С., Андерсон Г.Х. Моллард Р.С. и др. Appl Physiol Nutr Metab. 2014 дек;39(12):1360-5. doi: 10.1139/apnm-2014-0170. Epub 2014 2 августа. Appl Physiol Nutr Metab. 2014. PMID: 25302637 Клиническое испытание.
Обогащенный хлеб на основе злаков влияет на рейтинги аппетита и гликемические, инсулинемические и желудочно-кишечные гормональные реакции у здоровых взрослых в рандомизированном контролируемом исследовании.
Гонсалес-Антон С., Лопес-Миллан Б., Рико М.С., Санчес-Родригес Э., Руис-Лопес М.Д., Гил А., Меса М.Д. Гонсалес-Антон С. и др. Дж Нутр. 2015 февраль; 145 (2): 231-8. doi: 10.3945/jn.114.200386. Epub 2014 10 декабря. Дж Нутр. 2015. PMID: 25644342 Клиническое испытание.
Влияние кисломолочных и немолочных продуктов, добавленных к хлопьям для завтрака, на контроль уровня глюкозы в крови, чувство сытости, насыщение и кратковременный прием пищи у молодых женщин.

Мазер К., Боачи Р., Анини Ю., Панахи С., Андерсон Г.Х., Луховой Б.Л. Мазер К. и др. Appl Physiol Nutr Metab. 2020 окт;45(10):1118-1126. doi: 10.1139/apnm-2019-0772. Epub 2020 15 апр. Appl Physiol Nutr Metab. 2020. PMID: 32294394 Клиническое испытание.
Влияние белков риса, гороха и овса на ослабление гликемической реакции подслащенных сахаром напитков.
Tan SY, Siow PC, Peh E, Henry CJ. Тан С.И. и соавт. Евр Дж Нутр. 2018 декабрь; 57 (8): 2795-2803. doi: 10.1007/s00394-017-1547-3. Epub 2017 30 сентября. Евр Дж Нутр. 2018. PMID: 28965176 Клиническое испытание.
Посмотреть все похожие статьи
Типы публикаций
термины MeSH
вещества
Проблемы и ограничения — Документация по Python 3.
 10.7
10.7Числа с плавающей запятой представлены в аппаратном обеспечении компьютера как основание 2 (двоичное) дроби. Например, десятичная дробь
имеет значение 1/10 + 2/100 + 5/1000, и точно так же двоичная дробь
имеет значение 0/2 + 0/4 + 1/8. Эти две дроби имеют одинаковые значения, единственное реальная разница в том, что первый записан в дробной системе счисления по основанию 10, а второй в базе 2.
К сожалению, большинство десятичных дробей не могут быть точно представлены в двоичном виде. дроби. Следствием этого является то, что, как правило, десятичное число с плавающей запятой числа, которые вы вводите, только аппроксимируются двоичными числами с плавающей запятой фактически хранится в машине.
Задачу легче понять сначала в десятичной системе счисления. Рассмотрим дробь 1/3. Вы можете аппроксимировать это как десятичную дробь:
.или лучше
или лучше
и так далее. Независимо от того, сколько цифр вы готовы записать, результат
никогда не будет ровно 1/3, но будет все более и более лучшим приближением к
1/3.
Таким же образом, независимо от того, сколько цифр с основанием 2 вы хотите использовать, десятичное значение 0,1 не может быть представлено точно как дробь с основанием 2. В базе 2, 1/10 — бесконечно повторяющаяся дробь
0.0001100110011001100110011001100110011001100110011...
Остановитесь на любом конечном числе битов, и вы получите приближение. На большинстве
современных машинах числа с плавающей запятой аппроксимируются с помощью двоичной дроби с
числитель, использующий первые 53 бита, начиная со старшего бита и
со знаменателем как степень двойки. В случае 1/10 двоичная дробь
это 3602879701896397/2 ** 55 , что близко, но не совсем
равно истинному значению 1/10.
Многие пользователи не знают об аппроксимации из-за того, как значения
отображается. Python печатает только десятичное приближение к истинному десятичному
значение двоичной аппроксимации, сохраненное машиной. На большинстве машин, если
Python должен был печатать истинное десятичное значение сохраненного двоичного приближения.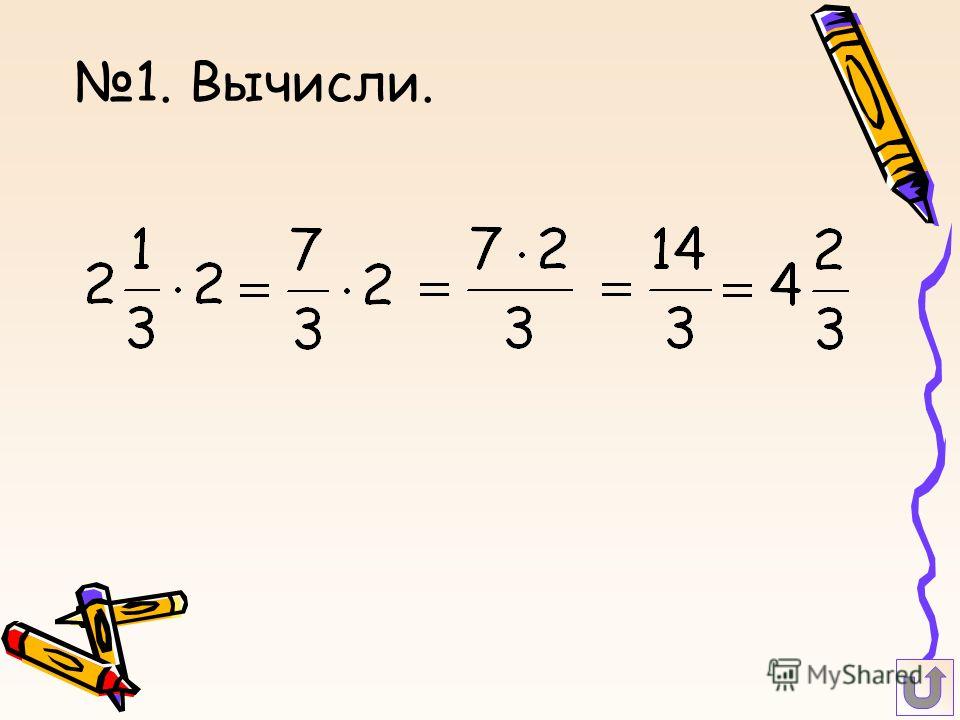 для 0.1 он должен отображать
для 0.1 он должен отображать
>>> 0,1 0,1000000000000000055511151231257827021181583404541015625
Это больше цифр, чем большинство людей считает нужным, поэтому Python сохраняет это число. цифр, управляемых отображением округленного значения вместо
>>> 1 / 10 0,1
Просто помните, даже если напечатанный результат выглядит как точное значение 1/10 фактическое сохраненное значение является ближайшей представимой двоичной дробью.
Интересно, что есть много разных десятичных чисел, которые имеют одинаковые
ближайшая приближенная двоичная дробь. Например, числа 0,1 и 0,10000000000000001 и 0.1000000000000000055511151231257827021181583404541015625 все
округляется на 3602879701896397/2**55 . Поскольку все эти десятичные
значения имеют одинаковое приближение, любое из них может быть отображено
сохраняя при этом инвариант eval(repr(x)) == x .
Исторически, приглашение Python и встроенная функция repr() выбирали
тот, у которого 17 значащих цифр, 0. . Начиная с
Python 3.1, Python (в большинстве систем) теперь может выбирать самый короткий из
эти и просто отображать 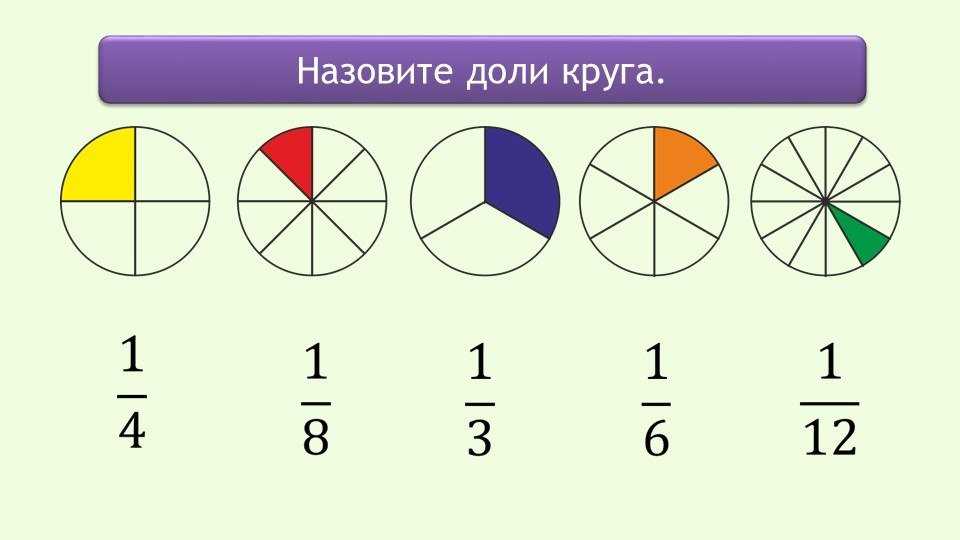 10000000000000001
10000000000000001 0,1 .
Обратите внимание, что это заложено в самой природе двоичных чисел с плавающей запятой: это не ошибка. в Python, и это также не ошибка в вашем коде. Вы увидите такой же вещь на всех языках, которые поддерживают арифметику с плавающей запятой вашего оборудования (хотя некоторые языки могут не отображать разницу по умолчанию или во всех режимы вывода).
Для более приятного вывода вы можете использовать форматирование строки для получения ограниченного количества значащих цифр:
>>> format(math.pi, '.12g') # дать 12 значащих цифр '3.14159265359' >>> format(math.pi, '.2f') # указать 2 цифры после точки «3.14» >>> repr(math.pi) '3.141592653589793'
Важно понимать, что это в действительности иллюзия: вы просто округляя , отображаем истинного машинного значения.
Одна иллюзия может породить другую. Например, поскольку 0,1 не совсем 1/10,
суммирование трех значений 0,1 также может не дать ровно 0,3:
Например, поскольку 0,1 не совсем 1/10,
суммирование трех значений 0,1 также может не дать ровно 0,3:
>>> .1 + .1 + .1 == .3 ЛОЖЬ
Кроме того, поскольку 0,1 не может приблизиться к точному значению 1/10 и
0,3 не может приблизиться к точному значению 3/10, тогда предварительное округление с Функция round() не может помочь:
>>> раунд(.1, 1) + раунд(.1, 1) + раунд(.1, 1) == раунд(.3, 1) ЛОЖЬ
Хотя числа нельзя приблизить к их предполагаемым точным значениям,
функция round() может быть полезна для последующего округления, чтобы результаты
с неточными значениями становятся сравнимыми друг с другом:
>>> раунд(.1 + .1 + .1, 10) == раунд(.3, 10) Истинный
Двоичная арифметика с плавающей запятой таит в себе много подобных сюрпризов. Проблема
с «0,1» подробно объясняется ниже, в разделе «Ошибка представления».
раздел. См. Опасности с плавающей запятой
для более полного описания других распространенных сюрпризов.
Как сказано в конце, «простых ответов не бывает». Тем не менее, не будьте чрезмерно опасайтесь чисел с плавающей запятой! Ошибки в операциях Python с плавающей запятой наследуются от оборудования с плавающей запятой, и на большинстве машин порядка нет более 1 части в 2**53 за операцию. Этого более чем достаточно для большинства задачи, но нужно иметь в виду, что это не десятичная арифметика и что каждая операция с плавающей запятой может привести к новой ошибке округления.
Несмотря на то, что патологические случаи существуют, для наиболее случайного использования операций с плавающей запятой
арифметики вы увидите результат, который вы ожидаете в конце, если вы просто округлите
отображение ваших окончательных результатов до ожидаемого количества десятичных цифр.
Обычно достаточно str() , а для более точного управления см. str.format() спецификаторы формата метода в синтаксисе строки формата.
Для случаев использования, требующих точного десятичного представления, попробуйте использовать decimal Модуль , который реализует десятичную арифметику, подходящую для
бухгалтерские приложения и высокоточные приложения.
Другая форма точной арифметики поддерживается модулем дробей .
который реализует арифметику, основанную на рациональных числах (такие числа, как
1/3 можно представить точно).
Если вы интенсивно используете операции с плавающей запятой, вам следует взглянуть
в пакете NumPy и многих других пакетах для математических и
статистические операции, предоставляемые проектом SciPy. См.
Python предоставляет инструменты, которые могут помочь в тех редких случаях, когда вы действительно do хотите узнать точное значение числа с плавающей запятой. метод float.as_integer_ratio() выражает значение числа с плавающей запятой как
дробь:
>>> х = 3,14159 >>> x.as_integer_ratio() (3537115888337719, 11258992624)
Поскольку соотношение является точным, его можно использовать для воссоздания без потерь исходное значение:
>>> х == 3537115888337719 / 11258992624 Истинный
Метод float. выражает число с плавающей запятой в шестнадцатеричном (базовое
16), снова давая точное значение, сохраненное вашим компьютером: hex()
hex()
>>> x.hex() '0x1.921f9f01b866ep+1'
Это точное шестнадцатеричное представление может быть использовано для восстановления значение с плавающей запятой точно:
>>> x == float.fromhex('0x1.921f9f01b866ep+1')
Истинный
Поскольку представление точное, оно полезно для надежного переноса значений между различными версиями Python (независимость от платформы) и обмен данные с другими языками, которые поддерживают тот же формат (например, Java и C99).
Еще один полезный инструмент — Функция math.fsum() , которая помогает смягчить
потеря точности при суммировании. Он отслеживает «потерянные цифры» по мере того, как значения
добавляется к нарастающей сумме. Это может повлиять на общую точность
чтобы ошибки не накапливались до такой степени, что они влияют на
окончательный итог:
>>> сумма([0.1] * 10) == 1.0 ЛОЖЬ >>> math.fsum([0.1] * 10) == 1.0 Истинный
В этом разделе подробно объясняется пример «0.1» и показано, как можно выполнить точный анализ подобных случаев самостоятельно. Базовое знакомство с бинарником предполагается представление с плавающей запятой.
Ошибка представления относится к тому факту, что некоторые (фактически большинство) десятичные дроби не могут быть представлены точно как двоичные дроби (с основанием 2). Это главная причина, по которой Python (или Perl, C, C++, Java, Fortran и многие другие) другие) часто не будет отображать точное десятичное число, которое вы ожидаете.
Почему? 1/10 нельзя точно представить в виде двоичной дроби. Почти все
машины сегодня (ноябрь 2000 г.) используют арифметику с плавающей запятой IEEE-754, и
почти все платформы отображают Python с плавающей запятой в соответствии с IEEE-754 «двойной точностью». 754
числа double содержат 53 бита точности, поэтому при вводе компьютер стремится
преобразовать 0,1 в ближайшую дробь, которую он может иметь в форме J /2** N , где J целое число, содержащее ровно 53 бита. Переписывание
Переписывание
1/10 ~= Дж/(2**Н)
как
Дж ~= 2**Н/10
и вспоминая, что J имеет ровно 53 бита ( >= 2**52 , но < 2**53 ),
лучшее значение для N 56:
>>> 2**52 <= 2**56 // 10 < 2**53 Истинный
То есть 56 — единственное значение для N , которое оставляет J ровно с 53 битами. наилучшее возможное значение для J - это округленное частное:
>>> q, r = divmod(2**56, 10) >>> г 6
Поскольку остаток больше половины от 10, получается наилучшее приближение округляя:
>>> д+1 7205759403792794
Следовательно, наилучшее возможное приближение к 1/10 в 754 с двойной точностью:
7205759403792794/2**56
Деление числителя и знаменателя на два уменьшает дробь до:
3602879701896397/2**55
Обратите внимание, что, поскольку мы округлили, на самом деле это немного больше, чем 1/10;
если бы мы не округляли, то частное было бы немного меньше, чем
1/10. Но ни в коем случае не может быть именно 1/10!
Но ни в коем случае не может быть именно 1/10!
Таким образом, компьютер никогда не «видит» 1/10: он видит точную заданную дробь. выше, лучшее 754 двойное приближение, которое он может получить:
>>> 0,1 * 2 ** 55 3602879701896397.0
Если мы умножим эту дробь на 10**55, мы увидим значение, равное 55 десятичных цифр:
>>> 3602879701896397 * 10 ** 55 // 2 ** 55 1000000000000000055511151231257827021181583404541015625
означает, что точное число, хранящееся в компьютере, равно десятичное значение 0,1000000000000000055511151231257827021181583404541015625. Вместо отображения полного десятичного значения многие языки (включая более старые версии Python), округлить результат до 17 значащих цифр:
>>> формат (0.1, '.17f') «0,10000000000000001»
дроби и десятичные модули делают эти расчеты
легко:
>>> из десятичного импорта Decimal >>> из дробей импорт дроби >>> Дробь.from_float(0.1) Дробь(3602879701896397, 36028797018963968) >>> (0.1).as_integer_ratio() (3602879701896397, 36028797018963968) >>> Десятичный.from_float(0.1) Десятичный('0.1000000000000000055511151231257827021181583404541015625') >>> формат(десятичный.from_float(0.1), '.17') «0,10000000000000001»
Двоичные дроби и числа с плавающей запятой
Двоичные дроби и числа с плавающей запятой!
Вполовину неплохо.
Введение
До сих пор мы имели дело с целыми числами. Распространить это на дроби не так уж сложно, поскольку на самом деле мы просто используем те же механизмы, с которыми мы уже знакомы. Двоичные дроби вводят некоторые интересные особенности, как мы увидим ниже.
В этом разделе мы начнем с рассмотрения того, как мы представляем дроби в двоичном формате. Затем мы рассмотрим двоичную плавающую точку, которая является средством представления чисел, позволяющим нам представлять как очень маленькие дроби, так и очень большие целые числа. Это значение по умолчанию, которое компьютеры используют для работы с этими типами чисел, и фактически официально определено IEEE. Он известен как IEEE 754.
Это значение по умолчанию, которое компьютеры используют для работы с этими типами чисел, и фактически официально определено IEEE. Он известен как IEEE 754.
Двоичные дроби
Двоичные числа — это позиционная система счисления. Это также система счисления с основанием . Чтобы освежить в памяти это, прочитайте наше Введение в системы счисления. Когда мы перемещаем позицию (или цифру) влево, степень, на которую мы умножаем основание (2 в двоичном формате), увеличивается на 1. Когда мы двигаемся вправо, мы уменьшаемся на 1 (в отрицательные числа).
Таким образом, в десятичном виде число 56,482 на самом деле переводится как:
| 5 * 10 1 | 50 |
| 6 * 10 0 | 6 |
| 4 * 10 -1 | 4/10 |
| 8 * 10 -2 | 8/100 |
| 2 * 10 -3 | 2/1000 |
В двоичном формате это тот же процесс, но вместо этого мы используем степень двойки.
Таким образом, в двоичном формате число 101.101 переводится как:
| 1 * 2 2 | 4 |
| 0 * 2 1 | 0 |
| 1 * 2 0 | 1 |
| 1 * 2 -1 | 1/2 |
| 0 * 2 -2 | 0 |
| 1 * 2 -3 | 1/8 |
В десятичном формате это довольно просто, так как мы перемещаем каждую позицию в дроби вправо, мы добавляем 0 в знаменатель. В двоичном формате мы удваиваем знаменатель.
По мере продвижения знаменатель удваивается, поэтому мы получаем следующие значения знаменателя:
| 2 -1 | 1/2 |
| 2 -2 | 1/4 |
| 2 -3 | 1/8 |
| 2 -4 | 1/16 |
| 2 -5 | 1/32 |
| 2 -6 | 1/64 |
и так далее.
Преобразование двоичной дроби в десятичную дробь — это просто вопрос сложения соответствующих значений для каждого бита, который представляет собой 1 .
Дроби, которые мы не можем представить
В десятичной системе есть различные дроби, которые мы не можем точно представить. 1/3 является одним из них. Мы можем подойти очень близко (например, 0,3333333333), но мы никогда не сможем точно представить значение. То же самое и с двоичными дробями, однако количество значений, которые мы можем не точно представить, на самом деле больше. Обычно это не проблема, потому что мы можем представлять значение в достаточном количестве двоичных разрядов, чтобы оно было достаточно близким для практических целей. Мы вернемся к этому, когда рассмотрим преобразование в двоичные дроби ниже.
Двоичная точка
До сих пор мы представляли наши двоичные дроби с помощью двоичной точки. Это нормально, когда мы работаем с вещами в обычном режиме, но в компьютере это невозможно, поскольку он может работать только с 0 и 1 . Мы обходим это, соглашаясь, где должна быть двоичная точка.
Мы обходим это, соглашаясь, где должна быть двоичная точка.
Так, например, если мы работаем с 8-битными числами, можно договориться, что двоичная точка будет располагаться между 4-м и 5-м битами. 9Тогда предполагается, что 0003
01101001 на самом деле представляет 0110.1001
Преобразование десятичной дроби в двоичную
Многие операции при работе с двоичными числами сводятся к простому запоминанию и применению простого набора шагов. Преобразование десятичных дробей в двоичные ничем не отличается.
Самый простой подход — это метод, при котором мы многократно умножаем дробь на 2 и записываем, является ли цифра слева от десятичной точки 0 или 1 (т. е. если результат больше 1), а затем отбрасываем 1, если Это. Как только вы закончите, вы читаете значение сверху вниз. Давайте посмотрим на некоторые примеры. Этот пример заканчивается через 8 бит справа от двоичной точки, но вы можете продолжать так долго, как хотите. (или пока вы не получите 0 в своем множителе или повторяющемся наборе битов).
0.
Результат в двоичном формате:
С плавающей запятой
Ранее мы рассмотрели так называемые двоичные дроби с фиксированной точкой. Это удобный способ представления чисел, но как только число, которое мы хотим представить, становится очень большим или очень маленьким, мы обнаруживаем, что для его представления требуется очень большое количество битов. Если мы хотим представить десятичное значение 128, нам потребуется 8 двоичных цифр (10000000). Это более чем в два раза превышает количество цифр для представления одного и того же значения. Это только ухудшается по мере того, как мы удаляемся от нуля.
Чтобы обойти это, мы используем метод представления чисел, называемый с плавающей запятой . Плавающая точка очень похожа на научную нотацию как средство представления чисел. Однако мы немного теряем точность при работе с очень большими или очень маленькими значениями, что обычно приемлемо. Здесь я расскажу о стандарте IEEE для чисел с плавающей запятой (поскольку это в значительной степени стандарт де-факто, который используют все).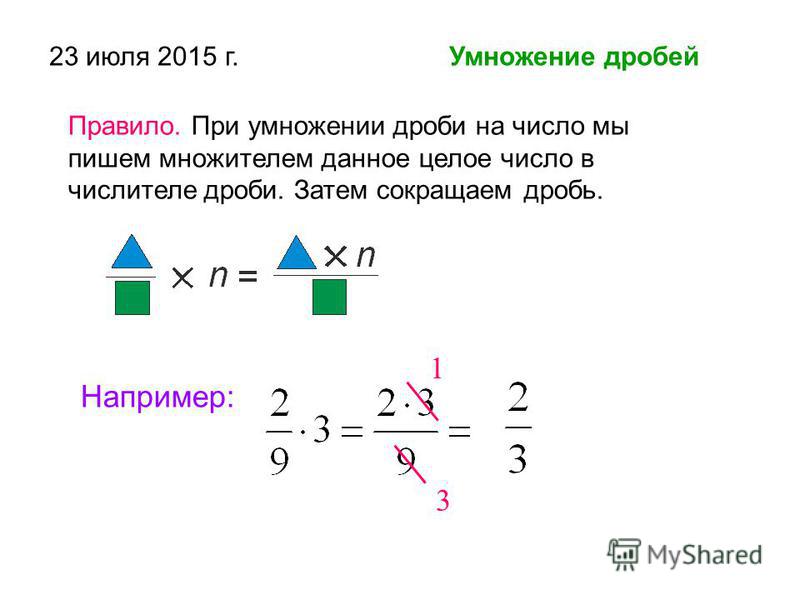
Напомните мне еще раз, как работает научная нотация
Некоторые из вас могут быть хорошо знакомы с научными обозначениями. Некоторые из вас, возможно, помнят, что выучили его некоторое время назад, но хотели бы освежить в памяти. Давайте рассмотрим, как это работает.
В приведенном выше 1.23 называется мантисса (мантисса), а 6 называется показателем степени. Мантисса всегда регулируется таким образом, чтобы слева от десятичной точки находилась только одна (ненулевая) цифра. Показатель степени говорит нам, на сколько мест нужно переместить точку. В этом случае мы перемещаем его на 6 позиций вправо. Если мы сделаем показатель степени отрицательным, то мы сдвинем его влево.
Если мы хотим представить 1230000 в экспоненциальном представлении, мы делаем следующее:
- Скорректируем число так, чтобы только одна цифра находилась слева от десятичной точки. 1,23
- Чтобы создать это новое число, мы переместили десятичную точку на 6 знаков.
 Это становится показателем степени.
Это становится показателем степени. - Таким образом, в экспоненциальном представлении это выглядит так: 1,23 x 10 6
Теперь то же самое в двоичном формате
Мы можем сделать то же самое в двоичном формате, и это формирует основу нашего числа с плавающей запятой.
Здесь мы перемещаем не десятичную точку, а двоичную точку, и поскольку она перемещается, она называется плавающей. Ниже мы рассмотрим то, что называется стандартом IEEE 754 для представления чисел с плавающей запятой. Стандарт определяет количество битов, используемых для каждого раздела (показатель степени, мантисса и знак), и порядок их представления.
Ничто не мешает вам представлять числа с плавающей запятой с помощью вашей собственной системы, однако почти все используют IEEE 754. Это касается производителей аппаратного обеспечения (включая процессоры) и означает, что в этих устройствах существует схема, специально предназначенная для обработки чисел с плавающей запятой IEEE 754. Используя стандарт для представления ваших чисел, ваш код может использовать это и работать намного быстрее. Это также означает, что улучшается функциональная совместимость, поскольку все представляют числа одинаково.
Используя стандарт для представления ваших чисел, ваш код может использовать это и работать намного быстрее. Это также означает, что улучшается функциональная совместимость, поскольку все представляют числа одинаково.
Стандарт определяет следующие форматы для чисел с плавающей запятой:
Одинарная точность , которая использует 32 бита и имеет следующую структуру:
- 1 бит для знака числа. 0 означает положительный, а 1 означает отрицательный.
- 8 бит для показателя степени.
- 23 бита для мантиссы.
Двойная точность , которая использует 64 бита и имеет следующую компоновку.
- 1 бит для знака числа. 0 означает положительный, а 1 означает отрицательный.
- 11 бит для показателя степени.
- 52 бита для мантиссы.
напр. 0 00011100010 010000100000000000000111010000011000000000000000000000
Двойная точность имеет больше битов, что позволяет представлять гораздо большие и гораздо меньшие числа. Поскольку мантисса также больше, степень точности также увеличивается (помните, что многие дроби не могут быть точно представлены в двоичном виде). Хотя числа с плавающей запятой двойной точности обладают этими преимуществами, они также требуют большей вычислительной мощности. С увеличением вычислительной мощности ЦП и переходом на 64-разрядные вычисления многие языки программирования и программное обеспечение просто по умолчанию используют двойную точность.
Поскольку мантисса также больше, степень точности также увеличивается (помните, что многие дроби не могут быть точно представлены в двоичном виде). Хотя числа с плавающей запятой двойной точности обладают этими преимуществами, они также требуют большей вычислительной мощности. С увеличением вычислительной мощности ЦП и переходом на 64-разрядные вычисления многие языки программирования и программное обеспечение просто по умолчанию используют двойную точность.
Ниже мы рассмотрим, как работают числа одинарной точности с плавающей запятой (просто потому, что это проще). Двойная точность работает точно так же, только с большим количеством битов.
Бит знака
Это первый бит (крайний левый бит) в числе с плавающей запятой, и это довольно просто. Как упоминалось выше, если ваш номер положительный, сделайте этот бит равным 0 . Если ваш номер отрицательный, сделайте его 1 .
Экспонента
Экспонента становится немного интереснее. Помните, что показатель степени может быть положительным (для представления больших чисел) или отрицательным (для представления небольших чисел, т. е. дробей). Ваше первое впечатление может состоять в том, что дополнение до двух было бы идеальным здесь, но стандарт имеет несколько иной подход. Это сделано для того, чтобы упростить обработку и манипулирование числами с плавающей запятой.
е. дробей). Ваше первое впечатление может состоять в том, что дополнение до двух было бы идеальным здесь, но стандарт имеет несколько иной подход. Это сделано для того, чтобы упростить обработку и манипулирование числами с плавающей запятой.
С 8 битами и беззнаковым двоичным кодом мы можем представить числа от 0 до 255. Чтобы разрешить использование отрицательных чисел с плавающей запятой, мы берем наш показатель степени и добавляем к нему 127. Диапазон показателей, которые мы можем представить, становится от 128 до -127. Однако 128 не допускается и сохраняется как особый случай для представления определенных специальных чисел, перечисленных ниже.
Напр. скажем:
- Мы хотим, чтобы наш показатель степени был равен 5. 5 + 127 равно 132, поэтому наш показатель степени становится - 10000100
- Мы хотим, чтобы показатель степени был равен -7. -7 + 127 равно 120, поэтому наш показатель степени равен - 01111000 .
Приятным дополнительным преимуществом этого метода является то, что если крайний левый бит равен 1, то мы знаем, что это положительный показатель степени, и это большое число, и если это 0, то мы знаем, что показатель степени отрицательный и это дробь (или небольшое число).
Здесь легко запутаться, так как бит знака для числа с плавающей запятой в целом имеет 0 для положительных и 1 для отрицательного значения, но оно переворачивается для экспоненты из-за использования механизма смещения. Это просто то, что вы должны иметь в виду при работе с числами с плавающей запятой.
Мантисса
Помните, что в научных обозначениях мы перемещаем точку так, чтобы слева от нее была только одна (не нулевая) цифра. Когда мы делаем это с двоичным кодом, эта цифра должна быть 1 , поскольку другой альтернативы нет. Создатели стандарта с плавающей запятой использовали это в своих интересах, чтобы получить немного больше данных, представленных в числе.
После преобразования двоичного числа в экспоненциальное представление перед сохранением в мантиссе мы удаляем начальный 1 . Это позволяет нам хранить в мантиссе еще 1 бит данных.
напр.
Если бы мы сохранили число 111.00101101, то в научной записи это было бы 1. 1100101101 с показателем степени 2 (мы переместили двоичную точку на 2 разряда влево). Мы отбрасываем начальные 1. и сохраняем только 1100101101.
1100101101 с показателем степени 2 (мы переместили двоичную точку на 2 разряда влево). Мы отбрасываем начальные 1. и сохраняем только 1100101101.
Если бы мы сохранили число 0,0001011011, то в экспоненте это было бы 1,011011 с показателем степени -4 (мы переместили двоичную точку на 4 знака вправо) . Отбрасываем ведущую 1. и нужно хранить только 011011.
Особые случаи
Следует учитывать несколько особых случаев.
Ноль
Нуль представляется путем создания бита знака либо 1 , либо 0 , а все остальные биты 0
, например. 1 00000000 000000000000000000000000 или 0 00000000 0000000000000000000000000
Это будет равно мантиссе 1 с показателем степени -127, что является наименьшим числом, которое мы можем представить в виде числа с плавающей запятой. Это не 0, но это довольно близко, и системы точно интерпретируют его как ноль.
Бесконечность
Можно представить как положительную, так и отрицательную бесконечность. Это просто вопрос переключения бита знака.
Это просто вопрос переключения бита знака.
Для представления бесконечности у нас есть показатель степени всех 1 с мантиссом всех 0 .
напр. 0 11111111 000000000000000000000000 или 1 11111111 0000000000000000000000000
Не число
Используется для обозначения того, что произошло нечто, что не может быть вычислено числом. Например, деление на ноль или квадратный корень из отрицательного числа. Это представлено показателем степени, равным всем 9.0133 1 и мантисса, которая представляет собой комбинацию 1 и 0 (но не все 0 , поскольку тогда это будет представлять бесконечность). Бит знака может быть 1 или 0.
например. 0 11111111 00001000000000100001000 или 1 11111111 11000000000000000000000
Образец 1 и 0 .
Итого:
| Ноль | 0 00000000 000000000000000000000000 |
| Отрицательный ноль | 1 00000000 000000000000000000000000 |
| Бесконечность | 0 11111111 000000000000000000000000 |
| Отрицательная бесконечность | 1 11111111 00000000000000000000000 |
| Не число (NaN) | 0 11111111 00001000000000100001000 |
Преобразование в число с плавающей запятой
Преобразование числа в число с плавающей запятой включает следующие шаги:
- Установите бит знака — если число положительное, установите бит знака на 0.
 Если число отрицательное, установите это до 1.
Если число отрицательное, установите это до 1. - Разделите номер на две части - целая часть числа и дробная часть.
- Преобразовать в двоичное число - преобразовать два числа в двоичное число, а затем соединить их вместе с двоичной точкой.
- Вычислить показатель степени . Это делается путем определения того, на сколько пробелов нужно переместить двоичную точку, чтобы она оказалась сразу после первого 1 в результате. Если вы переместите двоичную точку влево, то это число будет положительным. Если вы переместите его вправо, то число будет отрицательным. Добавьте к этому числу 127, а затем преобразуйте его в двоичное число.
- Форматирование мантиссы . Это делается путем отбрасывания первых 1 в числе и записи следующих 23 бит.
Давайте рассмотрим несколько примеров, чтобы увидеть это в действии.
Результат в двоичном формате:
Чтобы преобразовать число с плавающей запятой обратно в десятичное, просто выполните шаги в обратном порядке.


 И. Многочлены и алгебраические дроби. Учебник алгебры для 7 кл.
Выпуск 1. Конструктор книги Резник Н. А. – СПб.: Изд-во ЦПО «Информатизация образования», 2000.
И. Многочлены и алгебраические дроби. Учебник алгебры для 7 кл.
Выпуск 1. Конструктор книги Резник Н. А. – СПб.: Изд-во ЦПО «Информатизация образования», 2000.
 1139/апнм-2020-0571
1139/апнм-2020-0571
 1] * 10) == 1.0
ЛОЖЬ
>>> math.fsum([0.1] * 10) == 1.0
Истинный
1] * 10) == 1.0
ЛОЖЬ
>>> math.fsum([0.1] * 10) == 1.0
Истинный
 from_float(0.1)
Дробь(3602879701896397, 36028797018963968)
>>> (0.1).as_integer_ratio()
(3602879701896397, 36028797018963968)
>>> Десятичный.from_float(0.1)
Десятичный('0.1000000000000000055511151231257827021181583404541015625')
>>> формат(десятичный.from_float(0.1), '.17')
«0,10000000000000001»
from_float(0.1)
Дробь(3602879701896397, 36028797018963968)
>>> (0.1).as_integer_ratio()
(3602879701896397, 36028797018963968)
>>> Десятичный.from_float(0.1)
Десятичный('0.1000000000000000055511151231257827021181583404541015625')
>>> формат(десятичный.from_float(0.1), '.17')
«0,10000000000000001»
 Это становится показателем степени.
Это становится показателем степени. Если число отрицательное, установите это до 1.
Если число отрицательное, установите это до 1.