Дробное число в двоичной системе: Перевод дробных чисел из десятичной системы счисления в любую другую систему счисления — урок. Информатика, 10 класс.

{-2}\). Поскольку целая часть у нормализованного представления числа всегда (кроме числа 0) равна 1, то целая часть не хранится, а хранится только дробная часть мантиссы. Количество значащих знаков мантисcы, которое хранится, может быть различным для различных способов представления действительных чисел. Например, в типе данных двойной точности, который в языке Python соответствует типу float, в языке C — типу double, в языке Pascal — типу double, хранится 52 бита дробной части мантисы.

Стандарт IEEE754 определяет несколько типов представления действительных чисел, основными из которых являются числа одинарной точности (для их хранения требуется 4 байта), двойной точности (8 байт) и расширенной точности (10 байт).

Точность	Размер (байт)	C, C++	Pascal	Python	Мантисса (бит)	Точность, десятичных цифр	Максимальное значение	Минимальное положительное значение
одинарная	4	float	single	—	23	\(\approx 7{,}2\)	\(3{,}4\cdot10^{38}\)	\(1{,}4\cdot10^{-45}\)
двойная	8	double	double	float	52	\(\approx 15{,}9\)	\(1{,}7\cdot10^{308}\)	\(5{,}0\cdot10^{-324}\)
расширенная	10	long double (только в gnu gcc/g++)	extended	—	63	\(\approx 19{,}2\)	\(1{,}1\cdot10^{4932}\)	\(1{,}9\cdot10^{-4951}\)

Содержание

Неточность при представлении действительных чисел

Рациональные числа, которые не могут быть представлены в виде дроби со знаменателем, являющимся степенью двойки, не могут быть точно представлены в виде конечной двоичной дроби, а, значит, не могут быть в точности представлены в памяти компьютера. {-2}\) и хранятся только 52 цифры дробной части мантиссы числа. Дальнейшие цифры отбрасываются (с округлением), поэтому вместо числа \(\frac{1}{3}\), которое непредставимо в действительных типах данных, хранится другое ближайшее к нему представимое число. В случае с числом \(\frac{1}{3}\) записывается меньшее число, также меньшее число записывается и при записи в переменную двойной точности значений \(\frac{1}{10}\) и \(\frac{2}{10}\), а вот вместо числа \(\frac{3}{10}\) уже будет записано большее представимое число. Поэтому если записать в две переменные значения \(0.1\) и \(0.2\) (десятичные), а в третью переменную записать их сумму, то результат окажется меньше, чем \(\frac{3}{10}\), в то время как при записи в переменную значения \(\frac{3}{10}\) явно в виде \(0.3\), получится результат, больший чем \(\frac{3}{10}\). То есть при вычислении суммы чисел \(0.1\) и \(0.2\) результат получится отличным от значения \(0.3\), записанного в переменную явно, то есть с точки зрения компьютерной арифметики \(0. 1 + 0.2 \ne 0.3\). Эту проблему (неточное представление действительных чисел и выполнение арифметических операций с действительными числами) всегда следует иметь в виду.

Использование эпсилон при сравнении действительных чисел

Таким образом, сравнивать действительные числа в компьютерных программах на точное равенство нельзя. Вместо этого если нужно сравнить два числа \(a\) и \(b\) на равенство, правильным будет проверка условия, что эти два числа не сильно различаются, то есть что модуль их разности не превосходит некоторого небольшого значения \(\varepsilon\), то есть что \(|a-b|<\varepsilon\). Значение \(\varepsilon\) как правило определяется для каждой задачи исходя из той точности, с которой необходимо получить результат.

В следующей таблице указано, как нужно проверять различные сравнения действительных чисел с использованием \(\varepsilon\).

Условие	Как нужно проверять
\(a=b\)	\(\|a-b\|\lt\varepsilon\)
\(a\ne b\)	\(\|a-b\|\ge \varepsilon\)
\(a\lt b\)	\(a \le b — \varepsilon\)
\(a \le b\)	\(a \lt b + \varepsilon\)
\(a\gt b\)	\(a \ge b + \varepsilon\)
\(a\ge b\)	\(a \gt b — \varepsilon\)

Специальные значения действительных типов

При работе с действительными числами, как правило, в результате алгоритмических ошибок, возникают некоторые специальные значения, например, inf и nan.

Значение inf (от infinity) возникает при переполнении действительной переменной, когда результат становится очень большим. Например, если взять положительное число и умножать его на два в цикле, то довольно скоро получится значение inf. Максимальное значение, которое может быть сохранено до получения переполнения, различается для разных типов действительных чисел.

Значение inf отличается тем, что после получения результата inf из него уже нельзя получить “обычное” действительное число. При прибавлении и вычитании к inf любого действительного (неспециального) числа, умножении и делении

inf на положительное число, в результате всегда получается inf. То есть inf считается “очень большим”, настолько, что сложение, умножение и деление все равно оставляет результат “очень большим”. Значение inf считается больше любого действительного неспециального числа.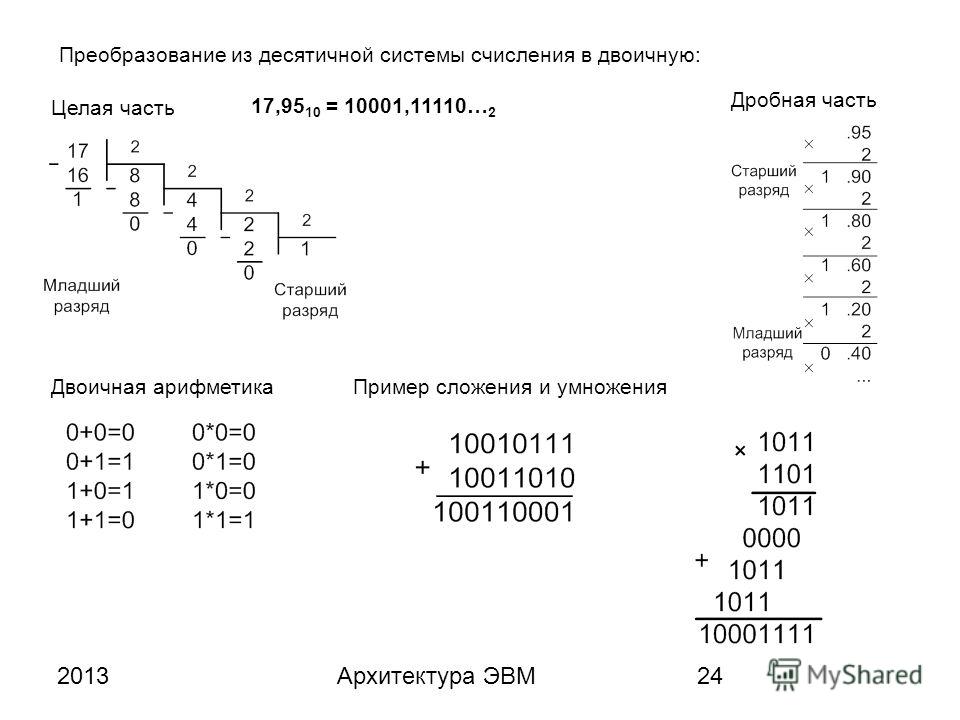

Также есть отрицательное значение -inf, которое считается “минус бесконечностью”.

При ряде операций со значением inf может возникнуть другое специальное значение nan (от not a number — не число). Примеры операций, дающих в результате nan:

\(inf — inf\)
\(inf \times 0\)
\(inf / inf\)

nan означает, что результат может быть “чем угодно”, то есть это непредсказуемая величина и работать с ней невозможно. Любые арифметические операции c

nan будут давать в результате nan. Более того, при любом сравнении nan с любым действительным числом при помощи любой из операций ==, <, <=, >, >= в результате будет получаться false. А при сравнении nan с любым действительным числом при помощи операции != всегда будет получаться true.

И даже если значения двух переменных a и b оба равны nan, то сравнение a == b будет давать false, а сравнение a != b будет давать true.

В заголовочном файле cmath определены две константы INFINITY и NAN, которые принимают значения inf и nan соответственно, а также две функции

bool isinf(x) и bool isnan(x), которые возвращают true, если аргумент x равен inf и nan соответственно или false в противном случае.

Электронный справочник по ИНФОРМАТИКЕ (Автор Панов В.А.)

Двоичная система счисления

Введение

Перевод чисел

Дробные числа

Отрицательные числа

Двоичная арифметика

Двоичная система счисления является основной системой представления информации в памяти компьютера.

В этой системе счисления используются две цифры: 0 и 1.

Двоичную цифру называют битом.

Первое опубликованное обсуждение двоичной системы счисления принадлежит испанскому священнику Хуану Карамюэлю Лобковицу ( 1670 г .). Всеобщее внимание к этой системе привлекла статья немецкого математика Готфрида Вильгельма Лейбница, опубликованная в 1703 г . В ней пояснялись двоичные операции сложения, вычитания, умножения и деления. Лейбниц не рекомендовал использовать эту систему для практических вычислений, но подчёркивал её важность для теоретических исследований. Со временем двоичная система счисления становится хорошо известной и получает развитие.

Большинство современных электронно-вычислительных машин используют в своей работе именно эту систему чисел.

Ей было тысяча сто лет.
Она в сто первый класс ходила,
В портфеле по сто книг носила —
Всё это правда, а не бред.

Когда пыля десятком ног,
Она шагала по дороге,
За ней всегда бежал щенок
С одним хвостом, зато стоногий.
Она ловила каждый звук
Своими десятью ушами,
И десять загорелых рук
Портфель и поводок держали.
И десять тёмно-синих глаз
Рассматривали мир привычно…

Но станет всё совсем обычным,
Когда поймёте наш рассказ.

———————

С помощью двоичной системы кодирования можно зафиксировать любые данные и знания. Это легко понять, если вспомнить принцип кодирования и передачи информации с помощью азбуки Морзе.

Телеграфист, используя только два символа этой азбуки — точки и тире, может передать практически любой текст.

Объём памяти компьютера измеряется в байтах. Каждый байт может выражать букву, число, пробел, знак препинания или какой-либо другой символ. Количество символов, которые компьютер может хранить в оперативной памяти, меняется в широких пределах от вида компьютера и его модели.

Объём памяти, хотя он и измеряется в байтах, обычно выражается в килобайтах. Слово «килобайт», вообще говоря, означает «1000 байт». (Напомним, что приставка «кило» означает «тысяча».)

Фактически же килобайт равен 1024 байтам: 1 Кбайт = 1024 байт.

Компьютер с объёмом памяти в 64 К может хранить 64 х 1024 = 65536 символов.

Объём памяти первых микрокомпьютеров составлял всего лишь 2 Кб. Нынешние компьютеры имеют объём памяти 128, 256, 512, 1024 Мб и более

Объём памяти новейших компьютеров так велик, что она выражается в гигабайтах, т. е. в миллиардах байтов.

1 Мбайт = 1024 Кбайт = 1 048 576 байт.

Итак, каждый символ алфавитно-цифровой информации представляется в компьютере кодом из восьми двоичных цифр. Следовательно, каждый символ в компьютере имеет код объёмом 1 байт.

имеет в двоичной форме объём 25 байт: 23 буквы и 2 символа «пробел» по 1 байту.

Пример. Измерим в байтах объём текстовой информации в книге из 258 страниц, если на одной странице размещается в среднем 45 строк по 60 символов (включая пробелы). Один символ в двоичной форме содержит 1 байт. Строка будет содержать 61 байт, учитывая и служебный символ окончания строки. Тогда

61 байт * 45 строк = 2745 байт.

Так как в книге 258 страниц текста и на каждой странице в среднем по 2745 байт информации, то объём алфавитно-цифровой информации в книге

2745 байт * 258 страниц = 708210 байт » 692 Кбайт

Таким образом, текст книги имеет объём около 692 Кбайт.

Перевод чисел

Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.

73₁₀ = 1001001₂

А вот как происходит перевод двоичного числа в десятичное:

В любой системе счисления нужно уметь представлять не только целые числа, но и дробные. С математической точки зрения это ординарная задача, которая давно решена. Однако с точки зрения компьютерной техники это далеко не тривиальная проблема, во многом связанная с архитектурой компьютера. Ресурсы компьютеров не бесконечны, и основной трудностью является представление периодических и непериодических дробей. Следовательно, такие дроби следует округлять, задавать класс точности участвующих (и могущих появиться в результате вычислений!) чисел без потери точности вычислений, а также следить за тем, чтобы потеря точности не произошла при переводе чисел из одной системы счисления в другую. Особенно важно аккуратно производить вычисления при операциях с плавающей точкой.

Запишем формулу представления дробного числа в позиционной системе счисления:

A_p = a_n-1·p^n-1+a_n-2·p^n-2 + … + a₁·p¹+a₀·p⁰ +a_-1·p^-1+a_-2·p^-2 + . .. + a_-m·p^-m,

В случае десятичной системы счисления получим:

24,73₁₀ = (2·10¹+4·10⁰+7·10^-1+3·10^-2)₁₀

Перевод дробного числа из двоичной системы счисления в десятичную производится по следующей схеме:

101101,101₂ = (1·2⁵+0·2⁴+1·2³+1·2²+0·2¹+1·2⁰+1·2^-1+0·2^-2+1·2^-3)₁₀=45,625₁₀

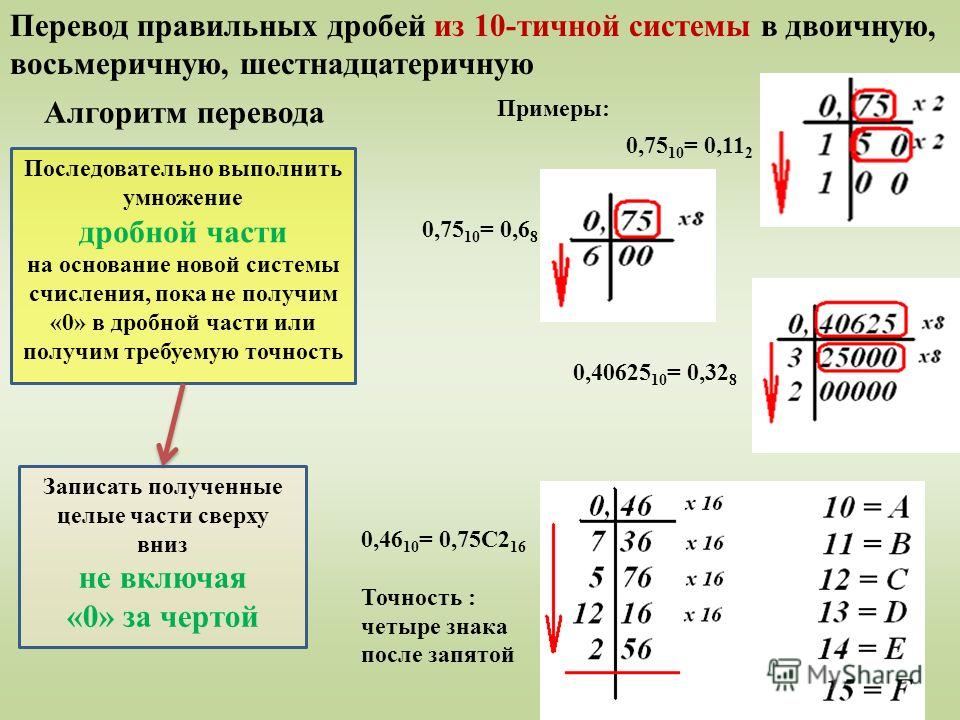
Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

· Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

· Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

· В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

· Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206₁₀=11001110₂ по ранее описанным алгоритмам; дробную часть умножаем на основание 2, занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

.116 • 2 = 0.232

.232 • 2 = 0.464

.464 • 2 = 0.928

.928 • 2 = 1.856

.856 • 2 = 1.612

. 612 • 2 = 1.224

.224 • 2 = 0.448

.448 • 2 = 0.896

.896 • 2 =1.792

.792 • 2 = 1.584

и т.д.

Получим: 206,116₁₀=11001110,0001110011₂

Таблицу степеней первых восьми отрицательных степеней двойки

Степень основания	2	8	16
0	1	1	1
1	2	8	16
2	4	64	256
3	8	512	4096
4	16	4096	65536
5	32	32768	1048576
6	64	262144	16777216
7	128	2097152	268435456
8	256	16777216	4294967296
9	512	134217728	68719476736
10	1024	1073741824	1099511627776
11	2048	8589934552	17592186044416
12	4096	68719476736	281474976710656
13	8192	549755813888	4503599627370496
14	16384	4398046511104	72057594037927936
15	32768	35184372088832	1152921504606846976
16	65536	281474976710756	18446744073709551616

Отрицательные числа

Перейдем теперь к вопросу представления отрицательных чисел. Для определенности рассмотрим тип byte, в котором любое число занимает ровно восемь бит. Из записи в двоичной системе счисления равенства (- 1) + 1 = 0 легко найти, какой вид должно иметь неизвестное нам пока двоичное представление xxxxxxxx числа — 1:

    xxxxxxxx + 00000001 = 00000000

Ясно, что на месте символов xxxxxxxx должно быть расположено число 11111111. Правильным результатом при этом, конечно, следовало бы считать 100000000, а не 00000000, но ведь мы имеем дело с типом byte и, так как результат обязан разместиться в байте, единица <<исчезает>>.

Итак, число — 1 должно кодироваться как 11111111. Дальнейшее уже совсем просто: для получения — 2 нужно — 1 уменьшить на единицу, что даст 11111110; число — 3 представляется как 11111101 и т. д.

Отрицательные числа всегда имеют в своем двоичном представлении единицу в самом старшем разряде, который поэтому называют знаковым, а абсолютная величина кодируемого числа получается как двоичное дополнение остальных бит (нули нужно заменить на единицы и наоборот), увеличенное на один.

Легко видеть, что при этом самым маленьким отрицательным числом, которое принадлежит типу byte, является число — 128 (двоичное представление 10000000), а самым большим — число 127 (представление 01111111). Все представимыe числа (а их 256) в данном случае могут быть получены как пересечение двух множеств: множества Z всех целых чисел и отрезка [ — 128; 127 ].

Интересным является следующее наблюдение: если число 01111111 увеличить на единицу, то получится 10000000, что означает следующее:

127 + 1 = — 128 !!!

Итак, множество элементов типа byte можно представлять себе в виде свернутого в кольцо отрезка
[ — 128; 127 ].

То, что для элементов множества , являющегося машинным аналогом Z, нарушено фундаментальное свойство целых чисел X + 1 > X, способно привести к различным невероятным на первый взгляд результатам, однако гораздо более странные вещи происходят при работе с вещественными числами.

Двоичная арифметика

Над числами в двоичной системе счисления можно выполнять арифметические действия.

При этом используются следующие таблицы:

Сложение	Вычитание	Умножение
0+0=0	0-0=0	0*0=0
1+0=1	1-0=1	1*0=0
0+1=1	1-1=0	0*1=0
1+1=10	10-1=1	1*1=1

Рассмотрим примеры:

1 1 0 1 0 1₂ + 1 1 0 1 1₂

1 1 0 1 1₂ — 1 1 0 1₂

1 1 0 1 1₂ * 1 0 1₂

Для деления в двоичной системе счисления нужно уметь сравнивать числа (определять, какое больше) и хорошо вычитать. Посмотри деление на анимированном примере

Пример:

Еще несколько примеров:

Несколько примеров для тренировки:

Простая математика, лежащая в основе алгоритмов преобразования десятичных чисел в двоичные

Если вы поищете в Интернете «Как преобразовать десятичные числа в двоичные», вы найдете четыре простых алгоритма: два для целых чисел и два для дробей. Они представлены на примерах ниже в первой части статьи. Но хотя почти всегда достаточно просто знать алгоритмы, я решил попытаться понять, почему они работают. Во второй части этой статьи объясняется самая основная математика, стоящая за каждым из них. Знание этого может помочь вам вспомнить любой из алгоритмов, если вы вдруг забудете их. Я настоятельно рекомендую вам взять блокнот и ручку и выполнять операции вместе со мной, чтобы лучше запомнить математику. Вот четыре алгоритма с примерами, которые вы можете найти в Интернете.

Преобразование десятичного целого числа в двоичное

Чтобы преобразовать целое число в двоичное, начните с рассматриваемого целого числа и разделите его на 2, обращая внимание на частное и остаток. Продолжайте делить частное на 2, пока не получите частное, равное нулю. Затем просто выпишите остатки в обратном порядке.

Вот пример такого преобразования с использованием целого числа 12.
Сначала разделим число на два, указав частное и остаток:

Теперь осталось просто выписать остаток в обратном порядке — 1100 . Итак, 12 в десятичной системе представляется как 1100 в двоичной.

Преобразование десятичной дроби в двоичную

Чтобы преобразовать дробь в двоичную, начните с рассматриваемой дроби и умножьте ее на 2 , обращая внимание на полученную целую и дробную части. Продолжайте умножать на 2, пока не получите в результате дробную часть, равную нулю. Затем просто выпишите целые части из результатов каждого умножения.

Вот пример такого преобразования с использованием дроби 0,375 .

Теперь просто выпишем полученную целую часть на каждом шаге — 0,011 . Итак, 0,375 в десятичной системе представляется как 0,011 в двоичной.

Только дроби со знаменателем, равным степени двойки, могут быть конечно представлены в двоичной форме. Например, знаменатели 0,1 (1/10) и 0,2 (1/5) не являются степенями двойки, поэтому эти числа не могут быть конечно представлены в двоичном формате. Чтобы сохранить их как числа с плавающей запятой IEEE-754, их необходимо округлить до количества доступных битов для мантиссы — 10 бит для половинной точности, 23 бита для одинарной точности или 52 бита для двойной точности. В зависимости от того, сколько битов точности доступно, приближения с плавающей запятой 0,1 и 0,2 могут быть немного меньше или больше, чем соответствующие десятичные представления, но никогда не равны. Из-за этого у вас никогда не будет 0,1+0,2 == 0,3.

Преобразование двоичного целого числа в десятичное

Чтобы преобразовать двоичное целое число в десятичное, начните слева. Возьмите текущую сумму, умножьте ее на два и добавьте текущую цифру. Продолжайте до тех пор, пока не останется цифр. Вот пример такого преобразования с использованием дроби 1011 .

Преобразование целой дроби в десятичную

Чтобы преобразовать двоичную дробь в десятичную, начните справа с суммы 0. Возьмите текущую сумму, добавьте текущую цифру и разделите результат на 2. Продолжайте, пока не останется цифр. . Вот пример такого преобразования с использованием дроби 0,1011 . Я просто заменил деление на 2 умножением на 1/2 .

Вот вам 4 простых алгоритма, которые позволят вам преобразовывать двоичные числа в десятичные и обратно.

Расширение числа по основанию q

Ключом к пониманию того, почему эти алгоритмы работают, является расширение числа по основанию q числа. Целое число в любой системе счисления может быть представлено в следующем виде:

где

N целое число
x цифра 82
q — базовое значение (10 для системы с основанием 10, 2 для системы с основанием 2 ) , или просто базовое расширение q . Посмотрим, как выглядит число 12 в десятичной и двоичной системах счисления:
Аналогично дробное число в любой системе счисления может быть представлено в следующем виде:
где,
4 — дробь
x — цифра (от 0 до 9 для системы счисления по основанию 10, 0 и 1 для системы с основанием 2)
q — базовое значение (10 для системы счисления по основанию 10, 2 для системы с основанием 2)
Для номера 2
14 в десятичной и двоичной системах представления выглядит следующим образом:
Преобразование десятичного целого числа в двоичное
Как оказалось, мы можем использовать эту форму расширения base-q для преобразования числа из десятичной системы в двоичную. Давайте сделаем это для того же числа 12 . Во-первых, давайте притворимся, что мы не знаем, как оно представлено в двоичном формате, и запишем его, заменив неизвестные цифры на x :
Наша задача — найти все x . Давайте посмотрим, что мы можем сделать здесь. Первое, на что мы должны обратить внимание, это то, что все слагаемые, кроме последнего, будут четными числами, потому что все они кратны двум. Теперь, используя эту информацию, мы можем вывести цифру для 9.0080 x0  — если преобразуемое целое четное, то x0  900 , если нечетно — то x0  должен быть 1 . Здесь у нас четное число 12, поэтому x0  равно нулю. Давайте запишем эту информацию:
Далее нам нужно найти значение для x1 . Поскольку все слагаемые от x1 до xN кратны двум, мы можем выделить 9014 . выделить x1 . Сделаем так:
Также легко увидеть, что сумма значений в скобках равна 6 . Итак, мы можем записать наш первый шаг как:
Продолжим поиск оставшихся x . Мы можем записать многочлен в скобках как отдельное утверждение:
Здесь, применяя ту же логику, что и выше, мы видим, что x1 равно 0 . Давайте перепишем его и снова вынесем 2:
Итак, наш второй шаг:
Теперь мы можем увидеть закономерность. Мы можем продолжить факторинг 2 , пока частное не станет равным нулю. Давайте последуем этой схеме и посмотрим, что у нас получится.
Поскольку частное равно 1, осталось только одно слагаемое, поэтому давайте перепишем предыдущее выражение:
Итак, наш третий шаг:
Итак, мы получаем следующее:
Понятно, что x3 равно 1 . Но, так как для нашего алгоритма нам нужно частное, перепишем предыдущее выражение так, чтобы оно имело частное:
Поскольку мы получили частное 0 , больше не с чем работать, и это был наш последний шаг. Запишем:
Итак, мы закончили преобразование. Вот как выглядит наше преобразование по шагам:
Теперь понятно, что остаток на каждом шаге соответствует значению x на соответствующих позициях: первый остаток соответствует первому x, второй остаток второму х и так далее. Итак, число 12 в двоичном виде с использованием описанного выше алгоритма представляется как 1100 .
Помните, что мы начали с идеи показать, почему алгоритм, который включает погружение на 2 , работает. Давайте выполним шаги, описанные выше, и переместим 2 в левую часть выражений:
Таким образом, вы можете увидеть, как мы пришли к алгоритму, описанному в начале. Мы также можем поместить вычисления для этих четырех шагов в одно представление, подобное этому 9.0003
Убедитесь, что вы понимаете, как мы пришли к этому представлению, так как оно понадобится нам при изучении того, как работает алгоритм преобразования из двоичного в десятичный.
Преобразование десятичной дроби в двоичную
Чтобы показать, почему мы умножаем на 2 и берем целую часть при преобразовании дробей в двоичную, я также буду использовать base-q форму расширения для дробей. Я буду использовать дробное число 0,375 из первой части статьи. Аналогично целой части, давайте представим, что мы не знаем, как это число представлено в двоичном виде, и запишем его, заменив неизвестные цифры на 9. 0080 x :
Как и в случае с целыми числами, наша задача состоит в том, чтобы найти все x , выделив x . Давайте посмотрим, как мы можем это сделать. Первое, на что следует обратить внимание, это то, что отрицательные степени числа 2 дают нам дроби со знаменателем числа 2 с положительными степенями. Давайте перепишем приведенное выше выражение:
Сразу видно, что мы можем просто вынести 1/2 в правой части выражения. Сделаем так:
и тогда мы можем переместить 1/2 в левую часть
Хорошо, здесь мы выделили x1 2 1 либо 2 , и мы знаем, что это может быть 90 или 0 . Чтобы определить, какая у него цифра, давайте посмотрим на оставшиеся слагаемые:
Давайте подумаем, насколько большой может быть сумма этих чисел. Если максимальное количество цифр x равно 1, то мы можем просто заменить x с единицами и запишите сумму в виде:
Ну, это геометрический ряд дробей, и сумма такого ряда лежит в границах [0 < сумма < 1], поэтому максимальное количество таких сумма может дать нам 1. Давайте теперь снова посмотрим на наше выражение:
Теперь здесь должно быть ясно, что если правая часть меньше 1, то x1 не может быть равно 1 и, следовательно, равно 0 , а оставшаяся часть равна 0,75 .
Именно так выглядит первый шаг алгоритма, представленного в начале:
Отнимем дробную часть от 0,75 и выделим еще 1/2 , чтобы выделить x2
:
:
и переместить 1/2 влево:
Теперь, если x2 равно 0 , то сумма левой части выражения не может быть больше 1 , но левая часть равна 1,5 2 , поэтому х 2 должно быть 1 а оставшаяся часть 0.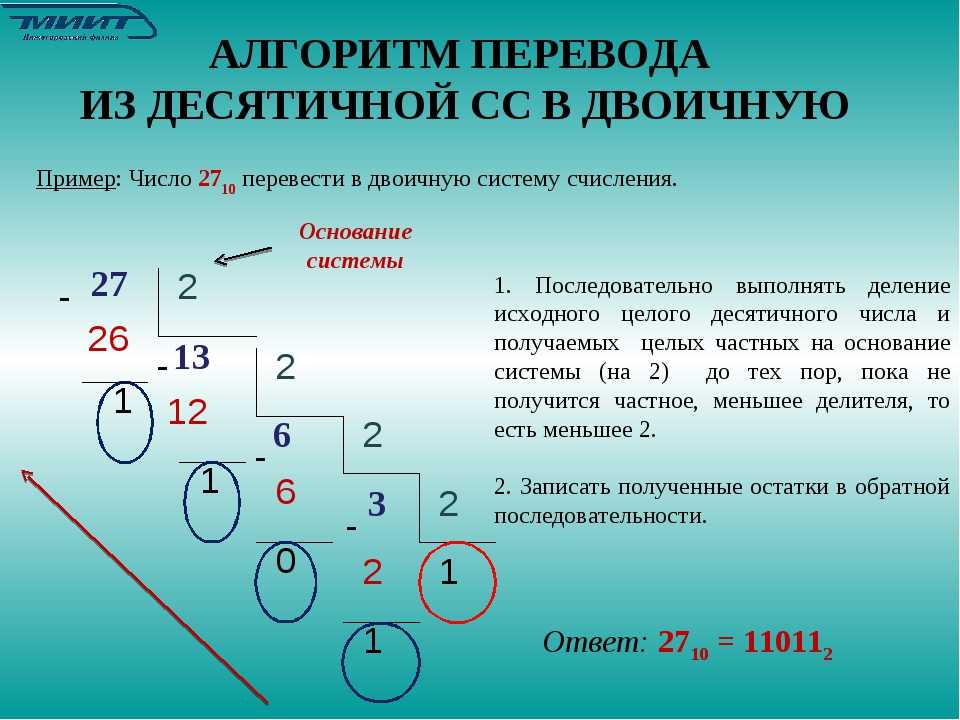 5 . Давайте запишем это:
Опять же, это следует схеме в алгоритме, представленном в начале:
Повторим те же действия для оставшейся дробной части 0,5 .
Используя ту же логику, что и выше, мы можем видеть, что x3 равно 1 и нет оставшейся дробной части:
вот как выглядит наш последний шаг:
Итак, давайте еще раз выпишем все шаги:
Это именно тот алгоритм, который я представил в начале. Точно так же, как мы делали с целыми числами, мы также можем поместить вычисления для этих трех шагов в одно представление, например:
Опять же, важно, чтобы вы полностью усвоили это представление, так как оно понадобится нам при изучении двоичного преобразования в десятичное.
Почему не все дроби могут быть конечно представлены в двоичной системе
Тот факт, что некоторые дроби, представленные конечно в десятичной системе, не могут быть представлены конечно в двоичной системе, является неожиданностью для многих разработчиков. Но именно эта путаница лежит в основе кажущегося странным результата прибавления 0,1 к 0,2. Так что же определяет, может ли дробь быть конечно представлена в системе счисления? Это довольно сложно. Но базовая версия такова — для конечного представления числа знаменатель в дроби должен быть степенью основания системы. Например, для системы с основанием 10 знаменатель должен быть степенью 10, поэтому мы можем конечно представить 0,625 в десятичном виде:
и не может конечно представлять 1/3:
То же самое касается системы с основанием 2:
Но если мы проверим 0,1, знаменатель будет равен 10, и это не степень 2, поэтому 0,1 будет бесконечная дробь в двоичной системе. Давайте посмотрим на это, используя алгоритм, который мы изучили выше:
Мы можем продолжать делать это бесконечно, но давайте запишем это в виде периодической цепной дроби:
Преобразование двоичного целого числа в десятичное
Я собираюсь использовать то же самое двоичное целое число 1011 из первого раздела, чтобы показать вам, почему работает алгоритм умножения на 2. Здесь мы также будем использовать расширение base-q от числа . Давайте запишем это в такой форме:
Поскольку все слагаемые кратны 2 , мы можем продолжать выносить на множители 2 , пока частное не станет равным нулю. Давайте сделаем так:
Теперь, если вы просто будете следовать порядку математических операций, вы получите точно такие же шаги, как я показал в начале, а именно:
Таким образом, 1011 в двоичном виде равно 11 в десятичном виде.
Преобразование двоичной дроби в десятичную
Вот мы и подошли к последнему алгоритму. Наверное, вы уже сами разобрались с механикой, стоящей за этим. Если нет, давайте посмотрим, почему это работает. Расширение числа base-q от числа также является ключевым здесь. Число 0,1011 возьмем из первого раздела. Запишем в развернутом виде:
Опять же, поскольку все слагаемые кратны 1/2 , мы можем продолжать разлагать 1/2 до тех пор, пока не останется дробной части. Сделаем так:
Следуя порядку математических операций, получается алгоритм, описанный в начале:
Таким образом, 0,1011 в двоичном виде равно 0,6875 в десятичном.
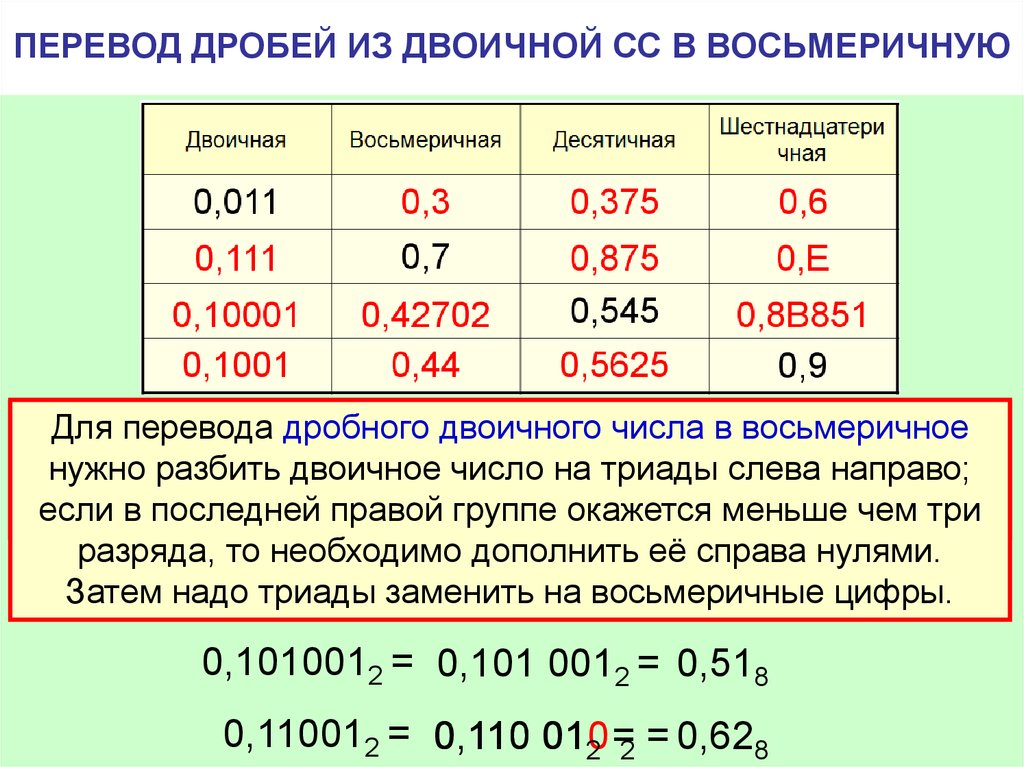
Двоичные дроби — Electronics-Lab.com
Двоичные дроби
Число, представляющее значение, может состоять из двух частей: целой и дробной части. Разделение между этими двумя частями представлено точкой (точкой). Дробная часть представляет собой значение между двумя целыми числами для выражения точности. Число также может быть представлено только целым числом без дроби, что просто зависит от степени точности, необходимой для представления значения. Число с дробной частью может принадлежать любой системе счисления, т. е. десятичной, двоичной, шестнадцатеричной и т. д.
Давайте сначала рассмотрим дроби в широко используемой десятичной системе счисления, которая является системой счисления с основанием 10. Будучи числом с основанием 10, он может выбрать любое из десяти (10) возможных чисел для представления значения цифры. Десять (10) возможных чисел: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Кроме того, каждая десятичная цифра имеет позиционный вес, который она несет, который увеличивается на десять (10) раз для каждого позиционного шага справа налево. И наоборот, позиционный вес каждой десятичной цифры уменьшается в десять (10) раз с каждым позиционным шагом слева направо. В выражении это может быть представлено как (10 ⁿ ), где «n» представляет позицию десятичной цифры. При движении слева направо позиции за пределами «n = 0» представлены отрицательными значениями, т. е. -1, -2, -3, … и т. д., и поэтому их позиционный вес уменьшается на десять (10) с каждым шаг. Эти отрицательные позиционные веса вместе с соответствующими цифровыми значениями составляют дробное число . Разделение между положительными («n=0») и отрицательными позиционными («n=-1») значениями представлено десятичной точкой .
Из предыдущих статей известно, что данное число является взвешенной суммой значений его цифр и относительных позиционных весов. Это можно выразить следующим образом:
Пример дробного числа
Рассмотрим пример (123,456 ₁₀ ) , который представляет собой десятичное число, состоящее из целой и дробной частей, разделенных десятичной точкой. Числа слева и справа от десятичной точки (.) составляют целое число и дробных частей соответственно. В соответствии с этим 123 ₁₀ является целой частью, тогда как 456 ₁₀ составляет дробную часть данного (123,456 ₁₀) числа. Позиционный вес каждой цифры зависит от ее относительного положения относительно десятичной точки. Это показано ниже:
Позиционные веса цифр 1, 2 и 3 слева от десятичной точки:0650 0 (1) соответственно. Точно так же цифры 4, 5 и 6 справа от запятой имеют позиционные веса 10 ^-1 (0,1), 10 ^-2 (0,01) и 10 ^-3 (0,001) соответственно. .
Состав числа (123,456 ₁₀ ) с использованием относительных позиционных весов цифр объясняется следующим образом:
Концепция позиционной записи для представления относительного веса каждой десятичной цифры может быть применена к другим системам счисления. Однако каждая система нумерации использует другую базу или 9.0012 множитель значение. Например, Octal использует систему счисления по основанию 8, и каждый позиционный шаг увеличивает или уменьшает вес в восемь (8) раз в зависимости от направления шага. Аналогично, в двоичных числах каждая двоичная цифра или бит имеет весовую разницу в два (2) раза по сравнению с соседним битом.
Двоичные дроби
Двоичное число использует систему счисления с основанием 2 , и каждая двоичная цифра (бит) имеет два варианта представления своего значения: «0» и «1». Как и десятичная цифра, каждая двоичная цифра (бит) имеет связанный с ней позиционный вес относительно двоичной точки (десятичной точки в случае десятичной цифры). Вес двоичных разрядов увеличивается в два (2) раза на каждый шаг разряда при движении справа налево. Более того, двоичные числа без знака также могут иметь дробные числа, т.е. прямо до двоичной точки. Вес двоичных цифр, представляющих дробные числа, уменьшается в два раза на каждом шаге при движении вправо от двоичной точки. Это означает, что двоичные цифры имеют позиционный вес 9.0012 2 ⁰ , 2 ¹ , 2 ² , и т. д. , начиная с левого двоичного числа, т. е. номера позиций 0, 1, 2 и т. д. соответственно. Точно так же двоичные цифры имеют позиционный вес 2 ^-1 , 2 ^-2 , 2 ^-3 и т. д. , начиная непосредственно справа от двоичной точки.
Относительные позиционные веса двоичных цифр поясняются ниже:
Учитывая двоичную дробь 0,1101 ₂ , считается, что позиционный вес каждой двоичной цифры или бита, составляющих двоичную дробь, составляет ее десятичный эквивалент. Это показано ниже:
Двоичная дробь 0,1101 ₂ дает эквивалентную десятичную дробь 0,8125 ₁₀ .
Примеры двоичных дробей
Следующие двоичные дроби преобразуются в эквивалентные им десятичные дроби с помощью описанного выше метода.
Сверху видно, что биты двоичной дроби имеют вес, уменьшающийся в два (2) раза с каждым позиционным шагом вправо или, наоборот, вес становится вдвое (1/2 раза) в пересчете на десятичный эквивалент.
Преобразование десятичной дроби в двоичную
Для преобразования десятичной дроби в ее двоичный эквивалент применяется метод, использованный ранее для преобразования десятичной дроби в двоичную. Однако вместо многократного деления на два (2) применяется умножение дробной части.
Десятичное число, состоящее из целой и дробной части, требует преобразования каждой части отдельно. Для целочисленной части требуется метод повторного деления на 2, тогда как для дробной части требуется повторное умножение на 2.
Обсуждавшийся ранее метод преобразования десятичной дроби в двоичную применяется только к целой части, составляющей положительные веса. Целая часть десятичного числа многократно делится на два (2), отмечая остаток в обратном порядке (от LSB к MSB), пока разделенное десятичное значение не станет «0». Это показано ниже путем преобразования 238 ₁₀ в его двоичный эквивалент.
Следовательно, двоичный эквивалент числа 238 ₁₀ , состоящий только из целой части, равен 11101110 ₂ .
Аналогично, двоичный эквивалент дробной части десятичного числа находится повторным умножением на 2 и отметкой переносов вниз в порядке пересылки, пока дробная часть не станет равной «0». Данную десятичную дробь, которая будет заведомо меньше 1, умножают на два (2), в результате чего получается значение, которое будет либо больше, либо меньше единицы (1). Если в результате умножения получается значение меньше единицы (1), перенос вперед не выполняется, т. е. «0», и процесс умножения повторяется с отметкой «0», пока результат не станет равным или больше единицы. Умножение, в результате которого получается значение, большее или равное единице (1), производит перенос вперед, т. е. «1», и процесс умножения повторяется только для его дробной части (для случаев, когда умножение приводит только к значению больше единицы). В случае, если значение становится равным единице (1), дальнейшее умножение не применяется.
В некоторых случаях может показаться, что повторное умножение не сходится к решению, т. е. дает точную единицу или результирующую дробь, равную «0». В таких случаях дробные числа имеют бесконечную длину, а умножения или числовые биты ограничены для получения желаемой степени точности.
Примеры преобразования десятичной дроби в двоичную
Следующие примеры преобразования десятичной дроби в двоичную объясняют вышеупомянутый метод.
Двоичный эквивалент 0,625 ₁₀ равно 0,101 ₂ . Точно так же смешанное десятичное число (43,375 ₁₀ ) можно преобразовать в его двоичный эквивалент, как показано ниже:
Таким образом, двоичный эквивалент смешанного десятичного числа (43,375 ₁₀ 2) 101011.011 _2.
Заключение
В двоичных числах используется система счисления с основанием 2, поэтому вес каждой двоичной цифры (бита) равен 2 ⁿ, где «n» представляет позицию этого бита относительно двоичной точки.
Биты слева от двоичной точки (.) имеют позиции в положительной последовательности, т. е. 0, 1, 2, 3 и т. д. Тогда как справа имеют позиции в отрицательной последовательности, т. е. -1, -2, -3, -4 и т. д., которые составляют двоичную дробь.
Для позиций прямой последовательности вес каждого бита увеличивается в два раза на каждый шаг увеличения позиции. В то время как для позиций обратной последовательности (двоичная дробь) вес каждого бита уменьшается в два раза для каждого шага уменьшения позиции.
No related posts.