Неравенства с модулем
Продолжаем изучать модуль числа. Сегодня мы научимся решать неравенства с модулем.
Чтобы решать неравенства с модулем, нужно прежде всего уметь решать простейшие линейные неравенства, а также знать что такое модуль и как его раскрывать.
Независимо от того, решаем мы уравнение или неравенство, нужно уметь раскрывать модуль.
Рассмотрим к примеру простейшее неравенство с модулем:
|x| > 2
Чтобы решить данное неравенство раскроем его модуль.
Если подмодульное выражение больше или равно нулю, то исходное неравенство примет вид:
x > 2
Решением этого неравенства является множество всех чисел, бóльших 2. Отметим их на координатной прямой:
А если подмодульное выражение меньше нуля, то исходное неравенство примет вид:
−x > 2
Умнóжим обе части этого неравенства на −1. Тогда полýчим неравенство x < −2. Решением этого неравенства является множество всех чисел, мéньших −2.
Забавно, но получившиеся промежутки x < −2 и x > 2 являются ответом к нашей задаче. Если в исходное неравенство |x| > 2 подставить какое-нибудь значение x, удовлетворяющее данному неравенству, то это значение будет принадлежать промежутку (−∞ ; −2) или промежутку (2 ; +∞).
То есть решением исходного неравенства является совокупность из x < −2 и x > 2
Совокупностью неравенств мы будем называть несколько неравенств, объединённых квадратной скобкой, и которые имеют множество решений, удовлетворяющих хотя бы одному из неравенств, входящих в данную совокупность.
Чтобы записать окончательный ответ, промежутки x < −2 и x > 2 следует объединить. В математике знаком объединения служит ∪. Тогда:
x ∈ (−∞ ; −2) ∪ (2 ; +∞)
Знак объединения ∪ читается как «или».
Тогда запись x ∈ (−∞ ; −2) ∪ (2 ; +∞) можно прочитать так:
Значение переменной x принадлежит промежутку (−∞ ; −2) или промежутку (2 ; +∞)
Действительно, если подставить какое-нибудь значение x, являющееся решением исходного неравенства, то это значение будет принадлежать промежутку (−∞ ; −2) или промежутку (2 ; +∞).
Например, число 3, является решением исходного неравенства |x| > 2
|3| > 2 ⇔ 3 > 2
Значение 3 принадлежит промежутку (2 ; +∞). Также оно удовлетворяет хотя бы одному из неравенств совокупности , а именно неравенству x>2.
Значение −4 тоже является решением исходного неравенства |x| > 2. Это значение принадлежит промежутку (−∞ ; −2)
|−4| > 2 ⇔ 4 > 2
Также значение −4 удовлетворяет хотя бы одному из неравенств совокупности , а именно неравенству x < −2.
Согласно определению, модуль числа x есть расстояние от начала координат до точки x.
В неравенстве |x| > 2 это расстояние больше чем 2.
Действительно, от начала координат (точка 0) любое расстояние бóльшее двух, будет решением неравенства |x| > 2
Ответ: x ∈ (−∞ ; −2) ∪ (2 ; +∞)
Обратите внимание, что границы −2 и 2 не включены в соответствующие промежутки. Это потому, что при подстановке этих чисел в исходное неравенство, получается неверное неравенство.
Теперь немного поменяем наш пример. В неравенстве|x| > 2 поменяем знак > на знак <
|x| < 2
Решим это неравенство.
Как и раньше для начала раскрываем модуль. Если подмодульное выражение больше или равно нулю, то получим неравенство x < 2. Решениями этого неравенства являются все числа, мéньшие двух. Отметим их:
А если подмодульное выражение меньше нуля, то получим неравенство −x < 2. Умнóжим обе части этого неравенства на −1. Тогда получим неравенство x > −2.
Решениями этого неравенства являются все числа, бóльшие −2. Отметим эти решения на том же рисунке, где мы отметили решения для неравенства x < 2.
Для наглядности, решения неравенства x > −2 отметим красным цветом:
Если выражение |x| это расстояние от начала координат до точки x, то неравенство |x| < 2 говорит, что это расстояние меньше чем 2. На рисунке видно, что от начала координат расстояния, мéньшие двух, лежат в промежутках от −2 до 0 и от 0 до 2
А эти расстояния одновременно будут принадлежать промежуткам x < 2 и x > −2
Обратите внимание, что в этот раз промежутки обрамлены знáком системы, а не знáком совокупности как в прошлом примере. Это означает, что значения x одновременно удовлетворяют обоим неравенствам (промежуткам x < 2 и x > −2)
То есть решением неравенства |x| < 2 является пересечение промежутков x < 2 и x > −2.
Напомним, что пересечением двух промежутков является промежуток, состоящий из чисел, которые принадлежат как первому промежутку так и второму:
x ∈ (−2 ; 0) ∩ (0 ; 2)
Знак пересечения ∩ читается как «и». Тогда запись x ∈ (−∞ ; 2) ∩ (−2 ; +∞) можно прочитать так:
Значение переменной x одновременно принадлежит промежутку (−∞ ; 2) и промежутку (−2 ; +∞)
Действительно, если подставить какое-нибудь значение x, являющееся решением неравенства |x| < 2, то это значение будет принадлежать одновременно промежутку (−∞ ; 2) и (−2 ; +∞).
Например, число 1 является решением исходного неравенства |x| < 2
|1| < 2 ⇔ 1 < 2
Значение 1 одновременно принадлежит промежутку (−∞ ; 2) и промежутку (−2 ; +∞)
Также, значение 1 удовлетворяет обоим неравенствам системы
А если к примеру подставить значение, не являющееся решением неравенства |x| < 2, то это значение не будет одновременно принадлежать промежуткам (−∞ ; 2) и (−2 ; +∞).
Например, значение 7
|7| < 2 ⇔ 7 < 2
Несмотря на то, что значение 7 принадлежит одному из промежутков, а именно промежутку (−2 ; +∞), данное значение не является решением исходного неравенства, поскольку оно не удовлетворяет ему. Также, данное значение не принадлежит одновременно обоим промежуткам: (−∞ ; 2) и (−2 ; +∞).
Для неравенства |x| < 2 ответ можно записать покороче:
x ∈ (−2 ; 2)
Из рассмотренных примеров видно, что решением неравенства с модулем может быть либо объединение промежутков либо их пересечение.
В первом примере мы решили неравенство |x| > 2, то есть неравенство вида |x| > a. Это неравенство при котором модуль больше какого-нибудь числа или буквенного выражения. Решением такого неравенства является объединение решений неравенств, получающихся после раскрытия модуля исходного неравенства. Неравенства, получающиеся после раскрытия модуля, следует записывать в виде совокупности:
Совокупность свóдится потому, что итоговые решения будут удовлетворять хотя бы одному из неравенств, полученных после раскрытия модуля исходного неравенства.
Во втором примере мы решили неравенство |x| < 2, то есть неравенство вида |x| < a. От предыдущего неравенства оно отличается только знáком. Но это неравенство при котором модуль меньше какого-нибудь числа или буквенного выражения. Решением такого неравенства является пересечение решений неравенств, получающихся после раскрытия модуля исходного неравенства. Неравенства, получающиеся после раскрытия модуля, следует записывать в виде системы:
Система записывается потому, что итоговые решения будут удовлетворять обоим неравенствам, полученным после раскрытия модуля исходного неравенства.
Эти же правила сохраняются и для неравенств, содержащих знаки ≥ и ≤
Например, решим неравенство |x| ≥ 1. Модуль больше или равен числу. Поэтому решением будет объединение
Решением служит объединение промежутков x ≤ −1 и x ≥ 1
x ∈ (−∞ ; −1] ∪ [1 ; +∞)
Обратите внимание, что границы −1 и 1 включены в соответствующие промежутки.
Это потому что при подстановке этих чисел в исходное неравенство, получается верное неравенство.
Решим теперь к примеру неравенство |x| ≤ 1. Модуль меньше или равен числу. Поэтому решением будет пересечение решений неравенств, которые получатся после раскрытия модуля. После раскрытия модуля и выполнения необходимых тождественных преобразований, получим систему неравенства: x ≤ 1 и x ≥ −1
Решением служит пересечение промежутков x ≤ 1 и x ≥ −1
x ∈ (−∞ ; 1] ∩ [−1 ; +∞)
или покороче:
x ∈ [−1 ; 1]
Обратите внимание, что границы −1 и 1 включены в соответствующие промежутки. Это потому что при подстановке этих чисел в исходное неравенство, получается верное неравенство.
Аналогично решаются неравенства, в левой части которого модуль, а справа не просто число, а буквенное выражение.
Пример 4. Решить неравенство |7x − 6| < x + 12
Решение
Для начала раскроем модуль. Вспоминаем, что если неравенство содержит знак < или ≤, то неравенства получившиеся после раскрытия модуля, следует записать в виде системы. Это будет означать, что итоговые решения будут удовлетворять обоим неравенствам.
Итак, после раскрытия модуля получим следующую систему:
В данном случае система содержит не совсем элементарные неравенства как в прошлых примерах. Данные неравенства следует упростить, используя известные тождественные преобразования.
Раскроем скобки во втором неравенстве. Тогда получим следующую систему:
В обоих неравенствах выражения, содержащие неизвестные, перенесём в левую часть, а числовые выражения — в правую. Затем приведём подобные слагаемые. Тогда получим систему:
В первом неравенстве разделим обе части на 6. Во втором неравенстве разделим обе части на −8.
Тогда получим окончательную систему:
Изобразим решения на координатной прямой:
Решением является пересечение промежутков (−∞ ; 3) и , то есть промежуток
Ответ:
Пример 5. Решить неравенство |1 − 2x| ≥ 4 − 5x
Решение
Для начала раскроем модуль. Вспоминаем, что если неравенство содержит знак > или ≥, то неравенства получившиеся после раскрытия модуля, следует записать в виде совокупности:
После раскрытия модуля получим следующую совокупность:
Выполним необходимые тождественные преобразования в обоих неравенствах. В результате получим:
Изобразим решения на координатной прямой:
Решением является объединение промежутков и [1 ; +∞), то есть промежуток
Ответ: .
Задание 1. Решить неравенство:
Решение:
Ответ: x ∈ (−36 ; 36).
Показать решение
Задание 2.
Решить неравенство:
Решение:
Ответ: x ∈ (−∞ ; −2) ∪ (2 ; +∞).
Показать решение
Задание 3. Решить неравенство:
Решение:
Ответ:
Показать решение
Задание 4. Решить неравенство:
Решение:
Ответ: x ∈ [−5 ; 2]
Показать решение
Задание 5. Решить неравенство:
Решение:
Ответ: x ∈ (−∞ ; 0)
Показать решение
Задание 6. Решить неравенство:
Решение:
Ответ:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
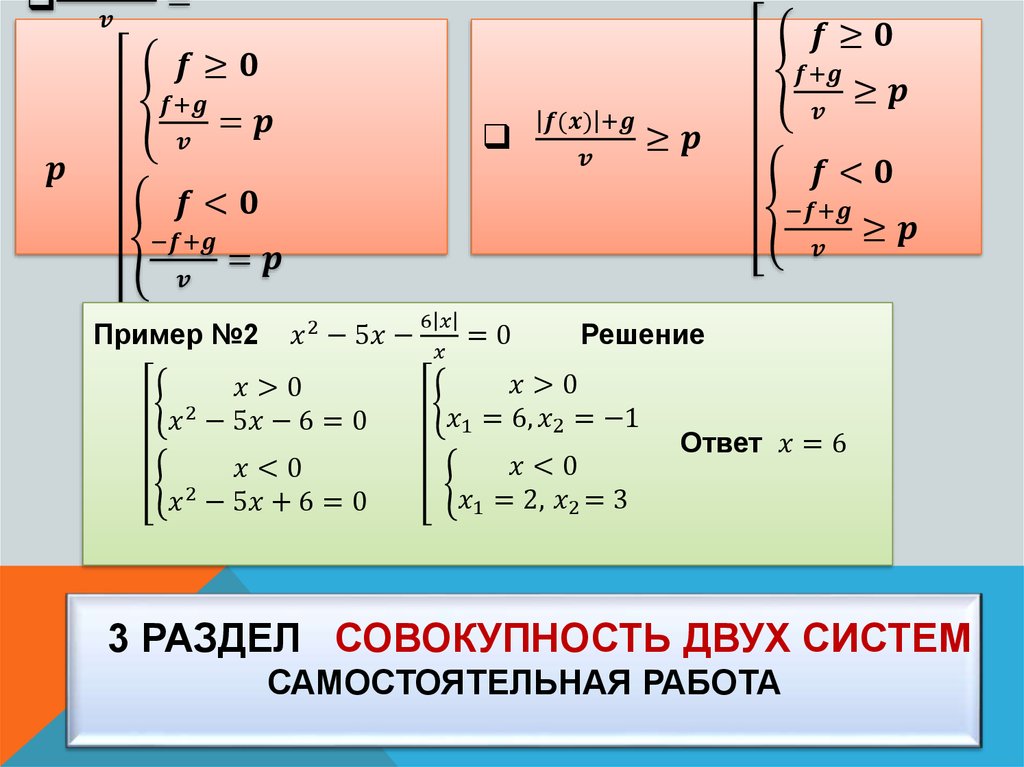
25.
Неравенства с модулемI тип: Неравенство содержит некоторое выражение под модулем и число вне модуля:
где (3.27)
Решение зависит от знака числа А.
1. Если то неравенство (3.27) не имеет решений.
2. Если то неравенство (3.27) равносильно системе неравенств
где (3.28)
1. Если то неравенство (3.28) не имеет решений.
2. Если то неравенство (3.28) равносильно уравнению
3. Если , то неравенство (3.28) равносильно системе неравенств
где (3.29)
1. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения
2. Если то решением неравенства (3.29) является множество всех значений Х из ОДЗ выражения таких, что
3. Если то неравенство (3.29) равносильно совокупности
где (3.30)
1. Если то решением неравенства (3.30) является множество всех значений Х из ОДЗ выражения
2. Если то неравенство (3.
30) равносильно совокупности
II тип: Неравенство, которое содержит выражение с переменной под знаком модуля и вне его:
(3.31)
Где – некоторые выражения с переменной Х.
Для решения неравенств типа (3.31) можно использовать следующие способы.
1-й способ: используя определение модуля, получаем равносильную совокупность систем:
2-й способ: Решаем аналогично решению неравенства (3.29) при дополнительном ограничении на знак выражения
1. Если
(3.32)
То решением является множество всех значений Х из ОДЗ выражения которые удовлетворяют условию (3.32).
2. Если
То решением является множество всех значений Х, которые удовлетворяют системе
3. Если решение определяется системой
Ответом в решении неравенства (3.31) является объединение всех решений, полученных на этапах 1–3.
3-й способ: метод интервалов.
Для решения необходимо:
1) найти значения Х, для которых
2) найденные значения Х нанести на числовую ось;
3) определить знак выражения на всех полученных промежутках;
4) нарисовать кривую знаков;
5) раскрыть модуль, пользуясь рисунком, и получить соответствующее неравенство, которое следует решить вместе с условием принадлежности переменной Х определенному промежутку;
6) в ответе неравенства указать совокупность полученных решений.
III тип: Неравенство содержит несколько модулей и решается двумя способами:
1-й способ: Можно использовать определение модуля и решать совокупность систем неравенств. Этот способ, как правило, не является рациональным.
2-й способ: использовать метод интервалов. Необходимо нарисовать столько числовых осей и кривых знаков, сколько модулей содержится в неравенстве. Для каждого промежутка следует решать полученное после раскрытия модулей неравенство при условии, что переменная Х принадлежит конкретному промежутку. В ответе указывают объединение всех полученных решений.
IV тип: Неравенство вида
где (3.33)
Решается двумя способами:
1-й способ: метод интервалов.
2-й способ: согласно теореме равносильности (см. свойства равносильности неравенств (3.22) и (3.23)) неравенство (3.33) можно возводить в квадрат:
Решение неравенства (3.33) сводится к решению неравенства
Аналогично решают неравенства IV типа (3.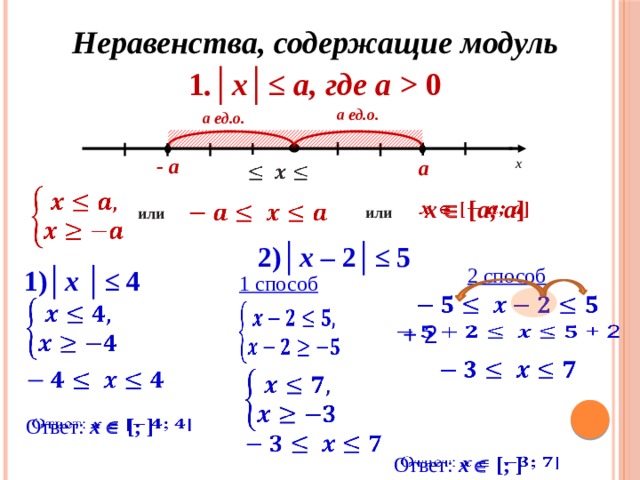
33), если они заданы со знаками
V тип: Неравенства, решаемые заменой переменной.
В таком случае выражение с модулем обозначают новой переменной. Неравенство с новой переменной решают до конца (т. е. до возможного получения промежутков решения для новой переменной). Затем возвращаются к старой переменной и решают полученные неравенства с модулем как неравенства I типа.
Пример 1. Решить неравенства:
1) 2)
3) 4)
5) 6)
Решение. 1) Решаем как неравенство I типа:
Получаем ответ:
2) Решаем как неравенство I типа:
Второе неравенство совокупности не имеет решения (соответствующая парабола лежит над осью Ох). Первое неравенство сводится к виду
Его решение: это и есть ответ.
3) Решаем как неравенство II типа. Оно имеет решение, если Поэтому получаем равносильную систему:
Получаем ответ:
4) Заданное неравенство может быть записано в виде
Заменим переменную Решаем неравенство
Его решение
Возвращаемся к переменной Х и решаем совокупность
Получаем
Т. е. приходим к ответу
5) Для решения неравенства используем метод интервалов. Запишем неравенство в виде
Построим числовые прямые и определим знаки выражений, стоящих под модулем (рис. 3.10).
ОДЗ:
Рис. 3.10
А) рассмотрим неравенство на 1-м промежутке. Получаем систему
(3.34)
Решаем неравенство
Получаем
Система (3.34) сводится к системе
На данном промежутке решений нет.
Б)
Если , то С учетом рассматриваемого промежутка имеем:
Получаем
В)
Решением является промежуток:
Объединим полученные решения и приходим к ответу:
6)
ОДЗ:
Введем новую переменную:
тогда и приходим к неравенству вида
Решаем его
Используем метод интервалов (рис. 3.11).
Рис.
3.11
Запишем полученное решение в виде совокупности:
Вернемся к переменной Х:
(3.35)
– выполняется при любых
С учетом ОДЗ второе неравенство системы (3.35) равносильно системе
Получаем ответ:
| < Предыдущая | Следующая > |
|---|
абсолютное значение — Двойной модуль в неравенстве
спросил
Изменено 10 лет, 6 месяцев назад
Просмотрено 2к раз
$\begingroup$
Может кто-нибудь объяснить мне (или дать ссылку на сайт, который делает), как решить эту проблему?
$$
||х+1| -1| \geq 3
$$
Я понятия не имею, как вычислить этот знак двойного абсолютного значения.
- неравенство
- абсолютное значение
$\endgroup$
1
$\begingroup$
Работа снаружи внутрь. Для начала у вас есть неравенство $|u-1|\ge 3$, где $u=|x+1|$. Это эквивалентно $$u-1\le -3\quad\mathbf{or}\quad u-1\ge 3\;.$$ Решая их, мы находим, что $$u\le-2\quad\mathbf {или}\quad u\ge 4\;,$$, что в терминах исходной переменной $x$ равно
$$|x+1|\le -2\quad\mathbf{or}\quad|x+1|\ge 4\;.\tag{1}$$
Абсолютное значение невозможно отрицательно, поэтому $(1)$ сводится к $|x+1|\ge 4$. Как и в самом первом шаге, это эквивалентно
$$x+1\le-4\quad\mathbf{or}\quad x+1\ge 4\;,$$, решение которого равно
$$x \le-5\quad\mathbf{or}\quad x\ge 3\;.$$
$\endgroup$
4
$\begingroup$
Так как у тебя уже есть раствор снаружи, я открою тебе изнанку.
Сначала возьмем случай $x+1\geq 0$. Таким образом, $||x+1|-1|=|x+1-1|=|x|$.
$|x|\geq3$ имеет решение $x\leq-3$ или $x\geq3$. Зная, что $x\geq-1$, первое невозможно.
Теперь рассмотрим $x+1\leq0$. Таким образом, $||x+1|-1|=|-(x+1)-1|=|-x-2|=|x+2|$. $|x+2|\geq3$ имеет решение $x\leq-5$ или $x\geq1$. Зная, что $x\leq-1$, второе невозможно.
92=(а-б)(а+б)\\
&\Longleftrightarrow (x-3)(x+5)\geq 0\\
&\Longleftrightarrow x\in(-\infty,-5]\cup[3,+\infty)
\end{выравнивание}
$$
$\endgroup$
$\begingroup$
Если бы я был перед классом, который столкнулся с этой проблемой, я бы изобразил ее на графике, проанализировав ее изнутри. Во-первых, $|x+1|$ имеет V-образный граф с вершиной в $(-1,0)$. Тогда $|x+1|-1$ также имеет V-образный граф с вершиной в $(-1,-1)$. Обратите внимание, что этот график пересекает ось $x$ в точке $(-2,0)$ и начале координат.
Когда вы берете абсолютное значение функции $|x+1|-1$, часть графика, расположенная ниже оси $x$, отражается выше. Результат теперь W -образный график с левым углом в $(-2,0)$, средним углом в $(-1,1)$ и прямым углом в начале координат. Слева от $(-2,0)$ график поднимается (по мере удаления от начала координат) с наклоном $-1$, т.е. имеет уравнение $y=-x-2$, а справа от начала координат, график поднимается с наклоном $1$, т.е. просто $y=x$. Чтобы значение этой функции было не меньше $3$, нужно справа $x\ge3$, а слева $x\le-5$.
$\endgroup$
Как решать неравенства с модулем
Как решать неравенства с модулем :
В этом разделе мы узнаем, как решить неравенство с модулем.
Решение неравенств по модулю — концепция
Если задан вопрос в любой из следующих форм, мы должны следовать данным методам для решения x.
Вопросы в форме | Первый шаг, который нужно сделать | Решение |
|х — а| < r | -г < х - а < г | (-р + а, г + а) |
|х — а| ≤ г | -r ≤ x — a ≤ r | [а- г, а + г] |
|х — а| > r | х — а < -r и х — а > r | (∞,a-r)U(a+r,∞) |
|х — а| ≥ р | х — а ≤ -r и х — а ≥ r | (∞,а-р]U[а+r,∞) Пример 1 < 2 и выразить решение в виде интервалов. Решение: -2 < x - 9 < 2 Добавьте 9 к уравнению -2 + 9 < x - 9 + 9 < 2 + 9 7 < x < 11 неравенство (7, 11). Пример 2 : Решите абсолютное неравенство, приведенное ниже |2/ (x — 4)| > 1 , x ≠ 4 и выразить решение в виде интервалов. Решение: Из данного неравенства получаем, что 2 > (x — 4) -2 < x - 4 < 2 Добавьте 4 по всему неравенству -2 + 4 < x - 4 + 4 < 2 + 4 2 < x < 6 Мы не можем выразить решение в виде (2 , 6). Потому что в середине 2 и 6 у нас есть значение 4. Итак, мы должны разбить его на два интервала. (2, 4) U (4, 6) Пример 3 : Решите абсолютное неравенство, приведенное ниже |3 — (3x/4)| ≤ 1/4 и выразить решение в виде интервалов. Решение: (-1/4) ≤ 3 — (3x/4) ≤ (1/4) (-1/4) ≤ (12 — 3x)/4 ≤ (1/4) Умножить на 4 во всем уравнении -1 ≤ (12 — 3x) ≤ 1 Вычесть 12 во всем уравнении -1 — 12 ≤ 12 — 3x — 12 ≤ 1 -12 -13 ≤ — ≤ -11 Делится на (-3) во всем уравнении -13/(-3) ≤ — 3x ≤ -11 13/3 ≤ x ≤ 11/3 11/3 ≤ x ≤ 13/ 3 Следовательно, набор решений приведенного выше абсолютного неравенства равен [11/3, 13/3]. |
