ГДЗ учебник по алгебре 8 класс Макарычев. 25. Решение дробных рациональных уравнений Номер 605
- Учебники
- 8 класс
- Алгебра 👍
- Макарычев
- №605
авторы: Макарычев, Миндюк, Нешков, Суворова.
издательство: «Просвещение» 2013 г
Раздел:
- Предыдущее
- Следующее
Найдите корни уравнения:
а)
x−4x−5+x−6x+5=2
;
б)
12−x−1=1x−2−6−x3x2−12
;
в)
;
г)
3y−2+7y+2=10y
;
д)
x+3x−3+x−3x+3=313
;
е)
5x+7x−2−2x+21x+2=823
.
reshalka.com
Решение а
x−4x−5+x−6x+5=2
|*(x − 5)(x + 5)
{(x−4)(x+5)+(x−6)(x−5)=2(x2−25)x≠±5
x2+x−20+x2−11x+30=2×2−50
−10x = −60
x = 6
{x=6x≠±5
Ответ: x = 6
Решение б
12−x−1=1x−2−6−x3x2−12
−12−x−1=1x−2−6−x3x2−12
2x−2−6−x3(x2−4)+1=0
|*3(x − 2)(x + 2)
{6(x+2)−(6−x)+3(x2−4)=0x≠±2
6x+12−6+x+3×2−12=0
3×2+7x−6=0
(3x − 2)(x + 3) = 0
x1=−3
x2=23
{x1=−3,x2=23x≠±2
Ответ:
x1=−3
x2=23
Решение в
7y−3y−y2=1y−1−5y(y−1)
−7y−3y2−y=1y−1−5y(y−1)
1y−1−5y(y−1)+7y−3y(y−1)=0
1y−1+7y−8y(y−1)=0
|* y(y − 1)
{y+7y−8=0y≠0;1
{8y=8y≠0;1
{y=1y≠0;1
Ответ: y = ∅ − нет решений
Решение г
3y−2+7y+2=10y
|* y(y − 2)(y + 2)
{3y(y+2)+7y(y−2)=10(y2−4)y≠0;±2
3y2+6y+7y2−14y=10y2−40
3y2+6y+7y2−14y−10y2+40=0
−8y = −40
y = 5
{y=5y≠0;±2
Ответ: y = 5
Решение д
x+3x−3+x−3x+3=313
|* 3(x − 3)(x + 3)
{3(x+3)2+3(x−3)2=10(x2−9)x≠±3
3(x2+6x+9)+3(x2−6x+9)=10×2−90
3×2+18x+27+3×2−18x+27−10×2+90=0
−4×2=−144
x2=36
x = ±6
{x=±6x≠±3
Ответ:
x1=−6
x2=6
.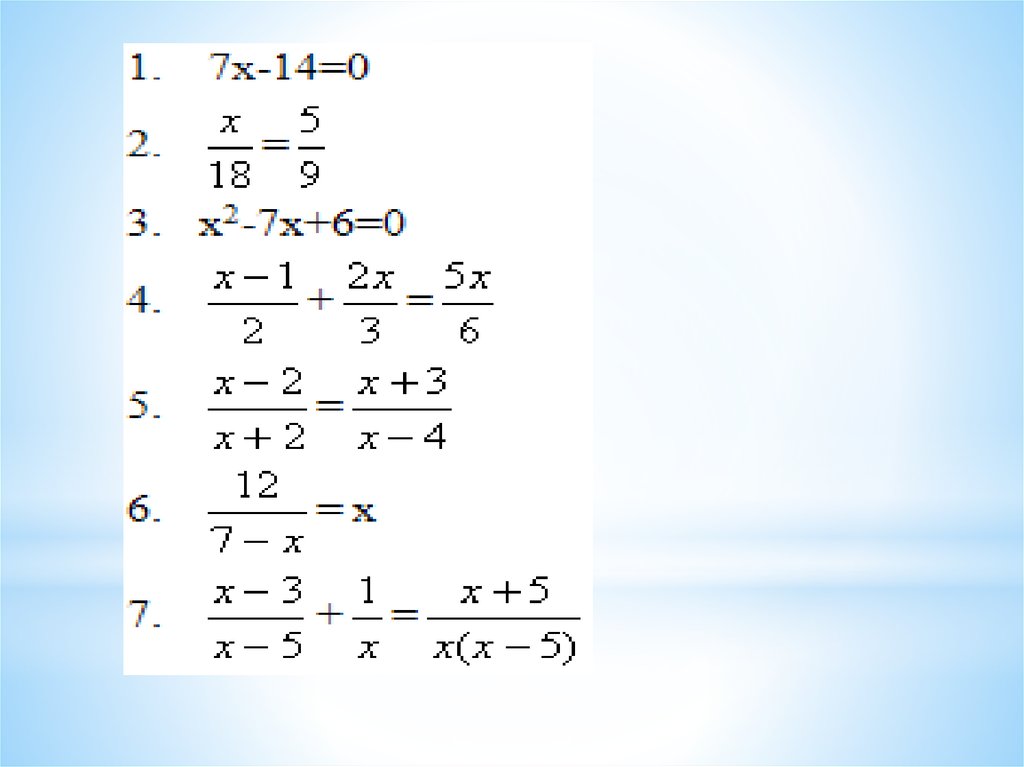
Решение е
5x+7x−2−2x+21x+2=823
|*3(x − 2)(x + 2)
{3(5x+7)(x+2)−3(2x+21)(x−2)=26(x2−4)x≠±2
3(5×2+17x+14)−3(2×2+17x−42)=26×2−104
15×2+21x+42−6×2−51x+126=26×2−104
9×2+168=26×2−104
17×2=272
x2=16
x = ±4
{x=±4x≠±2
Ответ:
x1=−4
;
x2=4
.
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом
Дробные рациональные уравнения
У р о к алгебры 9 класс
ТЕМА : дробные рациональные уравнения
Цели: Образовательные : продолжить формирование умения решать дробно-рациональные уравнения, используя алгоритм, известный учащимся из курса 8 класса; дать определение «дробно-рациональные уравнения», показать способы решения таких уравнений.
2. Развивающие: развитие умений и навыков решать примеры с данным типом уравнений, находить корни дробно-рациональных уравнений.
3. Воспитывающие: воспитывать внимание, внимательность, активность, аккуратность; уважительное отношение к матери; заинтересовать учеников предметом, показать важность умения решать разные уравнения и задачи.
Тип урока: комбинированный.
Ход урока
Организационный момент.
Проверить готовность к уроку. Проверка домашнего задания ( по готовым решениям)
II. Устная работа.
Верно ли, что выражение обращается в нуль:
а) при х = 2;
б) при х = –5;
в) при х = 1.
— Как называется данное уравнение? Сколько корней имеет данное уравнение?
Скажите, какой степени это уравнение? Сколько корней имеет данное уравнение?
Скажите, какой степени это уравнение? Сколько корней имеет данное уравнение?
Как называется данное уравнение?
III. Объяснение нового материала.
Объяснение нового материала.
В 8 классе учащиеся уже изучали данную тему. Сейчас необходимо расширить их знания.
Отличия дробно-рациональных уравнений, изучаемых в 9 классе, состоят в следующем:
1) получаемое в процессе решения целое уравнение имеет степень, большую двух;
2) некоторые дробно-рациональные уравнения возможно решить, только используя метод введения новой переменной.
1. И з у ч е н и е п о н я т и я дробно-рационального уравнения.
Уравнение y(x) =0 называют дробным рациональным уравнением, если выражение y(x) является дробным ( т.е. содержит деление на выражение с переменными).
Для решения рационального уравнения его необходимо преобразовать в линейное или квадратное уравнение, решить это уравнение и отбросить те корни, которые не входят в ОДЗ (область допустимых значений) исходного рационального уравнения.
Усвоение данного понятия проверяется при решении упражнения на распознавание этого вида уравнений.
З а д а н и е. Какие из следующих уравнений являются дробно-рациональными? Ответ объясните.
а) ; г) ;
б) ; д) ;
в) ; е) .
2. В ы в о д а л г о р и т м а решения дробно-рациональных уравнений
Алгоритм решения дробных рациональных уравнений:
Найти допустимые значения дробей, входящих в уравнение.
Найти общий знаменатель дробей, входящих в уравнение.
Умножить обе части уравнения на общий знаменатель.
Решить получившееся уравнение.
Исключить корни, не входящие в допустимые значения дробей уравнения
3. Р а с с м о т р е н и е п р и м е р о в решения дробно-рациональных уравнений по изученному алгоритму (пример 1 и пример 3 из учебника).
IV. Формирование умений и навыков.
Упражнения:
1. № 288 (а, в), № 289 (а).
2. № 290 (а), № 292 (б).
3. № 291 (в).
Р е ш е н и е
;
;
;
х (х – 2) = 4 (х + 2) – 16;
х2 – 2х – 4х – 8 + 16 = 0;
х2 – 6х + 8 = 0;
х1 = 2, х2 = 4;
х1 = 2 – не является корнем уравнения.
О т в е т: 4.
4. № 296 (а).
Р е ш е н и е
;
5а + 7 – 28а2 = 20а3;
5а + 7 – 4а2 (7 + 5а) = 0;
(5а + 7) (1 – 4а2) = 0;
5а + 7 = 0; или 5а = –7; а = –1,4. | 1 – 4а2 = 0; а2 = ; а = ± . |
О т в е т: –1,4; ±0,5.
Самостоятельная работа. Самоконтроль – 4 варианта.
В а р и а н т 1. | В а р и а н т 2. |
В а р и а н т 3. | В а р и а н т 4. |
О т в е т ы:
I вариант: , ( ; ).
II вариант: ( ; )
III вариант: ( )
IV вариант: , ( ; ).
VII. Физкультминутка.
Учитель: А теперь разминка.
— Повернитесь ко мне. Я проговариваю предложения. Если оно справедливо – вы встаёте, если нет – то остаётесь сидеть.
1) 5х = 7 имеет единственный корень.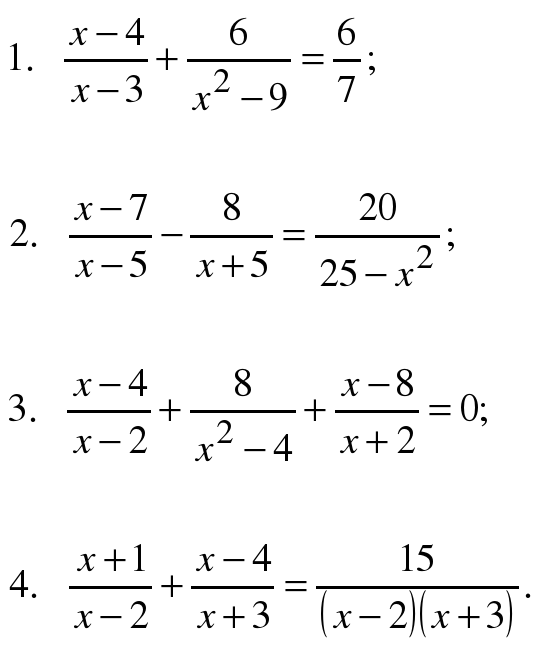
2) 0х = 0 не имеет корней.
3) Если Д 0, то квадратное уравнение имеет два корня.
4) Если Д
5) Количество корней не больше степени уравнения
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие уравнения называются дробно-рациональными?
– Являются ли следующие уравнения дробно-рациональными:
?
– Опишите алгоритм решения дробно-рациональных уравнений.
Домашнее задание: № 289 (б), № 290 (б), № 291 (б), № 295 (б).
Общие базовые стандарты для 7-го класса
Ниже приведены общие базовые стандарты для 7-го класса со ссылками на поддерживающие их ресурсы. Мы также поощряем множество упражнений и работу с книгами.
7 класс | Соотношения и пропорциональные отношения
Анализируйте пропорциональные отношения и используйте их для решения реальных и математических задач.
7.RP.A.1 Вычислить удельные нормы, связанные с отношениями дробей, включая соотношения длин, площадей и других величин, измеренных в одинаковых или разных единицах. Например, если человек проходит 1/2 мили каждые 1/4 часа, рассчитайте удельную скорость как комплексную дробь (1/2)/(1/4) мили в час, что эквивалентно 2 милям в час.
Соотношения
Эквивалентные фракции
Соотношение — Рецепт шоколадных чипсов
Соотношение — Приготовление шоколадных чипсов
7.RP.A.2 Распознавать и представлять пропорциональные отношения между величинами.
а. Определите, находятся ли две величины в пропорциональном соотношении, например, проверив эквивалентные отношения в таблице или нарисовав график на координатной плоскости и наблюдая, является ли график прямой линией, проходящей через начало координат.
с. Представьте пропорциональные отношения уравнениями. Например, если общая стоимость t пропорциональна количеству n товаров, купленных по постоянной цене p, соотношение между общей стоимостью и количеством товаров может быть выражено как t = pn.
д. Объясните, что означает точка (x, y) на графике пропорциональной зависимости с точки зрения ситуации, обратив особое внимание на точки (0, 0) и (1, r), где r — единичная ставка.
Коэффициенты
Цена за единицу
Игра с ценой за единицу
Головоломка «Стадо верблюдов»
Стадо верблюдов — решение
Задание: трава для сада
Ratio — Рецепт шоколадных чипсов
Ratio — Приготовьте шоколадные чипсы
7.RP.A.3Используйте пропорциональные соотношения для решения многошаговых задач на соотношение и проценты. Примеры: простые проценты, налоги, надбавки и уценки, чаевые и комиссионные, сборы, процентное увеличение и уменьшение, процентная ошибка.
Коэффициенты
процентная ошибка
процентное изменение
процентные пункты
процент калькулятора
Процент Разница
Проверьте свои проценты
Введение в проценты
процентные процентные процентные проценты Процент. Система счисления
Система счисления
Применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел.
7.NS.A.1 Применение и расширение предыдущего понимания сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями.
б. Под p + q понимается число, расположенное на расстоянии |q| от p в положительном или отрицательном направлении в зависимости от того, является ли q положительным или отрицательным. Покажите, что число и его противоположность имеют сумму 0 (аддитивные инверсии). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
с. Поймите вычитание рациональных чисел как добавление обратного аддитивного, p — q = p + (-q).
 Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира.
Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира. д. Применяйте свойства операций как стратегии сложения и вычитания рациональных чисел.
Обратное
Кейси Раннер
Абсолютное значение
Рациональные числа
Использование числовой строки
Сложение и вычитание положительных и отрицательных чисел
7.NS.A.2 Применить и расширить прежнее понимание умножения и деления и дробей для умножения и деления рациональных чисел.
а. Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (-1)(-1) = 1, и правилам умножения чисел со знаком. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
б. Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом.
с. Применяйте свойства операций как стратегии умножения и деления рациональных чисел.
д. Преобразование рационального числа в десятичное с использованием длинного деления; известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется.
Обратный
Взаимный
Long Division
Разделение на ноль
Разделительные фракции
Фракционные рабочие листы
Умножение фракции
. Рабочие листы деления
Обратная дробь
Умножение смешанных чисел
Полное деление — введение
Длинное деление на десятичные разряды
Умножение отрицательных значений дает положительное число
7.NS.A.3 Решите реальные и математические задачи, связанные с четырьмя операциями с рациональными числами. (Вычисления с рациональными числами расширяют правила обращения с дробями до сложных дробей.
Обратное
Длинное деление
Сложение дробей
Деление дробей
Таблицы дробей
Умножение дробей3
04 Вычитание фракций
с использованием номеров
с использованием рациональных номеров
Анимация длинного дивизиона
Математические листы по математике
Рабочие листы длинного подразделения
Умножение смешанных номеров
Долгое подразделение — Введение
Long Division To Decimal Places
Долгое подразделение. и вычитание смешанных дробей
Умножение отрицательных чисел дает положительное число
Сложение и вычитание положительных и отрицательных чисел
7 класс | Выражения и уравнения
Используйте свойства операций для создания эквивалентных выражений.
7.EE.A.1 Применение свойств операций в качестве стратегий для сложения, вычитания, факторизации и расширения линейных выражений с рациональными коэффициентами.
Подобные термины
Факторинг в алгебре
Наибольший общий делитель
7. EE.A.2 Поймите, что переписывание выражения в различных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равнозначно «умножению на 1,05».
EE.A.2 Поймите, что переписывание выражения в различных формах в контексте задачи может пролить свет на проблему и на то, как связаны в ней величины. Например, a + 0,05a = 1,05a означает, что «увеличение на 5%» равнозначно «умножению на 1,05».
Подобные термины
Рациональные числа
Использование рациональных чисел
Десятичные дроби и проценты
Решайте реальные и математические задачи, используя числовые и алгебраические выражения и уравнения.
7.EE.B.3 Решайте многоэтапные задачи из реальной жизни и математические задачи, связанные с положительными и отрицательными рациональными числами в любой форме (целые числа, дроби и десятичные дроби), стратегически используя инструменты. Применяйте свойства операций как стратегии для расчетов с числами в любой форме; конвертировать между формами по мере необходимости; и оценить обоснованность ответов, используя умственные вычисления и стратегии оценки. Например: если женщина, зарабатывающая 25 долларов в час, получает надбавку на 10%, она будет получать дополнительную 1/10 своей зарплаты в час, или 2,50 доллара, за новую зарплату в 27,50 долларов. Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
Если вы хотите разместить полотенцесушитель 93/4 дюйма длиной в центре двери шириной 27 1/2 дюйма, вам нужно будет разместить планку примерно в 9 дюймах от каждого края; эту оценку можно использовать в качестве проверки точного вычисления.
Оценка
Абсолютное значение
Рациональные номера
ЗАГРАНИЧЕНИЯ
Использование рациональных чисел
Советы по оценке и хитростям
Орден операции — BODMAS
Орден Орден0003
7.EE.B.4Используйте переменные для представления величин в реальной или математической задаче и создавайте простые уравнения и неравенства для решения задач, рассуждая о величинах.
а. Решите текстовые задачи, ведущие к уравнениям вида px + q = r и p(x + q) = r, где p, q и r — конкретные рациональные числа. Решите уравнения этих форм бегло. Сравните алгебраическое решение с арифметическим, указав последовательность операций, используемых в каждом подходе. Например, периметр прямоугольника равен 54 см. Его длина составляет 6 см. Какова его ширина?
Какова его ширина?
б. Решите текстовые задачи, ведущие к неравенствам вида px + q > r или px + q < r, где p, q и r — конкретные рациональные числа. Нарисуйте график множества решений неравенства и интерпретируйте его в контексте проблемы. Например: как продавец, вам платят 50 долларов в неделю плюс 3 доллара за продажу. На этой неделе вы хотите, чтобы ваша зарплата была не менее 100 долларов. Напишите неравенство для количества продаж, которое вам нужно сделать, и опишите решения.
Инверсия
Аналогичные термины
Решение уравнений
График неравенства
Решение неравенства
Решение вопросов Word
Введение в алгебру
Введение в неравенство
Баланс при добавлении и подключении
. | Геометрия
Рисовать, строить и описывать геометрические фигуры и описывать отношения между ними.
7.G.A.1 Решение задач, связанных с чертежами геометрических фигур в масштабе, включая вычисление фактических длин и площадей по чертежу в масштабе и воспроизведение чертежа в масштабе в другом масштабе.
Соотношения
Подобные
Подобные треугольники
Активность: Насколько высоко?
7.Г.А.2 Нарисуйте (от руки, с линейкой и транспортиром и с техникой) геометрические фигуры с заданными условиями. Сосредоточьтесь на построении треугольников по трем мерам углов или сторон, отмечая, когда условия определяют уникальный треугольник, более одного треугольника или отсутствие треугольника.
Градусы
Круговая диаграмма
3 4 5 Треугольник
Использование транспортира
Упражнение: Как высоко?
Интерактивные треугольники
Треугольники, содержащие 180 градусов
Построение треугольника с 3 известными сторонами
7.G.A.3 Опишите двумерные фигуры, которые получаются в результате разрезания трехмерных фигур, таких как плоские сечения прямоугольных призм и прямоугольных пирамид.
Пирамиды
Поперечные сечения
Призмы с примерами
Упражнение: Исследование твердых тел
Решайте реальные и математические задачи, связанные с измерением угла, площади, площади поверхности и объема.
7.R.B.4 Знать формулы площади и длины окружности и использовать их для решения задач; дать неформальный вывод отношения между длиной окружности и площадью круга.
Пи
Периметр
Калькулятор площади
Площадь круга
Упражнение: Олимпийская легкая атлетика
Упражнение: Найдите приблизительное значение числа Пи
Площадь круга Треугольник Квадрат Прямоугольник Параллелограмм Трапеция Эллипс и сектор
7.RUS5Используйте факты о дополнительных, дополнительных, вертикальных и смежных углах в многошаговой задаче, чтобы написать и решить простые уравнения для неизвестного угла в фигуре.
Градусы
Внешний уголок
Внутренний уголок
Прямые углы
Вертикальные углы
Комплементарные углы
Дополнительные углы
Вертикально противоположные углы
Внешние углы многоугольников
Треугольники содержат 180 градусов
углы
. Прямая линия Добавить к 180
Прямая линия Добавить к 180
7.RUS6Решение реальных и математических задач, связанных с площадью, объемом и площадью поверхности двух- и трехмерных объектов, состоящих из треугольников, четырехугольников, многоугольников, кубов и прямых призм.
Заливная жидкость
Площадь калькулятор
Активность: суп банка
Объем кубоидных
Призмы с примерами
Прямоугольные призмы и кубики
Площадь квадратной площади треугольника. Прямоугольная параллелограмма Trapezium ellipsse и сектор
4
карта 77 7. 700044 40004 карка 7 7. 700044 40004. Статистика и вероятность
Используйте случайную выборку, чтобы делать выводы о населении.
7.SP.A.1 Понимать, что статистику можно использовать для получения информации о населении путем изучения выборки населения; обобщения о совокупности из выборки действительны только в том случае, если выборка репрезентативна для этой совокупности. Поймите, что случайная выборка, как правило, дает репрезентативные выборки и поддерживает достоверные выводы.
Что такое данные?
Вопросы опроса
Как провести опрос
Упражнение: Оценка
Упражнение: Длина листьев
Отображение результатов опроса
7.SP.A.2Используйте данные из случайной выборки, чтобы сделать выводы о совокупности с неизвестной интересующей характеристикой. Создайте несколько выборок (или смоделированных выборок) одинакового размера, чтобы оценить различия в оценках или прогнозах. Например, оцените среднюю длину слова в книге путем случайной выборки слов из книги; предсказать победителя школьных выборов на основе случайно выбранных данных опроса. Оцените, насколько далеко может быть оценка или прогноз.
Вопросы опроса
Как провести опрос
Упражнение: Оценка
Демонстрация результатов опроса
Сделайте неформальные сравнительные выводы о двух популяциях.
7.SP.B.3 Неформально оценить степень визуального перекрытия двух распределений числовых данных с похожими вариациями, измеряя разницу между центрами, выражая ее как кратное мере вариации. Например, средний рост игроков баскетбольной команды на 10 см больше, чем средний рост игроков футбольной команды, что примерно вдвое превышает вариабельность (среднее абсолютное отклонение) в любой из команд; на точечном графике заметно разделение между двумя распределениями высот.
Например, средний рост игроков баскетбольной команды на 10 см больше, чем средний рост игроков футбольной команды, что примерно вдвое превышает вариабельность (среднее абсолютное отклонение) в любой из команд; на точечном графике заметно разделение между двумя распределениями высот.
Гистограммы
Построение гистограммы
Среднее значение
Поиск центрального значения
Как вычислить среднее значение
Демонстрация результатов опроса
7.SP.B.4 Используйте меры центра и меры изменчивости для числовых данных из случайных выборок, чтобы сделать неформальные сравнительные выводы о двух совокупностях. Например, решите, длиннее ли слова в главе учебника по естествознанию для седьмого класса, чем слова в главе из учебника по естествознанию для четвертого класса.
Квартили
Диапазон
Среднее значение
Поиск центрального значения
Как найти медианное значение
Как вычислить среднее значение
Как вычислить модальное значение
Исследование случайных процессов и разработка, использование и оценка вероятностных моделей.
7.SP.C.5 Поймите, что вероятность случайного события — это число от 0 до 1, которое выражает вероятность наступления события. Большие числа указывают на большую вероятность. Вероятность, близкая к 0, указывает на маловероятное событие, вероятность около 1/2 указывает на событие, которое не является ни маловероятным, ни вероятным, а вероятность, близкая к 1, указывает на вероятное событие.
Вероятность
Линия вероятности
7.SP.C.6 Аппроксимация вероятности случайного события путем сбора данных о случайном процессе, который его производит, и наблюдения за его долгосрочной относительной частотой, а также предсказание приблизительной относительной частоты с учетом вероятности. Например, подбрасывая числовой куб 600 раз, предскажите, что число 3 или 6 выпадет примерно 200 раз, но, вероятно, не ровно 200 раз.
Вероятность
Линия вероятности
Относительная частота
Действие: Оценка
Действие: Случайно или нет?
Упражнение: Игла Бюффона
Упражнение: Бросание монеты на сетку
7. SP.C.7 Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните вероятности из модели с наблюдаемыми частотами; если согласие неудовлетворительное, объясните возможные источники несоответствия.
SP.C.7 Разработайте вероятностную модель и используйте ее для определения вероятностей событий. Сравните вероятности из модели с наблюдаемыми частотами; если согласие неудовлетворительное, объясните возможные источники несоответствия.
а. Разработайте единую вероятностную модель, назначив всем исходам равную вероятность, и используйте эту модель для определения вероятностей событий. Например, если из класса случайным образом выбран ученик, найдите вероятность того, что будет выбрана Джейн, и вероятность того, что будет выбрана девочка.
б. Разработайте вероятностную модель (которая может быть неоднородной), наблюдая частоты в данных, полученных в результате случайного процесса. Например, найдите приблизительную вероятность того, что крутящийся пенни упадет решкой вверх или что брошенный бумажный стаканчик упадет открытым концом вниз. Судя по наблюдаемым частотам, результаты для крутящегося пенни кажутся равновероятными?
Вероятность
Линия вероятности
Пазл с мешочками шариков
Условная вероятность
Упражнение: Игла Бюффона
Диаграммы деревьев вероятностей
Спиннер — ваше лицо, принимающее решения
Упражнение: Бросание монеты на сетку
7. SP.C.8 Найдите вероятности составных событий, используя упорядоченные списки, таблицы, древовидные диаграммы и моделирование.
SP.C.8 Найдите вероятности составных событий, используя упорядоченные списки, таблицы, древовидные диаграммы и моделирование.
а. Поймите, что, как и в случае с простыми событиями, вероятность составного события представляет собой долю исходов в выборочном пространстве, для которого происходит составное событие.
б. Представляйте примеры пространств для составных событий, используя такие методы, как организованные списки, таблицы и древовидные диаграммы. Для события, описанного повседневным языком (например, «выпадение двойных шестерок»), определите исходы в выборочном пространстве, составляющие событие.
с. Разработайте и используйте симуляцию для генерации частот для составных событий. Например, используйте случайные числа в качестве инструмента моделирования, чтобы примерно ответить на вопрос: если 40% доноров имеют кровь группы А, какова вероятность того, что потребуется не менее 4 доноров, чтобы найти одного с кровью группы А?
Вероятность
Пазлы с мешочками шариков
Условная вероятность
Диаграммы деревьев вероятностей
Вероятность: типы событий
Вероятность: независимые события
6, 7 и 8 классы | Математика | Средняя школа | Алгебра — уравнения
Элементарный (1–2 классы) Начальный (3–5 классы) Средний (6–8 классы) Младший средний (9–10 классы) Старший (11–12 классы) Испанский (все возрастные категории) ESL (все ages)GamesCup of Tea (для всех возрастов)
- Домашний
- Средняя школа: 6, 7 и 8 классы
- Математика: Средняя школа: 6, 7 и 8 классы
- Алгебра – уравнения – дробные 0 Если вы не знаете 90 не получите полных оценок, попробуйте пройти этот тест еще раз!
Эта викторина по математике называется «Алгебра — Уравнения — Дробные числа» и была написана учителями, чтобы помочь вам, если вы изучаете предмет в средней школе. Играя в образовательные викторины, вы учитесь в 6-м, 7-м или 8-м классе в возрасте от 11 до 14 лет. школьная работа. Вы можете подписаться на странице Присоединяйтесь к нам
Играя в образовательные викторины, вы учитесь в 6-м, 7-м или 8-м классе в возрасте от 11 до 14 лет. школьная работа. Вы можете подписаться на странице Присоединяйтесь к нам
В дробных уравнениях появляются числители и знаменатели. Первые несколько вопросов в этой викторине по математике будут служить повторением того, что такое дроби, а затем мы перейдем к более интересным вещам.
Напрягите мышцы мозга и посмотрите, сможете ли вы получить максимальные оценки в этом тесте.
1.
Каково назначение дроби по словарю?
Чтобы усложнить математику
Чтобы досадить учителям
Чтобы запутать учеников
Чтобы представить часть целого
2.
Где можно найти «числитель» в дроби?
Выше черты
Ниже черты
Либо выше, либо ниже черты
Где угодно, только не там, где он должен быть
3.
Где можно найти «знаменатель» дроби?
Над чертой
Под чертой
Над или под чертой
Сокрытие
4.
Если у дроби числитель (над чертой) больше знаменателя (под чертой), то это что за дробь?
Важно
Невозможно
Маловероятно
Недопустимо
5.
Посмотрите на это дробное уравнение: a ⁄ 3 = 9 ⁄ 2 . Чтобы решить уравнение, что бы вы сделали в первую очередь?
Умножить a x 9
Умножить 3 x 2
Умножить a x 9 И умножить 3 x 2
Умножить a x 2 И умножить 3 x 9 не верно?
2 х а = 27
2а = 3 х 9
2а = 27
а = 14,5
7.
Посмотрите на это дробное уравнение: a ⁄ 9 = 9 ⁄ 4 . Какой из следующих шагов неверный?
4 x a = 9 x 9
4a = 81
a = 81/4
a = 20
8.
Посмотрите на следующее дробное уравнение и решите, каково правильное значение для a: 8 ⁄ 6 = 7 ⁄ 4 .
6,5
8,5
10,5
12,5
9.

