дробный калькулятор с корнями
Вы искали дробный калькулятор с корнями? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и калькулятор дробей с корнями, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «дробный калькулятор с корнями».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как дробный калькулятор с корнями,калькулятор дробей с корнями,калькулятор дробей со степенями и корнями,калькулятор дробей со степенями онлайн с решением,калькулятор квадратов чисел,калькулятор корень уравнения,калькулятор онлайн корней уравнений,калькулятор онлайн с дробями и корнями онлайн калькулятор,калькулятор онлайн с дробями и с корнями калькулятор,калькулятор онлайн с корнями и дробями онлайн калькулятор,калькулятор радикалов,калькулятор с дробями и корнями и степенями,калькулятор с корнями дробный,калькулятор с корнями и дробями,калькулятор с корнями и дробями и степенями,калькулятор с корнями и дробями онлайн,калькулятор с корнями и степенями и дробями,калькулятор с корнями с решением,калькулятор с кубами и квадратами,калькулятор сокращения дробей с буквами и степенями онлайн,калькулятор степеней с дробями онлайн,калькулятор уравнений с корнями,найти значение выражения с дробями и степенями онлайн,онлайн калькулятор квадратов,онлайн калькулятор корней с решением,онлайн калькулятор корней уравнений,онлайн решение выражений с корнями,онлайн решение примеров с корнями,онлайн решить пример с корнями,решение выражений с корнями онлайн,решение примеров онлайн с корнями,решение примеров с корнями онлайн,решение примеров с корнями онлайн калькулятор с решением,решить выражение онлайн с корнями,решить выражение с корнями онлайн,решить онлайн пример с корнями,решить пример онлайн с корнями,сложение корней калькулятор,сократить дробь с корнями онлайн калькулятор.
Где можно решить любую задачу по математике, а так же дробный калькулятор с корнями Онлайн?
Решить задачу дробный калькулятор с корнями вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Калькулятор корней — извлечь корень 2, 3, 4, 5 степени онлайн
Многие школьники, студенты, а также их родители в процессе проверки домашних заданий испытывают затруднения при вычислениях нестандартных корней n степени. Необходимость решения часто возникает для сложных примеров из таких наук как, алгебра, геометрия, высшая математика и т.д. Сделать эти математические расчеты более быстрыми и удобными позволяют root калькуляторы от «raschitat-online».
Необходимость решения часто возникает для сложных примеров из таких наук как, алгебра, геометрия, высшая математика и т.д. Сделать эти математические расчеты более быстрыми и удобными позволяют root калькуляторы от «raschitat-online».
Пользователи сайта могут всего за пару кликов узнать значение корня n-й степени (n=2,3,4,5,6…). Фактически, особый алгоритм помогает определить, какое неотрицательное число «b» возведено в «н» так, что под знаком корня получилось некоторое число «a». Другими словами, первое «b» является искомым параметром, которое умножено само на себя «энное» количество раз. Это выглядит, как запись:
n√a=b; bn=b∗b∗b∗…∗b n раз=a.
На странице предусмотрено отдельное поле для значений, созданное для указания имеющегося числового значения «а».
Если читать пример правильно, то «энная степень», расположенная над галочкой, называется показателем корня. Когда, перед учащимся пример, где n=2, то читается он как «корень 2-й степени» либо «обычный квадратный корень».
Особенности вычислений корневых решений: четной и нечетной степени
Необходимо четко отличать правила работы с четными и нечетными корневыми показателями. Определить значения с четным параметром «н» (2, 4, 6, 8 …) можно только из положительного числа. Для отрицательных подкоренных чисел и четным вариантом степени – решений не существует.
Для нечетной степени можно посчитать из любых действительных чисел. К ним относятся кубический «3», а также «5», «7» и т.д. Им соответствуют выражения 3√a=b, 5√a=b, 7√a=b.
Если под знаком с корневым определителем находится дробь, к примеру ½, то вычисление проводят для каждого числа по отдельности. Онлайн калькуляторы позволяют это пример решить следующим образом: n√(½)=n√1 / n√2.
Важным условием для возможности цифровых расчетов с дробными числами является правило: знаменатель не может быть равен нулю.
Формат математических расчетов
Онлайн калькулятор способен решение для любых единиц измерения, включая Deg – градусы, Rad – радианы, Grad – грады.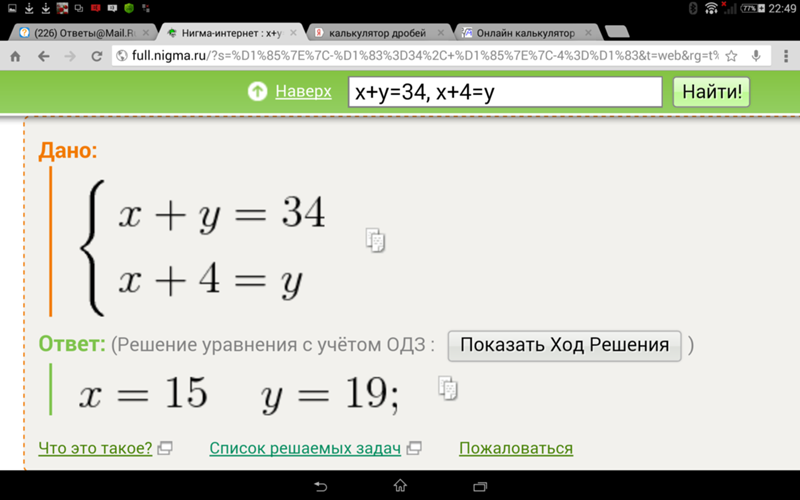
Примером перевода являются:
- 1 рад = 57,3°;
- круг с радиусом 360° = 2π рад.;
- 1 град = 0,9 Deg или 1 град = 0,015708 Rad.
Наиболее простым примером является синус 90 градусов. Для получения готового решения нажмите:
90;
sin;
=.
В области ответа будет результат 1.
Опция Deg помогает перевести угол из формата градусы, минуты и секунды в десятичные доли градуса для вычислений. Например, угол 35 o 14 минут 04 секунды 53 десятые доли секунды можно перевести в десятые доли. Эта запись выглядят так:
35,140453;
Deg;
=.
Ответом будет 35,2345916…..
Опция RAD позволяет выяснить значения углов в радианах. Единица Radian соответствует 1/2π от r длины окружности. А проведение измерений углов в этой системе исчисления называется «радианной мерой угла». Выражение выглядят так: 1 рад = 360/(2π).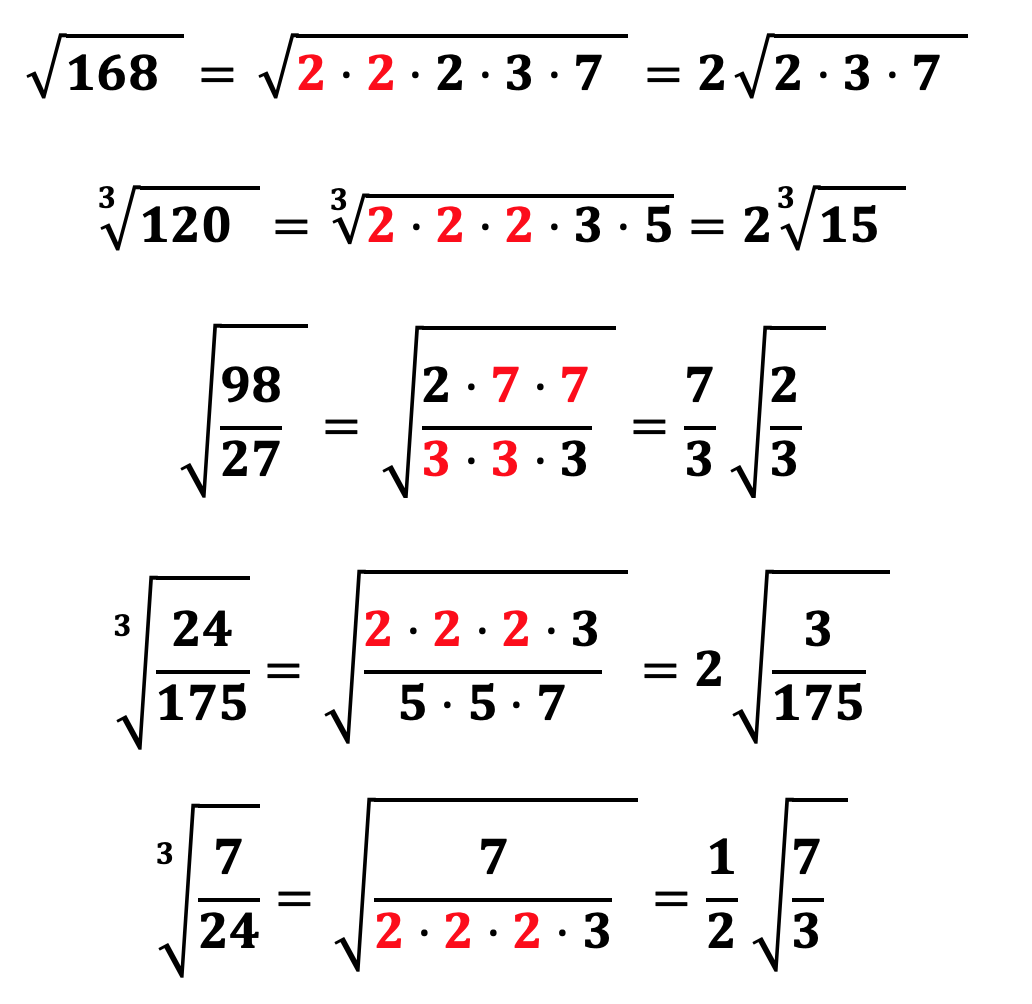
Опция Grad позволяет уточнить данные в режиме задания углов в градах. При этом, 1 град равен 1/400 длины окружности.
Благодаря этим приведеным примерам и встроенным опциям, любой пользователь сможет использовать онлайн калькуляторы для расчета корня н степени.
Другие калькуляторы
Алгоритм извлечения квадратного корня
Квадратный корень легко извлекается с помощью калькулятора. Для этого достаточно набрать на нём исходное число и нажать клавишу корня
Если калькулятора под рукой нет, то квадратный корень извлекают пользуясь алгоритмом извлечения квадратного корня.
Применение алгоритма может оказаться весьма полезным на контрольных и экзаменах. Ведь чаще всего на таких мероприятиях использовать калькулятор запрещено.
Предварительные навыкиКак пользоваться алгоритмом
Рассмотрим применение алгоритма извлечения квадратного корня на конкретных примерах. О том, почему алгоритм следует применять именно так, поговорим позже.
Пример 1. Извлечём квадратный корень из числа 4096 с помощью алгоритма извлечения квадратного корня.
Прежде всего сгруппируем число 4096 по две цифры. Двигаясь с конца влево сделаем небольшую мéтку:
Сгруппированные цифры исходного числа называют грáнями, а саму группировку по две цифры разделением на грáни. Количество грáней позволяет предположить сколько цифр будет содержаться в извлечённом корне. В нашем примере извлечённый корень будет содержать две цифры, поскольку исходное число содержит две грани.
Теперь нужно извлечь квадратный корень из числа 40 с точностью до целых, получаем 6. Записываем 6 после знака равенства:
Далее возвóдим число 6 в квадрат и полученный результат записываем под числом 40
Далее вычитаем из числа 40 число 36, получаем 4. Записываем это число под 36
Снóсим оставшиеся цифры из под корня, а именно 96. Получаем остаток 496
Теперь нужно найти следующую цифру корня. Её находят так. Первую найденную цифру корня, а именно 6 умножаем на 2, получаем 12. К числу 12 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 496 или хотя бы максимально близким к нему, но не превосходящим его.
Её находят так. Первую найденную цифру корня, а именно 6 умножаем на 2, получаем 12. К числу 12 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 496 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 5. Допишем её к числу 12 и умножим образовавшееся число 125 на 5
Получилось число 625, которое больше остатка 496. Значит цифра 5 не годится в качестве следующей цифры корня. Проверим тогда цифру 4. Допишем ее к числу 12 и умножим образовавшееся число 124 на 4
Получилось число 496, которое в точности является нашим остатком. Значит дописанная к числу 12 цифра 4 является следующей цифрой корня. Возвращаемся к исходному примеру и записываем цифру 4 в ответе после цифры 6
А число 496, которое получилось в результате умножения 124 на 4 записываем под остатком 496
Выполняем вычитание 496 − 496 = 0.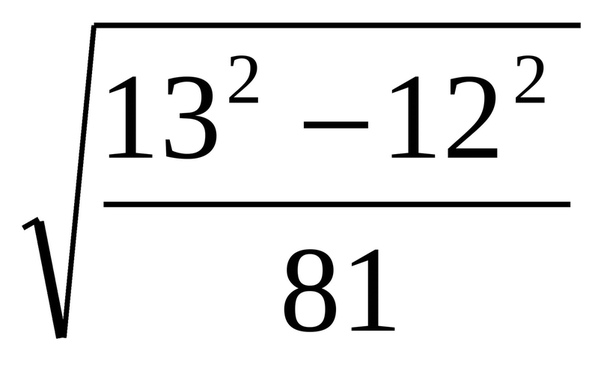 Ноль в остатке говорит о том, что решение окончено:
Ноль в остатке говорит о том, что решение окончено:
Для удобства поиска второй цифры, слева от остатка проводят вертикáльную линию и уже за этой линией записывают умножение. В нашем случае умножение 124 на 4. Результат умножение сразу записывают под остатком:
Итак, квадратный корень из числа 4096 равен 64
Пример 2. Извлечём квадрáтный корень из числа 441 с помощью алгоритма извлечения квадратного корня.
Прежде всего сгруппируем число 441 по две цифры. Двигаясь с конца влево сделаем небольшую мéтку. В данном случае в числе 441 только три цифры. Поэтому группируем цифры 4 и 1. Крайняя четвёрка слева будет сама по себе:
Теперь нужно извлечь квадратный корень из числа 4 с точностью до целых, получаем 2. Записываем 2 после знака равенства:
Далее возвóдим число 2 в квадрат и полученный результат записываем под числом 4
Вычитаем из числа 4 число 4, получаем 0. Ноль принято не записывать.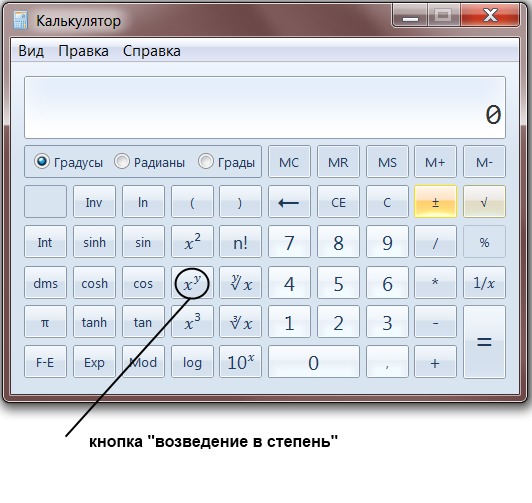 Снóсим оставшиеся цифры корня, а именно 41
Снóсим оставшиеся цифры корня, а именно 41
Теперь нахóдим следующую цифру корня. Первую найденную цифру корня, а именно 2 умножаем на 2, получаем 4. К числу 4 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить получившееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 41 или хотя бы максимально близким ему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 4 и умножим получившееся число 42 на ту же самую дописанную цифру 2. Результат умножения будем записывать сразу под остатком 41
Получилось число 84, которое больше остатка 41. Значит цифра 2 не годится в качестве следующей цифры корня. Проверим тогда цифру 1. Допишем ее к числу 4 и умножим получившееся число 41 на на ту же самую дописанную цифру 1
Получилось число 41, которое в точности является нашим остатком. Значит дописанная к числу 4 цифра 1 является следующей цифрой корня. Записываем цифру 1 после цифры 2
Записываем цифру 1 после цифры 2
А число 41, которое получилось в результате умножения 41 на 1, записываем под остатком 41
Выполняем вычитание 41 − 41 = 0. Ноль в остатке говорит о том, что решение окончено:
Пример 3. Извлечём квадратный корень из числа 101761 с помощью алгоритма извлечения квадратного корня.
Разбиваем число 101761 на грани:
Получилось три грани. Значит корень будет состоять из трёх цифр.
Извлекáем квадратный корень из первой грани (из числа 10) с точностью до целых, получаем 3. Записываем 3 после знака равенства:
Далее возвóдим число 3 в квадрат и полученный результат записываем под первой гранью (под числом 10)
Вычитаем из числа 10 число 9, получаем 1. Снóсим следующую грань, а именно число 17. Получаем остаток 117
Теперь нахóдим вторую цифру корня. Первую найденную цифру корня, а именно 3 умножаем на 2, получаем 6. К числу 6 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 117 или хотя бы максимально близким к нему, но не превосходящим его.
Полученное произведение должно быть равно остатку 117 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 6 и умножим образовавшееся число 62 на ту же самую дописанную цифру 2. Результат умножения будем записывать сразу под остатком 117
Получилось число 124, которое больше остатка 117. Значит цифра 2 не годится в качестве второй цифры корня. Проверим тогда цифру 1. Допишем ее к числу 6 и умножим образовавшееся число 61 на на ту же самую дописанную цифру 1
Получилось число 61, которое не превосходит остатка 117. Значит дописанная к числу 6 цифра 1 является второй цифрой корня. Записываем её в ответе после цифры 3
Теперь выполняем вычитание 117 − 61 = 56.
Снóсим следующую грань, а именно число 61. Получаем новый остаток 5661
Теперь нахóдим третью цифру корня. Первые две найденные цифры корня, а именно число 31 умножаем на 2, получаем 62. К числу 62 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет третьей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 5661 или хотя бы максимально близким к нему, но не превосходящим его.
Полученное произведение должно быть равно остатку 5661 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 9. Допишем её к числу 62 и умножим образовавшееся число 629 на ту же самую дописанную цифру 9. Результат умножения будем записывать сразу под остатком 5661
Получилось число 5661, которое в точности является нашим остатком. Значит дописанная к числу 62 цифра 9 является третьей цифрой корня. Записываем цифру 9 в ответе после цифры 1
Выполняем вычитание 5661 − 5661 = 0. Ноль в остатке говорит о том, что решение окончено:
Пример 4. Извлечём квадратный корень из числа 30,25 с помощью алгоритма извлечения квадратного корня.
Данное число является десятичной дробью. В данном случае на грани следует разбить целую и дробную часть. Целую часть на грани следует разбить, двигаясь влево от запятой. А дробную — двигаясь вправо от запятой:
Получилось по одной грани в каждой части. Это значит, что корень будет состоять из двух цифр: одна цифра будет в целой части корня и одна цифра в дробной.
Это значит, что корень будет состоять из двух цифр: одна цифра будет в целой части корня и одна цифра в дробной.
Извлечём квадратный корень из первой грани (из числа 30) с точностью до целых, получаем 5. Записываем 5 после знака равенства:
Далее возвóдим число 5 в квадрат и полученный результат записываем под первой гранью (под числом 30)
Вычитаем из числа 30 число 25, получаем 5.
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 30,25 с точностью до целых, получили ответ 5. Последний остаток 5 показывает, что целая часть 30 превосходит квадрат 52 на 5 квадратных единиц.
Чтобы дальше извлечь корень (с точностью до десятых), снесём следующую грань, а именно число 25, получим остаток 525. А в ответе после числа 5 следует поставить запятую, поскольку сейчас мы будем искать дробную часть корня.
Затем снóсим следующую грань, а именно число 25. Получаем остаток 525
Далее работаем по тому же принципу, что и раньше. Нахóдим следующую цифру корня. Для этого уже найденный корень, а именно число 5 умножим на 2 получим 10. К числу 10 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 525 или хотя бы максимально близким к нему, но не превосходящим его.
Нахóдим следующую цифру корня. Для этого уже найденный корень, а именно число 5 умножим на 2 получим 10. К числу 10 в конце нужно дописать ещё одну цифру (эта цифра впоследствии и станет следующей цифрой корня) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 525 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 5. Допишем её к числу 10 и умножим получившееся число 105 на ту же самую дописанную цифру 5
Получилось число 525, которое в точности является нашим остатком. Значит дописанная к числу 10 цифра 5 является следующей цифрой корня. Возвращаемся к исходному примеру и записываем цифру 5 после в ответе после запятой:
Выполняем вычитание 525 − 525 = 0. Ноль в остатке говорит о том, что решение окончено:
В подкоренном выражении можно было использовать следующий прием: умножить подкоренное число на 100 и получить под корнем число 3025. Далее извлечь из него квадратный корень, как из обычного целого числа. Тогда получился бы ответ 55
Далее извлечь из него квадратный корень, как из обычного целого числа. Тогда получился бы ответ 55
Затем можно обратно разделить 3025 на 100 (или сдвинуть запятую влево на две цифры). В результате под корнем полýчится прежнее число 30,25, а правая часть уменьшится в десять раз и полýчится квадратный корень из числа 30,25.
Пример 5. Извлечём квадратный корень из числа 632,5225 с помощью алгоритма извлечения квадратного корня.
Данное число является десятичной дробью. Разбиваем число на грани. На грани следует разбить целую и дробную часть. Целую часть на грани следует разбить, двигаясь влево от запятой. А дробную — двигаясь вправо от запятой:
Получилось четыре грани. При этом две грани в целой части, и две грани в дробной. Это значит, что корень будет состоять из четырёх цифр: две цифры будет в целой части корня, и две цифры после запятой.
Извлечём квадратный корень из первой грани (из числа 6) с точностью до целых, получаем 2. Записываем 2 после знака равенства:
Записываем 2 после знака равенства:
Далее возвóдим число 2 в квадрат и полученный результат записываем под первой гранью (под числом 6)
Вычитаем из числа 6 число 4, получаем 2. Затем снóсим следующую грань, а именно число 32. Получаем остаток 232
Теперь нахóдим вторую цифру корня. Первую уже найденную цифру корня, а именно 2 умножаем на 2, получаем 4. К числу 4 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня) и умножить получившееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 232 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 6. Допишем её к числу 4 и умножим получившееся число 46 на ту же самую дописанную цифру 6. Результат умножения будем записывать сразу под остатком 232
Получилось число 276, которое больше остатка 232. Значит цифра 6 не годится в качестве второй цифры корня. Проверим тогда цифру 5. Допишем ее к числу 4 и умножим получившееся число 45 на на ту же самую дописанную цифру 5
Проверим тогда цифру 5. Допишем ее к числу 4 и умножим получившееся число 45 на на ту же самую дописанную цифру 5
Получилось число 225, которое не превосходит остатка 232. Значит дописанная к числу 4 цифра 5 является второй цифрой корня. Записываем её в ответе после цифры 2
Теперь выполняем вычитание 232 − 225 = 7.
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 632,5225 с точностью до целых, получили ответ 25. Последний остаток 7 показывает, что целая часть 632 превосходит квадрат 252 на 7 квадратных единиц.
Чтобы дальше извлечь корень (с точностью до десятых и сотых), снесём следующую грань, а именно число 52, получим остаток 752. А в ответе после числа 25 поставим запятую, поскольку сейчас мы будем искать дробные части корня:
Далее работаем по тому же принципу, что и раньше. Нахóдим первую цифру корня после запятой. Для этого уже найденные цифры, а именно 25 умножим на 2 получим 50.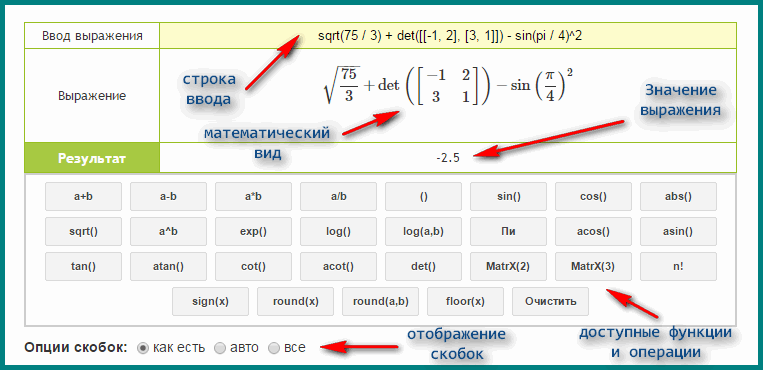 К числу 50 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет первой цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 752 или хотя бы максимально близким к нему, но не превосходящим его.
К числу 50 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет первой цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 752 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 2. Допишем её к числу 50 и умножим получившееся число 502 на ту же самую дописанную цифру 2. Можно интуитивно понять, что цифра 2 великá, поскольку 502 × 2 = 1004. А число 1004 больше остатка 752. Тогда очевидно, что первой цифрой после запятой будет цифра 1
Теперь выполняем вычитание 752 − 501 = 251. Сразу снóсим следующую грань 25. Полýчим остаток 25125
Теперь нахóдим вторую цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умнóжим на 2. Полýчим 502.
К числу 502 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 25125 или хотя бы максимально близким к нему, но не превосходящим его.
Полученное произведение должно быть равно остатку 25125 или хотя бы максимально близким к нему, но не превосходящим его.
Итак, проверим например цифру 6. Допишем её к числу 502 и умнóжим образовавшееся число 5026 на ту же самую дописанную цифру 6. Результат умножения будем записывать сразу под остатком 25125
Получилось число 30156, которое больше остатка 25125. Значит цифра 6 не годится в качестве второй цифры корня после запятой. Проверим тогда цифру 5. Допишем ее к числу 502 и умножим получившееся число 5025 на на ту же самую дописанную цифру 5
Получилось число 25125, которое в точности является нашим остатком. Значит дописанная к числу 502 цифра 5 является второй цифрой корня после запятой. Записываем цифру 5 в ответе после цифры 1
Теперь выполняем вычитание 25125 − 25125 = 0. Ноль в остатке говорит о том, что решение окончено:
В этом примере можно было воспользоваться методом умножения подкоренного выражения на 10000.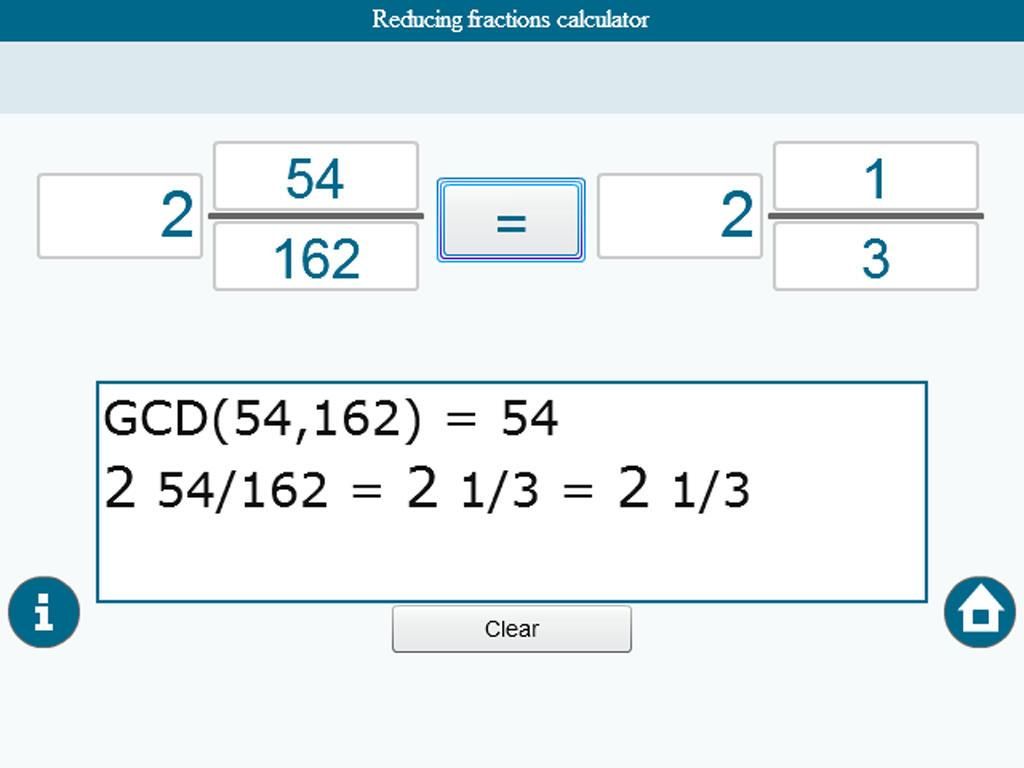 Тогда подкоренное число приняло бы вид 6325225. Его можно разделить на грани, двигаясь справа налево. В результате получился бы корень 2515
Тогда подкоренное число приняло бы вид 6325225. Его можно разделить на грани, двигаясь справа налево. В результате получился бы корень 2515
Затем подкоренное число 6325225 делят на 10000, чтобы вернуться к изначальному числу 632,5225. В результате этого деления ответ умéньшится в 100 раз и обратится в число 25,15.
Пример 4. Используя алгоритм извлечения квадратного корня, извлечь квадратный корень из числа 11 с точностью до тысячных:
В данном числе только одна грань 11. Извлечём из неё корень с точностью до целых, получим 3
Теперь возвóдим число 3 в квадрат и полученный результат записываем под первой гранью (под числом 11)
Выполним вычитание 11 − 9 = 2
Извлечение корня из целой части подкоренного выражения завершено. На данный момент мы извлекли корень из числа 11 с точностью до целых, получили ответ 3. Последний остаток 2 показывает, что целая часть 11 превосходит квадрат 32 на две квадратные единицы.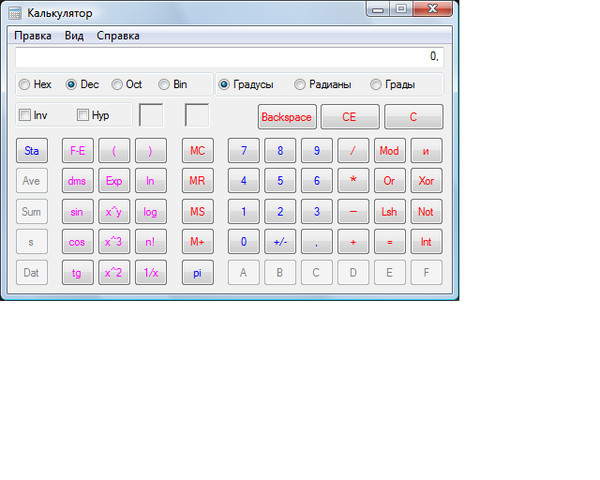
Наша задача была извлечь корень из числа 11 с точностью до тысячных. Значит нужно снести следующую грань, но её в данном случае нет.
Если после целого числа поставить запятую и написать сколько угодно нулей, то значение этого числа не измéнится. Так, после 11 можно поставить запятую и написать несколько нулей (несколько граней), которые в последствии можно будет снóсить к остаткам.
Если корень извлекáется с точностью до тысячных, то в ответе после запятой должно быть три цифры. Поэтому в подкоренном выражении поставим запятую и запишем три грани, состоящие из нулей:
Теперь можно снести следующую грань, а именно два нуля. Получим остаток 200. А в ответе после числа 3 поставим запятую, поскольку сейчас мы будем искать дробные части корня:
Теперь нахóдим первую цифру после запятой в ответе. Первую найденную цифру корня, а именно число 3 умножаем на 2, получаем 6. К числу 6 нужно дописáть ещё одну цифру (эта цифра впоследствии и станет первой цифрой после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 200 или хотя бы максимально близким к нему, но не превосходящим его.
Полученное произведение должно быть равно остатку 200 или хотя бы максимально близким к нему, но не превосходящим его.
В данном случае подойдёт цифра 3
Выполним вычитание 200 − 189 и снесём следующую грань 00
Нахóдим вторую цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умнóжим на 2. Полýчим 66.
К числу 66 в конце нужно дописáть ещё одну цифру (эта цифра впоследствии и станет второй цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 1100 или хотя бы максимально близким к нему, но не превосходящим его.
В данном случае подойдёт цифра 1
Выполним вычитание 1100−661 и снесём следующую грань 00
Нахóдим третью цифру корня после запятой. Не обращая внимания на запятую, найденные цифры корня умножим на 2. Получим 662.
К числу 662 нужно дописáть ещё одну цифру (эта цифра впоследствии и станет третьей цифрой корня после запятой) и умножить образовавшееся число на ту же самую дописанную цифру. Полученное произведение должно быть равно остатку 43900 или хотя бы максимально близким к нему, но не превосходящим его.
Полученное произведение должно быть равно остатку 43900 или хотя бы максимально близким к нему, но не превосходящим его.
Проверим цифру 7
Получилось число 46389, которое больше остатка 43900. Значит цифра 7 не годится в качестве третьей цифры корня после запятой. Проверим тогда цифру 6. Допишем ее к числу 662 и умножим получившееся число 6626 на на ту же самую дописанную цифру 6
Получилось число 39756, которое не превосходит остатка 43900. Значит дописанная к числу 662 цифра 6 является третьей цифрой корня после запятой. Записываем цифру 6 в ответе после цифры 1
Выполним вычитание 43900 − 39756 = 4144
Дальнейшее вычисление не требуется, поскольку корень нужно было извлечь с точностью до тысячных.
Но в таких примерах как этот, цифры после запятой можно находить бесконечно. Например, так можно продолжить данный пример, найдя значение корня с точностью до десятитысячных:
Как работает алгоритм
Алгоритм извлечения квадратного корня основан на формуле квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Геометрически эту формулу можно представить так:
То есть сторона a увеличивается на b. Это приводит к увеличению изначального квадрата. Чтобы вычислить площадь такого квадрата, нужно по отдельности вычислить площади квадратов и прямоугольников, входящих в этот квадрат и сложить полученные результаты. Нужно хорошо понимать данный рисунок. Без его понимания невозможно понять как работает алгоритм извлечения квадратного корня.
Это приводит к увеличению изначального квадрата. Чтобы вычислить площадь такого квадрата, нужно по отдельности вычислить площади квадратов и прямоугольников, входящих в этот квадрат и сложить полученные результаты. Нужно хорошо понимать данный рисунок. Без его понимания невозможно понять как работает алгоритм извлечения квадратного корня.
Отметим, что формула квадрата суммы двух выражений позволяет возвести в квадрат любое число. Используя разряды, исходное число представляют в виде суммы чисел и далее эту сумму возвóдят в квадрат.
Например, так можно возвести число 21 в квадрат: представить данное число в виде суммы двух десятков и одной единицы, и далее эту сумму возвести в квадрат :
212 = (20 + 1)2 = 202 + 2 × 20 × 1 + 12 = 400 + 40 + 1 = 441
Геометрически это будет выглядеть так: сторона квадрата равная 21 разбивается на две составляющие: 20 и 1.
Затем по отдельности вычисляются площади квадратов и прямоугольников, входящих в большой квадрат.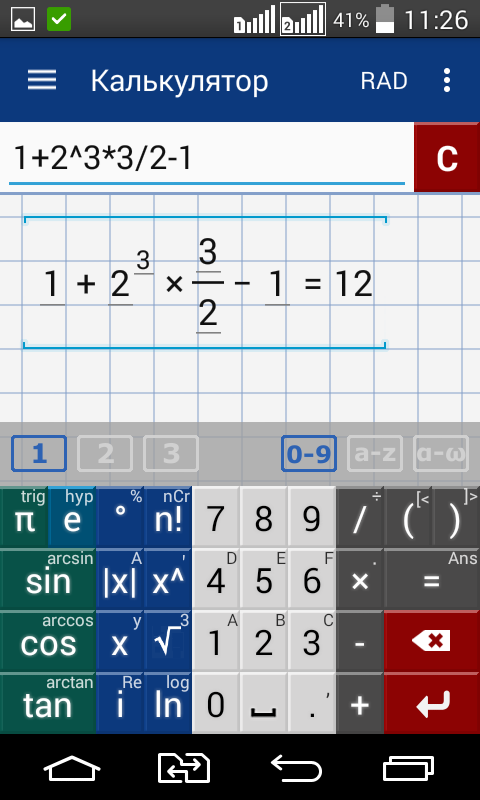 А именно: один квадрат со стороной 20 (получается площадь, равная 400), два прямоугольника со сторонами 20 и 1 (получается две площади по 20), один квадрат со стороной 1 (получается площадь, равная 1). Результаты вычисления площадей складываются и получается итоговое значение 441.
А именно: один квадрат со стороной 20 (получается площадь, равная 400), два прямоугольника со сторонами 20 и 1 (получается две площади по 20), один квадрат со стороной 1 (получается площадь, равная 1). Результаты вычисления площадей складываются и получается итоговое значение 441.
Заметим также, что при возведéнии десятков в квадрат получились сотни. В данном случае при возведéнии числа 20 в квадрат получилось число 400. Это позволяет предположить, что если корень является двузначным числом, то десятки этого корня следует искать в сотнях подкоренного числа. Действительно, . Десятки корня это цифра 2, является корнем числа 4, которое отвечает за сотни числа 441.
А при возведéнии сóтен в квадрат получаются десятки тысяч. Например, возведём в квадрат число 123, используя формулу квадрата суммы двух выражений. Число 123 это одна сотня, два десятка и три единицы:
1232 = (100 + 20 + 3)2
При изучении многочленов мы выяснили, что если многочлен содержит более двух членов и возникла необходимость применить формулу квадрата суммы, то некоторые из членов можно взять в скобки, чтобы получилось выражение вида (a + b)2
Рассмотрим подробное извлечение квадратного корня из числа 4096. Заодно пройдёмся по основным этапам алгоритма извлечения квадратного корня, рассмотренного в предыдущей теме.
Заодно пройдёмся по основным этапам алгоритма извлечения квадратного корня, рассмотренного в предыдущей теме.
Допустим, что число 4096 это площадь следующего квадрата:
Извлечь корень из числа 4096 означает найти длину стороны данного квадрата:
Для начала узнáем из скольких цифр будет состоять корень. Ближáйшие от 4096 известные нам квадраты это 3600 и 4900. Между ними располагается квадрат 4096. Запишем это в виде неравенства:
Запишем каждое число под знáком корня:
Квадратные корни из чисел 3600 и 4900 нам известны. Это корни 60 и 70 соответственно:
Корни 60 и 70 являются двузначными числами. Если квадратный корень из числа 4096 располагается между числами 60 и 70, то этот корень тоже будет двузначным числом.
Двузначное число состоит из десятков и единиц. Это значит, что квадратный корень из числа 4096 можно представить в виде суммы a + b, где a — десятки корня, b — единицы корня. Сумма a + b во второй степени будет равна 4096
Сумма a + b во второй степени будет равна 4096
(a + b)2 = 4096
Тогда сторона квадрата будет разбита на две составляющие: a и b
Перепишем в равенстве (a + b)2 = 4096 левую часть в виде a2 + 2ab + b2
a2 + 2ab + b2 = 4096
Тогда рисунок, иллюстрирующий квадрат площадью 4096, можно представить так:
Если мы узнáем значения переменных a и b, то узнáем длину стороны данного квадрата. Проще говоря, узнáем сам корень.
Вернёмся к извлечению корня. Мы выяснили, что корнем будет двузначное число. Двузначное число состоит из десятков и единиц. При возведéнии десятков в квадрат, получаются сотни. Тогда десятки искомого корня следует искать в сотнях подкоренного числа. В подкоренном числе 40 сотен. Отделим их небольшой помéткой:
Извлечём корень из числа 40. Из числа 40 корень не извлекается. Поэтому извлечение следует выполнить приближённо с точностью до целых.
Из числа 40 корень не извлекается. Поэтому извлечение следует выполнить приближённо с точностью до целых.
Ближáйший мéньший квадрат к числу 40 это 36. Извлечём корень из этого квадрата, получим 6. Тем сáмым полýчим первую цифру корня:
На самом деле корень извлечён не из числа 40, а из сорокá сотен. Метка, которая постáвлена после числа 40, отделяет разряды числа, находящегося под знáком корня. Нужно понимать, что в данном случае 40 это 4000.
Из 4000 как и 40 корень не извлекается, поэтому его тоже следует извлекать приближённо. Для этого следует найти ближáйший мéньший квадрат к числу 4000. Но нужно принимать во внимание следующий момент. Десятки это числа с одним нулем на конце. Примеры:
10 — один десяток
30 — три десятка
120 — двенадцать десятков
При возведéнии таких чисел в квадрат, получаются числа с двумя нулями на конце:
102 = 100
302 = 900
1202 = 14400
Мы ищем десятки корня в сотнях числá 4096, то есть в числе 4000. Но нет такого числá с нулем на конце, вторая степень которого равна 4000. Поэтому мы ищем ближáйший мéньший квадрат, но опять же с двумя нулями на конце. Таковым является квадрат 3600. Корень следует извлекать из этого квадрата.
Но нет такого числá с нулем на конце, вторая степень которого равна 4000. Поэтому мы ищем ближáйший мéньший квадрат, но опять же с двумя нулями на конце. Таковым является квадрат 3600. Корень следует извлекать из этого квадрата.
Вернемся к нашему рисунку. Большой квадрат со стороной a и площадью a2 это тот самый квадрат 3600. Укажем вместо a2 значение 3600
Теперь извлечём квадратный корень из квадрата 3600. Ранее мы говорили, что если число содержит уже знакомый нам квадрат и чётное количество нулей, то можно извлечь корень из этого числа. Для этого сначала следует извлечь корень из знакомого нам квадрата, а затем записать половину от количества нулей исходного числа:
Итак, мы нашли сторону квадрата, площадь которого 3600. Подпишем сторону a как 60
Но ранее в ответе мы написали не 60, а 6. Это является сокращённым вариантом. Число 6 в данном случае означает шесть десятков:
Итак, десятки корня найдены. Их шесть. Теперь нужно найти единицы корня. Единицы корня это длина оставшейся маленькой стороны квадрата, то есть значение переменной b.
Их шесть. Теперь нужно найти единицы корня. Единицы корня это длина оставшейся маленькой стороны квадрата, то есть значение переменной b.
Чтобы найти b, нужно из общего квадрата, площадь которого 4096 вычесть квадрат, площадь которого 3600. В результате останется фигура, площадь которой 4096 − 3600 = 496
На рисунке видно как из квадрата, площадь которого 4096 отделился квадрат, площадь которого 3600. Осталась фигура, площадь которой 496.
Именно поэтому в процессе применения алгоритма первая найденная цифра корня возводится в квадрат, чтобы результат возведения вычесть из сотен подкоренного выражения.
Так, из 40 сотен вычитаются 36 сотен, остаётся 4 сотни плюс сносятся девяносто шесть единиц. Эти четыре сотни и девяносто шесть единиц вместе образуют 496 единиц:
Оставшаяся фигура есть ни что иное как удвоенное произведение первого выражение a плюс квадрат второго выражения b
Сумма площадей 2ab + b2 должна вмещаться в число 496. Запишем это в виде следующего равенства:
Запишем это в виде следующего равенства:
2ab + b2 = 496
Значение a уже известно. Оно равно 60. Тогда равенство примет вид:
2 × 60 × b + b2 = 496
120b + b2 = 496
Теперь наша задача найти такое значение b, при котором левая часть станет равна 496 или хотя близкой к этому числу. Поскольку b является единицами искомого корня, то значение b является однозначным числом. То есть значение b это число от 1 до 9. Это число можно найти методом подбора. В данном случае очевидно, что числом b является 4
120 × 4 + 42 = 496
480 + 16 = 496
496 = 496
Но для удобства поиска этой цифры, переменную b выносят за скобки. Вернёмся к выражению 120b + b2 = 496 и вынесем b за скобки:
b(120 + b) = 496
Теперь правую часть можно понимать так: к 120 следует прибавить некоторое число b, которое при умножении с тем же сáмым b даст в результате 496.
Именно поэтому при использовании алгоритма, уже найденную цифру умножают на 2. Так, 6 мы умножили на 2 получили 12 и уже к 12 дописывали цифру и умножáли образовавшееся число на ту же дописанную цифру, пытаясь получить остаток 496.
Но это опять же упрощённый вариант. На самом деле на 2 умножается не просто 6, а найденные десятки (в нашем случае число 60), получается число 120. Затем следует нахождение числá вида b(120 + b). То есть к 120 прибавляется число b, которое при перемножении с b даёт остаток 496.
Итак, b = 4. Тогда:
4(120 + 4) = 496
4 × 124 = 496
496 = 496
При подстановке числá 4 вместо b получается остаток 496. Это значит, что единицы корня найдены. Квадрат, площадь которого 4096, имеет сторону равную 60 + 4, то есть 64.
Если из общей площади вычесть 3600, затем 496, полýчим 0. Остаток, равный нулю, говорит о том, что решение завершено:
4096 − 3600 − 496 = 0
Пример 2. Извлечь квадратный корень из числа 54756
Извлечь квадратный корень из числа 54756
Пусть число 54756 это площадь следующего квадрата:
Извлечь корень из числа 54756 означает найти длину стороны данного квадрата:
Пока неизвестно является ли квадратный корень из числа 54756 целым либо дробным числом. Узнáем для начала из скольких цифр будет состоять целый корень.
Число 54756 больше числá 10000, но меньше числá 90000
10000 < 54756 < 90000
Корни из 10000 и 90000 являются трёхзначными числами.
Тогда корень из 54756 тоже будет трёхзначным числом. А трёхзначное число состоит из сотен, десятков и единиц.
Квадратный корень из числа 54756 можно представить в виде суммы a + b + с, где a — сотни корня, b — десятки корня, с — единицы корня. Сумма a + b + с во второй степени будет равна 54756
(a + b + c)2 = 54756
Тогда сторона квадрата будет разбита на три составляющие: a, b и c
Выполним в левой части равенства (a + b + c)2 = 54756 возведéние в квадрат:
Тогда рисунок иллюстрирующий квадрат, площадью 54756 можно представить так:
Два прямоугольника площадью ab в приведённом ранее равенстве заменены на 2ab, а два прямоугольника площадью (a + b)c заменены на 2ac + 2bc, поскольку (a + b)c = ac + bc. Если повторить выражение ac + bc дважды, то полýчится 2ac + 2bc
Если повторить выражение ac + bc дважды, то полýчится 2ac + 2bc
2(ac + bc) = 2ac + 2bc
Если мы узнáем значения переменных a, b и c, то узнáем длину стороны данного квадрата. Проще говоря, узнáем сам корень.
Вернёмся к извлечению корня. Мы выяснили, что корнем будет трёхзначное число. Трёхзначное число состоит из сотен, десятков и единиц.
При возведéнии сотен в квадрат, получаются десятки тысяч. Тогда сотни искомого корня следует искать в десятках тысяч подкоренного числа. В подкоренном числе 5 десятков тысяч. Отделим их мéткой:
Извлечём корень из числа 5. Из числа 5 корень не извлекается. Поэтому извлечение следует выполнить приближённо с точностью до целых Ближáйший мéньший квадрат к 5 это 4. Извлечём корень из этого квадрата, получим 2. Тем самым полýчим первую цифру корня:
На самом деле корень извлечён не из числа 5, а из пяти десятков тысяч. Метка, которая поставлена после числá 5, отделяет разряды числá, находящегося под знáком корня. Нужно понимать, что в данном случае 5 это 50000.
Нужно понимать, что в данном случае 5 это 50000.
Из 50000 как и 5 корень не извлекается, поэтому его тоже следует извлекать приближённо. Для этого следует найти ближáйший мéньший квадрат к числу 50000. Но нужно принимать во внимание, что сотни это числа с двумя нулями на конце. Примеры:
100 — одна сотня
500 — пять сотен
900 — девять сотен
При возведéнии таких чисел в квадрат, получаются числа, у которых четыре нуля на конце:
1002 = 10000
5002 = 250000
9002 = 810000
Мы ищем сотни корня в десятках тысяч числа 54756, то есть в числе 50000. Но нет такого числá с двумя нулями на конце, вторая степень которого равна 50000. Поэтому мы ищем ближáйший мéньший квадрат, но опять же с четырьмя нулями на конце. Таковым является квадрат 40000.
Вернёмся к нашему рисунку. Большой квадрат со стороной a и площадью a2 это тот самый квадрат 40000. Укажем вместо a2 значение 40000
Теперь извлечём корень из квадрата 40000
Итак, мы нашли сторону квадрата, площадь которого 40000. Подпишем сторону a как 200
Подпишем сторону a как 200
Но ранее в ответе мы написали не 200, а 2. Это является сокращённым вариантом. Число 2 в данном случае означает две сотни:
Теперь вытаскиваем остаток. Из пяти десятков тысяч корень извлечён только из четырёх десятков тысяч. Значит в остатке остался один десяток тысяч. Вытащим его:
Опять же надо понимать, что 4 это 40000, а 1 это 10000. С помощью рисунка это можно пояснить так: квадрат, площадь которого 40000, вычитается от общего квадрата, площадь которого 54756. Остаётся фигура, площадь которой 54756 − 40000 = 14756
Теперь нужно найти десятки корня. Рассмотрим на рисунке сумму площадей ab + ab + b2 (или 2ab + b2). В эту сумму будет входить один десяток тысяч, который остался в результате нахождения сóтен корня, удвоенное произведение сотен и десятков корня 2ab, а также десятки корня в квадрате b2.
Десятки в квадрате составляют сотни. Поэтому десятки корня следует искать в сотнях подкоренного числа. Под корнем сейчас 47 сотен. Снесём их к остатку 1, предварительно отделив их под корнем мéткой:
Поэтому десятки корня следует искать в сотнях подкоренного числа. Под корнем сейчас 47 сотен. Снесём их к остатку 1, предварительно отделив их под корнем мéткой:
Один десяток тысяч это сто сотен, плюс снесено 47 сотен. Итого 100 + 47 = 147 сотен. В эти 147 сотен должна входить сумма 2ab + b2
2ab + b2 = 14700
Переменная a уже известна, она равна 200. Подставим это значение в данное равенство:
2 × 200 × b + b2 = 14700
400b + b2 = 14700
Теперь наша задача найти такое значение b, при котором левая часть станет равна 14700 или хотя близкой к этому числу, но не превосходящей его. Поскольку b является десятками искомого корня, то значение b является двузначным числом с одним нулём на конце. Такое число можно найти методом подбора. Для удобства вынесем в левой части за скобки b
b(400 + b) = 14700
Теперь левую часть можно понимать так: к 400 следует прибавить некоторое число b, которое при умножении с тем же самым b даст в результате 14700 или близкое к 14700 число, не превосходящее его. Подставим например 40
Подставим например 40
40(400 + 40) = 14700
17600 ≠ 14700
Получается 17600, которое превосходит число 14700. Значит число 40 не годится в качестве десятков корня. Проверим тогда число 30
30(400 + 30) = 14700
12900 ≤ 14700
Получилось число 12900, которое не превосходит 14700. Значит число 30 подходит в качестве десятков корня. Числа, расположенные между 30 до 40 проверять не нужно, поскольку сейчас нас интересуют только двузначные числа с одним нулем на конце:
Вернемся к нашему рисунку. Сторона b это десятки корня. Укажем вместо b найденные десятки 30. А квадрат, площадь которого b2 это найденные десятки во второй степени, то есть число 900. Также укажем площади прямоугольников ab. Они равны произведению сотен корня на десятки корня, то есть 200 × 30 = 6000
Ранее в ответе мы написали не 30, а 3. Это является сокращённым вариантом. Число 3 в данном случае означают три десятка.
Теперь вытаскиваем остаток. В 147 сотен вместилось только 129 сотен. Значит в остатке осталось 147 − 129 = 18 сотен плюс сносим число 56 из подкоренного выражения. В результате образýется новый остаток 1856
С помощью рисунка это можно пояснить так: от фигуры, площадь которой 14756, вычитается площадь 12900. Остаётся фигура, площадь которой 14756 − 12900 = 1856
Теперь нужно найти единицы корня. Рассмотрим на рисунке сумму площадей 2(a + b)c + c2. В эту сумму и должен входить последний остаток 1856
2(a + b)c + c2 = 1856
Переменные a и b уже известны, они равны 200 и 30 соответственно. Подставим эти значения в данное равенство:
2(200 + 30)c + c2 = 1856
2 × 230c + c2 = 1856
460c + c2 = 1856
Теперь наша задача найти такое значение c, при котором левая часть станет равна 1856 или хотя близкой к этому числу, но не превосходящей его. Поскольку c является единицами искомого корня, то значение с является однозначным числом. То есть значение с это число от 1 до 9. Это число можно найти методом подбора. Для удобства вынесем в левой части за скобки с
Поскольку c является единицами искомого корня, то значение с является однозначным числом. То есть значение с это число от 1 до 9. Это число можно найти методом подбора. Для удобства вынесем в левой части за скобки с
с(460 + c) = 1856
Теперь левую часть можно понимать так: к 460 следует прибавить нéкоторое число с, которое при умножении с тем же сáмым с даст в результате 1856 или близкое к 1856 число, не превосходящее его. Подставим, например, число 4
4(460 + 4) = 1856
4 × 464 = 1856
1856 = 1856
Именно поэтому при использовании алгоритма первые найденные цифры умножают на 2. Так, 23 мы умнóжили на 2, получили 46 и уже к 46 дописывали цифру и умножáли образовавшееся число на ту же самую дописанную цифру, пытаясь получить остаток 1856
Итак, с = 4. При подстановке вместо с числá 4 получается остаток 1856. Это значит, что единицы корня найдены.
Квадрат, площадь которого 54756, имеет сторону равную 200 + 30 + 4, то есть 234.
Если из общей площади 54756 вычесть 40000, 6000, 6000, 900, 920, 920 и 16, то получим 0. Остаток равный нулю говорит о том, что решение завершено:
54756 − 40000 − 6000 − 6000 − 900 − 920 − 920 − 16 = 0
Пример 3. Извлечь квадратный корень из числа 3
Квадратный корень из числа 3 не извлекается. Ранее мы говорили, что квадратные корни из таких чисел можно извлекать только приближённо с определенной точностью.
Пусть 3 это площадь следующего квадрата:
Извлечь корень из числа 3 значит найти длину стороны данного квадрата:
Корень из 3 больше корня из 1, но меньше корня из 4
√1 < √3 < √4
Корни из 1 и 4 являются целыми числами.
√1 < √3 < √4
1 < √3 < 2
Между числами 1 и 2 нет целых чисел. Значит корень из числа 3 будет десятичной дробью. Найдём этот корень с точностью до десятых.
Квадратный корень из числа 3 можно представить в виде суммы a + b, где a — целая часть корня, b — дробная часть. Тогда сторону квадрата можно разбить на две составляющие: a и b
Тогда сторону квадрата можно разбить на две составляющие: a и b
Сумма a + b во второй степени должна приближённо равняться 3.
(a + b)2 ≈ 3
Выполним в левой части данного равенства возведéние в квадрат:
a2 + 2ab + b2 ≈ 3
Тогда рисунок, иллюстрирующий квадрат площадью 3, можно представить так:
Найдём a. Извлечём корень из числа 3 с точностью до целых, получим 1
Если a2 это 1, а площадь всего квадрата равна 3, то в остатке останется 2. В этот остаток должна вмещаться площадь оставшейся фигуры:
Найдём b. Для этого рассмотрим сумму площадей 2ab + b2. Эта сумма должна приближённо равняться остатку 2, но не превосходить его
2ab + b2 ≈ 2
Значение a уже известно, оно равно единице:
2b + b2 ≈ 2
Вынесем за скобки b
b(2 + b) ≈ 2
Теперь в левой части к 2 следует прибавить нéкоторое число b, которое при умножении с тем же b будет приближённо равняться 2.
Значение b является дробным числом, а именно десятой частью. Оно равно какому-нибудь числу из промежутка [0,1; 0,9]. Возьмём любое число из этого промежутка и подставим его в равенство. Подставим к примеру 0,8
0,8(2 + 0,8) ≈ 2
2,24 ≈ 2
Получилось 2,24 которое превосходит 2. Значит 0,8 не годится в качестве значения b. Проверим тогда 0,7
0,7(2 + 0,7) ≈ 2
1,89 ≈ 2
Получилось 1,89 которое приближённо равно 2 и не превосходит его. Значит 0,7 является значением b
Значит квадратный корень из 3 с точностью до десятых приближённо равен 1 + 0,7
К сожалению, понять механизм алгоритма извлечения квадратного корня намного сложнее, чем использовать сам алгоритм. Решите несколько примеров на применение алгоритма, и понимание механизма его работы будет даваться вам значительно проще.
Задания для самостоятельного решения
Задание 1. Извлечь квадратный корень из числа 169, используя алгоритм извлечения квадратного корня
Решение:
Задание 2. Извлечь квадратный корень из числа 289, используя алгоритм извлечения квадратного корня
Извлечь квадратный корень из числа 289, используя алгоритм извлечения квадратного корня
Решение:
Задание 3. Извлечь квадратный корень из числа 1089, используя алгоритм извлечения квадратного корня
Решение:
Задание 4. Извлечь квадратный корень из числа 1764, используя алгоритм извлечения квадратного корня
Решение:
Задание 5. Извлечь квадратный корень из числа 4761, используя алгоритм извлечения квадратного корня
Решение:
Задание 6. Извлечь квадратный корень из числа 132496, используя алгоритм извлечения квадратного корня
Решение:
Задание 7. Извлечь квадратный корень из числа 157 с точностью до сотых, используя алгоритм извлечения квадратного корня
Решение:
Задание 8. Извлечь квадратный корень из числа 240,25 используя алгоритм извлечения квадратного корня
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
методы умножения, примеры с объяснением
Известно, что знак корня является квадратным корнем из некоторого числа. Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Однако знак корня означает не только алгебраическое действие, но и применяется в деревообрабатывающем производстве — в расчете относительных размеров.
Если вы хотите узнать, как умножить корни «с» или «без» множителей, то эта статья для вас. В ней мы рассмотрим методы умножения корней:
- без множителей;
- с множителями;
- с разными показателями.
Метод умножения корней без множителей
Алгоритм действий:
Убедиться, что у корня одинаковые показатели (степени). Вспомним, что степень записывается слева над знаком корня. Если нет обозначения степени, это значит, что корень квадратный, т.е. со степенью 2, и его можно умножать на другие корни со степенью 2.
ПримерПример 1: 18×2=?
Пример 2: 10×5=?
Пример 3: 33×93=?
Далее необходимо перемножить числа под корнем.
ПримерПример 1: 18×2=36
Пример 2: 10×5=50
Пример 3: 33×93=273
Упростить подкоренные выражения. Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
Когда мы умножаем корни друг на друга, мы можем упростить полученное подкоренное выражение до произведения числа (или выражения) на полный квадрат или куб:
Пример 1: 36=6. 36 — квадратный корень из шести (6×6=36).
Пример 2: 50=(25×2)=(5×5)×2=52. Число 50 раскладываем на произведение 25 и 2. Корень из 25 — 5, поэтому выносим 5 из-под знака корня и упрощаем выражение.
Пример 3: 273=3. Кубический корень из 27 равен 3: 3×3×3=27.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеМетод умножения показателей с множителями
Алгоритм действий:
Умножить множители. Множитель — число, которое стоит перед знаком корня. В случае отсутствия множителя, он, по умолчанию, считается единицей. Далее необходимо перемножить множители:
ПримерПример 1: 32×10=3?3×1=3
Пример 2: 43×36=12?4×3=12
Умножить числа под знаком корня. Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Как только вы перемножили множители, смело умножайте числа, стоящие под знаком корня:
Пример 1: 32×10=3(2×10)=320
Пример 2: 43×36=12(3×6)=1218
Упростить подкоренное выражение. Далее следует упростить значения, которые стоят под знаком корня, — требуется вынести соответствующие числа за знак корня. После этого, необходимо перемножить числа и множители, которые стоят перед знаком корня:
ПримерПример 1: 320=3(4×5)=3(2×2)×5=(3×2)5=65
Пример 2: 1218=12(9×2)=12(3×3)×2=(12×3)2=362
Метод умножения корней с разными показателями
Алгоритм действий:
Найти наименьшее общее кратное (НОК) показателей. Наименьшее общее кратное — наименьшее число, делящееся на оба показателя.
ПримерНеобходимо найти НОК показателей для следующего выражения:
53×22
Показатели равны 3 и 2. Для этих двух чисел наименьшим общим кратным является число 6 (оно делится без остатка и на 3, и на 2). Для умножения корней необходим показатель 6.
Для умножения корней необходим показатель 6.
Записать каждое выражение с новым показателем:
56×26
Найти числа, на которые нужно умножить показатели, чтобы получить НОК.
В выражении 53 необходимо умножить 3 на 2, чтобы получить 6. А в выражении 22 — наоборот, необходимо умножить на 3, чтобы получить 6.
Возвести число, которое стоит под знаком корня, в степень равную числу, которое было найдено в предыдущем шаге. Для первого выражения 5 нужно возвести в степень 2, а втором — 2 в степень 3:
2→56=5263→26=236
Возвести в степень выражения и записать результат под знаком корня:
526=(5×5)6=256236=(2×2×2)6=86
Перемножить числа под корнем:
(8×25)6
Записать результат:
(8×25)6=2006
По возможности необходимо упростить выражение, но в данном случае оно не упрощается.
Решение (корни) квадратного уравнения
Квадратным уравнением называется уравнение вида ax² + bx + c = 0,
где x — переменная, которая в уравнении присутствует в квадрате, a, b, c — некоторые числа, причём a ≠ 0.
Например, квадратным является уравнение
2x² — 3x + 1 = 0,
в котором a = 2, b = — 3, c = 1.
В квадратном уравнении ax² + bx + c = 0 коэффициент a называют первым коэффициентом, b — вторым коэффициентом, c — свободным членом.
Уравнения вида ax² + bx = 0,
где c =0,
ax² + c = 0,
где b =0, и
ax² = 0,
где a =0 и b =0,
называются неполными квадратными уравнениями.
Найти корни квадратного уравнения значит решить квадратное уравнение.
Для вычисления корней квадратного уравния служит выражение b² — 4ac,
которое называется дискриминантом квадратного уравнения и обозначается буквой D.
Корни квадратного уравнения имеют следующие сферы применения:
— для разложении квадратного трёхлена на множители, что, в свою очередь, является приёмом упрощения выражений (например, сокращения дробей, вынесение за скобки общего знаменателя и т.д.) в частности, при нахождении пределов, производных и интегралов;
— для решения задач на соотношения параметров меняющегося объекта (корни квадратного уравнения, чаще всего один, являются обычно конечным решением).
График квадратичного трёхлена ax² + bx + c —
левой части квадратного уравнения — представляет собой параболу, ось симметрии которой параллельна
оси 0y. Число точек пересечения параболы с осью
0x определяет число корней квадратного уравнения. Если точек
пересечения две, то квадратное уравнение имеет два действительных корня, если точка пересечения
одна, то квадратное уравнение имеет один действительный корень, если парабола не пересекает
ось 0x, то квадратное уравнение не имеет действительных
корней. На рисунке ниже изображены три упомянутых случая.
На рисунке ниже изображены три упомянутых случая.
Как видно на рисунке, красная парабола пересекает ось 0x в двух точках, зелёная — в одной точке, а жёлтая парабола не имеет точек пересечения с осью 0x.
1. Если дискриминант больше нуля (), то квадратное уравнение имеет два различных действительных корня.
Они вычисляются по формулам:
и
.
Часто пишется так: .
2. Если дискриминант равен нулю (), то квадратное уравнение имеет только один действительный корень, или, что то же самое — два равных действительных корня, которые равны .
3. Если дискриминант меньше нуля (),
то квадратное уравнение не имеет действительных корней, а имеет комплексные корни, но нахождение комплексных корней
в этой статье рассматривать не будем. В общем случае правильным решением является констатация того,
что квадратное уравнение не имеет действительных корней.
Пример 1. Определить, сколько действительных корней имеет квадратное уравнение:
.
Решение. Найдём дискриминант:
.
Дискриминант больше нуля, следовательно, квадратное уравнение имеет два действительных корня.
Путём преобразования в квадратное уравнение следует решать и дробные уравнения, в которых хотя бы одно из слагаемых — дробь, в знаменателе которой присутствует неизвестное, например, . О том, как это делается — в материале Решение дробных уравнений с преобразованием в квадратное уравнение.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Пример 2. Определить, сколько действительных корней имеет квадратное уравнение:
.
Решение. Найдём дискриминант:
.
Дискриминант равен нулю, следовательно, квадратное уравнение имеет один действительный корень.
Пример 3. Определить, сколько действительных корней имеет квадратное уравнение:
.
Решение. Найдём дискриминант:
.
Дискриминант меньше нуля, следовательно, квадратное уравнение не имеет действительных корней.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Находить корни квадратного уравнения требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.
Пример 4. Найти корни квадратного уравнения:
.
В примере 1 нашли дискриминант этого уравнения:
,
Решение квадратного уравнения найдём по формуле для корней:
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.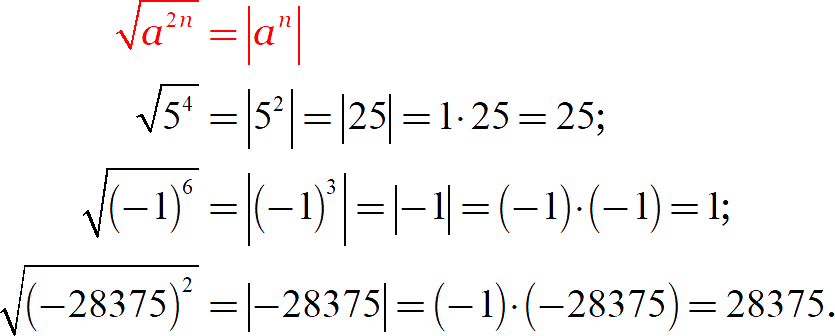
Корни приведённого квадратного уравнения
Формула корней приведённого уравнения имеет вид:
.
Существуют формулы, связывающие корни квадратного уравнения с его коэффициентами. Они впервые были получены французским математиком Ф.Виетом.
Теорема Виета. Если квадратное уравнение ax² + bx + c = 0 имеет действительные корни, то их сумма равна — b/a, а произведение равно с/a:
Следствие. Если приведённое квадратное уравнение x² + px + q = 0 имеет действительные корни и , то
Пояснение формул: сумма корней приведённого квадратного уравнения равна второму
коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному
члену.
Следовательно, теорему Виета можно применять и для поиска корней приведённого квадратного уравнения.
Если известны корни квадратного уравнения, то трёхчлен, представляющий собой левую часть уравнения, можно разложить на множители по следующей формуле:
.
Этот приём часто используется для упрощения выражений, особенно сокращения дробей.
Пример 9. Упростить выражение:
.
Решение. Числитель данной дроби можем рассматривать как квадратный трёхчлен в отношении x и разложить его на множители, предварительно найдя его корни. Найдём дискриминант квадратного уравнения:
.
Корни квадратного уравнения будут следующими:
.
Разложим квадратный многочлен на множители:
.
Упростили выражение, проще не бывает:
.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Пример 10. Упростить выражение:
.
Решение. И числитель, и знаменатель — квадратные трёхчлены. Значит, их можно разложить на множители, предварительно найдя корни соответствующих квадратных уравнений. Находим дискриминант первого квадратного уравнения:
.
Корни первого квадратного уравнения будут следующими:
.
Находим дискриминант второго квадратного уравнения:
.
Так как дискриминант равен нулю, второе квадратное уравнение имеет два совпадающих корня:
.
Подставим корни квадратных уравнений, разложим числитель и знаменатель на множители и получим:
.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Упрощать выражения путём решения квадратных уравнений требуется при решении многих задач высшей математики, например, при нахождении пределов, интегралов, исследовании функций на возрастание и убывание и других.
Разумеется, квадратного трёхчлена может может и не быть в выражении в первоначальном виде, он может быть получен в процессе предварительных преобразований выражения.
Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один
из первых дошедших до наших дней выводов этой формулы принажлежит индийскому математику
Брахмагупте (около 598 г.). Среднеазиатский учёный аль-Хорезми (IX в.) получил эту формулу
методом выделения полного квадрата с помощью геометрической иллюстрации. Суть его рассуждений
видна из рисунка ниже (он рассматривает уравнение x² + 10x = 39).
Площадь большого квадрата равна (x + 5)². Она складывается из площади x² + 10x заштрихованной фигуры, равной левой части рассматриваемого уравнения, и площади четырёх квадратов со стороной 5/2, равной 25. Получается следующее уравнение и его решение:
Пример 11. Отрезок ткани стоит 180 у.ед. Если бы ткани в отрезке было на 2,5 м больше и цена отрезка оставалась бы прежней, то цена 1 м ткани была бы на 1 у.ед. меньше. Сколько ткани в отрезке?
Решение. Примем количество ткани в отрезке за x и получим уравнение:
Приведём обе части уравнения к общему знаменателю:
Произведём дальнейшие преобразования:
Получили квадратное уравнение, которое и решим:
Ясно, что количество ткани не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь один корень — положительный.
Ответ: в отрезке 20 м ткани.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Пример 12. Товар, количество которого 187,5 кг, взвешивают в одинаковых ящиках. Если в каждом ящике количество товара уменьшить на 2 кг, то следовало бы использовать на 2 ящика больше и при этом 2 кг товара остались бы невзвешенными. Сколько кг товара взвешивают в каждом ящике?
Решение. Примем за x количество товара, взвешиваемого в одном ящике. Тогда получим уравнение:
Приведём обе части уравнения к общему знаменателю, произведём дальнейшие преобразования и получим квадратное уравнение. Процесс записывается так:
Найдём дискриминант:
Найдём корни квадратного уравнения:
Количество товара не может быть отрицательным, поэтому в качестве ответа из двух корней квадратного уравнения подходит лишь положительный корень.
Ответ: в одном ящике взвешивают 12,5 кг ткани.
Проверить решение можно с помощью онлайн калькулятора квадратных уравнений.
Другие темы в блоке «Школьная математика»
Извлечение корня. Внесение и вынесения множителя из под корня
Извлечь из данного числа корень какой-нибудь степени значит найти такое число, которое при возведении в эту степень, будет равно данному числу.
Из правил знаков при возведении в степень следует, что:
- Корень нечётной степени из положительного числа есть число положительное, а из отрицательного – отрицательное.
Примеры:
3√+27 = +3, так как (+3)3 = 27;
3√-27 = -3, так как (-3)3 = -27.
- Корень чётной степени из положительного числа может быть как положительным, так и отрицательным числом.

Примеры:
√+9 = ±3, так как (+3)2 = +9 и (-3)2 = +9;
4√+256 = ±4, так как (+4)4 = +256 и (-4)4 = +256.
- Корень чётной степени из отрицательного числа является невозможным выражением, потому что любое положительное или отрицательное число при возведении в чётную степень даёт только положительный результат. Таким образом,
√-49 , 4√-256 , 6√-64 — это невозможные выражения.
Невозможные выражения иначе называют мнимыми.
Извлечение корня из произведения, степени и дроби
Чтобы извлечь корень из произведения, надо извлечь его из каждого множителя отдельно.
Так же можно сказать, что корень произведения равен произведению корней всех его множителей:
Чтобы извлечь корень из степени, следует показатель степени разделить на показатель корня:
Чтобы извлечь корень из дроби, следует извлечь его отдельно из числителя и из знаменателя:
Примеры:
Вынесение множителя из-под знака корня
Когда нельзя извлечь корень из всего подкоренного числа или выражения, то подкоренное число или выражение раскладывают на множители и извлекают корень только из тех множителей, из которых это возможно сделать.
Внесение множителя под корень
Если нужно внести множитель под знак корня, то его следует возвести в степень, равную показателю корня.
Примеры:
Режимы работы калькулятора, использование памяти — КиберПедия
В обычном режиме на калькуляторе можно выполнять следующие операции: четыре арифметических действия (сложение, вычитание, деление, умножение), определение обратной величины любого числа (результат от деления 1 на данное число), противоположный, нахождение процента от числа и квадратного корня, использование в расчетах ячеек памяти.
Инженерный режим (Scientific view) позволяет работать с функциями: тригонометрическими (прямыми и обратными), логарифмическими, степенными и т.п., выполнять статистические расчеты.
Как вычислить среднее значение ряда чисел с помощью режима Статистика?
1. В меню Вид выберите команду Инженерный.
2. Введите первое число и нажмите кнопку Sta, чтобы открыть окно Статистика.
3. Нажмите кнопку RET, чтобы вернуться в окно калькулятора, а затем нажмите кнопку Dat, чтобы сохранить это значение.
4. Введите остальные числа, нажимая кнопку Dat после ввода каждого из них.
5.Нажмите кнопку Ave, Sum или s.
Как вычислить значение корня пятой степени из 312?
Чтобы извлечь корень введите два числа — основание (из чего извлекается корень) и степень. Калькулятор корней извлечет корень. Степень может быть как положительной, так и отрицательной. Число, из которого извлекается корень, должно быть больше нуля.
К примеру, чтобы извлечь квадратный корень из числа 312 мы вводим значения как на картинке ниже и нажимаем кнопку Посчитать. Результат увидим тут же. Помимо этого наш калькулятор может извлекать корни из дробных чисел (дробей), а также извлекать корень дробной степени.
Как вычислить arctg 0. 5?
5?
Введите значение тангенса угла и нажмите кнопку посчитать. В результате вы получите значение арктангенса выраженное в градусах и радианах.
Арктангенс числа x — это значение угла в радианах, для которого справедливо равенство tg a = m.
Выводы: В ходе лабораторной работы, я изучила способы выполнения расчётов различной сложности с помощью программы Калькулятор.
Федеральное государственное
бюджетное образовательное учреждение высшего
образования «Краснодарский государственный
Институт культуры»
Кафедра документоведения
и проектной деятельности
Отчет по лабораторной работе № 5
По теме: Графический редактор Paint
Выполнил: студент 2 курса ОФО
Информационно-библиотечного факультета
Группы: Док/бак-18
Самойловский Аристарх Михайлович
Проверил: доцент кафедры библиотечно-
Библиографической деятельности
информационных технологий, к. т.н.
т.н.
Багдасарян Рафаэль Хачикович
Краснодар 2020
Лабораторная №5
Тема: Графический редактор Paint
Цель работы:
Изучение графических возможностей редактора Paint
Содержание работы:
1. Панель инструментов редактора Paint.
2 Рисование графических объектов.
3 Работа с фрагментом изображения.
Результаты выполнения работы:
Нарисовать разными инструментами (Кистью и Карандашом) следующие геометрические фигуры:
— окружность, эллипс, прямоугольник, квадрат;
— прямые куб, параллелепипед, цилиндр, конус, пирамиду;
— наклонные куб, параллелепипед, цилиндр, конус, пирамиду;
— раскрасить грани фигур разными цветами с помощью инструментов Заливка и Распылитель;
— увеличить одну из фигур в 2 раза;
— наклонить одну из фигур на 30°.
Изобразить на экране произвольный пейзаж (горы с снежными шапками, солнце, облака, море, корабли, лес, деревья, дорогу, пшеничное поле, автомобиль, автобус, поезд, танк, самолёт и др. Обязательно над пейзажем изобразить семицветную радугу.
3. Нарисовать на экране электронные часы, показывающие текущее время. Уменьшить рисунок на 20% (чтобы он составлял 80% от исходного)
4. Изобразить на экране эскиз поздравительной открытки для какого-либо праздника (8 марта, Новый год, 1 или 9 мая, день рождения, свадьбы…). В нижней части эскиза написать свою фамилию и инициалы.
Контрольные вопросы
Калькулятор дробей
Калькулятор выполняет базовые и расширенные операции с дробями, выражениями с дробями, объединенными с целыми числами, десятичными знаками и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Решайте задачи с двумя, тремя или более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — используйте косую черту «/» между числителем и знаменателем, т.е.е., для пяти сотых введите 5/100 . Если вы используете смешанные числа, не забудьте оставить один пробел между целой и дробной частью.Косая черта разделяет числитель (число над дробной чертой) и знаменатель (число ниже).
Смешанные числа (смешанные дроби или смешанные числа) записываются как ненулевое целое число, разделенное одним пробелом и дробью, то есть 1 2/3 (с тем же знаком). Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком для дробной линии и деления, мы рекомендуем использовать двоеточие (:) в качестве оператора деления дробей, то есть 1/2: 3 .
Десятичные числа (десятичные числа) вводятся с десятичной запятой . , и они автоматически конвертируются в дроби — то есть 1,45 .
Двоеточие : и косая черта / являются символом деления. Может использоваться для деления смешанных чисел 1 2/3: 4 3/8 или может использоваться для записи сложных дробей i.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целого и дробного числа: 5 ÷ 1/2
• комплексные дроби: 5/8: 2 2/3
• десятичное дробное: 0,625
• Дробь в десятичную: 1/4
• Дробь в проценты: 1/8%
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt (1/16)
• уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение в скобках: 1 / 3 * (1/2 — 3 3/8)
• сложная дробь: 3/4 от 5/7
• кратная дробь: 2/3 от 3/5
• разделите, чтобы найти частное: 3/5 ÷ 2 / 3
Калькулятор следует известным правилам для порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — круглые скобки, экспоненты, умножение, деление, сложение, вычитание.
BEDMAS — Скобки, экспоненты, деление, умножение, сложение, вычитание
BODMAS — Скобки, порядок или, деление, умножение, сложение, вычитание.
GEMDAS — Группирующие символы — скобки () {}, экспоненты, умножение, деление, сложение, вычитание.
Будьте осторожны, всегда выполняйте умножение и деление перед сложением и вычитанием .Некоторые операторы (+ и -) и (* и /) имеют одинаковый приоритет и должны вычисляться слева направо.
Дроби в задачах со словами:
следующие математические задачи »
Калькулятор дробей квадратного корня
Наших пользователей:
Я учусь в 9-м классе и всегда удивлялся, почему некоторые ученики всегда получают хорошие отметки по математике, но никогда не могли представить, что я буду одним из них. Снимаю шляпу перед алгебратором! Теперь я твердо разбираюсь в алгебре, и мой подход к решению задач стал более методичным.
Шарлотта Бичем, IN
Я только что купил вашу программу. Я купил Personal Algebra Tutor (PAT), и я очень разочарован им. Причины: 1) если компьютер выйдет из строя, вы должны отправить им по электронной почте пароль (где я живу, на горе с сильным ветром, мы получаем много отключений электроэнергии), а также удары молнии; 2) они сказали, что проблемы можно набрать, и будет предложено решение. Половина математических задач, которые у меня были, не работают с их программой; 3) они говорят отправить им вопросы по электронной почте, и они предоставят решения, но это может занять до 24 часов, а иногда слишком долго, чтобы ждать ответа.Чтобы показать доказательство моей подтвержденной покупки программы PAT, я приложил копию квитанции, которую они мне прислали.
Я купил Personal Algebra Tutor (PAT), и я очень разочарован им. Причины: 1) если компьютер выйдет из строя, вы должны отправить им по электронной почте пароль (где я живу, на горе с сильным ветром, мы получаем много отключений электроэнергии), а также удары молнии; 2) они сказали, что проблемы можно набрать, и будет предложено решение. Половина математических задач, которые у меня были, не работают с их программой; 3) они говорят отправить им вопросы по электронной почте, и они предоставят решения, но это может занять до 24 часов, а иногда слишком долго, чтобы ждать ответа.Чтобы показать доказательство моей подтвержденной покупки программы PAT, я приложил копию квитанции, которую они мне прислали.
Дэн Мазерс, Мичиган
Доступно так много программ алгебры. Не знаю, как я застрял с вашим, но с академической точки зрения это лучшее, что когда-либо случалось со мной!
Хален Иден, MT
Мои методы обучения никогда не были достаточно хорошими; Таким образом, я всегда ищу более простой метод обучения и настоятельно рекомендую Алгебратор.
P.W., Иллинойс
Я очень внимательно отношусь к академическим потребностям моего сына и слежу за ними. Недавно я обнаружил, что у него проблемы с пониманием алгебраических уравнений. Я не мог уделять ему много времени из-за моего плотного графика. Затем это программное обеспечение пришло как дар, посланный Богом. Простой способ объяснения сложных концепций помог моему сыну быстро схватить предмет. Всем рекомендую эту программу.
B.F., Вермонт
Студенты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь.Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 2010-06-05:
- начальная школа «2-й класс» рабочий лист по математике
- как упростить десятичные уравнения
- 6 класс по алгебре бесплатные примеры
- радикальное упрощение онлайн
- рабочие листы уравнений неравенства
- Таблицы сочетаний и перестановок третьего класса Конвертер десятичных чисел в смешанные числа
- «сравните и упорядочите» положительные и отрицательные дроби загрузить домашнее обучение
- как разделить вручную
- стихов и вопросов к ответам для 3-х классов
- Образцы SAT для 9 класса
- подстановка алгебры ks2
- пересмотр математики для индексов, стандартной формы, квадратных выражений и уравнений, вариаций и пифагора от
- девятый класс алгебра граф функции квадратного корня
- Диаграммная статистика в бизнес-математике
- учить алгебру 1
- Предварительная алгебра для 5 класса
- устранение неравенства математика справка
- Рабочий лист сложения и вычитания целых чисел Какулятор фракций
- KS3 Рабочий лист по алгебре
- вопросов о самых сложных сложных комплексных событиях в мире
- решатель наименьшего общего знаменателя
- ответы на вопросы по алгебре 2
- крестики-нолики метод факторинга
- рабочие листы по алгебраическим уравнениям
- программа упрощения радикальных выражений
- рабочие листы умножения рациональных выражений
- ти 83 всепр программы
- функциональные машины рабочие листы для печати 4 класс
- рабочие листы по алгебре ks3
- Excel одновременные нелинейные уравнения
- комбинаций рабочий лист 8 класс по математике
- «Предварительный тест по алгебре» и ответы
- TN Algebra 1 Gateway Практические тесты Калькулятор рациональных выражений
- , бесплатно онлайн
- Флорида примечания о сложении и вычитании 5-го класса как дроби / без умножения и деления
- Онтарио вопросов для 8-го класса по математике
- листов по бесплатной алгебре за 9 год
- элемент алгебры
- ответы разделение рациональных выражений yourhomework Рабочий лист
- для 6-х классов
- ключ ответа «saxon math» алгебра электронная книга
- как хранить данные в TI89
- макет бумаги 8 класс
- Факторинговые приложения для TI-84
- рабочие листы по критическому мышлению 6
- делительные полиномы / калькулятор
- , Калифорния, средний курс математики и навыков, курс 1 скачать -amazon
- matlab + решение системы нелинейных уравнений
- факторинговых проектов по алгебре 2
- математические идеи стихотворений Факторинг
- с использованием метода переменного тока.
 Лист
Лист - ответов на домашнее задание по математике
- уравнений с распределительным свойством
- радикальная упрощенная схема
- рассказ + задачи пифагорейских троек
- Современная химия Глава 10 Домашнее задание 10-1
- «Планы занятий по алгебре»
- Распечатка практического теста GED в штате Вашингтон
- ti-89 квадратная формула символически
- практических задач на вычитание бесплатно
- сложение вычитание деление и умножение Калькулятор квадратного корня
- как решать уравнения с дробями и десятичными знаками
- читерские ответы по алгебре 1
- планов уроков по вероятности для первого класса
- решения задач алгебры холла II
- 10 класс по алгебре
- справка по квадратным уравнениям + gcse
- Algerbra I Help
- асимптотических программ
- почему так важно уметь переводить дроби, десятичные дроби, проценты
- 10 класс по математике Радикалы
- ks2 математика справка по факторам для детей
- коэффициент корня четвертой степени линейная математика
- Algebra Chicago Series Teachers Edition Mathbook
- Калькулятор упрощенных логических уравнений
- Знаменатель KS2
- Алгебра / игры с дробями для 5-х классов
- Программа предварительного расчета для домашних заданий
— CueMath
Калькулятор квадратного корня помогает найти квадратный корень из заданного числа.
Что такое калькулятор квадратного корня?
Калькулятор квадратного корня — это онлайн-инструмент, который вычисляет значение квадратного корня числа.
Онлайн-калькулятор квадратного корняCuemath поможет вам вычислить квадратный корень числа за несколько секунд.
Примечание. Введите цифры до 3 цифр.
Что такое квадратный корень числа?
Квадратный корень числа — это число, которое при умножении на само себя дает произведение как исходное число.Давайте лучше поймем это на примере.
Найдем квадратный корень из 5.
Мы знаем, что 5 2 = (5 × 5) = 25
Здесь 5 называется квадратным корнем из 25. 25 — это полный квадрат. Итак, квадратный корень из 25 равен 5.
Как пользоваться калькулятором квадратного корня?
Выполните следующие действия, которые помогут вам использовать калькулятор.
- Шаг 1 : Введите число в поле ввода.
- Шаг 2 : Щелкните « Calculate », чтобы найти значение квадратного корня из числа.

- Шаг 3 : Щелкните « Reset », чтобы очистить поле и ввести новый номер.
Как найти квадратный корень числа?
Квадратный корень из числа ‘ n’ можно записать как ‘ √n’ . Это означает, что есть число ‘a’ при повторном умножении на ‘a’ дает ‘n’:
а × а = п
Это также можно записать как:
a 2 = n или a = √nИтак, a равно квадратному корню из n.
Теперь, если n = 89, то a = √89 — квадратный корень из 89. В радикальной форме квадратный корень из 89 может быть представлен как √89.
Квадратный корень из 89 = 9,43 в десятичной форме с точностью до 2 знаков после запятой.
Хотите найти сложные математические решения за секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором для решения сложных вопросов. Cuemath находит решения простым и легким способом.
Забронируйте бесплатную пробную версию Класс
Решенный пример:Найдите квадратный корень из 64.
Раствор:Мы знаем, что квадратный корень из числа (n), a = \ (\ sqrt {number, n} \)
\ (a = \ sqrt {n} \\ \, \, \, = \ sqrt {64} \\ \, \, \, = \ sqrt {8 \ times 8} \\ \, \, \, = 8 \)
Следовательно, 8 — это квадратный корень из 64.
Теперь попробуйте вычислить на калькуляторе квадратный корень из следующих чисел.
| Автор | Сообщение | ||||||
|---|---|---|---|---|---|---|---|
| MoveliVadBoy Зарегистрирован: 06.03.2002 |
| ||||||
| К началу | |||||||
| nxu Зарегистрировано: 25.10.2006 |
| ||||||
| К началу | |||||||
| Koem Зарегистрировано: 22.10.2001 |
| ||||||
| К началу | |||||||
| ndrc Зарегистрировано: 22.09.2007 |
| ||||||
| К началу | |||||||
| Mibxrus Зарегистрировано: 19.10.2002 | |||||||
| К началу | |||||||
Калькулятор дробной степени
Этот калькулятор дробной степени подскажет вам — сюрприз, сюрприз — дробные показатели.Вы боретесь с концепцией дробных показателей? Отрицательные и дробные показатели — это для вас закрытая книга? Что ж, больше не о чем беспокоиться, прокрутите вниз, чтобы найти полезные объяснения.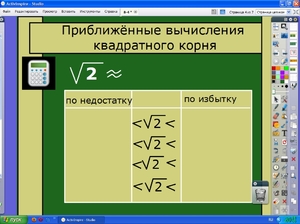
Дробные показатели с числителем 1
Дробные показатели — это способ выражения степеней, а также корней в одном представлении .
Что именно это означает? Давайте сначала рассмотрим несколько простых примеров, где наш числитель равен 1 :
.- 64 (1/2) = √64
- 27 (1/3) = ³√27
Из приведенных выше уравнений мы можем вывести, что:
- Показатель степени 1/2 — это квадратный корень
- Показатель степени 1/3 — кубический корень
- Показатель степени 1/4 — корень четвертой степени
- …
- Показатель степени 1 / k является корнем k-й степени
Но почему это так? Постараемся это доказать:
Давайте воспользуемся законом экспонент, который гласит, что мы можем складывать показатели при умножении двух степеней с одинаковым основанием:
x a + b = x a * x b
так, например, если n = 2
x² = x¹⁺¹ = x¹ * x¹ = x * x
Попробуйте это с любым числом, которое вам нравится, это всегда правда!
Затем давайте посмотрим на дробные показатели x:
x = x¹ = x (1/2 + 1/2) = x (1/2) * x (1/2)
Как позвонить по номеру, умножение которого само на себя дает другой номер? Конечно, это квадратный корень из ! Итак, мы выяснили, что:
x (1/2) = √x
Если хотите, вы можете аналогичным образом проверить другие корни, например.
 грамм. кубический корень:
грамм. кубический корень:x = x (1/3 + 1/3 + 1/3) = x (1/3) * x (1/3) * x (1/3) = ³√x * ³√x * ³√x
т.
x (1/3) = ³√x
Теперь мы знаем, что x в степени одной трети равен кубическому корню из x.
Дробные показатели с числителем, отличным от 1 (любая дробь)
Итак, что произойдет, если наш числитель не равен 1 (n 1)?
Все, что вам нужно сделать, это возвести это число в степень n и взять корень d-й степени .Порядок не имеет значения, дробь n / d может быть разделена на две части:
- целое число (n)
- дробная часть (1 / д)
Давайте посмотрим на пример, где дробная экспонента = 3/2 и x = 16:
- 16 3/2 = 16 (3 * 1/2) = (16 3 ) 1/2 = √ (16³) = √4096 = 64
Или, как вариант, можно написать, что
- 16 3/2 = 16 (1/2) * 3 = (16 1/2 ) 3 = (√16) ³ = 4³ = 64
И результат действительно тот же. Вы можете выбрать тот метод, который дает вам самый простой расчет, или вы можете просто использовать наш калькулятор дробной степени!
Вы можете выбрать тот метод, который дает вам самый простой расчет, или вы можете просто использовать наш калькулятор дробной степени!
Отрицательный и дробный показатель степени
Положительные показатели говорят нам, сколько раз мы используем число при умножении:
Но что произойдет, если наша экспонента будет отрицательным числом, вы можете догадаться? Да, он говорит вам, сколько раз вам нужно разделить на это число:
Кроме того, вы можете просто вычислить положительную экспоненту (например, x 4 ), а затем взять обратную величину (в нашем случае 1 / x 4 ).Конечно, аналогично, если у нас есть отрицательная И дробная экспонента.
Калькулятор степени дроби — как использовать
Мы считаем, что этот инструмент настолько интуитивно понятен и прост, что никаких дополнительных пояснений не требуется, но для записи мы быстро объясним, как вычислить дробные показатели:
- Введите базовое значение .
 Например, введите 7.
Например, введите 7. - Введите числитель и знаменатель дроби .Если вы хотите использовать этот калькулятор как простой инструмент экспоненты — с целым числом в качестве показателя степени вместо дроби — введите 1 в качестве знаменателя. Предположим, наша дробь равна -2/5. Введите -2 в числитель и 5 в поле знаменателя (также отметьте обратное действие).
- Наслаждайтесь результатом, отображаемым нашим калькулятором дробной степени! Это 0,4592 для нашей примерной задачи.
Надо ли говорить о гибкости нашего инструмента? Вам не нужно переходить калькулятор сверху вниз — вычислите любое неизвестное, какое захотите! Введите любые три значения, и четвертое появится в мгновение ока.
Еще одна полезная функция калькулятора — дробью может быть не только показатель степени, но и основание ! Например, если вы хотите вычислить (1/16) 1/2 , просто введите 1/16 в базовое поле. Отлично!
Отлично!
Работает для десятичных и целых подкоренных выражений
Что такое квадратные корни?
Определение квадратного корня: Противоположность возведению числа в квадрат. Например, найти квадратный корень из 81 — это то же самое, что спросить: «Какое число в квадрате равно 81?»
Конечно, если вы знаете, что 9 x 9 = 81, вы будете знать, что квадратный корень из 81 равен 9 (9 2 = 81).Однако вы можете не осознавать, что -9 также является квадратным корнем из 81, потому что -9 x -9 также равняется 81.
Другими словами, все числа больше нуля (ноль никогда не может быть отрицательным или положительным) имеют два квадратных корня — один положительный и один отрицательный. Вот почему при использовании онлайн-калькулятора квадратного корня результату всегда будет предшествовать знак ±.
Что касается отрицательных чисел, поскольку отрицательное значение, умноженное на отрицательное, всегда дает положительное число, отрицательные числа не могут иметь действительного квадратного корня.
Что такое идеальные квадраты?
Когда квадратный корень числа является целым числом, это число называется полным квадратом. Например, поскольку √4 имеет квадратный корень из 2, 4 называется полным квадратом. Вот список идеальных квадратов до 225:
Список идеальных квадратов до 225| √1 | = | 1 | с | 1 2 | = | 1 | ||||||||
| √4 | = | 2 | с | 2 2 | = | 4 | ||||||||
| √9 | = | 3 | с | 23 | с | 23 | с | 3 | 9 | |||||
| √16 | = | 4 | с | 4 2 | = | 16 | ||||||||
| √25 | = | 5 | = | 25 | ||||||||||
| √36 | = | 6 | с | 6 2 | = | 36 | ||||||||
| √49 | = 7 41 с | 7 2 | = | 49 | ||||||||||
| √64 | = | 8 | с | 8 2 | = | 64 | ||||||||
| 9 | с | 9 2 | = | 81 | ||||||||||
| √100 | = | 10 | с | 10 2 | 100 121 | = | 11 | с | 11 2 | = | 121 | |||
| √144 | = | 12 | с | 12 | с | 904 12 9044 2 9044 | ||||||||
| √169 | = | 13 | с | 13 2 | = | 169 | ||||||||
| √196 | = | 14 | с | 14 2 | = | 196 | ||||||||
| √225 | = | 15 | с | 15 2 | = | 225 9454000 9 все еще 9 Если вам сложно понять квадратные корни, сообщите мне об этом в форме обратной связи, расположенной под калькулятором, и я постараюсь улучшить свои пояснения на этой странице. Можно ли получить «рут! Рут!»? 🙂 Калькулятор дробейФракции/ Для ввода дроби формы 3/4. Щелкните число, затем щелкните полосу дробей, затем щелкните другое число. ↔ Вы можете использовать кнопку пробела, чтобы создать число в форме 5 3/4. Введите число, затем щелкните пробел дроби, щелкните другое число и затем щелкните кнопку полосы дроби, наконец, введите другое число. DEC
FRA
Кнопка десятичного формата и кнопка формата дроби работают как пара. Когда вы выбираете одно, другое отключается. а б / с а + б / с
Кнопка правильной дроби и кнопка неправильной дроби работают как пара. Когда вы выбираете одно, другое отключается. |


 Лист
Лист
 Я очень старался найти кого-нибудь, кто мог бы мне в этом помочь. Я также искал учителя, который научил бы меня решать мои задачи по разности кубов, умножению матриц и эквивалентным дробям. Хотя я нашел несколько человек, которые, возможно, могли бы решить мою проблему, я понял, что не могу за них платить. У меня тоже мало времени. Скоро мое задание. Я в отчаянии . Может ли кто-нибудь помочь мне в этой ситуации? Я был бы очень признателен за любую помощь или любое предложение.
Я очень старался найти кого-нибудь, кто мог бы мне в этом помочь. Я также искал учителя, который научил бы меня решать мои задачи по разности кубов, умножению матриц и эквивалентным дробям. Хотя я нашел несколько человек, которые, возможно, могли бы решить мою проблему, я понял, что не могу за них платить. У меня тоже мало времени. Скоро мое задание. Я в отчаянии . Может ли кто-нибудь помочь мне в этой ситуации? Я был бы очень признателен за любую помощь или любое предложение. Сначала вам нужно контролировать себя. Не паникуй. Устройтесь поудобнее, расслабьтесь и смотрите на книги непредвзято. Они будут казаться трудными, если вы думаете, что они трудные. Калькулятор квадратных корней с дробями легко понять, и вы можете решить практически любую задачу с помощью алгебратора. Так что расслабься.
Сначала вам нужно контролировать себя. Не паникуй. Устройтесь поудобнее, расслабьтесь и смотрите на книги непредвзято. Они будут казаться трудными, если вы думаете, что они трудные. Калькулятор квадратных корней с дробями легко понять, и вы можете решить практически любую задачу с помощью алгебратора. Так что расслабься.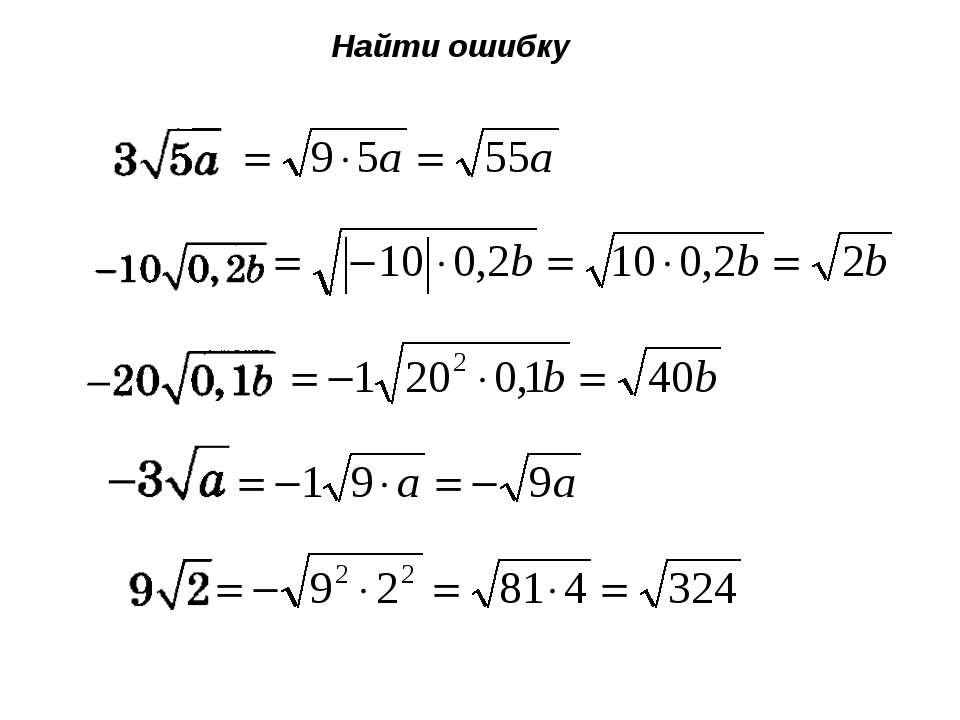 Я был удивлен, когда после нескольких недель разочарования я просто ввел линейные неравенства, и на этом мои проблемы с математикой закончились. Также здорово, что вы можете использовать программу на любом уровне: я использую ее уже несколько лет, я использовал ее в базовой математике, а также в промежуточной алгебре! Просто попробуйте и убедитесь в этом сами!
Я был удивлен, когда после нескольких недель разочарования я просто ввел линейные неравенства, и на этом мои проблемы с математикой закончились. Также здорово, что вы можете использовать программу на любом уровне: я использую ее уже несколько лет, я использовал ее в базовой математике, а также в промежуточной алгебре! Просто попробуйте и убедитесь в этом сами! Но всякий раз, когда я вижу эту книгу и груды классных работ, мне кажется, что я просто не могу удержать свои чувства. Большое спасибо за совет, обязательно воспользуюсь им. Где взять эту штуку?
Но всякий раз, когда я вижу эту книгу и груды классных работ, мне кажется, что я просто не могу удержать свои чувства. Большое спасибо за совет, обязательно воспользуюсь им. Где взять эту штуку? грамм. кубический корень:
грамм. кубический корень: Например, введите 7.
Например, введите 7. то есть 3/4 DEC x 6 =.
то есть 3/4 DEC x 6 =. 