Один факториал чему равен – Факториал числа — расчет онлайн

Содержание

Таблица факториалов до 50

Главная > ф >

Факториа́л числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно.
Например: 4! = 4 × 3 × 2 × 1 = 24.
Принято: 0! = 1.

В таблице приведены значения факториалов для чисел от 0 до 50.

число	факториал числа
0!	1
1!	1
2!	2
3!	6
4!	24
5!	120
6!	720
7!	5040
8!	40320
9!	362880
10!	3628800
11!	39916800
12!	479001600
13!	6227020800
14!	87178291200
15!	1307674368000
16!	20922789888000
17!	355687428096000
18!	6402373705728000
19!	121645100408832000
20!	2432902008176640000
21!	51090942171709440000
22!	1124000727777607680000
23!	25852016738884976640000
24!	620448401733239439360000
25!	15511210043330985984000000
26!	403291461126605635584000000
27!	10888869450418352160768000000
28!	304888344611713860501504000000
29!	8841761993739701954543616000000
30!	265252859812191058636308480000000
31!	8222838654177922817725562880000000
32!	263130836933693530167218012160000000
33!	8683317618811886495518194401280000000
34!	295232799039604140847618609643520000000
35!	10333147966386144929666651337523200000000
36!	371993326789901217467999448150835200000000
37!	13763753091226345046315979581580902400000000
38!	523022617466601111760007224100074291200000000
39!	20397882081197443358640281739902897356800000000
40!	815915283247897734345611269596115894272000000000
41!	33452526613163807108170062053440751665152000000000
42!	1405006117752879898543142606244511569936384000000000
43!	60415263063373835637355132068513997507264512000000000
44!	2658271574788448768043625811014615890319638528000000000
45!	119622220865480194561963161495657715064383733760000000000
46!	5502622159812088949850305428800254892961651752960000000000
47!	258623241511168180642964355153611979969197632389120000000000
48!	12413915592536072670862289047373375038521486354677760000000000
49!	608281864034267560872252163321295376887552831379210240000000000
50!	30414093201713378043612608166064768844377641568960512000000000000

comments powered by HyperComments

tab.wikimassa.org

Двойной факториал — это… Что такое Двойной факториал?

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно:

По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

Эта функция часто используется в комбинаторике, теории чисел и функциональном анализе.

Иногда словом «факториал» неформально называют восклицательный знак.

Свойства

Комбинаторное определение

В комбинаторике факториал определяется как количество перестановок множества из n элементов. Например, элементы множества {A,B,C,D} можно линейно упорядочить 4!=24 способами:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Связь с гамма-функцией

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

n! = Γ(n + 1)

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел. Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое. Коэффициенты этого разложения дают последовательность A001163 в OEIS (числители) и последовательность A001164 в OEIS (знаменатели).

Во многих случаях для приближенного значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые в степени

Таким образом,

где произведение берется по всем простым числам.

Другие свойства

x!² > x^x > x! > = x, при x>1

Обобщения

Двойной факториал

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Таким образом,

По определению полагают 0!! = 1.

Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

Убывающий факториал дает число размещений из n по k.

Возрастающий факториал

Возрастающим факториалом называется выражение

Праймориал или примориал

Примориал (англ. Primorial) числа n обозначается n# и определяется как произведение простых чисел, не превышающих n. Например,

Последовательность праймориалов начинается так:

2, 6, 30, 210, 2310, 30030, 510510, 9699690, … (последовательность A002110 в OEIS)

Суперфакториалы

Основная статья: Большие числа

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению суперфакториал четырёх равен (поскольку устоявшегося обозначения нет, используется функциональное)

В общем

Последовательность суперфакториалов начинается (с n = 0) с

1, 1, 2, 12, 288, 34560, 24883200, … (последовательность A000178 в OEIS)

Идея была обобщена в 2000 Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Super-duper-factorial), которые являются произведением первых n суперфакториалов. Первые члены (с n = 0) равны:

1, 1, 2, 24, 6912, 238878720, 5944066965504000, … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, где m-уровневый факториал n — произведение первых n (m − 1)-уровневых факториалов, то есть

где для n > 0 и .

Субфакториал

Субфакториал определяется как количество беспорядков порядка , то есть перестановок -элементного множества без неподвижных точек.

Ссылки

См. также

Wikimedia Foundation. 2010.

dic.academic.ru

что такое факториал? спасибо всем

факториал n!=1*2*..*n

Факториа́л числа n (обозначается n!) — произведение всех натуральных чисел до n включительно: n! = 1*2*….*n По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел. Эта функция часто используется в комбинаторике, теории чисел и функциональном анализе.

Факториалом называется перестановка из Н-элементов, каждое расположение этих элементов в определённом порядке и вычисляется по формуле Рн=н

Факториал — последовательное перемножение чисел 5!=1*2*3*4*5 Это перемножение чисел, заданных функцией (не путать с обычным факториалом) (2n+1)!!=3*5*7*…

Факториал — это произведение всех целых чисел от 1 до n, обозначается n! и равен 1 * 2 * 3 *…*n, Например, 4! = 1*2*3*4 = 24 Факториал используется в математике, и связанных с ней областях.

Факториа́л числа n (обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел до n включительно: Иногда словом «факториал» неформально называют восклицательный знак.

Произведение. Значение факториала показывает, до какого периода совершалось произведение.

чтобы вычислить факториал нужно эти все числа перемножить

Факториал это число обазночаеться так 3! 4! 2! И т. д. Это означает: 3!=3х2х1 можно сделать вывод что это число умноженное на предыдущие числа до единицы

Какое наибольшее число точек можно расположить на плоскости, так чтобы любые три точки не лежали на одной прямой и были вершинами равнобедренного треугольника.

факториал 2! = 1 *2 факториал 5 = 5*4*3*2*1 или 1*2*3*4*5 и т. д. Научным языком Факториал — это произведение последовательных множителей начиная с единицы. Pn=n! n!=1*2*3 *…* (n-1)*n n -количество элементов! m — количество в размещении! Pn -количество перестановок!

Произведение натуральных чисел от одного до данного. Допустим 5!=1•2•3•4•5=120

Факториа́л — функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л.

Факториал числа а = а * (а-1)*(а-2)* …*1 Пример: факториал 7 = 7*6*5*4*3*2*1 Ещё можно так: Факториал целого числа а = произведению всех целых чисел от 1 до а (вкл)

touch.otvet.mail.ru

Факториал — Википедия

Факториа́л числа n (лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:

Например:

По договорённости: . Также это равенство выполняется естественным образом:

Факториал определён только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так^[1]:

1, 1, 2, 6, 24, 120, 720, 5040, 40 320, 362 880, 3 628 800, 39 916 800, 479 001 600, 6 227 020 800, 87 178 291 200, 1 307 674 368 000, 20 922 789 888 000, 355 687 428 096 000, 6 402 373 705 728 000, 121 645 100 408 832 000, 2 432 902 008 176 640 000, …

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.

Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем многочлен любой степени, и быстрее, чем экспоненциальная функция (но медленнее, чем двойная экспоненциальная функция ).

Рекуррентная формула[править]

Комбинаторная интерпретация[править]

В комбинаторике факториал натурального числа n интерпретируется как количество перестановок (упорядочиваний) множества из n элементов. Например, для множества {A,B,C,D} из 4-х элементов существует 4! = 24 перестановки:

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, так как пустое множество упорядочено единственным способом.

Связь с гамма-функцией[править]

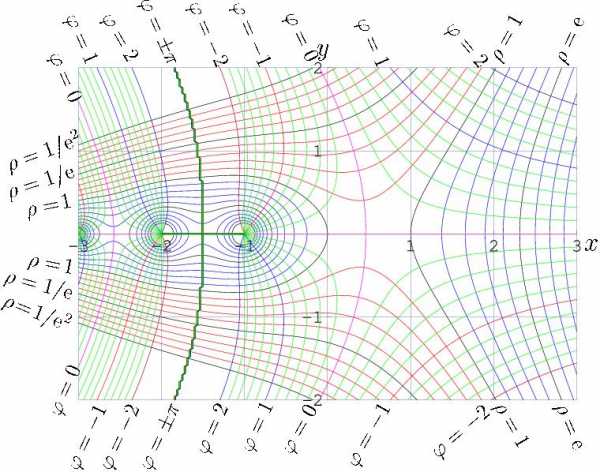Амплитуда и фаза факториала комплексного аргумента.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при .

Пи-функция, определённая для всех вещественных чисел, кроме отрицательных целых, и совпадающая при натуральных значениях аргумента с факториалом.

Более непосредственным обобщением факториала на множество вещественных (и комплексных) чисел является пи-функция, определяемая как

Поскольку то пи-функция натурального числа совпадает с его факториалом: Как факториал, пи-функция удовлетворяет рекурсивному соотношению

Формула Стирлинга[править]

Формула Стирлинга — асимптотическая формула для вычисления факториала:

см. O-большое^[2].

Во многих случаях для приближённого значения факториала достаточно рассматривать только главный член формулы Стирлинга:

При этом можно утверждать, что

Формула Стирлинга позволяет получить приближённые значения факториалов больших чисел без непосредственного перемножения последовательности натуральных чисел. Так, с помощью формулы Стирлинга легко подсчитать, что

100! ≈ 9,33×10¹⁵⁷;
1000! ≈ 4,02×10²⁵⁶⁷;
10 000! ≈ 2,85×10^35 659.

Разложение на простые числа[править]

Каждое простое число p входит в разложение n! на простые множители в степени

Таким образом,

где произведение берётся по всем простым числам. Нетрудно видеть, что для всякого простого p большего n соответствующий множитель в произведении равен 1, а потому произведение можно брать лишь по простым p, не превосходящим n.

Связь с производной от степенной функции[править]

Для целого неотрицательного числа n:

Например:

Другие свойства[править]

Для натурального числа n:

Двойной факториал[править]

Двойной факториал числа n обозначается n‼ и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность, что и n.

Для нечётного n:

Связь между двойными факториалами двух соседних целых неотрицательных чисел и обычным факториалом одного из них.

Для нечётного n:

Выведение формул

Осуществив замену для чётного n и для нечётного n соответственно, где — целое неотрицательное число, получим:

для чётного числа:

для нечётного числа:

По договорённости: . Также это равенство выполняется естественным образом:

</div></div>

Двойной факториал, также как и обычный факториал, определён только для целых неотрицательных чисел.

Последовательность значений n!! начинается так^[3]:

1, 1, 2, 3, 8, 15, 48, 105, 384, 945, 3840, 10 395, 46 080, 135 135, 645 120, 2 027 025, 10 321 920, 34 459 425, 185 794 560, 654 729 075, 3 715 891 200, 13 749 310 575, 81 749 606 400, 316 234 143 225, 1 961 990 553 600, 7 905 853 580 625, 51 011 754 393 600, …

Кратный факториал[править]

m-кратный факториал числа n обозначается и определяется следующим образом. Пусть число n представимо в виде где Тогда^[4]

Обычный и двойной факториалы являются частными случаями m-кратного факториала для m = 1 и m = 2 соответственно.

Кратный факториал связан с гамма-функцией следующим соотношением^[5]:

Неполный факториал[править]

Убывающий факториал[править]

Убывающим факториалом называется выражение

Например:

n = 7; k = 4,

(n − k) + 1 = 4,

3^k = 7 • 6 • 5 • 4 = 840.

Убывающий факториал даёт число размещений из n по k.

Возрастающий факториал[править]

Возрастающим факториалом называется выражение

Праймориал или примориал[править]

Праймориал или примориал (англ. primorial) числа n обозначается p_n# и определяется как произведение n первых простых чисел. Например,

Иногда праймориалом называют число , определяемое как произведение всех простых чисел, не превышающих заданное n.

Последовательность праймориалов (включая ) начинается так^[6]:

1, 2, 6, 30, 210, 2310, 30 030, 510 510, 9 699 690, 223 092 870, 6 469 693 230, 200 560 490 130, 7 420 738 134 810, 304 250 263 527 210, 13 082 761 331 670 030, 614 889 782 588 491 410, 32 589 158 477 190 044 730, 1 922 760 350 154 212 639 070, …

Суперфакториалы[править]

Нейл Слоан и Саймон Плоуф (англ.) в 1995 году определили суперфакториал как произведение первых n факториалов. Согласно этому определению, суперфакториал четырёх равен

(поскольку устоявшегося обозначения нет, используется функциональное).

В общем

Последовательность суперфакториалов чисел начинается так^[7]:

1, 1, 2, 12, 288, 34 560, 24 883 200, …

Идея была обобщена в 2000 году Генри Боттомли (англ.), что привело к гиперфакториалам (англ. Superduperfactorial), которые являются произведением первых n суперфакториалов. Последовательность гиперфакториалов чисел начинается так^[8]:

1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 745 453 331 864 786 829 312 000 000, 3 769 447 945 987 085 350 501 386 572 267 520 000 000 000, 6 916 686 207 999 802 072 984 424 331 678 589 933 649 915 805 696 000 000 000 000 000 …

Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение (m − 1)-уровневых факториалов чисел от 1 до n, то есть

где для и

Субфакториал[править]

Субфакториал !n определяется как количество беспорядков порядка n, то есть перестановок n-элементного множества без неподвижных точек.

wp.wiki-wiki.ru

Факториал — это… Что такое Факториал?

Факториа́л числа n (лат. factorialis — действующий, производящий умножающий; обозначается n!, произносится эн факториа́л) — произведение всех натуральных чисел от 1 до n включительно:

Например:

По определению полагают 0! = 1. Факториал определён только для целых неотрицательных чисел.

Последовательность факториалов неотрицательных целых чисел начинается так:

Факториалы часто используются в комбинаторике, теории чисел и функциональном анализе.

Свойства

Рекуррентная формула

Комбинаторная интерпретация

ABCD  BACD  CABD  DABC
ABDC  BADC  CADB  DACB
ACBD  BCAD  CBAD  DBAC
ACDB  BCDA  CBDA  DBCA
ADBC  BDAC  CDAB  DCAB
ADCB  BDCA  CDBA  DCBA

Комбинаторная интерпретация факториала служит обоснованием тождества 0! = 1, т. к. пустое множество упорядочено единственным способом.

Связь с гамма-функцией

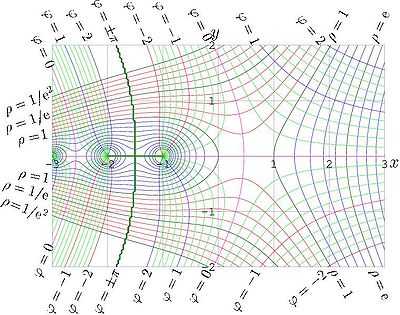Амплитуда и фаза факториала комплексного аргумента.

Факториал связан с гамма-функцией от целочисленного аргумента соотношением:

Таким образом, гамма-функцию рассматривают как обобщение факториала для положительных вещественных чисел.

Путём аналитического продолжения её также расширяют и на всю комплексную плоскость, исключая особые точки при

Формула Стирлинга

Формула Стирлинга — асимптотическая формула для вычисления факториала:

При этом можно утверждать, что

100! ≈ 9,33×10¹⁵⁷;
1000! ≈ 4,02×10²⁵⁶⁷;
10 000! ≈ 2,85×10^35 659.

Разложение на простые числа

Каждое простое число p входит в разложение n! на простые множители в степени

Таким образом,

Другие свойства

Для натурального числа n

Обобщения

Двойной факториал

По определению полагают 0!! = 1.

Последовательность значений n!! начинается так:

Кратный факториал

m-Кратный факториал числа n обозначается и определяется следующим образом:

Пусть число n представимо в виде где Тогда^[1]

Двойной факториал является частным случаем m-кратного факториала для m = 2.

Кратный факториал связан с гамма-функцией следующим соотношением^[2]:

Убывающий факториал

Убывающим факториалом (или неполным факториалом) называется выражение

Убывающий факториал даёт число размещений из n по k.

Возрастающий факториал

Возрастающим факториалом называется выражение

Праймориал или примориал

Праймориал или примориал (англ. primorial) числа n обозначается n# и определяется как произведение всех простых чисел, не превышающих n. Например,

11# = 12# = 2 · 3 · 5 · 7 · 11 = 2310.

Последовательность праймориалов (включая ) начинается так:

Суперфакториалы

(поскольку устоявшегося обозначения нет, используется функциональное).

В общем

Последовательность суперфакториалов чисел n⩾0 начинается так:

1, 1, 2, 12, 288, 34 560, 24 883 200, … (последовательность A000178 в OEIS).

1, 1, 2, 24, 6912, 238 878 720, 5 944 066 965 504 000, 125 411 328 000, 5 056 584 744 960 000, 1 834 933 472 251 084 800 000, 6 658 606 584 104 736 522 240 000 000, 265 790 267 296 391 946 810 949 632 000 000 000, 127 313 963 299 399 416 749 559 771 247 411 200 000 000 000 … (последовательность A055462 в OEIS)

Продолжая рекуррентно, можно определить факториал кратного уровня, или m-уровневый факториал числа n, как произведение первых n (m−1)-уровневых факториалов, то есть

где для и

Субфакториал

Ссылки

См. также

Примечания

↑ «Энциклопедия для детей» Аванта+. Математика.
↑ wolframalpha.com.

dal.academic.ru

Чему равен (x+3)! =????Факториал от (х+3)

Двойной факториал числа n обозначается n!! и определяется как произведение всех натуральных чисел в отрезке [1,n], имеющих ту же чётность что и n. Вот формулы в виде рисунков, вам нужно подставить в эту формулу своё значение (в первой формуле вместо 2к подставьте n, а во второй вместо 2к+1 подставьте n+3,естевственно что остальные значения нужно будет коректировать под ваши данные), если вы хоть немного знакомы с математикой то у вас всё получится :)<img src=»//otvet.imgsmail.ru/download/a49d56cc33ea15e2f5b5f27d1fa9cb59_i-39.jpg» ><img src=»//otvet.imgsmail.ru/download/a49d56cc33ea15e2f5b5f27d1fa9cb59_i-40.jpg» > У меня к сожалению нет возможности записать такую сложную математическую формулу на компе, еслиб могла я бы написала вам ответ…

блин, что такое факториал?

А через что выразить? Можно так: (x+3)! = x! (x+3)(x+2)(x+1)

Люди тут даже не знают что такое факториал?? ? К примеру факториал 5! = 5*4*3*2*1=120

touch.otvet.mail.ru

Факториал — Википедия

Материал из Википедии — свободной энциклопедии

Факториа́л — функция, определённая на множестве неотрицательных целых чисел. Название происходит от лат. factorialis — действующий, производящий, умножающий; обозначается n!, произносится эн факториа́л. Факториал натурального числа n определяется как произведение всех натуральных чисел от 1 до n включительно:

n!=1⋅2⋅…⋅n=∏k=1nk{\displaystyle n!=1\cdot 2\cdot \ldots \cdot n=\prod _{k=1}^{n}k}.

Например,

5!=1⋅2⋅3⋅4⋅5=120{\displaystyle 5!=1\cdot 2\cdot 3\cdot 4\cdot 5=120}.

Из определения факториала следует соотношение (n−1)!=n!n{\displaystyle (n-1)!={\frac {n!}{n}}}, откуда при n=1{\displaystyle n=1} формально находим

0!=1{\displaystyle 0!=1}.

Последнее равенство обычно принимают в качестве соглашения, хотя, как показано выше, оно следует из определения факториала для натуральных чисел при условии, что все значения функции связаны единым рекуррентным соотношением.

Факториалы всех чисел составляют последовательность в OEIS; значения в научной нотации округляются
n	n!
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5040
8	40320
9	362880
10	3628800
11	39916800
12	479001600
13	6227020800
14	87178291200
15	1307674368000
16	20922789888000
17	355687428096000
18	6402373705728000
19	121645100408832000
20	2432902008176640000
25	≈1,551121004⋅10²⁵
50	≈3,041409320⋅10⁶⁴
70	≈1,197857167⋅10¹⁰⁰
100	≈9,332621544⋅10¹⁵⁷
450	≈1,733368733⋅10¹⁰⁰⁰
1000	≈4,023872601⋅10²⁵⁶⁷
3249	≈6,412337688⋅10¹⁰⁰⁰⁰
10000	≈2,846259681⋅10³⁵⁶⁵⁹
25206	≈1,205703438⋅10¹⁰⁰⁰⁰⁰
100000	≈2,824229408⋅10⁴⁵⁶⁵⁷³
205023	≈2,503898932⋅10^1000004
1000000	≈8,263931688⋅10^5565708
10¹⁰⁰	≈10^{9,956570552⋅10¹⁰¹}
10¹⁰⁰⁰	≈10^10¹⁰⁰³
10^10 000	≈10^{10^10 004}
10^100 000	≈10^{10^100 005}
10^10¹⁰⁰	≈10^{10^10¹⁰⁰}

Факториал активно используется в различных разделах математики: комбинаторике, математическом анализе, теории чисел, функциональном анализе и др.

Факториал является чрезвычайно быстро растущей функцией. Он растёт быстрее, чем любая показательная функция или любая степенная функция, а также быстрее, чем любая сумма произведений этих функций. Однако, степенно-показательная функция nn{\displaystyle n^{n}} растёт быстрее факториала, так же как и большинство двойных степенных, например een

encyclopaedia.bid

Таблица факториалов до 50

В таблице приведены значения факториалов для чисел от 0 до 50.

Двойной факториал — это… Что такое Двойной факториал?

Свойства

Комбинаторное определение

Связь с гамма-функцией

Формула Стирлинга

Разложение на простые числа

Другие свойства

Обобщения

Двойной факториал

Убывающий факториал

Возрастающий факториал

Праймориал или примориал

Суперфакториалы

Субфакториал

Ссылки

См. также

что такое факториал? спасибо всем

Факториал — Википедия

Рекуррентная формула[править]

Комбинаторная интерпретация[править]

Связь с гамма-функцией[править]

Формула Стирлинга[править]

Разложение на простые числа[править]

Связь с производной от степенной функции[править]

Другие свойства[править]

Двойной факториал[править]

Кратный факториал[править]

Неполный факториал[править]

Убывающий факториал[править]

Возрастающий факториал[править]

Праймориал или примориал[править]

Суперфакториалы[править]

Субфакториал[править]

Факториал — это… Что такое Факториал?

Свойства

Рекуррентная формула

Комбинаторная интерпретация

Связь с гамма-функцией

Формула Стирлинга

Разложение на простые числа

Другие свойства

Обобщения

Двойной факториал

Кратный факториал

Убывающий факториал

Возрастающий факториал

Праймориал или примориал

Суперфакториалы

Субфакториал

Ссылки

См. также

Примечания

Чему равен (x+3)! =????Факториал от (х+3)

Факториал — Википедия

Добавить комментарий Отменить ответ