Урок 36. рациональные числа — Математика — 6 класс
Математика
6 класс
Урок № 36
Рациональные числа
Перечень рассматриваемых вопросов:
- Понятие рациональных чисел.
- Характеристики множества рациональных чисел.
Тезаурус
Натуральные числа – числа, которые используются при счёте.
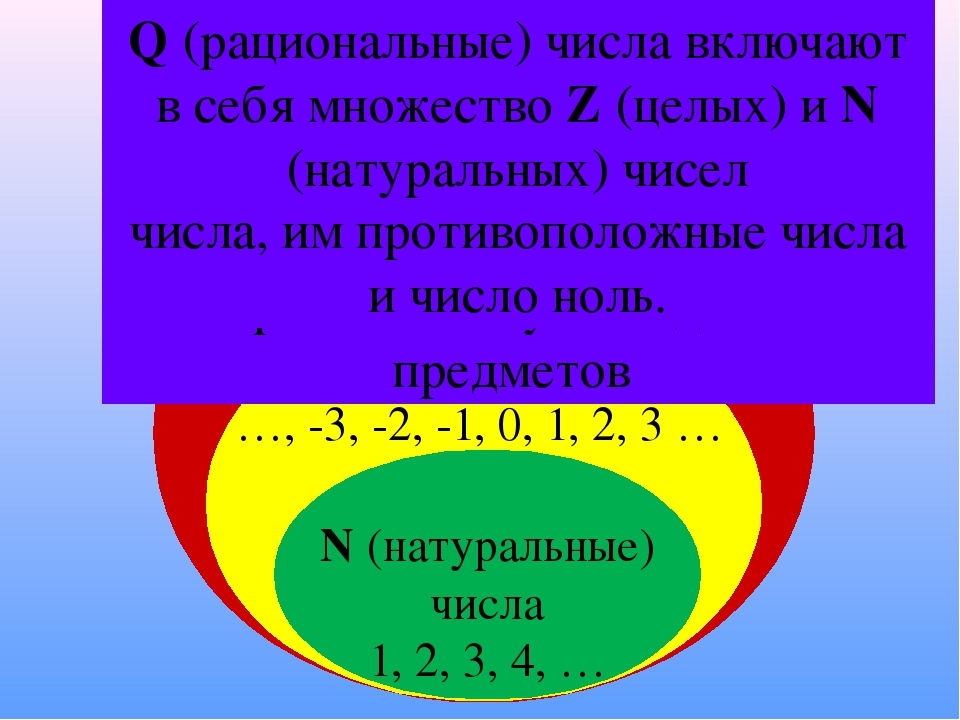
Целые числа – натуральные числа, число нуль, а также числа, противоположные натуральным.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.

Теоретический материал для самостоятельного изучения
Рассмотрим на координатной оси
натуральные, целые и дробные числа.
Натуральные (целые положительные): 1, 2, 3
Целые отрицательные: 1, 2, 3
Нуль: 0
Все эти числа можно записать в виде обыкновенных дробей. Поэтому они имеют общее название — рациональные числа.
Некоторые дроби считают равными. Равенство дробей устанавливают при помощи основного свойства дроби.
Если числитель и знаменатель дроби умножить на одно и то же целое, не равное нулю число, то получится равная ей дробь.
Равенство (2) означает, что если числитель и знаменатель дроби имеют общий множитель n (целое, не равное нулю число), то дробь можно сократить на n. При этом получается дробь, равная данной.
Итак, две дроби равны, когда одна из них может быть получена из другой сокращением на общий множитель её числителя и знаменателя.
Либо, сформулируем так:
две дроби равны, когда одна из них может быть получена из другой умножением её числителя и знаменателя на одно и тоже число, не равное нулю.
Таким образом, любое целое число является рациональным числом.
Чтобы привести дроби к наименьшему общему знаменателю, надо:
1. найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2. разделить наименьший общий знаменатель на знаменатели данных дробей, т. е. найти для каждой дроби дополнительный множитель;
3. умножить числитель и знаменатель каждой дроби на её дополнительный множитель.
Приведём дроби к положительному знаменателю
Это интересно
Название «рациональные числа» происходит от слова «рацио», что означает «отношение».
Мы выяснили, что рациональное число представляется виде дроби.
Уже в V веке до нашей эры люди понимали, что с помощью деления «единицы измерения» можно гораздо точнее приблизить любую величину.
Бывают случаи, когда без дробных чисел нам нельзя обойтись.
Например, кусок проволоки, длиной 4 метра, необходимо разрезать на три равные части. Сколько метров приходится на каждую часть?
Сколько метров приходится на каждую часть?
Можем составить равенство:
3 ∙ х = 4,
где х – и есть то количество метров, которое приходится на каждую часть.
Ясно, что ответ:
Для решения подобных задач в далёком прошлом и появились дробные числа.
Интерес к ним не ослабевает и в наше время. Стремительное развитие вычислительной техники – главная причина этого интереса, так как компьютер может иметь дело только с рациональными числами.
Разбор заданий тренировочного модуля
Тип 1. Разместите нужные подписи под изображениями.
Варианты ответов:
смешанная дробь
положительная дробь
отрицательная дробь
целое положительное число
целое отрицательное
Для выполнения задания вспомним определения известных нам числовых множеств.
Правильный ответ:
- положительная дробь
- целое положительное число
- отрицательная дробь
Тип 2. Вставьте в текст нужные слова.
Если … и знаменатель дроби умножить на одно и то же целое, … нулю число, то получится … ей дробь.
Варианты слов для вставки:
знаменатель
числитель
не равное
равное
не равная
равная
Для выполнения задания обратимся к теоретическому материалу урока.
Правильный ответ
Если числитель и знаменатель дроби умножить на одно и то же целое, не равное нулю число, то получится равная ей дробь.
Какие числа называются Рациональными? Примеры и Определение
Определение рациональных чисел
Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.
Рациональные числа — это те, которые можно представить в виде
где числитель m — целое число, а знаменатель n — натуральное число.
Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.
Множество рациональных чисел принято обозначать латинской буквой Q.
Примеры рациональных чисел:
- десятичная дробь 1,15 — это 115/100;
- десятичная дробь 0,2 — это 1/2;
- целое число 0 — это 0/1;
- целое число 6 — это 6/1;
- целое число 1 — это 1/1;
- бесконечная периодическая дробь 0,33333… — это 1/3;
- смешанное число — это 25/10;
- отрицательная десятичная дробь -3,16 — это -316/100.
Подружиться с математикой и повысить оценки в школе — проще, чем кажется. В детской школе Skysmart знают, как увлечь ребенка предметом и объяснить самую коварную тему.
Записывайте ребенка на бесплатный пробный урок: познакомим с платформой, решим пару задач в интерактивном формате и наметим программу обучения.
Свойства рациональных чисел
У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.
Основные свойства действий с рациональными числами
|
Кроме основных перечисленных есть еще ряд свойств:
- Правило умножения рациональных чисел с разными знаками: (-a) * b = -ab.
 Такая фраза поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус».
Такая фраза поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус». - Правило умножения отрицательных рациональных чисел: (−a) * (−b) = ab. Запомнить поможет фраза: «минус на минус есть плюс».
- Правило умножении произвольного рационального числа на нуль: a * 0 = 0 или 0 * a = 0. Докажем это свойство.
Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).
Распределительный закон позволяет переписать выражение:
a * d + a * (−d), а так как a * (−d) = -ad, то a * d + a * (-d) = a * d + (-ad).
Так получилась сумма двух противоположных чисел, которая в результате дает нуль, что доказывает равенство a * 0 = 0.
Мы перечислили только свойства сложения и умножения. На множестве рациональных чисел вычитание и деление можно записать, как обратные к сложению и умножению. То есть, разность (a — b) можно записать, как сумму a + (-b), а частное a/b равно произведению a * b−1, при b ≠ 0.
Определение иррационального числа
Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби
Оно может быть выражено в форме бесконечной непериодической десятичной дроби.
Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.
Примеры:
- π = 3,1415926…
- √2 = 1,41421356…
- e = 2,71828182…
- √8 = 2.828427…
- -√11= -3.31662…
Обозначение множества иррациональных чисел: латинская буква I.
Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.
Свойства иррациональных чисел:
- результат суммы иррационального числа и рационального равен иррациональному числу;
- результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
- результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
- результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).

Различие между целыми, натуральными и рациональными числами
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.
А вот, что точно не является натуральным числом:
- Нуль — целое число, которое при сложении или вычитании с любыми числами в результате даст то же число. Умножение на ноль дает ноль.
- Отрицательные числа: -1, -2, -3, -4.
- Дроби: 1/2, 3/4, 5/6.
Целые числа — это натуральные числа, противоположные им и нуль.
Если два числа отличаются друг от друга знаком — их называют противоположными: +2 и -2, +7 и -7. Знак «плюс» обычно не пишут, и если перед числом нет никакого знака, значит оно положительное. Числа, перед которыми стоит знак «минус», называют отрицательными.
Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.
Рациональные числа — это конечные дроби и бесконечные периодические дроби.
Например:
Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.
Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.
Вот и разобрались! А если не совсем — приходите на увлекательные уроки математики в онлайн-школу Skysmart. Никаких скучных учебников: ребенка ждут интерактивные занятия, математические комиксы и учителя, которые никогда не оставят в беде.
Целые числа. Рациональные числа
Представим себе такую историю…
– Привет, Паша! – поздоровался с другом Саша. – Извини, что опоздал.
– Что случилось? – поинтересовался Паша.
–
Ничего не случилось. Просто когда мы договаривались встретиться в кафе, ты
сказал, что мне нужно выйти из автобуса и пройти дальше по тротуару 100
метров. Но ты не сказал, в какую сторону надо идти, – говорил немного
расстроенный Саша.
Просто когда мы договаривались встретиться в кафе, ты
сказал, что мне нужно выйти из автобуса и пройти дальше по тротуару 100
метров. Но ты не сказал, в какую сторону надо идти, – говорил немного
расстроенный Саша.
– После того, как ты вышел из автобуса, надо было идти дальше по направлению движения автобуса, то есть повернуть налево и пройти 100 метров, – пояснил Паша.
– А я повернул направо и прошёл 100 метров, – сказал Саша.
– Извини, что так вышло. Ты прошёл 100 метров, но в противоположном направлении. А давай мы об этом поговорим с Мудряшом, – предложил другу Паша.
– Давай, – согласился с ним Саша.
– Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!
–
А сейчас можем вернуться к вашему вопросу, – начал Мудряш.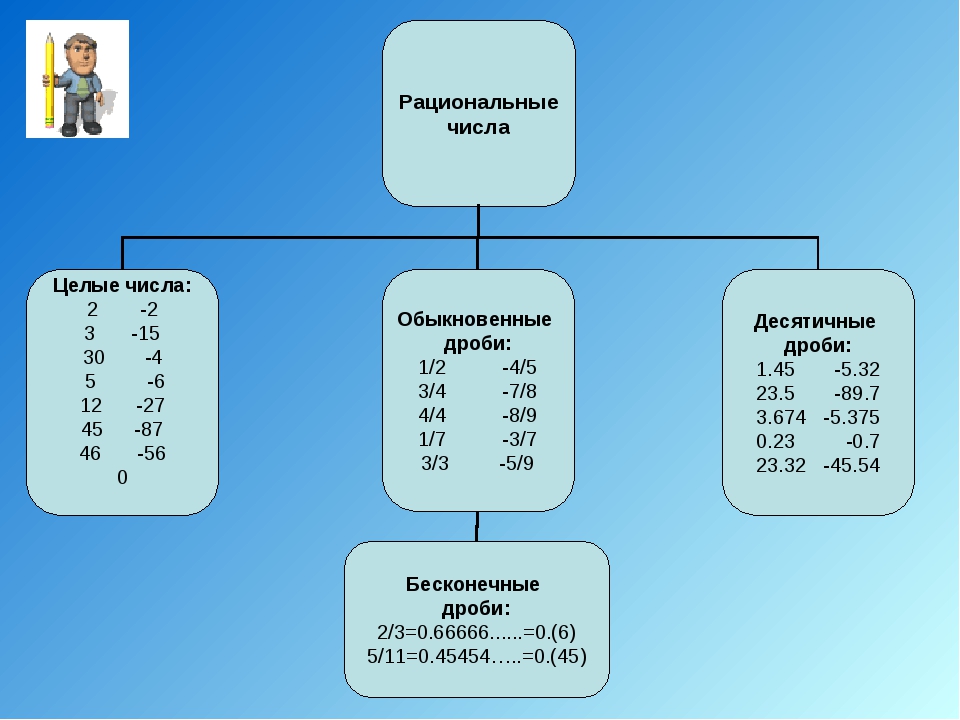 – На прошлом уроке
мы с вами ввели понятие координатной прямой. Напомним, что координатной
прямой называют прямую, на которой выбрали начало отсчёта, единичный
отрезок и направление.
– На прошлом уроке
мы с вами ввели понятие координатной прямой. Напомним, что координатной
прямой называют прямую, на которой выбрали начало отсчёта, единичный
отрезок и направление.
Начертим координатную прямую. Отметим на ней начало отсчёта. Пусть длина единичного отрезка равна 20 метрам. Представим, что автобусная остановка, на которой вышел Саша, расположена в начале отсчёта. Паша сказал Саше, что кафе находится в 100 метрах от автобусной остановки, но не уточнил, в какую сторону нужно идти Саше.
Если бы кафе было расположено справа от автобусной остановки, то есть от начала отсчёта, то на координатной прямой ему бы соответствовала точка 100. А если бы слева, то ему бы соответствовала бы точка .
То
есть получается, чтобы попасть из начала в эти точки, надо пройти одинаковые
расстояния, но в противоположных направлениях. Тогда числа 100
и называют
противоположными. Будем говорить, что число 100
противоположно числу ,
а число противоположно
числу 100.
Будем говорить, что число 100
противоположно числу ,
а число противоположно
числу 100.
Давайте ещё приведём примеры противоположных чисел.
– и 7; 30,9 и ; и , – начали перечислять мальчики, и у них возник вопрос, – а какое число является противоположным числу 0?
– Запомните! – сказал Мудряш. – Число 0 противоположно самому себе. Число, противоположное числу a, обозначают как .
– Обратите внимание, – продолжил Мудряш, – что, поставив, например, перед положительным числом 15 знак «», мы получим число , противоположное 15. Приписав перед отрицательным числом знак «», мы получим число 15, противоположное .
–
Запомните! – сказал Мудряш. – Число, противоположное числу ,
равно числу а. То есть верно следующее равенство: .
Обратите внимание, что использование скобок в этом равенстве обязательно.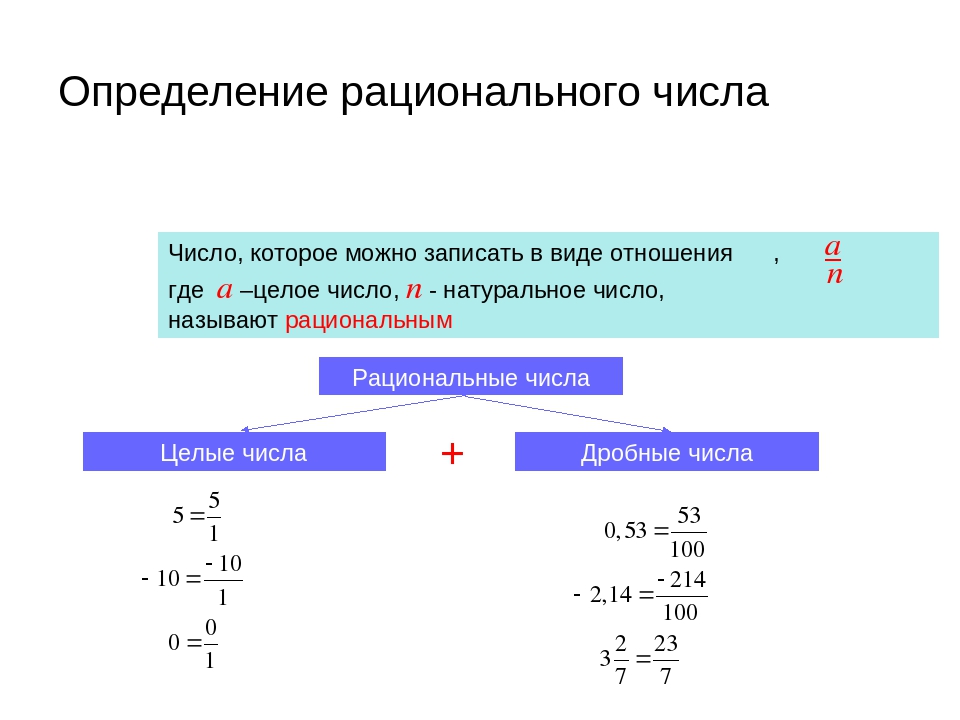
– Получается, что каждое число имеет противоположное ему число? – спросили ребята.
– Да, и только одно, – сказал Мудряш и добавил, – запомните! Все натуральные числа, противоположные им числа и 0 называют целыми числами. Натуральные числа называют целыми положительными числами. А числа, противоположные натуральным, называют целыми отрицательными числами.
– Тогда как называют числа, например, ; 3,5; ? – спросили мальчишки.
– Такие числа называются дробными числами, – ответил Мудряш. – Запомните! Целые и дробные числа называют рациональными числами.
– Давайте приведём примеры рациональных чисел, – предложил Мудряш.
– ; 2; 105; ; 0; ; , – привели примеры Саша и Паша.
–
Хорошо! А сейчас составим следующую схему, – сказал Мудряш. – Мы сказали, что
рациональными называют целые и дробные числа. Целыми числами называют
натуральные числа, 0 и числа, противоположные
натуральным. Дробными числами являются положительные и отрицательные дроби.
Целыми числами называют
натуральные числа, 0 и числа, противоположные
натуральным. Дробными числами являются положительные и отрицательные дроби.
А теперь давайте выполним несколько заданий.
Задание первое: найдите числа, противоположные числам .
Решение: первое число у нас 12. Припишем перед ним знак «» и получим противоположное ему число .
Второе число у нас . Припишем перед ним знак «». Воспользовавшись равенством , получим противоположное ему число .
Следующее число у нас . Поставим перед ним знак «». Воспользовавшись равенством , получим противоположное число .
Перед числом поставим знак «» и получим противоположное число .
Противоположным числу 0 является само число 0.
Следующее число у нас . Припишем перед ним знак «» и получим противоположное число .
Перед
числом припишем
знак «». Воспользовавшись равенством ,
получим противоположное число .
Воспользовавшись равенством ,
получим противоположное число .
Следующее задание: выберите из чисел натуральные, целые, отрицательные, неотрицательные, дробные.
Решение: давайте заполним следующую таблицу.
Число 8 мы можем отнести к натуральным числам, целым и неотрицательным. Напомним, что к неотрицательным числам относятся положительные числа и 0.
отнесём к неотрицательным и дробным.
у нас – целое отрицательное число.
также отнесём к целым и отрицательным.
0 отнесём к целым и неотрицательным.
к отрицательным числам и дробным.
150 запишем к натуральным, целым и неотрицательным.
6,3 отнесём к неотрицательным числам и дробным.
И последнее число у нас . Его мы запишем к отрицательным числам и дробным.
И
ещё одно задание: решите уравнения: а) ;
б) ;
в) .
Решение: первое уравнение: . Чтобы его решить, воспользуемся уже известным нам равенством , но справа налево. Тогда можем записать, что . Подставим вместо . И получим, что . Следовательно, .
Второе уравнение: . Также воспользуемся равенством . Тогда можем записать, что . Подставим вместо . Получим, что . Откуда .
И последнее уравнение: . Снова воспользуемся равенством , но справа налево: . Подставим вместо . И получим, что .
Рациональные числа, зачем нужны рациональные числа, в чем их особенность
Рациональным числом называют число, которое можно записать в виде отношения mn, где m — целое число, a n — натуральное число. Чтобы понимать значение рационального числа, необходимо знать, что такое натуральные числа, целые числа, дроби (правильные \(\frac{2}{3}\), неправильные \(\frac{3}{2}\), бесконечные периодические 0,(4) и смешанные \(4 \frac{2}{3}\),).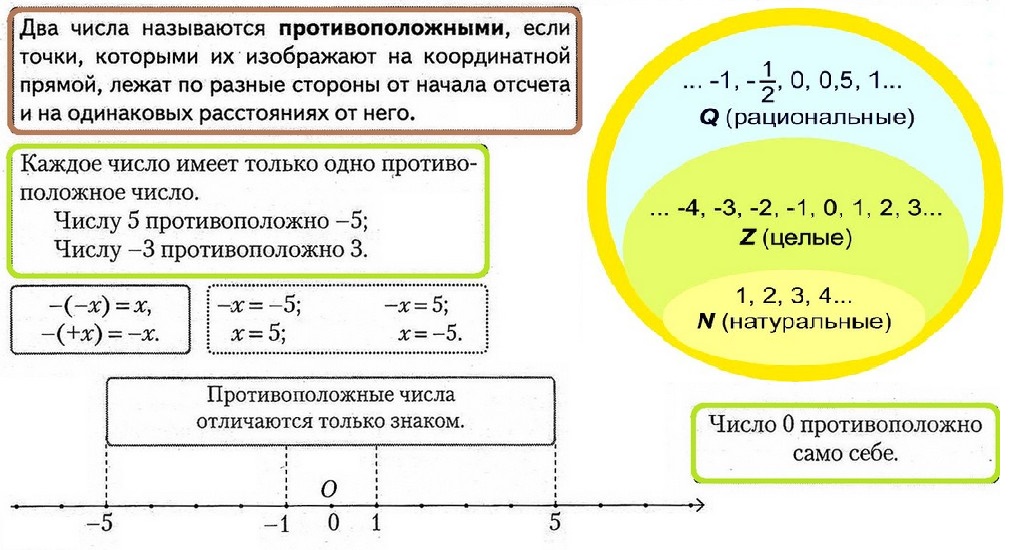 Натуральные числа представляют собой числа, которые мы используем при счете (1, 2, 3…). В свою очередь целые числа – это натуральные числа, а также противоположные им и ноль (1, 2, 0, -1, -2…). Дробью называется число, записанное в виде отношения mn (\(\frac{2}{3}\)), где m – целое, а n – натуральное число. Понятие дроби берет свое начало еще с древних времен, когда людям в торговых делах и бытовых нуждах требовалось определить часть какого-либо целого.
Натуральные числа представляют собой числа, которые мы используем при счете (1, 2, 3…). В свою очередь целые числа – это натуральные числа, а также противоположные им и ноль (1, 2, 0, -1, -2…). Дробью называется число, записанное в виде отношения mn (\(\frac{2}{3}\)), где m – целое, а n – натуральное число. Понятие дроби берет свое начало еще с древних времен, когда людям в торговых делах и бытовых нуждах требовалось определить часть какого-либо целого.
История рациональных чисел началась с возникновением финансово-кредитных отношений между людьми. Чтобы в численном виде представить задолженность человека, нужно было записывать числа, противоположные натуральным. Так появились отрицательные числа (-3, -167). А для того, чтобы записывать часть целого (например, возвращение долга частями), стали использовать дроби. Именно поэтому математикам необходимо было как-то объединить такие характерные числа, дать им общее название. Так появились рациональные числа (от латинского ratio – «отношение»).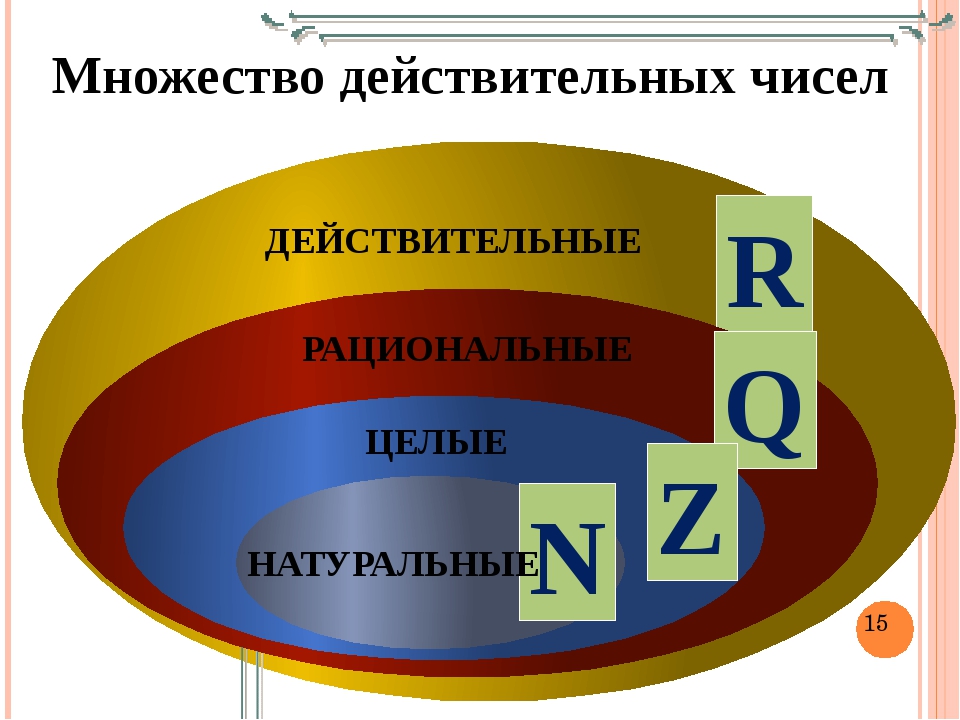
Для усвоения материала приведем пример задания на определение рациональных чисел из ряда чисел.
Задача. Даны числа: -34, 480, 0,11, \(\frac{1}{2}\), 8. Какие из них рациональные?
Решение.
Рассмотрим отдельно каждое из заданных чисел:
- Число -34 – целое число;
- Число 480 – натуральное число;
- Число 0,11 = \(\frac{11}{100} \) – десятичная дробь;
- Число \(\frac{1}{2}\) — правильная дробь;
- Число 8 – натуральное число.
Каждое из заданных чисел можно представить в виде дроби с целым и натуральным знаменателем. Значит, все 5 чисел являются рациональными числами.
Ответ: все числа являются рациональными.
Чтобы хорошо понимать специфику рациональных чисел, нужно усвоить два правила:
- Сумма рациональных чисел является рациональным числом.
- Произведение рациональных чисел является рациональным числом.

Теория в математике очень важна. Умение отличать натуральные числа от целых, рациональные от иррациональных поможет Вам не запутаться и не ошибиться в практике. Удачи!
«Целые числа. Рациональные числа» Математика 6 класс
Просмотр содержимого документа
«»Целые числа. Рациональные числа» Математика 6 класс»
Целые числа Рациональные числа
МАТЕМАТИКА
6 класс
ЗАДАНИЕ
Начертите координатную прямую, приняв за единичный отрезок 1 клетку тетради. Отметьте на координатной прямой точки:
М (0)
А (-3) В (2)
С(5) D (3)
E (-1,5)
Определение
- Числа, имеющие разные знаки, но удаленные от начала отсчета на одинаковое расстояние, называют противоположными
3
-1
-2
-3
-4
2
1
0
4
ЗАДАНИЕ
- Найти и отметить на координатной прямой противоположные данным числа:
М (0)
А (-3) В (2)
С(5) D (3)
E (-1,5)
Для каждого числа есть только одно
противоположное ему число
Знаки «+» и «-» называются
противоположными знаками
Число, противоположное положительному числу,
есть число отрицательное
Число, противоположное отрицательному числу.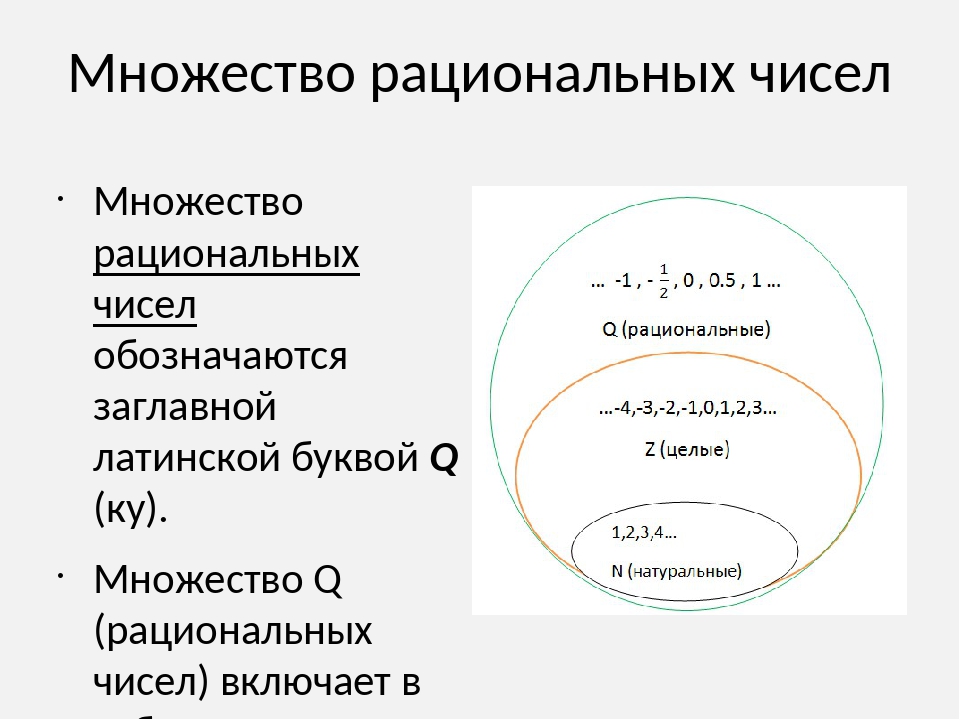
есть число положительное
Число 0 противоположно самому себе
ПРАВИЛО
- Приписав противоположный знак к данному числу, получаем число, противоположное данному
а и –а
- (-а) = а
- Запись скобок обязательна!
Правила знаков
Если перед скобкой стоит знак «+» ,
то при записи без скобок знаки чисел сохраняются
+(+6)=+6
+(-7)=-7
Если перед скобкой стоит знак «-» ,
то при записи без скобок знак числа меняется на противоположный
-(+4) = -4
-(-9)=+9
Целые числа
Множество
целых
чисел
Z
Числа, противоположные
натуральным
( отрицательные, не 0 )
Натуральные
числа
N
(положительные, не 0)
Число 0
Рациональные числа
Целые числа
Дробные числа
Положительные и отрицательные
Множество
рациональных чисел
Q
Q
рациональные
… , -1, -0,5, 0, 1/2, 1 …
Z
целые
… , -3, -2, -1, 0, 1, 2, 3 …
N
натуральные
1, 2, 3, 4, …
Работа в классе
№ 871
№ 873
№ 874 (1–5)
№ 875
№ 876
№ 877
Домашнее задание
- § 31, вопросы 1–10 – учить теорию!
Урок 1-2 по теме «Целые и рациональные числа.
 Действительные числа»
Действительные числа»Уроки 1-2. «Целые и рациональные числа. Действительные числа»
Цели занятия:
— рассмотреть множество натуральных чисел;— рассмотреть множество целых чисел;
— рассмотреть множество рациональных чисел;
— ввести понятие конечной и бесконечной десятичной дроби;
— дать определение бесконечной периодической десятичной дроби.
— сформировать желание самостоятельно изучать материал;
Воспитательные:
— воспитывать положительное отношение к приобретению новых знаний;
— воспитывать ответственность за свои действия и поступки;
— вызвать заинтересованность новым для студентов подходом изучения математики.
Развивающие:
— формировать навыки познавательного мышления;
— формировать умения и навыки учебного труда.
Задачи занятия: сформировать умение переводить обыкновенную дробь в десятичную; сформировать умение переводить бесконечную периодическую дробь в обыкновенную.
Планируемый результат: студент знает определение бесконечной периодической десятичной дроби. Знает множество натуральных чисел. Знает множество целых чисел. Знает множество рациональных чисел. Умеет представлять обыкновенную дробь в виде десятичной. Умеет представлять бесконечную периодическую дробь в виде обыкновенной дроби.
Структура занятия:
1. Организованный момент.
2. Актуализация.
3. Объяснение темы «Целые и рациональные числа. Действительные числа»
Множество натуральных чисел
Множество целых чисел
Множество рациональных чисел
Конечные десятичные дроби
Бесконечные десятичные дроби
Бесконечная периодическая десятичная дробь.
4. Решение ключевых задач.
Представить обыкновенную дробь в виде десятичной.
Представить бесконечную периодическую дробь в виде обыкновенной дроби.
5. Решение упражнений.
6. Подведение итогов урока. Домашнее задание.
Ход занятия:
1. Организованный момент. Приветствие учащихся. Сообщение темы и целей занятия. Проверка готовности студентов к занятию.
2. Актуализация
Вычислить: 1) , 2) , 3)
3. Объяснение нового материала:
Определение: числа, которые мы используем при счете предметов, называются натуральными. При сложении и умножении натуральных чисел всегда получаются натуральные числа.Утверждение: разность и частное натуральных чисел не всегда являются натуральными числами.
Натуральные числа используются при счете предметов.
Множество целых чисел
Дополним множество натуральных чисел, нулем и отрицательными числами.Мы получим множество целых чисел. Надо заметить, что при сложении, вычитании, умножении целых чисел, всегда образуются целые числа.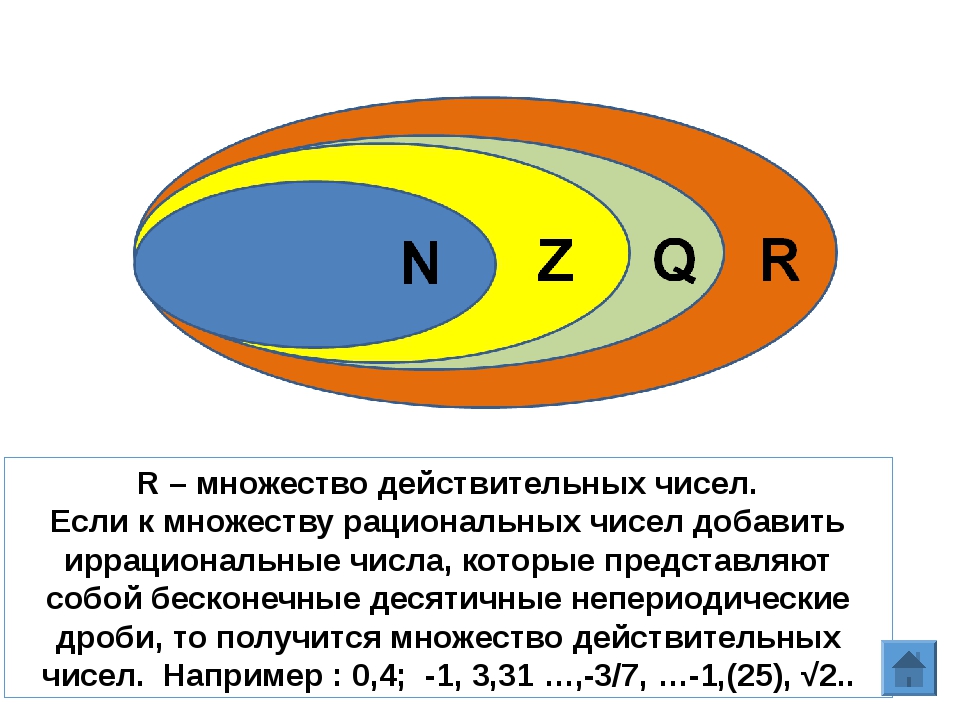 Однако частное двух целых чисел, не обязятельно будет целым числом.
Однако частное двух целых чисел, не обязятельно будет целым числом.
Множество рациональных чисел
Введение рациональных чисел, то есть чисел вида , где – целое число, – натуральное число, дает возможность находить частное двух рациональных чисел при условии, что делитель не равен нулю.
Каждое целое число также является рациональным, так как его можно представить в виде .
Утверждение: при выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа.
Конечные десятичные дроби
Если рациональное число можно представить в виде дроби , где – целое число, – натуральное число, то его можно записать в виде конечной десятичной дроби.
Например, .
Бесконечные десятичные дроби
Существуют рациональные числа, которые нельзя записать в виде конечной десятичной дроби.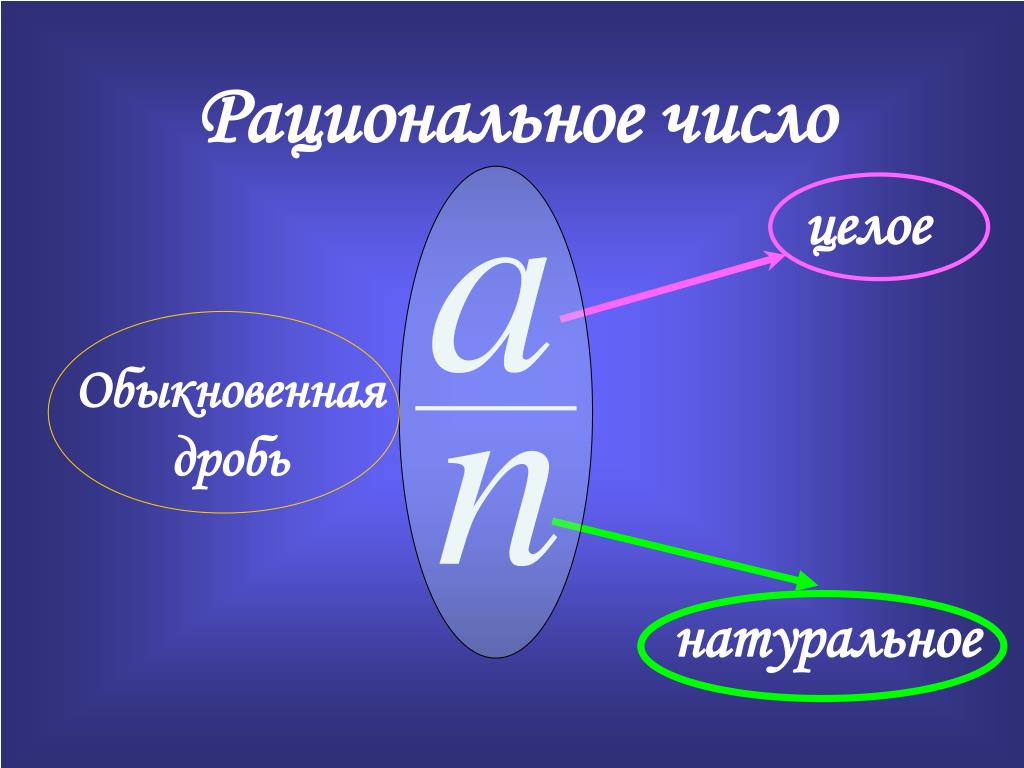
Если, например, попытаться записать число в виде десятичной дроби, разделив числитель на знаменатель, то получится бесконечная десятичная дробь
Бесконечную деятичную дробь называют периодической, а повторяющуюся цифру 3 — ее периодом.
Коротко записывают так: (ноль целых три десятых в периоде)
Бесконечная периодическая десятичная дробь
Периодическая дробь – это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби.
Например,
Утверждение. Каждая бесконечная периодическая дробь является рациональным числом, так как может быть представлена в виде , где — это целое число, — натуральное число.
4. Решение ключевых задач.
1. Представить в виде десятичной дроби
2) Записать бесконечную периодическую дробь в виде обыкновенной дроби.
Решение. Распишем период дроби:
Ответ: .
3) Записать бесконечную периодическую дробь в виде обыкновенной дроби.
Решение. Распишем период дроби:
,
Ответ: .
5. Решение упражнений.
1) Записать в виде десятичной дроби:
1) ; 2) ; 3) ; 4) ; 5) .
2) Выполнить действия и записать результат в виде десятичной дроби:
1) , 2)
3) Представить в виде обыкновенной дроби:
1)
.
2)
.
3)
.
4) 0,2(18)
.
Резерв – задания 1,2,3 (четные).
1) Представить обыкновенную дробь в виде десятичной периодической дроби
1. ; 2.; 3. ; 4.;
5. ; 6. ; 7. ; 8. ;
9. ; 10. ; 11. ; 12. .
2) Записать в виде обыкновенной дроби бесконечную периодическую десятичную дробь
1. ; 2. ; 3.
4. ; 5. ; 6. ;
7. ; 8. ; 9. ;
10. ; 11. ; 12. ;
3) Найти значение следующих дробей
1. .
6. Подведение итогов. Выставление оценок. Домашнее задание: выучить теоретический материал, задания 1, 2 (нечетные).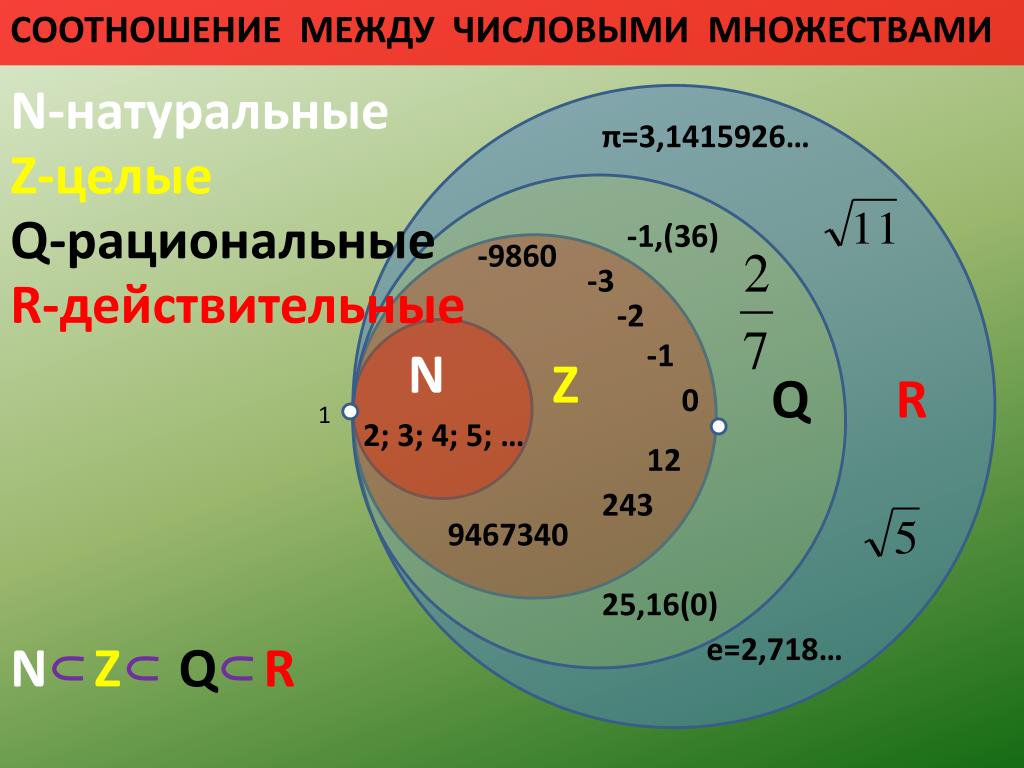
1 | Устная работа: | ||||||||||||||
Вычислите: | Вычислите: | Вычислите: | Вычислите: | ||||||||||||
2 | Объяснение новой темы: | ||||||||||||||
| Числа, которые мы используем при счете предметов, называются натуральными. При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел не всегда являются натуральными числами. | ||||||||||||||
| Дополним множество натуральных чисел, нулем и отрицательными числами(т. | ||||||||||||||
| Введение рациональных чисел, то есть чисел вида , где – целое число, – натуральное число, дает возможность находить частное двух рациональных чисел при условии, что делитель не равен нулю. Каждое целое число также является рациональным, так как его можно представить в виде При выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа. | ||||||||||||||
| Если рациональное число можно представить в виде дроби – целое число, – натуральное число, то его можно записать в виде конечной десятичной дроби. Например, можно записать Например, | ||||||||||||||
| Существуют рациональные числа, которые нельзя записать в виде конечной десятичной дроби, например Если, например, попытаться записать число в виде десятичной дроби, разделив числитель на знаменатель, то получится бесконечная десятичная дробь Бесконечную деятичную дробь называют периодической, а повторяющуюся цифру 3 — ее периодом. Коротко записывают так: (ноль целых три десятых в периоде) | ||||||||||||||
| Определение Периодическая дробь – это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби. | ||||||||||||||
3 | Решение ключевых задач. | Задача 1. Записать число в виде бесконечной десятичной дроби. Решение: | |||||||||||||
Задача 2. Представить бесконечную периодическую десятичную дробь в виде обыкновенной. Решение: 1.Пусть Так как в записи этого числа до периода содержится только один десятичный знак, то, умножая на 10, получаем (1) 2)Период этой дроби состоит из двух цифр. Поэтому, умножая обе части последнего равенства на находим (2) 3)Вычитая из равенства (2) равенство (1), получаем | |||||||||||||||
4 | Решение тренировочных упражнений из учебника «Алгебра и начала анализа 10-11» на закрепление темы: | ||||||||||||||
№1. Решение: | |||||||||||||||
№2. Выполнить действия и записать результат в виде десятичной дроби: | |||||||||||||||
№4.Вычислить: | |||||||||||||||
| |||||||||||||||
| |||||||||||||||
№5. | |||||||||||||||
5 | Самостоятельная работа | ||||||||||||||
1 вариант | 2 вариант | ||||||||||||||
Закончите предложения таким образом, чтобы высказывание стало истинным | |||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
Представьте бесконечную периодическую десятичную дробь в виде десятичной | |||||||||||||||
Решение: Так как в записи нашего числа до периода содержится только один десятичный знак, то, умножая на 10, получаем Период нашей дроби состоит из одной цифры. Поэтому, умножая обе части последнего равенства на находим
Вычитая из равенства (2) равенство (1), получаем | Решение: Так как в записи нашего числа до периода содержится только один десятичный знак, то, умножая на 10, получаем Период нашей дроби состоит из одной цифры. Вычитая из равенства (2) равенство (1), получаем | ||||||||||||||
7.1: Рациональные и иррациональные числа
Поздравляем! Вы прочитали первые шесть глав этой книги! Пришло время подвести итоги того, что вы уже сделали в этом курсе, и подумать о том, что вас ждет впереди. Вы узнали, как складывать, вычитать, умножать и делить целые числа, дроби, целые числа и десятичные дроби. Вы познакомились с языком и символами алгебры, а также упростили и оценили алгебраические выражения. Вы решили много разных типов приложений.Вы заложили хорошую прочную основу, необходимую для достижения успеха в алгебре.
В этой главе мы убедимся, что ваши навыки твердо закреплены. Мы еще раз взглянем на типы чисел, с которыми мы работали во всех предыдущих главах. Мы будем работать со свойствами чисел, которые помогут вам улучшить ваше понимание чисел. И мы попрактикуемся в их использовании, как и при решении уравнений и выполнении других процедур в алгебре.
И мы попрактикуемся в их использовании, как и при решении уравнений и выполнении других процедур в алгебре.
Мы уже описали числа как счетные числа, целые числа и целые числа.Вы помните, в чем разница между этими типами чисел?
Рациональные числа
Какой тип чисел вы получите, если начнете со всех целых чисел, а затем включите все дроби? Числа, которые у вас будут, образуют набор рациональных чисел. Рациональное число — это число, которое можно записать как отношение двух целых чисел.
Определение: рациональные числа
Рациональное число — это число, которое можно записать в форме \ (\ dfrac {p} {q} \), где p и q — целые числа, а q 0.
Все дроби, как положительные, так и отрицательные, являются рациональными числами. Несколько примеров:
\ [\ dfrac {4} {5}, — \ dfrac {7} {8}, \ dfrac {13} {4}, \; а также\; — \ dfrac {20} {3} \]
Каждый числитель и каждый знаменатель — целое число.
Нам нужно посмотреть на все числа, которые мы использовали до сих пор, и убедиться, что они рациональны. Определение рациональных чисел говорит нам, что все дроби рациональны. Теперь мы посмотрим на счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.
Определение рациональных чисел говорит нам, что все дроби рациональны. Теперь мы посмотрим на счетные числа, целые числа, целые числа и десятичные дроби, чтобы убедиться, что они рациональны.
Целые числа являются рациональными числами? Чтобы решить, является ли целое число рациональным числом, мы пытаемся записать его как отношение двух целых чисел. Легкий способ сделать это — записать дробь со знаминателем один.
\ [3 = \ dfrac {3} {1} \ quad -8 = \ dfrac {-8} {1} \ quad 0 = \ dfrac {0} {1} \]
Поскольку любое целое число можно записать как отношение двух целых чисел, все целые числа являются рациональными числами. Помните, что все счетные числа и все целые числа также являются целыми числами, а значит, они тоже рациональны.
А как насчет десятичных знаков? Они рациональны? Давайте посмотрим на несколько, чтобы увидеть, можем ли мы записать каждое из них как отношение двух целых чисел. Мы уже видели, что целые числа — это рациональные числа. Целое число -8 можно записать как десятичное -8,0. Итак, очевидно, что некоторые десятичные дроби рациональны.
Итак, очевидно, что некоторые десятичные дроби рациональны.
Подумайте о десятичной системе счисления 7.3. Можем ли мы записать это как отношение двух целых чисел? Поскольку 7.3 означает \ (7 \ dfrac {3} {10} \), мы можем записать это как неправильную дробь, \ (7 \ dfrac {3} {10} \). Итак, 7,3 — это соотношение целых чисел 73 и 10.Это рациональное число.
В общем, любое десятичное число, которое заканчивается рядом цифр (например, 7,3 или -1,2684), является рациональным числом. Мы можем использовать обратное (или мультипликативное обратное) значение разряда последней цифры в качестве знаменателя при записи десятичной дроби в виде дроби.
Пример \ (\ PageIndex {1} \):
Запишите каждое как отношение двух целых чисел: (a) −15 (b) 6,81 (c) \ (- 3 \ dfrac {6} {7} \).
Решение
(а) −15
| Запишите целое число в виде дроби со знаминателем 1. | $$ \ dfrac {-15} {1} $$ |
(б) 6,81
Запишите десятичную дробь как смешанное число. | $$ 6 \ dfrac {81} {100} $$ |
| Затем преобразовать его в неправильную дробь. | $$ \ dfrac {681} {100} $$ |
(c) \ (- 3 \ dfrac {6} {7} \)
| Преобразует смешанное число в неправильную дробь. | $$ — \ dfrac {27} {7} $$ |
Упражнение \ (\ PageIndex {1} \):
Запишите каждое как отношение двух целых чисел: (a) −24 (b) 3.57.
- Ответьте на
\ (\ frac {-24} {1} \)
- Ответ б
\ (\ frac {357} {100} \)
Упражнение \ (\ PageIndex {2} \):
Запишите каждое как отношение двух целых чисел: (a) −19 (b) 8,41.
- Ответьте на
\ (\ frac {-19} {1} \)
- Ответ б
\ (\ frac {841} {100} \)
Давайте посмотрим на десятичную форму рациональных чисел. Мы видели, что каждое целое число является рациональным числом, поскольку a = \ (\ dfrac {a} {1} \) для любого целого числа, a. Мы также можем преобразовать любое целое число в десятичное, добавив десятичную точку и ноль.
Мы видели, что каждое целое число является рациональным числом, поскольку a = \ (\ dfrac {a} {1} \) для любого целого числа, a. Мы также можем преобразовать любое целое число в десятичное, добавив десятичную точку и ноль.
\ [\ begin {split} Integer \ qquad & -2, \ quad -1, \ quad 0, \ quad 1, \; \; 2, \; 3 \\ Десятичный \ qquad & -2.0, -1.0, 0.0, 1.0, 2.0, 3.0 \ end {split} \]
Эти десятичные числа останавливаются.
Мы также видели, что каждая дробь является рациональным числом. Посмотрите на десятичную форму только что рассмотренных дробей.
\ [\ begin {split} Коэффициент \; из\; Целые числа \ qquad \ dfrac {4} {5}, \ quad — \ dfrac {7} {8}, \ quad \ dfrac {13} {4}, \; & — \ dfrac {20} {3} \\ Decimal \; формы \ qquad 0.8, -0.875, 3.25, & -6.666 \ ldots \\ & -6. \ overline {66} \ end {split} \]
Эти десятичные дроби либо останавливаются, либо повторяются.
Что вам говорят эти примеры? Каждое рациональное число может быть записано как в виде отношения целых чисел, так и в виде десятичной дроби, которая либо останавливается, либо повторяется. В таблице ниже показаны числа, которые мы рассматривали, выраженные как отношение целых чисел и десятичной дроби.
В таблице ниже показаны числа, которые мы рассматривали, выраженные как отношение целых чисел и десятичной дроби.
| Рациональные числа | ||
|---|---|---|
| Дроби | Целые числа | |
| Номер | $$ \ dfrac {4} {5}, — \ dfrac {7} {8}, \ dfrac {13} {4}, \ dfrac {-20} {3} $$ | $$ — 2, -1, 0, 1, 2, 3 $$ |
| Целое число | $$ \ dfrac {4} {5}, \ dfrac {-7} {8}, \ dfrac {13} {4}, \ dfrac {-20} {3} $$ | $$ \ dfrac {-2} {1}, \ dfrac {-1} {1}, \ dfrac {0} {1}, \ dfrac {1} {1}, \ dfrac {2} {1}, \ dfrac {3} {1} $$ |
| Десятичное число | $$ 0.8, -0,875, 3,25, -6. \ Overline {6} $$ \ Overline {6} $$ | $$ — 2,0, -1,0, 0,0, 1,0, 2,0, 3,0 $$ |
Иррациональные числа
Есть ли десятичные дроби, которые не останавливаются и не повторяются? Да. Число \ (\ пи \) (греческая буква пи, произносится как «пирог»), которое очень важно при описании кругов, имеет десятичную форму, которая не останавливается и не повторяется.
\ [\ pi = 3,141592654 \ ldots \ ldots \]
Точно так же десятичные представления квадратных корней из целых чисел, которые не являются точными квадратами, никогда не прекращаются и никогда не повторяются.Например,
\ [\ sqrt {5} = 2.236067978 \ ldots \ ldots \]
Десятичная дробь, которая не останавливается и не повторяется, не может быть записана как отношение целых чисел. Мы называем такой номер иррациональным числом .
Определение: Иррациональное число
Иррациональное число — это число, которое нельзя записать как отношение двух целых чисел. Его десятичная форма не останавливается и не повторяется.
Его десятичная форма не останавливается и не повторяется.
Давайте резюмируем метод, который мы можем использовать, чтобы определить, является ли число рациональным или иррациональным.
Если десятичная форма числа
- останавливается или повторяется, число рациональное.
- не останавливается и не повторяется, цифра иррациональна.
Пример \ (\ PageIndex {2} \):
Определите каждое из следующего как рациональное или иррациональное: (a) 0,58 \ (\ overline {3} \) (b) 0,475 (c) 3,605551275…
Решение
(а) 0,58 \ (\ overline {3} \)
Полоса над цифрой 3 указывает на то, что это повторяется.Следовательно, 0,583 — это повторяющееся десятичное число, а значит, является рациональным числом.
(б) 0,475
Эта десятичная дробь заканчивается после 5, так что это рациональное число.
(в) 3.605551275…
Многоточие (…) означает, что это число не останавливается. Нет повторяющегося рисунка цифр. Поскольку число не останавливается и не повторяется, это нерационально.
Нет повторяющегося рисунка цифр. Поскольку число не останавливается и не повторяется, это нерационально.
Упражнение \ (\ PageIndex {3} \):
Определите каждое из следующего как рациональное или иррациональное: (a) 0.29 (б) 0,81 \ (\ overline {6} \) (в) 2,515115111…
- Ответьте на
рациональное
- Ответ б
рациональное
- Ответ c
иррациональный
Упражнение \ (\ PageIndex {4} \):
Определите каждое из следующего как рациональное или иррациональное: (a) 0,2 \ (\ overline {3} \) (b) 0,125 (c) 0,418302…
- Ответьте на
рациональное
- Ответ б
рациональное
- Ответ c
иррациональный
Давайте теперь подумаем о квадратных корнях.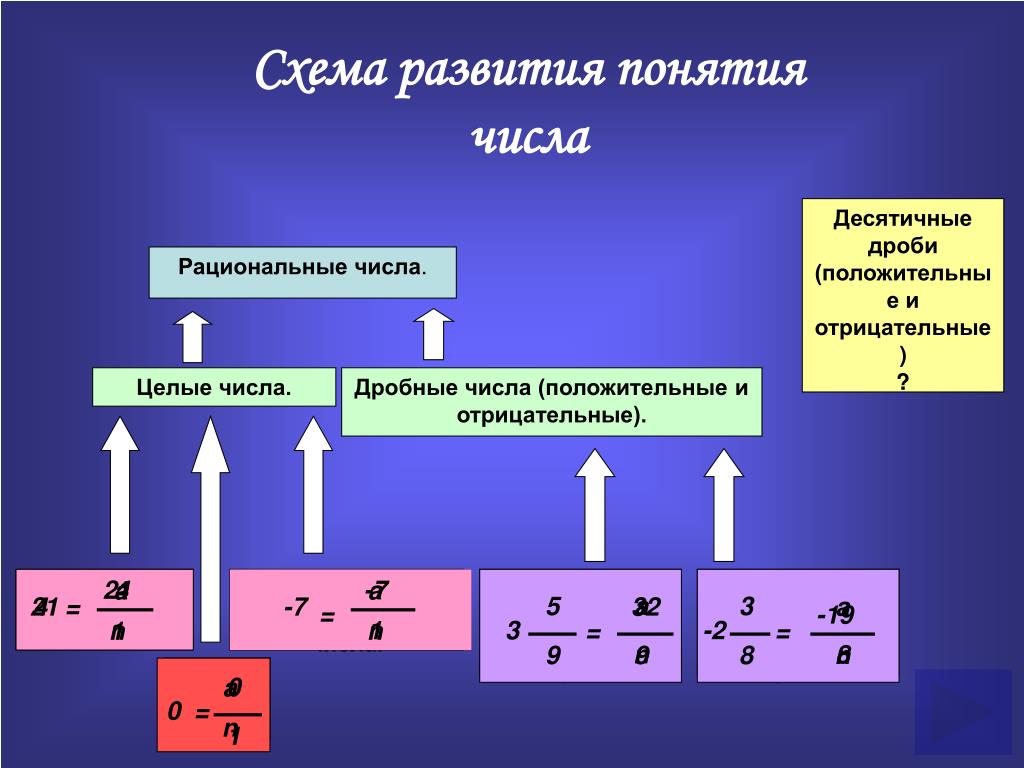 Квадратные корни из полных квадратов всегда целые числа, поэтому они рациональны. Но десятичные формы квадратных корней чисел, которые не являются точными квадратами, никогда не останавливаются и никогда не повторяются, поэтому эти квадратные корни иррациональны.
Квадратные корни из полных квадратов всегда целые числа, поэтому они рациональны. Но десятичные формы квадратных корней чисел, которые не являются точными квадратами, никогда не останавливаются и никогда не повторяются, поэтому эти квадратные корни иррациональны.
Пример \ (\ PageIndex {3} \):
Определите каждое из следующего как рациональное или иррациональное: (a) 36 (b) 44
Решение
(a) Число 36 — полный квадрат, так как 6 2 = 36. Итак, \ (\ sqrt {36} \) = 6. Следовательно, \ (\ sqrt {36} \) рационально.
(б) Помните, что 6 2 = 36 и 7 2 = 49, поэтому 44 не является полным квадратом. Это означает, что \ (\ sqrt {44} \) иррационально.
Упражнение \ (\ PageIndex {5} \):
Определите каждое из следующего как рациональное или иррациональное: (a) \ (\ sqrt {81} \) (b) \ (\ sqrt {17} \)
- Ответьте на
рациональное
- Ответ б
иррациональный
Упражнение \ (\ PageIndex {6} \):
Определите каждое из следующего как рациональное или иррациональное: (a) \ (\ sqrt {116} \) (b) \ (\ sqrt {121} \)
- Ответьте на
иррациональный
- Ответ б
рациональное
Обучение рациональным числам: десятичные дроби, дроби и многое другое
Важным свойством как действительных, так и рациональных чисел является свойство плотности .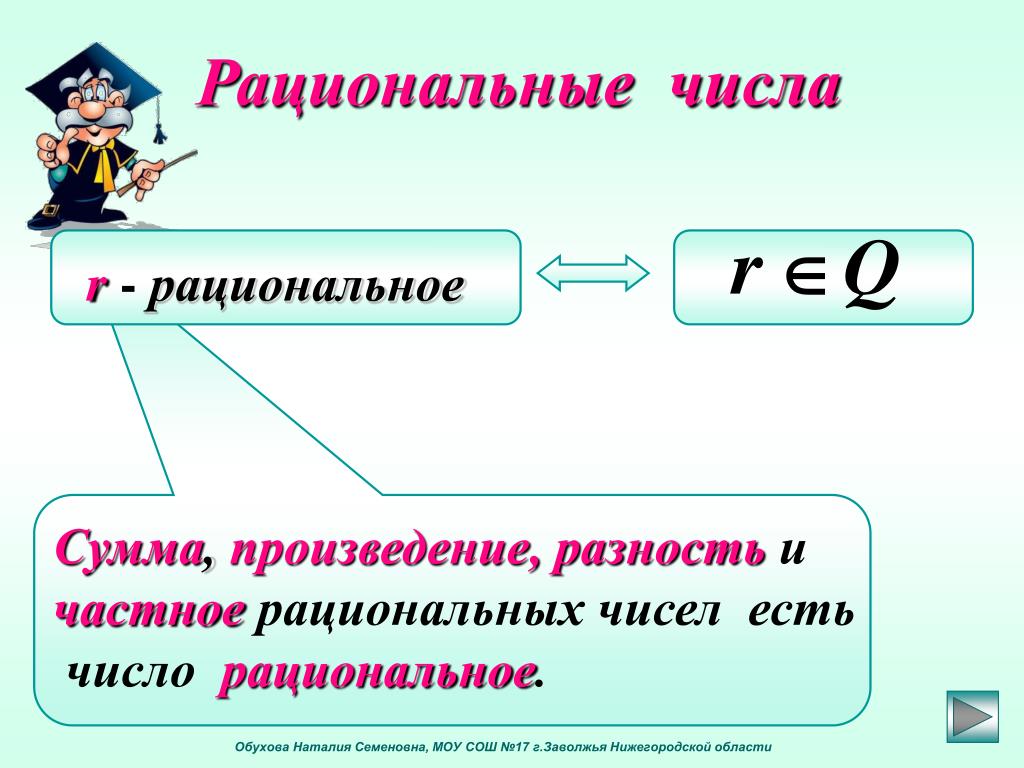 Он говорит, что между любыми двумя действительными числами всегда есть другое действительное число. Например, между 0,4588 и 0,4589 существует число 0,45887 (и бесконечно много других). Обратите внимание, что рисунок выше предназначен для демонстрации того, что действительные числа — это самая большая категория, которая включает в себя все; однако нет ни рациональных, ни иррациональных чисел. Другими словами, все действительные числа попадают либо в рациональную часть, либо в иррациональную часть.
Он говорит, что между любыми двумя действительными числами всегда есть другое действительное число. Например, между 0,4588 и 0,4589 существует число 0,45887 (и бесконечно много других). Обратите внимание, что рисунок выше предназначен для демонстрации того, что действительные числа — это самая большая категория, которая включает в себя все; однако нет ни рациональных, ни иррациональных чисел. Другими словами, все действительные числа попадают либо в рациональную часть, либо в иррациональную часть.
Итак, вот все возможные действительные числа:
Действительные числа: рациональный
Основной стандарт: под рациональным числом понимается отношение двух целых чисел и точки на числовой прямой.(6 класс)
Рациональные числа: Любое число, которое может быть записано как отношение (или дробь) двух целых чисел, является рациональным числом. Студенты часто спрашивают, являются ли дроби рациональными числами? Ответ — да, но дроби составляют большую категорию, в которую также входят целые числа, завершающие десятичные дроби, повторяющиеся десятичные дроби и дроби.
- Целое число можно записать в виде дроби, задав ему знаменатель, равный единице, поэтому любое целое число является рациональным числом.
\ (6 = \ frac {6} {1} \)
\ (0 = \ frac {0} {1} \)
\ (- 4 = \ frac {-4} {1} \) или \ ( \ frac {4} {- 1} \) или \ (- \ frac {4} {1} \) - Конечная десятичная дробь может быть записана как дробь, используя свойства разряда. Например, 3,75 = три и семьдесят пять сотых или \ (3 \ frac {75} {100} \), что равно неправильной дроби \ (\ frac {375} {100} \).
- Повторяющаяся десятичная дробь всегда можно записать в виде дроби, используя алгебраические методы, которые выходят за рамки данной статьи.Однако важно понимать, что любой десятичный разделитель с одной или несколькими цифрами, который повторяется бесконечно, например \ (2.111 \) … (который может быть записан как \ (2. \ bar {1} \)) или \ ( 0.8890 \) … (или \ (0. \ bar {89} \)), является рациональным числом.
 Распространенный вопрос: «Повторяются ли десятичные дроби рациональными числами?» Ответ положительный!
Распространенный вопрос: «Повторяются ли десятичные дроби рациональными числами?» Ответ положительный!
Целые числа: Счетные числа (1, 2, 3, …), их противоположности (–1, –2, –3, …) и 0 являются целыми числами. Распространенная ошибка учащихся 6–8 классов — считать, что целые числа относятся к отрицательным числам.Точно так же многие студенты задаются вопросом, являются ли десятичные дроби целыми числами? Это верно только тогда, когда десятичная дробь заканчивается на «.000 …», как в 3.000 …, что равно 3. (Технически это также верно, когда десятичная дробь заканчивается на «.999 …», поскольку 0,999 … = 1. Это встречается нечасто, но цифра 3 на самом деле может быть записана как 2,999 ….)
Целые числа: Ноль и положительные целые числа являются целыми числами.
Натуральные числа: Этот набор, также называемый счетными числами, включает в себя все целые числа, кроме нуля (1, 2, 3 ,…).
Вещественные числа: иррационально
Ключевой стандарт: знайте, что есть числа, которые не являются рациональными. (8 класс)
(8 класс)
Иррациональные числа: Любое действительное число, которое нельзя записать в виде дроби, является иррациональным числом. Эти числа включают неповторяющиеся, неповторяющиеся десятичные дроби, например \ (\ pi \), 0,45445544455544445555 … или \ (\ sqrt {2} \). Любой квадратный корень, не являющийся точным корнем, является иррациональным числом. Например, \ (\ sqrt {1} \) и \ (\ sqrt {4} \) рациональны, потому что \ (\ sqrt {1} = 1 \) и \ (\ sqrt {4} = 2 \), но \ (\ sqrt {2} \) и \ (\ sqrt {3} \) иррациональны.2 + 3 = 0 \) (решение которого \ (\ pm \ sqrt {3} \)).
В некотором смысле это «конец» чисел, хотя математики всегда придумывают новые способы описания и представления чисел по-разному. Поощряйте своих учеников быть математиками! Как бы они описали число, которого нет среди представленных здесь типов чисел? Почему ученый или математик может пытаться это сделать?
***
Ищете бесплатные уроки математики и задания для учеников 6-х классов и выше, в которых используются рациональные и иррациональные числа? Изучите наш постоянно расширяющийся центр бесплатных ресурсов!
Набор чисел (действительные, целые, рациональные, натуральные и иррациональные числа)
В этом разделе мы дадим краткое, но более содержательное введение в концепции наборов чисел, причем набор действительных чисел является наиболее важным и обозначается $$ \ mathbb {R} $$.
Но сначала, чтобы перейти к действительным числам, мы начнем с набора натуральных чисел.
Натуральные числа $$ \ mathbb {N} $$
Натуральные числа — это числа, которые с незапамятных времен использовались для счета. В большинстве стран они приняли арабские цифры, названные так потому, что именно арабы ввели их в Европу, но именно в Индии они были изобретены.
Набор натуральных чисел обозначается как $$ \ mathbb {N} $$; итак:
$$$ \ mathbb {N} = \ {1,2,3,4,5,6 \ ldots \} $$$
Натуральные числа характеризуются двумя свойствами:
- Число 1 — это первое натуральное число, и каждое натуральное число образуется путем прибавления 1 к предыдущему.
- Когда мы вычитаем или делим два натуральных числа, результат не обязательно является натуральным числом, поэтому мы говорим, что натуральные числа не закрываются при этих двух операциях. Натуральные числа закрываются только при сложении и умножении, т. Е. Сложение или умножение двух натуральных чисел всегда приводит к другому натуральному числу.

Целые числа $$ \ mathbb {Z} $$
Когда возникает необходимость отличать одни значения от других от исходной позиции, возникает необходимость в отрицательных числах.Например, с уровня 0 (уровня моря) мы проводим различие над уровнем моря или глубоким морем. Или в случае отрицательной или положительной температуры. Таким образом, мы можем быть на высоте 700 м, $$ + 700 $$, или нырнуть на глубину 10 м, $$ — 10 $$, и она может быть примерно на 25 градусов $$ + 25 $$ или на 5 градусов ниже 0, $$ — 5 $$.
Для обозначения отрицательных чисел мы добавляем знак минус перед числом.
Короче говоря, набор, образованный отрицательными целыми числами, числом ноль и положительными целыми числами (или натуральными числами), называется набором целых чисел.
Они обозначаются символом $$ \ mathbb {Z} $$ и могут быть записаны как:
$$$ \ mathbb {Z} = \ {\ ldots, -2, -1,0,1,2, \ ldots \} $$$
Обозначим их на числовой строке следующим образом:
Важным свойством целых чисел является то, что они закрываются при сложении, умножении и вычитании, то есть любое сложение, вычитание и умножение двух целых чисел приводит к получению другого целого числа. Обратите внимание, что частное двух целых чисел, например $$ 3 $$ и $$ 7 $$, не обязательно является целым числом.Таким образом, набор не замыкается на деление.
Обратите внимание, что частное двух целых чисел, например $$ 3 $$ и $$ 7 $$, не обязательно является целым числом.Таким образом, набор не замыкается на деление.
Рациональные числа $$ \ mathbb {Q} $$
Рациональные числа — это числа, которые можно выразить как деление между двумя целыми числами. Набор рациональных чисел обозначается как $$ \ mathbb {Q} $$, поэтому:
$$$ \ mathbb {Q} = \ Big \ {\ dfrac {p} {q} \ | \ p, q \ in \ mathbb {Z} \ Big \} $$$
Результатом рационального числа может быть целое число ($$ — \ dfrac {8} {4} = — 2 $$) или десятичное ($$ \ dfrac {6} {5} = 1,2 $$) число, положительное или отрицательное. Кроме того, среди десятичных дробей есть два разных типа: один с ограниченным числом цифр, который называется точным десятичным числом, ($$ \ dfrac {88} {25} = 3,52 $$), а другой — с неограниченным числом. цифр, которые он называется повторяющимся десятичным числом ($$ \ dfrac {5} {9} = 0,5555 \ ldots = 0, \ widehat {5} $$).
Мы называем их повторяющимися десятичными знаками, потому что некоторые цифры в десятичной части повторяются снова и снова.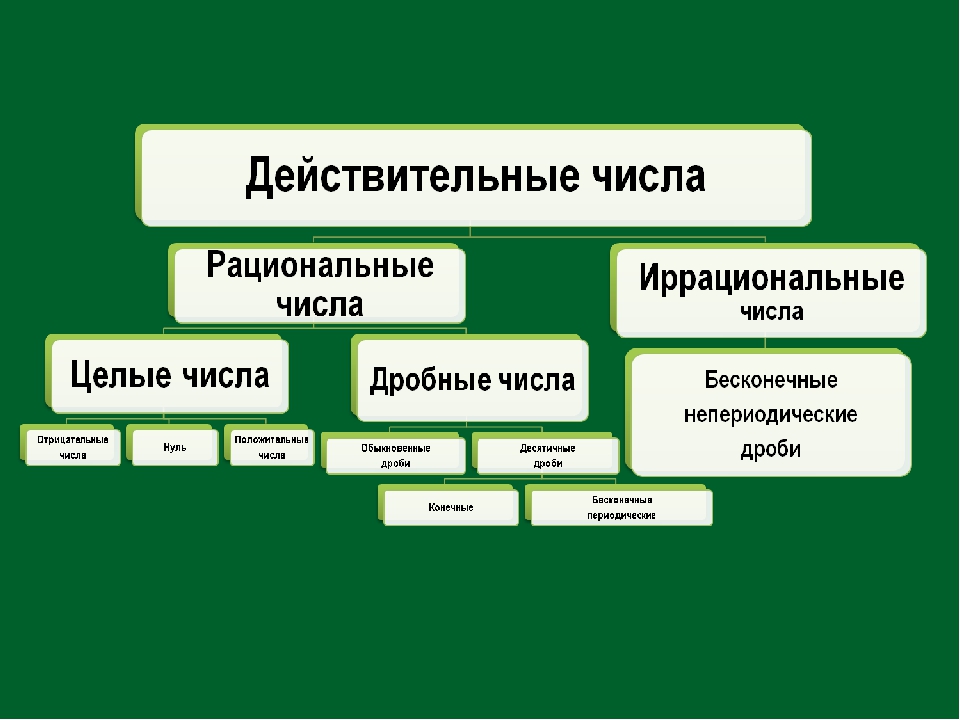 Если просто повторяющиеся цифры начинаются с десятой, мы называем их чистыми повторяющимися десятичными знаками ($$ 6,8888 \ ldots = 6, \ widehat {8} $$), в противном случае мы называем их смешанными повторяющимися десятичными знаками ($$ 3,415626262 \ ldots = 3,415 \ widehat {62} $$).
Если просто повторяющиеся цифры начинаются с десятой, мы называем их чистыми повторяющимися десятичными знаками ($$ 6,8888 \ ldots = 6, \ widehat {8} $$), в противном случае мы называем их смешанными повторяющимися десятичными знаками ($$ 3,415626262 \ ldots = 3,415 \ widehat {62} $$).
Обратите внимание, что каждое целое число является рациональным числом, так как, например, $$ 5 = \ dfrac {5} {1} $$; следовательно, $$ \ mathbb {Z} $$ является подмножеством $$ \ mathbb {Q} $$. Таким же образом каждое натуральное число также является целым числом, в частности положительным целым числом.Таким образом имеем:
$$$ \ mathbb {N} \ subset \ mathbb {Z} \ subset \ mathbb {Q} $$$
Рациональные числа замыкаются не только сложением, умножением и вычитанием, но и делением (кроме $$ 0 $$).
Иррациональные числа $$ \ mathbb {I} $$
Мы видели, что любое рациональное число может быть выражено целым, десятичным или точным десятичным числом.
Однако не все десятичные числа являются точными или повторяющимися десятичными числами, и поэтому не все десятичные числа могут быть выражены как дробь двух целых чисел.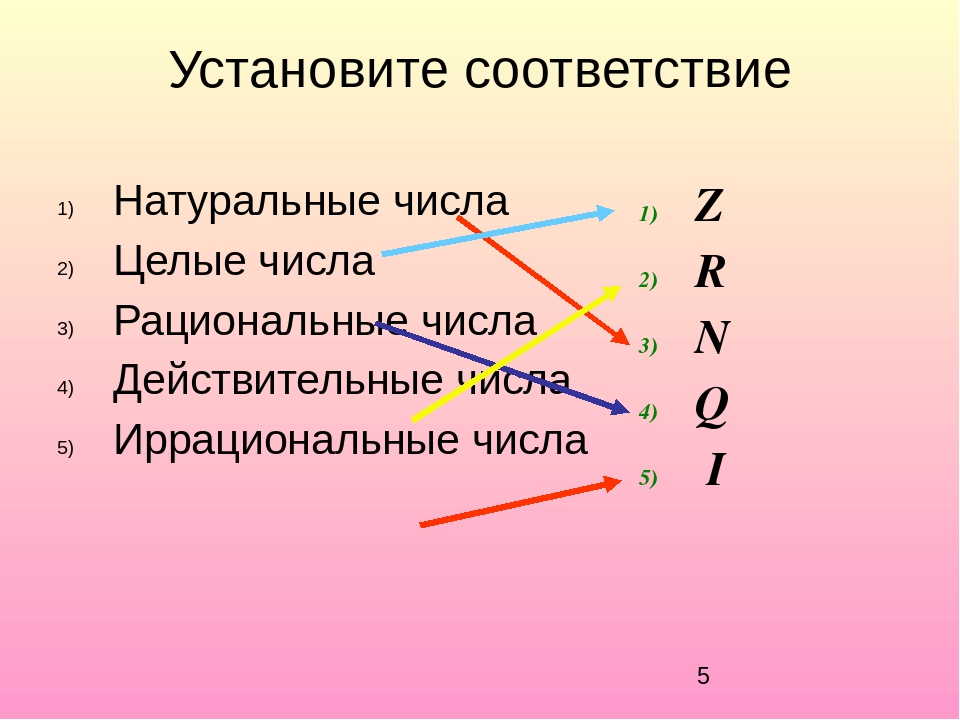
Эти десятичные числа, которые не являются ни точными, ни повторяющимися десятичными знаками, характеризуются бесконечными непериодическими десятичными цифрами, т. Е. Никогда не заканчиваются и не имеют повторяющегося образца.
Обратите внимание, что набор иррациональных чисел является дополнением набора рациональных чисел.
Некоторые примеры иррациональных чисел: $$ \ sqrt {2}, \ pi, \ sqrt [3] {5}, $$ и, например, $$ \ pi = 3,1415926535 \ ldots $$ происходит из отношения между длина круга и его диаметр.
Действительные числа $$ \ mathbb {R} $$
Набор, состоящий из рациональных и иррациональных чисел, называется множеством действительных чисел и обозначается как $$ \ mathbb {R} $$.
Таким образом имеем:
$$$ \ mathbb {R} = \ mathbb {Q} \ cup \ mathbb {I} $$$
И рациональные, и иррациональные числа являются действительными числами.
Одним из наиболее важных свойств действительных чисел является то, что они могут быть представлены в виде точек на прямой. Мы выбираем точку под названием origin, чтобы обозначить $$ 0 $$, и другую точку, обычно справа, чтобы обозначить $$ 1 $$.
Мы выбираем точку под названием origin, чтобы обозначить $$ 0 $$, и другую точку, обычно справа, чтобы обозначить $$ 1 $$.
Соответствие между точками на линии и действительными числами возникает естественным образом; другими словами, каждая точка на линии представляет собой одно действительное число, а каждое действительное число имеет одну точку на линии.Мы называем это настоящей линией. На следующем рисунке вы можете увидеть пример:
Рациональные числа — OeisWiki
Эта статья требует дополнительной доработки. Помогите, пожалуйста, расширив его! Рациональные числа — это числа, которые могут быть выражены как отношение двух целых чисел. Если и являются целыми числами, то их отношение, обозначаемое как или, является рациональным числом. Например, дробь и целое число являются рациональными числами. с другой стороны, это не рациональное число.Рациональные числа, будучи алгебраическими числами степени 1, являются корнями непостоянного линейного уравнения с целыми коэффициентами
- a1x + a0 = 0, {\ displaystyle {\ begin {array} {l} \ displaystyle {a_ {1} x + a_ {0} = 0,} \ end {array}}}
a 1, a 0 ∈ ℤ, a 1 ≥ 1. |
Целые рациональные числа
Целые рациональные числа (целые алгебраические числа степени 1) — нули линейного монического полинома с целыми коэффициентами
- x + a0, {\ displaystyle {\ begin {array} {l} \ displaystyle {x + a_ {0} {\! \, \!},} \ End {array}}}
Деление в длину дает указанное выше десятичное разложение, хотя без явного акцента на геометрические ряды, участвующие в десятичном разложении.
- 90n = 100n − 10n = abc.ccccc …− ab.cccccc … = abc − ab, {\ displaystyle {\ begin {array} {l} \ displaystyle {90n = 100n-10n = {\ mbox {abc.ccccc …}} — {\ mbox {ab.cccccc …}} = {\ mbox {abc}} — {\ mbox {ab}},} \ end {array}}}
- n = abc − ab90. {\ Displaystyle {\ begin {array} {l} \ displaystyle {n = {\ frac {{\ mbox {abc}} — {\ mbox {ab}}} {90}}. } \ end {array}}}
Двойные представления и стандартная форма
Любое рациональное число, знаменатель которого не является взаимно простым с фиксированным основанием, используемым для представления, имеет два представления из-за того, что| 1 = 1.00000000… = 0.9999999999… |
 Рассмотрение подразумевает
Рассмотрение подразумевает- 9n = 10n − n = 9.99999999… −0.99999999… = 9, {\ displaystyle {\ begin {array} {l} \ displaystyle {9n = 10n-n = 9.99999999 \ ldots -0.99999999 \ ldots = 9,} \ end {array}}}
таким образом
- n = 1. {\ Displaystyle {\ begin {array} {l} \ displaystyle {n = 1.} \ End {array}}}
База
b разложения иррациональных чисел Разложения иррациональных чисел никогда не бывают периодическими ни по какой базе. , приблизительно| 3,1415926535897932384626433832795… |

Непрерывные дроби для рациональных чисел
Все непрерывные дроби для рациональных чисел конечны (см. Категория: Непрерывные дроби для рациональных чисел).
Градуированное упорядочение рациональных чисел
Рациональные числа (в сокращенной форме)| , a ∈ ℤ, b ∈ ℤ +, |
| gcd (числитель, знаменатель) = 1 |
Гипотеза Шинцеля
В предположении гипотезы Шинцеля-Серпинского каждое положительное рациональное число может быть представлено бесконечным числом способов в виде
- ab = p + 1q + 1 {\ displaystyle {\ begin {array} {l} \ displaystyle {{\ frac {a} {b}} = {\ frac {p + 1} {q + 1}}} \ end {array}}}
и
- ab = p − 1q − 1, {\ displaystyle {\ begin {array} {l} \ displaystyle {{\ frac {a} {b}} = {\ frac {p-1} {q-1}} ,} \ end {array}}}
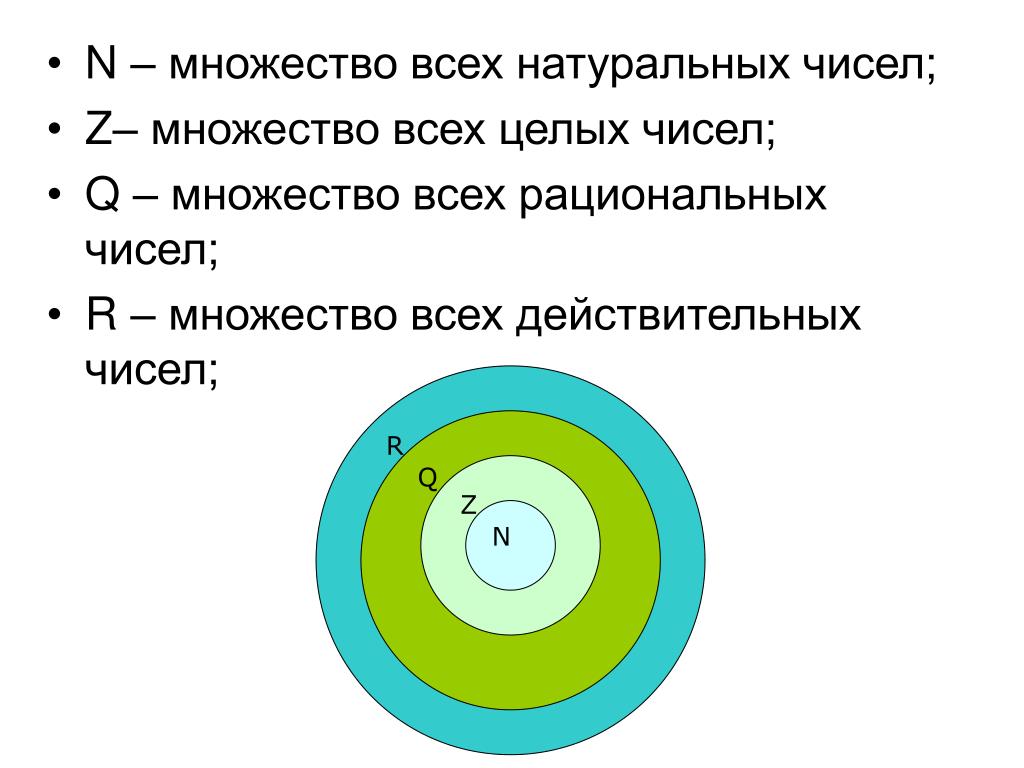
Рациональные числа среди алгебраических чисел
- Рациональные числа: алгебраические числа первой степени (целые рациональные числа: алгебраические целые числа первой степени)
- Квадратичные числа: алгебраические числа второй степени (квадратичные целые числа: алгебраические целые числа второй степени)
- Кубические числа: алгебраические числа третьей степени (кубические целые числа: алгебраические целые числа третьей степени)
- Четвертые числа: алгебраические числа четвертой степени (четвертые целые числа: алгебраические целые четвертой степени)
- Пятые числа: алгебраические числа пятой степени (пятые целые числа: алгебраические целые числа пятой степени)
- …
См. Также
Банкноты
Что такое рациональное число?
Рациональные числа
Привет, и добро пожаловать в это видео о рациональных и иррациональных числах!
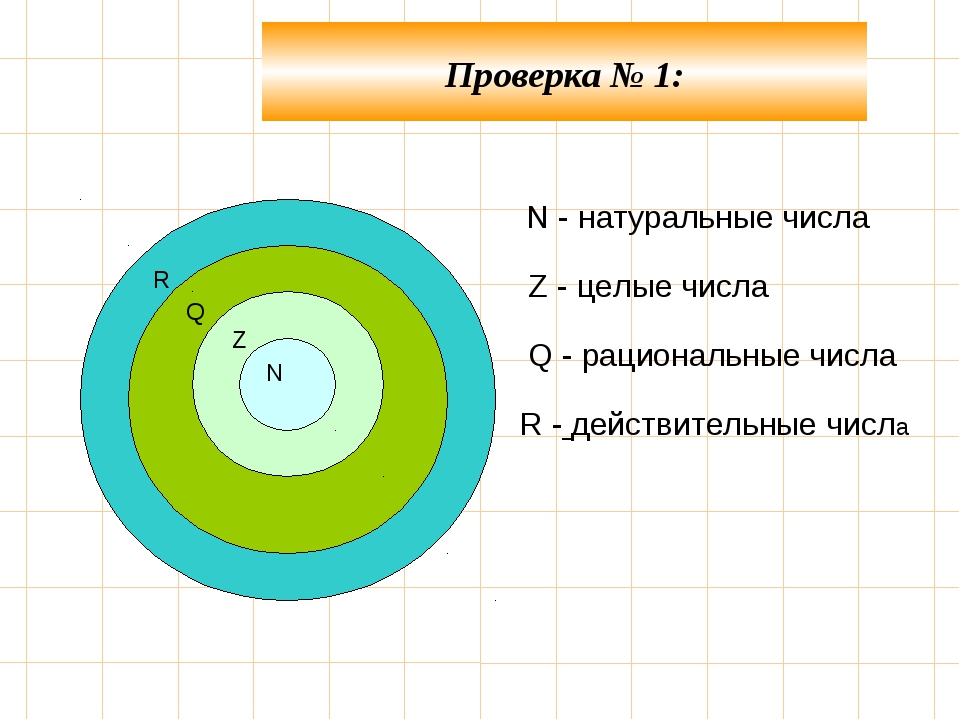
Рациональные и иррациональные числа образуют систему действительных чисел . Эта диаграмма Венна показывает визуальное представление того, как классифицируются действительные числа.
Эта диаграмма Венна показывает визуальное представление того, как классифицируются действительные числа.
натуральных чисел составляют наименьшее подмножество, которое также известно как набор «счетных» чисел.Все это положительные недесятичные значения, начинающиеся с единицы. Целые числа — это натуральные числа плюс значение нуля. Целочисленный набор чисел включает целые числа и все отрицательные, недесятичные значения.
Рациональные числа включают наборы, показанные здесь, в дополнение к дробным значениям между ними.
Легкий способ запомнить это — слово «ratio» есть в названии этой классификации. Все числа, входящие в набор рациональных чисел, могут быть записаны как отношение целых чисел:
Если a и b являются целыми числами: рациональные числа могут быть записаны как \ (\ frac {a} {b} \), если b ≠ 0.
Очевидно, что набор целых чисел можно записать как отношения, потому что любое целое число, деленное на «1», дает исходное целое число. Как показано здесь, целые числа могут быть выражены в виде дробей бесконечным числом способов.
Как показано здесь, целые числа могут быть выражены в виде дробей бесконечным числом способов.
Целое число 3 можно представить в виде дробей \ (\ frac {3} {1}, \ frac {6} {2}, \ frac {-24} {- 8} \)
Целое число -5 может быть представлены в виде следующих дробей \ (\ frac {-5} {1}, \ frac {5} {- 1}, \ frac {-25} {5} \)
, а целое число 0 может быть представлено в виде дробей \ (\ frac {0} {3}, \ frac {0} {- 2}, \ frac {0} {123} \)
Кстати, это не единственные дроби, которые приводят к этим целым числам, они это лишь некоторые из множества существующих примеров.
Примеры:
| Целое число | дробное представление |
| 3 | \ (\ frac {3} {1}, \ frac {6} {2}, \ frac {-24} {- 8} \)… |
| -5 | \ (\ frac {-5} {1}, \ frac {5} {- 1}, \ frac {-125} {5} \)… |
| 0 | \ (\ frac {0} {3}, \ frac {0} {- 2}, \ frac {0} {123} \)… |
Дроби также могут быть записаны как десятичные. Например,
Например,
.1 эквивалентно \ (\ frac {1} {10} \), потому что «1» находится в десятичном разряде «десятых»
.13 эквивалентно \ (\ frac {13} {100} \), потому что «3» находится в «сотых» десятичных разрядах, а единица — в десятых долях после запятой
. 237 эквивалентно \ (\ frac { 237} {1,000} \), потому что «7» находится в «тысячных» десятичных долях, и так далее.
Эти десятичные дроби могут быть записаны как дроби, поэтому они считаются рациональными.
Остальные десятичные числа содержат повторяющихся шаблонов. Они также считаются рациональными, потому что их можно выразить в виде дроби на основании следующего доказательства:
Повторяющаяся десятичная дробь \ (2.\ overline {17} \) представляет собой цифры 2.1717171717…
И так далее. Итак, давайте попробуем это на практике.
Пусть \ (x = 2. \ Overline {17} \) повторяется. Повторяющаяся десятичная дробь состоит из двух цифр, что соответствует сотым разрядам.
Итак, давайте умножим обе части уравнения на 100:
. В результате получим:
В результате получим:
100x = 217,17171717… ..
Что равно 217,17 повторения.
Мы перемещаем десятичную дробь на две точки, потому что мы умножили на 100.Теперь давайте вычтем исходное уравнение из этого:
100x = 217,171717…
— x = 2,171717…
—————————
Итак, у нас 99x = 215
. Обратите внимание, что повторяющаяся часть десятичной дроби сейчас устранено.
Решение для x приводит к \ (x = \ frac {215} {99} \),
Итак, у нас 99x равно 215. Обратите внимание, что повторяющаяся часть десятичной дроби теперь удалена. Решение относительно x приводит к делению обеих сторон на 99, \ (x = \ frac {215} {99} \).
Это дробное представление \ (x = 2.\ overline {17} \).
Это доказательство показывает, что повторяющиеся десятичные дроби также считаются рациональными, поскольку их можно записать как дробь целых чисел. Если вы подключите это к своему калькулятору, вы получите что-то близкое к повторению 2,17 (возможно, округленное).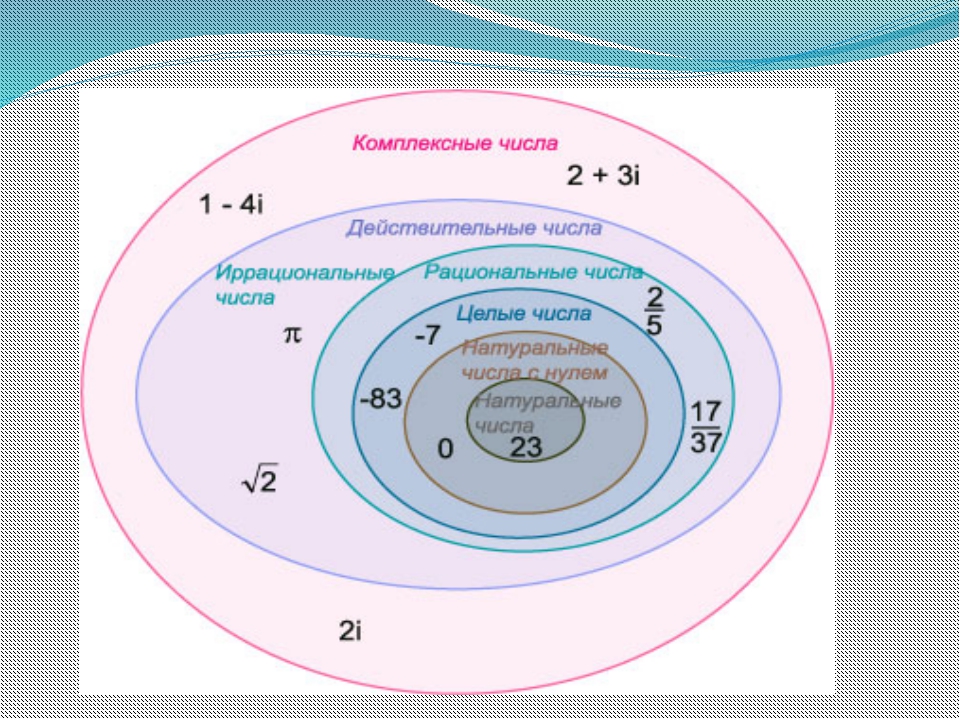
Важно отметить, что не все десятичные дроби повторяются. Некоторые десятичные дроби имеют бесконечное число из неповторяющихся цифр и, следовательно, не могут быть выражены как дробная часть целых чисел. Эти типы действительных чисел классифицируются как иррациональные .Хотя в действительной системе счисления существует бесконечное количество иррациональных чисел, в математике чаще всего используются квадратные корни из неполных квадратов, например, квадратный корень из 2, и константы π и e. Обозначение иррациональных чисел обеспечивает эффективность в математических приложениях.
Что касается геометрии, вы можете вспомнить, что π = 3,14159… для бесконечности. Это вычисляется из длины окружности любого круга и его диаметра. Поскольку десятичное значение не повторяется и бесконечно, мы используем приблизительное значение в математических приложениях.Бизнес-приложения, касающиеся непрерывно начисляемых процентов, используют иррациональное значение e, которое снова имеет приблизительное значение 2,718 для бесконечности.
Спасибо за просмотр и удачной учебы!
Классификация чисел — MathsTips.com
Ниже приведены классификации чисел.
1. Натуральные числа:
- Каждое из 1,2,3,4,… .. и т. Д. Является натуральным числом.
- Наименьшее натуральное число — 1, наибольшее натуральное число не может быть получено.
- Последовательные натуральные числа отличаются на 1.
- Позвольте быть любое натуральное число, тогда натуральные числа, которые идут сразу после, и т. Д.
2. Четные натуральные числа:
Система натуральных чисел, которые делятся на 2 или кратны 2, называется набором четных чисел.
E = (2,4,6,8,10,12 …… ..)
Есть бесконечные четные числа.
3. Нечетные натуральные числа:
Система натуральных чисел, которые не делятся на 2, называется набором нечетных чисел.
O = (1,3,5,7,9 ………)
Есть бесконечное количество нечетных чисел.
Соединяя нечетные и четные числа, мы получаем натуральные числа.
4. Целые числа:
- 0,1, 2,3,4, …… и т. Д. — целые числа.
- Наименьшее целое число равно нулю, тогда как наибольшее целое число получить невозможно.
- Целые числа, идущие подряд, отличаются на 1.
- За исключением нуля, каждое целое число является натуральным числом, поэтому:
- Каждое четное натуральное число является четным целым числом
- Каждое нечетное натуральное число является нечетным целым числом.
5. Простые числа:
- Целые числа больше 1, которые делятся только на единицу и только на себя.
- Все остальные простые числа, кроме 2, нечетные. P = 2,3,5,7,11,13, ………. пр.
6. Составные номера:
Составное число — это целое число (больше 1), которое не является простым.
Составные числа C = (4,6,8,9 …… .. и т. Д.)
7. Целые числа:
- Целые числа состоят из натуральных чисел, нуля и отрицательного числа из натуральных чисел.
 Таким образом, Z или I = …………………, -4, -3, -2, -1, 0, 1,2,3,4 …………….
Таким образом, Z или I = …………………, -4, -3, -2, -1, 0, 1,2,3,4 ……………. - Есть бесконечные целые числа в положительную сторону и бесконечные целые числа в отрицательную сторону.
- Положительные целые числа — это натуральные числа.
Использование целых чисел
Целые числа используются для математического выражения наших повседневных ситуаций.
- Если прибыль представлена целыми положительными числами, тогда потери — отрицательными целыми числами.
- Если высота над уровнем моря выражается положительными целыми числами, то глубины ниже уровня моря выражаются отрицательными целыми числами.
- Если рост цены представлен целыми положительными числами, то падение цены — отрицательными целыми числами и так далее.
8. Рациональные числа:
Любое число, которое может быть выражено в форме, где a и b оба являются целыми числами, а, — рациональным числом.
- — рациональное число, поскольку 2, 5 — целые числа, а 5 не равно нулю.

- и т. Д. Не являются рациональными числами, поскольку эти числа не могут быть выражены как.
Итак, мы можем сказать, что рациональные числа содержат все целые числа и все дроби (включая десятичные).Существует бесконечное количество рациональных чисел.
- Каждое целое число является рациональным числом, но обратное неверно. Тот же результат верен для натуральных чисел, целых чисел, дробей и т. Д.
9. Иррациональные числа:
Тогда числа, которые не являются рациональными, называются иррациональными числами.
Каждое из и т.д. — это иррациональное число.
Число не является ни рациональным, ни иррациональным, если.
10. Реальные числа:
Каждое число, которое является рациональным или иррациональным, называется действительным числом.
- Каждое натуральное число является действительным числом.
- Каждое целое число является действительным числом.
- Каждое целое число является действительным числом.

- Каждое рациональное число является действительным числом.
- Каждое иррациональное число является действительным числом и т. Д.
Абсолютное значение числа:
Абсолютным значением целого числа является его числовое значение независимо от его знака.
Абсолютное значение
Абсолютное значение
Следовательно, если представляет собой целое число, его абсолютное значение представлено и всегда неотрицательно
Помните:
- , когда положительный или нулевой
- , когда отрицательно.
Рациональное определение числа
Рациональное число — это любое число, которое может быть выражено как отношение двух целых чисел (отсюда и название «рациональное»). Его можно записать в виде дроби, в которой верхнее число (числитель) делится на нижнее число (знаменатель).
Все целые числа являются рациональными числами, так как их можно разделить на 1, что дает отношение двух целых чисел. Многие числа с плавающей запятой также являются рациональными числами, поскольку их можно выразить дробями.Например, 1,5 является рациональным, поскольку его можно записать как 3/2, 6/4, 9/6 или другую дробь или два целых числа. Пи (π) равно иррациональным , так как оно не может быть записано в виде дроби.
Многие числа с плавающей запятой также являются рациональными числами, поскольку их можно выразить дробями.Например, 1,5 является рациональным, поскольку его можно записать как 3/2, 6/4, 9/6 или другую дробь или два целых числа. Пи (π) равно иррациональным , так как оно не может быть записано в виде дроби.
Число с плавающей запятой является рациональным, если оно соответствует одному из следующих критериев:
- он имеет ограниченное количество цифр после десятичной точки (например, 5,4321)
- он имеет бесконечно повторяющееся число после десятичной точки (например, 2.333333 …)
- он имеет бесконечно повторяющийся образец чисел после десятичной точки (например,грамм. 3,151515 …)
Если числа после десятичной точки повторяются бесконечно без единого образца, это означает, что число не является рациональным или «иррациональным». Ниже приведены примеры рациональных и иррациональных чисел.
- 1 — рациональный
- 0,5 — рациональное
- 2.
 0 — рациональный
0 — рациональный - √2 — иррациональный
- 3,14 — рациональный
- π (3,14159265359 …) — иррациональное
- √4 — рациональный
- √5 — иррациональный
- 16/9 — рациональное
- 1000000.0000001 — рациональный
В информатике важно, является ли число рациональным или иррациональным. Рациональное число может быть сохранено как точное числовое значение, а иррациональное число должно быть оценено.
ПРИМЕЧАНИЕ: Число ноль (0) является рациональным числом, потому что его можно записать как 0/1, что равно 0.
Обновлено: 5 июня 2018 г.
TechTerms — Компьютерный словарь технических терминов
Эта страница содержит техническое определение Rational Number.Он объясняет в компьютерной терминологии, что означает Rational Number, и является одним из многих технических терминов в словаре TechTerms.
Все определения на веб-сайте TechTerms составлены так, чтобы быть технически точными, но также простыми для понимания.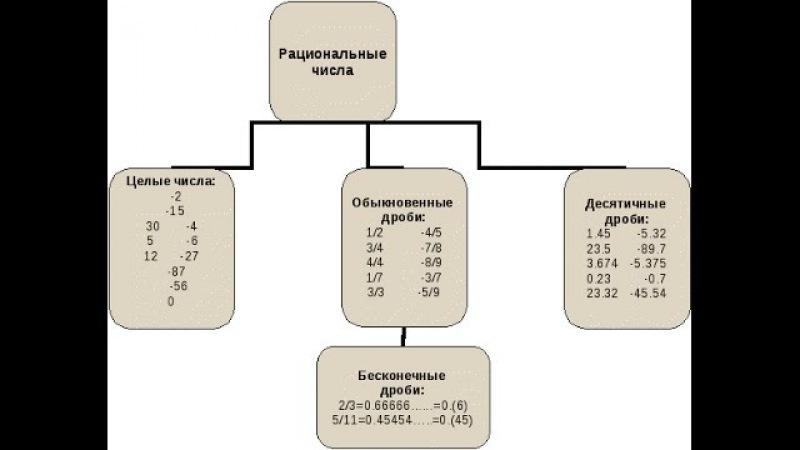

 Такая фраза поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус».
Такая фраза поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус».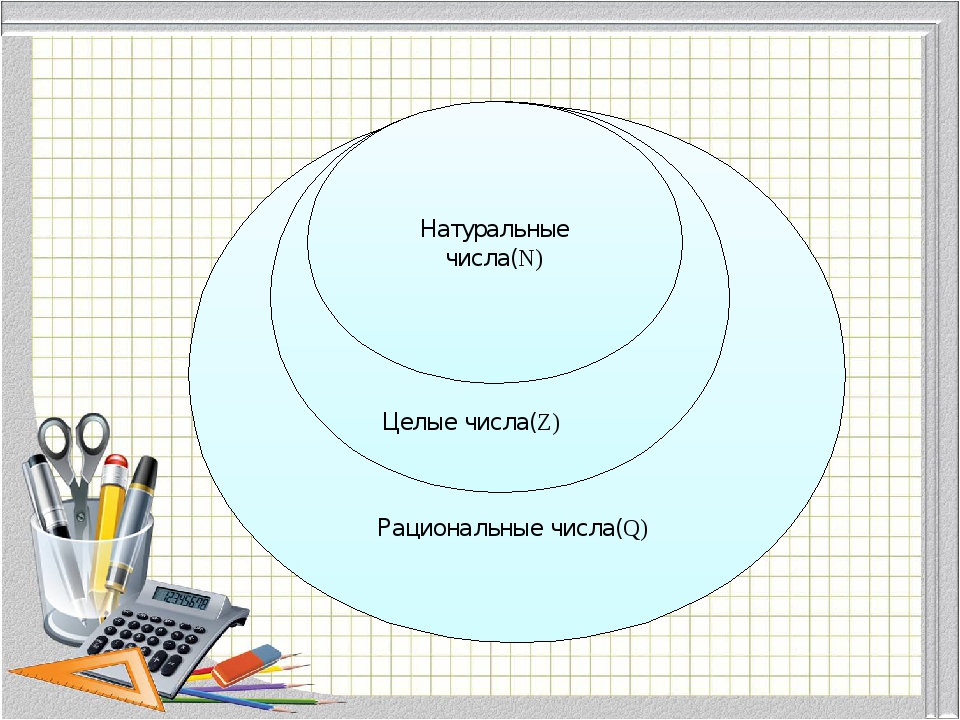

 е. числами противоположными натуральным). Мы получим множество целых чисел. Надо заметить, что при сложении, вычитании, умножении целых чисел, всегда образуются целые числа. Однако частное двух целых чисел, не обязятельно будет целым числом.
е. числами противоположными натуральным). Мы получим множество целых чисел. Надо заметить, что при сложении, вычитании, умножении целых чисел, всегда образуются целые числа. Однако частное двух целых чисел, не обязятельно будет целым числом.

 Записать в виде десятичной дроби:
Записать в виде десятичной дроби: 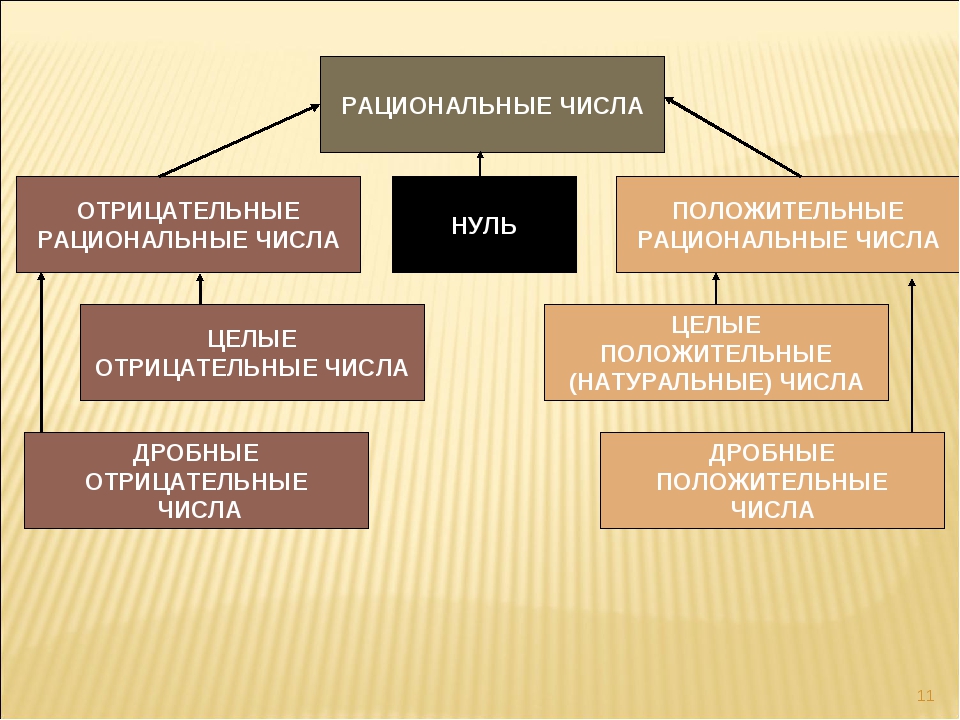 Вычислить:
Вычислить: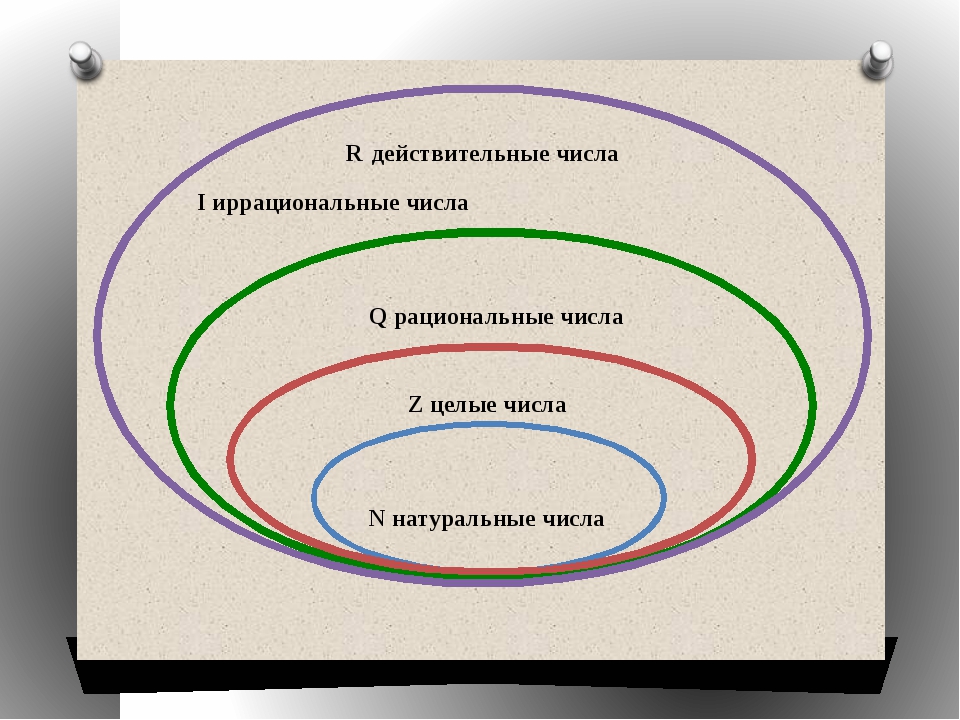 сумма цифр этого числа делится на 9
сумма цифр этого числа делится на 9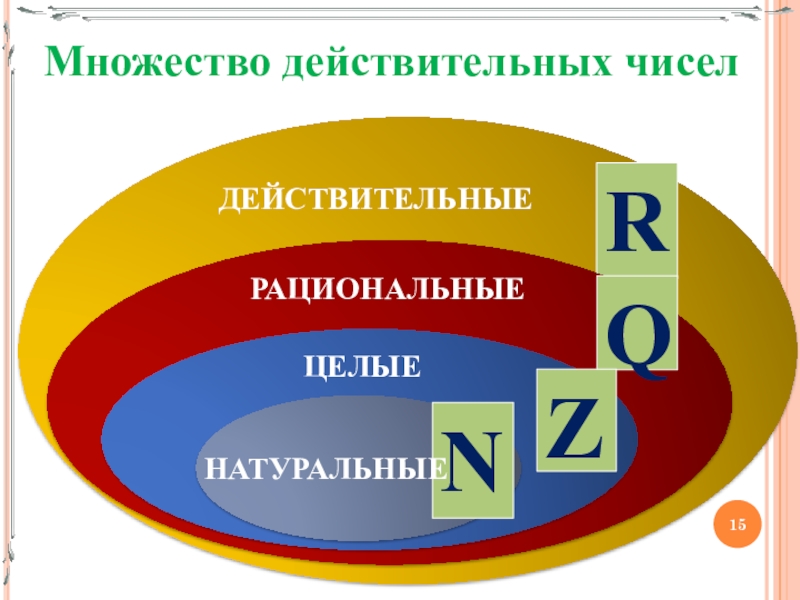 Поэтому, умножая обе части последнего равенства на находим
Поэтому, умножая обе части последнего равенства на находим Распространенный вопрос: «Повторяются ли десятичные дроби рациональными числами?» Ответ положительный!
Распространенный вопрос: «Повторяются ли десятичные дроби рациональными числами?» Ответ положительный!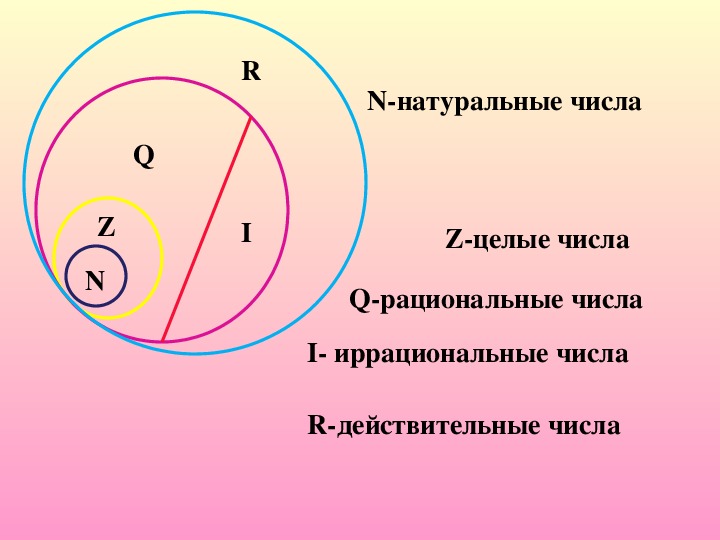
 Таким образом, Z или I = …………………, -4, -3, -2, -1, 0, 1,2,3,4 …………….
Таким образом, Z или I = …………………, -4, -3, -2, -1, 0, 1,2,3,4 …………….
 0 — рациональный
0 — рациональный