3.4. Решение примера
3.4.1. Дана структурная схема, которая изображена на рис.3.1. Требуется, пользуясь критерием устойчивости Рауса-Гурвица:
а) исследовать устойчивость системы при К = 10 с -1 ;
б) определить критическое значение К кр общего коэффициента усиления разомкнутой системы.
X(p)
Y(p)
+
Рис.3.1
Решение
Исследование устойчивости системы при К = 10 1/с :
а) определение характеристического полинома А(p) и проверка положительности коэффициентов а i :
;
A(p) = p (p
+ 1) 2 (0,2
p + 1) + K (2 p +1) = 0,2 p
а 0 = K = 10 > 0 ; а 1 = 1 + 2K = 21 > 0 ; а 2 = 2,2 > 0 ; а 3 = 1,4 >0 ; а 4 = 0,2 > 0;
б) исследование устойчивости системы, составление определителя Гурвица :
Для системы 4-го порядка справедливо следующее неравенство :
а 3 (а 1 а 2 — а 0а 3) — а 4а 12 > 0 ,
1,4 (21 2,2 — 10 1,4) — 0,2 441 > 0 ; — 43,12 > 0,
что несправедливо. Это значит, что система неустойчива при К = 10 1/с .
Определение К кр.Определяется из условия равенства нулю определителя или известного неравенства (для системы с 1-го по 4-й порядок характеристического полинома). К кр = 4,975 1/с.
а 3 (а 1 а 2 — а 0а 3) — а 4а 12 = 0.
1,4 [(1+2K) 2,2 — 1,4 K] — 0,2 (1 + 2 K) 2 = 2,88 + 3,4 K — 0,8 K 2 = 0 .
3.4.2. Исследовать на устойчивость систему автоматического регулирования по критерию Рауса -Гурвица и построить области устойчивости по двум параметрам, если передаточная функция разомкнутой системы имеет вид : .
Решение
Характеристическое уравнение найдем с помощью выражения :
;
;
A(p) = T1 T2 p3 + (T1 + T2 ) p2 + p + K = 0,
откуда получим
Из этого выражения найдем определители Гурвица
; ; 3 = 2 .
Отсюда условия устойчивости будут:
; ; .
Так как Т1 > 0, T2 > 0, K > 0 , то остается одно условие устойчивости
, которое сводится к неравенству .
С помощью неравенства построим границу устойчивости системы по параметрам К и Т1 при Т2 = 0,5 с (см.рис.3.2, а) ; К и Т2 при Т1 = 0,005 с (см.рис.3.2, б). На этих рисунках области устойчивости заштрихованы.
а) б)
Рис.3.2
3.5.Частотный критерий устойчивости Найквиста
Данный критерий позволяет исследовать устойчивость замкнутой системы, структурная схема которой имеет вид, показанный на рис.3.3, по годографу частотной характеристики разомкнутой системы:
.
X(p)
Y(p)
Рис.3.3
Предположим, что разомкнутая система устойчива. Тогда частотный критерий Найквиста формулируется следующим образом: если разомкнутая система устойчива, то для того, чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы годограф разомкнутой системы при изменении от 0 до не охватывал точку с координатами (- 1; j0) (см.рис.3.4).
Рис.3.4
Если годограф АФХ проходит через точку (- 1; j0) , то система находится на границе устойчивости. Годограф АФХ разомкнутой системы , содержащий интегрирующие звенья, при 0 уходит в бесконечность вдоль одной из осей. В этом случае для определения устойчивости по критерию Найквиста, необходимо дополнить годограф АФХ дугой достаточно большого радиуса, как показано на рис.3.5 пунктирной линией. Дугу следует вести от АФХ до вещественной оси против часовой стрелки. Формулировка критерия в этом случае остается неизменной.
При определении устойчивости по логарифмическим частотным характеристикам для систем, устойчивых в разомкнутом состоянии, частотный критерий Найквиста формулируется следующим образом: для того, чтобы система , устойчивая в разомкнутом состоянии, была устойчива в замкнутом состоянии, необходимо и достаточно при положительных значениях логарифмической амплитудной частотной характеристики разность числа переходов логарифмической фазовой частотной характеристики через ось — сверху вниз и снизу вверх была равна нулю, или должно выполняться условие с < — (см.рис.3.6).
Рис.3.5 Рис.3.6
Устойчивые системы обладают запасами устойчивости:
по фазе и определяются равенством (рис.3.6)
з = 180 0 — ( c) ,
где c — частота среза, на которой L() = 0 [A() = 1];
по амплитуде и определяются равенством (см.рис.3.6)
L з = — L( ) ,
где — частота, удовлетворяющая условию
( ) = arg W(j ) = — 180 0 .
studfiles.net
3.4. Решение задачи 4
Решение нелинейных уравнений вида F(x)=0заключается в поиске одного или всех таких значенийxна интервале [a,b], при подстановке которых функцияF(x)обращается в нуль.
Работу по решению этой задачи целесообразно провести в два этапа.
На первом этапе оценивается характер изменения функции F(x)при изменении аргументаxна интервале [a,b] и проверяется, имеет ли место перемена ее знака (переход через нуль). Количество таких переходов определяет и количество корней.
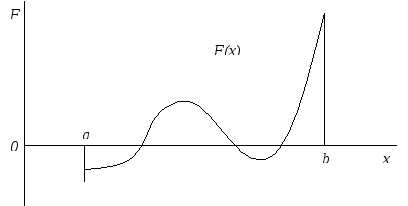
Рис. 3. Графическое представление функции F(x)
Для этого интервал [ a,b] разбивается наnучастков, гдеnпринимается равным 10..15, и вычисляется функцияF(x)на каждом участке, т.е. при измененииxотa доbс шагомh=(b—a)/n.
Из полученной таким образом таблицы будет виден и характер изменения функции, и количество переходов через нуль.
На втором этапе путем последовательных приближений производится поиск корней одним из предлагаемых методов.
Метод итерацийоснован на последовательном задании аргументаxи вычислении по нему функцииF1(x), причем очередное значениеxприращивается предыдущему значению функцииx(n+1)=F1(x(n))до тех пор, пока соблюдается условие|x(
Метод половинного деления (дихотомии)состоит в следующем.
Определяем начальное значение x=(a+b)/2(как результат деления интервала [a,b] пополам).
Вычисляем F(x).
Если F(x)>0 иF(a)>0 илиF(x)<0 иF(a)<0(т.е. перемена знака функцииF(x)не произошла), то задаемa=x(т.е. перемещаем левую границу интервала в середину), уменьшая интервал вдвое и исключая при этом левую половину, на которой либо нет корней, либо есть четное число корней, иначе задаем b=x(исключаем правую половину интервала). См. рис. 4.
Проверяем условие b—a<E, если оно выполняется, то возвращаемся к п.1. с новыми значениями границ интервала, иначе заканчиваем вычисления и считаем, что последнее значениеx и будет корнем уравнения с заданной точностьюE.

Рис.4. Геометрическое представление метода половинного деления
Метод Ньютона (касательных)основан также на последовательном задании значенийxи вычислении функцииF(x), причем очередное значениеxопределяется формулой:
x(n+1)=x(n)-F(x(n))/F’(x(n))
где F’(x(n))– производная от функцииF(x)в точкеx(n).
Геометрически производная от F(x), как известно, по величине равна тангенсу угла наклона касательной к кривойF(x)в точкеx. Тогда точкаx(n+1)есть точка пересечения с осью абсцисс касательной к кривойF(x), проведенной в точкеx=x(n). См. рис. 5.

Рис. 5. Геометрическое представление метода Ньютона
Как и в методе итераций, начальное значение xзадается как ближайшее табличное к месту перехода функцииF(x)через нуль.
Выражение для производной F’(x)получают аналитически в результате дифференцирования функцииF(x). Значение производной может быть получено приближенно и численным методом:
F’(x)=(F(x+E)-F(x))/E.
Итерационный процесс приближения к корню (последовательное вычисление x(n+1)) продолжается до тех пор, пока будет выполняться условие|x(n+1)-x(n)|>=E.
Следует иметь ввиду, что при выполнении задания и алгоритм, и программа должны предусматривать оба этапа работы: табулирование функции F(x)с выбором начального приближения и процесс поиска корней с заданной точностью.
studfiles.net
4.3. Решение уравнений состояния методом Гаусса
60
точности. К итерационным методам относится метод простой итерации, метод Зейделя, градиентные методы.
Воснове практически всех прямых методов решения линейных систем -алгебраических уравнений установившихся режимов электрических систем лежит метод Гаусса или его модификации.
4.3.1. Метод Гаусса с обратным ходом
Это наиболее рациональный и распространенный метод решения систем уравнений произвольного порядка, реализующий последовательное исключение переменных и затем последующую подстановку для получения решений.
Решение системы n алгебраических уравнений вида
AX = в
по данному алгоритму состоит из двух этапов. На первом этапе в результате преобразований, заключающихся в исключении всех неизвестных, расположенных ниже главной диагонали, матрица коэффициентов А превращается в верхнюю треугольную, а последнее уравнение оказывается разрешенным относительно неизвестного. На втором этапе определяются все неизвестные системы уравнений.
Рассмотрим применение метода Гаусса на примере системы из трех уравне-
ний:
a11x1+ a12x2+ a13x3= b1 |
|
a21x1+ a22x2+ a23x3= b2 | (4.1) |
a31x1+ a32x2+ a33x3= b3 |
|
При исключении по методу Гаусса применяется стандартная операция, которая позволяет упорядочить исключение и получить удобный алгоритм для реализации этого метода на ЭВМ.
Решение состоит в том, что на каждом шаге преобразования системы (число шагов равно (n -1),гдеn — порядок решаемой системы) исключается одна из переменных из всех нижестоящих уравнений системы. Особенностью метода является то, что для проведения операции исключения на каждом шаге используется главный диагональный элемент, каковым является коэффициент при исключаемом неизвестном в главном уравнении, т.е. в уравнении, в котором это неизвестное остается.
Так как главный диагональный элемент входит в коэффициент преобразования в знаменателе, то обязательным условием возможности применения этого метода является неравенство нулю главного диагонального элемента на каждом шаге преобразований. Если все же он оказался равным нулю, то перед выполнением
61
очередного шага уравнения преобразуемой системы должны быть так переставлены, чтобы главный диагональный элемент не оказался нулевым.
Первый шаг. Будем считать, чтоa11 ¹ 0 . Запишем коэффициенты преобразования для каждого уравнения. Первое уравнение является главным, из второго и третьего исключается неизвестноеx1 .
m(1 ) | = | a21 | ; m(1) | = | a31 | . |
|
| |||||
2 |
| a11 | 3 |
| a11 | |
|
|
|
| |||
Чтобы исключить из второго уравнения неизвестноеx1 , умножим первое уравне-
ние на коэффициент m2(1) и вычтем результат из второго уравнения:
æ | (1) | ö | æ | (1) | ö |
| æ | (1) | ö | (1) | × b1 |
ça21 | — m2 | × a11÷x1 | + ça22 -m2 | × a12÷x2 | + ça23 | — m2 | × a13÷x3 | = b2 -m2 | |||
è |
| ø | è |
| ø |
| è |
| ø | 1442443 | |
144424443 | 144424443 |
| 144424443 | b2(1 ) |
| ||||||
| 0 |
|
| a22(1 ) |
|
|
| a23(1 ) |
|
| |
| Для исключения | неизвестного x1 | из третьего уравнения умножим | первое | |||||||
уравнение на коэффициент m3(1) и результат умножения вычтем из третьего уравнения:
(a | 31 | — m(1) ×a | )x+ (a | 32 | — m(1) ×a | )x | 2 | + (a -m(1) | × a | )x= b- m(1) | × b | |||||||
| 3 | 11 | 1 |
|
| 3 | 12 |
| 33 | 3 | 13 | 3 | 3 | 3 | 1 | |||
1442443 | 1442443 |
| 1442443 | 14243 | ||||||||||||||
|
| 0 |
|
|
|
| a | (1 ) |
|
|
| a | (1 ) |
|
|
| b(1 ) |
|
|
|
|
|
|
|
|
| 32 |
|
|
|
| 33 |
|
|
| 3 |
|
Таким образом, исходная система уравнений преобразуется к виду: |
| |||||||||||||||||
|
|
|
|
|
|
|
| a11x1+ a12x2+ a13x3= b1 |
|
|
|
| ||||||
|
|
|
|
|
|
|
| 0 ×x1 +a22(1 )x2 +a23(1 )x3 =b2(1 ) |
|
|
| (4.2) | ||||||
|
|
|
|
|
|
|
| 0 ×x1 +a32(1 )x2 +a33(1 )x3 =b3(1 ) |
|
|
|
| ||||||
Второй шаг. Аналогичные преобразования производятся при условии, что главным уравнением является второе уравнение, так как будет исключаться второе неизвестное из уравнения ниже второго. Главным элементом будет считаться
элемент a22(1). Операция производится совершенно аналогично первому шагу. По-
скольку рассматривается система из трех уравнений, то преобразованию подвергается только третье уравнение.
Определим коэффициент преобразования для третьего уравнения:
(2 )a(1)
m = 32( ) . 3 a221
Умножим коэффициент m3(2) на второе уравнение и результат умножения вычтем из третьего уравнения:
0 ×x +(a (1) | — m(2) | × a | (1))x | 2 | + (a | (1) | — m(2) | × a | 23 | )x | 3 | = b(1) | — m(2) | ×b | (1). | |
1 | 32 | 3 |
| 22 |
| 33 | 3 |
|
| 3 | 3 |
| 2 | |||
| 1442443 |
| 1442443 |
| 1442443 | |||||||||||
|
| 0 |
|
|
|
|
| a(2 ) |
|
|
|
|
| b(2 ) |
|
|
|
|
|
|
|
|
|
| 33 |
|
|
|
|
| 3 |
|
|
В результате получим:
62
a11x1+ a12x2+ a13x3= b1 |
|
0 ×x1 +a22(1 )x2 +a23(1 )x3 =b2(1 ) | (4.3) |
0 ×x1 +0 ×x2 +a33(2 )x3 =b3(2 ) |
|
На этом заканчивается первый этап решения(прямой ход), так как все коэффициенты ниже главной диагонали нулевые.
Обратный ход (второй этап, процесс подстановки):
|
|
|
|
|
|
| b(2) |
|
|
|
|
|
|
|
| ||||
|
|
|
|
| x = |
| 3 |
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
| 3 |
| a | (2 ) |
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| 33 |
|
|
|
|
|
|
|
|
| |
|
|
| æ |
|
|
|
|
|
| b(2 )ö |
|
| 1 |
| |||||
| x |
| = çb(1 ) -a | (1 ) | × |
|
| 3 | ÷ | × |
|
|
|
| |||||
| 2 | 23 |
|
|
|
| a | (1 ) |
| ||||||||||
|
| ç | 2 |
|
|
| a | (2 )÷ |
|
| |||||||||
|
|
| è |
|
|
|
|
|
|
|
|
| 33 | ø |
|
|
| 22 |
|
x | = | 1 | (b | — a |
|
| × x | 2 | — a |
|
| × x ). | |||||||
|
|
|
|
| |||||||||||||||
1 |
|
| a11 | 1 | 12 |
|
|
|
| 13 |
| 3 | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Для данного метода может быть использована модификация – преобразуются не только ниже стоящие уравнения по отношению к главному, но и само глав-
ное уравнение. В этом случае главный диагональный элемент превращается в единицу.
Рассмотренная последовательность выполнения операций достаточно легко реализуется с помощью ЭВМ.
4.3.2.Метод Гаусса без обратного хода (метод Жордана)
Вотличие от метода Гаусса с обратным ходом, метод Гаусса без обратного хода в процессе реализации прямого хода решения разрешает систему относительно неизвестных, то есть уже к концу прямого хода фактически получается решение системы уравнений, и нет необходимости в обратной подстановке. Реализация этого метода совершенно аналогична методу Гаусса с обратным ходом. Отличие состоит лишь в том, что операции по исключению неизвестных ведутся не только с элементами, стоящими ниже диагонали, но и с элементами, стоящими выше диагонали.
Как и в методе Гаусса с обратным ходом, необходимым условием является неравенство нулю главного диагонального элемента.
Рассмотрим данный метод на примере решения системы из трех уравнений
(4.1):
a11x1+ a12x2+ a13x3= b1a21x1+ a22x2+ a23x3= b2
a31x1+ a32x2+ a33x3= b3.
Первый шаг. Определим коэффициенты преобразований для второго и третьего уравнений:
63
m2(1) = a21, a11
m3(1) = a31. a11
Умножая поочередно первое уравнение на коэффициенты m2(1) и m3(1) и вы-
читая результат соответственно из второго и третьего уравнений, получим:
a11x1+ a12x2+ a13x3= b10x1+ a22(1 )x2+ a23(1 )x3= b2(1 )
0x1+ a32(1 )x2+ a33x3(1 ) = b3(1 ).
Второй шаг. Для исключения неизвестногох2 из первого и третьего уравнений определим соответствующие коэффициенты преобразований:
m(2 )= | a12 | , |
|
|
|
|
| ||||
a22(1 ) |
|
|
|
|
| ||||||
1 |
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
| |
(2 ) |
|
| a32(1 ) |
|
|
|
|
|
|
| |
m2 | = |
|
|
| . |
|
|
|
|
| |
| a22(1 ) |
|
|
| и m(2) |
| |||||
|
|
|
|
|
|
|
|
| |||
Умножая второе уравнение поочередно на m(2) |
| и вычитая результат | |||||||||
|
|
|
|
|
|
|
| 1 |
| 3 |
|
умножения соответственно из первого и третьего уравнений, получим: | |||||||||||
a x | + 0x | 2 | + a(2)x | = b(2) |
| ||||||
11 | 1 |
|
|
| 13 | 3 | 1 |
| |||
0x | + a(1 )x | 2 | + a | (1 )x | = b(1 ) | (4.4) | |||||
1 |
| 22 |
|
| 23 | 3 | 2 |
| |||
0x | + 0x | 2 | + a(2 )x | = b(2 ). |
| ||||||
1 |
|
|
|
|
| 33 | 3 |
| 3 |
| |
Третий шаг. Определим коэффициенты преобразований для первого и второго уравнений:
m(3 )= | a (2) |
| ||
13 | , | |||
1 |
| a22(1 ) |
| |
|
|
| ||
(3 ) |
| a23(1 ) |
| |
m2 | = |
| . | |
a33(2 ) | ||||
|
|
| ||
В результате произведения операций, аналогичных выполненным на первом и втором шагах, получим:
a x | + 0x | 2 | + | 0x |
| = b(3) |
| |||
11 | 1 |
|
|
| 3 | 1 |
| |||
0x | + a(1 )x | 2 | + 0x |
| = b(3 ) | (4.5) | ||||
1 |
| 22 |
|
| 3 | 2 |
| |||
0x | + 0x | 2 | + a | (2 )x | 3 | = b(2 ). |
| |||
1 |
|
|
|
|
| 33 | 3 |
| ||
studfiles.net
4.3. Решение уравнений состояния методом Гаусса
60
точности. К итерационным методам относится метод простой итерации, метод Зейделя, градиентные методы.
Воснове практически всех прямых методов решения линейных систем -алгебраических уравнений установившихся режимов электрических систем лежит метод Гаусса или его модификации.
4.3.1. Метод Гаусса с обратным ходом
Это наиболее рациональный и распространенный метод решения систем уравнений произвольного порядка, реализующий последовательное исключение переменных и затем последующую подстановку для получения решений.
Решение системы n алгебраических уравнений вида
AX = в
по данному алгоритму состоит из двух этапов. На первом этапе в результате преобразований, заключающихся в исключении всех неизвестных, расположенных ниже главной диагонали, матрица коэффициентов А превращается в верхнюю треугольную, а последнее уравнение оказывается разрешенным относительно неизвестного. На втором этапе определяются все неизвестные системы уравнений.
Рассмотрим применение метода Гаусса на примере системы из трех уравне-
ний:
a11x1+ a12x2+ a13x3= b1 |
|
a21x1+ a22x2+ a23x3= b2 | (4.1) |
a31x1+ a32x2+ a33x3= b3 |
|
При исключении по методу Гаусса применяется стандартная операция, которая позволяет упорядочить исключение и получить удобный алгоритм для реализации этого метода на ЭВМ.
Решение состоит в том, что на каждом шаге преобразования системы (число шагов равно (n -1),гдеn — порядок решаемой системы) исключается одна из переменных из всех нижестоящих уравнений системы. Особенностью метода является то, что для проведения операции исключения на каждом шаге используется главный диагональный элемент, каковым является коэффициент при исключаемом неизвестном в главном уравнении, т.е. в уравнении, в котором это неизвестное остается.
Так как главный диагональный элемент входит в коэффициент преобразования в знаменателе, то обязательным условием возможности применения этого метода является неравенство нулю главного диагонального элемента на каждом шаге преобразований. Если все же он оказался равным нулю, то перед выполнением
61
очередного шага уравнения преобразуемой системы должны быть так переставлены, чтобы главный диагональный элемент не оказался нулевым.
Первый шаг. Будем считать, чтоa11 ¹ 0 . Запишем коэффициенты преобразования для каждого уравнения. Первое уравнение является главным, из второго и третьего исключается неизвестноеx1 .
m(1 ) | = | a21 | ; m(1) | = | a31 | . |
|
| |||||
2 |
| a11 | 3 |
| a11 | |
|
|
|
| |||
Чтобы исключить из второго уравнения неизвестноеx1 , умножим первое уравне-
ние на коэффициент m2(1) и вычтем результат из второго уравнения:
æ | (1) | ö | æ | (1) | ö |
| æ | (1) | ö | (1) | × b1 |
ça21 | — m2 | × a11÷x1 | + ça22 -m2 | × a12÷x2 | + ça23 | — m2 | × a13÷x3 | = b2 -m2 | |||
è |
| ø | è |
| ø |
| è |
| ø | 1442443 | |
144424443 | 144424443 |
| 144424443 | b2(1 ) |
| ||||||
| 0 |
|
| a22(1 ) |
|
|
| a23(1 ) |
|
| |
| Для исключения | неизвестного x1 | из третьего уравнения умножим | первое | |||||||
уравнение на коэффициент m3(1) и результат умножения вычтем из третьего уравнения:
(a | 31 | — m(1) ×a | )x+ (a | 32 | — m(1) ×a | )x | 2 | + (a -m(1) | × a | )x= b- m(1) | × b | |||||||
| 3 | 11 | 1 |
|
| 3 | 12 |
| 33 | 3 | 13 | 3 | 3 | 3 | 1 | |||
1442443 | 1442443 |
| 1442443 | 14243 | ||||||||||||||
|
| 0 |
|
|
|
| a | (1 ) |
|
|
| a | (1 ) |
|
|
| b(1 ) |
|
|
|
|
|
|
|
|
| 32 |
|
|
|
| 33 |
|
|
| 3 |
|
Таким образом, исходная система уравнений преобразуется к виду: |
| |||||||||||||||||
|
|
|
|
|
|
|
| a11x1+ a12x2+ a13x3= b1 |
|
|
|
| ||||||
|
|
|
|
|
|
|
| 0 ×x1 +a22(1 )x2 +a23(1 )x3 =b2(1 ) |
|
|
| (4.2) | ||||||
|
|
|
|
|
|
|
| 0 ×x1 +a32(1 )x2 +a33(1 )x3 =b3(1 ) |
|
|
|
| ||||||
Второй шаг. Аналогичные преобразования производятся при условии, что главным уравнением является второе уравнение, так как будет исключаться второе неизвестное из уравнения ниже второго. Главным элементом будет считаться
элемент a22(1). Операция производится совершенно аналогично первому шагу. По-
скольку рассматривается система из трех уравнений, то преобразованию подвергается только третье уравнение.
Определим коэффициент преобразования для третьего уравнения:
(2 )a(1)
m = 32( ) . 3 a221
Умножим коэффициент m3(2) на второе уравнение и результат умножения вычтем из третьего уравнения:
0 ×x +(a (1) | — m(2) | × a | (1))x | 2 | + (a | (1) | — m(2) | × a | 23 | )x | 3 | = b(1) | — m(2) | ×b | (1). | |
1 | 32 | 3 |
| 22 |
| 33 | 3 |
|
| 3 | 3 |
| 2 | |||
| 1442443 |
| 1442443 |
| 1442443 | |||||||||||
|
| 0 |
|
|
|
|
| a(2 ) |
|
|
|
|
| b(2 ) |
|
|
|
|
|
|
|
|
|
| 33 |
|
|
|
|
| 3 |
|
|
В результате получим:
62
a11x1+ a12x2+ a13x3= b1 |
|
0 ×x1 +a22(1 )x2 +a23(1 )x3 =b2(1 ) | (4.3) |
0 ×x1 +0 ×x2 +a33(2 )x3 =b3(2 ) |
|
На этом заканчивается первый этап решения(прямой ход), так как все коэффициенты ниже главной диагонали нулевые.
Обратный ход (второй этап, процесс подстановки):
|
|
|
|
|
|
| b(2) |
|
|
|
|
|
|
|
| ||||
|
|
|
|
| x = |
| 3 |
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
| 3 |
| a | (2 ) |
|
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
|
| 33 |
|
|
|
|
|
|
|
|
| |
|
|
| æ |
|
|
|
|
|
| b(2 )ö |
|
| 1 |
| |||||
| x |
| = çb(1 ) -a | (1 ) | × |
|
| 3 | ÷ | × |
|
|
|
| |||||
| 2 | 23 |
|
|
|
| a | (1 ) |
| ||||||||||
|
| ç | 2 |
|
|
| a | (2 )÷ |
|
| |||||||||
|
|
| è |
|
|
|
|
|
|
|
|
| 33 | ø |
|
|
| 22 |
|
x | = | 1 | (b | — a |
|
| × x | 2 | — a |
|
| × x ). | |||||||
|
|
|
|
| |||||||||||||||
1 |
|
| a11 | 1 | 12 |
|
|
|
| 13 |
| 3 | |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Для данного метода может быть использована модификация – преобразуются не только ниже стоящие уравнения по отношению к главному, но и само глав-
ное уравнение. В этом случае главный диагональный элемент превращается в единицу.
Рассмотренная последовательность выполнения операций достаточно легко реализуется с помощью ЭВМ.
4.3.2.Метод Гаусса без обратного хода (метод Жордана)
Вотличие от метода Гаусса с обратным ходом, метод Гаусса без обратного хода в процессе реализации прямого хода решения разрешает систему относительно неизвестных, то есть уже к концу прямого хода фактически получается решение системы уравнений, и нет необходимости в обратной подстановке. Реализация этого метода совершенно аналогична методу Гаусса с обратным ходом. Отличие состоит лишь в том, что операции по исключению неизвестных ведутся не только с элементами, стоящими ниже диагонали, но и с элементами, стоящими выше диагонали.
Как и в методе Гаусса с обратным ходом, необходимым условием является неравенство нулю главного диагонального элемента.
Рассмотрим данный метод на примере решения системы из трех уравнений
(4.1):
a11x1+ a12x2+ a13x3= b1a21x1+ a22x2+ a23x3= b2
a31x1+ a32x2+ a33x3= b3.
Первый шаг. Определим коэффициенты преобразований для второго и третьего уравнений:
63
m2(1) = a21, a11
m3(1) = a31. a11
Умножая поочередно первое уравнение на коэффициенты m2(1) и m3(1) и вы-
читая результат соответственно из второго и третьего уравнений, получим:
a11x1+ a12x2+ a13x3= b10x1+ a22(1 )x2+ a23(1 )x3= b2(1 )
0x1+ a32(1 )x2+ a33x3(1 ) = b3(1 ).
Второй шаг. Для исключения неизвестногох2 из первого и третьего уравнений определим соответствующие коэффициенты преобразований:
m(2 )= | a12 | , |
|
|
|
|
| ||||
a22(1 ) |
|
|
|
|
| ||||||
1 |
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
| |
(2 ) |
|
| a32(1 ) |
|
|
|
|
|
|
| |
m2 | = |
|
|
| . |
|
|
|
|
| |
| a22(1 ) |
|
|
| и m(2) |
| |||||
|
|
|
|
|
|
|
|
| |||
Умножая второе уравнение поочередно на m(2) |
| и вычитая результат | |||||||||
|
|
|
|
|
|
|
| 1 |
| 3 |
|
умножения соответственно из первого и третьего уравнений, получим: | |||||||||||
a x | + 0x | 2 | + a(2)x | = b(2) |
| ||||||
11 | 1 |
|
|
| 13 | 3 | 1 |
| |||
0x | + a(1 )x | 2 | + a | (1 )x | = b(1 ) | (4.4) | |||||
1 |
| 22 |
|
| 23 | 3 | 2 |
| |||
0x | + 0x | 2 | + a(2 )x | = b(2 ). |
| ||||||
1 |
|
|
|
|
| 33 | 3 |
| 3 |
| |
Третий шаг. Определим коэффициенты преобразований для первого и второго уравнений:
m(3 )= | a (2) |
| ||
13 | , | |||
1 |
| a22(1 ) |
| |
|
|
| ||
(3 ) |
| a23(1 ) |
| |
m2 | = |
| . | |
a33(2 ) | ||||
|
|
| ||
В результате произведения операций, аналогичных выполненным на первом и втором шагах, получим:
a x | + 0x | 2 | + | 0x |
| = b(3) |
| |||
11 | 1 |
|
|
| 3 | 1 |
| |||
0x | + a(1 )x | 2 | + 0x |
| = b(3 ) | (4.5) | ||||
1 |
| 22 |
|
| 3 | 2 |
| |||
0x | + 0x | 2 | + a | (2 )x | 3 | = b(2 ). |
| |||
1 |
|
|
|
|
| 33 | 3 |
| ||
studfiles.net
