Формулы треугольника, формулы для расчета площади и периметра треугольника
Содержание:
Треугольник — фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — его сторонами.
Формулы площади треугольника
Площадь геометрической фигуры — часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади выражается числом заключающихся в него квадратных единиц.
1-ая формула
S — площадь треугольника
a, b — длины 2-х сторон треугольника
С — угол между сторонами a и b
2-ая формула
S — площадь треугольника
a — длина стороны треугольника
h — длина высоты, опущенной на сторону a
3-ья формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
p — полупериметр треугольника
4-ая формула
S — площадь треугольника
r — радиус вписанной окружности
p — полупериметр треугольника
5-ая формула
S — площадь треугольника
a, b, c — длины 3-х сторон треугольника
R — радиус описанной окружности
См. также: Программа для расчета площади треугольника.
также: Программа для расчета площади треугольника.
Формула периметра треугольника
Периметр геометрической фигуры — суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.
1) Периметр треугольника равен сумме 3-ех его сторон (a, b, c).
P — периметр треугольника
a, b, c — длины сторон треугольника
См. также: Программа для расчета периметра треугольника.
Слишком сложно?
Формулы треугольника не по зубам? Тебе ответит эксперт через 10 минут!
Как находить периметр треугольника
В статье на примерах покажем, как находить периметр треугольника. Рассмотрим все основные случая, как найти периметры треугольников, даже когда не все значения сторон известны.
Треугольником называется простая геометрическая фигура состоящая из трех прямых линий пересекающих друг друга. В которой точки пересечения прямых, называются вершинами, а прямые линии соединяющие их, называются сторонами.
В которой точки пересечения прямых, называются вершинами, а прямые линии соединяющие их, называются сторонами.
Периметром треугольника называется сумма длин сторон треугольника. От того сколько мы имеем изначальных данных, для вычисления периметра треугольника, зависит каким из вариантов мы воспользуемся, для его вычисления.
Если мы знаем длины сторон n, y и z треугольника, то периметр мы можем определить с помощью следующей формулы: в которой P — это периметр, n, y, z- стороны треугольника
периметр прямоугольника формула
P = n + y + z
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =8см. найти его периметр.
Пользуясь формулой получаем 10 + 10 + 8 = 28.
Ответ: Р = 28см.
Для равностороннего треугольника находим периметр так — длина одной стороны умноженная на три. формула выглядит следующим образом :
Р = 3n
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =10см. найти его периметр.
найти его периметр.
Пользуясь формулой получаем 10 * 3 = 30
Ответ: Р = 30см.
Для равнобедренного треугольника находим периметр так — к длине одной боковой стороны умноженной на два, прибавляем сторону основания
P = 2n + z
Рассмотрим на примере:
Дан треугольник ksv стороны которого k = 10см, s = 10 см, v =7см. найти его периметр.
Пользуясь формулой получаем 2 * 10 + 7 = 27.
Ответ: Р = 27см.
Второй вариант
Когда нам не известна длина одной стороны, но мы знаем величины длины двух других сторон и угла между ними, а периметр треугольника возможно найти только после того как мы узнаем длину третьей стороны. В этом случае неизвестная сторона будет равна корню квадратному из выражения в2 + с2 — 2 ∙ в ∙ с ∙ cosβ
P = n + y + √ ( n2 + y2 — 2 ∙ n ∙ y ∙ cos α )
n, y — длины сторон
α — размер угла между известными нам сторонами
Третий вариант
Когда нам не известны стороны n и y, но мы знаем длину стороны z и величины прилегающих к ней.
P = z + sinα ∙ z / (sin ( 180°-α — β )) + sinβ ∙ z / (sin ( 180°-α — β ))
z — длина известной нам стороны
α, β — размеры известных нам углов
Четвертый вариант
Так же можно найти периметр треугольника по радиусу вписанному в его окружность и площади треугольника. Определяем периметр по формуле
P = 2S / r
S — площадь треугольника
r — радиус вписанной в него окружности
Мы с вами разобрали четыре разных варианта, как можно найти периметр треугольника.
Находить периметр треугольника в принципе не сложно. Если у вас появились какие то вопросы по статье, дополнения, то обязательно пишите их в комментариях.
Кстати, на referatplus.ru вы можете скачать рефераты по математике бесплатно.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Расчет периметра и площади треугольника
Треугольник имеет три угла или вершины, и три стороны, которые являются прямыми отрезками.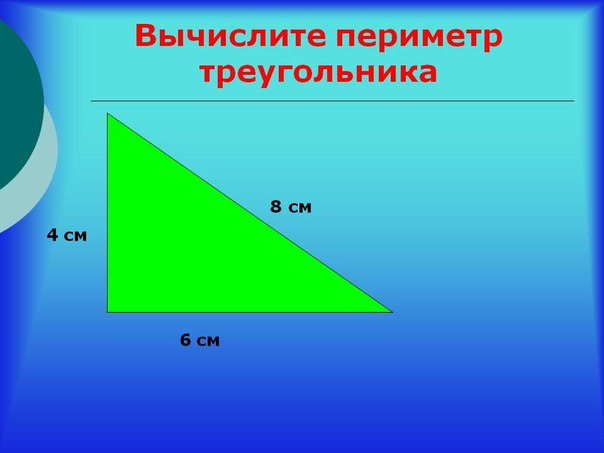
Равносторонним треугольником является треугольник, который имеет равную длину всех трех сторон.
Если две стороны треугольника и два прилегающих к ним угла равны между собой — такой треугольник называется равнобедренным
Площадь треугольника через основание и высоту: a×h/2
Периметр треугольника: (a + b + c)
Площадь равностороннего треугольника: (√(3)/4)×a²
Площадь равнобедренного треугольника(2 стороны и угол): ½×a×b×SinC
Формулы площади треугольника:
- Площадь треугольника = a * h/2
- Периметр треугольника = a + b + c
- Площадь равностороннего треугольника = (√(3) / 4) * a²
- Площадь равнобедренного треугольника = ½ * a * b * SinC
где,
- h — высота треугольника,
- a, b, c = стороны треугольника
Примеры :
Задача 1: Найдите площадь треугольника у которого высота = 3, а длина основания = 4.
Шаг 1: Найдем площадь.
Площадь = h * b/2 = 3 * 4/2 = 12/2 = 6.
Задача 2: Найдите периметр треугольника, если известна длина его трех сторон = 1, 2, 3.
Шаг 1: Найдем периметр.
Периметр = a + b + c = 1 + 2 + 3 = 6.
Задача 3: Найдите площадь равностороннего треугольника, если длина его стороны равна 3.
Шаг 1: Найдем площадь.
Площадь = (√(3) / 4) * a² = (1.73 / 4) * 3² = 0.43 * 9 = 3.87.
Задача 4: Найдите площадь равнобедренного треугольника если сторона его равна 3, основание = 4 и угол между ними 28.
Шаг 1: Найдем площадь.
Площадь = ½ * a * b * SinC = 0.5 * 3 * 4 * Sin(28) = 6 * 0.27 = 1.62.
Приведенные выше примеры показывают, как вычислить площадь и периметр треугольника, равностороннего треугольника,
равнобедренного треугольника вручную.
Как найти периметр треугольника — wikihow
Площадь
Для измерения треугольника можно сравнить его с параллелограммом. Рассмотрим треугольник ABC:
Рассмотрим треугольник ABC:
Если взять равный ему треугольник и приставить его так, чтобы получился параллелограмм, то получится параллелограмм с той же высотой и основанием, что и у данного треугольника:
В данном случае общая сторона сложенных вместе треугольников является диагональю образованного параллелограмма. Из свойства параллелограммов известно, что диагональ всегда делит параллелограмм на два равных треугольника, значит площадь каждого треугольника равна половине площади параллелограмма.
Так как площадь параллелограмма равна произведению его основания на высоту, то площадь треугольника будет равна половине этого произведения. Значит для ΔABC площадь будет равна
Теперь рассмотрим прямоугольный треугольник:
Два равных прямоугольных треугольника можно сложить в прямоугольник, если прислонить их друг к другу гипотенузой. Так как площадь прямоугольника равна произведению его смежных сторон, то площадь данного треугольника равна:
Из это можно сделать вывод, что площадь любого прямоугольного треугольника равна произведению катетов, разделённому на 2.
Из данных примеров можно сделать вывод, что площадь любого треугольника равна произведению длин основания и высоты, опущенной на основание, разделённому на 2. Общая формула для нахождения площади треугольников будет выглядеть так:
где S – это площадь треугольника, a – его основание, h a – высота, опущенная на основание a.
Полупериметр
Если периметр – это сумма длин всех сторон фигуры, то полупериметр – сумма одной длины и одной ширины. Мы находим полупериметр, когда работаем по формуле нахождения периметра прямоугольника (когда мы выполняем первое действие в скобках – (a+b)).
Список литературы
- Александрова Э.И. Математика. 2 класс. – М.: Дрофа, 2004.
- Башмаков М.И., Нефёдова М.Г. Математика. 2 класс. – М.: Астрель, 2006.
- Дорофеев Г.В., Миракова Т.И. Математика. 2 класс. – М.: Просвещение, 2012.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Festival.1september.ru (Источник).

- Nsportal.ru (Источник).
- Math-prosto.ru (Источник).
Домашнее задание
- Найти периметр прямоугольника, у которого длина 13 метров, а ширина – 7 метров.
- Найти полупериметр прямоугольника, если его длина – 8 см, а ширина – 4 см.
- Найти периметр прямоугольника, если его полупериметр – 21 дм.
Треугольник прямоугольный
Главным отличием прямоугольного треугольника от других геометрических фигур этой категории является наличие угла 90°. По этому признаку и определяется вид фигуры. Прежде, чем определить, как найти периметр прямоугольного треугольника, стоит заметить, что данная величина для любой плоской геометрической фигуры составляет сумму всех сторон. Так и в этом случае самый простой способ узнать результат – суммировать три величины.
В научной терминологии те стороны, которые прилегают к прямому углу, имеют название «катеты», а противоположная к углу 90º – гипотенуза. Особенности этой фигуры исследовались еще древнегреческим ученым Пифагором. Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
Согласно с теоремой Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
На основании данной теоремы выведена еще одна формула, объясняющая, как найти периметр треугольника по двум известным сторонам. Рассчитать периметр при указанной длине катетов можно, используя следующий способ.
Чтобы узнать периметр, имея информацию о размере одного катета и гипотенузы, нужно определить длину второй гипотенузы. С этой целью используют такие формулы:
Также периметр описанного вида фигуры определяется и без данных о размерах катетов.
Вам потребуется знать длину гипотенузы, а также угол, прилегающий к ней. Зная длину одного из катетов, если имеется угол, прилегающий к нему, периметр фигуры рассчитывают по формуле:
Треугольник, у которого есть угол 90°
Его называют прямоугольным. Наличие прямого угла дает возможность находить неизвестные стороны, пользуясь определением тригонометрических функций и теоремой Пифагора. Самая длинная сторона называется гипотенуза и обозначается c. Имеются еще две стороны, a и b. Следуя теореме, носящей имя Пифагора, имеем c2 = a2 + b2. Катеты a = √ (c2 – b2) и b = √ (c2 – а2). Зная длину двух катетов a и b, вычисляем гипотенузу. Затем находим сумму сторон фигуры, сложив эти значения. Задание: Катеты прямоугольного треугольника имеют длину 8,3 сантиметра и 6,2 сантиметра. Периметр треугольника нужно вычислить. Решаем: Обозначим катеты a = 8,3 см, b = 6,2 см. За теоремой Пифагора гипотенуза c = √ (8,32 + 6,22) = √ (68,89 + 38,44) = √107,33 = 10,4 (см). P = 24,9 (см). Или P = 8,3 + 6,2 + √ (8,32 + 6,22) = 24,9 (см). Ответ: P = 24,9 см. Значения корней брали с точностью до десятых. Если нам известны значения гипотенузы и катета, то значение Р получим, вычислив Р=√ (c2 – b2) + b + c. Задача 2: Отрезок земельного участка, лежащий против угла в 90 градусов, 12 км, один из катетов – 8 км. За какое время можно обойти весь участок, если двигаться со скоростью 4 километра в час? Решение: если наибольший отрезок — 12 км, меньший b = 8 км, то длина всего пути составит P = 8 + 12 + √ (122 – 82) = 20 + √80 = 20 + 8,9 = 28,9 (км).
Имеются еще две стороны, a и b. Следуя теореме, носящей имя Пифагора, имеем c2 = a2 + b2. Катеты a = √ (c2 – b2) и b = √ (c2 – а2). Зная длину двух катетов a и b, вычисляем гипотенузу. Затем находим сумму сторон фигуры, сложив эти значения. Задание: Катеты прямоугольного треугольника имеют длину 8,3 сантиметра и 6,2 сантиметра. Периметр треугольника нужно вычислить. Решаем: Обозначим катеты a = 8,3 см, b = 6,2 см. За теоремой Пифагора гипотенуза c = √ (8,32 + 6,22) = √ (68,89 + 38,44) = √107,33 = 10,4 (см). P = 24,9 (см). Или P = 8,3 + 6,2 + √ (8,32 + 6,22) = 24,9 (см). Ответ: P = 24,9 см. Значения корней брали с точностью до десятых. Если нам известны значения гипотенузы и катета, то значение Р получим, вычислив Р=√ (c2 – b2) + b + c. Задача 2: Отрезок земельного участка, лежащий против угла в 90 градусов, 12 км, один из катетов – 8 км. За какое время можно обойти весь участок, если двигаться со скоростью 4 километра в час? Решение: если наибольший отрезок — 12 км, меньший b = 8 км, то длина всего пути составит P = 8 + 12 + √ (122 – 82) = 20 + √80 = 20 + 8,9 = 28,9 (км). Время найдем, разделив путь на скорость. 28,9:4 = 7,225 (ч). Ответ: можно обойти за 7,3 ч. Значение квадратных корней и ответа берем с точностью до десятых. Можно найти сумму сторон прямоугольного треугольника, если дана одна из сторон и значение одного из острых углов. Зная длину катета b и значение противолежащего ему угла β, найдем неизвестную сторону a = b/ tg β. Находим гипотенузу c = a: sinα. Периметр такой фигуры находим, сложив полученные значения. P = a + a/ sinα + a/ tg α, или P = a(1 / sin α+ 1+1 / tg α). Задание: В прямоугольном Δ АВС с прямым углом С катет ВС имеет длину 10 м, угол А – 29 градусов. Нужно найти сумму сторон Δ АВС. Решение: Обозначим известный катет ВС = a = 10 м, угол, лежащий напротив него, ∟А = α = 30°, тогда катет АС = b = 10: 0,58 = 17,2 (м), гипотенуза АВ = c = 10: 0,5 = 20 (м). Р = 10 + 17,2 + 20 = 47,2 (м). Или Р = 10 · (1 + 1,72 + 2) = 47,2 м. Имеем: P = 47,2 м. Значение тригонометрических функций берем с точностью до сотых, значение длины сторон и периметра округляем до десятых.
Время найдем, разделив путь на скорость. 28,9:4 = 7,225 (ч). Ответ: можно обойти за 7,3 ч. Значение квадратных корней и ответа берем с точностью до десятых. Можно найти сумму сторон прямоугольного треугольника, если дана одна из сторон и значение одного из острых углов. Зная длину катета b и значение противолежащего ему угла β, найдем неизвестную сторону a = b/ tg β. Находим гипотенузу c = a: sinα. Периметр такой фигуры находим, сложив полученные значения. P = a + a/ sinα + a/ tg α, или P = a(1 / sin α+ 1+1 / tg α). Задание: В прямоугольном Δ АВС с прямым углом С катет ВС имеет длину 10 м, угол А – 29 градусов. Нужно найти сумму сторон Δ АВС. Решение: Обозначим известный катет ВС = a = 10 м, угол, лежащий напротив него, ∟А = α = 30°, тогда катет АС = b = 10: 0,58 = 17,2 (м), гипотенуза АВ = c = 10: 0,5 = 20 (м). Р = 10 + 17,2 + 20 = 47,2 (м). Или Р = 10 · (1 + 1,72 + 2) = 47,2 м. Имеем: P = 47,2 м. Значение тригонометрических функций берем с точностью до сотых, значение длины сторон и периметра округляем до десятых. Имея значение катета α и прилежащего угла β, узнаем, чему равен второй катет: b = a tg β. Гипотенуза в таком случае будет равна катету, разделенному на косинус угла β. Периметр узнаем по формуле P = a + a tg β + a: cos β = (tg β + 1+1: cos β)·a. Задание: Катет треугольника с углом 90 градусов 18 см, прилежащий угол – 40 градусов. Найти P. Решение: Обозначим известный катет ВС = 18 см, ∟β = 40°. Тогда неизвестный катет АС = b = 18 · 0,83 = 14,9 (см), гипотенуза АВ = c = 18: 0,77 = 23,4 (см). Сумма сторон фигуры равна Р = 56,3 (см). Или Р = (1 + 1,3+0,83)*18 = 56,3 см. Ответ: P = 56,3 см. Если известна длина гипотенузы c и какой-нибудь угол α, то катеты будут равны произведению гипотенузы для первого – на синус и для второго – на косинус этого угла. Периметр этой фигуры P = (sin α + 1+ cos α)*c. Задание: Гипотенуза прямоугольного треугольника АВ = 9,1 сантиметр, а угол 50 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим гипотенузу: AB = c = 9,1 см, ∟A= α = 50°, тогда один из катетов BC имеет длину a = 9,1 · 0,77 = 7 (см), катет АС = b = 9,1 · 0,64 = 5,8 (см).
Имея значение катета α и прилежащего угла β, узнаем, чему равен второй катет: b = a tg β. Гипотенуза в таком случае будет равна катету, разделенному на косинус угла β. Периметр узнаем по формуле P = a + a tg β + a: cos β = (tg β + 1+1: cos β)·a. Задание: Катет треугольника с углом 90 градусов 18 см, прилежащий угол – 40 градусов. Найти P. Решение: Обозначим известный катет ВС = 18 см, ∟β = 40°. Тогда неизвестный катет АС = b = 18 · 0,83 = 14,9 (см), гипотенуза АВ = c = 18: 0,77 = 23,4 (см). Сумма сторон фигуры равна Р = 56,3 (см). Или Р = (1 + 1,3+0,83)*18 = 56,3 см. Ответ: P = 56,3 см. Если известна длина гипотенузы c и какой-нибудь угол α, то катеты будут равны произведению гипотенузы для первого – на синус и для второго – на косинус этого угла. Периметр этой фигуры P = (sin α + 1+ cos α)*c. Задание: Гипотенуза прямоугольного треугольника АВ = 9,1 сантиметр, а угол 50 градусов. Найти сумму сторон данной фигуры. Решение: Обозначим гипотенузу: AB = c = 9,1 см, ∟A= α = 50°, тогда один из катетов BC имеет длину a = 9,1 · 0,77 = 7 (см), катет АС = b = 9,1 · 0,64 = 5,8 (см). 2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.
2 — (2 * a * b * cos(C)), где a,b,c — стандартно длины граней, а A,B и С — это углы, которые лежат напротив соответствующих граней треугольника. То есть, A — угол, противолежащий стороне a и так далее.
Представим, что описан треугольник, стороны а и б которого составляют 100 см и 120 см соответственно, а угол, лежащий между ними, составляет 97 градусов. То есть а = 100 см, б = 120 см, C = 97 градусов.
Все, что нужно сделать в данном случае — это подставить все известные значения в теорему косинусов. Длины известных граней возводятся в квадрат, после чего известные стороны перемножаются между друг другом и на два и умножаются на косинус угла между ними. Далее, необходимо сложить квадраты граней и отнять от них второе полученное значение. Из итоговой величины извлекается квадратный корень — это будет третья, неизвестная до этого сторона.
После того как все три грани фигуры известны, осталось воспользоваться уже полюбившейся нам стандартной формулой поиска периметра описываемой фигуры из первого метода.
Задача решена.
Задача 1: подсчет периметра прямоугольника
Рассмотрим следующую задачу:
Задача 1 (рис. 2)
Вокруг земельного участка строителям понадобилось поставить забор. Ширина этого участка – 5 метров, длина – 10 метров. Забор какой длины получится у строителей?
Рис. 2. Иллюстрация к задаче 1
Забор ставят по границам участка, поэтому, чтобы узнать длину забора, нужно знать длину каждой из сторон. У данного прямоугольника стороны равны: 5 метров, 10 метров, 5 метров, 10 метров. Составим выражение для подсчета длины забора: 5+10+5+10. Воспользуемся переместительным законом сложения: 5+10+5+10=5+5+10+10. В данном выражении есть суммы одинаковых слагаемых (5+5 и 10+10). Заменим суммы одинаковых слагаемых произведениями: 5+5+10+10=5·2+10·2. Теперь воспользуемся распределительным законом умножения относительно сложения: 5·2+10·2=(5+10)·2.
Найдем значение выражения (5+10)·2. Сначала выполняем действие в скобках: 5+10=15. А затем повторяем число 15 два раза: 15·2=30.
(5+10)·2=30
Ответ: 30 метров.
Периметр по двум сторонам
Для расчета периметра не обязательно знать все данные геометрической фигуры. Рассмотрим способы расчета по двум сторонам.
Равнобедренный треугольник
Равнобедренным называется такой треугольник, не меньше двух сторон которого имеют одинаковую длину. Они называются боковыми, а третья сторона – основанием. Равные прямые образовывают вершинный угол. Особенностью в равнобедренном треугольнике является наличие одной оси симметрии. Ось – вертикальная линия, выходящая из вершинного угла и заканчивающаяся посредине основания. По своей сути ось симметрии включает в себя такие понятия:
- биссектриса вершинного угла;
- медиана к основанию;
- высота треугольника;
- срединный перпендикуляр.
Чтобы определить периметр равнобедренного вида треугольной фигуры, воспользуйтесь формулой.
P = 2a + b.
В данном случае вам необходимо знать только две величины: основание и длину одной стороны. Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
Обозначение «2а» подразумевает умножение длины боковой стороны на 2. К полученной цифре нужно добавить величину основания – «b».
В исключительном случае, когда длина основания равнобедренного треугольника равна его боковой прямой, можно воспользоваться более простым способом. Он выражается в следующей формуле:
P = 3a.
Для получения результата достаточно умножить это число на три. Эта формула используется для того, чтобы найти периметр правильного треугольника.
Задача 2
Если в задаче дается острый угол прямоугольного треугольника, значит в любом случае в решении нужно использовать тригонометрические функции. Иначе для нахождения результата просто не хватит данных.
В этой задаче есть два возможных варианта. Острый угол может быть расположен у известного катета, а может противолежать ему. В любом случае придется использовать тригонометрические функции, но результаты могут разница. Обычно в задаче этот момент прописывается, но иногда от решающего требуется предоставить оба варианта решения. Это ясно из условия, в котором не говорится, какой из острых углов дан.
Это ясно из условия, в котором не говорится, какой из острых углов дан.
Рассмотрим вариант, при котором дан острый угол при известном катете. Тогда воспользуемся функцией косинуса:
$$Cos(BAC)={AB\over AC}={\sqrt{3}\over2}$$
$$AC={AB\over {cos(BAC)}}$$
$$AC={8\over{\sqrt{3}\over 2}}={16\over\sqrt{3}}=9,24$$ – значение округлим до сотых
BC найдем через значение тангенса.
$$tg(BAC)={BC\over AB}={1\over\sqrt{3}}$$
$$BC=AB*{1\over\sqrt{3}}={AB\over\sqrt{3}}$$
$$BC={8\over\sqrt{3}}=4,62$$
Вычисление периметра произведем по общей формуле:
P=8+9,24+4,62=21,86
Если острый угол противолежит известному катету, то решение будет выглядеть немного иначе.
Найдем BC через значение тангенса.
$$tg(ACB)={AB\over BC}={1\over\sqrt{3}}$$
$$BC={AB\over {1\over\sqrt{3}}}=AB*\sqrt{3}=8*\sqrt{3}=13,86$$
Гипотенузу найдем через значение синуса.
$$sin(ACB)={AB\over AC}={1\over 2}$$
$$AC={AB\over sin(ACB)}={AB\over {1\over 2}}=2*AB=2*8=16$$
Если в расчетах присутствуют округления, то лучше округленный результат не использовать в дальнейших вычислениях. То есть, если мы посчитали BC, то AC лучше найти через синус, а не через косинус или теорему Пифагора, если есть такая возможность. Использование точных значений избавляет от больших погрешностей в результатах.
То есть, если мы посчитали BC, то AC лучше найти через синус, а не через косинус или теорему Пифагора, если есть такая возможность. Использование точных значений избавляет от больших погрешностей в результатах.
Что мы узнали?
Мы узнали, что отличия между формулой периметра для прямоугольного и произвольного треугольника нет. Разница в пути решения. Найти периметр прямоугольного треугольника можно через теорему Пифагора, площадь или тригонометрические функции, можно комбинировать различные методы между собой. Главное, это возможность решения задачи без дополнительных построений.
Классическая формула
Самым простым способом найти периметр фигуры, если есть данные всех сторон. В этом случае используется следующая формула:
P = a + b + c.
Буквой «P» обозначается сама величина периметра. В свою очередь «a», «b» и «c» – это длины сторон.
Зная размер трех величин, достаточно будет получить их сумму, которая и является периметром.
Альтернативный вариант
В математических задачах все данные длины редко бывают известны. В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
В таких случаях рекомендуется воспользоваться альтернативным способом поиска нужной величины. Когда в условиях указана длина двух прямых, а также угол, находящийся между ними, расчет производится через поиск третьей. Для поиска этого числа необходимо добыть квадратный корень по формуле:
Далее рассчитывайте Р по такой формуле:
Пример
Сложную задачу на нахождение периметра правильного треугольника придумать нелегко. Поэтому решим интересную, но простую задачу на заданную тематику. В процессе решения рассмотрим применение теоремы Пифагора для решения задач с правильным треугольником.
Площадь правильного треугольника АВС равняется $9\sqrt{3}$
Рис. 2. Рисунок к задаче.
Любую характеристику правильного треугольника можно найти, если есть хотя бы одна из длин
Неважно, будет это сторона, площадь, периметр, медиана или биссектриса. Любой длины будет достаточно для решения задачи
Вспомним формулу площади треугольника и упростим ее для правильного треугольника. 2*{\sqrt{3}\over{4}}$$
2*{\sqrt{3}\over{4}}$$
Из этой формулы выразим значение стороны:
$$a=\sqrt{4S\over{\sqrt{3}}}=\sqrt{{4*{9\over{\sqrt{3}}}}\over{\sqrt{3}}}=6$$
Теперь найти периметр не составит проблем.
$$P=3a=3*6=18$$
Что мы узнали?
Мы привели формулу периметра правильного треугольника. На примере показали, как можно найти площадь правильного треугольника через площадь. На том же примере показали примерный ход решения любой задачи на решение правильного треугольника.
Совет 5: Как обнаружить площадь и периметр квадрата
Квадрат представляет собой геометрическую фигуру, состоящую из четырех сторон идентичной длины и четырех прямых углов, всякий из которых равен 90°. Определение площади либо периметра четырехугольника, причем всякого, требуется не только при решении задач по геометрии, но и в повседневной жизни. Эти знания могут стать пригодными, скажем, во время ремонта при расчете необходимого числа материалов – покрытий для пола, стен либо потолка, а также для разбивки газонов и грядок и т. д.
д.
1. Для определения площади квадрата умножьте величину длины на величину ширины. Потому что в квадрате длина и ширина идентичны, то значение одной стороны довольно построить в квадрат. Таким образом, площадь квадрата равна длине его стороны, возведенной в квадрат. Единицей измерения площади могут быть квадратные миллиметры, сантиметры, дециметры, метры, километры.Дабы определить площадь квадрата, дозволено воспользоваться формулойS = aa, где S – площадь квадрата,а – сторона квадрата.2. Пример № 1. Комната имеет форму квадрата. Сколько ламината (в кв.м) понадобится для того, дабы всецело покрыть пол, если длина одной стороны комнаты составляет 5 метров.Запишите формулу: S = aa. Подставьте в нее указанные в условии данные.Потому что а = 5 м, следственно, площадь будет равнаS (комнаты) = 5х5= 25 кв.м, значит, и S (ламината) = 25 кв.м.3. Периметр представляет собой всеобщую длину границы фигуры. В квадрате периметр – это длина всех четырех, причем идентичных, сторон. То есть, периметр квадрата представляет собой сумму всех его четырех сторон. Дабы вычислить периметр квадрата, довольно знать длину одной его стороны. Измеряется периметр в миллиметрах, сантиметрах, дециметрах, метрах, километрах.Для определения периметра имеется формула:P = a + а + а + а илиP = 4a, гдеР – периметр,а – длина стороны.4. Пример № 2. Для отделочных работ помещения в форме квадрата требуются потолочные плинтуса. Вычислите всеобщую длину (периметр) плинтусов, если величина одной стороны комнаты равна 6 метров. Запишите формулу P = 4a.Подставьте в нее указанные в условии данные:Р (комнаты) = 4 х 6 = 24 метра.Следственно, длина потолочных плинтусов тоже будет равна 24 метров.Видео по теме
Дабы вычислить периметр квадрата, довольно знать длину одной его стороны. Измеряется периметр в миллиметрах, сантиметрах, дециметрах, метрах, километрах.Для определения периметра имеется формула:P = a + а + а + а илиP = 4a, гдеР – периметр,а – длина стороны.4. Пример № 2. Для отделочных работ помещения в форме квадрата требуются потолочные плинтуса. Вычислите всеобщую длину (периметр) плинтусов, если величина одной стороны комнаты равна 6 метров. Запишите формулу P = 4a.Подставьте в нее указанные в условии данные:Р (комнаты) = 4 х 6 = 24 метра.Следственно, длина потолочных плинтусов тоже будет равна 24 метров.Видео по теме
Периметром треугольника, как в прочем и любой фигуры, называется сумма длин всех сторон. Довольно часто это значение помогает найти площадь или используется для расчета других параметров фигуры.
Формула периметра треугольника выглядит так:
P=a+b+c
Формула расчета периметра равнобедренного треугольника будет выглядеть так:
P=2a+b
Формула расчета периметра равностороннего треугольника:
P=3a
В общем, когда все стороны даны, найти периметр довольно просто. В остальных же ситуациях требуется найти размер недостающей стороны. В прямоугольном треугольнике можно найти третью сторону по теореме Пифагора.
Совет 3: Как обнаружить стороны прямоугольника
Частный случай параллелограмма – прямоугольник – знаменит только в геометрии Евклида. У прямоугольника равны все углы, и всякий из них по отдельности составляет 90 градусов. Исходя из частных свойств прямоугольника , а также из свойств параллелограмма о параллельности противолежащих сторон дозволено обнаружить стороны фигуры по заданным диагоналям и углу от их пересечения. Вычисление сторон прямоугольника базируется на дополнительных построениях и использовании свойств получаемых фигур.
1. Постройте прямоугольник EFGH. Запишите знаменитые данные: диагональ прямоугольника EG и угол α, полученный от пересечения 2-х равных диагоналей FH и EG. Постройте на рисунке диагонали и подметьте между ними угол α.2. Буквой А подметьте точку пересечения диагоналей. Разглядите образованный построениями треугольник EFА. Согласно свойству прямоугольника его диагонали равны и делятся напополам точкой пересечения А. Вычислите значения FА и EА. Потому что треугольник EFА является равнобедренным и его стороны EА и FА равны между собой и соответственно равны половине диагонали EG.3. Дальше вычислите первую сторону EF прямоугольника . Данная сторона является третьей неведомой стороной рассматриваемого треугольника EFА. Согласно теореме косинусов по соответствующей формуле обнаружьте сторону EF. Для этого подставьте в формулу косинусов полученные ранее значения сторон FА равна EА и косинус знаменитого угла между ними α. Вычислите и запишите полученное значение EF.4. Обнаружьте вторую сторону прямоугольника FG. Для этого разглядите иной треугольник EFG. Он является прямоугольным, где знамениты гипотенуза EG и катет EF. Согласно теореме Пифагора обнаружьте 2-й катет FG по соответствующей формуле.5. В соответствии со свойствами прямоугольника его противолежащие ребра равны. Таким образом сторона GH равна обнаруженной стороне EF, а HЕ = FG. Запишите в результат все вычисленные стороны прямоугольника .
Для этого разглядите иной треугольник EFG. Он является прямоугольным, где знамениты гипотенуза EG и катет EF. Согласно теореме Пифагора обнаружьте 2-й катет FG по соответствующей формуле.5. В соответствии со свойствами прямоугольника его противолежащие ребра равны. Таким образом сторона GH равна обнаруженной стороне EF, а HЕ = FG. Запишите в результат все вычисленные стороны прямоугольника .
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия
Фигуру называют выпуклой, если для любых двух точек этой фигуры соединяющий их отрезок полностью принадлежит фигуре.
Правильными многоугольниками называют выпуклые многоугольники, у которых все углы равны и все стороны равны.
Замечание 1. В любой правильный многоугольник можно вписать окружность.
Замечание 2. Около любого правильного многоугольника можно описать окружность.
Замечание 3. Центры вписанной в правильный многоугольник окружности и описанной около правильного многоугольника окружности совпадают. Эту точку называют центром правильного многоугольника.
Используемые обозначения
| Число вершин правильного многоугольника | Сторона правильного многоугольника | Радиус вписанной окружности | Радиус описанной окружности | Периметр | Площадь |
| n | a | r | R | P | S |
| Число вершин правильного многоугольника | n |
| Сторона правильного многоугольника | a |
| Радиус вписанной окружности | r |
| Радиус описанной окружности | R |
| Периметр | P |
| Площадь | S |
Формулы для стороны, периметра и площади правильного
n – угольника| Формулы для периметра правильного n – угольника |
Выражение периметра через сторону P = an Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности |
| Формулы для площади правильного n – угольника |
Выражение площади через сторону и радиус вписанной окружности Выражение площади через сторону Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности |
| Формулы для стороны правильного n – угольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного треугольника
| Формулы для периметра правильного треугольника |
Выражение периметра через сторону P = 3a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности |
| Формулы для площади правильного треугольника |
Выражение площади через сторону Посмотреть вывод формулы Выражение площади через сторону и радиус вписанной окружности Выражение площади через радиус вписанной окружности Посмотреть вывод формулы Выражение площади через радиус описанной окружности Посмотреть вывод формулы |
| Формулы для стороны правильного треугольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности |
Формулы для стороны, периметра и площади правильного шестиугольника
| Формулы для периметра правильного шестиугольника |
Выражение периметра через сторону P = 6a Выражение периметра через радиус вписанной окружности Выражение периметра через радиус описанной окружности P = 6R |
| Формулы для площади правильного шестиугольника |
Выражение площади через сторон Выражение площади через сторону и радиус вписанной окружности S = 3ar Выражение площади через радиус вписанной окружности Выражение площади через радиус описанной окружности |
| Формулы для стороны правильного шестиугольника |
Выражение стороны через радиус вписанной окружности Выражение стороны через радиус описанной окружности a = R |
Формулы для стороны, периметра и площади квадрата
| Формулы для периметра квадрата |
Выражение периметра через сторону P = 4a Выражение периметра через радиус вписанной окружности P = 8r Выражение периметра через радиус описанной окружности |
| Формулы для площади квадрата |
Выражение площади через сторону S = a2 Выражение площади через радиус вписанной окружности S = 4r2 Выражение площади через радиус описанной окружности S = 2R2 |
| Формулы для стороны квадрата |
Выражение стороны через радиус вписанной окружности a = 2r Выражение стороны через радиус описанной окружности |
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Как найти периметр равностороннего треугольника
Равносторонний треугольник наряду с квадратом является, пожалуй, самой простой и симметричной фигурой в планиметрии. Разумеется, все соотношения, справедливые для обычного треугольника, верны также и для равностороннего. Однако для правильного треугольника все формулы становятся намного проще.Вам понадобитсяЧтобы найти периметр равностороннего треугольника измерьте длину одной из его сторон и умножьте результат измерения на три. В виде формулы это правило можно записать следующим образом:
Прт = Дс * 3,
где:
Прт – периметр равностороннего треугольника,
Дс – длина любой из его сторон.
Периметр треугольника получится в тех же единицах измерения, что и длина его стороны.
Пример.
Длина стороны равностороннего треугольника равна 10 мм. Требуется определить его периметр.
Решение.
Прт = 10 * 3= 30 (мм)
Так как равносторонний треугольник обладает высокой степенью симметрии, то для вычисления его периметра достаточно одного из параметров. Например, площади, высоты, радиуса вписанной или описанной окружности.
Например, площади, высоты, радиуса вписанной или описанной окружности.
Если известен радиус вписанной окружности равностороннего треугольника, то для вычисления его периметра воспользуйтесь следующей формулой:
Прт = 6 * √3 * r,
где: r — радиус вписанной окружности.
Это правило следует из того, что радиус вписанной окружности равностороннего треугольника выражается через длину его стороны следующим соотношением:
r = √3/6 * Дс.
Чтобы вычислить периметр правильного треугольника через радиус описанной окружности, примените формулу:
Прт = 3 * √3 * R,
где: R — радиус описанной окружности.
Данная формула легко выводится из того факта, что радиус описанной окружности правильного треугольника выражается через длину его стороны следующим соотношением: R = √3/3 * Дс.
Для вычисления периметра равностороннего треугольника через известную площадь воспользуйтесь следующим соотношением:
Sрт = Дст² * √3 / 4,
где: Sрт – площадь равностороннего треугольника. ¼.
¼.
Вычисление площади и периметра треугольника с помощью Python?
Эй, ребята, у меня возникли проблемы с выводом площади и периметра треугольника с учетом сторон по формуле цапли. Вот мой код:
def main():
a = int(input('Enter first side: '))
b = int(input('Enter second side: '))
c = int(input('Enter third side: '))
def area():
# calculate the sides
s = (a + b + c) / 2
# calculate the area
area = (s*(s-a)*(s-b)*(s-c)) ** 0.5
return area
area()
def perimeter():
# Calculate the perimeter
perim = a + b + c
return perim
perimeter()
print( 'Area is: ',format(area,'.1f'))
print( 'Perimeter is: ',format(perim,',.1f'))
main()
Я получаю много ошибок, таких как
- TypeError: непустая строка формата, переданная объекту. формат
- NameError: имя ‘perim’ не определено
Я должен сделать это, запросив стороны в основной функции, а затем вызвав вторую, а затем выведя ответы с одним десятичным знаком.
Может кто-нибудь сказать мне, что я делаю не так?
pythonПоделиться Источник AvenNova 11 февраля 2015 в 22:01
3 ответа
- Python вычисление периметра окружности
Я работаю над калькулятором площади в python году, и все кажется нормальным…пока я не доберусь до вычисления периметра круга… Может ли кто-нибудь указать мне правильное направление? import math from math import pi menu = Pick a shape(1-3): 1) Square (area) 2) Rectangle (area) 3) Circle (area)…
- площадь треугольника-python 27
Программа настроена на вычисление площади треугольника. Стороны треугольника (a,b, c) являются входными данными. Код отлично работает только с сертификационными числами, а не с другими. E.g. когда a, b и c соответственно: 2,3,4 код OK. 2,3,5 выход в 0.00, который является неправильным. 2,3,6.
 ..
..
2
Вам нужно присвоить возвращаемые значения и сделать три длины сторон глобальными. Честно говоря, вы должны прочитать больше о области видимости переменных, которые являются уровнями, на которых определяются переменные. Кроме того, имена переменных не должны перезаписывать имена функций. Таким образом, вы можете повторно использовать эти небольшие функции позже в любом месте вашего скрипта, просто вызвав их и передав три параметра.
Например:
def area(a, b, c):
# calculate the sides
s = (a + b + c) / 2
# calculate the area
area = (s*(s-a)*(s-b)*(s-c)) ** 0.5
return area
def perimeter(a, b, c):
# Calculate the perimeter
perim = a + b + c
return perim
def main():
a = int(input('Enter first side: '))
b = int(input('Enter second side: '))
c = int(input('Enter third side: '))
print "Area is:", area(a, b, c)
print "Perimeter is:", perimeter(a, b, c)
main()
Это должен быть более чистый способ сделать это, и вы вызываете только одну функцию из основного потока. Вы избежите объявления глобальных переменных и целого беспорядка, который у вас есть (без обид) в вашем исходном коде.
Вы избежите объявления глобальных переменных и целого беспорядка, который у вас есть (без обид) в вашем исходном коде.
Поделиться Onedot618 11 февраля 2015 в 22:10
0
Вам нужно присвоить возвращаемые значения и сделать три длины сторон глобальными. Честно говоря, вы должны прочитать больше о области видимости переменных, которые являются уровнями, на которых определяются переменные. Кроме того, имена переменных не должны перезаписывать имена функций.
a = int(input('Enter first side: '))
b = int(input('Enter second side: '))
c = int(input('Enter third side: '))
def area():
# calculate the sides
s = (a + b + c) / 2
# calculate the area
area = (s*(s-a)*(s-b)*(s-c)) ** 0.5
return area
areaValue = area()
def perimeter():
# Calculate the perimeter
perim = a + b + c
return perim
perim = perimeter()
print( 'Area is: ', format(areaValue,'. 1f'))
print( 'Perimeter is: ', format(perim,',.1f'))
1f'))
print( 'Perimeter is: ', format(perim,',.1f'))
Поделиться Malik Brahimi 11 февраля 2015 в 22:06
0
TypeError: обязательно отметьте параметры форматирования парой фигурных скобок.
'Area is {}, perimeter is {}.'.format(first_value, second_value)NameError : возможно,вы захотите прочитать о переменных областях.
def perimeter(a, b, c): # Calculate the perimeter perim = a + b + c return perim # Call the function with the parameters # you want it to compute : print "Perimeter is {}."format( perimeter(3, 4, 5) ) # output : "Perimeter is 12."
Поделиться mcadorel 11 февраля 2015 в 22:25
- Вычисление периметра любого треугольника [python 3]
Я следую онлайн-курсу по python и застрял на этом занятии: Предположим, что distance2D (x1, y1, x2, y2) уже определен.
 Используя его, определите функцию trianglePerimeter (xA, yA, xB, yB, xC, yC), которая вычисляет периметр треугольника, тремя точками которого являются (xA, yA), (xB, yB) и (xC,…
Используя его, определите функцию trianglePerimeter (xA, yA, xB, yB, xC, yC), которая вычисляет периметр треугольника, тремя точками которого являются (xA, yA), (xB, yB) и (xC,… - Расчет периметра и площади прямоугольника
Мы должны создать программу, которая создает класс с атрибутами length и width, значения по умолчанию которых равны 1.0, а также имеет методы для получения периметра и площади. Я закончил с созданием класса, но мы должны проверить его в программе. Вот как выглядит мой код: public class Rectangle {…
Похожие вопросы:
C# расчет площади и периметра
Итак, я использую Microsoft Visual C# 2010 Express. я пытаюсь создать программу, которая вычисляет площадь и периметр. у меня есть 2 текстовых поля для длины и ширины. у меня есть 2 текстовых поля…
Невозможно напечатать значения площади и периметра внутри моего форматированного столбца
Это мой код для программы, в которой я должен печатать площадь и периметр прямоугольников, используя все возможные комбинации длин и Ширин от 1 до 10. Я в основном настроил таблицу, но не знаю, как…
Я в основном настроил таблицу, но не знаю, как…
Вычисление площади треугольника
Я использую этот код для вычисления площади треугольника со значениями 2, 2 и 1. Когда я делаю расчет в своем карманном калькуляторе, я получаю 0.97, но в C# это 0. Я предполагаю, что это как-то…
Python вычисление периметра окружности
Я работаю над калькулятором площади в python году, и все кажется нормальным…пока я не доберусь до вычисления периметра круга… Может ли кто-нибудь указать мне правильное направление? import math…
площадь треугольника-python 27
Программа настроена на вычисление площади треугольника. Стороны треугольника (a,b, c) являются входными данными. Код отлично работает только с сертификационными числами, а не с другими. E.g. когда…
Вычисление периметра любого треугольника [python 3]
Я следую онлайн-курсу по python и застрял на этом занятии: Предположим, что distance2D (x1, y1, x2, y2) уже определен. Используя его, определите функцию trianglePerimeter (xA, yA, xB, yB, xC, yC),…
Используя его, определите функцию trianglePerimeter (xA, yA, xB, yB, xC, yC),…
Расчет периметра и площади прямоугольника
Мы должны создать программу, которая создает класс с атрибутами length и width, значения по умолчанию которых равны 1.0, а также имеет методы для получения периметра и площади. Я закончил с…
детерминантный метод против площади поперечного произведения треугольника
Мне было интересно, какой метод (детерминантный метод или кросс-продукт) более эффективен для вычисления площади треугольника? С детерминантами я думал, что в области = 1/2*det() для этого метода я…
Вычисление площади треугольника
Я новичок в Java. Я пытаюсь вычислить площадь треугольника по формуле: s = (сторона 1 + сторона 2 + сторона 3)/2 площадь = квадратный корень (сторона (сторона — сторона 1)(сторона — сторона 2)…
Woocommerce расчет цены продукта на основе размеров площади и периметра
Пожалуйста, посоветуйте, какой плагин подойдет для следующих расчетов ниже: Прямоугольник Продукта: a = длина b = ширина p1 = цена за кв. м (площадь) p2 = цена за м (периметр) Расчет на основе общей…
м (площадь) p2 = цена за м (периметр) Расчет на основе общей…
Как найти периметр прямоугольного треугольника
Объяснение:Для определения периметра прямоугольного треугольника используются три основных метода.
- Если указаны длины сторон, сложите их вместе.
- Найдите недостающую сторону, используя теорему Пифагора.
- Если нам известна информация о стороне, углу, стороне, найдите недостающую сторону, используя закон косинусов.
Метод 1:
Этот метод покажет вам, как рассчитать периметр треугольника, когда известны длины всех сторон.Рассмотрим следующую цифру:
Если нам известны длины сторон, и, то мы можем просто сложить их вместе, чтобы найти периметр треугольника. Важно отметить несколько моментов. Во-первых, нам нужно убедиться, что все заданные единицы соответствуют друг другу. Во-вторых, когда все длины сторон известны, формула периметра может использоваться для всех типов треугольников (например, правого, острого, тупого, равностороннего, равнобедренного и разностороннего). Формула периметра записывается формально в следующем формате:
Формула периметра записывается формально в следующем формате:
Метод 2:
В прямоугольных треугольниках мы можем вычислить периметр треугольника, когда нам предоставлены только две стороны.Мы можем сделать это, используя теорему Пифагора. Давайте сначала обсудим прямоугольные треугольники в общем смысле. Прямоугольный треугольник — это треугольник с одним углом. Это особый треугольник, и его нужно пометить соответствующим образом. Катушки треугольника образуют угол, они обозначены и. Сторона треугольника, противоположная углу и соединяющая два катета, известна как гипотенуза. Гипотенуза — это самая длинная сторона треугольника, обозначенная как.
Если треугольник появляется в этом формате, то мы можем использовать теорему Пифагора, чтобы найти любую недостающую сторону.Эта формула записывается следующим образом:
Мы можем переставить его разными способами, чтобы решить для каждой из сторон треугольника. Переставим его, чтобы найти гипотенузу,.
Переставим его, чтобы найти гипотенузу,.
Переставьте и извлеките квадратный корень из обеих частей.
Упростить.
Теперь давайте воспользуемся теоремой Пифагора, чтобы найти один из катетов,.
Вычтем из обеих частей уравнения.
Извлеките квадратный корень из обеих частей.
Упростить.
Наконец, давайте воспользуемся теоремой Пифагора, чтобы найти соседнюю ногу,.
Вычтем из обеих частей уравнения.
Извлеките квадратный корень из обеих частей.
Упростить.
Важно отметить, что мы можем использовать следующие формулы для поиска недостающей стороны прямоугольного треугольника, только если известны две другие стороны:
После того, как мы найдем недостающую сторону, мы можем использовать формулу периметра для вычисления периметра треугольника.
Метод 3:
Этот метод является наиболее сложным и может использоваться только в том случае, если мы знаем длины двух сторон треугольника, а также меру угла между ними. Когда мы знаем информацию о стороне, углу, стороне (SAS), мы можем использовать закон косинусов, чтобы найти недостающую сторону. Чтобы эта формула могла точно вычислить недостающую сторону, нам нужно обозначить треугольник следующим образом:
Когда треугольник обозначен таким образом, каждая сторона прямо соответствует углу, прямо противоположному ему.Если мы тщательно помечаем наш треугольник, мы можем использовать следующие формулы для поиска недостающих сторон в любом треугольнике с учетом информации SAS:
После того, как мы вычислим правую часть уравнения, нам нужно извлечь квадратный корень из обеих частей, чтобы получить окончательную длину стороны недостающей стороны. Наконец, нам нужно использовать формулу периметра, чтобы получить расстояние длин сторон многоугольника.
Решение:
Теперь, когда мы обсудили три метода вычисления периметра треугольника, мы можем использовать эту информацию для решения проблемы.Периметр треугольника — это просто сумма трех его сторон. Наша проблема в том, что мы знаем только две стороны. Ключевым моментом для нас является тот факт, что у нас есть прямоугольный треугольник (на что указывает маленький прямоугольник в одном углу). Знать две стороны прямоугольного треугольника и нуждаться в третьей — классический случай использования теоремы Пифагора. Проще говоря, теорема Пифагора гласит, что сумма квадратов длин катетов прямоугольного треугольника равна квадрату длины его гипотенузы.
Каждый прямоугольный треугольник имеет три стороны и прямой угол. Сторона, лежащая напротив прямого угла (также самая длинная), называется гипотенузой. Две другие стороны называются ногами. Это означает, что в нашем треугольнике сторона длиной 17 является гипотенузой, а сторона длиной 8 и та, которую нам нужно найти, — это катеты.
Теорема Пифагора говорит нам, что если мы возведем в квадрат длины наших двух катетов и сложим эти два числа вместе, мы получим то же число, что и при возведении в квадрат длины нашей гипотенузы.Поскольку мы не знаем длины нашей второй ноги, мы можем идентифицировать ее с помощью переменной.
Это позволяет нам создать следующее алгебраическое уравнение:
, который упрощен, становится
Чтобы решить это уравнение, нам сначала нужно получить переменную отдельно, что можно сделать, вычтя 64 из обеих частей, что даст нам
Отсюда мы просто извлекаем квадратный корень из обеих частей.
Технически, это также будет квадратный корень из 225, но поскольку сторона треугольника может иметь только положительную длину, мы будем придерживаться 15 в качестве нашего ответа.
Но мы еще не закончили. Теперь мы знаем длину отсутствующей стороны, но нам все еще нужно сложить три длины стороны вместе, чтобы найти периметр.
Наш ответ — 40.
Что такое периметр треугольника?
Периметр треугольникаПериметр фигуры — это длина ее границы или общая длина вокруг фигуры. Периметр двумерной замкнутой формы = сумма всех ее сторон.
Треугольник
Треугольник — это многоугольник с тремя сторонами.Другими словами, это замкнутая двухмерная фигура с тремя прямыми сторонами.
В данном треугольнике a, b и c — стороны треугольника.
Периметр треугольника
Периметр треугольника — это сумма всех трех его сторон. Мы можем рассчитать периметр по следующей формуле:
Периметр треугольника = сумма всех трех сторон |
Если a, b и c — стороны треугольника, то
Периметр треугольника = a + b + c
Кроме того, единица измерения периметра треугольника такая же, как и единицы длины его сторон. В случае, если единицы длины его сторон различаются, сначала преобразуйте их в одинаковые единицы.
В случае, если единицы длины его сторон различаются, сначала преобразуйте их в одинаковые единицы.
Пример 1 : Найдите периметр данного треугольника.
Здесь стороны треугольника равны AB = 3 см, BC = 4 см и AC = 3 см
Периметр треугольника = сумма всех трех сторон
Следовательно, периметр данного треугольника = 3 см + 4 см + 3 см = 10 см
Периметр равнобедренного треугольника:
Периметр равнобедренного треугольника = a + b + c
Здесь стороны AB и AC равны по длине, поэтому мы можем записать приведенную выше формулу, как показано ниже.
Периметр равнобедренного треугольника = a + a + c или b + b + c
Это также может быть записано как 2a + c или 2b + c или 2✕ равная сторона + c
Периметр равностороннего треугольника:
Периметр равностороннего треугольника = a + b + c
Как известно, стороны равносторонности равны по длине.
Итак, периметр равностороннего треугольника = a + a + a = 3a
Эту формулу также можно записать как:
Периметр равностороннего треугольника = сторона 3 ✕
Использование периметра треугольника в повседневной жизни
Ниже приведены примеры использования периметра треугольника в повседневной жизни:
Интересные факты |
Как найти периметр треугольника (формула и видео) // Репетиторы.com
Периметр треугольника (формула и примеры)
видео Определения Формула Примеры Вызов
Возможно, один из самых простых способов работы с многоугольниками — это найти их периметр или расстояние по их сторонам. Треугольник — самый простой многоугольник, поэтому найти его периметр несложно!
Что вы узнаете:
Пройдя этот урок и видео, вы сможете:
- Определить периметр
- Распознавать типы треугольников
- Вспомните и объясните метод нахождения периметра треугольников
- Определите длины сторон треугольника с помощью алгебры, если известен периметр
Что такое периметр?
Периметр — это расстояние по сторонам многоугольника или другой формы. Периметр — это всегда та же линейная единица измерения, что и для сторон.
Периметр — это всегда та же линейная единица измерения, что и для сторон.
В равностороннем треугольнике ниже △ WUT имеет стороны WU, UT и TW. Маленькие отметки по бокам показывают, что все три стороны одинаковы, поэтому размер WU, равный 27 метрам, также верен для двух других сторон.
[вставить равносторонний △ WUT, как описано]
Чтобы найти периметр треугольника, сложите длины трех сторон:
П = 27 + 27 + 27
P = 81 метр
Классификация треугольников
Треугольник — это трехсторонняя плоская форма, закрывающаяся в пространстве.Три стороны образуют три внутренних угла. Треугольники бывают разных конфигураций, в зависимости от вашего выбора, чтобы сфокусироваться на их сторонах или углах:
Сторонами
- Равносторонний — три стороны одинаковой длины
- Равнобедренный — Две стороны равной длины, называемые ногами
- Скален — без сторон одинаковой длины
По углам
- Острый — Три внутренних угла <90 °
- Тупой — один внутренний угол> 90 °
- Справа — один внутренний угол = 90 °
Острый и тупой треугольники относятся к категории наклонный треугольник s, что означает, что у них нет прямых углов.
Формула периметра треугольника
Вы можете найти периметр каждого из этих треугольников, используя следующую формулу:
Это всегда верно, если P — периметр, а a, b и c — длины сторон.
Периметр равносторонних треугольников
Только с равносторонними треугольниками можно заменить умножением на сложение. Поскольку у равносторонних треугольников три равные стороны, P = 3 × a или P = 3a, где P — периметр, а a — длина любой стороны.
Как найти периметр треугольника
Вот разносторонний треугольник DOT с измеренными сторонами 9 ярдов, 11 ярдов и 13 ярдов:
[вставить △ ТОЧКА, как описано]
Сложите три длины:
П = 9 + 11 + 13
P = 33 ярда
Вот равнобедренный треугольник LEG с размером основания 175 мм. Измеряется только одна ножка, LE = 200 мм.
[вставить △ НОЖКА, как описано]
Какова длина бокового GL? Они не сказали вам, как долго был GL!
Думай. Все будет хорошо.
Все будет хорошо.
В равнобедренном треугольнике другая сторона равна идентифицированной стороне, поэтому вы также знаете, что GL = 200 мм! Сложите стороны:
P = 175 + 200 + 200
P = 575 мм
Вызов по периметру алгебры
Некоторые учебники и учителя математики могут взять простую концепцию, например, периметр треугольников, в сложную задачу. Вот △ ЯК с заданным периметром 118 км (да, это большой треугольник), но стороны обозначены необычным образом.
[вставить △ YAK, как описано]
У нас есть сторона YA как «5 более чем в два раза больше», и YK как «10 меньше, чем в шесть раз больше того же числа», а сторона AK как «15 больше, чем в четыре раза больше загадочного числа». Что нам со всем этим делать?
Превратите каждое предложение в алгебраическое выражение. Пусть x будет неизвестным числом:
«5 более чем в два раза больше» становится:
2x + 5 =
лет назад«10 меньше, чем в шесть раз больше того же числа» становится:
6x — 10 =
йен«Загадочное число в 15 раз больше, чем в четыре раза» становится:
4x + 15 = АК
Периметр — это сумма сторон, поэтому, если сложить эти выражения вместе, получится:
2x + 5 + 6x — 10 + 4x + 15 = 118 км
Объедините термины:
12x + 10 = 118 км
Вычтите 10 с обеих сторон, чтобы изолировать переменную:
12x = 108 км
Разделите обе стороны на 12:
x = 9 км
Вернитесь к каждому выражению и замените x на 9 км:
2x + 5 =
лет назад2 (9) + 5 =
YA23 =
YA.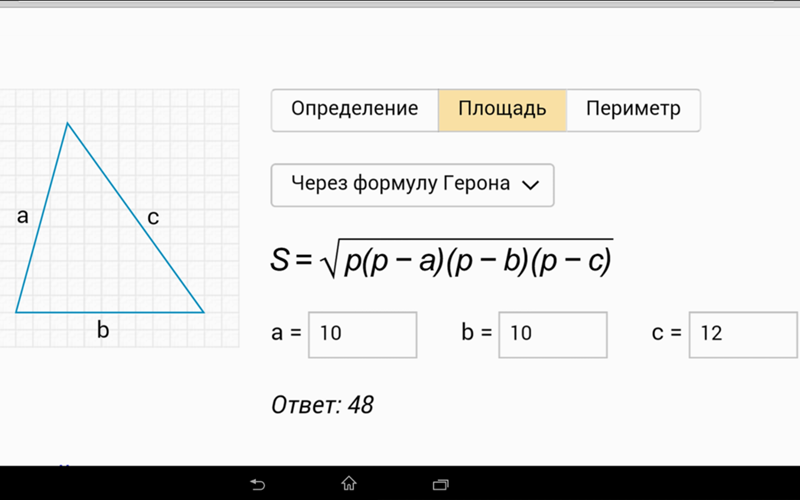 ..
..
6x — 10 =
йен6 (9) — 10 =
йен44 =
юаней…
4x + 15 = АК
4 (9) + 15 = АК
51 = АК
Чтобы подтвердить наши стороны, добавьте, чтобы проверить, равны ли они заданному периметру:
23 + 44 + 51 = 118 км
Молодец! Вы использовали алгебру для решения задачи о периметре!
Краткое содержание урока
Теперь, когда вы прошли урок, вы можете определять периметр, распознавать типы треугольников, вспоминать и объяснять метод определения периметра треугольников путем сложения длин их сторон и, учитывая периметр, решать для длин сторон треугольника с помощью алгебры.
Следующий урок:
Как найти периметр прямоугольника
Математическое выражение: периметр треугольника
ЧАСТЬ 2
00:00: 04.020
Разобравшись с основами периметра треугольника, давайте посмотрим на нем несколько примеров.
00:00: 12. 010
010
Найдите периметр этого треугольника, когда его стороны равны 3 см, 4 см и 5 см.
00:00: 22.090
Начнем с формулы для периметра треугольника «P», равного a + b + c.
00:00: 30.180
Одна из сторон составляет 3 см. Следовательно, мы можем заменить «а» на 3.
00: 00: 38.200
Точно так же мы можем заменить «b» на «4» и заменить «c» на 5.
00: 00: 47.130
Давайте упростим это. 4 складывается с 5, дает 9. 3 складывается с 9, дает 12.
00: 00: 59.130
Теперь у нас P равно 12.
00: 01: 04.010
Обратите внимание, что это число не имеет значения, если мы не укажем для него единицу измерения.
00: 01: 10.030
Поскольку эти длины указаны в сантиметрах, единицей измерения периметра также будет сантиметр.
00: 01: 17.070
Следовательно, периметр этого треугольника равен 12 сантиметрам.
00: 01: 24.130
В следующем примере периметр этого треугольника составляет 21 фут. Его стороны длиной 7 футов, 9 футов и x футов. Найдите x.
Найдите x.
00: 01: 40.070
Опять же, мы начинаем с формулы для периметра треугольника: «P» равно a + b + c.
00: 01: 49.190
Поскольку периметр задан как 21 фут, мы можем заменить ‘P’ на 21.
00: 01: 57.090
Теперь длина одной из сторон задается как x. Следовательно, мы можем заменить «a» на x.
00: 02: 06.090
Точно так же мы можем заменить «b» на 7, а «c» на 9.
00: 02: 15.090
Мы можем упростить это уравнение, добавив 7 к 9. Это дает 16.
00: 02: 22.210
Теперь у нас есть x + 16, что равно 21.
00: 02: 29.080
Давайте перепишем это так, чтобы оно выглядело аккуратнее.
00: 02: 33.200
Обратите внимание: чтобы найти x, нам нужно удалить 16.
00: 02: 39.230
Мы можем сделать это, добавив -16 к обеим сторонам уравнения. Следовательно, получаем, что x равно 21 минус 16.
00: 02: 53.060
21, минус 16, получаем 5.
00: 02: 57.210
Теперь у нас есть x, равное 5. Обратите внимание, что важно включить единицу измерения.
Обратите внимание, что важно включить единицу измерения.
00:03:07.130
Отсюда очевидно, что у нас есть 5 футов.
00: 03: 12.200
Наконец, x = 5 футов.
00: 03: 18.010
Это все для урока. Попробуйте ответить на практический вопрос, чтобы углубить свое понимание.
Как найти периметр треугольника
Определение расстояния вокруг треугольника — это определение периметра треугольника. Вот пошаговое руководство, как найти периметр треугольника тремя разными способами.
Существует три основных метода определения периметра прямоугольного треугольника.
- Если указаны длины сторон, сложите их.
- Найдите недостающую сторону, используя теорему Пифагора.
- Если мы знаем информацию о сторонах, углах, сторонах, найдите недостающую сторону, используя закон косинусов.
Как
найти периметр треугольника, когда известны три длины сторон- Запомните и запишите формулу для нахождения периметра треугольника.

Для треугольника со сторонами a , b и c периметр P определяется как
- Посмотрите на свой треугольник и определите длины трех сторон.
Например: Пусть три стороны треугольника равны a = 5 см, b = 4 см, c = 2 см
- Сложите три стороны длины вместе, чтобы найти периметр.
- Не забудьте добавить единиц к окончательному ответу.
Следовательно, ответ — 11 см.
Как
Найти периметр прямоугольного треугольника, когда известны две стороныПрямоугольный треугольник — это треугольник, имеющий один прямой (90 градусов) угол. Сторона треугольника, противоположная прямому углу, всегда является самой длинной стороной и называется гипотенузой.
- Напомним теорему Пифагора. Теорема Пифагора говорит нам, что для любого прямоугольного треугольника со сторонами длиной a и b и гипотенузой длины c a 2 + b 2 = c 2
- Обозначьте стороны «a, ”“ B ”и“ c ” и самая длинная сторона треугольника будут находиться напротив прямого угла и должны быть помечены как c .

- Введите длины сторон, которые вы знаете, в теорему Пифагора.
Например, вы знаете, что сторона a = 3 и сторона b = 4 , затем подставьте эти значения в формулу следующим образом: 3 2 + 4 2 = c 2 . - Решите уравнение, чтобы найти недостающую длину стороны.
- Сложите длины трех сторон, чтобы найти периметр.
P = a + b + c
P = 3 + 4 + 5
P = 12
Как
Найти периметр бокового треугольника по закону косинусов Закон косинусов Косинусы позволяют решить любой треугольник, если вам известны длины двух сторон и измерение угла между ними.Работает на любом треугольнике. Закон косинусов гласит, что для любого треугольника со сторонами a , b и c с противоположными углами A , B и C : c 2 = a 2 + b 2 — 2ab cos (C) .
- Посмотрите на свой треугольник и присвойте переменные буквы его компонентам.
Например, треугольник с длинами сторон 12 и 14 и углом между ними 110 °.Мы назначим переменные следующим образом: a = 12, b = 14, C = 110 °
- Подставьте ваши данные в уравнение и решите для стороны c.
- Используйте длину стороны c , чтобы найти периметр треугольника.
P = a + b + c
P = 12 + 14 + 21.32
P = 59.32
Периметр прямоугольного треугольника — DewWool
Периметр треугольника можно определить как сумму всех трех сторон.В большинстве случаев формула для периметра проста как a + b + c. Но в некоторых случаях одна или две стороны могут быть неизвестны. Таким образом, мы должны применить некоторые теоремы или использовать некоторые формулы, чтобы найти периметр. В этой статье мы рассмотрим методы, как узнать периметр прямоугольного треугольника
В этой статье мы рассмотрим методы, как узнать периметр прямоугольного треугольника
- Простой метод: сложить все стороны
- Теорема: использовать теорему Пифагора для вычисления гипотенузы.
- Используйте закон косинусов, чтобы найти неизвестную сторону
- Используйте закон синуса [a sin A = b sin B = c sin C]
- Используйте формулу для площади
Это основной метод определения периметра прямоугольного треугольника. Складываем все стороны треугольника.
Формула периметра прямоугольного треугольника = a + b + c
Например, в приведенном ниже случае:
Метод 1: сложите все стороны треугольникаa = 4 см; b = 3 см и c = 5 см
Периметр этого прямоугольного треугольника будет = a + b + c = 4 + 3 + 5 = 12 см. Единицей измерения периметра всегда будет см, м, км и т. Д.
Единицей измерения периметра всегда будет см, м, км и т. Д.
Иногда бывает, что мы не знаем всех сторон прямоугольного треугольника. Предположим, что если нам неизвестна сторона, противоположная прямому углу (90 o ), то мы можем использовать теорему Пифагора, чтобы найти ее.
Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон.
c 2 = a 2 + b 2
Периметр треугольника, когда гипотенуза неизвестнаНа изображении выше a = 4; b = 3; c неизвестно. Мы можем найти это по теореме Пифагора.
с 2 = 4 2 + 3 2
c = sqrt (25)
с = 5
3) Использование закона косинусов Этот закон можно использовать, когда какая-либо одна сторона неизвестна, и мы знаем меру противоположного угла. Этот закон применим к любому треугольнику в целом.
Этот закон применим к любому треугольнику в целом.
В приведенном выше уравнении неизвестная сторона — это c, a и b известны, а y — угол, противоположный неизвестной стороне. Если c — гипотенуза, тогда y будет 90 o . Поскольку cos (90) равен нулю, уравнение сводится к sqrt (a 2 + b 2 ). Это доказывает, что этот закон согласуется с теоремой Пифагора.
периметр прямоугольного треугольника, когда заданы две стороны и хотя бы один уголНапример, на изображении выше две стороны известны как 3 см и 4.24 см (гипотенуза), длина стороны x неизвестна. Применяя закон косинуса, получаем:
x = sqrt {(3) 2 + (4,24) 2 — 2 * 3 * 4,24} = ~ 3 см
Проверим наш ответ с помощью теоремы Пифагора:
LHS: квадрат гипотенузы = (4,24) 2 = ~ 18
RHS: сумма квадратов двух других сторон = (3) 2 + (3) 2 = 18
LHS = RHS. Значит, наш ответ проверен.
Значит, наш ответ проверен.
Теперь мы можем вычислить периметр прямоугольного треугольника, который является суммой трех сторон: 3 + 3 + 4.24 = 13,24 см.
Вы можете использовать этот инструмент для вычисления значений косинуса.
4) Использование закона синусовЭтот закон можно использовать, когда известны как минимум два угла и две стороны. Этот закон также можно использовать в сочетании с другими законами и формулами для определения периметра любого треугольника. В прямоугольном треугольнике мы уже знаем один угол как 90 o , поэтому этот закон может быть предпочтительным для вычисления периметра прямоугольных треугольников.
Закон синусов Периметр прямоугольного треугольника, когда заданы два угла и хотя бы одна сторонаВ приведенном выше примере известны две стороны и два угла. Вычислим неизвестную сторону x, используя закон синусов.
грех (45) / х = грех (45) / 3
х = 3
Давайте проверим наш ответ, используя также и другую сторону.
грех (45) / х = грех (90) /4,24
0,707 / х = 1 / 4,24
x = 0,707 * 4,240 = 3 см
Значит, наш ответ проверен.Этот метод очень полезен, когда известны два угла и хотя бы одна сторона. Периметр этого прямоугольного треугольника теперь можно рассчитать как 3 + 3 + 4,24 = 10,24 см.
Вы можете использовать этот инструмент для вычисления значений синуса.
5) Используя формулу площади прямоугольного треугольникаМы видели случаи, когда известны все три стороны или известны хотя бы две стороны. Бывают случаи, когда известна только одна сторона. Затем требуется, чтобы мы использовали 2 или более формул, чтобы прийти к периметру прямоугольного треугольника.
Мы знаем, что формула площади прямоугольного треугольника равна ab / 2. Это уравнение можно использовать с другими законами, если известны две стороны. Затем мы можем решить два уравнения с двумя переменными, чтобы получить две другие стороны, а затем соответственно вычислить периметр прямоугольного треугольника.
В приведенном выше примере площадь = 4 см 2 , а одна сторона известна как 3 см.
Формула площади прямоугольного треугольника = a * b / 2
6 = 1/2 * 3 * (х)
x = 4 см
Теперь давайте вычислим гипотенузу по теореме Пифагора:
H 2 = 3 2 + 4 2
H = 5 см
Следовательно, периметр этого треугольника будет: 3 + 4 + 5 = 12 см.
Численные задачи по периметру прямоугольного треугольникаНайдите периметр прямоугольных треугольников, показанных ниже:
Найдите периметр прямоугольного треугольникаЗдесь мы знаем два угла (A = 60 и B = 30) и одну сторону (c = 12). В этом сценарии мы можем использовать закон синусов:
а / грех (60) = 12 / грех (90)
а / 0,866 = 12/1
a = 10,4 см
Найдите периметр прямоугольного треугольника Здесь известна площадь прямоугольного треугольника и длина одной стороны (b = 12).
Площадь = ab / 2 = (a * 12) / 2
36 = а * 6
a = 6 см
с использованием теоремы Пифагора,
c = sqrt (144 + 36)
c = 13,4 см
Периметр = a + b + c = 12 + 6 + 13,4 = 31,4 см
Найдите периметр этого прямоугольного треугольникаЗдесь представлены две стороны (c = 7,01 см и b = 5 см) и один угол (A = 45 o ). Здесь мы можем применить закон косинуса, чтобы найти неизвестную сторону.
а = sqrt (49,14 + 25 — 24,5)
а = 5,9
Следовательно, периметр прямоугольного треугольника будет = 5 + 5,9 + 7,01 = 16,91 см
Найдите периметр этого прямоугольного треугольникаВот один угол (B = 45 o ) и одна сторона (c = 7,01 см). Мы можем использовать закон синусов, чтобы найти две другие стороны. Мы можем найти другой угол A = 45 o (используя A + B + C = 180).
Sin45 / a = sin (90) / 7,01
а = ~ 5 см
sin45 / b = sin (90) / 7. 01
01
b = ~ 5 см
Следовательно, периметр = 5 + 5 + 7,01 = 17,01 см
См. ТакжеПлощадь треугольника — веб-формулы
Треугольник — это многоугольник с тремя сторонами, который можно разделить на следующие типы:
· Равносторонний треугольник имеет равные стороны и равные углы.
· Равнобедренный треугольник имеет две равные стороны и два равных угла.
· Разносторонний треугольник имеет три неравные стороны и три неравных угла.
· Прямоугольный треугольник имеет один прямой угол (90 °).
· Остроугольный треугольник имеет все углы менее 90 °.
· Тупоугольный треугольник имеет один угол больше 90 °.
Периметр треугольника = Сумма трех сторон.
На рисунке рядом с ΔABC периметр представляет собой сумму AB + BC + AC.
Площадь треугольника определяется как:
A = ½ × основание × высота
Любая сторона треугольника может считаться его основанием.
Тогда длина перпендикулярной линии от противоположной вершины принимается за соответствующую высоту или высоту.
Таким образом, на приведенном выше рисунке площадь задается как: ½ × AC × BD .
Дополнительные формулы для определения площади треугольника:
Площадь треугольника = √ (s (sa) (sb) (sc)) по формуле Герона (или формуле Героя), где a , b и c — длины сторон треугольника, и s = ½ ( a + b + c ) — это полупериметр треугольника.
Площадь равностороннего треугольника
A = √ (3) · ¼ · сторона, где сторона = a = b = c
Площадь равнобедренного треугольника
A = ¼ · b · √ (4a 2 — b 2 )
Площадь прямоугольного треугольника
A = ½ × Произведение сторон, содержащих прямой угол.
Если даны две стороны и угол между ними, то площадь треугольника можно определить по следующей формуле:
Площадь = ½ · a · b · sinC = ½ · b · c · sinA = ½ · a · c · sin B
Пример 1: Найдите площадь треугольника с основанием 14 см и высотой 10 см.
Решение :
b = 14 см
h = 10 см
A = ½ · 14 · 10 = 70 см 2
Пример 2: Найдите площадь треугольника, стороны и угол между которыми задаются следующим образом:
a = 5 см и b = 7 см
C = 45 o
Решение:
Площадь треугольника = ½ · a · b · sinC
Площадь = ½ × 5 × 7 × 0. 707 (поскольку sin 45 ° = 0,707)
707 (поскольку sin 45 ° = 0,707)
Площадь = ½ × 24,745 = 12,3725 м 2
Пример 3: Найдите площадь (в м 2 ) равнобедренного треугольника со сторонами 10 м и основанием 12 м.
Решение:
Площадь равнобедренного треугольника определяется по:
A = ¼ · b · √ (4a 2 — b 2 )
A = ¼ · 12 · √ (4 (10) 2 — (12) 2 )
A = 48 м 2
Пример 4: Найдите площадь треугольника со сторонами 8, 9 и 11 соответственно.Все единицы измеряются в метрах (м).
Решение :
Дано: стороны a = 8, b = 9 и c = 11
Согласно формуле Герона площадь треугольника может быть определена по следующей формуле:
A = √ (s (s-a) (s-b) (s-c))
Прежде всего, нам нужно определить s, который является полупериметром треугольника:
s = ½ ( a + b + c ) = ½ ( 8 + 9 + 11 ) = 14
Теперь, подставив значение полупериметра в формулу Герона, мы можем определить площадь треугольника:
A = √ ( s · ( s-a ) · ( s-b ) · ( s-c ))
A = √ ( 14 · ( 14-8 ) · ( 14-9 ) · ( 14-11 ))
A = √ ( 1260 ) = 35. 50 м 2
50 м 2
Пример 5: Фермер Муннабхай владеет треугольным участком земли. Длина забора АВ — 150 м. Длина забора БЦ 231 м. Угол между ограждением AB и ограждением BC составляет 123º.
Сколько земли в собственности фермера Муннабхаи?
Решение: Прежде всего мы должны решить, какие длины и углы нам известны:
- AB = c = 150 м
- г. до н.э. = а = 231 м
- и угол B = 123º
Для определения площади земли мы можем использовать следующую формулу:
Площадь = ½ · c · a · sin B
Площадь = ½ × 150 × 231 × sin (123º)
Площадь = 17,325 × 0.8386
Площадь = 14 529 м 2
Таким образом, у фермера Муннабхаи 14 529 м 2 земли.


 ..
.. 1f'))
print( 'Perimeter is: ', format(perim,',.1f'))
1f'))
print( 'Perimeter is: ', format(perim,',.1f'))
 Используя его, определите функцию trianglePerimeter (xA, yA, xB, yB, xC, yC), которая вычисляет периметр треугольника, тремя точками которого являются (xA, yA), (xB, yB) и (xC,…
Используя его, определите функцию trianglePerimeter (xA, yA, xB, yB, xC, yC), которая вычисляет периметр треугольника, тремя точками которого являются (xA, yA), (xB, yB) и (xC,…