Дуга окружности это: Дуга окружности | это… Что такое Дуга окружности?

Длина дуги окружности калькулятор и формулы

{L = \dfrac{\pi R \alpha}{180\degree}}

Найти длину дуги

через радиус и уголпо формуле Гюйгенса

Радиус окружности R

ммсмдммкмдюймы (in)футы (ft)

Угол α

градусы (°)радианы (рад)грады (град)обороты (об)минуты (′)секунды (″)миллирадианымикрорадианы

Результат в

ммсмдммкмдюймы (in)футы (ft)

Виджет

Ссылка на расчет

Сообщить об ошибке

Сохранить расчет

Печатать

Длина дуги окружности — важный параметр, который используется в геометрии и математике для решения различных задач. На этой странице приведены две формулы для расчета длины дуги окружности — через радиус и угол между радиусами и по формуле Гюйгенса.

Также вы можете рассчитать длину дуги окружности с помощью калькулятора, которые используют эти формулы.

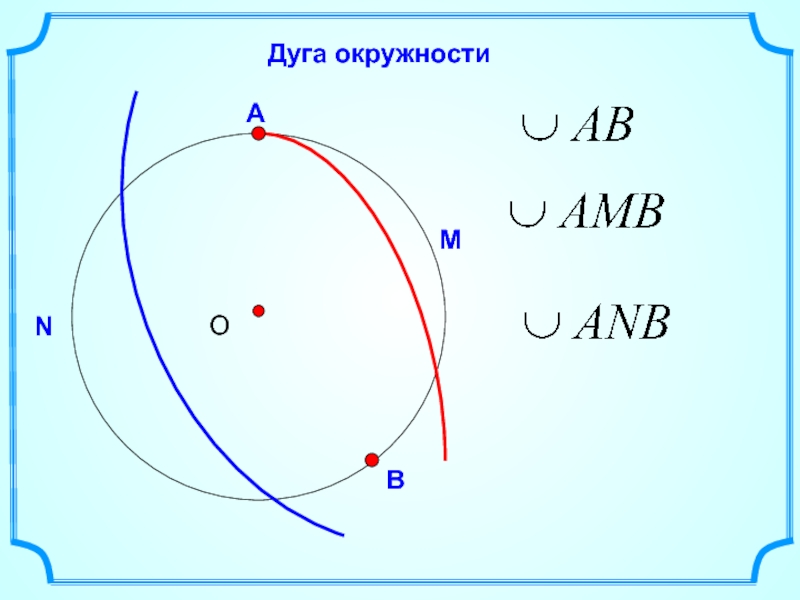
Дуга — одно из двух подмножеств окружности, на которые её разбивают любые две различные принадлежащие ей точки. Любые две точки окружности разбивают её на две части, при этом каждая из частей является дугой.

Содержание:

1. калькулятор длины дуги окружности
2. формула длины дуги окружности через радиус и угол
3. формула длины дуги окружности по формуле Гюйгенса
4. примеры задач

Если обобщить, то дуга окружности — это часть окружности, ограниченная двумя ее точками. Ниже приведены несколько примеров дуг окружностей:

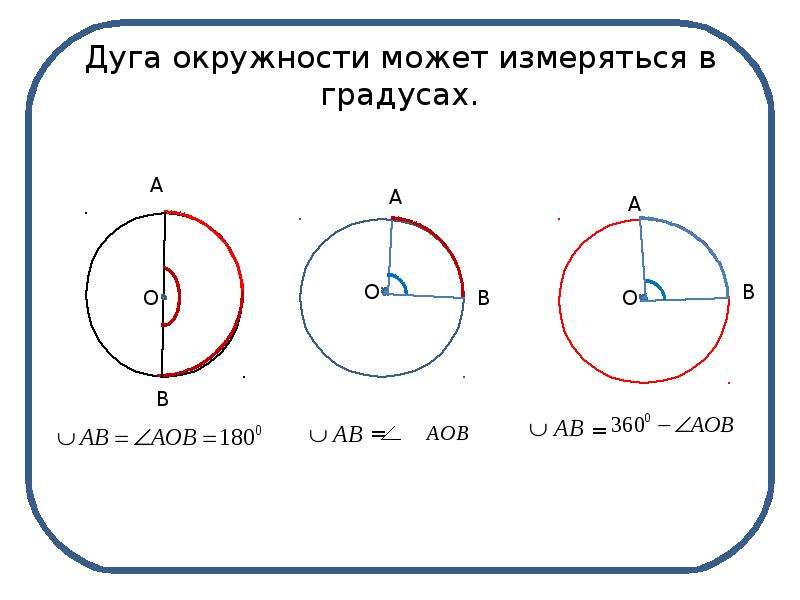
• Полная окружность — это дуга, которая охватывает всю окружность. Угол, определяющий полную окружность, равен 360° или 2π радиан. Длина дуги полной окружности равна общей длине окружности, которая может быть вычислена по формуле

  L = 2πr, где r — радиус окружности.

• Полуокружность — это дуга, которая охватывает половину окружности. Угол, определяющий полуокружность, равен 180° или π радиан. Длина дуги полуокружности равна половине общей длины окружности и может быть вычислена по формуле L = πr.

• Сектор окружности — это область, ограниченная дугой окружности и двумя ее радиусами.

Это только несколько примеров дуг окружности. Дуги могут быть разных размеров и форм, в зависимости от угла, определяющего их, и расположения на окружности.

Формула длины дуги окружности через радиус и угол

{L = \dfrac{\pi R \alpha}{180\degree}}

R — радиус окружности

α — центральный угол (угол между радиусами)

в градусах

{L = R \alpha}

R — радиус окружности

α — центральный угол (угол между радиусами) в радианах

Формула длины дуги окружности по формуле Гюйгенса

{L \approxeq 2m + \dfrac{2m-M}{3}}

m — длина хорды m

M — длина хорды M

Обратите внимание, что в данной формуле используется не привычный знак равно «=», а знак «равно или почти равно», который записывается так — «\approxeq». Это связано с тем, что формула Гюйгенса дает погрешность при вычислении. Хоть величина погрешности невелика, знать об этом надо.

Относительная погрешность формулы Гюйгенса составляет порядка 0,5% когда угол дуги равен 60°. Если же угловая мера дуги уменьшается, то уменьшается и погрешность. Например, для дуги в 45° относительная погрешность будет равна примерно 0,02%.

Примеры задач на нахождение длины дуги

Задача 1

Найдите длину дуги окружности радиуса 6см, если ее градусная мера равна 30.

Решение

Для решения этой задачи нам подойдет первая формула. Подставим в нее значение радиуса и угла и произведем вычисления:

L = \dfrac{\pi R \alpha}{180\degree} = \dfrac{\pi \cdot 6 \cdot 30\degree}{180\degree} = \dfrac{\pi \cdot 180\degree}{180\degree} = \pi \: см \approx 3.14 \: см.

Ответ: {\pi \: см \approx 3.14 \: см.}

Введем известные значения в калькулятор для проверки полученного ответа.

Задача 2

Найдите длину дуги окружности радиуса 3см, если ее градусная мера равна 150 градусов.

Решение

Задача аналогична предыдущей. Также воспользуемся первой формулой.

L = \dfrac{\pi R \alpha}{180\degree} = \dfrac{\pi \cdot 3 \cdot 150\degree}{180\degree} = \dfrac{\pi \cdot 3 \cdot 5}{6} = \dfrac{\pi \cdot 5}{2} = \dfrac{5}{2} \pi \: см = 2.5 \pi \: см \approx 7.85398 \: см.

Ответ: {2.5 \pi \: см \approx 7.85398 \: см.}

В проверке ответа нам снова поможет калькулятор .

Длина дуги окружности имеет множество применений в математике и ее приложениях. Например, она используется для вычисления длины дуги графика функции, заданной в полярных координатах. Также длина дуги окружности используется при вычислении пути, пройденного телом при движении по окружности, а также для вычисления объема тела, полученного путем вращения дуги окружности вокруг ее диаметра.

Создание дуг окружностей—ArcGIS Pro | Документация

На панели Создать объекты среди инструментов построения линейных и полигональных объектов есть метод создания дуг окружности. Они доступны на панели инструментов построения и в контекстном меню при создании объекта.

Дуга окружности — это часть линии круга. Геометрия задается радиусом и длиной хорды либо углом дельта. Вы можете создавать их в виде части непрерывной линии или контура полигона или как двухточечный дуговой элемент.

Шаги для получения линии или дуги из сегмента см. в разделе Изменение сегментов объектов.

Создание сегмента дуги

Сегмент дуги задается начальной точкой, точкой, через которую проходит дуга, и конечной точкой. Вы можете поставить все эти три точки, перетащить курсор либо указать радиус либо воспользоваться диалоговым окном дуги окружности, чтобы задать значения для геометрии.

1. На панели Каталог выполните следующие действия для добавления слоя полилиний к своей карте:
   • Разверните Базы данных , затем базу, содержащую ваши данные, и перетащите класс объектов на карту.
   • Щелкните правой кнопкой базу данных по умолчанию и создайте новый линейный или полигональный класс объектов.

   Перетаскивание на карту или создание класса объектов приводит к добавлению слоя на текущую карту и созданию шаблона объектов с настройками по умолчанию.

2. На закладке Редактирование в группе Замыкание задайте свои предпочтительные настройки замыкания.
3. Если вы работаете с объектами, имеющими z-значения, на вкладке Редактировать в группе Высота выберите способ добавления z-значений к объектам.

   Шаги для добавления z-значений при создании объектов с z-значениями см. в разделе Указание высоты для 3D-объектов.
4. На вкладке Редактировать в группе Объекты щелкните Создать .

   Появится панель Создать объекты.

5. На панели щелкните шаблон полилинейного или полигонального объекта.
   • Для создания вершины линии щелкните Линия .
   • Чтобы создать вершину полигона, щелкните Полигон.

   Внизу карты появляется панель инструментов Построение.

6. На панели инструментов построения щелкните инструмент Сегмент дуги .
7. Создайте начальную точку одним из следующих способов:
   • Щелкните карту.
   • Щелкните правой кнопкой мыши и используйте команды в контекстном меню, чтобы задать координаты x,y,z местоположения, а также расстояние и направление.
   • Начальной точкой является последняя точка предыдущего сегмента.
8. Создайте вторую точку, которая описывает путь дуги, одним из следующих способов:
   • Щелкните карту.
   • Щелкните правой кнопкой мыши и используйте команды в контекстном меню, чтобы задать координаты x,y,z местоположения, а также расстояние и направление.

   Путь дуги замкнется на эту новую точку.

9. Создайте конечную точку и задайте радиус, используя один из следующих способов:
   • Переместите указатель мыши, чтобы задать радиус, и снова щелкните на карте, чтобы создать конечную точку.
   • Нажмите клавишу R, введите радиус, нажмите Enter и щелкните карту, чтобы создать конечную точку.
   • Щелкните правой кнопкой, нажмите Дуга окружности , укажите радиус и другие значения геометрии и нажмите Enter, чтобы закрыть диалоговое окно и создать дугу.

     Значения геометрии по умолчанию для новой дуги основаны на расположении точек, которые вы нарисовали на карте.

10. Чтобы продолжить создание остальных сегментов дуги, используйте инструменты на панели инструментов построения.
11. На панели инструментов построения нажмите Готово или нажмите клавишу F2.

Создание дуги по конечным точкам

Сегмент дуги по конечным точкам задается начальной точкой, конечной точкой и радиусом. Вы можете поставить все эти три точки, перетащить курсор либо указать радиус, или воспользоваться диалоговым окном дуги окружности, чтобы задать значения ограничений для геометрии.

1. На панели Каталог выполните следующие действия для добавления слоя полилиний к своей карте:
   • Разверните Базы данных , затем разверните базу, содержащую ваши данные, и перетащите класс объектов на карту.
   • Щелкните правой кнопкой базу данных по умолчанию и создайте новый линейный или полигональный класс объектов.

   Перетаскивание на карту или создание класса объектов приводит к добавлению слоя на текущую карту и созданию шаблона объектов с настройками по умолчанию.

2. На закладке Редактирование в группе Замыкание задайте свои предпочтительные настройки замыкания.
3. На вкладке Редактировать в группе Объекты щелкните Создать .

   Появится панель Создать объекты.

4. На панели щелкните шаблон полилинейного или полигонального объекта.
   • Для создания вершины линии щелкните Линия .
   • Чтобы создать вершину полигона, щелкните Полигон.

   Внизу карты появляется панель инструментов Построение.

5. Если вы работаете с объектами, имеющими z-значения, на вкладке Редактировать в группе Высота выберите способ добавления z-значений к объектам.

   Шаги для добавления z-значений при создании объектов с z-значениями см. в разделе Указание высоты для 3D-объектов.

6. На панели инструментов построения щелкните инструмент Сегмент дуги конечной точки .

   Вы можете выбирать между прямыми и дуговыми сегментами в любой момент создания объекта.

7. Создайте начальную и конечную точки дуги одним из следующих способов:
   • Щелкните карту.
   • Щелкните правой кнопкой мыши и используйте команды в контекстном меню, чтобы задать координаты x,y,z местоположения, а также расстояние и направление.
   • Начальной точкой является последняя точка предыдущего сегмента.

   Между начальной и конечной точками будет создана дуга.

8. Создайте конечную точку и задайте радиус, используя один из следующих способов:
   • Переместите курсор, чтобы задать радиус, и щелкните на карте.
   • Нажмите клавишу R, введите радиус и нажмите Enter.
   • Щелкните правой кнопкой, нажмите Дуга окружности , укажите радиус и другие значения геометрии и нажмите Enter, чтобы закрыть диалоговое окно и создать дугу.

     Значения геометрии по умолчанию для новой дуги основаны на расположении точек, которые вы нарисовали на карте.

9. Чтобы продолжить создание остальных сегментов дуги, используйте инструменты на панели инструментов построения.
10. На панели инструментов построения нажмите Готово или нажмите клавишу F2.

Связанные разделы

---

Отзыв по этому разделу?

Длина дуги — формула, как найти длину дуги

Длину дуги лучше определить как расстояние вдоль части окружности любого круга или любой кривой (дуги). Любое расстояние вдоль изогнутой линии, образующей дугу, называется длиной дуги. Часть кривой или часть окружности окружности называется Дугой. Все они имеют кривую форму. Длина дуги больше, чем любое расстояние по прямой линии между ее концами (хорда).

В частности, длина дуги окружности радиуса r, образующей угол θ в центре, рассчитывается по формуле rθ × (π/180), если угол выражен в градусах, а если угол выражен в радианы, тогда длина дуги равна rθ. Давайте посмотрим, как вывести эти формулы.

1.	Что такое длина дуги?
2.	Формула длины дуги
3.	Как найти длину дуги кривой?
4.	Часто задаваемые вопросы о длине дуги

Что такое длина дуги?

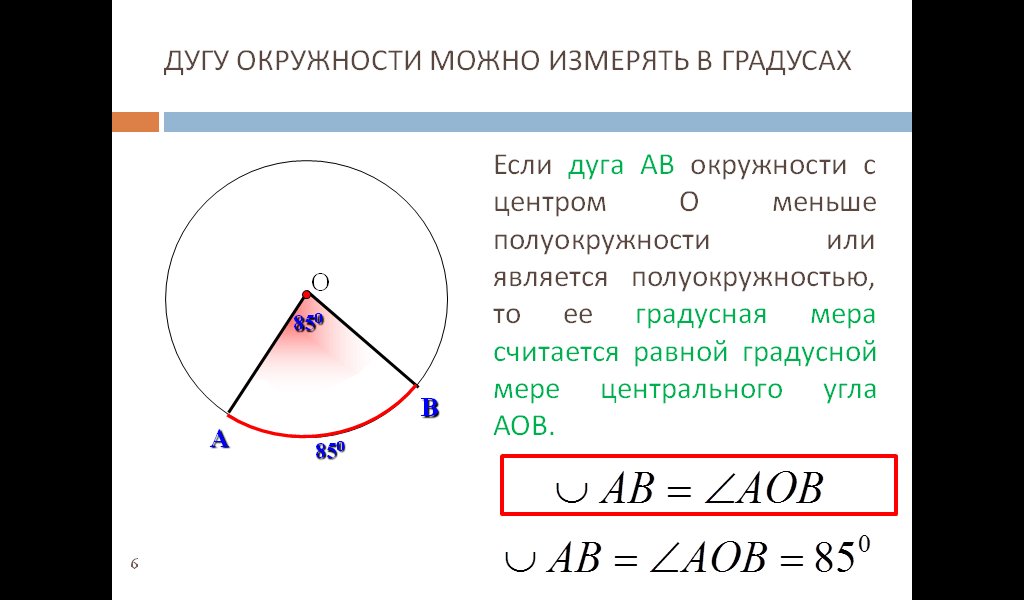
Длина дуги определяется как промежуток между двумя точками на участке кривой. Дуга окружности – это любая часть окружности. Угол, образуемый дугой в любой точке, — это угол, образованный между двумя отрезками, соединяющими центр с конечными точками дуги. Например, в окружности, показанной ниже, OP — это дуга окружности с центром Q. Длина дуги этой дуги OP равна L.

Формула длины дуги

Чтобы вывести формулу длины дуги, вспомним, какова длина полной окружности, радиус которой равен r. Это 2πr. Но дуга — это всего лишь часть (на самом деле часть) всей окружности. Мы знаем, что угол в центре полной окружности равен 360°. Если угол, образуемый дугой, равен θ°, то это означает, что дуга занимает долю θ/360 от общей окружности. Таким образом:

Длина дуги = θ/360 из 2πr = θ/360 × 2πr = rθ × π/180.

Это формула длины дуги, когда угол выражен в градусах. Длину дуги можно рассчитать по разным формулам, исходя из единицы центрального угла дуги. Измерения центрального угла могут быть даны в градусах или радианах, и соответственно мы вычисляем длину дуги окружности.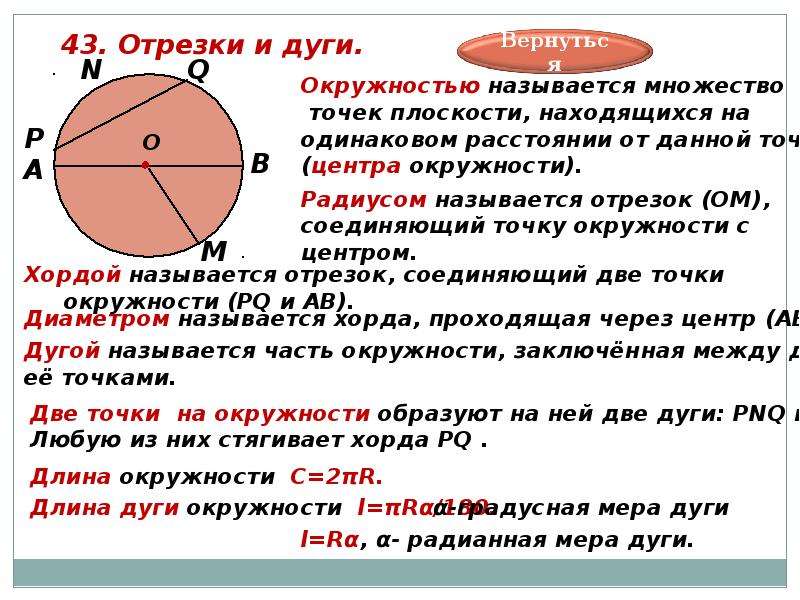

Если θ в радианах, то угол в градусах = θ × 180/π. Подставив это в приведенную выше формулу,

Длина дуги = rθ × π/180 × 180/π = rθ.

Таким образом, формула дуги окружности равна радиусу окружности, умноженному на θ, если угол выражен в радианах.

Формула длины дуги может быть выражена следующим образом:

длина дуги, L = θ × r, когда θ выражено в радианах;

длина дуги, L = θ × (π/180) × r, где θ в градусах,

где,

• L = длина дуги
• θ = центральный угол дуги
• r = радиус окружности

Формула длины дуги в радианах

Длина дуги окружности может быть рассчитана с использованием различных формул, основанных на единице измерения центрального угла дуги. Формула длины дуги в радианах может быть выражена следующим образом:

Длина дуги = θ × r

, где

• L = длина дуги
• θ = Центральный угол дуги в радианах
• r = радиус окружности

Как найти длину дуги кривой?

Длина дуги окружности может быть рассчитана с использованием различных методов и формул на основе заданных данных. Некоторые важные случаи приведены ниже,

• найти длину дуги по радиусу и центральному углу
• найти длину дуги без радиуса
• найти длину дуги без центрального угла

Как найти длину дуги по радиусу и центральному углу?

Длину дуги окружности можно рассчитать с помощью радиуса и центрального угла, используя формулу длины дуги:

• Длина дуги = θ × r, где θ в радианах.
• Длина дуги = θ × (π/180) × r, где θ в градусах.

Как найти длину дуги без радиуса?

Длину дуги окружности можно рассчитать без радиуса, используя:

Центральный угол и площадь сектора:

• Формула площади сектора: (θ/360º) × πr ² , если θ в градусах (или) (1/2) r ² θ, если θ в радианах.
• Используйте эту формулу и найдите радиус ‘r’. Нам нужно использовать квадратный корень в этом процессе.
• Затем найдите длину дуги по соответствующей формуле.

Пример: Рассчитайте длину дуги кривой с площадью сектора 25 квадратных единиц и центральным углом, равным 2 радианам.

Имеем,

Площадь сектора = 25 единиц

Центральный угол = 2 радиана

• Шаг 1: Площадь сектора = 25 ⇒ (1/2) r ² ( 2) = 25
• Шаг 2: Это дает r ² = 25. Извлекая квадратный корень с обеих сторон, r = 5.
• Шаг 3: Длина дуги = rθ = 5 × 2 = 10 шт.

Таким образом, длина дуги = 10 единиц

Центральный угол и длина хорды:

• Формула длины хорды: 2r sin (θ/2).
• Используйте эту формулу и найдите радиус ‘r’.
• Тогда легко найти длину дуги по подходящей формуле.

Пример : Вычислить длину дуги кривой, концы которой касаются хорды окружности размером 5 единиц. Центральный угол, образуемый дугой, равен 2 радианам.

Имеем,

Длина хорды = 5 единиц

Центральный угол = 2 радиана

• Шаг 1: Длина хорды = 5 ⇒ 2r sin (2/2) = 5
• Шаг 2: 2r sin (1) = 5 ⇒ r = 5 / (2 × sin 1) = 2,97 единицы
• Шаг 3: Длина дуги = радиус × центральный угол = 2,97 × 2 = 5,94 единицы

Таким образом, длина дуги = 5,94 единицы

Как найти длину дуги без центрального угла?

Длину дуги окружности можно рассчитать без угла, используя:

Радиус и площадь сектора :

• Подставьте значения радиуса и площади сектора в формулу площади сектора.
• Решите для центрального угла.
• Найдите длину дуги.

Пример: Рассчитайте длину дуги кривой с площадью сектора 25 квадратных единиц и радиусом 2 единицы.

Имеем,

Площадь сектора = 25 единиц

Центральный угол = 2 единицы

• Шаг 1: Площадь сектора = 25 ⇒ (1/2) (2) ² θ = 25,
• Шаг 2: Решая приведенное выше уравнение, мы получаем θ = 12,5 радиан.
• Шаг 3: Длина дуги = радиус × центральный угол = 2 × 12,5 = 25 единиц

Таким образом, длина дуги = 25 единиц

Радиус и длина хорды:

• Подставьте значения радиуса и длины хорды в формулу длины хорды.
• Затем найдите центральный угол.
• Рассчитать длину дуги.

Пример : Вычислить длину дуги кривой, концы которой касаются хорды окружности размером 3 единицы. Радиус круга равен 2 единицам.

Имеем,

Длина хорды = 5 единиц

Центральный угол = 2 единицы

• Шаг 1: Длина хорды = 3 ⇒ 2(2) sin (θ/2) = 3
• Шаг 2: Решая это, получаем: sin (θ/2) = 0,75 ⇒ θ/2 = sin ^-1 (0,75) = 0,848 ⇒ θ = 1,696.
• Шаг 3: Длина дуги = радиус × центральный угол = 2 × 1,696 = 3,392 единицы

Таким образом, длина дуги = 3,392 единицы

☛ Важные примечания по дуге окружности:

Ниже приведены основные моменты концепции длины дуги.

• Длина дуги = θ × r, где θ в радианах.
• Длина дуги = θ × (π/180) × r, где θ в градусах.

☛ Темы, связанные с длиной дуги

Ознакомьтесь с еще несколькими интересными статьями, связанными с длиной дуги, чтобы лучше понять тему.

• Калькулятор длины дуги
• Калькулятор дуги окружности

 

Примеры длины дуги

1. Пример 1: Найдите длину дуги окружности, отсеченной центральным углом 4 радиана в окружности радиусом 6 дюймов.

   Решение:

   Центральный угол, θ = 4 радиана, радиус, r = 6 дюймов. Используйте формулу длины дуги: L = θ × r = 4 × 6 = 24 дюйма.

   Ответ: ∴ Длина дуги (PQ) = 24 дюйма

2. Вопрос 2: Радиус окружности составляет 14 единиц, а дуга стягивается в центре на 65°. Какова длина дуги с использованием длины окружности?

   Решение: Мы знаем, что

   Длина окружности = 2πr

   C = 2π × 14 = 28π

   длина дуги = (θ/360) × C = (65°/360°)28π = 15,882 единицы

   Ответ: Длина дуги = 15,882 единицы.

3. Пример 3: Рассчитайте длину дуги, отсеченной центральным углом θ = 40º в окружности с радиусом 4 дюйма.

   Решение:

   Радиус, r = 4 дюйма, θ = 40º. Используйте формулу длины дуги: L = π × (r) × (θ/180º) = π × (4) × (40º/180º) = 2,79дюймы.

   Ответ: ∴ Длина дуги данного круга = 2,79 дюйма

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных эффектов.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по длине дуги

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о длине дуги

Что такое дуга окружности?

Дуга окружности определяется как длина части окружности, которая лежит между любыми двумя точками на ней. т. е. дуга окружности — это любая часть окружности. Угол, образуемый дугой в любой точке, — это угол, образованный между двумя отрезками прямой, соединяющими эту точку с конечными точками дуги.

Что такое формула длины дуги окружности?

Формула длины дуги окружности включает ее радиус (r) и центральный угол (θ). Обозначается буквой L и рассчитывается как

• по формуле L = rθ × (π/180), если θ выражено в градусах
.
• формула с использованием L = rθ, если θ выражена в радианах

Как найти длину дуги без радиуса?

Чтобы найти длину дуги, нам обязательно нужны радиус окружности и центральный угол. Но когда радиус не указан, то можно было бы указать либо площадь сектора, либо длину хорды. Используйте следующие формулы для определения радиуса, а затем примените формулу длины дуги.

• Площадь сектора = (θ/360º) × πr ² , если θ в градусах (или) (1/2) r ² θ
• Длина хорды = 2r sin (θ/2)

Что вы понимаете под уравнением длины дуги?

Есть два уравнения, связанные с длиной дуги. Ниже приведены два уравнения длины дуги.

• Длина дуги = θ × r, где θ в радианах.
• Длина дуги = rθ × (π/180), где θ в градусах

Как рассчитать длину дуги в радианах?

Длину дуги можно рассчитать, если центральный угол задан в радианах, используя формулу дуги окружности: Длина дуги = θ × r, когда θ выражено в радианах.

• L = длина дуги
• θ = Центральный угол дуги
• r = радиус окружности

Должна ли длина дуги быть в радианах?

Нет, длина дуги не может быть указана в радианах. Это измерение расстояния, поэтому не может быть в радианах. Центральный угол, стягиваемый в центре, может быть выражен в радианах, градусах или угловых секундах соответственно.

Как найти длину окружности дуги?

Если длина дуги (L) дана с центральным углом θ, то длина окружности (C) рассчитывается по уравнению L / C = θ/360º.

Какова длина большой дуги с использованием формулы длины дуги?

Большая дуга в окружности больше, чем полуокружность. Центральный угол больше 180°. Используя формулу ℓ = rθ, мы можем найти длину дуги окружности, где θ в радианах.

Калькулятор длины дуги

Создано Bogna Szyk

Отзыв Стивена Вудинга и Джека Боуотера из площадь дуги и сектора: пример

Часто задаваемые вопросы

Этот калькулятор длины дуги представляет собой инструмент, который может рассчитать длину дуги и площадь сектора круга. В этой статье подробно объясняется формула длины дуги и приводятся пошаговые инструкции о том, как найти длину дуги. Вы также узнаете уравнение площади сектора.

Если вы новичок в кругах, вычисление длины и площади секторов может быть немного сложным, и вам нужно начать с более простых инструментов, таких как длина круга и окружность и площадь круга калькуляторы.

Формула длины дуги

Длина дуги зависит от радиуса окружности и центрального угла θ . Мы знаем, что для угла, равного 360 градусам (2π), длина дуги равна длине окружности. Следовательно, поскольку пропорция между углом и длиной дуги постоянна, мы можем сказать, что:

L / θ = C / 2π

Как длина окружности C = 2πr ,

L / θ = 2πr / 2π

90 493 L / θ = r
Находим формулу длины дуги, когда умножив это уравнение на θ:

L = r * θ

Следовательно, длина дуги равна радиусу, умноженному на центральный угол (в радианах).

Площадь сектора круга

Аналогичным образом можно найти площадь сектора круга. Мы знаем, что площадь всего круга равна πr². Из пропорций

A / θ = πr² / 2π

A / θ = r² / 2

Формула площади сектора:

A = r² * θ / 2

Как найти длина дуги и площадь сектора: пример

1. Определите радиус окружности. Например, она может быть равна 15 см. (Вместо этого вы также можете ввести диаметр в калькулятор длины дуги.)
2. Какой будет угол между концами дуги? Допустим, он равен 45 градусам, или π/4.
3. Рассчитайте длину дуги по приведенной выше формуле: L = r * θ = 15 * π/4 = 11,78 см .
4. Вычислите площадь сектора: A = r² * θ / 2 = 15² * π/4 / 2 = 88,36 см² .
5. Вы также можете использовать калькулятор длины дуги, чтобы найти центральный угол или радиус окружности. Просто введите любые два значения в соответствующие поля и наблюдайте, как он выполняет все расчеты за вас.

Не забудьте также воспользоваться калькулятором уравнения окружности!

Часто задаваемые вопросы

Как найти длину дуги без радиуса?

Чтобы рассчитать длину дуги без радиуса, вам нужен центральный угол и площадь сектора :

1. Умножьте площадь на 2 и разделите результат на центральный угол в радианах.
2. Найдите квадратный корень из этого деления.
3. Умножьте этот корень на центральный угол еще раз, чтобы получить длину дуги.
4. Единицы будут квадратным корнем из единиц площади сектора.

Или центральный угол и длина хорды :

1. Разделить центральный угол в радианах на 2 и применить к нему функцию синуса.
2. Разделите длину хорды на удвоенный результат шага 1. Это вычисление даст вам радиус.
3. Умножьте радиус на центральный угол, чтобы получить длину дуги.

Как найти длину дуги в радианах?

1. Умножьте центральный угол в радианах на радиус окружности.
2. Вот оно! Результатом является просто это умножение.

Как рассчитать длину дуги без учета угла?

Чтобы рассчитать длину дуги без угла, вам нужен радиус и площадь сектора :

1. Умножьте площадь на 2.
2. Затем разделите результат на квадрат радиуса (убедитесь, что единицы измерения совпадают), чтобы получить центральный угол в радианах.

Или вы можете использовать радиус и длину хорды :

1. Разделите длину хорды на удвоенный радиус.

   No related posts.