Итоговый зачет по геометрии 8 класс | Методическая разработка:
Опубликовано 09.05.2017 — 14:26 — Носкова Яна Хачатуровна
Весь список вопросов для подготовки к итоговому зачету по геометрии 8 класс
Скачать:
Предварительный просмотр:
Зачёт по геометрии (8 класс) __________________________
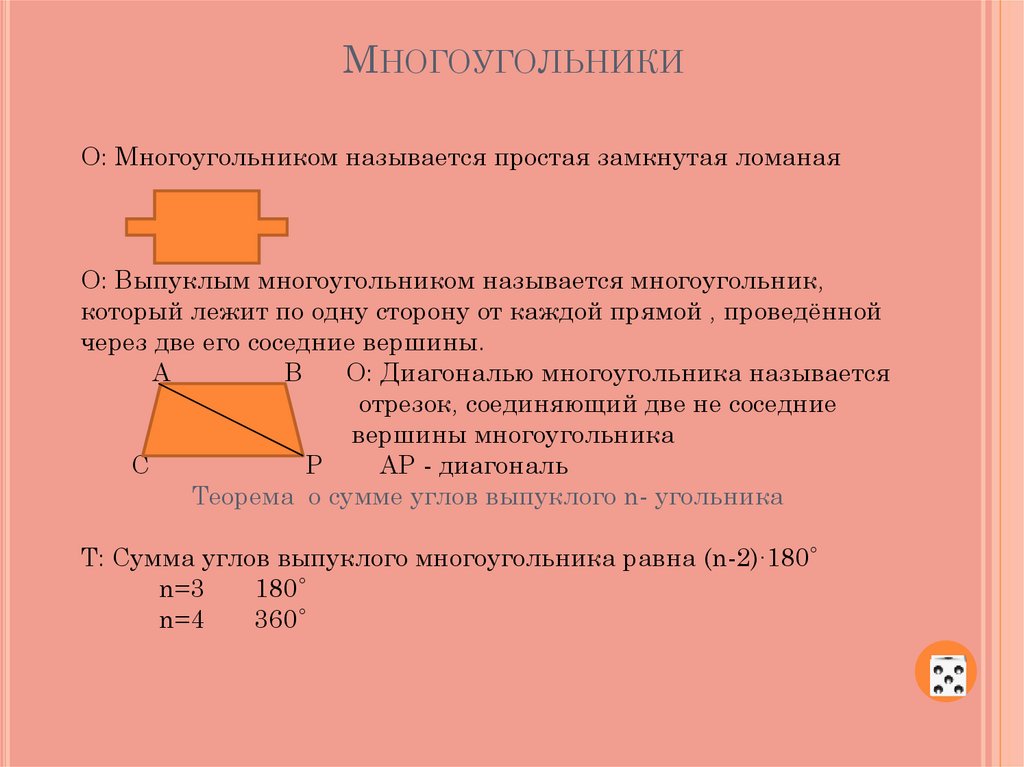
- Многоугольник — это фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.
- Сумма длин всех сторон многоугольника называется периметром многоугольника.
- Две вершины многоугольника, принадлежащие одной стороне, называются соседними.
- Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.
- Многоугольник называется выпуклым, если он лежит по одну сторону от каждой прямой, проходящей через две его соседние вершины.
- Сумма углов выпуклого n-угольника равна (n–2)·180°.
- Четырёхугольник – это многоугольник у которого четыре вершины и четыре стороны.

- Две несмежные стороны четырёхугольника называются противоположными.
- Две вершины, не являющиеся соседними, называются противоположными.
- Сумма углов выпуклого четырехугольника равна 360°.
- Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
- (Свойства параллелограмма) В параллелограмме противоположные стороны равны и противоположные углы равны. Диагонали параллелограмма точкой пересечения делятся пополам.
- (Признак параллелограмма) Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
- (Признак параллелограмма) Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
- (Признак параллелограмма) Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
- Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
 Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами. - Трапеция называется равнобедренной, если её боковые стороны равны.
- Трапеция называется прямоугольной, если один из её углов прямой.
- (Т. Фалеса) Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
- Прямоугольником называется параллелограмм, у которого все углы прямые.
- (Особое свойство прямоугольника) Диагонали прямоугольника равны.
- (Признак прямоугольника) Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.
- Ромбом называется параллелограмм, у которого все стороны равны.
- (Особое свойство ромба) Диагонали ромба взаимно перпендикулярны и делят его углы пополам.
- Квадратом называется прямоугольник, у которого все стороны равны.
- (Основные свойства квадрата) Все углы квадрата прямые.
 Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам. - Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
- Две точки А и А1 называются симметричными относительно точки О, если О – середина отрезка АА1.
- (Основные свойства площадей) Равные многоугольники имеют равные площади.
Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников.
- Площадь квадрата равна квадрату его стороны ( S=a2).
- (Т.)Площадь прямоугольника равна произведению его смежных сторон (S=ab).
- (Т.)Площадь параллелограмма равна произведению его основания на высоту (S=ah).
- (Т.)Площадь треугольника равна половине произведения его основания на высоту (S= ah).
- Площадь прямоугольного треугольника равна половине произведения его катетов (S= ab).

- Если высоты двух треугольников равны, то их площади относятся как основания.
- Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
- Площадь трапеции равна произведению полусуммы её оснований на высоту ( S= ·h ).
- (Теорема Пифагора) В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (с2=a2+b2)
- (Теорема, обратная теореме Пифагора) Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
- Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
- (Формула Герона) Площадь треугольника со сторонами a, b, c выражается формулой S=, где p = (a+b+c) — полупериметр треугольника.
- Говорят, что отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1 , если =.
- Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

- Число k, равное отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
- (Т.)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
- (Т. Первый признак подобия треугольников) Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- (Т. Второй признак подобия треугольников) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
- (Т. Третий признак подобия треугольников) Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
- Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон.
- (Т. о средней линии треугольника) Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
- Медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

- Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
- Отрезок XY называется средним пропорциональным (или средним геометрическим) для отрезков АВ и CD, если XY=
- Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые делится гипотенуза этой высотой.
- Средняя линия трапеции — это отрезок, соединяющий середины ее боковых сторон.
- (Т. о средней линии трапеции) Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме.
- Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
- Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
- Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

- Тангенс угла равен отношению синуса к косинусу этого угла.
- sin2A+cos2A=1 – основное тригонометрическое тождество.
- Если расстояние от центра окружности до прямой меньше радиуса окружности, то прямая и окружность имеют две общие точки.
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют одну общую точку.
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.
- Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
- (Т. о свойстве касательной к окружности) Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
- (Свойство отрезков касательных, проведённых из одной точки) Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

- (Т. Признак касательной) Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна к этому радиусу, то она является касательной
- Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром окружности.
- Угол с вершиной в центре окружности называется её центральным углом.
- Центральный угол измеряется дугой, на которую он опирается.
- Сумма градусных мер двух дуг окружности с общими концами равна 360°.
- Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.
- (Т.) Вписанный угол измеряется половиной дуги, на которую он опирается.
- Вписанные углы, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на полуокружность – прямой.
- (Теорема о произведении отрезков пересекающихся хорд) Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
- Каждая точка биссектрисы неразвёрнутого угла равноудалена от его сторон.
 Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе. - Биссектрисы треугольника пересекаются в одной точке.
- Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему.
- (Теорема о серединном перпендикуляре к отрезку) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к нему.
- Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
- Высоты треугольника (или их продолжения) пересекаются в одной точке.
- Четыре точки: точка пересечения медиан, точка пересечения биссектрис, точка пересечения серединных перпендикуляров к сторонам и точка пересечения высот(или их продолжений) называются замечательными точками треугольника.
- Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.

- (Теорема об окружности, вписанной в треугольник) В любой треугольник можно вписать окружность.
- В треугольник можно вписать только одну окружность.
- Не во всякий четырёхугольник можно вписать окружность.
- В любом описанном четырёхугольнике суммы противоположных сторон равны.
- Если суммы противоположных сторон выпуклого четырёхугольника равны то в него можно вписать окружность.
- Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в эту окружность.
- (Теорема об окружности, описанной около треугольника) Около любого треугольника можно описать окружность.
- Около треугольника можно описать только одну окружность.
- Около четырёхугольника не всегда можно описать окружность.
- В любом вписанном четырёхугольнике сумма противоположных углов равна 180°.
- Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.

По теме: методические разработки, презентации и конспекты
Рабочая программа по геометрии 11 класс Атанасян
Рабочая программа составлена на основе книги Яровенко ПОУРОЧНЫЕ РАЗРАБОТКИ по геометрии…
Урок геометрии в 8 классе по теме «Теорема Пифагора. Вычисление площадей фигур».
На изучение тем «Теорема Пифагора. Вычисление площадей фигур» в 8 классе по программе Л.С. Атанасяна отводится 14 часов.По типу «Урок повторения и отработки приобретённых навыков и полученных ранее зн…
Рабочая программа дисциплины «Математика: алгебра и начала математического анализа, геометрия » для специальности 44.02.02 «Преподавание в начальных классах»
Аннотация рабочей программы дисциплины «Математика: алгебра и начала математического анализа, геометрия »по специальности 44.02.02 Преподавание в началь…
Итоговая контрольная работа 7 класс
Контрольная работа к учебнику «Алгебра» 7 класс Ю.Н.Макарычев…
Методическая разработка «Химический диктант как итоговая форма контроля индивидуальной проверки знаний по органической химии в рамках зачета».

Данная работа посвящается проблеме подведения итогов изучения органической химии на первом курсе в системе НПО и СПО.Методическая разработка может быть полезна педагогам химии и биологии и рекомендова…
Итоговый тест по учебной дисциплине Математика: алгебра и начала математического анализа; геометрия
Итоговый тест содержит 5 вариантов с ответами…
Тема 5.2 «Итоговое занятие. Дифф. зачет».
…
Поделиться:
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
какой график отражает процесс вытекания воды из наполненного сосуда после открытия крана
Двум классам поручено расчистить школьный каток длина которого 20 м а ширина 10 м . в одном классе 26 учеников а в другом 24 сколько квадратных метров должен расчистить каждый класс если
в одном классе 26 учеников а в другом 24 сколько квадратных метров должен расчистить каждый класс если
Решено
сумма цифр трёхзначного натурального числа А делится на 12.Сумма цифр числа А+6 также делится на 12.Найти наименьшее возможное число А
У мальчика в коллекции 24 болгарских марки и 40 российских марок. Он поместил их в альбом, поровну на каждую страницу. Российские марки заняли на 2…
В труппе театра 40 актеров.Часть из них являются ведущими артистами.Половина из остальных-артисты второго плана. Сколько артистов второго плана играет в театре?
Пользуйтесь нашим приложением
Минимум по геометрии 8 класса. Модуль 1 для школьников
- четырёхугольник
- внутренние и внешние углы четырехугольника
- виды четырехугольников
- средняя линия треугольника
Четырёхугольник
Четырёхугольник — это фигура, которая состоит из четырёх точек и четырёх последовательно соединяющих их отрезков. При этом, никакие три из указанных точек не должны быть расположены на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырёхугольника, а соединяющие их отрезки — сторонами четырёхугольника.
При этом, никакие три из указанных точек не должны быть расположены на одной прямой, а соединяющие их отрезки не должны пересекаться. Данные точки называются вершинами четырёхугольника, а соединяющие их отрезки — сторонами четырёхугольника.
Вершины, являющиеся концами одной стороны четырёхугольника, называются соседними, а вершины, не принадлежащие одной стороне — противолежащими. Стороны, имеющие общую вершину, называются соседними сторонами, а не имеющие общих вершин — противолежащими сторонами. Отрезки, соединяющие противолежащие вершины, называются диагоналями четырёхугольника. Точки, принадлежащие четырёхугольнику, делят плоскость q на два множества, которые образуют две области — внутреннюю и внешнюю.
Четырёхугольник называется выпуклым, если все точки, принадлежащие внутренней области, находятся в одной полуплоскости от линии, содержащей любую сторону четырёхугольника; если эти точки находятся в разных полуплоскостях, то четырёхугольник называется невыпуклым (вогнутым).
Если соединить любые две точки внутренней области выпуклого многоугольника, то отрезок, соединяющий эти точки, целиком находится во внутренней области четырёхугольника. Диагонали выпуклого четырёхугольника находятся во внутренней области. У невыпуклого четырёхугольника одна из диагоналей находится во внешней области. Каждая из двух диагоналей выпуклого четырёхугольника делит его на два треугольника.
Внутренние и внешние углы четырехугольника
Угол, смежный любому углу выпуклого четырёхугольника, называется внешним углом. Из любой вершины четырёхугольника можно провести два внешних угла, которые являются вертикальными углами и соответственно равны друг другу. Поэтому, говоря о внешнем угле четырёхугольника, мы будем иметь в виду, один из них. На рисунке для внутренних углов α, β, γ, δ углы α’, β’, γ’, δ’ являются внешними.
Каждый внутренний угол выпуклого четырёхугольника меньше 180°.
Градусная мера внутреннего угла невыпуклого четырёхугольника может быть больше 180°.
Сумма внутренних углов выпуклого четырёхугольника
∡A+∡B+∡C+∡D=360°
Сумма внешних углов выпуклого четырёхугольника
Теорема. Сумма внешних углов выпуклого четырёхугольника, взятых по одному при каждой вершине, равна 360°.
Свойства сторон
- Каждая сторона четырехугольника меньше суммы всех его других сторон.
- Сумма диагоналей меньше его периметра.
Виды четырехугольников
Параллелограмм
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны.
Свойства параллелограмма
- Противоположные стороны параллелограмма равны
- Противоположные углы параллелограмма равны
- Диагонали параллелограмма точкой пересечения делятся пополам: BO=OD, AO=OC
- Диагональ делит параллелограмм на два равных треугольника: треугольники ABC и CDA равны.
- Сумма соседних углов равна 180°.

- Накрест лежащие углы при диагонали равны: ∡BAC=∡ACD, ∡BCA=∡CAD
- Сумма всех углов равна 360°.
- Биссектриса отсекает от параллелограмма равнобедренный треугольник.
- Биссектрисы углов параллелограмма, прилежащих к одной стороне, взаимно перпендикулярны.
- Биссектрисы двух противолежащих углов параллелограмма параллельны.
- Периметр параллелограмма равен удвоенной сумме соседних сторон.
- Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен острому углу параллелограмма. ∡MBN=∡C
Признаки параллелограмма
- Две противоположные стороны одновременно равны и параллельны.
- Все противолежащие углы попарно равны.
- Все противоположные стороны попарно равны.
- Все противоположные стороны попарно параллельны.
- Обе диагонали в точке пересечения делятся пополам.
Прямоугольник
Прямоугольник — это четырехугольник, у которого все углы равны 90° (т.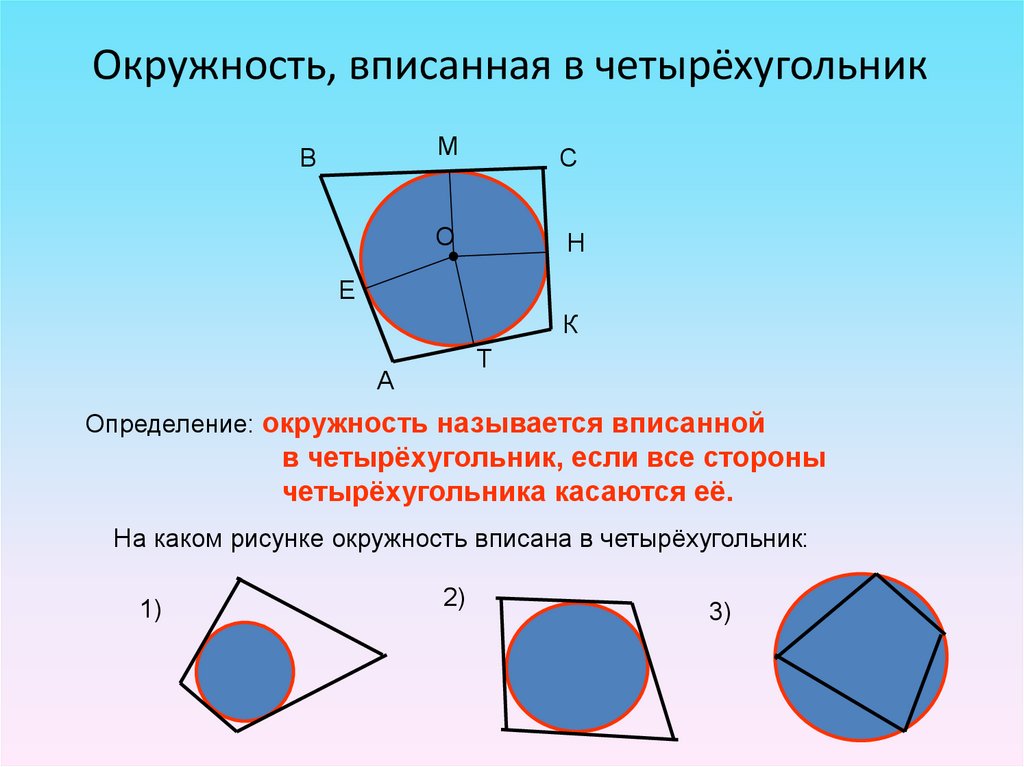 е. являются прямыми).
∡ABC=∡BCD=∡BAD=∡ADC=90°
е. являются прямыми).
∡ABC=∡BCD=∡BAD=∡ADC=90°
Если один угол параллелограмма прямой, то этот параллелограмм является
Свойства прямоугольника
- Прямоугольник имеет все свойства параллелограмма.
- Все углы прямые.
- Диагонали прямоугольника равны.
- Периметр прямоугольника равен удвоенной сумме соседних сторон.
- При пересечении биссектрис внутренних углов произвольного параллелограмма образуется прямоугольник.
Признаки прямоугольников
- Если три угла четырёхугольника прямые, то этот четырёхугольник является прямоугольником.
- Если один угол параллелограмма прямой, то этот параллелограмм является прямоугольником.
- Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.
Ромб
Ромб — это четырехугольник, у которого все стороны равны.
Ромб — это параллелограмм, у которого соседние стороны равны.
Свойства ромба
- Так как ромб является параллелограммом, то он обладает всеми свойствами параллелограмма.
- Диагонали ромба взаимно перпендикулярны: AC⊥BD.
- Диагонали ромба являются также биссектрисами его углов (делят углы ромба пополам).
- Диагонали делят ромб на четыре равных прямоугольных треугольника. Треугольники ABO, СBO, CDO, ADO — равные прямоугольные треугольники.
- PABCD=4·AB
- Высоты ромба равны.
Признаки ромба
- Если диагонали параллелограмма перпендикулярны, то данный параллелограмм является ромбом.
- Если две смежные стороны параллелограмма равны, то данный параллелограмм является ромбом.
- Если диагонали параллелограмма являются биссектрисами его углов, то данный параллелограмм является ромбом.
- Если все стороны четырёхугольника равны, то данный четырёхугольник является ромбом.
Квадрат
Квадрат — это это четырёхугольник, у которого все углы равны и все стороны равны.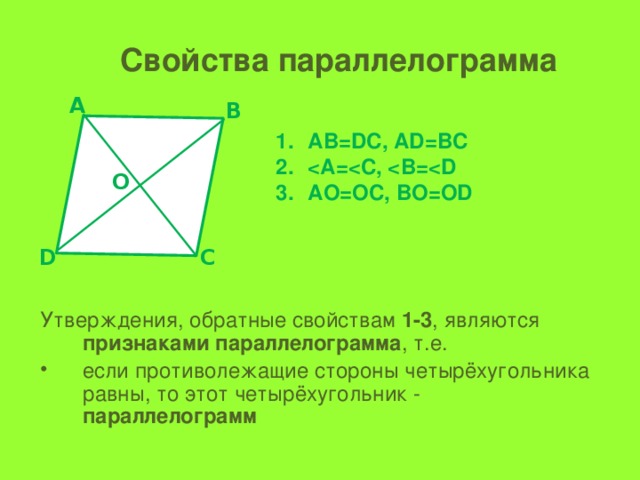
Квадрат — это параллелограмм, у которого есть прямой угол и соседние стороны равны.
Квадрат — это прямоугольник, у которого соседние стороны равны.
Квадрат — это ромб, у которого есть прямой угол.
Свойства квадрата
- Квадрату присущи все свойства параллелограмма, прямоугольника и ромба.
- Диагонали квадрата делят его на четыре равных прямоугольных равнобедренных треугольника.
Признаки квадрата
- Если две смежные стороны прямоугольника равны, то этот прямоугольник является квадратом.
- Если диагонали прямоугольника перпендикулярны, то этот прямоугольник является квадратом.
- Если один из углов ромба прямой, то этот ромб является квадратом.
- Если диагонали ромба равны, то этот ромб является квадратом.
Средняя линия треугольника
Определение
Средняя линия треугольника — это отрезок, соединяющий середины двух сторон треугольника.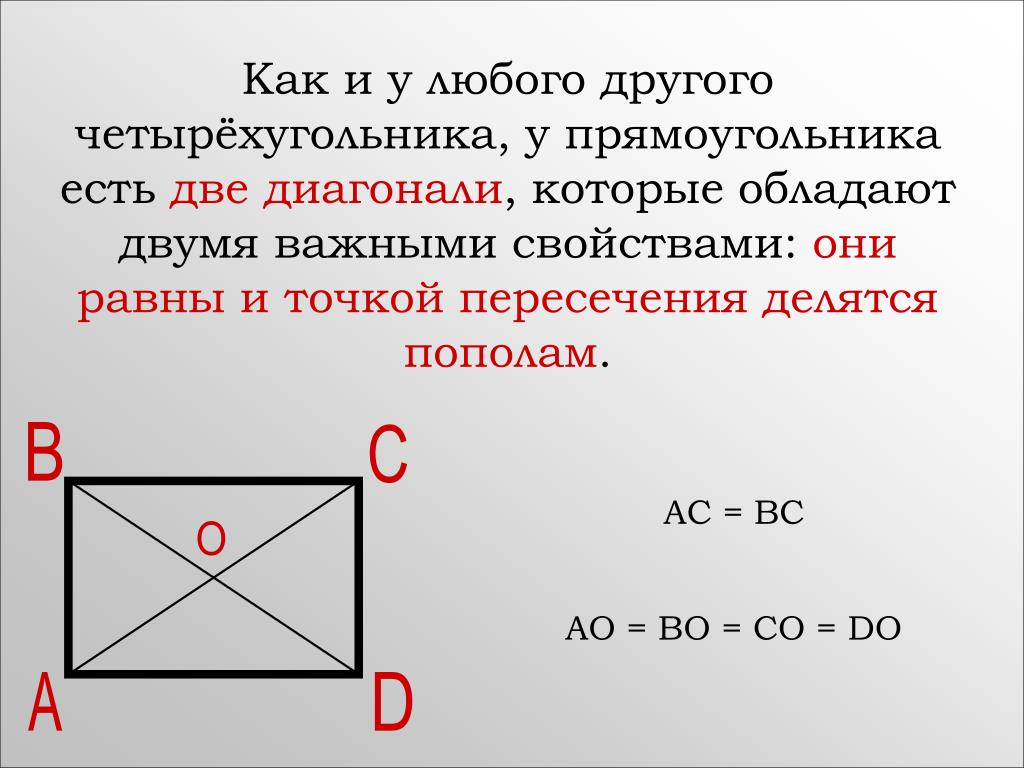 В каждом треугольнике — три средних линии.
В каждом треугольнике — три средних линии.
Средние линии DE, EF, DF.
Свойства
-
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
DE∥AC; EF=12АС -
Три средних линии делят треугольник на 4 равных треугольника ADF, DBE, ECF, DEF.
-
Середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
-
Средние линии треугольника образуют треугольник, периметр которого в два раза меньше периметра исходного треугольника.
P∆DEF=12·P∆ABC
- Коротко о важном
- Таблицы
- Формулы
- Формулы по геометрии
- Теория по математике
- МЫ В СЕТИ
|
|
Фигура, состоящая
из четырех точек и четырех последовательно
соединяющих их отрезков, называется четырехугольником. При этом, никакие три из данных
точек не должны лежать на одной прямой, а
соединяющие их отрезки не должны
пересекаться. Вершины четырехугольника, не являющиеся соседними, называются противолежащими вершинами четырехугольника. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями. У четырехугольника есть две пары противолежащих вершин и четыре пары соседних вершин. Стороны четырехугольника, имеющие общую точку, называются соседними сторонами четырехугольника. Cтороны, не имеющие общей точки,
называются противолежащими сторонами
четырехугольника. Периметр часто обозначают буквой P. Понятие площади. Понятие площади нам известно из повседневного опыта. Каждый понимает смысл слов: площадь комнаты равна 16 квадратным метрам, площадь садового участка- восьми соткам и т.д.Площадь -это величина той части плоскости, которую занимает многоугольник. Измерение площадей
проводится с помощью выбранной единицы
измерения аналогично измерению длин
отрезков. За единицу измерения площадей
принимают квадрат, сторона которого равна
единице измерения отрезков. Так, если за
единицу измерения площадей принимают
квадрат со стороной 1 см. Такой квадрат
называется квадратным сантиметром и
обозначается квадратным сантиметром. Четырехугольники
a, b — стороны
параллелограмма.
d12+d22=2(a2+b2)
Виртуальная
школа «Кирилл и Мефодий» http://www. Интересные задачи http://www.zaba.ru Глазомер http://www.citycat.ru/iq/trening/trensqu.html
Наверх
|
Четырехугольник и площади четырехугольника кратко Планометрия
Привет, мой друг, тебе интересно узнать все про четырехугольник, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое четырехугольник, четырехугольники, площади четырехугольника , настоятельно рекомендую прочитать все из категории Планометрия.
четырехугольник (греч. τετραγωνον) — это геометрическая фигура (многоугольник), состоящая из четырех точек (вершин), никакие три из которых не лежат на одной прямой, и четырех отрезков (сторон), последовательно соединяющих эти точки. Различают выпуклые и невыпуклые
четырехугольники , невыпуклый четырехугольник может быть самопересекающимся (см.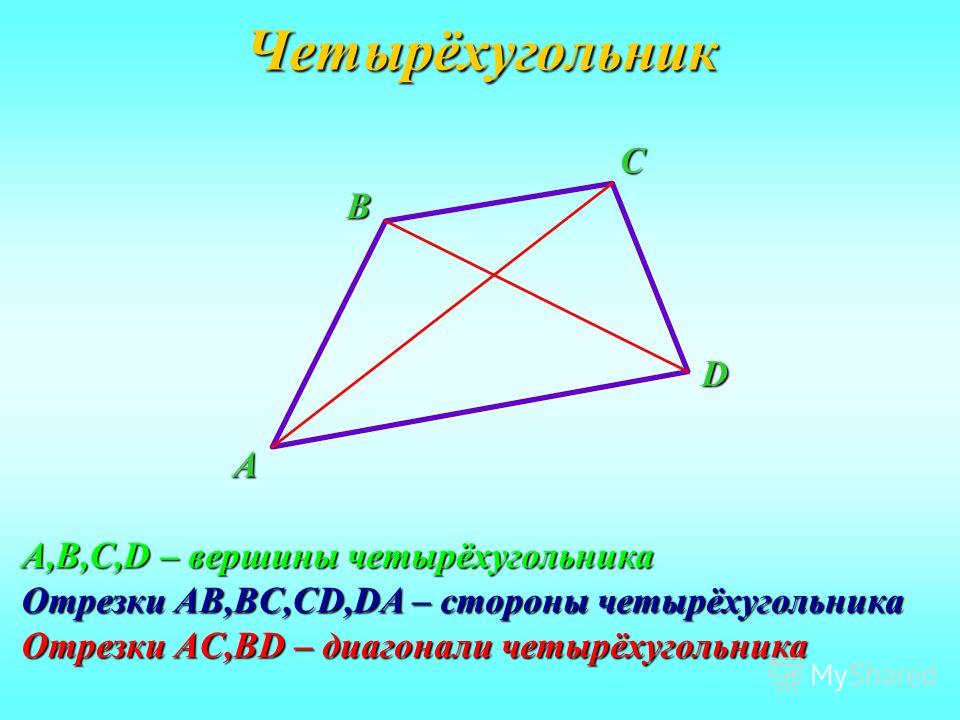 рис.). Четырехугольник без самопересечений называется простым, часто под термином «четырехугольник» имеется в виду только простые четырехугольники
рис.). Четырехугольник без самопересечений называется простым, часто под термином «четырехугольник» имеется в виду только простые четырехугольники
Четырехугольником называется фигура, которая состоит из четырех точек (вершины четырехугольника) и четырех последовательно соединяющих эти точки отрезков (стороны четырехугольника). При этом:
1. ни какие три данные точки не лежат на одной прямой;
2. соединяющие эти точки отрезки не должны не пересекаться.
Точки A, B, C, D – вершины четырех угольника.
Отрезки AB, BC, CD, DA – стороны четырехугольника.
Вершины четырех угольника называются соседними вершинами, если они являются концами одной из его сторон. Например, вершины A и B – соседние.
Вершины, не являющиеся соседними, называются противолежащими вершинами. Например, вершины A и С – противолежащие. Отрезки, которые соединяют противолежащие вершины четырехугольника, называются диагоналями. AC и BD – диагонали четырехугольника.
Стороны четырехугольника, исходящие из одной вершины, называются соседними (смежными) сторонами. Например, AB и BC – соседние стороны. Стороны не имеющие общих вершин, называются противолежащими сторонами. Например, AB и CD – противолежащие стороны.
Четырехугольник обозначается указанием его вершин, например ABCD. В обозначение четырехугольника стоящие рядом вершины должны быть соседними . Об этом говорит сайт https://intellect.icu . Т.е. обозначить четырехугольник ABDС нельзя (B и D – не соседние вершины).
Четырехугольники A1B1C1D1 и ABCD отличаются тем, что у одного диагонали пересекаются, а у другого нет. Четырехугольники у которых диагонали пересекаются будем называть выпуклыми. Сумму длин всех сторон четырехугольника будем называть периметром. P = AB + BC + CD + DA.
Диаграмма Эйлера некоторых типов простых четырехугольников. (UK) обозначает британский английский, а (US) обозначает американский английский.
Выпуклые четырехугольники по симметрии, представленные диаграммой Хассе .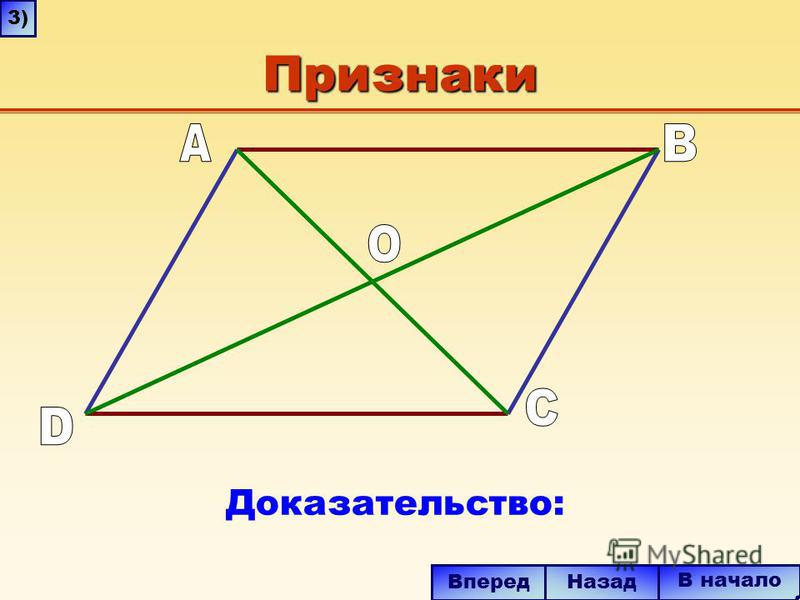
История
В древности египтяне и некоторые другие народы использовали для определения площади четырехугольника неверную формулу — произведение полусумм его противоположных сторон a, b, c, d[27]:
.
Для непрямоугольных четырехугольников эта формула дает завышенное значение площади. Можно предположить, что она использовалась только для определения площади почти прямоугольных участков земли. При неточном измерении сторон прямоугольника эта формула позволяет повысить точность результата за счет усреднения исходных измерений.
площади четырехугольника
Площадь четырехугольника — это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
Для вычисления площади произвольного четырехугольника применяются различные формулы, в зависимости от известных исходных данных.
Площадь частных случаев четырехугольников
Для вычисления частных случаев четырехугольников можно воспользоваться формулами и калькуляторами, приведенными в других статьях сайта:
- площадь квадрата
- площадь трапеции
- площадь параллелограмма
- площадь прямоугольника
- площадь ромба
Таблица с формулами площади четырехугольника
| исходные данные | Чертеж | формула | |
| 1 | диагональ и угол между ними | | |
| 2 | стороны и углы между этими сторонами |
|
|
| 3 | стороны (по Формуле Брахмагупты) |
|
|
| 4 | стороны и радиус вписанной окружности |
|
|
| 5 | стороны и углы между ними | |
См.
 также
также- Квадрат
- Прямоугольник
- Параллелограмм
- Антипараллелограмм
- Робм
-
Дельтоид
-
Трапеция
-
Специальные прямые линии четырехугольника
-
Специальные точки четырехугольника
-
Симметрия четырехугольников
- Лемма о шестой окружности
- Четырехугольник Саккери
- Теорема Тебо 1
- Теорема Кейси
- Теорема косинусов для четырехугольника
- Теорема о бабочке
- площадь прямоугольника , площадь квадрата ,
- площадь треугольника ,
- вычисление площадей плоских фигур в полярных координатах ,
- площадь трапеции ,
- вычисление площадей плоских фигур ,
- площадь параллелограмма ,
- площадь кругового сектора ,
- площадь фигуры ,
- площадь круга ,
- площадь боковой поверхности цилиндра ,
- площадь сферы ,
Понравилась статья про четырехугольник? Откомментируйте её Надеюсь, что теперь ты понял что такое четырехугольник, четырехугольники, площади четырехугольника
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Планометрия
Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Планометрия
Из статьи мы узнали кратко, но емко про четырехугольник
Лекция 54. Свойства геометрических фигур на плоскости
План:
4. Треугольники, четырехугольники, многоугольники. Формулы площадей треугольника, прямоугольника, параллелограмма, трапеции.
5. Окружность, круг.
- Треугольники
Треугольник – одна из простейших геометрических фигур. Но его изучение породило целую науку – тригонометрию, которая возникла из практических потребностей при измерении земельных участков, составлении карт местности, конструировании различных механизмов.
Треугольникомназывается геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех попарно соединяющих их отрезков.
Любой треугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из треугольника и его внутренней области, также называют треугольником ( или плоским треугольником).
В любом треугольнике выделяют следующие элементы: стороны, углы, высоты, биссектрисы, медианы, средние линии.
Углом треугольника АВС при вершине А называется угол, образованный полупрямыми АВ и АС.
Высотойтреугольника, опущенной из данной вершины, называется перпендикуляр, проведенный из этой вершины к прямой, содержащей противоположную сторону.
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющей вершину с точкой на противоположной стороне.
Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.
На практике и в теоретических построениях часто пользуются признаками равенства треугольников, обеспечивающих более быстрое решение вопроса об отношениях ме5жду ними. Таких признаков три:
1. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
3. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.
Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми, а третья сторона называется основанием треугольника.
Равнобедренные треугольники обладают рядом свойств, например:
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Отметим несколько свойств треугольников.
1. Сумма углов треугольника равна 180º.
Из этого свойства следует, что в любом треугольнике хотя бы два угла острые.
2. Средняя линия треугольника, соединяющая середины двух сторон, параллельна третьей стороне и равна ее половине.
3. В любом треугольнике каждая сторона меньше суммы двух других сторон.
Для прямоугольного треугольника верна теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
- Четырехугольники
Четырехугольником называется фигура, которая состоит из четырех точек и четырех последовательно соединяющих их отрезков, причем никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться.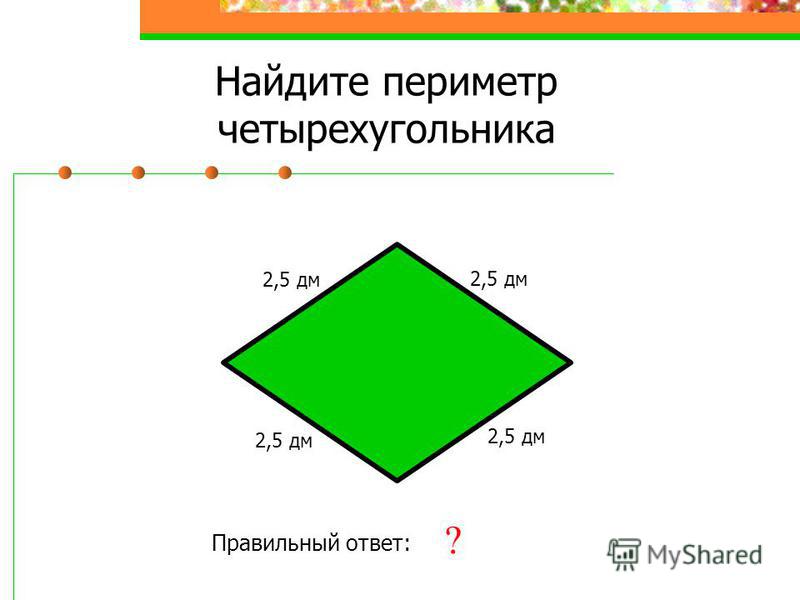 Данные точки называются вершинами четырехугольника, а соединяющие их отрезки – его сторонами.
Данные точки называются вершинами четырехугольника, а соединяющие их отрезки – его сторонами.
Любой четырехугольник разделяет плоскость на две части: внутреннюю и внешнюю. Фигуру, состоящую из четырехугольника и его внутренней области, также называется четырехугольником (или плоским четырехугольником).
Вершины четырехугольника называют соседними, если они являются концами одной из его сторон. Вершины, не являющиеся соседними, называются противолежащими. Отрезки, соединяющие противолежащие вершины четырехугольника, называются диагоналями.
Стороны четырехугольника, исходящие из одной вершины, называются соседними. Стороны, не имеющие общего конца, называются противолежащими. У четырехугольника АВСD вершины А и В – противолежащие, стороны АВ и ВС – соседние, ВС и АD – противолежащие; отрезки АС и ВD – диагонали данного четырехугольника.
В С Р М Т
АD К
Четырехугольники бывают выпуклые и невыпуклые.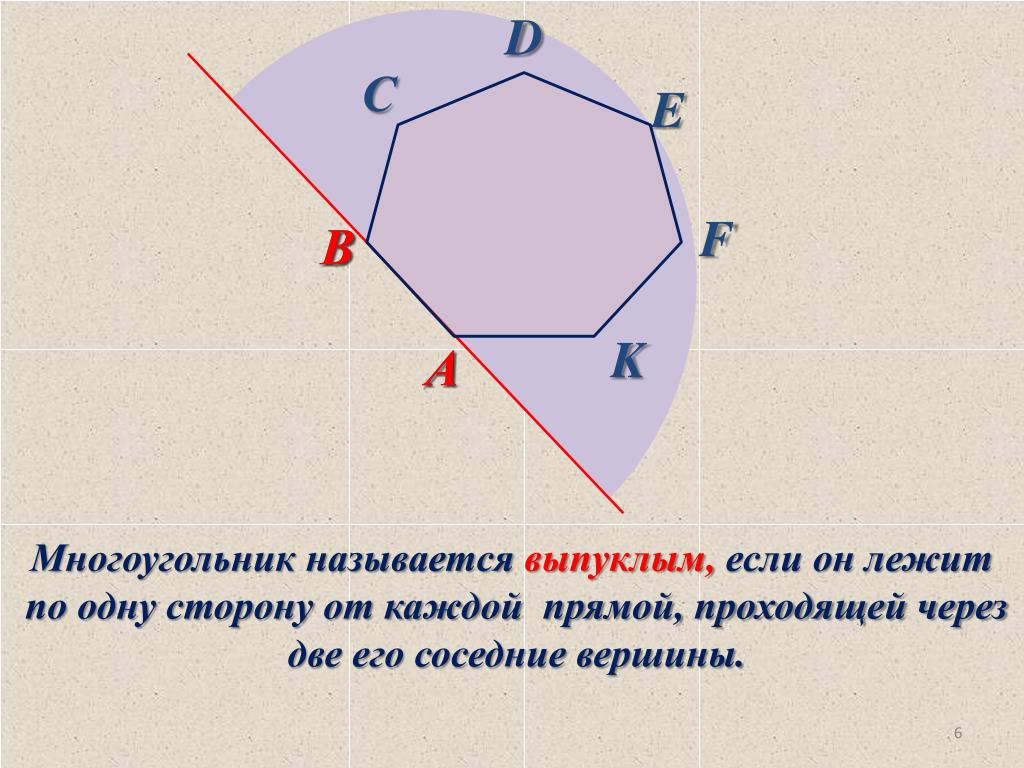 Так, четырехугольник АВСD – выпуклый, а четырехугольник КРМТ – невыпуклый. Среди выпуклых четырехугольников выделяют параллелограммы и трапеции.
Так, четырехугольник АВСD – выпуклый, а четырехугольник КРМТ – невыпуклый. Среди выпуклых четырехугольников выделяют параллелограммы и трапеции.
Параллелограммом называется четырехугольник, у которого противолежащие стороны параллельны.
Пусть АВСD – параллелограмм. Из вершины В на прямую АD опустим перпендикуляр ВЕ. Тогда отрезок ВЕ называется высотой параллелограмма, соответствующей сторонам ВС и АD. Отрезок
М
А Е D
СМ – высота параллелограмм, соответствующая сторонам СD и АВ.
Чтобы упростить распознавание параллелограммов, рассматривают следующий признак: если диагонали четырехугольника пересекаются и точкой пересечения делятся пополам, то данный четырехугольник – параллелограмм.
Ряд свойств параллелограмма, которые не содержатся в его определении, формулируют в виде теорем и доказывают. Среди них:
1. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
2. У параллелограмма противолежащие стороны и противолежащие углы равны.
У параллелограмма противолежащие стороны и противолежащие углы равны.
Рассмотрим теперь определение трапеции и ее основное свойство.
Трапециейназывается четырехугольник, у которого только две противолежащие стороны параллельны.
Эти параллельные стороны называются основаниями трапеции. Две другие стороны называются боковыми.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Средняя линия трапеции обладает свойством: она параллельна основаниям и равна их полусумме.
Из множества параллелограммов выделяют прямоугольники и ромбы.
Прямоугольником называется параллелограмм, у которого все углы прямые.
Исходя из этого определения, можно доказать, что диагонали прямоугольника равны.
Ромбом называется параллелограмм, у которого все стороны равны.
Пользуясь этим определением, можно доказать, что диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
Из множества прямоугольников выделяют квадраты.
Квадратом называют прямоугольник, у которого все стороны равны.
Так как стороны квадрата равны, то он является также ромбом. Следовательно, квадрат обладает свойствами прямоугольника и ромба.
- Многоугольники
Обобщением понятия треугольника и четырехугольника является понятие многоугольника. Определяется оно через понятие ломаной.
Ломаной А₁А₂А₃…Аn называется фигура, которая состоит из точек А₁, А₂, А₃, …, Аn и соединяющих их отрезков А₁А₂, А₂А₃, …, Аn-₁Аn. Точки А₁, А₂, А₃, …, Аn называются вершинами ломаной, а отрезки А₁А₂, А₂А₃, …, Аn-₁Аn – ее звеньями.
Если ломаная не имеет самопересечений, то она называется простой. Если ее концы совпадают, то она называется замкнутой. О ломаных, изображенных на рисунке можно сказать: а) – простая; б) – простая замкнутая; в) – замкнутая ломаная, не являющаяся простой.
А) б) в)
Длиной ломаной называется сумма длин ее звеньев.
Известно, что длина ломаной не меньше длины отрезка, соединяющего ее концы.
Многоугольникомназывается простая замкнутая ломаная, если ее соседние звенья не лежат на одной прямой.
Вершины ломаной называют вершинами многоугольника, а ее звенья – его сторонами. Отрезки, соединяющие несоседние вершины, называются диагоналями.
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая – внешней областью многоугольника (или плоским многоугольником).
Различают выпуклые и невыпуклые многоугольники.
Выпуклый многоугольник называется правильным, если у него все стороны и все углы равны.
Правильным является равносторонний треугольник, правильным четырехугольником – квадрат.
Углом выпуклого многоугольника при данной вершине называется угол, образуемый его сторонами, сходящимися в этой вершине.
Известно, что сумма углов выпуклого n-угольника равна 180º• (n – 2).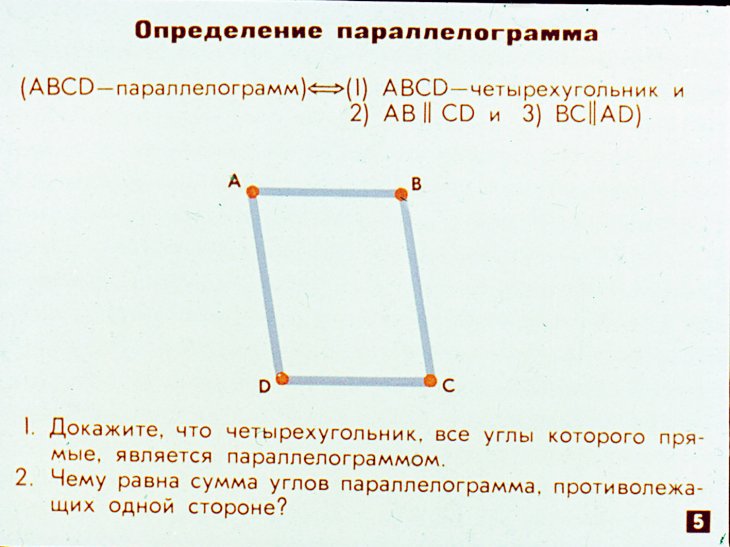
В геометрии, кроме выпуклых и невыпуклых многоугольников, рассматривают еще многоугольные фигуры.
Многоугольной фигурой называется объединение конечного множества многоугольников.
А) б) в)
Многоугольники, из которых состоит многоугольная фигура, могут не иметь общих внутренних точек, могут иметь общие внутренние точки.
Говорят, что многоугольная фигура F состоит из многоугольных фигур, если она является их объединением, а сами фигуры не имеют общих внутренних точек. Например, о многоугольных фигурах, изображенных на рисунке а) и в), можно сказать, что они состоят из двух многоугольных фигур или что они разбиты на две многоугольные фигуры.
- Окружность и круг
Окружностью называется фигура, которая состоит из всех точек плоскости, равноудаленных от данной точки, называемой центром.
Любой отрезок, соединяющий точку окружности с ее центром, называется радиусом окружности.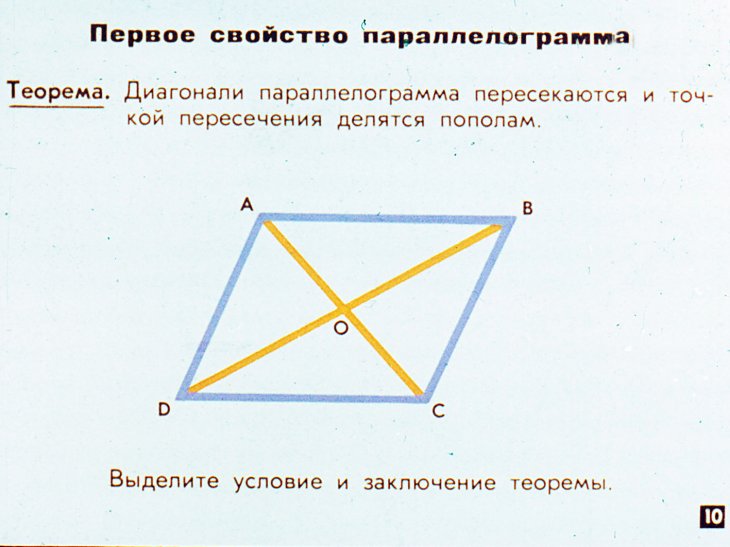 Радиусом называется также расстояние от любой точки окружности до ее центра.
Радиусом называется также расстояние от любой точки окружности до ее центра.
Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр, называется диаметром.
Кругом называется фигура, которая состоит из всех точек плоскости, находящихся на расстоянии, не большем данного, от данной точки. Эта точка называется центром круга, а данное расстояние – радиусом круга.
Границей круга является окружность с теми же центром и радиусом.
Напомним некоторые свойства окружности и круга.
Говорят, что прямая и окружность касаются, если они имеют единственную общую точку. Такую прямую называют касательной, а общую точку прямой и окружности – точкой касания. Доказано, что если прямая касается окружности, то она перпендикулярна радиусу, проведенному в точку касания. Справедливо и обратное утверждение (рис. а).
Центральным углом в окружности называется плоский угол с вершиной в ее центре. Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу (рис.б).
Часть окружности, расположенная внутри плоского угла, называется дугой окружности, соответствующей этому центральному углу (рис.б).
а) б) в)
Угол, вершина которого лежит на окружности, а стороны пересекают ее, называется вписанным в эту окружность (рис.в).
Угол, вписанный в окружность, обладает следующим свойством: он равен половине соответствующего центрального угла. В частности, углы, опирающиеся на диаметр – прямые.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Чтобы описать окружность около треугольника, надо найти ее центр. Правило его нахождения обосновывается следующей теоремой:
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к его сторонам, проведенных через середины этих сторон (рис.а).
а) б)
Окружность называется вписанной в треугольник, если она касается всех его сторон.
Правило нахождения центра такой окружности обосновывается теоремой:
Центр окружности, вписанной в треугольник, является точкой пересечения его биссектрис (рис.б)
Таким образом, серединные перпендикуляры и биссектрисы пересекаются в одной точке соответственно. В геометрии доказано, что медианы треугольника пересекаются в одной точке. Эту точку называют центром тяжести треугольника, а точку пересечения высот – ортоцентром.
Таким образом, во всяком треугольнике существует четыре замечательные точки: центр тяжести, центры вписанной и описанной окружностей и ортоцентр.
Около всякого правильного многоугольника можно описать окружность и во всякий правильный многоугольник можно вписать окружность, причем центры описанной и вписанной окружностей совпадают.
Живите по правилу: МАЛО ЛИ ЧТО НА СВЕТЕ СУЩЕСТВУЕТ? Я неслучайно подчеркиваю, что место в голове ограничено, а информации вокруг много, и что ваше право. ..
..
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала…
ЧТО ПРОИСХОДИТ, КОГДА МЫ ССОРИМСЯ Не понимая различий, существующих между мужчинами и женщинами, очень легко довести дело до ссоры…
Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Понимание четырехугольников 8 | Блог
Мы узнали о разных формах. Давайте посмотрим это видео, чтобы узнать эти формы и то, как мы их называем.
Обратите внимание, что стороны или края двери представляют собой прямые линии. Вы бы видели больше таких объектов вокруг себя. Некоторые из них показаны ниже.
Каждая из этих фигур состоит из отрезков. Чтобы использовать эти формы в зданиях или других реальных конструкциях, нам важно знать
Мы знаем, что многие объекты, которые мы используем в реальной жизни, имеют четырехстороннюю форму.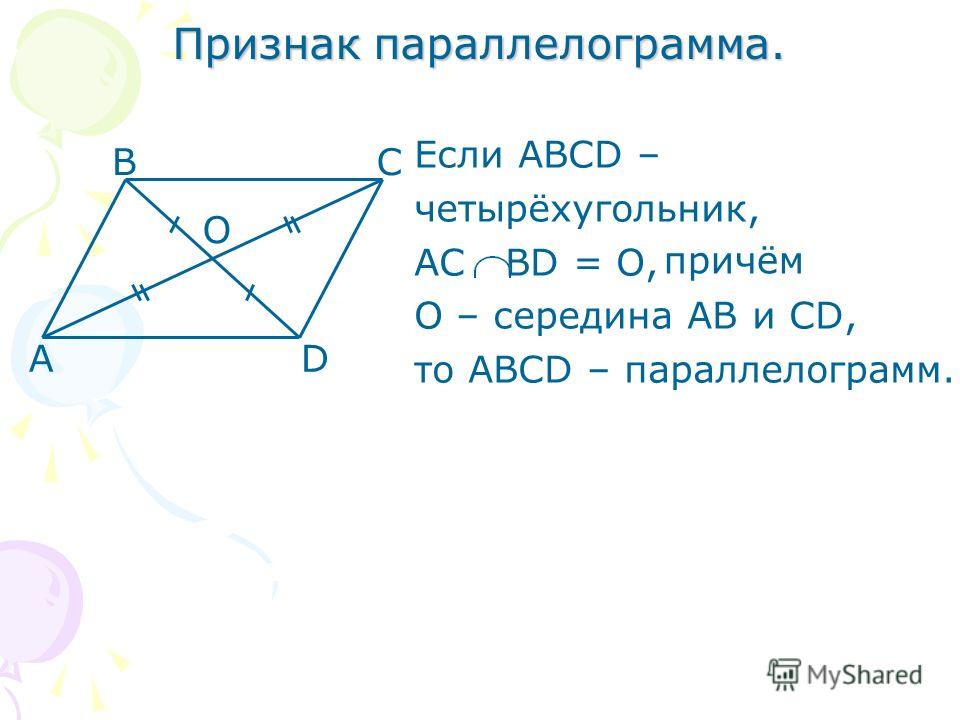 Стороны каждого из них были отрезками. Такие фигуры называются четырехугольниками.
Стороны каждого из них были отрезками. Такие фигуры называются четырехугольниками.
Четырехугольник — замкнутая геометрическая фигура, состоящая из четырех отрезков, называемых сторонами.
Чтобы построить их, важно знать больше о свойствах этих фигур.
Повторное посещение многоугольников
Многоугольник — это замкнутая фигура, состоящая только из отрезков. Примеры:
Чтобы фигуру можно было назвать многоугольником, она должна быть замкнутой.
Мы узнали о свойствах многоугольника. Итак, чтобы идентифицировать полигон, мы должны проверить эти свойства. Если данная фигура обладает всеми свойствами, то фигура является многоугольником. Свойства, которые необходимо проверить на данном рисунке:
Подробнее о многоугольниках
Многоугольник с наименьшим числом сторон (то есть с тремя сторонами) называется треугольником. Точно так же многоугольники с разным количеством сторон имеют разные имена.
Теперь давайте посмотрим на некоторые объекты многоугольной формы, которые мы видим в нашей повседневной жизни.
Классифицируем эти фигуры по количеству сторон многоугольников.
Знаете ли вы, почему многоугольник с тремя сторонами называется треугольником? Термин «три» означает три. Итак, треугольник означает три угла. Многоугольник с тремя сторонами имеет три угла, поэтому его называют треугольником.
Точно так же и другие многоугольники называются по количеству сторон.
Обычно многоугольник с числом сторон n называется n-угольником. Префиксы — это греческие слова, обозначающие определенные числа. Например, «пента» — это греческое слово, означающее «пять». Итак, многоугольник с 5 сторонами/углами называется пятиугольником.
Рассмотрим пятиугольник внизу.
Мы видим, что каждая пара сторон многоугольника пересекается в одной точке. Эта точка называется вершиной многоугольника. В любом многоугольнике количество вершин равно количеству сторон многоугольника. Назовем вершины многоугольника выше.
Мы можем назвать этот пятиугольник пятиугольником ABCDE.
Заметим, что отрезки:
- AE и AB являются сторонами многоугольника.
- AD и AC не являются сторонами многоугольника.
Здесь все четырехпрямые отрезки проведены из одной вершины A в другие вершины многоугольника. Но две из них являются сторонами многоугольника, а две другие — нет. Как мы различаем?
На рисунке видно, что вершины B и E смежны (последовательны) с вершиной A. Но вершины C и D не смежны с вершиной A. Таким образом, каждая сторона многоугольника соединяет две последовательные вершины полигон. Тогда как мы называем те отрезки, которые соединяют две непоследовательные вершины?
Они называются диагоналями многоугольника.
Диагональ многоугольника соединяет только непоследовательные вершины многоугольника. Каждый отрезок, соединяющий две непоследовательные вершины многоугольника, является его диагональю.
Пример:
PR — диагональ многоугольника PQRS.
Теперь рассмотрим шестиугольник.
Из каждой из 6 вершин шестиугольника можно провести по три диагонали. Но у нас всего 9 неповторяющихся диагоналей.
Количество диагоналей у разных полигонов разное. Как это меняется?
Есть ли связь между количеством сторон многоугольника и количеством его диагоналей? Начнем с четырехугольника.
Рассмотрим четырехугольник ABCD. Сколько у него вершин? Все четырехугольники имеют 4 стороны и 4 вершины. Теперь рассмотрим вершину A.
Сколько вершин четырехугольника ABCD не являются смежными с вершиной A? Только одна, то есть вершина C. Значит, из вершины A нельзя провести диагонали к вершинам B и D. Также нельзя провести диагональ из любой вершины в саму себя. Только к вершине C можно провести диагональ из вершины A. Аналогично и для других вершин. Из любой вершины четырехугольника можно провести только одну диагональ.
Итак, всего в четырехугольнике должно быть 4 диагонали. Но находим только 2. Почему так? Не забывайте, что каждую диагональ делят 2 вершины. Если вы посчитаете одну и ту же диагональ для обеих вершин, то вы получите количество диагоналей в два раза больше, чем оно есть на самом деле.
Если вы посчитаете одну и ту же диагональ для обеих вершин, то вы получите количество диагоналей в два раза больше, чем оно есть на самом деле.
Значит, у четырехугольника 2 диагонали.
Рассмотрим пятиугольник PQRST.
Сколько диагоналей можно провести из вершины T?
Из пяти вершин P и S следуют за T. Следовательно, из T к ним нельзя провести диагонали. Также нельзя провести диагональ к самой себе. Значит, из 5 вершин нельзя провести диагонали из T к трем вершинам.
Итак, количество возможных диагоналей из точки T = 5 – 3 = 2
Аналогично и для других вершин. Значит, из всех пяти вершин можно провести только две диагонали.
Всего 5 вершин.
Итак, сумма будет 5 × 2 = 10.
т. е. 5 × (5 – 3)
Но, таким образом, при счете мы рассмотрели каждую диагональ дважды.
Например, диагональ TR считается диагональю как от T, так и от R. То есть считается дважды. Это касается каждой диагонали. Следовательно, чтобы получить реальный счет, мы должны разделить 5 × (5 – 3) на 2,9.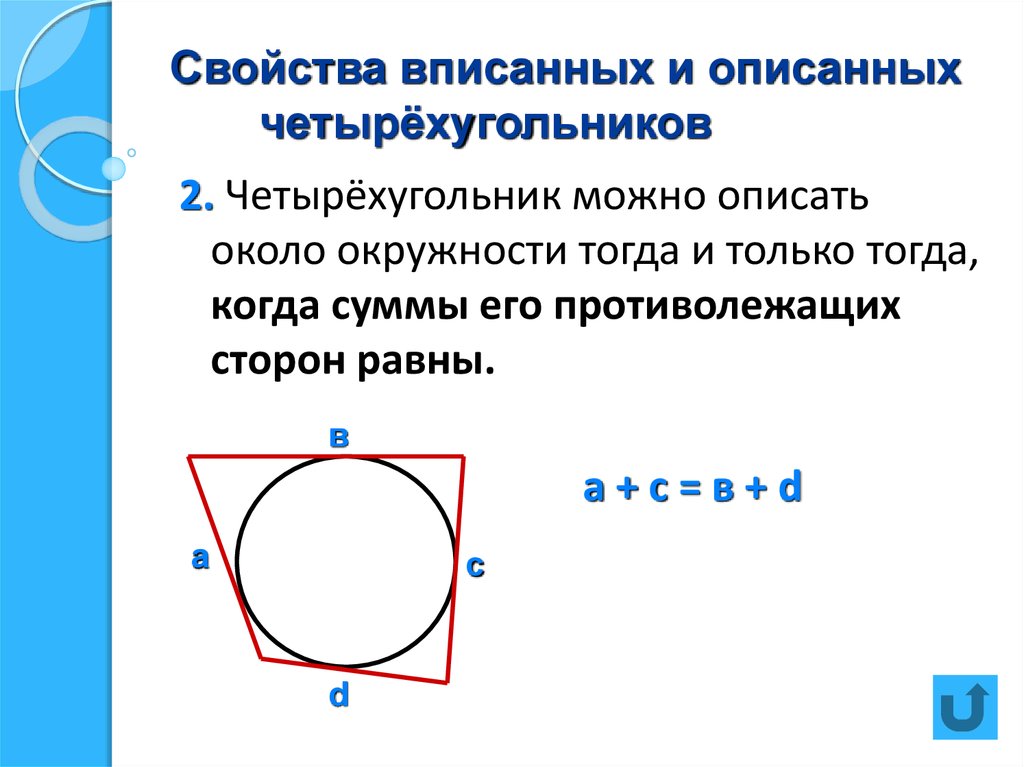 0003
0003
Таким образом, количество диагоналей пятиугольника 5 × (5 – 3) 2 = 5
В общем случае для многоугольника с «n» сторонами
- Из каждой вершины возможны (n – 3) диагоналей.
- Всего n вершин. Таким образом, общее количество будет n (n — 3).
- Каждая диагональ делится на две вершины. Таким образом, общее количество дает двойное фактическое количество диагоналей многоугольника. Вот почему общее количество нужно разделить на 2, чтобы получить фактическое количество диагоналей в многоугольнике.
Количество диагоналей многоугольника с «n» сторонами = п × (п – 3) 2
Типы многоугольников
Обратите внимание на цифры ниже:
Находите ли вы разницу между двумя многоугольниками, данными в предыдущем вопросе?
Конечно, нет никакой разницы в количестве сторон многоугольников, потому что оба имеют 6 сторон.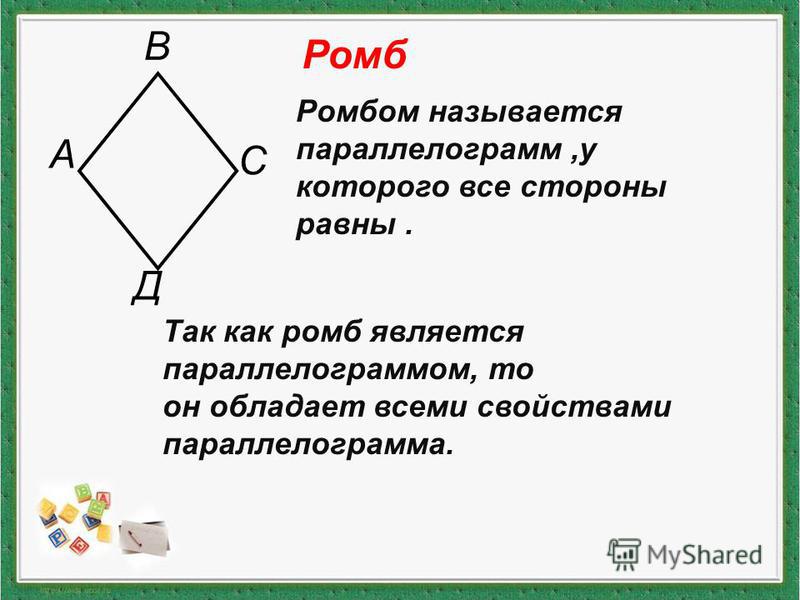
Итак, давайте посмотрим, чем эти два полигона отличаются друг от друга.
Чтобы найти разницу, вы должны наблюдать за внутренними углами двух многоугольников.
Мы находим разницу между двумя многоугольниками в их внутренних углах.
- В многоугольнике PQRSTU ни один из внутренних углов не является рефлекторным.
- Но в многоугольнике EFGHIJ один из внутренних углов является рефлекторным.
Такие многоугольники называются вогнутыми многоугольниками.
Диагонали вогнутого многоугольника, который мы видели в предыдущем примере, показаны на рисунке ниже.
Диагонали нескольких выпуклых многоугольников также показаны на рисунках ниже.
Находите ли вы разницу между диагоналями вогнутого многоугольника и диагоналями выпуклого многоугольника?
Вы можете заметить, что ни одна из диагоналей выпуклых многоугольников не имеет своей части, лежащей снаружи многоугольника.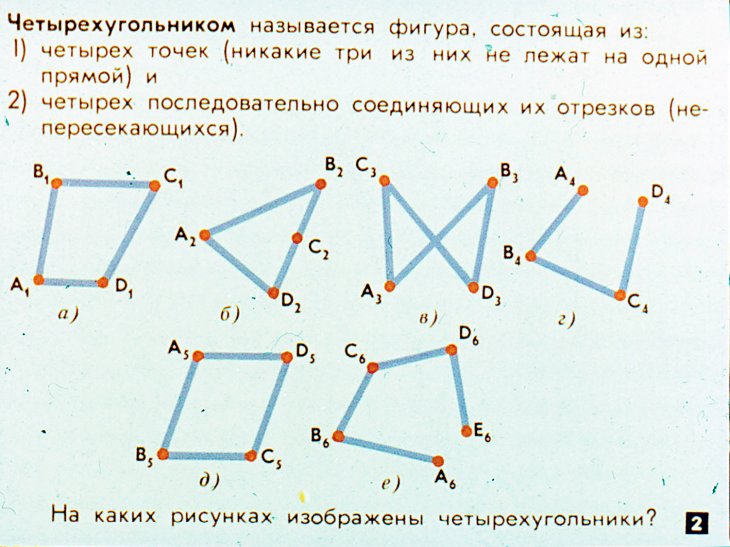
А диагонали вогнутого многоугольника?
Вы можете заметить, что в вогнутом многоугольнике несколько диагоналей имеют свою часть, лежащую снаружи многоугольника.
Теперь рассмотрим две точки A и B внутри вогнутого многоугольника, как показано ниже.
Соедините точки отрезком.
Итак:
- Многоугольник, имеющий хотя бы один внутренний угол отражения, называется вогнутым многоугольником.
- Многоугольник, у которого все внутренние углы непрямые, называется выпуклым многоугольником.
Другими словами, многоугольники без внутреннего угла отражения являются выпуклыми многоугольниками.
Перечислим свойства выпуклых и вогнутых многоугольников.
Многоугольник называется правильным, только если он не только равносторонний, но и равноугольный. Другими словами, правильный многоугольник имеет равные стороны и равные углы. Два очень знакомых примера правильного многоугольника — это равносторонний треугольник и квадрат.
- Равносторонний треугольник, как говорит само его название, имеет равные стороны.
- Равносторонние треугольники также называют равноугольными треугольниками, так как они имеют равные углы.
- Квадрат – это четырехугольник с равными сторонами и внутренним углом, равным 90°.
- Таким образом, квадрат, будучи равносторонним и равноугольным, является правильным многоугольником.
Рассмотрим еще несколько правильных многоугольников.
Мы знаем, что многоугольники можно классифицировать по количеству сторон как треугольники, четырехугольники, пятиугольники, шестиугольники и так далее.
Если эти многоугольники являются правильными многоугольниками, мы добавляем префикс «обычный» к их соответствующим именам. Например, пятиугольник с равными сторонами и равными углами называется правильным пятиугольником.
В следующей таблице приведены имена правильных многоугольников.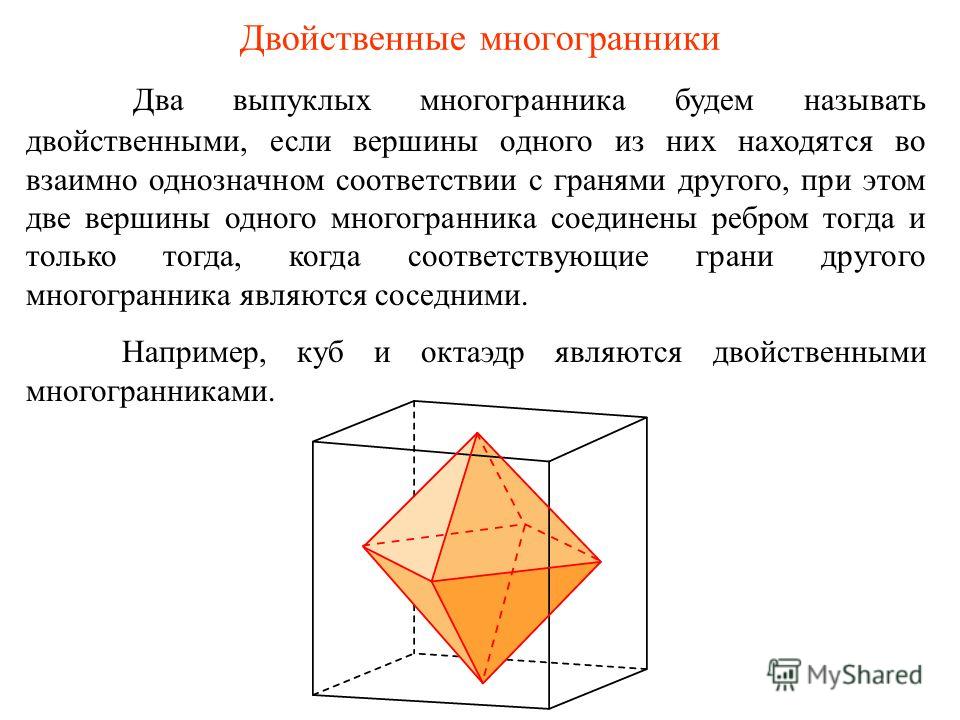
У прямоугольника равны только противоположные стороны, а каждый внутренний угол равен 90°. Таким образом, прямоугольник равноугольный, но не равносторонний, следовательно, прямоугольник является неправильным многоугольником.
Рассмотрим следующий вогнутый многоугольник с равными сторонами.
Этот многоугольник имеет равные стороны, но не равные углы. Таким образом, вогнутый многоугольник равносторонний, но не равноугольный. Значит, это неправильный многоугольник.
- У правильного многоугольника все стороны равны и все углы равны.
- Неправильный многоугольник будет иметь разную длину сторон или разную меру углов.
Вы знаете, что сумма всех внутренних углов четырехугольника равна 360°.
Теперь рассмотрим пятиугольник.
Теперь из вершины А проведите все возможные диагонали, чтобы разделить пятиугольник на треугольники.
Сколько треугольников у нас получилось? Три.
Теперь мы видим, что внутренние углы многоугольника делятся на внутренние углы всех треугольников, как показано на рисунке ниже.
Сумма внутренних углов каждого треугольника равна 180°.
Сумма внутренних углов трех треугольников дает сумму внутренних углов пятиугольника. В данном пятиугольнике 3 таких треугольника.
Итак, сумма внутренних углов всех треугольников = 3 × 180° = 540°
Таким образом, мы получаем сумму внутренних углов пятиугольника как 540°.
Для двух многоугольников, которые мы обсуждали, давайте сравним количество сторон/углов и сумму внутренних углов.
Теперь давайте рассмотрим пример вогнутого многоугольника. Рассмотрим:
Теперь давайте разделим многоугольник на треугольники.
Здесь мы также видим, что внутренние углы многоугольника делятся как внутренние углы треугольников. У многоугольника 6 сторон, и он разделен на 4 треугольника.
Отсюда сумма внутренних углов
= 4 × 180° = 720°
т.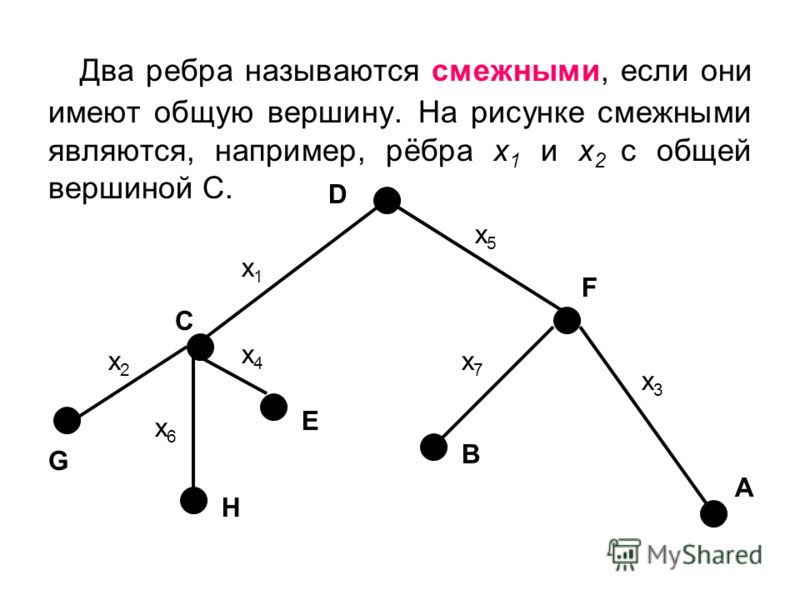 е. сумма внутренних углов
е. сумма внутренних углов
= (6 – 2) × 180°
Сумма внутренних углов многоугольник с n сторонами = (n – 2) × 180°
Кроме того, (n – 2) = сумма внутренних углов 180°
н = сумма внутренних углов 180° + 2
Итак, мы можем изменить формулу, чтобы найти количество сторон многоугольника.
Чтобы найти величину каждого внутреннего угла многоугольника, разделите сумму внутренних углов на количество углов многоугольника:
Каждый внутренний угол = сумма внутренних углов количество углов
Чтобы найти меру недостающего угла многоугольника с «n» сторонами, когда дана сумма (n – 1) углов:
- Найдите сумму внутренних углов многоугольника с n сторонами
- Недостающий угол = Сумма внутренних углов – Сумма оставшихся (n – 1) углов.

Мы знаем, что при удлинении стороны треугольника угол, образованный снаружи треугольника, называется его внешним углом. Рассмотрим многоугольник ABCD. Сторона BC многоугольника расширяется до точки E.
Теперь ∠DCE формируется снаружи многоугольника путем удлинения стороны многоугольника. Значит, это внешний угол многоугольника ABCD.
Теперь рассмотрим пятиугольник.
Теперь давайте расширим стороны пятиугольника, как показано ниже, чтобы получить внешние углы.
Если мы поместим все внешние углы смежными друг с другом, мы получим полный угол.
∠1, ∠2, ∠3, ∠4 и ∠5 в сумме дают полный угол.
т. е. сумма ∠1, ∠2, ∠3, ∠4 и ∠5 равна 360°.
(Можно попытаться доказать это логически, используя формулу суммы внутренних углов многоугольника.)
Аналогично, для любого другого многоугольника сумма внешних углов равна 360°.
Чтобы найти меру одного внешнего угла многоугольника, когда известны меры других углов, выполните следующие действия:
Сначала найдите сумму внешних углов, меры которых даны.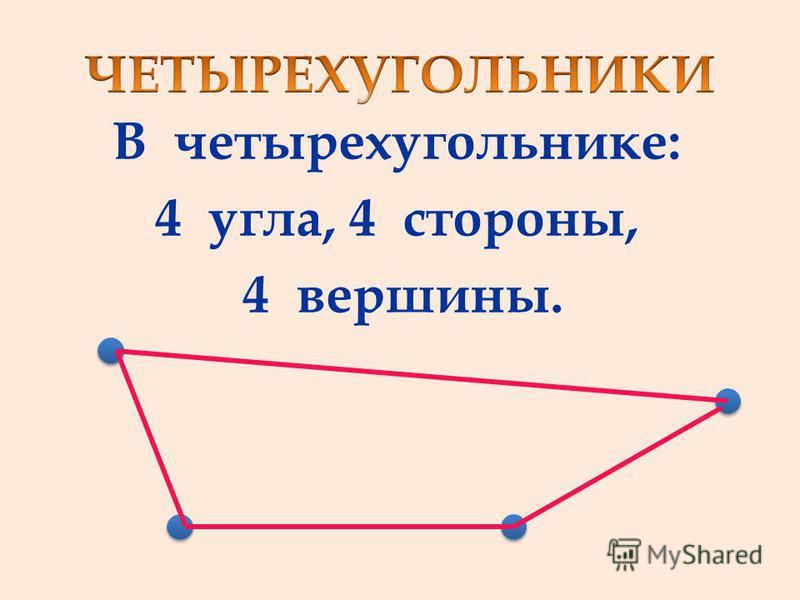
Затем вычтите сумму из 360⁰, чтобы получить величину недостающего угла.
В многоугольнике количество сторон, количество внутренних углов и количество внешних углов равны. Таким образом, для правильного многоугольника с числом сторон «n» число внешних углов также равно «n».
Сумма внешних углов любого многоугольника равна 360°.
Отсюда получаем,
n × мера каждого внешнего угла
= сумма всех внешних углов
Отсюда получаем
Число сторон правильного многоугольника получается делением 360° на меру каждого внешнего угла.
Теперь
Следовательно, имеем
Теперь вы знаете, как найти количество сторон правильного многоугольника, если задан внешний угол.
Мы знаем, что внутренний угол и соответствующий ему внешний угол многоугольника образуют линейную пару.
Таким образом, мы имеем следующее соотношение между ними.
Внутренний угол + Внешний угол = 180°
Используя это соотношение между внутренним углом и соответствующим внешним углом, мы можем найти количество сторон правильного многоугольника, если мера внутреннего угла многоугольника задана следующим образом: шаги:
Вычислить меру соответствующего внешнего угла.
Используйте результат «Сумма внешних углов многоугольника = 360°».
Вычислить значение ‘n’
- Внешние углы правильного многоугольника равны.
- Количество внутренних углов равно количеству сторон.
Используйте соотношение
Виды четырехугольников
Трапеция
- Трапеция – это четырехугольник, у которого одна пара противоположных сторон параллельна.
- Другая пара сторон будет непараллельной.
- Сумма углов на одной стороне, соединяющих параллельные стороны, будет 180°.
- Так как это четырехугольник, сумма всех углов трапеции будет 360°.
Ниже приведены несколько реальных примеров трапеций.
ABCD и PQRS — две трапеции. Какая разница между двумя?
А углы равнобедренной трапеции?
Мы можем резюмировать свойства трапеции следующим образом:
Так как это четырехугольник, сумма всех углов трапеции будет 360°.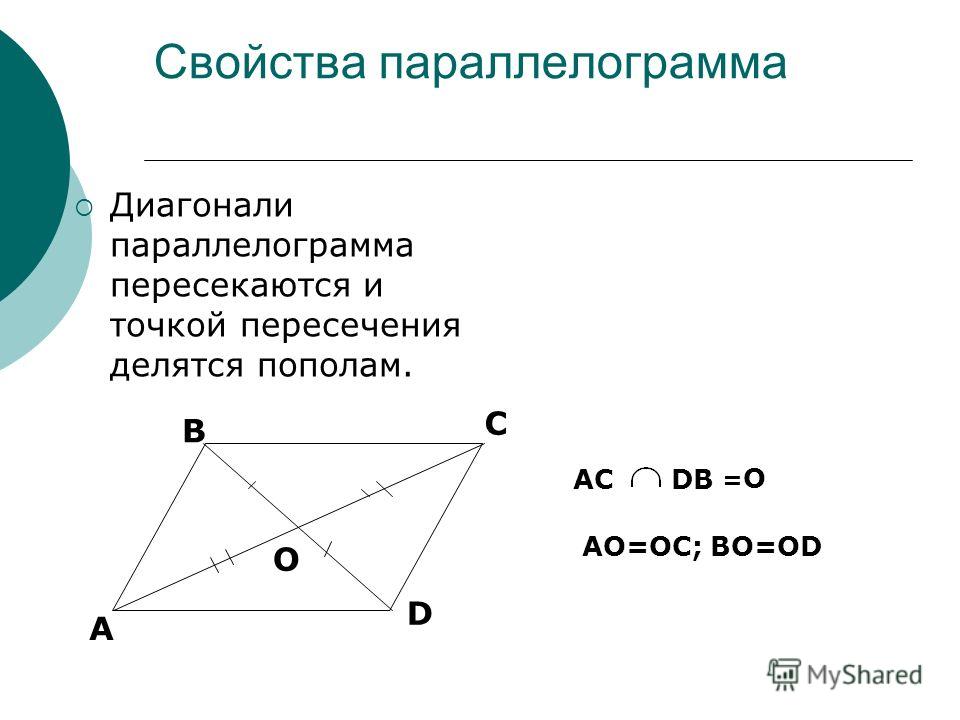
Откуда мы знаем, что четырехугольник является трапецией?
Откуда мы знаем, что четырехугольник является равнобедренной трапецией?
Воздушный змей
Стороны AB и BC являются смежными сторонами. Точно так же стороны AD и CD являются смежными сторонами.
Этот тип четырехугольника называется воздушным змеем.
В воздушном змее самая длинная диагональ делит воздушного змея на два равных треугольника.
- Углы, образованные каждой парой неравных смежных сторон, будут соответствующими углами и будут равны.
- Более короткая диагональ не делит воздушного змея на конгруэнтные треугольники.
Это означает, что другая пара противоположных углов не равна.
Таким образом, мы можем сказать, что у воздушного змея одна пара противоположных углов равна.
Как мы можем это сказать? У квадрата или ромба каждая пара смежных сторон равна. Следовательно, мы можем сказать, что квадрат и ромб также могут быть воздушным змеем.
Смежные стороны прямоугольника не равны. Следовательно, это не может быть воздушный змей.
Итак, воздушный змей — это четырехугольник со следующими свойствами
- Две различные пары смежных сторон равны.
- Одна пара противоположных углов равна (Углы, образованные неравными смежными сторонами).
- Диагонали пересекаются под углом 90°.
Как мы можем сказать, что четырехугольник — воздушный змей? Четырехугольник является воздушным змеем, если:
Параллелограмм
Рассмотрим две параллельные прямые a и b.
Две линии «x» и «y» пересекают эти параллельные линии.
‘x’ и ‘y’ также параллельны друг другу.
Форма PQRS представляет собой четырехугольник, в котором
- пара противоположных сторон параллельны.
- Пара противоположных сторон равны.
Такой четырехугольник называется параллелограммом.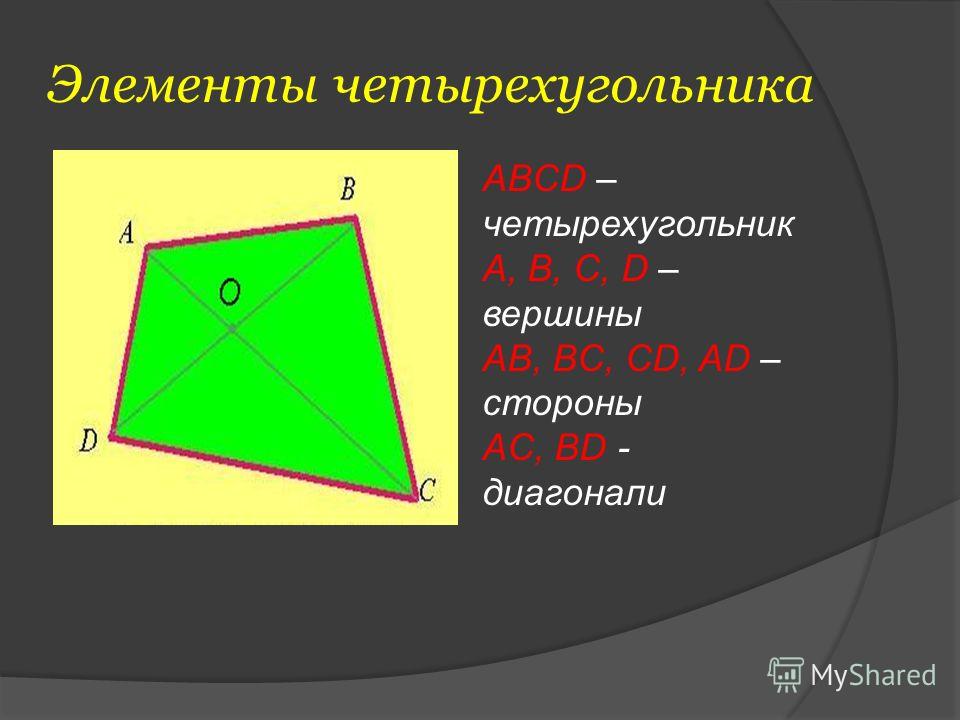
Вот несколько примеров параллелограммов, которые мы встречаем в повседневной жизни.
Параллелограмм – это четырехугольник, у которого:
- Пары противоположных сторон параллельны и равны.
- Пара противоположных углов равны.
- Пара смежных углов дополнительных.
- Диагонали, делящие друг друга пополам.
Четырехугольник является параллелограммом,
Когда мы должны найти длины сторон параллелограмма, зная длины смежных сторон, мы применяем следующее свойство:
- Противоположные стороны параллелограмма равны.
Пример:
В параллелограмме ABCD AB = 6 см и AD = 4,5 см. Мы можем найти длины двух других сторон BC и CD, как указано ниже:
Противоположные стороны параллелограмма равны.
Следовательно, AB = CD = 6 см
AD = BC = 4,5 см
Чтобы найти длины диагоналей параллелограмма, мы применяем следующее свойство:
- Диагонали параллелограмма делят друг друга пополам.

Пример:
В параллелограмме PARL диагонали PR и AL делятся пополам в точке O.
PO = 5,2 см и OL = 4 см
Какова длина диагоналей? Дано, что диагонали PR и AL пересекаются пополам в точке O.
Это означает, что PO = OR
и AO = OL.
Отсюда имеем
РО = ИЛИ = 5,2 см
ПР = РО + ИЛИ
= 5,2 + 5,2
= 5,2 + 5,2
Аналогично, АО = 9003
Аналогично, АО = 9003
= 03 см ПР
= 4 + 4
= 8 см
Чтобы найти неизвестные углы параллелограмма, мы должны применить следующие свойства углов:
- Пары противоположных углов параллелограмма равны.
- Пара смежных углов являются дополнительными.
Чтобы найти длину сторон параллелограмма, зная периметр и отношение сторон, выполните следующие действия:
Чтобы найти длину сторон, зная периметр параллелограмма и отношение сторон, мы выполняем следующие шаги:
Чтобы найти угол, если измерение смежных углов задано в алгебраической форме, выполните следующие действия:
Чтобы найти угол, если задано отношение смежных углов, выполните следующие действия:
Что означает выражение «Противоположные углы?»
Противоположные углы — это
- Углы, которые противоположны друг другу при пересечении двух прямых.

- Формируется в каждой из противоположных вершин.
Смежные углы — это углы, смежные с другим углом, имеющим ту же сторону, что и другой угол.
Ромб
Вы знаете, как называется красная фигура на карточке?
При игре в карты его обычно называют «алмаз». Но он представляет собой геометрическую фигуру «Ромб».
Ромб — особый параллелограмм, у которого все стороны равны. Ромб также имеет равные противоположные углы.
Это означает, что у ромба противоположные стороны параллельны. Помните, что диагонали ромба делятся пополам под прямым углом (9угол 0°) в точке их пересечения.
Диагонали ромба перпендикулярно делятся пополам.
Как узнать, является ли четырехугольник ромбом?
Чтобы найти длины сторон или диагоналей ромба, применим следующие свойства:
- Все стороны ромба равны.
- Диагонали делятся пополам.
Чтобы найти меры углов ромба, мы применяем следующие свойства:
- Пара противоположных углов равны.

- Пара смежных углов являются дополнительными.
Чтобы найти длину стороны ромба, зная периметр, выполните следующие действия:
Чтобы найти длину стороны ромба, зная длину диагонали, выполните следующие действия:
Запомнить :
Прямоугольник
Рассмотрим набор параллельных прямых ‘a’ и ‘b’.
Давайте нарисуем еще один набор параллельных линий, которые будут перпендикулярны линиям «a» и «b».
- Образованная фигура ABCD представляет собой параллелограмм.
- Четыре угла ∠A, ∠B, ∠C и ∠D равны 90°.
Фигура ABCD — прямоугольник. Прямоугольник является параллелограммом со следующими свойствами:
Прямоугольник является особым параллелограммом, так как его диагонали равны по длине.
В прямоугольнике RANG мы можем сказать, что
диагональ RN = диагональ AG
Чтобы найти длины сторон прямоугольника, применим следующее свойство:
- Пара противоположных сторон равны.

Чтобы найти длины диагоналей, применим следующее свойство:
- Диагонали прямоугольника равны и делят друг друга пополам.
Квадрат
Квадрат – это параллелограмм, у которого все стороны равны и все углы прямые.
- Квадрат — это особый тип параллелограмма, у которого все стороны равны по длине, все углы равны по размеру и все углы прямые.
- Все углы квадрата прямые.
- Диагонали квадрата равны по длине.
- Диагонали квадрата делятся пополам, образуя прямые углы.
Диагонали квадрата:
- Равны.
- Они пересекают друг друга перпендикулярно.
В квадрате:
- Когда известен периметр, мы можем найти длину стороны, разделив периметр на 4.
- Мы можем найти длину диагоналей, когда стороны заданы, применяя теорему Пифагора.

- Когда длина диагонали известна, мы можем найти длины сторон, применяя теорему Пифагора.
На рисунке ниже показана классификация четырехугольников.
Четырехугольники взаимосвязаны? Давайте сначала исследуем связь между трапецией и параллелограммом:
- Все параллелограммы являются трапециями, так как у них хотя бы одна пара противоположных сторон параллельна.
- Но трапеция не может быть параллелограммом, так как у нее нет двух пар противоположных сторон, параллельных и равных.
Теперь давайте посмотрим на связь между прямоугольником и квадратом:
- Мы можем считать, что квадрат имеет пару противоположных сторон, параллельных и равных.
- Все углы квадрата равны 90°.
- Квадрат также может быть прямоугольником.
- Прямоугольник не может быть квадратом, так как у него не все стороны равны.

Какая связь между ромбом и другими параллелограммами?
- Квадрат может быть ромбом, так как все его стороны равны, а диагонали делятся пополам под углом 90°.
- Ромб не может быть квадратом, так как его углы не прямые.
- Ромб не может быть прямоугольником, а прямоугольник не может быть ромбом.
- Ромб может быть воздушным змеем, так как его смежные стороны можно считать равными.
Помните:
- Если только одна пара противоположных сторон параллельна, то это трапеция.
- Если равны только две пары соседних сторон, то это воздушный змей.
- Если противоположные стороны и углы равны, а диагонали делят друг друга пополам, то это параллелограмм.
- Если все стороны равны, все углы равны 90⁰, диагонали равны и перпендикулярно делят друг друга пополам, то это квадрат.

- Если противоположные стороны равны и все углы равны 90⁰, то это прямоугольник.
- Если все стороны равны и противоположные углы равны, то это ромб.
Различные типы фигур | Вершина, стороны, части, 2D и 3D
Граница или контур объекта называется его формой. Мы сталкиваемся со многими формами в нашей повседневной жизни, и дети начинают узнавать эти формы еще до того, как на самом деле изучают их. Алфавиты английских фигур — это все фигуры разных типов. Солнце, земля и другие планеты, горы и все остальное в мире имеют определенные формы. Давайте узнаем больше об этих формах.
Для начала важно понять, как мы классифицируем различные формы? Первая базовая категоризация основана на характере линейных сегментов, из которых они состоят, т. е. образуют ли эти линейные сегменты замкнутый контур или открытые концы. В зависимости от структуры фигуры делятся на две категории:
- Открытые фигуры
- Закрытые фигуры
Далее у нас есть количество отрезков, необходимых для формирования фигуры.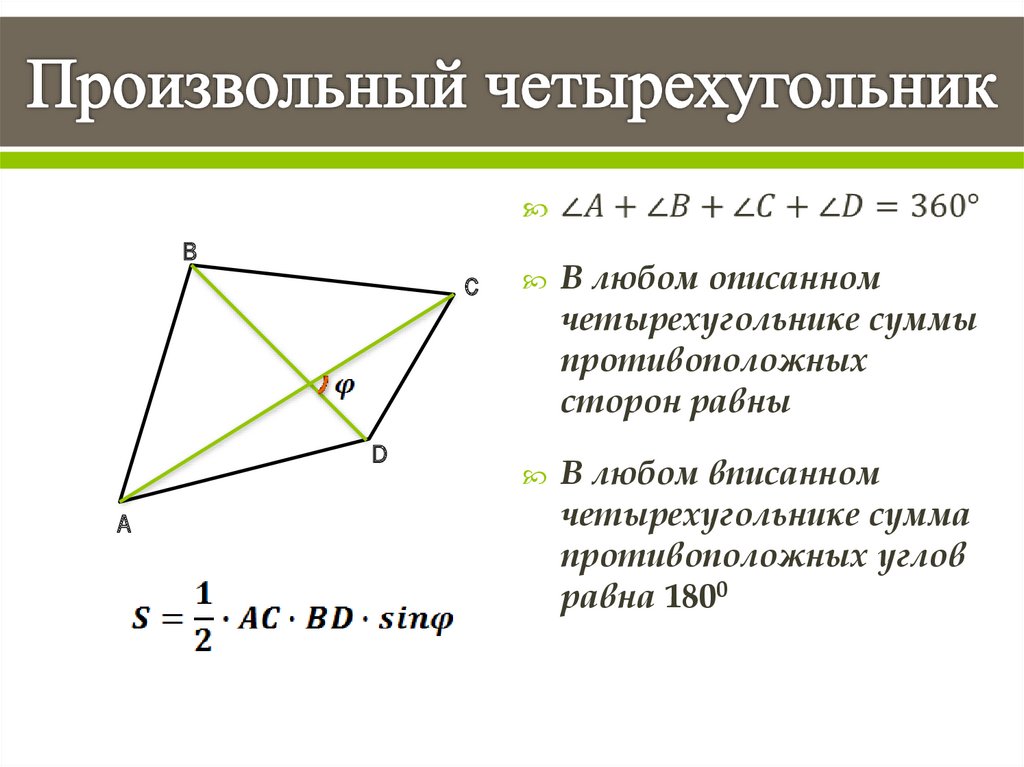 Например, нам может понадобиться три отрезка для определенной фигуры, в то время как для другой формы могут потребоваться отрезки. Таким образом, в зависимости от количества отрезков линии можно разделить на треугольники, четырехугольники, пятиугольники, шестиугольники и т. д.
Например, нам может понадобиться три отрезка для определенной фигуры, в то время как для другой формы могут потребоваться отрезки. Таким образом, в зависимости от количества отрезков линии можно разделить на треугольники, четырехугольники, пятиугольники, шестиугольники и т. д.
Кроме того, формы можно классифицировать на основе их размеров. Форма может быть:
- 2-мерной
- 3-мерной
Рассмотрим эти формы более подробно.
Открытые и замкнутые формы
Как мы узнали, первая базовая категоризация основана на природе линейных сегментов, из которых они состоят, т. е. образуют ли эти линейные сегменты замкнутый контур или открытые концы.
Открытые фигуры – Фигуры, состоящие из не пересекающихся отрезков, называются открытыми фигурами. Это означает, что эти формы имеют открытые концы и не закрыты, например, буква C является открытой формой, так как ее концы не встречаются.
Замкнутые фигуры — Замкнутыми фигурами называются фигуры, состоящие из сегментов линий, образующих замкнутые петли. Они начинаются и заканчиваются в одной и той же точке. Например, шар представляет собой замкнутую форму. Простая замкнутая фигура, состоящая из трех или более отрезков, называется многоугольником .
Они начинаются и заканчиваются в одной и той же точке. Например, шар представляет собой замкнутую форму. Простая замкнутая фигура, состоящая из трех или более отрезков, называется многоугольником .
2D- и 3D-формы
Формы можно классифицировать на основе их размеров. Три измерения: длина, ширина и высота.
2D-формы — 2-мерные формы или 2D-формы — это формы, которые имеют только длину и ширину. Например, такие формы, как прямоугольники и квадраты, являются двумерными.
3D-формы – 3-мерные формы или 3D-формы – это формы, которые имеют все три измерения, т. е. длину, ширину и высоту.
Вершина – Точка встречи пары сторон многоугольника называется его вершиной. Например, такие формы, как куб и прямоугольный параллелепипед, являются трехмерными фигурами. Например, на приведенном ниже рисунке ABCD вершинами являются A, B, C и D.
Сторона — Линия, соединяющая две вершины, называется стороной.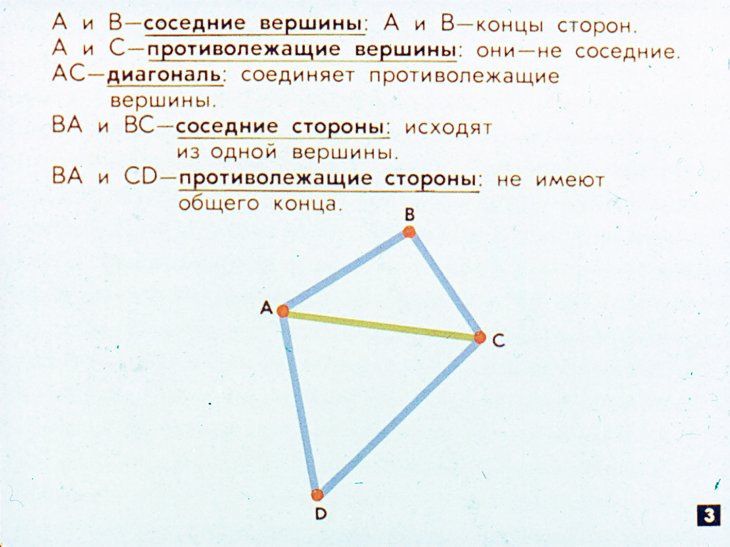 Например, в приведенном выше многоугольнике ABCD AB является одной из сторон многоугольника.
Например, в приведенном выше многоугольнике ABCD AB является одной из сторон многоугольника.
Смежные стороны – Любые две стороны многоугольника, имеющие общую конечную точку, называются его смежными сторонами. Например, в заданном многоугольнике ABCD четыре соседние пары сторон равны (AB, BC), (BC, CD), (CD, DA) и (DA, AB).
Углы – Три угла – это углы, образованные в этих вершинах, то есть ∠A, ∠B и ∠C. Угол, образованный при A, также можно записать как ∠BAC. Точно так же мы можем написать ∠ABC и ∠ACB. Эти углы также называются 9.0691 внутренних углов треугольника . Внешний угол треугольника образован любой стороной треугольника и продолжением прилежащей к нему стороны.
Диагонали – Отрезок, соединяющий две несмежные вершины многоугольника, называется его диагональю. Например, в данном многоугольнике ABCD вершины A и C являются несмежными. Точно так же B и D — несмежные вершины.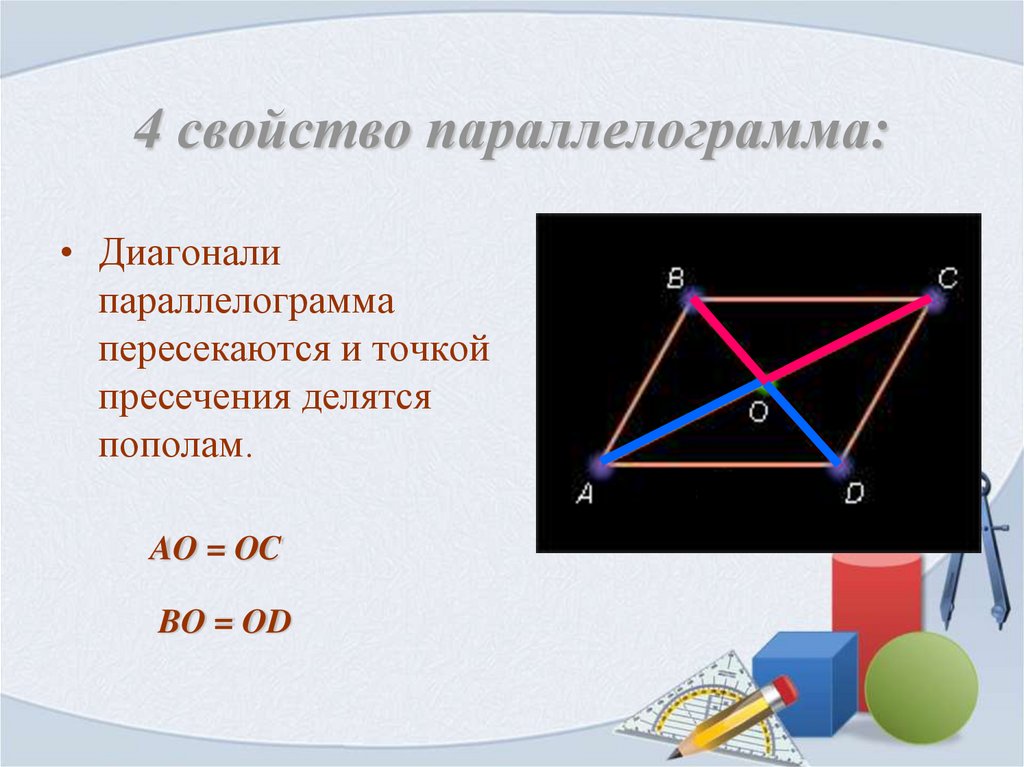 Следовательно, прямые BD и AC являются диагоналями многоугольника ABCD.
Следовательно, прямые BD и AC являются диагоналями многоугольника ABCD.
Давайте теперь изучим некоторые часто используемые формы в математике, а также в повседневной жизни.
Поскольку у нас есть исследования, то формы, которые имеют только длину и ширину, называются двумерными формами. Эти формы дополнительно классифицируются в зависимости от количества сегментов линии, из которых они состоят. Некоторыми из распространенных форм являются треугольники, четырехугольники, пятиугольники и другие многоугольники. Давайте разберемся в этом подробно.
Треугольник
Треугольник — это многоугольник, состоящий из трех сторон, трех углов и трех вершин. Например, пусть у нас есть треугольник ABC, как показано на рисунке ниже.
В этом треугольнике
- три вершины — A, B и C
- три стороны — AB, BC и AC
- три угла — ∠A, ∠B и ∠C
Свойства треугольник
Свойства треугольника:
- Стороны, углы и вершины – Мы уже знаем, что треугольник всегда имеет ровно три стороны и три вершины.
 Это основное свойство любого треугольника.
Это основное свойство любого треугольника. - Свойство суммы углов треугольника – Сумма трех внутренних углов треугольника всегда равна 180 o .
- Теорема Пифагора – Если один из углов треугольника равен 90 o , стороны, образующие прямой угол, называются основанием, а перпендикуляр – третьей стороной, а третья сторона называется гипотенузой.
Четырехугольники
Четырехугольник — это замкнутая фигура, образованная соединением четырех точек, среди которых любые три точки не лежат на одной прямой. Другими словами, четырехугольник — это многоугольник, состоящий из четырех сторон. При именовании четырехугольника необходимо помнить о порядке вершин.
Например, ниже у нас есть четырехугольник ABCD
Этот четырехугольник нельзя назвать ABDC, так как вершины B и D не смежны.
Также все четырехугольники имеют одинаковое количество сторон и углов, может быть разница в измерении этих сторон и углов из-за чего мы имеем разные виды четырехугольников.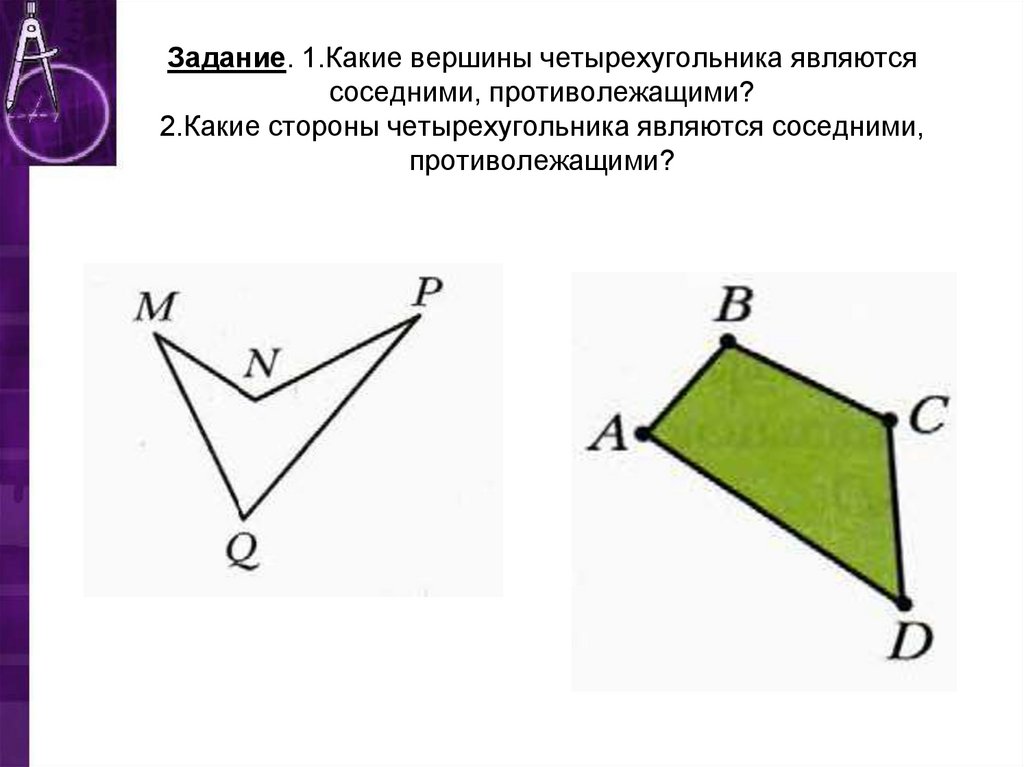 Но есть некоторые свойства четырехугольников, которые применимы ко всем, независимо от их уникальных свойств. Эти свойства:
Но есть некоторые свойства четырехугольников, которые применимы ко всем, независимо от их уникальных свойств. Эти свойства:
- Все четырехугольники имеют четыре стороны.
- Все четырехугольники имеют четыре угла
- Все четырехугольники имеют четыре вершины
- Сумма четырех углов четырехугольника равна 360 o
- Все четырехугольники имеют две диагонали четырехугольников.
Прямоугольник
Прямоугольник — это тип четырехугольника, который имеет равные противоположные стороны и четыре прямых угла. Свойства прямоугольника:
- У прямоугольника две пары параллельных сторон
- У прямоугольника четыре прямых угла
- У прямоугольника противоположные стороны одинаковой длины
- Диагонали прямоугольника делят друг друга пополам
Давайте разберемся с каждым из вышеперечисленных свойств через нижний прямоугольник ABCD.
- Прямоугольник ABCD имеет две пары параллельных сторон, а именно (AB и CD) и (AD и BC)
- Прямоугольник ABCD имеет четыре прямых угла, а именно при ∠A, ∠B, ∠C и ∠D.

- Прямоугольник ABCD имеет противоположные стороны равной длины, т.е. AB = CD и AD = BC
- Диагонали прямоугольника делят друг друга пополам, т.е. AP = PC и BP = PD
Квадрат
Квадрат – это четырехугольник, у которого четыре равные стороны и четыре прямых угла.
Свойства квадрата:
- У квадрата четыре равные стороны, т.е. все стороны квадрата равны.
- У квадрата четыре прямых угла
- У квадрата две пары параллельных сторон
- Диагонали квадрата делят друг друга пополам
- Диагонали квадрата перпендикулярны друг другу
Давайте разберем каждое из вышеуказанных свойств через приведенный ниже квадрат ABCD.
- Квадрат ABCD имеет две пары параллельных сторон, а именно (AB и CD) и (AD и BC)
- Квадрат ABCD имеет четыре прямых угла, а именно при ∠A, ∠B, ∠C и ∠D.
- У квадрата ABCD все стороны равны, т.е. AB = CD = AD = BC
- Диагонали квадрата ABCD делят друг друга пополам, т.
 е. AP = PC и BP = PD
е. AP = PC и BP = PD - Диагонали квадрата ABCD перпендикулярны друг другу, т.е. АС ⟂ BD.
Параллелограмм
Параллелограмм – это четырехугольник, в котором обе пары противоположных сторон параллельны.
Свойства параллелограмма:
- Параллелограмм имеет противоположные стороны одинаковой длины.
- Противоположные углы параллелограмма равны.
- Параллелограмм имеет две пары параллельных сторон
- Диагонали параллелограмма делят друг друга пополам
Давайте разберем каждое из вышеперечисленных свойств через приведенный ниже параллелограмм ABCD.
- Параллелограмм ABCD имеет две пары параллельных сторон, а именно (AB и CD) и (AD и BC)
- У параллелограмма ABCD противоположные углы равны, то есть ∠A = ∠C и ∠B = ∠D.
- Параллелограмм ABCD имеет противоположные стороны равной длины, т.е. AB = CD и AD = BC
- Диагонали параллелограмма делят друг друга пополам, т.
 е. AP = PC и BP = PD
е. AP = PC и BP = PD
Трапеция
Трапеция – это четырехугольник, у которого одна пара противоположных сторон параллельна.
Свойства трапеции:
- Трапеция имеет одну пару параллельных сторон
- Трапеция не имеет прямых углов
- Трапеция имеет одну пару противоположных сторон равной длины
вышеуказанные свойства через нижнюю трапецию ABCD.
- Трапеция ABCD имеет одну пару параллелей, а именно (AB и CD)
- В трапеции нет прямых углов.
- У трапеции ABCD одна пара противоположных сторон одинаковой длины, т.е. AD и BC
Ромб
Ромб – четырехугольник с четырьмя равными сторонами.
Свойства ромба:
- У ромба две пары параллельных сторон
- Противоположные углы в ромбе равны.
- У ромба четыре равные стороны. Это означает, что все его стороны равны.
- Диагонали ромба делят друг друга пополам
- Диагонали ромба перпендикулярны друг другу
Давайте разберем каждое из вышеуказанных свойств через изображенный ниже ромб ABCD.

Давайте разберем каждое из вышеперечисленных свойств через приведенный ниже ромб ABCD.
- Ромб ABCD имеет две пары параллельных сторон, а именно (AB и CD) и (AD и BC)
- У ромба ABCD все стороны равны, т.е. AB = CD = AD = BC
- У ромба ABCD противоположные углы равны, то есть ∠A = ∠C и ∠B = ∠D.
- Диагонали ромба делят друг друга пополам, т.е. AP = PC и BP = PD
- Диагонали ромба ABCD перпендикулярны друг другу, т.е. АС ⟂ BD.
Окружность — это двумерная фигура, образованная набором точек, находящихся на постоянном или фиксированном расстоянии от фиксированной точки на плоскости. Это фиксированное расстояние называется радиусом окружности, а фиксированная точка называется центром окружности.
Части круга
Окружность – Длина окружности – это расстояние вокруг границы окружности. Другими словами, это периметр круга.
Радиус – Радиус – это расстояние от центра круга до любой точки на границе круга.

Диаметр – Диаметр – это линия от одной точки на границе круга до другой точки, проходящая через центр круга. Это в два раза больше длины радиуса.
Хорда окружности – Хорда окружности – это линия, проведенная из одной точки на границе окружности в другую точку. Диаметр — это самая длинная хорда окружности.
Дуга окружности – Часть части окружности окружности называется ее дугой.
Давайте поймем вышеуказанные части круга через следующий рисунок.
В круге выше
O — центр круга.
Отрезок линии АО является радиусом окружности.
Отдельный сегмент PQ представляет собой диаметр круга. Заметим, что отрезок PQ проходит через центр O
Отрезок AQ — это хорда окружности, соединяющая две точки A и Q, лежащие на границе окружности.
Кривая, образованная AQ, является дугой окружности.
3-мерные формы или трехмерные формы — это формы, которые имеют все три измерения, т.
 е. длину, ширину и высоту. Комната дома является распространенным примером трехмерной формы. Давайте разберем некоторые из этих форм в деталях. Некоторые общие термины, используемые для определения 3D-форм:
е. длину, ширину и высоту. Комната дома является распространенным примером трехмерной формы. Давайте разберем некоторые из этих форм в деталях. Некоторые общие термины, используемые для определения 3D-форм:- Грани — гранью называется любая отдельная плоская поверхность трехмерной формы.
- Ребра – Ребро – это отрезок линии на границе, соединяющий одну вершину (угловую точку) с другой. Это похоже на стороны, которые мы имеем в 2D-фигурах.
- Вершины – Точка пересечения пары сторон многоугольника называется его вершиной.
Давайте теперь разберемся с некоторыми распространенными трехмерными формами.
Кубоид
Трехмерная фигура с шестью прямоугольными гранями называется кубоидом. Например, спичечный коробок, кирпич, книга и т. д. Другими словами, это расширение прямоугольника в трехмерной плоскости.

Ниже представлена общая схема прямоугольного параллелепипеда
Грани : Прямоугольный параллелепипед имеет 6 прямоугольных граней, противоположные стороны которых идентичны.
Ребра : Прямоугольный параллелепипед имеет 12 ребер
Вершина : Прямоугольный параллелепипед имеет 8 вершин
Куб
Кубоид, у которого длина, ширина и высота равны, называется кубом. Примерами куба являются кубики сахара, кубики сыра и кубики льда. Другими словами, это расширение квадрата в трехмерной плоскости.
Ниже представлена общая схема куба
Грани : Куб имеет 6 прямоугольных граней, все из которых идентичны.
Ребра : Куб имеет 12 ребер
Vertx : Куб имеет 8 вершин
Цилиндр
Цилиндр представляет собой тело с двумя конгруэнтными окружностями, соединенными криволинейной поверхностью.
Ниже представлена общая схема цилиндра
Грани : Цилиндр имеет одну изогнутую поверхность и две плоские грани.

Кромки : Цилиндр имеет две изогнутые кромки.
Vertx : Цилиндр не имеет вершин.
Конус
Круглый конус имеет круглое основание, соединенное изогнутой поверхностью с вершиной. Конус называется прямым круговым конусом, если прямая, проведенная из его вершины к центру основания, перпендикулярна основанию. Рожок мороженого является примером конуса
Ниже приведена общая схема конуса
Грани : Конус имеет одну плоскую поверхность и одну изогнутую поверхность.
Ребра : Конус имеет одно изогнутое ребро.
Вершина : Конус имеет одну вершину.
Сфера
Сфера — это твердое тело, образованное всеми точками пространства, которые находятся на одинаковом расстоянии от фиксированной точки, называемой центром. Другими словами, это расширение окружности в трехмерной плоскости.
Ниже представлена общая схема Сферы
Грани : Конус имеет одну изогнутую поверхность.

Ребра : Конус не имеет ребра.
Вершина : Конус не имеет вершины.
2-D и 3-D формы Рабочие листы по математике для детского сада
Площадь круга (на тему «Украшение дома и мебель») Рабочие листы
Преобразование фигур (на тему Международного дня грамотности) Рабочие листы по математикеПросмотреть все рабочие листы
Мы много тратим времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
ПОНИМАНИЕ ЧЕТЫРЕХСТОРОННИХ
Математика 09 августа 2020 г.
Четырехугольник: Замкнутым четырехугольником называется фигура, имеющая четыре сегмента линии.
Четырехугольник — это многоугольник с четырьмя отрезками.
Замкнутая фигура, состоящая из четырех отрезков, называется называется четырехугольником.

В этом четырехугольнике ABCD
его сторонами являются четыре отрезка AB, BC, CD и DA.
Четыре точки A, B, C и D являются его вершинами.
∠ A, ∠ B, ∠ C и ∠ D называются его углами.
АС и БД являются его диагоналями.
Диагональ отрезок, соединяющий две противоположные вершины.
Диагональ – это линия отрезок, соединяющий две непоследовательные вершины.
Соседний стороны четырехугольника
Любые два Стороны четырехугольника, имеющие общую точку, называются смежными сторонами.
На приведенном выше рисунке AD и AB являются смежными сторонами.
, которые имеют между собой общую точку «А».
Точно так же AB и BC являются смежными сторонами.
, которые имеют между собой общую точку «В».
Аналогично можно найти еще две пары смежных сторон (BC, CD) и (CD, DA), которые имеют общие точки C и D соответственно.
Противоположный стороны четырехугольника
Любые две стороны четырехугольника, не имеющие общей точки, называются противоположными сторонами.
Стороны, которые не являются смежными, называются противоположными сторонами.
На приведенном выше рисунке AB и CD являются противоположными сторонами.
, которые не являются соседними.
Точно так же BC и AD являются противоположными сторонами.
, которые не являются смежными и не имеют между собой общей точки.
Соседний углы четырехугольника
Смежные углы имеют общую сторону.
В приведенном выше четырехугольнике ABCD(∠ A, ∠ B), (∠ B, ∠ C) (∠ C, ∠ D) и (∠ D ∠ A) являются смежными углами.
Противоположный углы четырехугольника
Углы, которые не являются смежными, называются противолежащими углами четырехугольника.

В приведенном выше четырехугольнике ABCD
(∠ A, ∠ C) и (∠ B, ∠ D) противоположные углы.
Выпуклый четырехугольник и вогнутый четырехугольник
Четырехугольник, каждый угол которого меньше 180 0 , называется выпуклым четырехугольником.
Четырехугольник , у которого любой угол больше 180 0 , называется вогнутым. четырехугольник.
Правильный многоугольник
Многоугольник (здесь четырехугольник), у которого все стороны и все углы равны, называется правильным многоугольником.
Сумма углов свойство четырехугольника
Сумма углы четырехугольника 360 0 .
В любом четырехугольнике ∠ A + ∠B + ∠C +∠D = 360 0 .
Особые типы четырехугольников
Параллелограмм: Параллелограмм – это четырехугольник, в котором обе пары противоположных сторон параллельны.

Свойства параллелограмма
Противоположные стороны параллелограмма равны.
Противолежащие углы параллелограмма равны.
Диагонали параллелограмма делят друг друга пополам.
Каждая диагональ делит параллелограмм на два равных треугольника.
Одна пара противоположных сторон параллельна и равна.Прямоугольник: Параллелограмм, в котором все четыре угла прямые, называется прямоугольником.
Свойства прямоугольника
Каждый угол прямоугольника прямой.
Диагонали прямоугольника равны.
Диагонали прямоугольника делят друг друга пополам.
Диагонали прямоугольника делят друг друга пополам под разными углами.
Одна пара вертикально противоположных углов является острым, а другая пара углов тупым.Ромб: параллелограмм, у которого все четыре стороны равны.
Ромб: Параллелограмм, у которого две смежные стороны равны, называется ромбом.
Свойства ромба
Все стороны ромба равны.

Противоположные углы ромба равны.
Диагонали ромба не равны.
Диагонали ромба пересекаются под прямым углом пополам.Квадрат: Квадрат представляет собой параллелограмм, все стороны которого равны, а каждый угол равен 90 0 .
Свойства квадрата
Все стороны квадрата равны.
Каждый угол квадрата прямой.
Диагонали квадрата равны.
Диагонали квадрата делятся пополам под прямым углом.Трапеция: Трапеция – это четырехугольник , у которого одна пара противоположных сторон параллельна.
Равнобедренная трапеция: Трапеция, у которой две непараллельные стороны равны.
В равнобедренной трапеции каждая пара углов при основании равна.Воздушный змей: Четырехугольник, в котором две пары смежных сторон равны, называется воздушным змеем.
Свойства воздушного змея
Противоположные стороны воздушного змея не равны.
Диагонали перпендикулярны друг другу.
Любая диагональ перпендикулярна биссектрисе другой.
Решения NCERT для класса 8 Math Chapter 16
- Решения НЦЭРТ
- Класс 8
- Математика
- понимание форм ii четырехугольников
NCERT Solutions for Class 8 Math Глава 16 Понимание форм Ii Четырехугольники представлены здесь с простыми пошаговыми объяснениями. Эти решения для понимания четырехугольников фигур II чрезвычайно популярны среди учащихся 8-го класса по математике. Все вопросы и ответы из книги NCERT по математике для 8-го класса, глава 16, предоставляются здесь для вас бесплатно. Вам также понравится возможность без рекламы в решениях NCERT от Meritnation.
 Все решения NCERT для класса 8 по математике подготовлены экспертами и на 100% точны.
Все решения NCERT для класса 8 по математике подготовлены экспертами и на 100% точны.Страница № 16.15:
Вопрос 1:
Дайте определение следующим терминам:
(i) Четырехугольник
(ii) Выпуклый четырехугольникОтвет:
(i) Четырехугольник – это многоугольник, который имеет четыре стороны (или ребра) и четыре вершины (или углы).
Это может быть любая четырехсторонняя замкнутая форма.(ii) Выпуклый четырехугольник – это математическая фигура, каждый внутренний угол которой меньше или равен 180 градусам.
Страница № 16.15:
Вопрос 2:
В четырехугольнике определите каждое из следующего:
(i) Стороны
(ii) Вершины
(iii) Углы
(iv) Диагонали
(v) Смежные углы
(vi) Смежные стороны
(vii) Противоположные стороны
(viii) Противоположные углы
(ix) Внутренние
(x) ВнешниеОтвет:
(i) В четырехугольнике ABCD четыре отрезка прямой AB, BC, CD и DA называются его сторонами.
 (ii) вершины четырехугольника являются углами четырехугольника. Четырехугольник имеет четыре вершины. (iii) Точка встречи двух сторон четырехугольника называется углом. Четырехугольник имеет четыре угла. (iv) В четырехугольнике ABCD отрезки AC и BD называются его диагоналями. (v) Углы, имеющие общую сторону в качестве плеча, называются смежными углами. (vi) Две стороны смежны. если они имеют общую конечную точку. (vii) Две стороны противоположны, если они не имеют общей конечной точки. (viii) Два угла четырехугольника, которые не являются смежными, называются противоположными углами. (ix) Часть плоскость, образованная всеми такими точками, заключенными в четырехугольник, называется внутренней. (x) Часть плоскости, образованная всеми точками, не заключенными в четырехугольнике, называется внешней.
(ii) вершины четырехугольника являются углами четырехугольника. Четырехугольник имеет четыре вершины. (iii) Точка встречи двух сторон четырехугольника называется углом. Четырехугольник имеет четыре угла. (iv) В четырехугольнике ABCD отрезки AC и BD называются его диагоналями. (v) Углы, имеющие общую сторону в качестве плеча, называются смежными углами. (vi) Две стороны смежны. если они имеют общую конечную точку. (vii) Две стороны противоположны, если они не имеют общей конечной точки. (viii) Два угла четырехугольника, которые не являются смежными, называются противоположными углами. (ix) Часть плоскость, образованная всеми такими точками, заключенными в четырехугольник, называется внутренней. (x) Часть плоскости, образованная всеми точками, не заключенными в четырехугольнике, называется внешней.Стр. № 16.15:
Вопрос 3:
Дополните каждое из следующих утверждений так, чтобы получить верное утверждение:
(i) Четырехугольник имеет ……. сторон.
(ii) Четырехугольник имеет . ….. углов.
….. углов.
(iii) Четырехугольник имеет ….. вершин, никакие три из которых не являются …..
(iv) Четырехугольник имеет …. диагоналей.
(v) Количество пар смежных углов четырехугольника …….
(vi) Количество пар противоположных углов четырехугольника …….
(vii) Сумма углов четырехугольника равна ……
(viii) Диагональ четырехугольника — это отрезок, соединяющий две …… вершины четырехугольника.
(ix) Сумма углов четырехугольника равна …. прямым углам.
(x) Каждый угол выпуклого четырехугольника равен ….. 180°.
(xi) В четырехугольнике точка пересечения диагоналей лежит в …. четырехугольника.
(xii) Точка находится внутри выпуклого четырехугольника, если она лежит в ….. двух его противоположных углов.
(xiii) Четырехугольник выпуклый, если для каждой стороны остальные …. лежат по одну сторону от прямой, содержащей сторону.Ответ:
(i) четыре
(ii) четыре
(iii) четыре, коллинеарные
(iv) два
(v) четыре
(vi) два
(vii) 360°
(viii) напротив
( ix) четыре
(x) меньше
(xi) внутренность
(xii) внутренности
(xiii) вершиныСтраница № 16.
 16:
16:Вопрос 4:
На рис.
(i) Назовите пару смежных сторон.
(ii) Назовите пару противоположных сторон.
(iii) Сколько пар смежных сторон?
(iv) Сколько пар противоположных сторон?
(v) Назовите пару смежных углов.
(vi) Назовите пару противоположных углов.
(vii) Сколько пар смежных углов?
(viii) Сколько пар противоположных углов?Ответ:
(i) (AB, BC) или (BC, CD) или (CD, DA) или (AD, AB)(ii) (AB, CD) или (BC, DA) (iii ) Четыре (iv) Два (v) (∠A, ∠B) или (∠B, ∠C) или (∠C, ∠D) или (∠D, ∠A)(vi) (∠A, ∠C) или (∠B, ∠D)(vii) Четыре(viii) Два
Страница № 16.16:
Вопрос 5:
Углы четырехугольника равны 110°, 72°, 55° и х °. Найдите значение x .
Ответ:
Сумма углов четырехугольника равна 360°. Получаем 110°+72°+55°+x=360°⇒237°+x=360°⇒x=360°-237° ∴ x=123°
Страница № 16.16:
Вопрос 6:
Три угла четырехугольника соответственно равны 110°, 50° и 40°.
 Найдите его четвертый угол.
Найдите его четвертый угол.Ответ:
Пусть x — четвертый угол. Поскольку сумма всех углов четырехугольника равна 360°, имеем: 110°+50°+40°+x=360°⇒200°+x=360°⇒ x=160°∴. Четвертый угол равен 160°.
Страница № 16.16:
Вопрос 7:
Четырехугольник имеет три острых угла, каждый из которых равен 80°. Чему равен четвертый угол?
Ответ:
Пусть x будет четвертым углом. Поскольку сумма всех углов четырехугольника равна 360°, мы имеем: 80°+80°+80°+x=360°⇒240°+x=360 °⇒x=120°∴ Четвертый угол равен 120°.
Страница № 16.16:
Вопрос 8:
Четырехугольник имеет все четыре угла одинаковой меры. Какова мера каждого?
Ответ:
Пусть x — мера каждого угла. Поскольку сумма всех углов четырехугольника равна 360°, имеем: x°+x°+x°+x°=360°⇒4x° =360°⇒x°=90°∴ Размер каждого угла равен 90°.
Страница № 16.16:
Вопрос 9:
Два угла четырехугольника равны 65°, а два других угла равны. Какова мера каждого из этих двух углов?
Ответ:
Пусть x — мера каждого угла.
 Поскольку сумма всех углов четырехугольника равна 360°, имеем: 65°+65°+x°+x°=360°⇒2x° +130°=360°⇒2x°=230°⇒x°=115°∴ Размер каждого угла равен 115°.
Поскольку сумма всех углов четырехугольника равна 360°, имеем: 65°+65°+x°+x°=360°⇒2x° +130°=360°⇒2x°=230°⇒x°=115°∴ Размер каждого угла равен 115°.Страница № 16.16:
Вопрос 10:
Три угла четырехугольника равны. Четвертый угол равен 150°. Чему равна мера равных углов.
Ответ:
Пусть x — мера равных углов четырехугольника. Поскольку сумма всех углов четырехугольника равна 360°, имеем: x°+x°+x°+150°=360 °⇒3x°=360°-150°⇒x°=210°∴ Размер каждого угла равен 70°.
Страница № 16.16:
Вопрос 11:
Четыре угла четырехугольника равны 3 : 5 : 7 : 9. Найдите углы.
Ответ:
Пусть углы находятся в соотношении 3x : 5x : 7x : 9x. Поскольку сумма всех углов четырехугольника равна 360°, имеем: 3x+5x+7x+9x=360°⇒ 24x=360°⇒x=15° Таким образом, углы равны:3x=45°5x=75°7x=105°9x=135°
Страница № 16.16:
Вопрос 12:
Если сумма двух углы четырехугольника равны 180°. Чему равна сумма оставшихся двух углов?
Ответ:
Пусть x+y – сумма оставшихся двух углов.
 Поскольку сумма всех углов четырехугольника равна 360°, имеем: 180°+x+y°=360°⇒x+ y°=180°∴ Сумма оставшихся двух углов равна 180°.
Поскольку сумма всех углов четырехугольника равна 360°, имеем: 180°+x+y°=360°⇒x+ y°=180°∴ Сумма оставшихся двух углов равна 180°.Страница № 16.16:
Вопрос 13:
На рис. 16.20 найдите меру ∠MPN .
Ответ:
Поскольку сумма всех углов четырехугольника равна 360°, имеем: 45°+90°+90°+∠MPN=360°⇒225°+∠MPN=360°∴∠ MPN=135°
Страница № 16.16:
Вопрос 14:
Стороны четырехугольника производятся по порядку. Чему равна сумма четырех внешних углов?
Ответ:
Стороны четырехугольника ABCD производятся по порядку (согласно рисунку). Теперь нам нужно найти сумму внешних углов. , линейная пара, имеем: a+x+b+y+c+z+w+d=180°+180°+180°+180°=720°ИЛИ сумма внутренних углов+сумма внешних углов= 180 ° × 4 = 720 °. Поскольку сумма внутренних углов четырехугольника равна 360 °, мы имеем: w + x + y + z = 360 °. Подставляя значение, мы получаем: a + b + c + d = 360 °∴ Сумма внешних углов = 360°
Страница № 16.
 16:
16:Вопрос 15:
На рис. Если ∠C = 100° и ∠D = 50°, найдите меру ∠APB .
Ответ:
∠A+∠B+∠C+∠D=360°⇒∠A+∠B+100°+50°=360°⇒∠A+∠B=210° …(i)In △APB , имеем: 12∠A+12∠B+∠APB=180°⇒∠APB=180°-12∠A+∠BИз (i) получаем:⇒∠APB=180°-12×210° ∴∠APB= 75°
Страница № 16.17:
Вопрос 16:
В четырехугольнике ABCD углы A, B, C и D относятся как 1 : 2 : 4 : 5. Найдите величину каждого угла четырехугольника.
Ответ:
Пусть x — мера каждого угла. Тогда отношение становится x : 2x : 4x : 5x. Поскольку сумма всех углов четырехугольника равна 360°, имеем: x+2x+4x+ 5x=360°⇒12x=360°⇒x=360°12⇒x=30° Таким образом, углы равны:x=30°2x=60°4x=120°5x=150°
Страница № 16.17:
Вопрос 17:
В четырехугольнике ABCD, CO и DO являются биссектрисами ∠C и ∠D соответственно. Докажите, что ∠COD=12(∠A+∠B).
Ответ:
∠COD =180°-∠OCD+∠ODC=180°-12∠C+∠D=180°-12360°-∠A+∠B=180°-180°+12∠A+∠B =12∠A+∠B= RHSHОтсюда доказано.
Страница № 16.17:
Вопрос 18:
Найдите количество сторон правильного многоугольника, если каждый из его углов имеет меру
(i) 160°
(ii) 135°
(iii) 175°
(iv) 162°
(v) 150°Ответ:
(i) Каждый внутренний угол = 2n-4n×90°So ,2n-4n×90°=160°⇒2n-4n=160°90°⇒2n-4n=169⇒18n-36=16n⇒2n=36∴ n=18(ii) Каждый внутренний угол=2n-4n× 90°So,2n-4n×90°=135°⇒2n-4n=135°90°⇒2n-4n=32⇒4n-8=3n∴ n=8(iii) Каждый внутренний угол=2n-4n×90 ° Итак, 2n-4n×90°=175°⇒2n-4n=175°90°⇒2n-4n=3518⇒36n-72=35n∴ n=72(iv) Каждый внутренний угол=2n-4n×90° Итак, 2n-4n×90°=162°⇒2n-4n=162°90°⇒2n-4n=95⇒10n-20=9n∴ n=20(v) Каждый внутренний угол=2n-4n×90°So, 2n-4n×90°=150°⇒2n-4n=150°90°⇒2n-4n=53⇒6n-12=5n∴ n=12
Страница № 16.17:
Вопрос 19:
Найдите количество градусов в каждом внешнем внешнем угле правильного пятиугольника.
Ответ:
Каждый внешний угол = 360n° Для правильного пятиугольника n = 5.∴ Внешний угол = 3605° = 72° х °, ( х — 5)°, ( х — 5)°, (2 х — 5)°, (2 х — 5)°, (2 х + 20)°.
 Найдите значение x .
Найдите значение x .Ответ:
Так как сумма всех углов шестиугольника равна 720°, мы получаем:x°+x-5°+x-5°+2x-5°+2x-5°+2x+20° =720°⇒x°+x°-5°+x°-5°+2x-5°+2x-5°+2x+20°=720°⇒9x-20°+20°=720°⇒9x= 720°∴ x=80
Страница № 16.17:
Вопрос 21:
В выпуклом шестиугольнике докажите, что сумма всех внутренних углов равна удвоенной сумме его внешних углов, образованных путем создания сторон одного и того же шестиугольника. заказ.
Ответ:
Для выпуклого шестиугольника внутренний угол = 2n-4n × 90° Для шестиугольника n = 6∴ Внутренний угол = 12–46 × 90° = 86 × 90° = 120° Итак, сумма все внутренние углы = 120°+120°+120°+120°+120°+120°=720°∴ Внешний угол=360n°=3606°=60°Итак, сумма всех внешних углов=60°+60 °+60°+60°+60°+60°=360°Теперь сумма всех внутренних углов=720°=2360°=удвоение внешних углов.
Страница № 16.17:
Вопрос 22:
Сумма внутренних углов многоугольника в три раза больше суммы его внешних углов.
 Определить количество сторон многоугольника.
Определить количество сторон многоугольника.Ответ:
2n-4×90°=3×360°n×n⇒n-2×180=3×360⇒n-2=6∴ n=8
Номер страницы 16.17:
Вопрос 23 :
Определить количество сторон многоугольника, внешний и внутренний углы которого относятся как 1 : 5.
Ответ:
Пусть n будет количеством сторон многоугольника. Пусть x и 5x будут внешним и внутренним углов. Поскольку сумма внутреннего и соответствующего внешнего угла равна 180°, мы имеем: x+5x=180°⇒6x=180°⇒x=30°Многоугольник имеет n сторон. Итак, сумма всех внешних углов = 30n°. Мы знаем, что сумма всех внешних углов многоугольника равна 360°, т.е. 30n=360∴ n=12
Страница № 16.17:
Вопрос 24:
ПКРТУ – правильный шестиугольник. Определите каждый угол Δ PQT .
Ответ:
Правильный шестиугольник состоит из 6 равносторонних треугольников. Таким образом, ∠PQT=60° и ∠QTP=30°. Поскольку сумма углов ∆PQT равна 180°, имеем: ∠P+∠ Q+∠T=180°⇒∠P+60°+30°=180°⇒∠P=180°-90°⇒∠QPT=90°∴ Углы треугольника равны 90°, 60° и 30°.
Свойства полигонов
Ресурсы ·
·
·
·
·
·Поиск
Свойства многоугольника (Математика | Геометрия | Свойства полигона) Что такое полигон?
Замкнутая плоская фигура, состоящая из нескольких отрезков, соединенных вместе. Стороны не пересекаются друг с другом. Встретятся ровно две стороны
каждая вершина.
Стороны не пересекаются друг с другом. Встретятся ровно две стороны
каждая вершина.Типы | Формулы | Части | Специальные полигоны | Имена
Типы многоугольников
Обычные — все углы равны и все стороны имеют одинаковую длину. Правильные многоугольники бывают равноугольными и равносторонними.
Равноугольный — все углы равны.
Равносторонний — все стороны одинаковой длины.Выпуклая — прямая, проведенная через выпуклый многоугольник пересекает не более двух сторон . Каждый внутренний угол меньше 180°. Вогнутая — через нее можно провести хотя бы одну прямую линию вогнутый многоугольник, который пересекает более чем с двух сторон . По крайней мере один внутренний угол больше 180°. 
Формулы многоугольника
(N = количество сторон и S = длина от центра до угла)Площадь правильного многоугольника = (1/2) N sin(360°/N) S 2
Сумма внутренних углов многоугольника = (N — 2) x 180°
количество диагоналей в многоугольнике = 1/2 N(N-3)
число треугольников (при проведении всех диагоналей из одного вершина) в многоугольнике = (N — 2)Многоугольные детали
Сторона — один из отрезков линии которые составляют многоугольник.
Вершина — точка, где две стороны встретиться. Две или более таких точек называются вершинами.
Диагональ — линия соединительная две вершины, не являющиеся стороной.

Внутренний угол — Угол сформированный по двум смежным сторонам внутри многоугольника.
Внешний угол — Угол сформированный двумя соседними сторонами вне многоугольника.
Особые полигоны
Особые Четырехугольники — квадрат, ромб, параллелограмм, прямоугольник и т. трапеция.Специальный Треугольники — прямоугольные, равнобедренные, равнобедренные, разносторонние, остроугольные, тупоугольные.
Полигон Имена
Общепринятые именаСтороны
Имя п
Н-гон 3
Треугольник 4
Четырехугольник 5
Пентагон 6
Шестигранник 7
Гептагон 8
Октагон 10
Декагон 12
Додекагон Были предложены имена для других полигонов.

Стороны
Имя 9
Нонагон, Эннеагон 11
Ундекагон, Хендекагон 13
Тридекагон, Трискайдекагон 14
Тетрадекагон, Тетракаидекагон 15
Пятиугольник, Пятидесятиугольник 16
Шестидесятиугольник, Шестидесятиугольник 17
Гептадекагон, Гептадекагон 18
Октадекагон, Октакаидекагон 19
Эннеадекагон, Эннеакаидекагон 20
Икосагон 30
Триаконтагон 40
Тетраконтагон 50
Пентаконтагон 60
Гексаконтагон 70
Гептаконтагон 80
Октаконтагон 90
Эннеаконтагон 100
Гекатогон, Гекатонтагон 1000
Чилиагон 10 000
Мириагон Чтобы составить имя, объедините префикс+суффикс
Стороны
Префикс 20
Икосикай.  ..
..30
Триаконтакай… 40
Тетраконтака… 50
Пентаконтактная… 60
Гексаконтака… 70
Гептаконтак… 80
Октаконтакаи… 90
Эннеаконтакаи… +
Стороны
Суффикс +1
.  .. энагон
.. энагон+2
…дигон +3
… тригон +4
… четырехугольник +5
…пятиугольник +6
… шестигранник +7
… семиугольник +8
… восьмиугольник +9
.  ..эннагон
..эннагонПримеры:
46-сторонний многоугольник — Tetracontakaihexagon28-сторонний многоугольник — Icosikaioctagon
Однако многие люди вместо этого используют форму n-угольника, например, 46-угольника или 28-угольника. из этих имён.
Связаться с нами | Реклама и спонсорство | Товарищество | Ссылка на нас© 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика.
Четырехугольники
Четырехугольник представляет собой замкнутую плоскую фигуру, ограниченную четырьмя линиями сегменты.
 Например, показанная здесь цифра ABCD представляет собой
четырехугольник.
Например, показанная здесь цифра ABCD представляет собой
четырехугольник.Отрезок, проведенный из одной вершины четырехугольника в противоположную вершина называется диагональю четырехугольника. Например, AC является диагональю четырехугольника ABCD , а также BD .
Типы четырехугольников и их свойстваСуществует шесть основных типов четырехугольников:
1. Прямоугольник
- Противоположные стороны параллельны и равны.
- Все углы равны 90.
- Диагонали делятся пополам.
2. Квадрат- Противоположные стороны параллельны и все стороны равны.

- Все углы равны 90.
- Диагонали делят друг друга пополам под прямым углом.
3. Параллелограмм- Противоположные стороны параллельны и равны.
- Противоположные углы равны.
- Диагонали делят друг друга пополам.
4. Ромб- Все стороны равны, а противоположные стороны параллельны.
- Противоположные углы равны.
- Диагонали делятся пополам под прямым углом.
5. Трапеция- У трапеции одна пара противоположных сторон параллельна.
- У правильной трапеции непараллельные стороны равны, а углы при основании
равны, как показано на следующей диаграмме.

6. Воздушный змей- Две пары смежных сторон равны.
- Одна пара противоположных углов равна.
- Диагонали пересекаются под прямым углом.
- Самая длинная диагональ делит самую короткую пополам на две равные части. части.
Теорема 3Докажите, что сумма углов четырехугольника равна 360.
Доказательство:
Следовательно, сумма углов четырехугольника равна 360.
Применение свойств углов в четырехугольникахДоказанные теоремы можно использовать для доказательства других теорем. Они также может быть использован для нахождения значений прочислительных в задаче.

Пример 14
Найдите значение местоимения x на прилагаемой диаграмме. Обоснуйте свой ответ.
Решение:
Пример 15Найдите значение каждой процифры в изображенном здесь воздушном змее. Назови причины за ваши ответы.
Решение:
Пример 16Найдите значение каждой из прочислительных на прилагаемой диаграмме. Дайте причины ваших ответов.
Решение:
Пример 17Найдите значение прочислительного на прилагаемой диаграмме. Дайте причины вашего ответа.



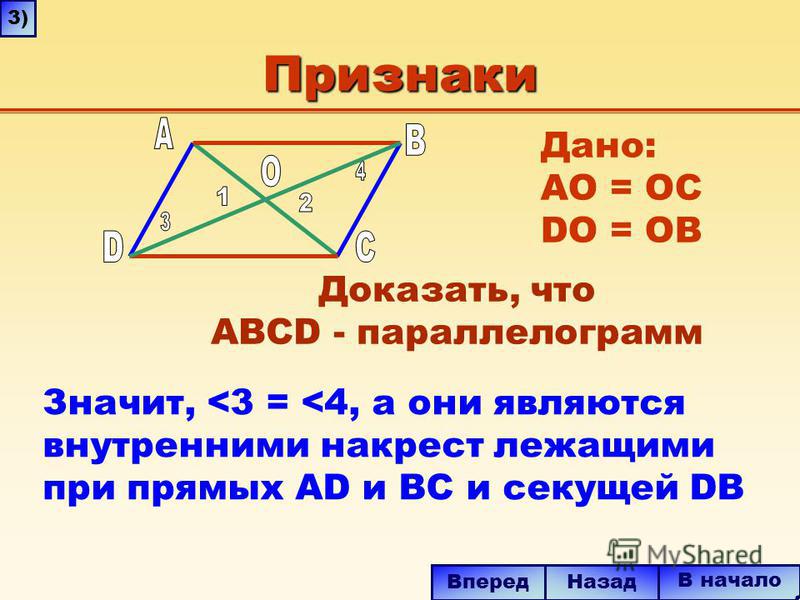 Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами.
Параллельные стороны трапеции называются ее основаниями, а две другие стороны — боковыми сторонами. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.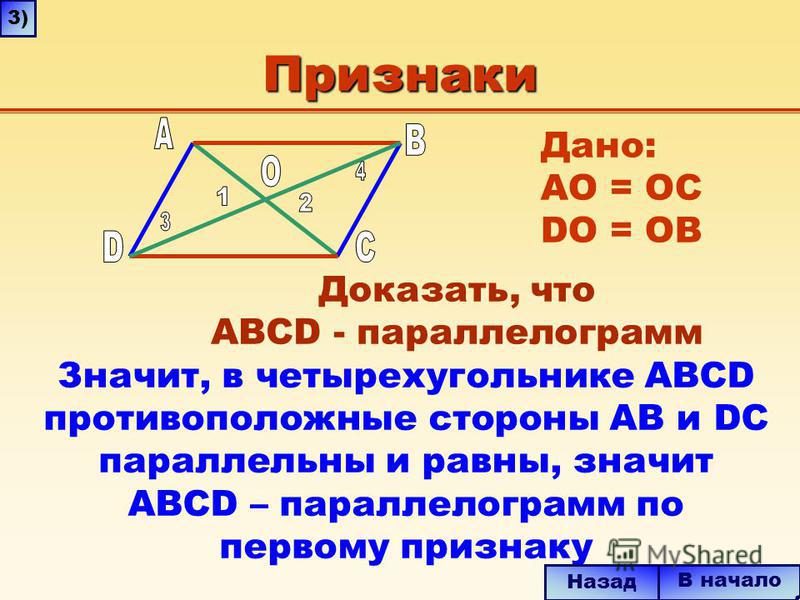

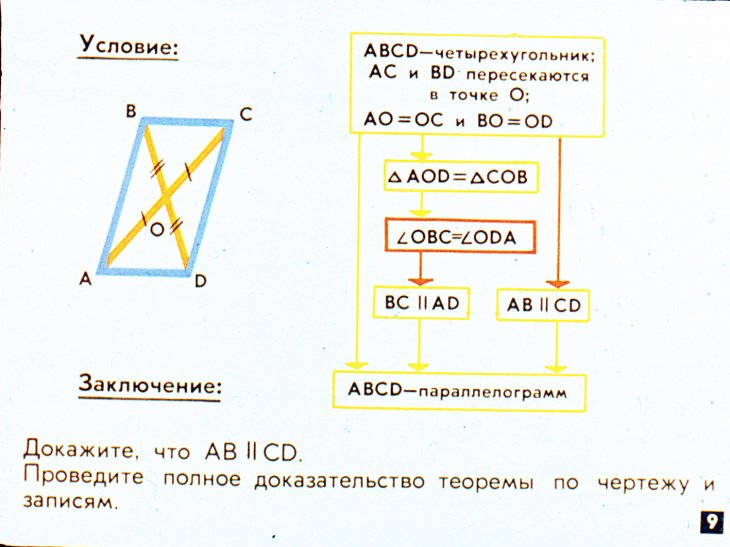

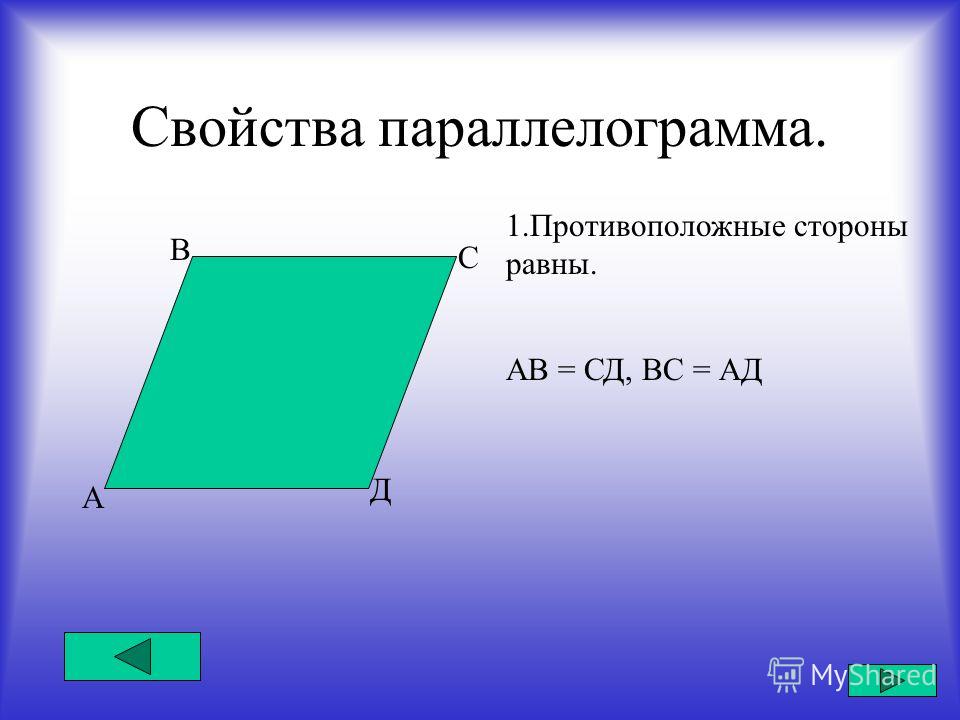
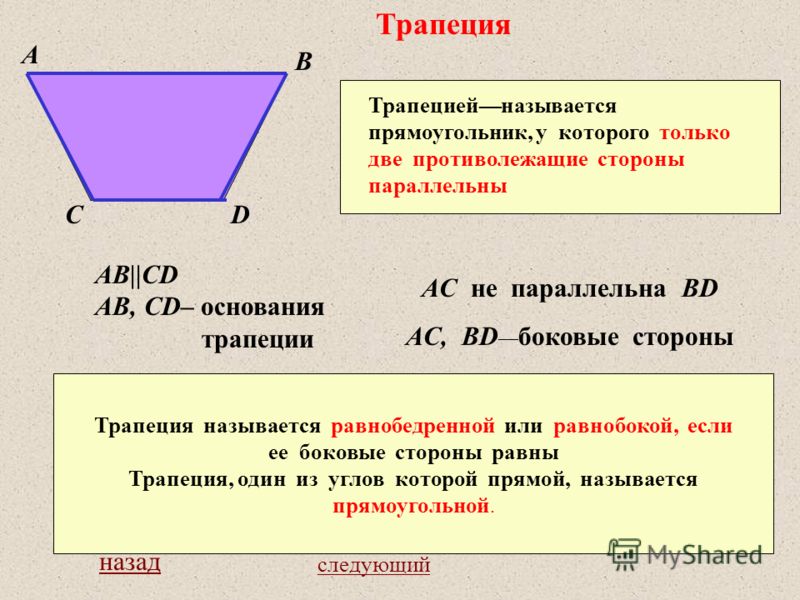 Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.
Обратно: каждая точка, лежащая внутри угла и равноудалённая от сторон угла, лежит на его биссектрисе.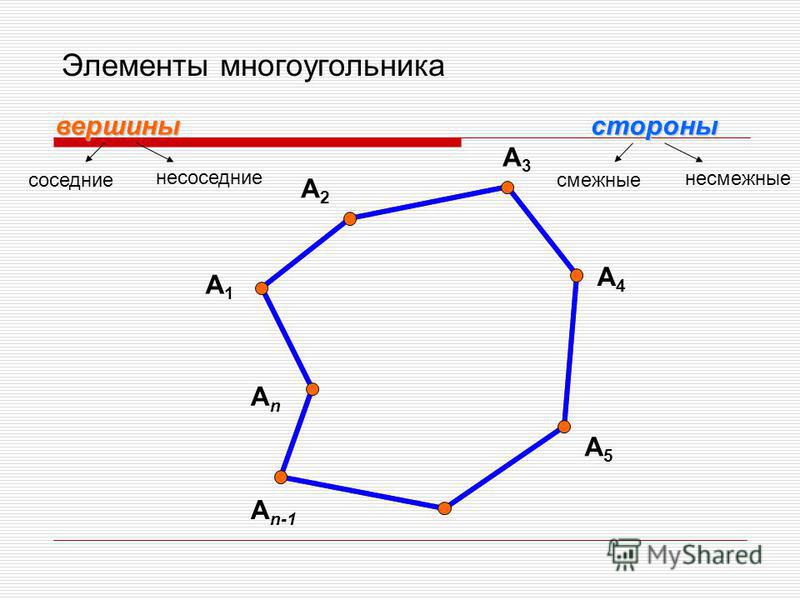

 Вершины, не являющиеся соседними, называются противоположными.
Вершины, не являющиеся соседними, называются противоположными.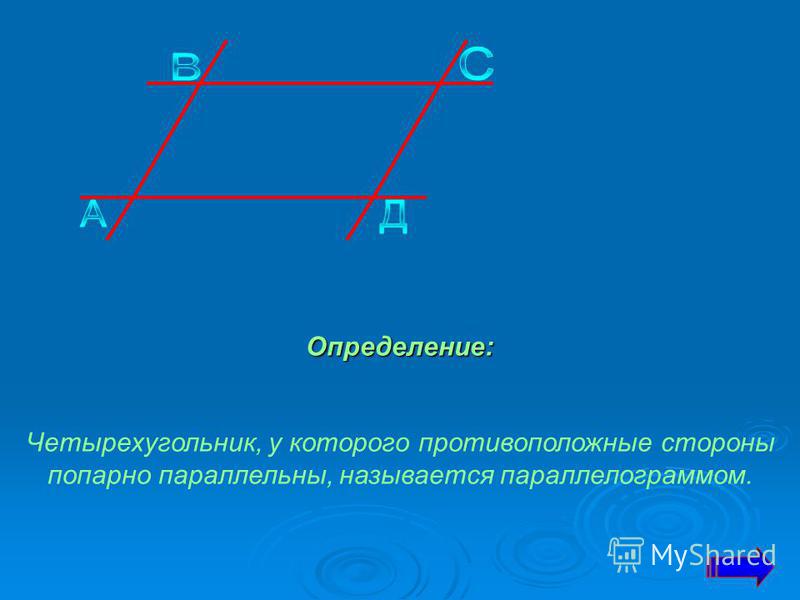
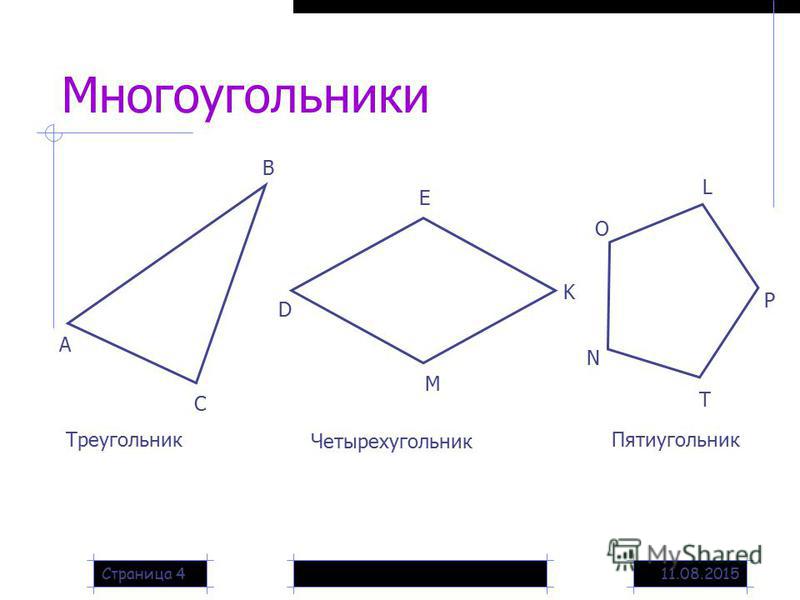
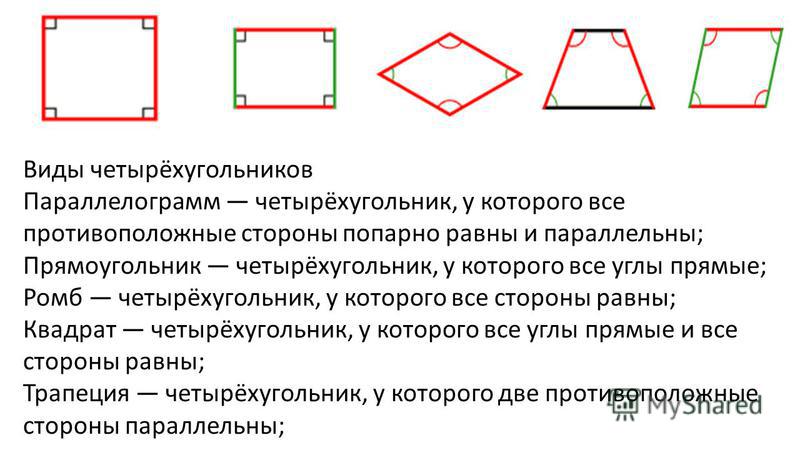
 Аналогично определяется квадратный метр,
квадратный миллиметр и т.д.
Аналогично определяется квадратный метр,
квадратный миллиметр и т.д. 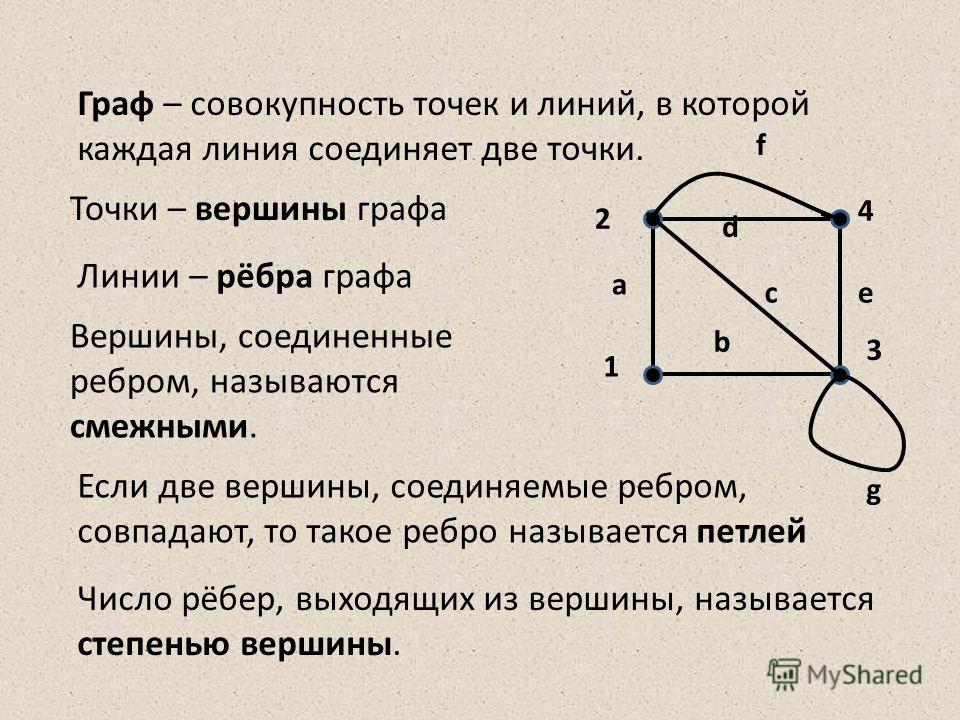 km.ru
km.ru
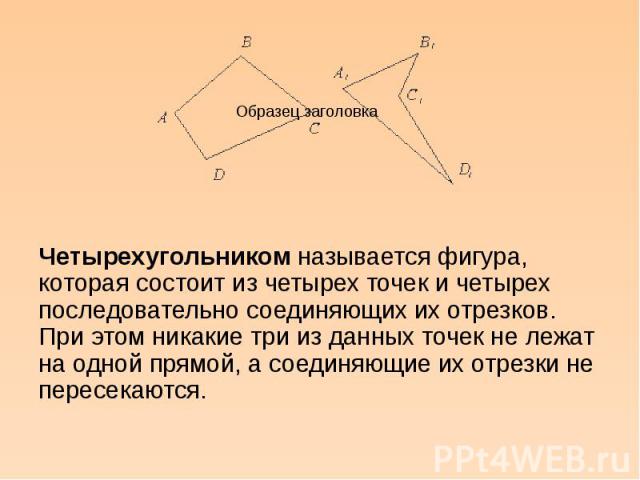



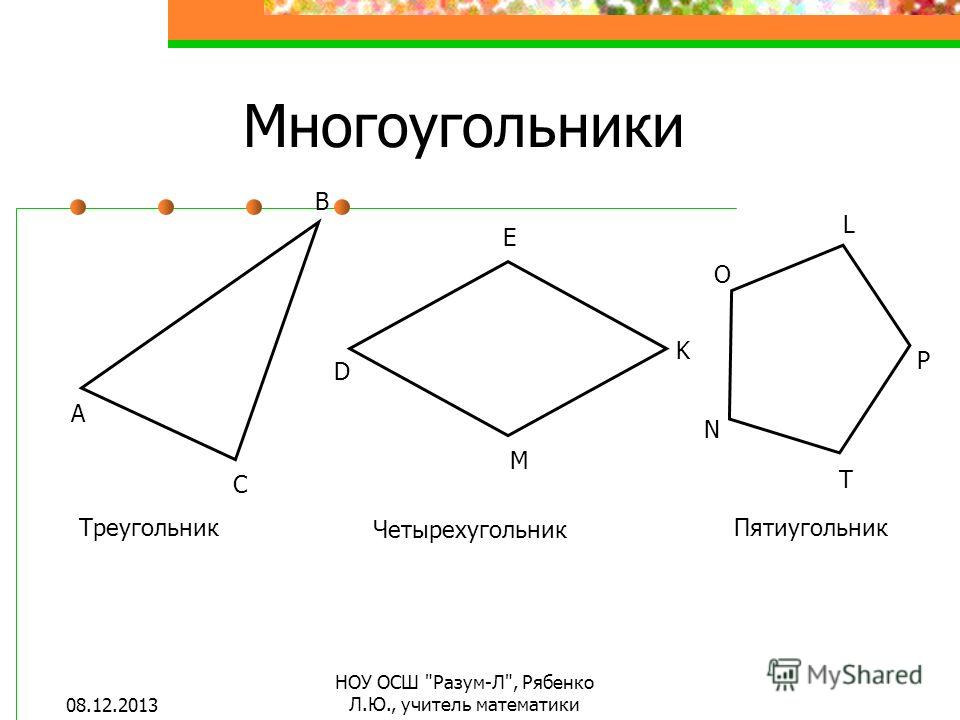


 Это основное свойство любого треугольника.
Это основное свойство любого треугольника.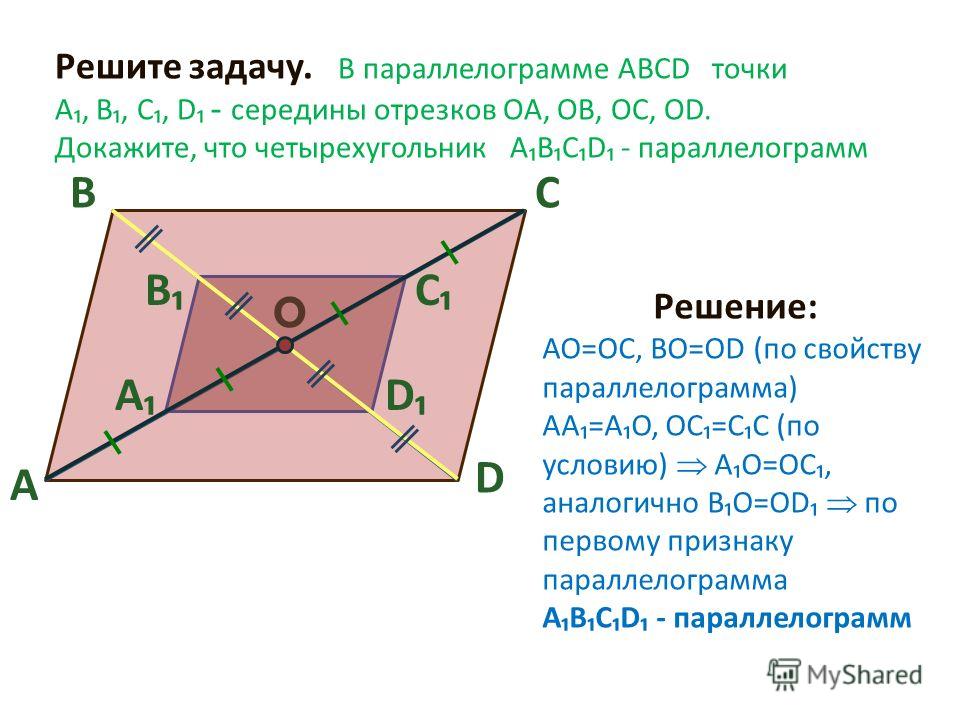
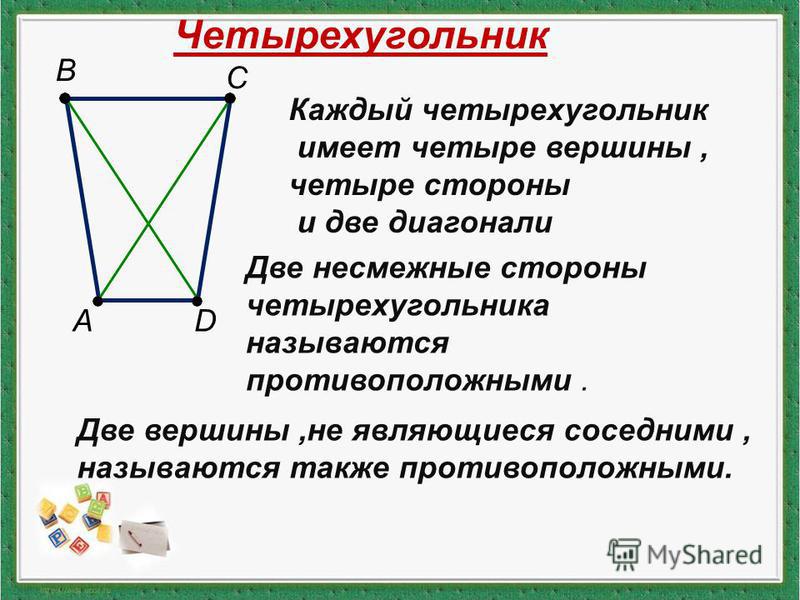 е. AP = PC и BP = PD
е. AP = PC и BP = PD е. AP = PC и BP = PD
е. AP = PC и BP = PD
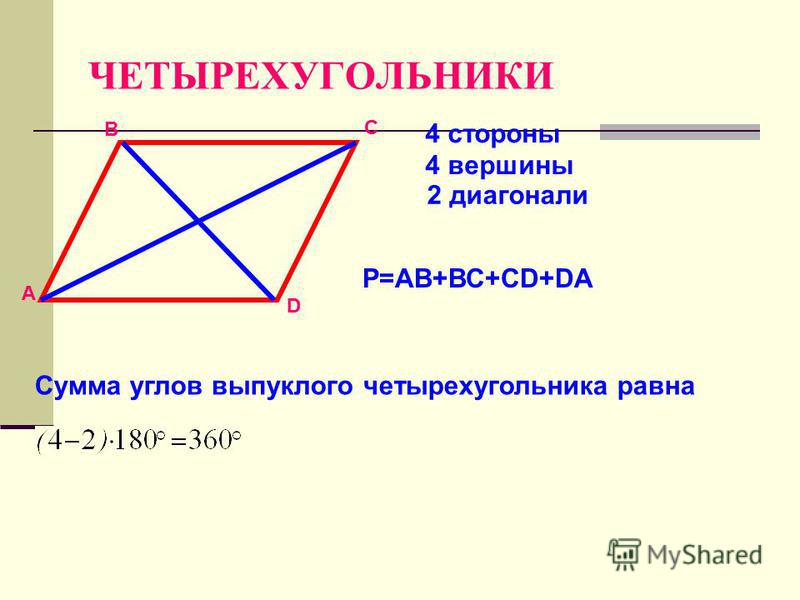
 е. длину, ширину и высоту. Комната дома является распространенным примером трехмерной формы. Давайте разберем некоторые из этих форм в деталях. Некоторые общие термины, используемые для определения 3D-форм:
е. длину, ширину и высоту. Комната дома является распространенным примером трехмерной формы. Давайте разберем некоторые из этих форм в деталях. Некоторые общие термины, используемые для определения 3D-форм: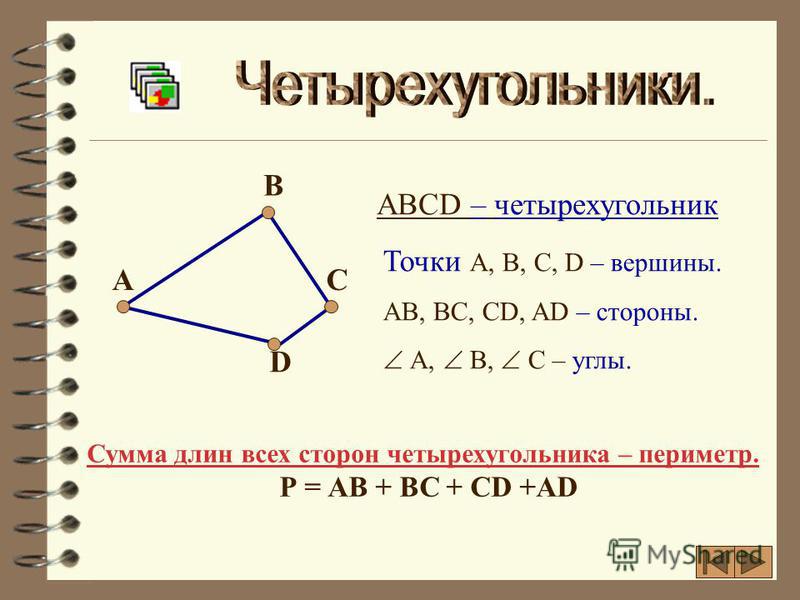


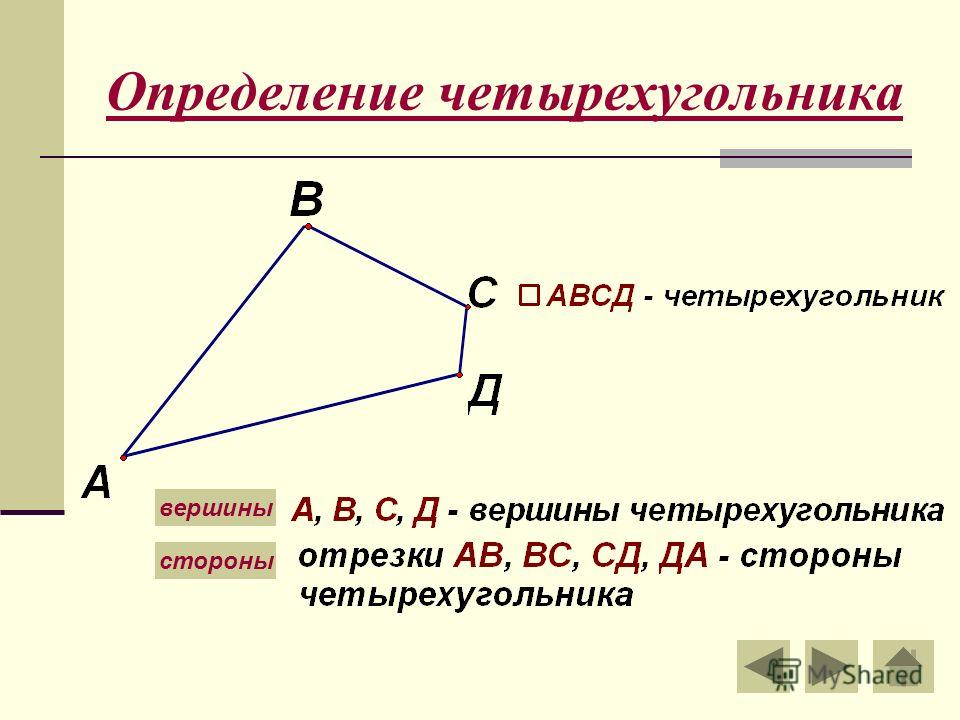

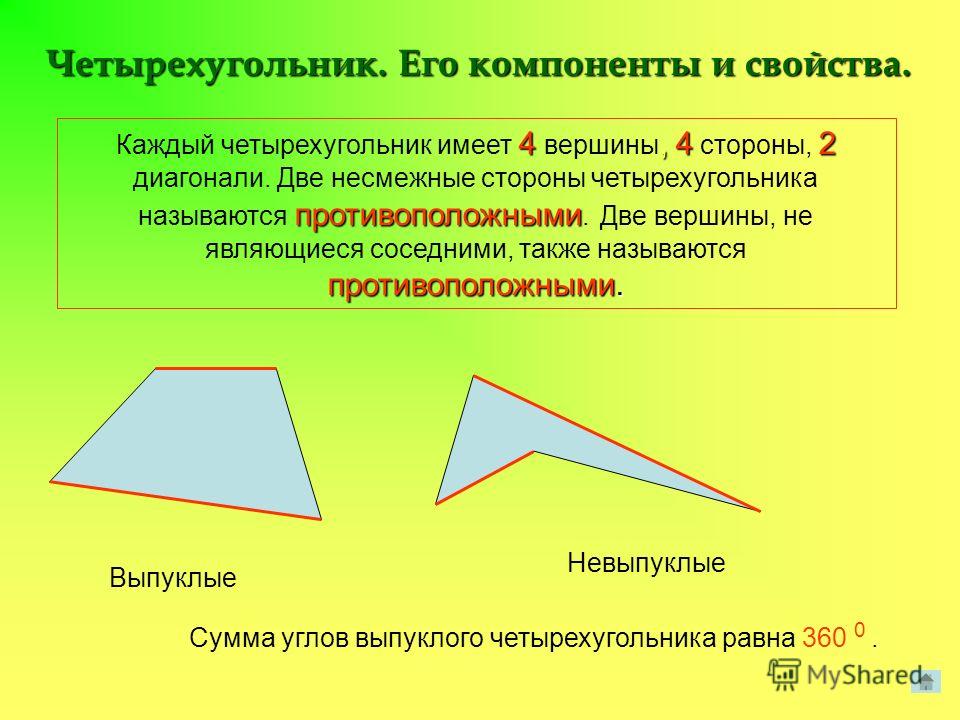
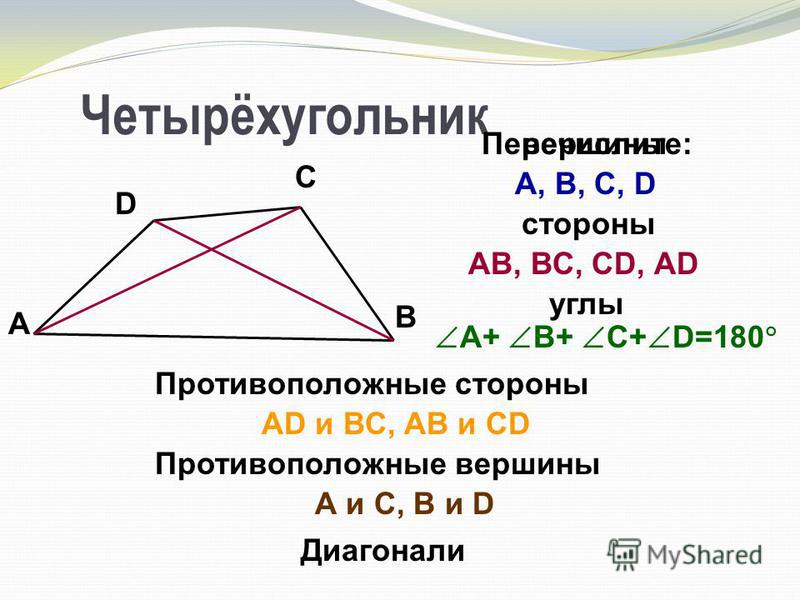


 Все решения NCERT для класса 8 по математике подготовлены экспертами и на 100% точны.
Все решения NCERT для класса 8 по математике подготовлены экспертами и на 100% точны.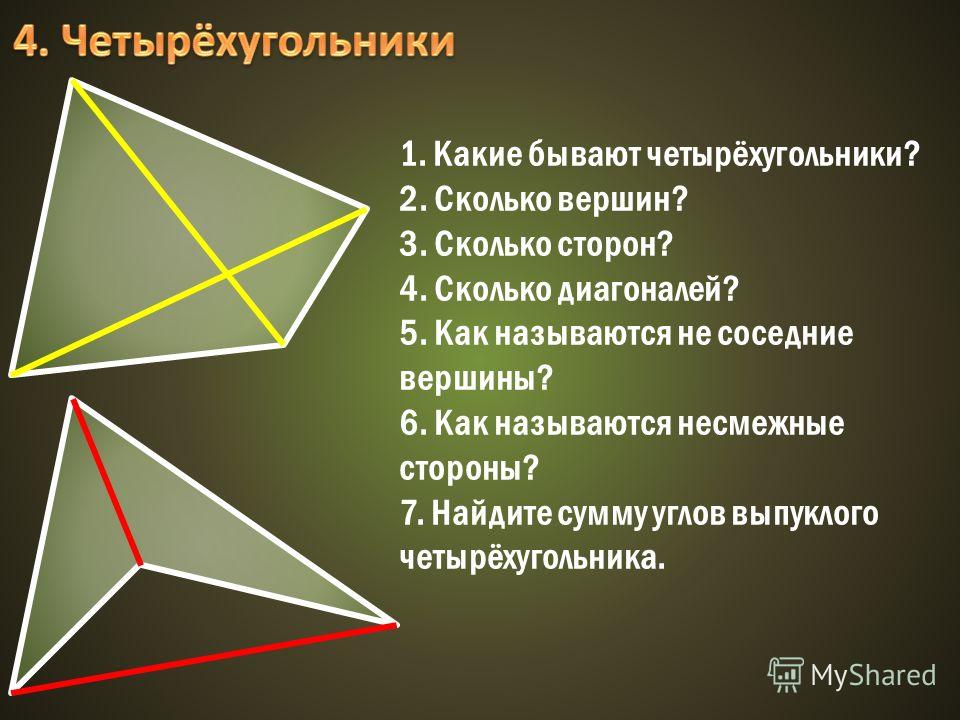 (ii) вершины четырехугольника являются углами четырехугольника. Четырехугольник имеет четыре вершины. (iii) Точка встречи двух сторон четырехугольника называется углом. Четырехугольник имеет четыре угла. (iv) В четырехугольнике ABCD отрезки AC и BD называются его диагоналями. (v) Углы, имеющие общую сторону в качестве плеча, называются смежными углами. (vi) Две стороны смежны. если они имеют общую конечную точку. (vii) Две стороны противоположны, если они не имеют общей конечной точки. (viii) Два угла четырехугольника, которые не являются смежными, называются противоположными углами. (ix) Часть плоскость, образованная всеми такими точками, заключенными в четырехугольник, называется внутренней. (x) Часть плоскости, образованная всеми точками, не заключенными в четырехугольнике, называется внешней.
(ii) вершины четырехугольника являются углами четырехугольника. Четырехугольник имеет четыре вершины. (iii) Точка встречи двух сторон четырехугольника называется углом. Четырехугольник имеет четыре угла. (iv) В четырехугольнике ABCD отрезки AC и BD называются его диагоналями. (v) Углы, имеющие общую сторону в качестве плеча, называются смежными углами. (vi) Две стороны смежны. если они имеют общую конечную точку. (vii) Две стороны противоположны, если они не имеют общей конечной точки. (viii) Два угла четырехугольника, которые не являются смежными, называются противоположными углами. (ix) Часть плоскость, образованная всеми такими точками, заключенными в четырехугольник, называется внутренней. (x) Часть плоскости, образованная всеми точками, не заключенными в четырехугольнике, называется внешней.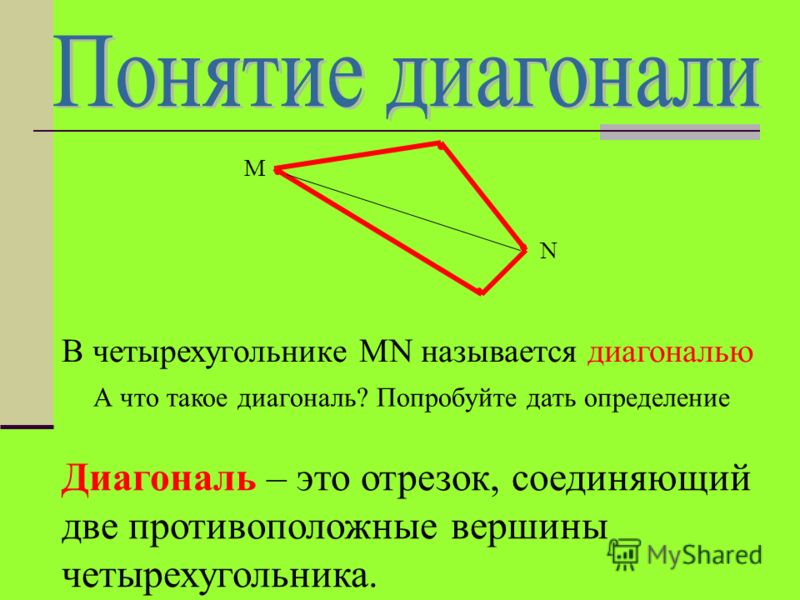 ….. углов.
….. углов.  16:
16: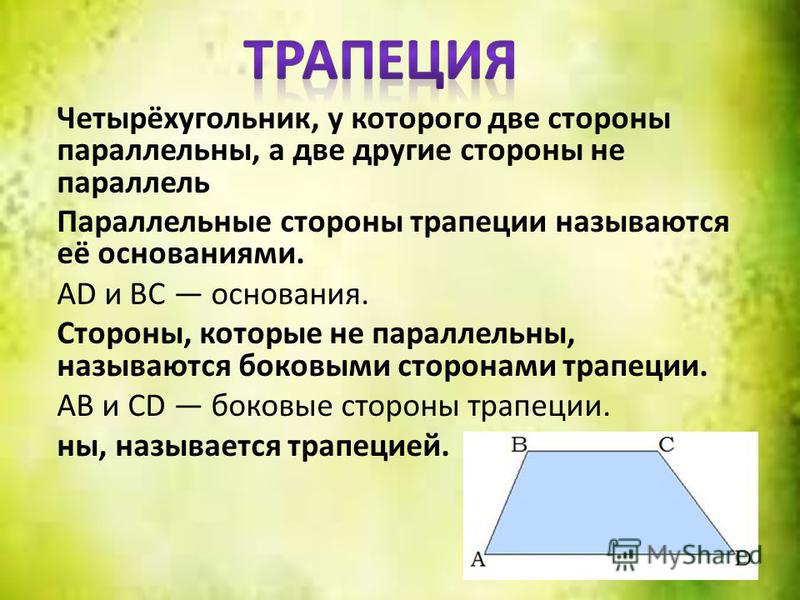 Найдите его четвертый угол.
Найдите его четвертый угол.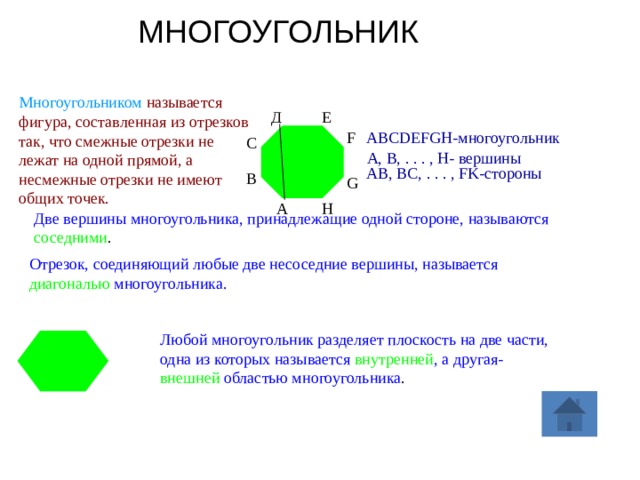 Поскольку сумма всех углов четырехугольника равна 360°, имеем: 65°+65°+x°+x°=360°⇒2x° +130°=360°⇒2x°=230°⇒x°=115°∴ Размер каждого угла равен 115°.
Поскольку сумма всех углов четырехугольника равна 360°, имеем: 65°+65°+x°+x°=360°⇒2x° +130°=360°⇒2x°=230°⇒x°=115°∴ Размер каждого угла равен 115°. Поскольку сумма всех углов четырехугольника равна 360°, имеем: 180°+x+y°=360°⇒x+ y°=180°∴ Сумма оставшихся двух углов равна 180°.
Поскольку сумма всех углов четырехугольника равна 360°, имеем: 180°+x+y°=360°⇒x+ y°=180°∴ Сумма оставшихся двух углов равна 180°. 16:
16: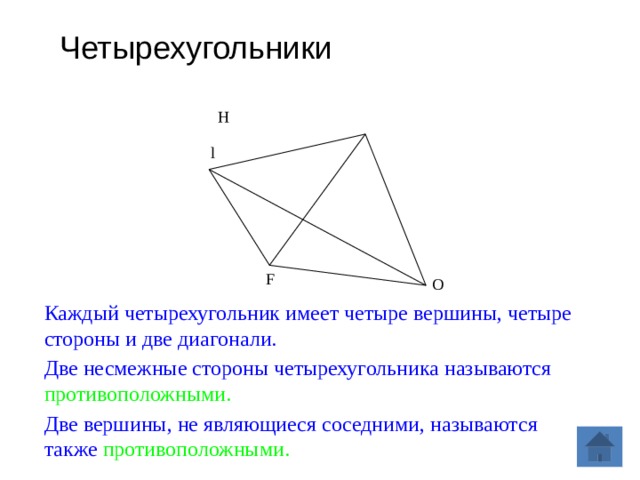
 Найдите значение x .
Найдите значение x . Определить количество сторон многоугольника.
Определить количество сторон многоугольника.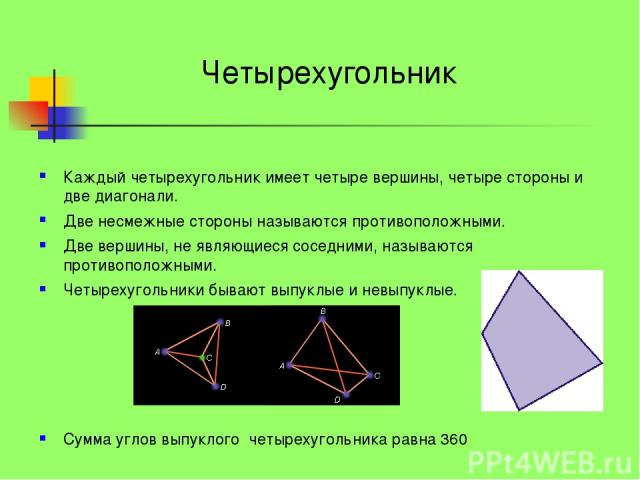
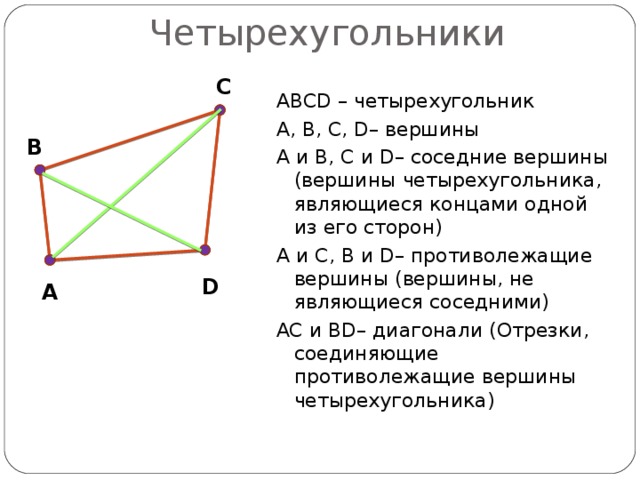 Стороны не пересекаются друг с другом. Встретятся ровно две стороны
каждая вершина.
Стороны не пересекаются друг с другом. Встретятся ровно две стороны
каждая вершина.


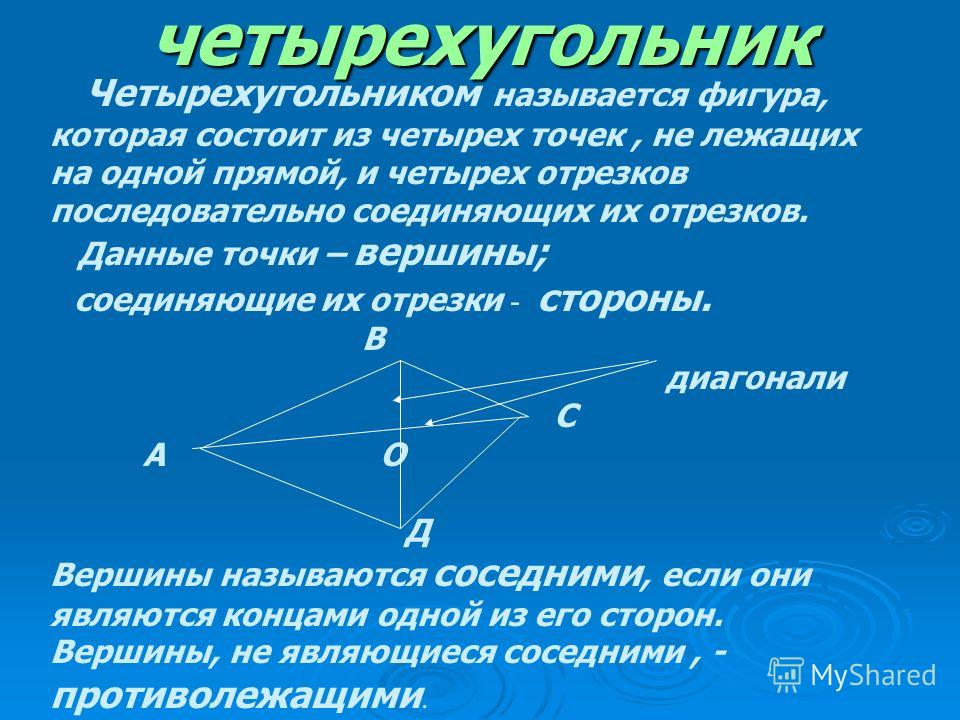 ..
.. .. энагон
.. энагон ..эннагон
..эннагон Например, показанная здесь цифра ABCD представляет собой
четырехугольник.
Например, показанная здесь цифра ABCD представляет собой
четырехугольник.