Как посчитать lg на калькуляторе
Десятичный логарифм
Логарифм, взятый по основанию 10 , носит название — десятичный логарифм.
Десятичные логарифмы принято обозначать так: lg N.
Десятичный логарифм единицы равен нулю.
Десятичный логарифм чисел 10 , 100 , 1000 равен соответвенно 1 , 2 , 3 , и т.д. т.е. имеют столько положительных единиц сколько нулей стоит после единицы.
Десятичный логарифм чисел 0.1 , 0.01 , 0.001 равен соответвенно -1 , -2 , -3 , и т.д. т.е. имеют столько отрицательных единиц сколько нулей стоит перед единицей, считая и ноль целых.
Как вычислить lg
Десятичные логарифмы применяются при решении уравнений, содержащих неизвестные показатели степеней. Из названия этого типа логарифмов вытекает, что основанием его является число десять. Десятичный логарифм определяет, в какую степень надо возвести десятку, чтобы получить указанный в нем аргумент. Вычисление такого рода логарифмов при наличии компьютера не представляет сложности.
Воспользуйтесь, например, поисковой системой Google для вычисления десятичного логарифма. Этот поисковик имеет встроенный калькулятор, который очень прост в использовании, не требует разбираться в его интерфейсе и запускать какие-либо дополнительные программы. Все что от вас требуется — перейти на сайт Google и ввести соответствующий запрос в единственное поле на этой странице. Например, для вычисления десятичного логарифма для числа 900 введите в поле поискового запроса lg 900 и сразу (даже без нажатия кнопки) получите ответ 2.95424251.
Используйте калькулятор, если нет доступа к поисковой системе. Это может быть и программный калькулятор из стандартного набора ОС Windows. Самый простой способ запустить его — нажать сочетание клавиш WIN +R, ввести команду calc и щелкнуть кнопку «OK». Другой способ — раскрыть меню на кнопке «Пуск» и выбрать в нем пункт «Все программы». Затем надо открыть раздел «Стандартные» и перейти в подраздел «Служебные», чтобы щелкнуть там ссылку «Калькулятор». При использовании ОС Windows 7 можно нажать клавишу WIN и ввести в поле поиска «Калькулятор», а затем щелкнуть соответствующую ссылку в результатах поиска.
При использовании ОС Windows 7 можно нажать клавишу WIN и ввести в поле поиска «Калькулятор», а затем щелкнуть соответствующую ссылку в результатах поиска.
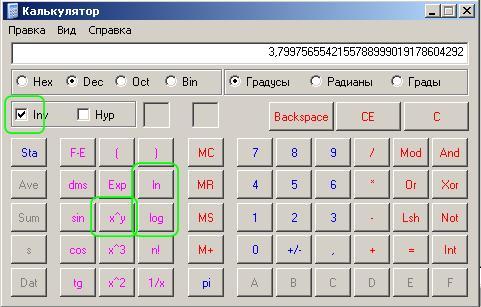
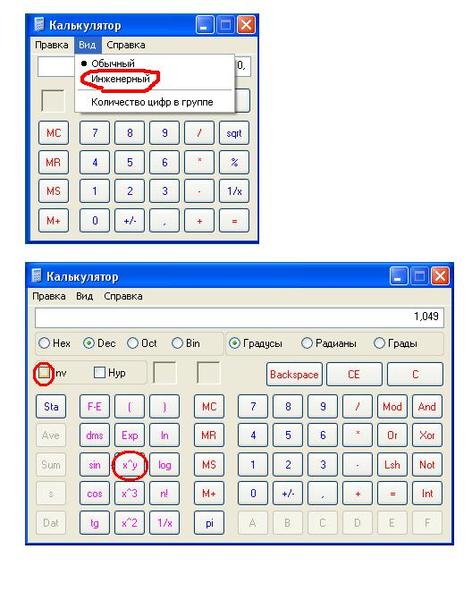
Переключите интерфейс калькулятора в расширенный режим, так как в открываемом по умолчанию базовом варианте нужная вам операция не предусмотрена. Для этого раскройте в меню программы раздел «Вид» и выберите пункт «научный» либо «инженерный» — в зависимости от того, которая версия операционной системы установлена в вашем компьютере.
Введите число, десятичный логарифм для которого нужно рассчитать, а затем щелкните кнопку с надписью log — в этом калькуляторе функция вычисления десятичного логарифма обозначена именно так, а не lg. Программа посчитает и отобразит результат.
Математический калькулятор
Математический калькулятор вычисляет значение заданного математического выражения. В выражении можно использовать операции сложения, умножения, вычитания, деления возведения в степень, константу pi, различные математические функции: sqrt — квадратный корень, exp — e в указанной степени, lb — логарифм по основанию 2, lg — логарифм по основанию 10, ln — натуральный логарифм (по основанию e), sin — синус, cos — косинус, tg — тангенс, ctg — котангенс, sec — секанс, cosec — косеканс, arcsin — арксинус, arccos — арккосинус, arctg — арктангенс, arcctg — арккотангенс, arcsec — арксеканс, arccosec — арккосеканс, versin — версинус, vercos — коверсинус, haversin — гаверсинус, exsec — экссеканс, excsc — экскосеканс, sh — гиперболический синус, ch — гиперболический косинус, th — гиперболический тангенс, cth — гиперболический котангенс, sech — гиперболический секанс, csch — гиперболический косеканс, root3 — кубический корень, rootN — корень указанной степени, logN — логарифм с заданным основанием.
Калькулятор был создан в ответ на многочисленные запросы наших пользователей, которые желают воспользоваться нашим сервисом чтобы посчитать результат какого-либо математического выражения, например, что-нибудь сложить, вычесть, поделить возвести в степень, извлечь корень и т. п. Вводите последовательность математических выражений в поле математическое выражение и получайте результат.
Все тригонометрические функции принимают аргументы в радианах, а не в градусах. Обратные тригонометрические функции, также возвращают угол в радианах. Для преобразования градусов в радианы — умножайте градусы на pi/180, например, sin 30 градусов надо записывать как sin(30*pi/180).
Калькулятор десятичных логарифмов
Для обозначения десятичного логарифма существует несколько способов:
- lg
- log10
- log 10
Так же возможно написание прописными буквами.
Что такое десятичный логарифм
Десятичный логарифм очень прост для понимания. К примеру, десятичный логарифм числа 100 равен 2. А числа 100 000 — 5. Таким образом,
К примеру, десятичный логарифм числа 100 равен 2. А числа 100 000 — 5. Таким образом,
Здесь y — число, логарифм которого мы ищем, а x — это искомый логарифм.
То есть десятичный логарифм — это степень, в которую нужно возвести число 10 для получения исходного числа, логарифм которого мы ищем. Как мы видим, для чисел кратных 10 десятичный логарифм находится просто. Для чисел, не кратных 10 логарифм будет дробным. К примерку, десятичный логарифм числа 7 равен 0.84509804001426. И тут наш калькулятор поможет с расчетом.
Как считать логарифмы без калькулятора
Как посчитать логарифм без калькулятора?
и перейти от натуральных логарифмов к логарифмам с другим основанием.
Я где-то читал, что посчитать логарифм можно и без таблицы, но для этого надо пройти очень длинную процедуру предварительных рассуждений. А в них очень легко запутаться. Следует идти более легким путем!
Приблизительно можно посчитать любой логарифм, и ошибка будет не такой же уж и большой.
Возьмем десятичный логарифм lg. Известно, что lg 10 = 1, а lg 1 = 0. Допустим вам надо найти логарифм числа, лежащего между 1 и 10. Например, 5. Любому человеку ясно, что это где-то посередине между 1 и 10. Значит и логарифм его будет приблизительно посередине. Берем складываем 0+1=1. Делим пополам, будет 0,5. Смотрим в таблицу десятичных логарифмов. Получаем 0,69897000433601880478626110527551 (эт я на калькуляторе вычислил в Виндовсе). Ну разница должен сказать небольшая. Всего-то 0,19. Для нормальной жизни пойдет. Нам же не ракету в космос запускать!
Логарифм. Как вычислить логарифм?
Объясним проще. Например, \(\log_\) равен степени, в которую надо возвести \(2\), чтоб получить \(8\). Отсюда понятно, что \(\log_=3\).
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:
Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
а) В какую степень надо возвести \(4\), чтобы получить \(16\)? Очевидно во вторую. Поэтому:
б) В какую степень надо возвести \(3\), чтобы получить \(\frac\) ? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени ).
в) В какую степень надо возвести \(\sqrt\), чтобы получить \(1\)? А какая степень делает любое число единицей? Ноль, конечно!
г) В какую степень надо возвести \(\sqrt\), чтобы получить \(\sqrt\)? В первую – любое число в первой степени равно самому себе.
д) В какую степень надо возвести \(3\), чтобы получить \(\sqrt\)? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень — это степень \(\frac\) .
В сложных случаях для вычисления логарифма удобно переводить его в показательное уравнение.
 =c\) \(\Leftrightarrow\) \(\log_=b\)
=c\) \(\Leftrightarrow\) \(\log_=b\)Зеркально перевернем уравнение, чтобы икс был слева
И не пугайтесь логарифма, относитесь к нему как к обычному числу.
Поделим уравнение на 5
Вот наш корень. Да, выглядит непривычно, но ответ не выбирают.
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы \((a>0, a\neq1)\). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание — число Эйлера \(e\) (равное примерно \(2,7182818…\)), и записывается такой логарифм как \(\ln\).
Десятичный логарифм: логарифм, у которого основание равно 10, записывается \(\lg\).
Основное логарифмическое тождество
У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:
| \(a^>=c\) |
Это свойство вытекает напрямую из определения. \), а так же то, что множители можно менять местами, преобразовываем выражение
\), а так же то, что множители можно менять местами, преобразовываем выражение
Вот теперь спокойно пользуемся основным логарифмическим тождеством.
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что \(\log_\) равен двум. Тогда можно вместо двойки писать \(\log_\).
Но \(\log_\) тоже равен \(2\), значит, также можно записать \(2=\log_\) . Аналогично и с \(\log_\), и с \(\log_\), и т.д. То есть, получается
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как \(\log_\), или как \(\log_\), или как \(\log_\)… Здесь мы как аргумент пишем основание в кубе:
Что такое логарифм. Как посчитать логарифм. Свойства логарифмов.
 Примеры решения логарифмов
Примеры решения логарифмовМногие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.
Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.
В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.
Итак, давайте разбираться, что такое логарифм.
Что такое логарифм и как его посчитатьЛогарифм имеет следующий вид:
где a – это основание логарифма,
b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X.и преобразовываем вЗапомните, что именно основание (оно выделено красным) возводится в степень.
Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:А в какую степень нужно возвести 2, чтобы получилось 8? Конечно же в третью степень, таким образом:
Еще раз обращаю ваше внимание, что основание (в нашем случае это – 2) всегда находится внизу и именно оно возводится в степень.
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифмДесятичный логарифм обозначается lg и имеет основание 10, т.е.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Например, вычислим lg100
Натуральный логарифмНатуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Основные свойства логарифмовЛогарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:
Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:
Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!
Рассмотрим свойства логарифмов на примерах.
Логарифмический ноль и логарифмическая единицаЭто следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.
Запомните, что логарифм от a по основанию а всегда равен единице:
loga a = 1 – это логарифмическая единица.
Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a 0 = 1:
loga 1 = 0 – логарифмический ноль.
Основное логарифмическое тождествоВ первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.
Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.
Вторая формула по сути является просто переформулированным определением логарифма
Разберем применение тождества на примере:
Необходимо найти значение выраженияСначала преобразуем логарифм
Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:Теперь применим основное логарифмическое тождество и получим:
Сумма логарифмов. Разница логарифмовЛогарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!
Вынесение показателя степени из логарифмаВынесение показателя степени из логарифма:
Переход к новому основаниюКогда мы разбирали формулы суммы и разности логарифмов, то обращали внимание на то, что основания логарифмов должны быть при этом одинаковыми. А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.
А что же делать, если основания логарифмов разные? Воспользоваться свойством перехода к новому основанию.
Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.
Разберем на примере.
Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:
Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:
10 примеров логарифмов с решением1. Найти значение выражения2. Найти значение выражения3. Найти значение выражения4. Найти значение выражения5. Найти значение выражения6. Найти значение выраженияСначала найдем значениеДля этого приравняем его к Х:Тогда изначальное выражение принимает вид:
7. Найти значение выраженияПреобразуем наше выражение:Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим: 8. Найти значение выраженияТак как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:9. Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:
Найти значение выраженияТак как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:Подставляем полученные значения в исходное выражение:
10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log216. Поэтому сначала найдем значение log216, а затем подставим полученный результат в log4:
Добро пожаловать в калькулятор логарифмов онлайн. Для чего нужен этот калькулятор. Ну, в первую очередь для того, что бы свериться со своими письменными или умственными расчетами. С логарифмами (в российских школах) столкнуться можно уже в 10-том классе. И эта тема считается достаточно сложной. Решение логарифмов, особенно с большими или дробными числами, знаете ли, дело не легкое. В данном калькуляторе, вам предстоит заполнить всего два поля. Поле для числа и поле для основания. Ну что ж, давайте попробуем обуздать калькулятор на практике. К примеру, вам нужно найти log 2 8 (логарифм 8-ми по основанию 2 или логарифм по основанию 2 числа 8, не пугайтесь разного произношения). Итак, вводим 2 в поле «введите основание», а 8 вводим в поле «введите число». После чего нажимаем «найти логарифм» или enter. Далее калькулятор логарифмов логарифмирует заданное выражение и выводит на ваши экраны такой результат. Калькулятор логарифмов (вещественных) – этот калькулятор находит логарифм по заданному основанию онлайн.
Понятие вещественного логарифма: Существует множество разных определений логарифма. Сперва, неплохо было бы узнать, что логарифм — это некая алгебраическая запись, обозначенная как log a b, где а – основание, b – число. А читается эта запись так: Логарифм по основанию a числа b. Иногда используется обозначение log b . А теперь собственно, определение самого логарифма: Логарифмом положительного числа b по основанию a (где a>0, a≠1)называется степень, в которую нужно возвести число а, чтобы получить число b. Кстати, не только основание должно быть в положительной форме. Число(аргумент), так же должно быть положительным.  В противном случае калькулятор логарифмов включит неприятную тревогу. Логарифмирование – это операция нахождения логарифма, по заданному основанию. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием. Сравните: В противном случае калькулятор логарифмов включит неприятную тревогу. Логарифмирование – это операция нахождения логарифма, по заданному основанию. Эта операция является обратной по отношению к возведению в степень с соответствующим основанием. Сравните:
А операция обратная логарифмированию это – Потенцирование. |
что такое в математике, вычисление, как правильно решать LG, примеры
Содержание:
- Десятичный логарифм числа – что это такое в математике
- Определение и формулы десятичного логарифма
- График десятичного логарифма
- Как правильно решать задачи на десятичных логарифмах, примеры
Содержание
- Десятичный логарифм числа – что это такое в математике
- Определение и формулы десятичного логарифма
- График десятичного логарифма
- Как правильно решать задачи на десятичных логарифмах, примеры
Десятичные логарифмы широко применялись в вычислениях до появления компактных калькуляторов. m\)
m\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Логарифм будет иметь смысл только при соблюдении ряда условий:
\(k>0,\;\;k\neq1,\;\;n>0\)
Примечание
Если за основание логарифма взята цифра 10, то такой логарифм называется десятичным. Его принято обозначать знаком lg и не указывать основание, равное 10. Например, правильно записывать lg 20, а не log10 20.
Десятичные логарифмы обладают теми же особенностями, что и любые другие логарифмы при основании больше, чем 1. Например, большему из нескольких положительных чисел будет соответствовать и больший десятичный логарифм. Десятичный логарифм числа, которое больше 0, но меньше 1, будет отрицательным, а больше единицы – положительным.
Десятичные логарифмы обладают рядом характерных признаков:
- Десятичный логарифм положительного целого числа, представленного единицей и следующими за ней нулями, представляет собой целое неотрицательное число, которое будет равно количеству нулей в записи выбранного числа: lg 10=1, lg 10000=4.

- Десятичный логарифм десятичной неотрицательной дроби, записанной как единица с предыдущими нулями, будет равен (-m). В этом случае m – количество нулей, предшествующих единице, в том числе с учетом и нулевой целой части: lg 0,1=-1, lg 0,0001=-4.
- Если умножить число на 10m, то десятичный логарифм увеличится на число m. Это можно записать формулой: lg (a10m) = lg a + lg 10m = lg a + m.
- Если разделить число на 10k, то его десятичный логарифм станет меньше на k.
Определение и формулы десятичного логарифма
Определение
Десятичным логарифмом числа k является решение уравнения: 10n=k
В алгебре свойства десятичных логарифмов описываются целым рядом формул. Их использование позволяет значительно проще решать сложные задачи, снижает вероятность ошибок.
Основными формулами десятичных логарифмов являются:
\(1. m\right)\;=\;mlg\;(x)\\6.\;lg\;\sqrt[p]x\;=\;\frac{lg\;(x)}p\)
m\right)\;=\;mlg\;(x)\\6.\;lg\;\sqrt[p]x\;=\;\frac{lg\;(x)}p\)
До изобретения калькуляторов вышеописанные формулы использовались очень широко. Например, они позволяют с легкостью выполнить умножение многозначных чисел. Для этого необходимо воспользоваться простым алгоритмом:
- найти по таблице логарифмы заданных чисел;
- в соответствии с третьим свойством сложить их и получить логарифм произведения;
- по полученному логарифму используя таблицу найти и само произведение чисел.
Аналогичным образом можно выполнить и деление многозначных чисел. Только в данном случае логарифмы следует не складывать, а вычитать.
Использование десятичных логарифмов дает возможность даже без калькулятора выполнить извлечение из корня или возведение в степень.
В настоящее время десятичные логарифмы практически полностью вытеснены натуральными. Они сохраняются только в исторически укоренившихся областях математики, например, в построении логарифмической шкалы.
Отрицательные десятичные логарифмы представляют в искусственной форме. В ней они имеют отрицательную характеристику и положительную мантиссу.
Рассмотрим пример:
\(lg\;(0.005)\;=\;\overset-3.69897\\\)
Иначе эту запись можно представить так:
\(lg\;(0.005)\;=\;\overset-3.69897=\;-3\;=\;0.69897=\;-2.30103\\\)
Для перевода десятичного отрицательного логарифма в искусственную форму необходимо увеличить на единицу абсолютную величину характеристики. Над полученным числом поставить знак «минус». Вычесть из девяти все цифры мантиссы кроме последней, не равной нулю.
Ее следует вычесть из десяти. Полученные в ходе вычитания разности записать на тех же местах мантиссы, где находились вычитаемые числа. Нули на конце остаются без изменений.
График десятичного логарифма
При рассмотрении логарифмируемого числа в качестве переменной получаем функцию:
\(y\;=\;lg\;(x)\\\)
Она будет определена при всех значениях x больше нуля. Область значений функции лежит в пределе:
Область значений функции лежит в пределе:
\(E_{(y)}=(-\infty;\;+\infty)\\\)
График десятичного логарифма представляет кривую линию, называемую логарифмикой.
Всюду, где функция определена, она дифференцируема, непрерывна и монотонно возрастает. Ее производную можно задать формулой:
\(\frac d{d_x}=lg\;x\;=\frac{lg\;e}x\\\)
Ось ординат рассматриваемой функции является вертикальной асимптотой, так как
\(\underset{x\rightarrow0+0}{\lim\;lg\;x}=\;-\infty\\\)
Как правильно решать задачи на десятичных логарифмах, примеры
Рассмотрим примеры решения задач с использованием десятичных логарифмов.
Задача 1. Вычислить значение выражения
\(lg\;\left(400\right)\;+\;lg\;\frac1{40}\)
Для решения данного примера воспользуемся формулой суммы:
\(lg\;\left(400\right)\;+\;lg\;\frac1{40}\;=\;lg\;\left(\frac{400\times1}{40}\right)=\;lg\;10\;=\;1\)
Задача 2. Упростите выражение:
\(lg\;\frac18\;-\;3\;lg\;4\)
В данном случае необходимо воспользоваться формулой степени:
\(lg\;\frac18\;-\;3\;lg\;4\;=\;lg\;2^{-3}\;-\;3\;lg\;2^2\;=\;-3lg\;-\;3\times2\;lg\;2\;=\;-9\;lg\;2\)
Задача 3.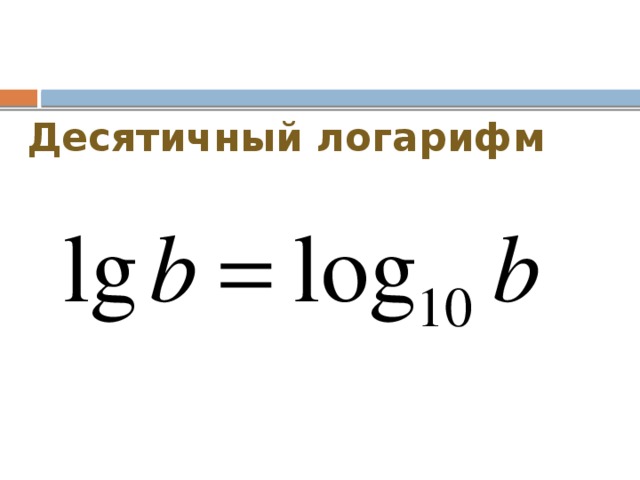 3\;=\;3\times2\;lg\frac3{10}\;-\;2\times3\;lg\;3\;=\;6\;lg\;\frac3{10}\;-\;6\;lg\;3\)
3\;=\;3\times2\;lg\frac3{10}\;-\;2\times3\;lg\;3\;=\;6\;lg\;\frac3{10}\;-\;6\;lg\;3\)
Теперь применим свойство частного, откроем скобки и приведем подобные слагаемые:
\(6\;lg\;\frac3{10}\;-\;6\;lg\;3\;=\;6\;(lg\;3\;-\;lg\;10)\;-\;6\;lg3\;=\;6\;lg\;3\;-\;6\;lg\;10\;-\;6\;lg\;3=\;-\;6\;lg\;10=\;-6\times1\;=\;-6\)
Насколько полезной была для вас статья?
Рейтинг: 1.75 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
7 лучших советов и хитростей для калькулятора iPhone
Вам не нужны специальные знания, чтобы использовать калькулятор по умолчанию на вашем iPhone — по крайней мере, для базовых расчетов. Однако есть некоторые не столь очевидные особенности приложения, о существовании которых многие пользователи iPhone не знают.
В этом руководстве мы перечислим несколько полезных советов и приемов калькулятора iPhone, которые помогут вам более эффективно использовать приложение.
1. Проведите по экрану, чтобы удалить номера.
В калькуляторе iPhone отсутствует специальная кнопка возврата. Вот почему многие ошибочно полагают, что ввод неправильной цифры при выполнении вычислений означает, что вам придется начинать с нуля. Что ж, это неправда.
Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)
В калькуляторе iPhone есть скрытый жест возврата, который позволяет удалить последнюю введенную цифру. Все, что вам нужно сделать, это провести пальцем влево или вправо в области дисплея калькулятора.
Вы можете провести пальцем несколько раз, чтобы удалить несколько записей.
2. Поверните, чтобы получить доступ к научному калькулятору
При использовании вашего iPhone в портретной ориентации отобразится стандартная версия приложения «Калькулятор», в которой вы сможете выполнять только базовые вычисления, такие как сложение, вычитание и т. Д. Чтобы получить доступ к полноценному калькулятору с научными функциями, просто поверните iPhone боком в альбомную ориентацию.
Если на вашем iPhone не отображается научный калькулятор, когда вы поворачиваете его набок, откройте Центр управления и коснитесь значка красного замка, чтобы отключить блокировку портретной ориентации.
3. Скопируйте и вставьте цифры
Хотите отправить результат расчета другу в WhatsApp или iMessage? Просто нажмите и удерживайте цифры, выберите «Копировать» и вставьте результаты в свое приложение для обмена сообщениями.
Вы также можете вставлять цифры из документа или других приложений в приложение «Калькулятор». Коснитесь и удерживайте раздел дисплея калькулятора и выберите «Вставить».
4. Быстрый просмотр и копирование последних результатов
iOS предоставляет ярлык, который позволяет просматривать и копировать результат последнего расчета, не открывая приложение «Калькулятор». Это пригодится, если вы заблокируете свой iPhone или переключитесь на другое приложение после выполнения расчета. Для этого откройте Центр управления и нажмите и удерживайте значок калькулятора.
Вы найдете результат своего последнего расчета на всплывающей карточке калькулятора. Коснитесь параметра «Копировать последний результат», чтобы скопировать результат в буфер обмена.
Примечание. Вы не сможете просмотреть или скопировать последние результаты из Центра управления или в приложении «Калькулятор», если вы нажали AC после выполнения расчета. Нажатие AC сбрасывает калькулятор и очищает все предыдущие расчеты.
Если значка «Калькулятор» нет в Центре управления вашего устройства, перейдите в «Настройки»> «Центр управления» и коснитесь значка «плюс» (+) рядом с «Калькулятором».
5. Легко рассчитывать советы на iPhone
Неправильная математика может привести к недооценке или перерасчету. Вот два способа использовать калькулятор iPhone, чтобы точно определить размер чаевых за услуги.
Расчет подсказок с помощью Siri
если ты используйте Siri на своем iPhone, вы можете попросить цифрового помощника рассчитать, сколько чаевых добавить к вашему счету. Сказать что-то вроде «Привет, Siri. Сколько чаевых в 15% от 30 долларов? » Siri отобразит карточку калькулятора в верхней части экрана, показывающую сумму чаевых и общую сумму к оплате.
Сказать что-то вроде «Привет, Siri. Сколько чаевых в 15% от 30 долларов? » Siri отобразит карточку калькулятора в верхней части экрана, показывающую сумму чаевых и общую сумму к оплате.
Вы также можете сказать «Привет, Siri. Какие 20% чаевые? ». Siri спросит, сколько стоит счет.
Ответьте, указав сумму, указанную в счете, и Siri отобразит расчет чаевых в верхней части экрана. Щелкнув по результатам расчета, вы перейдете в приложение «Калькулятор».
Рассчитать подсказки вручную
Если вы не используете Siri или вы один из многих пользователей iPhone, которые стесняются использовать Siri в общественных местах, следуйте инструкциям, чтобы вручную рассчитать подсказки на своем iPhone.
- Запустите приложение «Калькулятор» и введите сумму, указанную в счете.
Коснитесь знака «плюс» (+) и введите процент, который вы хотите дать.
После этого коснитесь знака процента (%).
Наконец, коснитесь символа равенства (=), чтобы узнать общую сумму, которую вы платите.

Чтобы определить, сколько чаевых составляет 20% от счета в 567,84 доллара, откройте калькулятор iPhone и введите 567,84. Нажмите знак плюса (+), введите 20 и нажмите знак процента (%), чтобы получить сумму чаевых.
Наконец, коснитесь знака равенства (=), чтобы получить общую сумму.
6. Расчеты прожекторов
Как и Siri, калькулятор iPhone также интегрирован для работы с поиском Spotlight. Вместо того чтобы открывать приложение «Калькулятор», вы можете решать простые и сложные уравнения, вводя их непосредственно в поиске Spotlight.
Проведите пальцем вправо от главного экрана вашего iPhone, чтобы получить доступ к поиску Spotlight. Введите свой расчет в строку поиска, и вы должны увидеть результаты под своей записью. Например, ввод «пи 4» отобразит результат для 3,1415 * 4.
Вы можете щелкнуть результат, чтобы открыть приложение «Калькулятор».
Вот некоторые поддерживаемые буквы, знаки, константы и символы, которые можно использовать для выполнения вычислений в поиске Spotlight:
- — — минус / вычитание
- + — сложение
- x или * — умножение
- ^ — показатель степени
- Пи — 3,14
- ! — факториал
- % — процент
7.
 Выполнение сложных расчетов
Выполнение сложных расчетовКак упоминалось ранее, вы можете получить доступ к научной версии приложения iPhone Calculator, установив альбомный формат. Это позволяет выполнять сложные вычисления, такие как дроби, квадратные корни, экспоненты, логарифмы и т. Д. Мы покажем вам, как использовать научный калькулятор iPhone для выполнения некоторых сложных функций.
Как вычислить квадратный корень на iPhone
Коснитесь числа, квадратный корень которого вы хотите вычислить, и коснитесь знака квадратного корня (2√x).
Чтобы найти кубический корень числа, введите число и коснитесь знака кубического корня (3√x).
В научном калькуляторе также есть функция корня n-й степени, которая позволяет вычислять другие значения корня числа. Чтобы использовать эту функцию, введите базовое число (т.е. значение x), коснитесь знака корня n-й степени (y√x), введите радикальное число или значение y (т.е. корень n-й степени, который вы ищете) и коснитесь равного знак (=).
Например, если вы хотите вычислить корень 5-й степени из 25, все, что вам нужно сделать, это ввести 25, коснуться знака корня n-й степени (y√x), ввести 5 и щелкнуть знак равенства.
Как считать дроби на iPhone
Вычислить дроби легко. Просто разделите числитель на знаменатель с помощью стандартного или научного калькулятора. Например, чтобы решить 11/4, введите 11, коснитесь знака деления (÷), введите 4 и коснитесь знака равенства (=).
Научный калькулятор iOS также имеет встроенную функцию для вычисления доли единицы числа. Введите число и коснитесь знака единичной дроби (1 / x), чтобы найти единичную дробь числа.
Как рассчитать экспоненты на iPhone
Вам также потребуется использовать научный калькулятор для выполнения экспоненциальных вычислений, т. Е. Многократных умножений числа. Есть специальные кнопки для выполнения вычислений «в квадрате» и «в кубе». Чтобы возвести число в степень 2 или 3, введите число в калькулятор и нажмите знак экспоненты в квадрате (x2) или кубе (x3) соответственно.
Хотите возвести число в степень больше 3? Используйте знак настраиваемой экспоненты (xy) для выполнения вычисления. Введите основную цифру, коснитесь знака настраиваемой экспоненты (xy), введите показатель степени (то есть степень или количество раз, которое вы хотите умножить на основание само по себе) и коснитесь знака равенства (=).
Расчет как профессионал
Эти советы помогут вам выполнять повседневные вычисления быстрее и лучше, чем раньше. Оставьте комментарий ниже, если вы узнали что-то новое или если у вас есть очень полезный трюк с калькулятором для iPhone, которым вы можете поделиться с нами.
Программы для Windows, мобильные приложения, игры — ВСЁ БЕСПЛАТНО, в нашем закрытом телеграмм канале — Подписывайтесь:)
Лучшие фишки приложения Калькулятор на Айфоне
Каждый из нас хоть изредка, но пользуется калькулятором на своем iPhone. Сам я пользуюсь им, пожалуй, раза в три больше, чем остальные. И дело совсем не в профессиональной необходимости. Просто в работе я не сталкиваюсь с вычислениями вообще никогда, поэтому сейчас настолько отвык от вычислений, что дважды два складываю только через приложение. На первый взгляд калькулятор на Айфоне предельно простой, но если копнуть чуть-чуть глубже, становится понятно, что это не так. Сегодня хочу поделиться с вами самыми необходимыми фишками, с которыми вы можете столкнуться в повседневной жизни.
Просто в работе я не сталкиваюсь с вычислениями вообще никогда, поэтому сейчас настолько отвык от вычислений, что дважды два складываю только через приложение. На первый взгляд калькулятор на Айфоне предельно простой, но если копнуть чуть-чуть глубже, становится понятно, что это не так. Сегодня хочу поделиться с вами самыми необходимыми фишками, с которыми вы можете столкнуться в повседневной жизни.
Фишки калькулятора, о которых мало кто знал.
Крейг Федериги объяснил, почему на iPad нет приложения «Калькулятор».
Содержание
- 1 Где найти калькулятор на Айфоне
- 2 Что умеет Siri
- 3 Как активировать научный калькулятор на Айфоне
- 4 Как удалить цифру на калькуляторе Айфона
- 5 Как скопировать последнее действие на калькуляторе Айфона
Где найти калькулятор на Айфоне
Оказывается, запустить калькулятор можно даже на заблокированном Айфоне. Для этого вам необходимо:
- Смахнуть с верхнего правого угла на iPhone X и новее или смахнуть снизу вверх на iPhone 8 и cтарше.

- В нижней части пункта управления нажать на иконку калькулятора.
Запускайте калькулятор в два тапа.
Если вдруг там калькулятора нет, его всегда можно добавить в настройках смартфона. Для этого:
- Перейдите в Настройки вашего iPhone.
- Затем перейдите в раздел Пункт управления.
- Далее найдите Калькулятор в предложенном списке.
- Нажмите на Плюс рядом с ним.
Добавьте Калькулятор в пункт управления на Айфоне.
Готово. Теперь вы всегда можете быстро открывать калькулятор прямо из меню Пункта управления. Из минусов важно сказать про историю поиска. Допустим вы посчитали денежные расходы за январь, закрыли калькулятор и заблокировали Айфон. Тот, кто зайдет в калькулятор через заблокированный экран сможет посмотреть последний результат. Кто-то скажет мелочь, а кто-то попадет по-крупному.
Что умеет Siri
Если вдруг вы не знали, Сири умеет считать и с радостью сделает это за вас. Скажите ей что-нибудь вроде «Привет, Siri, сколько будет шесть умножить на шесть» и голосовой помощник вам ответит.
Внимание! Фишка работает на iPad.
Также она справится с несколькими действиями. Правда, далеко не со всеми. Например, возвести выражение в скобки уже не получится. Если работаете с деньгами и валютой, в Siri встроен конвертер валют. Перевести фунты в доллары, доллары в рубли — все, что вам угодно.
Как активировать научный калькулятор на Айфоне
Если у вас вдруг появилась необходимость посчитать корень на калькуляторе Айфона или возвести число в степень, вам поможет научный калькулятор. Активировать его можно повернув смартфон на 90 градусов (в режим просмотра видео).
Вот так выглядит инженерный калькулятор.
Здесь вы найдете множество разных инструментов, которые пригодятся на все случаи жизни — синусы, косинусы, логарифмы, степени, факториалы.
До сих пор не подписаны на нас в Яндекс.Дзен? Это вы зря!
Как удалить цифру на калькуляторе Айфона
Необходимость удаления какой-нибудь цифры возникает у каждого пользователя. При этом далеко не каждый знает, как это сделать. Конечно, есть отдельная кнопка C, с помощью которой можно напрочь удалить все число, но иногда это не самое удобное решение.
При этом далеко не каждый знает, как это сделать. Конечно, есть отдельная кнопка C, с помощью которой можно напрочь удалить все число, но иногда это не самое удобное решение.
Удалить цифру в калькуляторе на iPhone можно с помощью простого свайпа слева направо или справа налево. Так айфон будет удалять по одной цифре, а если она останется одна, удалит все полностью. Отменить последнее действие на калькуляторе iPhone или убрать запятую и поставить ее в другое место не получится, поэтому будьте аккуратны.
Как скопировать последнее действие на калькуляторе Айфона
Чтобы скопировать результат вычислений на калькуляторе iPhone, просто нажмите и удерживайте готовое число в поле ввода. Также можно скопировать число из любого приложения или веб-сайта и ввести его в калькулятор.
Есть еще один способ, который подойдет тем, кто много работает с числами:
- Закройте приложение калькулятор.
- На экране Домой нажмите и удерживайте иконку приложения.

- Нажмите Скопировать последний результат.
Два способа копирования текста в калькуляторе на Айфоне.
Плюс, есть еще пару фичей, которые могут облегчить привычное использование Калькулятора на iPhone:
- Если нажать два раза на знак равенства, то последнее действие повторится.
- Нажатие на кнопку AC приводит к аннулированию текущего ввода, а кнопка C отменяет последнюю из введенных операций.
Ну, а если вам вдруг не хватает нативного калькулятора, мы уже рассказывали вам про несколько других вариантов.
Остались вопросы? Может быть вы находили какие-то свои уникальные фичи? Дайте обратную связь в нашем Телеграм-чате или в комментариях ниже, будет интересно прочесть.
Обзоры приложений для iOS и MacСмартфоны AppleСоветы по работе с Apple
Простой способ вычислить логарифмы без калькулятора?
Спросил
Изменено 2 года, 3 месяца назад
Просмотрено 170 тысяч раз
$\begingroup$
Мне нужно уметь вычислять логарифмы без использования калькулятора, только на бумаге. Результат должен быть дробным, чтобы он был наиболее точным. Например, я видел это на уроке математики, вычисленное одним из моих одноклассников без помощи калькулятора. 93)}=\dfrac{7\log_a2}{3\log_a2}=?$$
Результат должен быть дробным, чтобы он был наиболее точным. Например, я видел это на уроке математики, вычисленное одним из моих одноклассников без помощи калькулятора. 93)}=\dfrac{7\log_a2}{3\log_a2}=?$$
Ясно, что $\log_a2$ ненулевое конечное число для конечного вещественного $a>0,\ne1$
См. Законы логарифмов
$\endgroup$
$\begingroup$
Как вы уже видели, вычислить их вручную может быть уйма работы. Итак, в контексте «без калькулятора» я хотел бы отметить, что логарифмическая линейка была сделана почти точно для этого типа расчета!
$\endgroup$
3 92 $ и так $\sqrt 2 \приблизительно 10 / 7 = 1,4 $
После некоторой практики вы сможете очень быстро получать приближения в пределах 1%, часто в уме.
При наличии карандаша и бумаги часто можно быстро удвоить точность за одну итерацию метода Ньютона. Например:
Например:
$\sqrt 2 / 1,4 \приблизительно 1,42857 $, поэтому более точное приближение равно $\sqrt 2 \приблизительно (1,4 + 1,42857)/2 = 1,414285 $.
Повторение снова дает $\sqrt 2 \приблизительно 1,41421356 $, что так же точно, как многие ручные калькуляторы. 98 = 25 600 000 000\\ \log_{20} 25 600 000 000 \приблизительно 8\\ \ln 25 600 000 000 \приблизительно 8 \cdot 3 = 24\\ \ln 34 627 486 221 = \ln 25 600 000 000 + \ln (34 627 486 221 / 25 600 000 000) \приблизительно 24 + \ln 1,35 \приблизительно 24,35$$
Ответ: скидка всего 0,13%, что очень точно.
Надеюсь, это поможет!
$\endgroup$
$\begingroup$
В учебнике Апостола «Исчисление», том 1, разработана формула вычисления логарифма. Приводится конкретный пример $\log 2$, в результате чего получается 0,69 доллара США{1/n} — 1 \right)$$
Если $n$ является степенью $2$, вы получите много квадратных корней. См. в материалах HHC 2018 статью о вычислении логарифмов.
См. в материалах HHC 2018 статью о вычислении логарифмов.
Как правило, степенные ряды эффективны для натуральных логарифмов чисел, близких к $1$. Вы можете сделать что-нибудь, чтобы приблизить свое число к 1 доллару, например, умножить на степень десяти или извлечь квадратный корень, а затем скорректировать полученный логарифм.
Тем временем запомните число $0,4343$. Это приблизительный логарифм $e$. Используйте это, чтобы преобразовать натуральные журналы в десятичные журналы.
$\endgroup$
2
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Использование калькуляторов для выполнения логарифмических и антилогарифмических функций
Логарифмы (-логарифмы) и (-)антилогарифмы с калькуляторами
Std 5f
Чтобы найти pH решения, которое вы должны принять — log [H + ]
Найти pOH решения, которое вы должны принять — журнал [OH — ]
Чтобы найти [H + ] , вы должны взять (-) анти -логарифм pH
Чтобы найти [OH — ] , вы должны взять (-) анти -логарифм pH
(Для более полное объяснение этого см. в разделе Изменение pH или pOH до их соответствующих концентраций)
Большинство калькуляторов (включая TI-30Xa и Casio fx-250HC ):
1. Если pH = 3,5 и вас просят найти [H + ] (это расчет антилога)
Введите 3,5 (или любое другой pH вам может быть предоставлен)
Нажмите +/- клавиша (переворачивает знак)
Нажмите 10 x клавиша (нажав клавиши 2 и , а затем нажав ключ журнала)
Ответ 0,000316 или 3,16 x 10 -4
2. Если [H + ] = 3,16 x 10 -4 и вас просят ввести , найдите pH (это вычисление -LOG). TI-30Xa и Casio fx-250HC одинаковы, если не указано иное.
Если [H + ] = 3,16 x 10 -4 и вас просят ввести , найдите pH (это вычисление -LOG). TI-30Xa и Casio fx-250HC одинаковы, если не указано иное.
Введите 3.16 (3 значащие цифры [H + ] )
а. на TI пресс EE ключ
б. на Casio нажмите кнопку EXP клавиша
Нажмите +/- клавиша (это меняет знак степени, которую вы войдет)
Введите 4 (это отрицательный показатель степени 10 в [H + ] )
Нажмите клавишу LOG (это фактически вычисляет LOG введенного вами [H + ])
Нажмите +/- клавишу (это делает LOG вычислением LOG )
Ответ 3,5
3. Если [H + ] = 3,16 x 10 -4 и вас попросят найти pH выше
, но теперь мы решим ту же проблему, что и # использовать другой метод) (этот вычисляет -LOG)
TI-30Xa и Casio fx-250HC одинаковы для всех этих операций.
Введите 3,16 ( 3 значащие цифры [H + ] )
Нажмите клавишу X (клавиша времени)
Введите 10
Нажмите x y клавиша (который может быть помечен как y x ключ, или xy или yx. Это позволяет
поставить следующее число, введенное как показатель степени 10)
Введите 4 (это отрицательный показатель степени 10 в [H + ] )
Нажмите +/- клавишу (это делает знак степени, которую вы ввел отрицательный)
Press = key
Press LOG key
Ans pH = 3.5
Only use this method if you really like
это, в противном случае придерживайтесь # 2 выше.
То же самое
расчеты на графическом калькуляторе
вроде — ТИ-85 .
Все калькуляторы
которые имеют клавиши влево-вправо, вверх-вниз, обычно используют этот
логика. Модели, которые я определил
пока что используют эту логику:
Модели, которые я определил
пока что используют эту логику:
Casio fx-115MS, Casio fx-300MS и Casio fx-991s
Sharp EL-531V, Sharp 520W и Sharp EL-531; но для Шарпа EL-500L близко, но не точно, поработайте с ним немного и/или до встречи)
TI 30X IIS (Texas Instruments)
Hp 30S (Hewlett Packard)
1. Если pH = 3,5 и вас просят найти [H + ] (это вычисление -антилогарифма)
Нажмите 2 nd клавишу (действует как клавиша Shift)
Нажмите LOG клавишу (примечание: LOG изменен на функцию 10 x , напротив журнала)
Нажмите (-) клавишу (это изменяет следующее введенное число на отрицательный)
Введите 3,5 (или другой pH, который вы пытаетесь найти)
Нажмите Введите клавишу (это завершит расчет и даст ты концентрация)
ANS Вы увидите 3,16 E 4 показано , что такое же, как 3,16 x 10 -4
2. Если [H +
Если [H +
2. Если [H +
2. Если [H +
2. Если [H +
2. Если [H +
2. Если [H +
2. Если = 3,16 x 10 -4 и вас попросят найти pH (это вычисление -LOG)
Нажмите (-), чтобы изменить введенное число ( а отрицательный)
Нажмите LOG ключ (это устанавливает, что что бы ни было введено дальше, калькулятор рассчитает ЛОГ числового значения)
Нажмите (клавиша (это заставит калькулятор считать все внутри (до того, как он возьмет журнал чисел)
Введите 3.16 (три значащие цифры из [H + ] )
Нажмите клавишу EE (теперь калькулятор предполагает, что вы хотите введите степень 10 и умножьте на 3,16. E теперь будет отображается)
Нажмите кнопку (-) (это сделает следующее введенное число отрицательным)
Введите 4 ) ключ (этот номер будет использоваться как отрицательная экспонента числа 10)
Нажмите клавишу ENTER (или ANS) (теперь это позволит калькулятору рассчитать LOG вашего [H + ] )
Ans pH = 3,5
ПРИМЕЧАНИЕ: после
сделано выше, с расчетами, где вы не в идеальном экспоненциальном представлении (например, 53,2 x 10 -23 ), нажмите клавишу =, и он будет скорректирован до
научное обозначение 5,32 x 10 -22 .
Экспоненты из 10 и научной нотации Casio и TI
Здесь мы берем число в степени 10 и изменить его на научную нотацию, а затем, если мы хотим, легко изменить его на десятичная дробь.
1. Поместите число 85,3 x 10 -5 в экспоненциальную запись, а затем в десятичная форма
Сначала мы меняем показатель степени на десятичная форма:
1. Введите 85,3 , затем:
a. на Casio нажмите клавишу EXP (позволяет ввести показатель степени)
b. на ТИ нажмите клавишу EE (позволяет ввести показатель степени)
2. Нажмите клавишу +/- , а затем введите показатель степени 5 (это вводит показатель степени как )
3. Когда вы нажимаете кнопку = ключ число появится в десятичной форме. (0,000853)
Затем мы меняем десятичную дробь на показатель степени в научном обозначение
4.
 Поставить число в научный
обозначение:
Поставить число в научный
обозначение:а. на Casio нажмите Клавиша РЕЖИМ а затем номер 9 (научное обозначение)
b. на TI нажмите клавишу 2 nd и затем номер 5 (научная запись)
На любом калькуляторе число будет теперь покажите в правильном экспоненциальном представлении
Ответ : 8,53 x 10 -4
2. Измените число 8,53 х 10 -4 назад до десятичной дроби:
а. на Касио , нажмите кнопку РЕЖИМ , а затем номер 9 еще раз
б. на прессе TI 2 й ключ и затем число 4
На любом калькуляторе число не будет показать в десятичной форме.
Ответ : 0,000853
Калькулятор логарифмов — Калькулятор логарифмов
Выберите для расчета:
РЕЗУЛЬТАТЫ
Заполните форму калькулятора и нажмите кнопку «Рассчитать», чтобы получить результат здесь
Получить Индивидуальный калькулятор Для вашего веб-сайта
Получить сейчас
ИЛИ
Получить Калькулятор журналов Для вашего веб-сайта
Получить сейчас
| 1 | Что такое логарифм? |
| 2 | Как посчитать логарифм на нашем калькуляторе |
| 3 | Как посчитать логарифм? |
| 4 | Что такое функция ln? |
| 5 | Product Law: |
| 6 | Quotient Law: |
| 7 | Proof of Power Rule Law: |
| 8 | Proof of Change of base Rule Law: |
Наш калькулятор логарифмов определяет логарифмическое значение числа, учитывая указанную вами базу журнала. Когда база журнала предусмотрена, вы можете рассчитать значения натурального журнала, общего журнала и двоичного журнала. Это просто вопрос выбора. Этот решатель логарифмических уравнений является бесплатным инструментом для помощи математикам, инженерам, физикам и, в частности, студентам.
Когда база журнала предусмотрена, вы можете рассчитать значения натурального журнала, общего журнала и двоичного журнала. Это просто вопрос выбора. Этот решатель логарифмических уравнений является бесплатным инструментом для помощи математикам, инженерам, физикам и, в частности, студентам.
Что такое логарифм?
В математике логарифм — это функция, обратная возведению в степень. Это означает, что логарифм данного числа, скажем, x, является показателем степени, до которой должно быть возведено другое статическое число, основание (скажем, b), чтобы воспроизвести число x.
В простейшем случае журнал суммирует количество вхождений одного и того же множителя при многократном умножении; например, поскольку 10000=10×10×10×10=10410000 = 10 х 10 х 10 х 10 = 10410000 = 10 х 10 х 10 х 10 = 104, «логарифм по основанию 10» числа 10000 равен 4. log x по основанию b представлен как log b (x). Вот как вы можете написать журнал.
Как рассчитать бревно с помощью нашего калькулятора
Этот наш калькулятор базы бревна исключительно прост в использовании. Вы должны выполнить очень простые шаги, чтобы сделать расчет. Пользовательский интерфейс этого калькулятора ln гарантирует, что даже в этом нет необходимости, но мы перечислим шаги на всякий случай.
Вы должны выполнить очень простые шаги, чтобы сделать расчет. Пользовательский интерфейс этого калькулятора ln гарантирует, что даже в этом нет необходимости, но мы перечислим шаги на всякий случай.
- Сначала выберите журнал, который вы хотите рассчитать, например: натуральный журнал, общий журнал, двоичный журнал или пользовательский журнал.
- Во-вторых, введите базовое значение.
- В-третьих, нажмите «вычислить»
- Вот и все. вы получите ответ
Как вычислить логарифм?
Журналы очень полезны при измерении или вычислении больших значений, которые недоступны для простого калькулятора, таких как расстояние между двумя галактиками, прирост населения или объем воды на Земле. Он вычисляет эти и подобные типы вычислений с большой точностью.
Стандартное уравнение для логарифмической функции: logb(x)=y\log b(x) = ylogb(x)=y
В этом уравнении y — это логарифм, то есть число умножений на него, x — это число, которое дается для расчета журнала, а b — это основание, которое умножается на себя.
Что такое функция ln?
Ln — натуральный логарифм с основанием e. e — иррациональное число, которое приблизительно оценивается как 2,718281828459. Некоторые люди путают функцию ln с антилогарифмом. Не используйте его как антилог, потому что это не антилог. Натуральный логарифм полезен для расчета времени, необходимого для достижения определенного уровня роста. 9{x + y} = MNNowax×ay=MNorax+y=MN
Следовательно, по определению имеем
loga(MN)=x+y=logaM+logaN\log_a(MN) = x + y = \log_a M + \log_a Nloga(MN)=x+y=logaM+logaN [подставляя значения x и y]
Следствие:
Закон верен для более чем двух положительные факторы, т.е. logaN+logaP
, так как loga(MNP)=loga(MN)+logaP=+logaM++logaN+logaP\log_a(MNP) = \log_a (MN) + \log_a P = + \log_a M + + \log_a N + \log_a P loga(MNP)=loga(MN)+logaP=+logaM++logaN+logaP 9{x — y} = M/NNowax/ay=M/Nor,ax-y=M/N
Следовательно, по определению имеем
loga(MN)=x-y=logaM-log aN\log_a(\dfrac{M}{N}) = x — y = \log_a M — \log_a Nloga(NM)=x−y=logaM−logaN [положив значения x и y]
Следствие:
loga[Mx×Nx×PRx×Sx×T]\log_a[ \dfrac{M x \times N x \times P}{R x \times S x \times T}] loga[Rx×Sx×TMx×Nx×P]
=loga(Mx×Nx×P)−loga(Rx×Sx×T) = log_a (M x \times N x \times P) — log_a ( R x \times S x \times T) = loga(Mx×Nx×P) − loga(Rx×Sx×T) 9yzNowax=M=by-(az)y=ayz
Следовательноx=yz или logaM=logbM×logab\mathbf{Поэтому} x = yz \space \mathbf{or} \space \log_a M = \log_b M \times \log_a b Следовательно, x=yz или logaM=logbM×logab [подставляя значения x , y и z]
Следствие:
(i) Полагая M = a в обе стороны от формулы изменения базового правила [logaM=logbM×logb\log_a M = \log_b M \times \log_b logaM=logbM×logb] получаем,
logaa=logba×logab=1\log_a a = \log_b a \times \log_a b = 1logaa=logba×logab=1 [так как log a a = 1]
logba=1logab\log_b a = \dfrac{1}{\log_a b}logba=logab1
logbM= logaMlogab\log_b M = \dfrac{\log_a M}{\log_a b} logbM=logablogaM
Другие языки
Рейтинги пользователей
- Всего отзывов 1
- Общий рейтинг 5/5
- Звезды
Спасибо! Для вашего рассмотрения
Ваш отзыв скоро появится.
Отправить свой отзыв Закрыть
Отзывы
Пожалуйста, заполните 1 строку
Обратная связь
Отправьте нам свой отзыв!
Нужна помощь? Вы можете связаться с нами в любое время.
Логарифмы с помощью калькулятора | Функции III
Выполнить 3 мин чтения
Логарифмы с помощью калькулятора
Содержание
- Логарифмы с помощью калькулятора
- Вычисление логарифмического значения
- Пример
- Вопрос
- Используйте общую функцию логарифма на вашем калькуляторе
- Напишите окончательный ответ
- Пример
- Вопрос
- Используйте вторую функцию и общую функцию Logarithm. ответ
- Пример
- Вопрос
- Решение
- Используйте замену основания для преобразования заданного логарифма в основание \(\text{10}\)
- Используйте функцию десятичного логарифма на своем калькуляторе
- Запишите окончательный ответ
- Важно:
Существует множество различных типов и моделей научных калькуляторов. Очень важно хорошо знать свой собственный калькулятор и различные функциональные кнопки. Некоторые калькуляторы имеют только две кнопки для логарифмов: одну для вычисления десятичного логарифма (основание равно \(\text{10}\)) и другую для вычисления натурального логарифма (основание равно \(e\)). Более новые модели будут иметь третью кнопку, которая позволит пользователю вычислить логарифм числа по определенному основанию.
Очень важно хорошо знать свой собственный калькулятор и различные функциональные кнопки. Некоторые калькуляторы имеют только две кнопки для логарифмов: одну для вычисления десятичного логарифма (основание равно \(\text{10}\)) и другую для вычисления натурального логарифма (основание равно \(e\)). Более новые модели будут иметь третью кнопку, которая позволит пользователю вычислить логарифм числа по определенному основанию.
Пример
Вопрос
С помощью калькулятора определите следующие значения (с точностью до \(\text{3}\) знаков после запятой):
- \(\log{9}\)
- \( \log{\text{0.3}}\)
- \(\log{\cfrac{3}{4}}\)
- \(\log{(-2)}\)
Используйте десятичный логарифм функция на вашем калькуляторе
Убедитесь, что вы знакомы с функцией «LOG» на вашем калькуляторе. Обратите внимание, что основание для каждого из приведенных выше логарифмов равно \(\text{10}\).
Запишите окончательный ответ
- \(\log{9} = \text{0,954}\)
- \(\log{\text{0,3}} = -\text{0,523}\)
- \(\log{\cfrac{3}{4}} = -\text{0,125}\)
- \(\log{(-2)} =\) undefined
Пример
Вопрос
Используйте a калькулятор для определения следующих значений (с точностью до \(\text{3}\) знаков после запятой):
- \(\log{x} = \text{1.
 7}\)
7}\) - \(\log{t} = \cfrac{2}{7}\)
- \(\log{y} = -\text{3}\) 9{x}\)» на калькуляторе, что правильно, поскольку экспоненты являются обратными логарифмами.
Запишите окончательный ответ
- \(x = \text{50.119}\)
- \(t = \text{1.930}\)
- \(y = \text{0.001}\)
- 4
Пример
Вопрос
Используйте калькулятор, чтобы найти \(\log_{2}{5}\) с точностью до двух знаков после запятой.
Решение
\[\log_{2}{5} = \cfrac{\log{5}}{\log{2}}\]
Используйте замену основания для преобразования заданного логарифма в основание \(\ текст{10}\)
\[\log_{2}{5} = \cfrac{\log{5}}{\log{2}}\]
Воспользуйтесь функцией десятичного логарифма на калькуляторе
Запишите окончательный ответ
\[\log_{2}{5} = \text{2.32}\]
Важно:Не записывайте промежуточный шаг при выполнении этого типа вычислений:
\begin{align* } \log_{2}{5} &= \cfrac{\log{5}}{\log{2}} \\ &= \cfrac{\text{0.
 7}}{\text{0.3}} \quad ( \text{этот шаг может привести к ошибкам округления}) \\ &= \text{2.33} \end{align*}
7}}{\text{0.3}} \quad ( \text{этот шаг может привести к ошибкам округления}) \\ &= \text{2.33} \end{align*}Выполните одношаговое вычисление на калькуляторе:
\begin{align*} \log_{2}{5} &= \cfrac{\log{5}}{\log{2}} \\ &= \text{2.32} \end{align*}
Не округляйте перед окончательным ответом, так как это может повлиять на точность ответа.
Убедитесь, что вы определили правильную последовательность и порядок операций при использовании калькулятора.
Продолжить через мобильное приложение | Доступно в Google Play 9{c}\)
\(a_{b}\)
\(\sqrt{a}\)
\(\sqrt[b]{a}\)
\(\frac{a}{ б}\)
\(\cfrac{a}{b}\)
\(+\)
\(-\)
\(\times\)
\(\div\)
\(\pm\)
\(\cdot\)
\(\amalg\)
\(\ast\)
\(\barwedge\)
\(\bigcirc\)
\( \bigodot\)
\(\bigoplus\)
\(\bigotimes\)
\(\bigsqcup\)
\(\bigstar\)
\(\bigtriangledown\)
\(\bigtriangleup\)
\(\blacklozenge\)
\(\blacksquare\)
\(\blacktriangle\)
\(\
5\) \(\bullet\)
\(\cap\)
\(\cup\)
\(\circ\)
\(\circledcirc\)
\(\dagger\)
\( \ddagger\)
\(\diamond\)
\(\dotplus\)
\(\lozenge\)
\(\mp\)
\(\ominus\)
\(\oplus \)
\(\oslash\)
\(\otimes\)
\(\setminus\)
\(\sqcap\)
\(\sqcup\)
\(\square\)
\(\star\)
\(\triangle\)
\(\triangledown\)
\(\triangleleft\)
\(\Cap\)
\(\Cup\)
\( \upplus\)
\(\vee\)
\(\veebar\)
\(\клин\)
\(\wr\)
\(\следовательно\)
\(\left ( a \right )\)
\(\left \| a \right \|\)
\(\влево [ a \вправо ]\)
\(\влево \{ a \вправо \}\)
\(\влево \lceil a \вправо \rceil\)
\(\влево \ lfloor a \right \rfloor\)
\(\left ( a \right )\)
\(\vert a \vert\)
\(\leftarrow\)
\(\leftharpoondown\)
\(\leftharpoonup\)
\(\leftrightarrow\)
\(\leftrightharpoons\)
\(\mapsto\)
\(\rightarrow\)
\(\rightharpoondown\)
\( \правый гарпунвверх\)
\(\rightleftharpoons\)
\(\to\)
\(\Leftarrow\)
\(\Leftrightarrow\)
\(\Rightarrow\)
\(\overset{a}{ \leftarrow}\)
\(\overset{a}{\rightarrow}\)
\(\приблизительно \)
\(\asymp\)
\(\cong \)
\(\dashv \)
\(\doteq \)
\(= \)
\(\equiv \)
\(\frown \)
\(\geq \)
\(\geqslant \)
\(\гг\)
\(\gt \)
\(| \)
\(\leq \)
\(\leqslant \)
\(\ll \)
\(\lt \)
\( \models\)
\(\neq \)
\(\ngeqslant \)
\(\ngtr \)
\(\nleqslant \)
\(\nless \)
\(\not \equiv \)
\(\overset{\underset{\mathrm{def}}{}}{=} \)
\(\parallel \)
\(\perp \)
\(\prec \)
\(\preceq \)
\(\sim \)
\(\simeq\)
\(\smile\)
\(\succ\)
\(\succeq\)
\(\vdash\)
\(\in\)
\ (\ni \)
\(\notin \)
\(\nsubseteq \)
\(\nsupseteq \)
\(\sqsubset \)
\(\sqsubseteq \)
\(\ sqsupset \)
\(\sqsupseteq \)
\(\subset \)
\(\subseteq \)
\(\subseteqq \)
\(\supset \)
\(\supseteq )
\(\supseteqq \)
\(\emptyset\)
\(\mathbb{N}\)
\(\mathbb{Z}\)
\(\mathbb{Q}\)
\(\mathbb{R}\)
\(\mathbb{C}\)
\(\alpha\)
\(\beta\)
\(\gamma\)
\(\delta \)
\(\эпсилон\)
\(\дзета\)
\(\эта\)
\(\тета\)
\(\йота\)
\(\каппа\)
\(\lambda\)
\(\mu\)
\(\nu\)
\(\xi\)
\(\pi\)
\(\rho\)
\(\sigma\)
\(\tau\)
\(\upsilon\)
\(\phi\)
\(\chi\)
\(\psi\)
\(\omega\)
\(\Gamma\)
\(\Delta\)
\(\Theta\)
\( \Lambda\)
\(\Xi\)
\(\Pi\)
\(\Sigma\)
\(\Upsilon\)
\(\Phi\)
\(\Psi \)
\(\Омега\)
\((а)\)
\([а]\) 9{} a\)
Редактировать математику с помощью TeX:
Предварительный просмотр математики:
Мысленно вычислять функции научного калькулятора
На этой странице показано, как грубо вычислять функции, распространенные в научных калькуляторах — экспоненты и логарифмы, тригонометрические функции, корни — и одна функция, которая, как я считаю, должна быть более распространена на научном калькуляторе: гамма-функция [1].

В целом приближения на этой странице хороши до пары значащих цифр. Более подробная информация приводится для каждого приближения.
Логарифмы
В этом разделе показано, как мысленно вычислять логарифмы по основанию 10, e и 2. x ≤ 3.
В более общем случае логарифмическая база b может быть сведена к случаю 1/√ b ≤ x ≤ √ b.
Основание 10
Для 0,3 ≤ x ≤ 3.
log 10 х ≈ ( х -1)/( х +1).
This approximation has a maximum error of about 0.03, and is very accurate for x near 1.
Base
eFor 1/√ e ≤ x ≤ √ e,
log e x ≈ 2 ( x – 1)/( x + 1).
Это приближение имеет максимальную ошибку около 0,03 и очень точно для x около 1.
Подробнее здесь.

Основание 2
Для 1/√2 ≤ x ≤ √2.
log 2 х ≈ 3( х – 1)/( х + 1).
Это приближение имеет максимальную ошибку около 0,015 и очень точно для x около 1.
Подробнее здесь.
Все вместе
Между прочим,
лог 2 x ≈ лог e x + журнал 10 x .
Подробнее здесь.
Экспоненты
В этом разделе показано, как вычислить в уме 10 x и e x .
Нам нужно рассмотреть только x между -0,5 и 0,5, потому что мы можем свести общий случай к этому случаю.
Base 10
Для x между -0,5 и 0,5,
10 x ≈ (1+ x )/(1- х ).
Максимальная относительная ошибка составляет около 0,08. Простая вариация может уменьшить это значение до 0,03.
 Подробнее здесь.
Подробнее здесь.Основание
Eдля x между -0,5 и 0,5,
E x ≈ (2 + x )/(2–).
Это приближение имеет максимальную относительную погрешность около 0,01. Подробнее здесь.
Основание 2
Часто, когда вычислительная мощность равна 2, показатель степени является целым числом, и вам нужен точный целочисленный результат, а не приближение. Поэтому стоит запомнить цифры 2 N для N Integer до 10.
, если вам необходимо вычислять 2 x для реального x , между -0,5 и 0,5, приблизительно
9000 2 020202020202020202020202020202.9151, между -0,5 и 0,5. ≈ (3+ x )/(3- x )хорошо с точностью до 0,015.
Корни
В этом разделе дается несколько методов мысленного вычисления корней. Обратите внимание, что вы также можете вычислять корни, используя логарифмы и экспоненты с помощью описанных выше приемов.

Квадратные корни
Чтобы вычислить квадратный корень из числа x , возьмите g и вычислите среднее значение g и x / g . Вы можете получить столько точности, сколько захотите, повторив этот процесс достаточное количество раз.
Подробнее здесь.
Высшие корни
Существует способ вычисления корней высших порядков, связанный с описанными выше методами вычисления логарифмических и экспоненциальных величин.
См. этот пост для деталей.
Триггерные функции
Для малых углов (в радианах) триггерные функции проще всего вычислить из одночленного ряда Тейлора. Все следующие приближения имеют точность в пределах 1%.
- sin x ≈ x для | х | < 0,244.
- cos x ≈ 1 – x ²/2 для | х | < 0,662.
- загар x ≈ x для | х | < 0,173.
- угловых углов x ≈ x для | х | < 0,242.

- arccos x ≈ π/2 – x для | х | < 0,4.
- арктан x ≈ x для | х | < 0,173.
Вы можете использовать тригонометрические тождества, чтобы свести задачу вычисления любой тригонометрической функции для любого угла к задаче вычисления тригонометрической функции для углов от 0 до π/4 радиан = 45°.
Для углов в градусах с x между 0 и 45 справедливы следующие приближения:
Синусоидальная аппроксимация с точностью до 0,02 и косинусная аппроксимация с точностью до 0,005. Ошибка тангенсной аппроксимации может достигать 0,1, но более точным является отношение синусоидальной и косинусной аппроксимаций. Смотрите этот пост для ссылок и деталей.
Следующая аппроксимация для косинуса верна с точностью до 0,001 для x между 0 и 40.0002 См. этот пост для ссылок и подробностей.
Гамма-функция
Задачу вычисления гамма-функции для любого вещественного аргумента можно свести к задаче вычисления гамма-функции на интервале длины 1.

Для 2 ≤ x ≤ 3,
х ) ≈ 2/(4 – х ).
Это приближение имеет максимальную относительную погрешность около 0,009. Смотрите этот пост для деталей.
[1] Обычно в калькуляторе есть кнопка факториала. Если этот факториал примет нецелочисленный аргумент, то, по-видимому, он вычисляет Γ( х +1).
Почему до появления калькуляторов было выгодно использовать логарифмы для вычисления корней?
Тригонометрия
Белла Б.
спросил 27.11.13Почему до появления калькуляторов было выгодно использовать логарифмы для вычисления корней?
Спасибо,
Белла
Подписаться І 4
Подробнее
Отчет
3 ответа от опытных наставников
Лучший Новейшие Самый старыйАвтор: ЛучшиеНовыеСамыеСтарые
Эндрю.
 ответил 27.11.13
ответил 27.11.13Репетитор
5 (3)
Дружелюбный репетитор для ВСЕХ курсов математики и физики
Смотрите таких репетиторов
Посмотреть таких репетиторов
Привет Белла,
Это интересный вопрос, так как логарифмы существуют гораздо дольше, чем калькуляторы!
До появления калькуляторов люди использовали таблицы для вычислений, выходящих за рамки основных арифметических операций сложения, вычитания, умножения и деления. Квадратные и кубические корни были известны с древних времен. Конечно, были таблицы для квадратных корней, кубических корней, четвертых корней и т. д., но они позволяли вычислять только ограниченное количество значений.
Затем, в 16 веке, английский математик по имени Джон Нэпьер открыл логарифмы. Как вы знаете, у логарифмов есть одно удивительное свойство: они превращают произведения в суммы, например log(a*b)=log(a)+log(b).
 Это означает, что показатели степени становятся множителями, как в log(a 2 )=2 log(a) и log(√a)=1/2 log(a) (помните, что извлечение квадратного корня равносильно возведению этого числа в в степени 1/2). Нейпир свел в таблицу тысячи логарифмов и разработал простое устройство, называемое логарифмической линейкой, которое позволяет вычислять любой логарифм с точностью до трех знаков или выше. Многие математики после Нейпира усовершенствовали его таблицы до такого количества значений, что они заняли целые книги. Итак, если вы хотите вычислить, скажем, √2, вы должны использовать тот факт, что log(√2)= (1/2) log(2). Вы бы посмотрели значение log(2) в таблице, получили 0,3010 (обычно они табулировали десятичные логарифмы или логарифмы по основанию 10), разделили его на 2, получили 0,1505, а затем посмотрели, какой журнал даст вам 0,1505. , и это будет 1,414, что √2 округляется до 4 значащих цифр. Это действительно аккуратно!
Это означает, что показатели степени становятся множителями, как в log(a 2 )=2 log(a) и log(√a)=1/2 log(a) (помните, что извлечение квадратного корня равносильно возведению этого числа в в степени 1/2). Нейпир свел в таблицу тысячи логарифмов и разработал простое устройство, называемое логарифмической линейкой, которое позволяет вычислять любой логарифм с точностью до трех знаков или выше. Многие математики после Нейпира усовершенствовали его таблицы до такого количества значений, что они заняли целые книги. Итак, если вы хотите вычислить, скажем, √2, вы должны использовать тот факт, что log(√2)= (1/2) log(2). Вы бы посмотрели значение log(2) в таблице, получили 0,3010 (обычно они табулировали десятичные логарифмы или логарифмы по основанию 10), разделили его на 2, получили 0,1505, а затем посмотрели, какой журнал даст вам 0,1505. , и это будет 1,414, что √2 округляется до 4 значащих цифр. Это действительно аккуратно!Голосовать за 0 Понизить
Подробнее
Отчет
Вивиан Л.
 ответил 27.11.13
ответил 27.11.13Репетитор
3 (1)
Microsoft Word/Excel/Outlook, составление эссе, математика; Я ЛЮБЛЮ УЧИТЬ
Смотрите таких репетиторов
Посмотреть таких репетиторов
Привет Белла;
Я так понимаю ситуацию.
Изобретение калькуляторов не проблема. Логарифмы были разработаны для облегчения построения графиков в тех случаях, когда количество одной переменной изменяется экспоненциально, а количество другой переменной изменяется незначительно.
Например, предположим, что Любой город из Любой штат в США каждые десять лет оценивался Бюро переписи населения США как имеющий статистические данные о населении…
1900, 1 000
1910, 10 000
1920, 100 000
Мы можем изобразить это, характеризуя ось X как десятилетие, а ось Y как население.
 Потребуется длинный лист бумаги. Или мы можем использовать логарифмы для характеристики статистики как …
Потребуется длинный лист бумаги. Или мы можем использовать логарифмы для характеристики статистики как …1900, log 10 1000 = 3
1910, log 10 10000 = 4
1920, log 10 100000 = 5
1920, log 10 100000 = 5 1920Для этого потребуется стандартный лист бумаги размером 8,5 x 11 дюймов.
Проще говоря, дело не в скорости вычислений, а в размере бумаги.
Голосовать за 0 Понизить
Подробнее
Отчет
Эдвард Б. ответил 27.11.13
Репетитор
4 (1)
Все уровни Математика, информатика и программирование, SAT Math 9(-1) 0,6666666…
х ~ 4,64159
Голосовать за 0 Понизить
Подробнее
Отчет
Все еще ищете помощи? Получите правильный ответ, быстро.


 А именно, десятичные логарифмы характеризуются исключительно для положительных чисел. Десятичные логарифмы чисел, больших единицы, положительны, а чисел, меньших единицы, отрицательны; из двух не отрицательных чисел большему эквивалентен и больший десятичный логарифм и т. д. Дополнительно, десятичные логарифмы имеют отличительные черты и своеобразные признаки, которыми и поясняется, зачем в качестве основания логарифмов комфортно предпочитать именно цифру десять.
А именно, десятичные логарифмы характеризуются исключительно для положительных чисел. Десятичные логарифмы чисел, больших единицы, положительны, а чисел, меньших единицы, отрицательны; из двух не отрицательных чисел большему эквивалентен и больший десятичный логарифм и т. д. Дополнительно, десятичные логарифмы имеют отличительные черты и своеобразные признаки, которыми и поясняется, зачем в качестве основания логарифмов комфортно предпочитать именно цифру десять.


 В обратном случае «a» преобразуется в «у» и обладает трансцендентными и иррациональными признаками. Также стоит отметить, что натуральная величина рассчитывается специальным уравнением, где доказательством становится теория, изучаемая за пределами школьной программы старших классов.
В обратном случае «a» преобразуется в «у» и обладает трансцендентными и иррациональными признаками. Также стоит отметить, что натуральная величина рассчитывается специальным уравнением, где доказательством становится теория, изучаемая за пределами школьной программы старших классов. Показательное уравнение является практически точной копией логарифмических расчетов, если смотреть со стороны правильности решения. Просто первый вариант включает в себя специализированное число, помогающее быстрее разобраться в условии, а второй заменяет log на обыкновенную степень. При этом вычисления с применением последней формулы должны включать в себя переменное значение.
Показательное уравнение является практически точной копией логарифмических расчетов, если смотреть со стороны правильности решения. Просто первый вариант включает в себя специализированное число, помогающее быстрее разобраться в условии, а второй заменяет log на обыкновенную степень. При этом вычисления с применением последней формулы должны включать в себя переменное значение.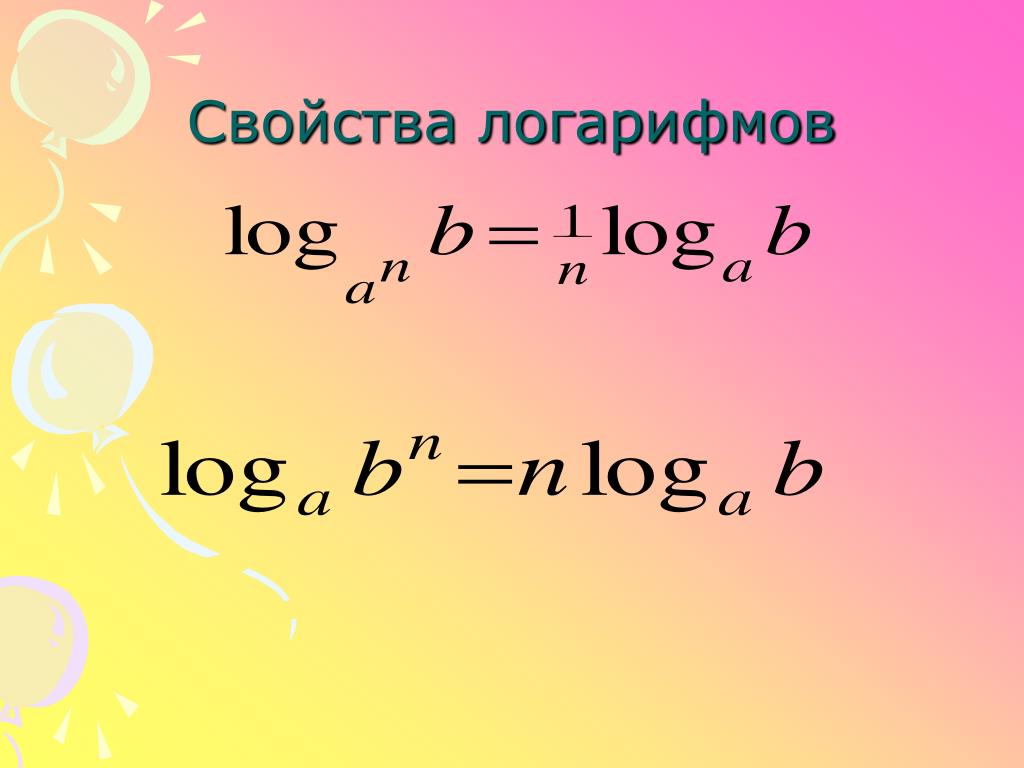

 При этом все базовые расчеты должны были упираться в последнюю величину. Таким же образом ученые интегрировали и вычитание.
При этом все базовые расчеты должны были упираться в последнюю величину. Таким же образом ученые интегрировали и вычитание.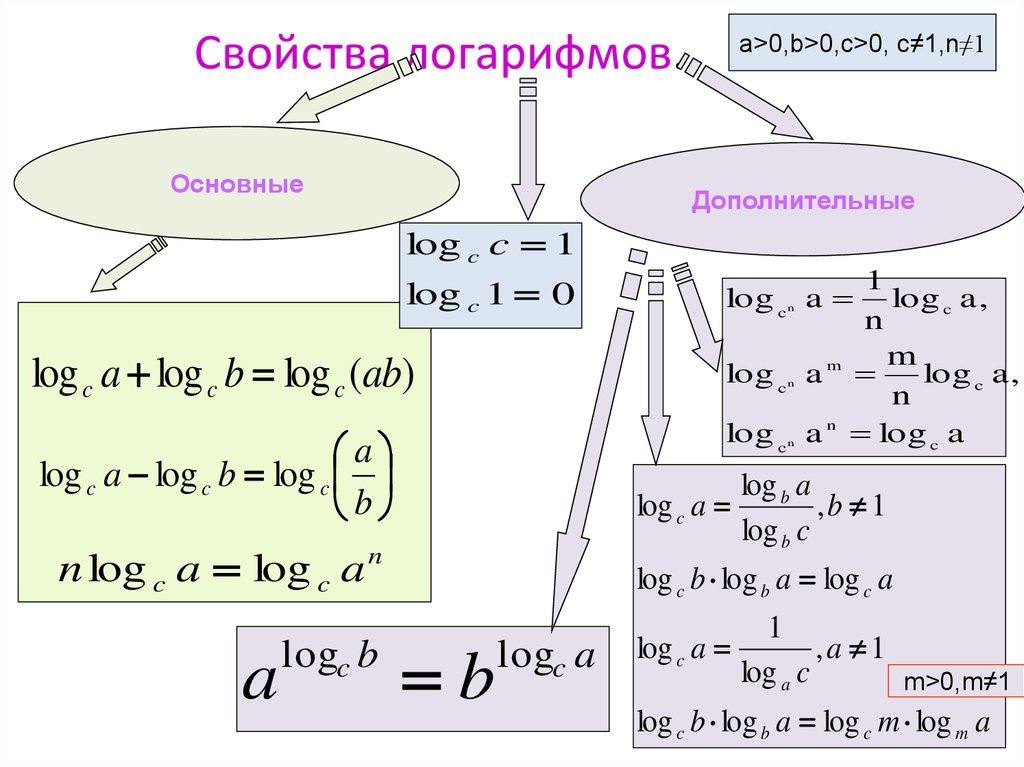 В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.
В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики.


 Однако a b не равно b a , за исключением единственного случая, когда 2 2 = 4 2 . В выражении a b = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы.
Однако a b не равно b a , за исключением единственного случая, когда 2 2 = 4 2 . В выражении a b = с, мы можем выразить a как корень b-ой степени из c, но как выразить b? Вот тут на сцене и появляются логарифмы. Это и есть ответ, которого строгим математикам достаточно. Если вы хотите выразить это число точно, то вычислите его при помощи инженерного калькулятора. В этом случае log2 20 = 4,32192809489. Это иррациональное бесконечное число, а log2 20 — его компактная запись.
Это и есть ответ, которого строгим математикам достаточно. Если вы хотите выразить это число точно, то вычислите его при помощи инженерного калькулятора. В этом случае log2 20 = 4,32192809489. Это иррациональное бесконечное число, а log2 20 — его компактная запись. Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно.
Точно также log10 50 и log10 360 записываются как lg50 и lg360 соответственно. По сути, это тоже возведение в степень и обратная операция для логарифмирования.
По сути, это тоже возведение в степень и обратная операция для логарифмирования. Для решения подобной проблемы используются десятичный логарифм, которой позволяет построить график функции, адекватно отображающий все ее значения.
Для решения подобной проблемы используются десятичный логарифм, которой позволяет построить график функции, адекватно отображающий все ее значения. Однако если логарифм вычисляется, вы обязаны представить его в виде целого числа. Пусть вы решили 5 примеров по алгебре, и вам требуется проверить результаты на возможность целочисленного представления. Давайте проверим их при помощи калькулятора логарифма по любому основанию:
Однако если логарифм вычисляется, вы обязаны представить его в виде целого числа. Пусть вы решили 5 примеров по алгебре, и вам требуется проверить результаты на возможность целочисленного представления. Давайте проверим их при помощи калькулятора логарифма по любому основанию: Представим, что ВВП страны Кракожия увеличилось с 5,5 миллиардов долларов до 7,8 за 10 лет. Давайте определим ежегодный прирост ВВП в процентах при помощи калькулятора натурального логарифма. Для этого нам надо подсчитать натуральный логарифм ln(7,8/5,5), что равнозначно ln(1,418). Введем это значение в ячейку калькулятора и получим результат 0,882 или 88,2% за все время. Так как ВВП рос в течение 10 лет, то ежегодный его прирост составит 88,2 / 10 = 8,82%.
Представим, что ВВП страны Кракожия увеличилось с 5,5 миллиардов долларов до 7,8 за 10 лет. Давайте определим ежегодный прирост ВВП в процентах при помощи калькулятора натурального логарифма. Для этого нам надо подсчитать натуральный логарифм ln(7,8/5,5), что равнозначно ln(1,418). Введем это значение в ячейку калькулятора и получим результат 0,882 или 88,2% за все время. Так как ВВП рос в течение 10 лет, то ежегодный его прирост составит 88,2 / 10 = 8,82%. Используйте наш сборник онлайн-калькуляторов для решения школьных заданий, а также задач из разных научных сфер.
Используйте наш сборник онлайн-калькуляторов для решения школьных заданий, а также задач из разных научных сфер.



 7}\)
7}\) 7}}{\text{0.3}} \quad ( \text{этот шаг может привести к ошибкам округления}) \\ &= \text{2.33} \end{align*}
7}}{\text{0.3}} \quad ( \text{этот шаг может привести к ошибкам округления}) \\ &= \text{2.33} \end{align*}
 Подробнее здесь.
Подробнее здесь.


 ответил 27.11.13
ответил 27.11.13 Это означает, что показатели степени становятся множителями, как в log(a 2 )=2 log(a) и log(√a)=1/2 log(a) (помните, что извлечение квадратного корня равносильно возведению этого числа в в степени 1/2). Нейпир свел в таблицу тысячи логарифмов и разработал простое устройство, называемое логарифмической линейкой, которое позволяет вычислять любой логарифм с точностью до трех знаков или выше. Многие математики после Нейпира усовершенствовали его таблицы до такого количества значений, что они заняли целые книги. Итак, если вы хотите вычислить, скажем, √2, вы должны использовать тот факт, что log(√2)= (1/2) log(2). Вы бы посмотрели значение log(2) в таблице, получили 0,3010 (обычно они табулировали десятичные логарифмы или логарифмы по основанию 10), разделили его на 2, получили 0,1505, а затем посмотрели, какой журнал даст вам 0,1505. , и это будет 1,414, что √2 округляется до 4 значащих цифр. Это действительно аккуратно!
Это означает, что показатели степени становятся множителями, как в log(a 2 )=2 log(a) и log(√a)=1/2 log(a) (помните, что извлечение квадратного корня равносильно возведению этого числа в в степени 1/2). Нейпир свел в таблицу тысячи логарифмов и разработал простое устройство, называемое логарифмической линейкой, которое позволяет вычислять любой логарифм с точностью до трех знаков или выше. Многие математики после Нейпира усовершенствовали его таблицы до такого количества значений, что они заняли целые книги. Итак, если вы хотите вычислить, скажем, √2, вы должны использовать тот факт, что log(√2)= (1/2) log(2). Вы бы посмотрели значение log(2) в таблице, получили 0,3010 (обычно они табулировали десятичные логарифмы или логарифмы по основанию 10), разделили его на 2, получили 0,1505, а затем посмотрели, какой журнал даст вам 0,1505. , и это будет 1,414, что √2 округляется до 4 значащих цифр. Это действительно аккуратно! ответил 27.11.13
ответил 27.11.13 Потребуется длинный лист бумаги. Или мы можем использовать логарифмы для характеристики статистики как …
Потребуется длинный лист бумаги. Или мы можем использовать логарифмы для характеристики статистики как …