Двойной интеграл в полярных координатах калькулятор онлайн: ∫∫ Двойной интеграл — Калькулятор Онлайн

2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x)

Интегральный синус от x

Ci(x)

Интегральный косинус от x

Shi(x)

Интегральный гиперболический синус от x

Chi(x)

Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа

вводить в виде 7. 3

— возведение в степень

x + 7

— сложение

x — 6

— вычитание

15/7

— дробь

Другие функции:

asec(x)

Функция — арксеканс от x

acsc(x)

Функция — арккосеканс от x

sec(x)

Функция — секанс от

x

csc(x)

Функция — косеканс от x

floor(x)

Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)

ceiling(x)

Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)

sign(x)

Функция — Знак x

erf(x)

Функция ошибок (или интеграл вероятности)

laplace(x)

Функция Лапласа

asech(x)

Функция — гиперболический арксеканс от x

csch(x)

Функция — гиперболический косеканс от x

sech(x)

Функция — гиперболический секанс от x

acsch(x)

Функция — гиперболический арккосеканс от x

Постоянные:

pi

Число «Пи», которое примерно равно ~3. 14159..

e

Число e — основание натурального логарифма, примерно равно ~2,7183..

i

Комплексная единица

oo

Символ бесконечности — знак для бесконечности

Двойной интеграл в полярных координатах

Алгоритм вычисления двойных интегралов при переходе к полярным координатам детально приведен как в настоящей статье, так и предыдущих публикациях с теорией. Для перехода к полярным координатам нужно найти якобиан, который несколько раз здесь повторим. Дальше сами уравнения кривых, которые ограничивают область интегрирования следует также перевести в полярные координаты. В теории все хорошо описано и выглядит понятным, однако на практике во многих студентов возникают трудности и немало вопросов, поэтому внимательно пересмотрите приведенные дальше решения.

Пример 2.1 Вычислить двойной интеграл, используя полярные координаты:

Решение: Построим область интегрирования ограниченную кривыми
-3≤x≤3
Эти кривые записываем из пределов интегрирования, внимательно пересмотрите в каких пределах изменяются «икс» и «игрек».
Нижний предел по оси «игреков» приведем к каноническому виду

x²+y²=9.
Получили уравнение круга с центром в точке O(0;0) и радиусом 3 (нижняя половина).

Перейдем к полярной системе координат с помощью превращения координат:

найдем якобиан перехода:

Найдем подынтегральную функцию в полярных координатах:

Внимательно пересмотрите формулы двойного синуса, косинуса и им подобных.
Они достаточно часто встречаются при упрощении подынтегральных функций, все сделано умышленно для того, чтобы Вы без проблем могли интегрировать.
Запишем пределы интегрирования в полярной системе координат:
0≤r≤3, π≤φ≤2 π.
Вычислим двойной интеграл:

Поскольку переменные разделены, то интегрирование не тяжелое, достаточно воспользоваться табличными интегралами и подставить пределы.

 

Пример 2.2 Найти двойной интеграл, используя полярные координаты:

Решение: Из интеграла выписываем область интегрирования
0≤x≤1
Она ограничена прямыми, которые совпадают с-осями координат  
, y²=12-x²,x²+y²=1² — дуга круга в I четверти.

Получили круг с центром в точке O(0;0) и радиусом r=1 (верхняя половина).
Якобиан перехода к ПСК I=r.
Запишем подынтегральную функцию в полярной системе координат:

Для круговых областей не трудно записать пределы интегрирования при переходе к полярной системе координат:
0≤r≤1, 0≤φ≤π/2.
Находим двойной интеграл:

В результате интегрирования в ответе получили выражение которое содержит логарифм двойки, и число Пи.

 

Пример 2.3 Вычислить значение двойного интеграла, перейдя к полярным координатам:

Решение: Выпишем область интегрирования, которая ограничена кривыми
— 2≤x≤2,
По «игреку» имеем ограничения ветками круга , y²=4-x², x²+y²=2² с центром в начале координат O(0;0) и радиусом 2.

Перейдем к полярной системе координат:
якобиан переходу: I=r.
С учетом формул перехода подынтегральная функция в полярной системе координат примет вид корневой зависимости:

Пределы интегрирования в ПСК следующие:
0≤r≤2, 0≤φ≤2π.
Переходим от двойного интеграла в декартовых координатах к двойному в полярных координатах и находим его значение:

Интеграл равен 16π/3.

 

Пример 2.4 Найти двойной интеграл, используя полярные координаты:

D: {x²+y²=π²/9; x²+y²=π²/4}.
Решение: Выпишем область интегрирования ограниченную кривыми
Первая кривая x²+y²=π²/9 — круг с центром в начале координат O(0;0) и радиусом π/3;
второе уравнение описывает x²+y²=π²/4 — больший круг с центром в той же точке O(0;0) и радиусом π/2.
Область между кругами образует кольцо, по которому выполняем интегрирование.

Найдем подынтегральную функцию в полярной СК:

Круги в полярной системе координат можно задать радиусами и центрами:
, отсюда r= π/3;
, имеем r= π/2.
Пределы интегрирования в полярной системе координат следующие:
π/3≤r≤π/2, 0≤φ≤2π.
Выполняем вычисление двойного интеграла:

Переход к полярной СК значительно упрощает вычисление интегралов для круговых и кольцевых областей.

 

Пример 2.5 Найти двойной интеграл, используя полярные координаты:

D: {x²+y²— 2y=0; x²+y²— 4y=0}.
Решение: На основе предыдущих примеров делаем вывод, что область интегрирования, ограниченная x²+(y-1)²=1 — кругом с центром в точке O(0;1) и радиусом 1;
Вторая кривая x²+(y-2)²=2- круг с центром в точке O(0;2) и радиусом 2.
Графически они формируют следующую область интегрирования.

Переходим к полярной системе координат с помощью якобиана перехода I=r.
Дальше записываем кривые в полярной системе координат:


расставляем корректные пределы интегрирования:
2sin(φ)≤r≤4sin(φ), 0≤φ≤2π.
Вычисляем двойной интеграл в полярной СК:

Нахождение двойных интегралов не тяжелое занятие, если часто самостоятельно практиковать и иметь перед собой таблицу основных интегралов.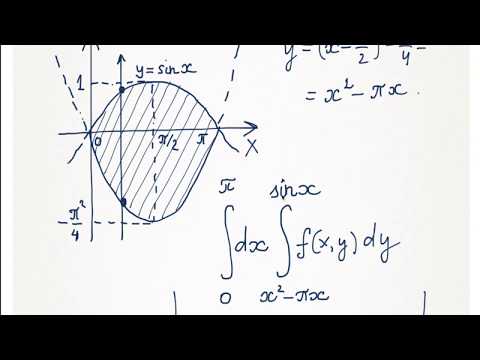
Все остальные манипуляции не тяжелые и их Вы повсюду в математике выполняете.
Дальше рассмотрим еще несколько примеров на вычисление двойных интегралов в полярных координатах.

Калькулятор двойного интеграла с шагами (прямоугольный и полярный)

1. Выберите тип координат, который вы будете использовать для вычисления двойного интеграла: Выберите параметр «Прямоугольный», чтобы вычислить двойной интеграл по прямоугольным областям, или выберите параметр «Полярный», чтобы вычислить двойные интегралы в полярных координатах.
2. Выберите дифференциал интегрирования: если вы выбрали прямоугольные координаты, у вас есть два выпадающих списка для этого. В случае, если вы выбрали полярные координаты, дифференциал интегрирования будет равен
   rdrdt , где переменная t относится к греческой букве тета.
3. Введите в калькулятор функцию, которая будет подынтегральной функцией двойного интеграла. Для этого следует иметь в виду таблицу допустимых функций, представленную в этом разделе.
4. Затем введите пределы интегрирования, которые могут быть числовыми или математическими выражениями, использующими переменные, присутствующие в дифференциале интегрирования. Обратите внимание, что для ввода числа пи необходимо написать пи и если вы хотите написать ∞ вы должны написать inf .
5. Выберите точность десятичных разрядов.
6. Наконец, нажмите кнопку «Рассчитать», чтобы получить результат. Решение будет развернуто автоматически, показывая этапы процесса интеграции.

Для просмотра примеров двойных интегралов нажмите кнопку «Примеры».

Допустимые функции и символы	Описание
квт()	Квадратный корень
лн()	Натуральный логарифм
лог()	Основание логарифма 10
^	Экспоненты
абс()	Абсолютное значение
sin(), cos(), tan(), csc(), sec(), cot()	Основные тригонометрические функции
asin(), acos(), atan(), acsc(), asec(), acot()	Обратные тригонометрические функции
sinh(), cosh(), tanh(), csch(), sech(), coth()	Гиперболические функции
asinh(), acosh(), atanh(), acsch(), asech(), acoth()	Обратные гиперболические функции
число пи	PI-номер (π = 3,14159. ..)
е	Число Непера (e= 2,71828…)
я	Для обозначения мнимой составляющей комплексного числа.
инф	∞

Калькулятор двойных интегралов с шагами и решателем

Онлайн-калькулятор двойных интегралов с бесплатными шагами поможет вам решить задачи двумерного интегрирования с функциями двух переменных. Вычисление двух последовательных интегралов позволяет вычислить площади функций с двумя переменными для интегрирования по заданным интервалам. Здесь вы можете научиться решать двойные интегралы и многое другое! 9n_{j = 1} f(y_{ij}, x_{ij})△A \).
В основном используется для определения области поверхности двухмерной фигуры, которую дарит «∫∫». Двойным интегрированием можно найти площадь прямоугольной области. Если вы хорошо разбираетесь в простой интеграции, то вам будет очень легко решать задачи двойной интеграции. Итак, начнем с некоторых основных правил двойной интеграции.

Правило двойного интегрирования:

Здесь мы обсудим некоторые важные формулы и правила, которые используются калькулятором двойного интеграла по области для выполнения двойного интегрирования. Для решения задач интеграции вы должны изучить различные методы, такие как интегрирование подстановками и интегрирование по частям или формулам. В двойных интегралах правило двойного интегрирования по частям упоминается ниже и также учитывается этим лучшим решателем двойного интегрирования при выполнении вычислений. 9b f (x, y) dx . dy $$

$$ ∫∫( f(x, y) ± g (x, y)) dA = ∫∫ g (x,y) ± dA ∫∫ f(x, y) dA $$

Если f(x, y) < g(x, y), то ∫∫g (x, y) dA > ∫∫ f(x, y) dA 

$$ k ∫∫ f (x, y) . dA = ∫∫ k. f (х, у). dA $$

$$ ∫∫ R ∪ S f (x, y) . dA = ∫∫ R f (x, y). dA + ∫∫ sf (x, y). dA $$

Площадь двойного интеграла:

Когда нам нужно найти двойное интегрирование переменной M, пусть M = f(x, y) определяется по области K в плане xy. Если мы найдем конечные точки для x и y как границы области и разделим определенную область на вертикальные полосы, то мы используем формулу: 9{r_2} _{r_1} f (r, θ) dθ, dr $$

Сначала мы должны проинтегрировать f(θ, r) по r в пределах \( r_1 и r_2 \), где θ является постоянным, и интегрируем полученное уравнение как θ от \( θ_1 до θ_2, \text {где } r_1 и r_2 \) являются постоянными. А для решения таких вопросов также можно воспользоваться онлайн-калькулятором двойного интеграла в полярных координатах. 2 + xy с предельными значениями (0, 1) для переменных x и y. 92 + 3 года) / 12 + константа $$

Помимо ручных вычислений, которые кажутся достаточно сложными, вы должны перепроверить и ускорить свои вычисления с помощью этого итерированного интегрального калькулятора с шагами.

Однако онлайн-калькулятор тройного интеграла поможет вам найти значения тройного интеграла заданной функции.

Как работает калькулятор двойных интегралов с шагами?

Онлайн-решатель двойных интегралов определяет двойной интеграл заданной функции с пределами x и y, выполнив следующие шаги:

Ввод:

• Сначала введите функцию для интегрирования и выберите интервалы из раскрывающегося списка.
• Если вы знаете пределы, выберите определенные значения и подставьте определенные значения для верхнего и нижнего пределов.
• С другой стороны, если вы не знаете предельных значений определенной функции, выберите неопределенное.
• Нажмите кнопку «Вычислить двойной интеграл».

Вывод:

• Калькулятор двойных интегралов отображает определенный и неопределенный двойной интеграл с шагами относительно заданной функции с исчерпывающими вычислениями.

Часто задаваемые вопросы:

Каково применение двойного интеграла?

• Используется для определения площади области, ограниченной кривой конкретной функции.
• В основном используется для нахождения подповерхностного объема.
• Двойные интегралы используются для вычисления среднего значения функции двух переменных.

Влияет ли порядок на двойную интеграцию?

Обычно порядок двойного интеграла не имеет значения. Если важно, то следует переписать повторный интеграл при изменении порядка интегрирования.

Можно ли разделить двойной интеграл?

Теорема Фубини гласит: «Мы можем разбить двойные интегралы на несколько повторных интегралов». Для получения дополнительной помощи вы можете позволить этому калькулятору теорем Фубини разделить интегралы и отобразить весь сценарий вычислений, связанных с процессом.

Как преобразовать полярный интеграл в декартов интеграл?

Преобразование полярных координат в другую систему осуществляется тремя способами, перечисленными ниже:

• Вам необходимо отобразить прямоугольник D в левой плоскости
• Кроме того, вам также необходимо сопоставить прямоугольник D с областью D на плоскости (x, y).
• Чтобы ускорить преобразование, вы можете позволить этому калькулятору двухполярных интегралов сделать это за вас.

Заключение:

Используйте этот онлайн-калькулятор двойных интегралов шаг за шагом, который предоставляет результирующие значения как для определенных, так и для неопределенных двойных интегралов в любом порядке с использованием системы алгебры. При символическом интегрировании решатель двойных интегралов использует интегральные и алгебраические правила для получения первообразной заданной функции перед применением основной теоремы исчисления для двойного интегрирования.