Как узнать решение по заявке на кредит
Сколько рассматривается заявка на кредит?
Обычно узнать решение по онлайн-заявке на кредит наличными можно в течение одного дня. В некоторых случаях банк рассматривает заявку на кредит дольше. Когда решение примут, банк пришлет уведомление.
Как узнать статус заявки на кредит?
Статус заявки на кредит появится через час после ее отправки в приложении Тинькофф и на сайте tinkoff.ru. Чтобы узнать решение банка на сайте tinkoff.ru, проверьте статус заявки, введя мобильный номер, который вы указали при ее оформлении.
Даже если вы еще не стали клиентом Тинькофф, скачайте наше мобильное приложение — в нем удобно оставить заявку на кредит, следить за ее рассмотрением, а потом согласовать предложенные банком условия.
Когда кредит одобрят, прямо в приложении можно будет назначить встречу с представителем банка для получения денег.
Также вы можете позвонить в банк по номеру 8 800 555‑77‑78 и спросить робота: «Что с моей заявкой на кредит наличными?»
Кто и как рассматривает заявку на кредит?
Сначала банк проверяет сведения, которые вы указали в заявке. При необходимости наш сотрудник позвонит вам или вашему работодателю, чтобы проверить актуальность этих данных.
Затем на основании этой информации банк устанавливает размер кредита, который готов вам предоставить. Мы свяжемся с вами, чтобы согласовать окончательные условия кредита после одобрения заявки.
Что произойдет после предварительного одобрения заявки?
Если вы сразу не выбрали время и место для доставки кредитного договора и дебетовой карты, сотрудник банка позвонит в течение 1–3 дней, чтобы назначить встречу.
Как назначить встречу с представителем или перенести ее
Зачем подтверждать доход через Госуслуги?
Это увеличит шансы на одобрение кредита, а также на то, что банк выдаст всю запрашиваемую сумму.
Процедура подтверждения работает так: на этапе рассмотрения заявки на кредит вам придет СМС от портала госуслуг с просьбой разрешить банку доступ к данным вашего счета в Пенсионном фонде РФ. Если вы согласитесь, мы получим сведения о вашем доходе в виде выписки из Пенсионного фонда, доступ к другой информации останется закрыт.
Это бесплатная услуга, и ваше ответное СМС на номер портала госуслуг тоже будет бесплатным. Но, чтобы всё сработало, у вас должна быть подтвержденная учетная запись на портале госуслуг.
Подтвердить учетную запись на Госуслугах можно прямо в личном кабинете на сайте tinkoff.
ru или в мобильном приложении Тинькофф:
При желании вы можете просто проигнорировать сообщение от портала госуслуг, тогда мы продолжим рассмотрение вашей заявки на кредит в стандартном порядке.
Подтверждать доход через Госуслуги не обязательно, но это увеличивает шансы на одобрение кредитаКак я узнаю, какую ставку и сумму кредита мне в итоге одобрят?
Свою ставку и максимальную сумму кредита, которую вам одобрит банк, вы сможете узнать после того, как подадите заявку, — вам позвонит менеджер Тинькофф, чтобы согласовать параметры вашего кредита.Если у вас уже есть кредит в нашем банке, вы можете посмотреть информацию о нем в приложении Тинькофф и в личном кабинете на сайте tinkoff.ru. Узнать информацию по действующему кредиту
Если переживаете, что в будущем могут возникнуть финансовые трудности, которые помешают спокойно платить по кредиту, подключите дополнительную услугу «Снижение платежа».
Она позволяет ненадолго снизить свою долговую нагрузку, чтобы было время разобраться с финансами. Как подключить услугу «Снижение платежа»
Есть проблема, а где решение?
Как оплачивать газ, свет, теплоснабжение и холодную воду, если нет счетчика? А кто-то из прописанных по тем или иным причинам долгое время не проживает по данному адресу. Таких ситуаций достаточно, а четко прописанных правил, как действовать, – нет.
Четыре – по факту, два – в уме
В редакцию обратился А. Абдумуминов из г. Ташкента: «В квартире прописаны 6 человек, но проживают 4. Дочь и сын учатся за рубежом. Как я должен оплачивать услуги газоснабжения, при условии, что у меня нет газового счетчика. Я слышал, что по количеству фактически проживающих. Однако сотрудник райгаза настаивает на том, чтобы я платил по числу прописанных. В Правилах пользования природным газом ответа на этот вопрос не нашел».
Мы адресовали этот вопрос в территориальный филиал газоснабжения АО «Узтрансгаз» по городу Ташкенту.
Получили ответ и. о. начальника филиала А. Саидвалиева, в котором он ссылается на старые Правила пользования газом в быту на территории Республики Узбекистан, утвержденные Министерством коммунального обслуживания в 1997 году (рег. МЮ N 370 от 14.10.1997 г., далее – Правила 1997 г.). В них сказано, что при отсутствии прибора учета газа начисление за природный газ производится по тарифу ежемесячно. Периодичность, сроки оплаты, ответственность сторон определяются договором. При выезде с места постоянного жительства на срок более полугода, а также при продаже или сносе жилых домов, принадлежащих гражданам на праве частной собственности, собственники жилых домов и квартир должны уведомить об этом организацию газового хозяйства. Вот, пожалуй, и весь ответ по существу вопроса. При этом возникает множество других.
Прежде всего почему руководитель филиала ссылается на старые Правила 1997 года? По словам сотрудников городской газоснабжающей организации, в новых Правилах пользования природным газом (прил.
N 2 к ПКМ N 22 от 12.01.2018 г., далее – Правила 2018 г.) решение этого вопроса не рассматривается. Они составлены с учетом перспективы создания автоматической системы контроля и учета газа (АСКУГ). Но предыдущие Правила 1997 года еще не отменены. В соответствии с Законом «О нормативно-правовых актах» действия представителя газоснабжающей организации не вызывают нареканий.
Правилами 1997 года установлено, что при отсутствии приборов учета расхода газа (газовых счетчиков) использованный газ оплачивается по нормам месячного расхода природного газа на 1 человека, на 1 м2 отапливаемой площади (п. 24).
Но каков порядок представления информации об изменениях числа проживающих? Почему нужно уведомлять, только если жилец выезжает более чем на 6 месяцев? Полгода – это большой срок, и за него набегает солидная сумма. Почему столько лет вопрос остается открытым? Почему на ситуацию не обратили внимания при разработке Правил 2018 года? Если нормотворцы считают решение этого вопроса слишком мелким для такого глобального документа, как Правила, то можно было бы разработать ведомственный акт, регулирующий подобные ситуации.
Сделать это не поздно и сейчас. Вопрос будет актуальным как минимум до 2021 года. Предполагается, что к тому времени системой будут охвачены все потребители без исключения. Поэтому газовики должны как можно скорее устранить пробелы в законодательстве.
А как у других?
При решении вопроса газовикам необязательно изобретать велосипед. Полезным может оказаться изучение опыта «коллег по цеху».
В пункте 103 Правил пользования электрической энергией (прил. N 1 к ПКМ N 22) определено: «Бытовой потребитель, не имеющий прибора учета электрической энергии и (или) временно не проживающий на данной жилой площади по каким-либо причинам, обязан письменно известить об этом Бюро и предприятие территориальных электрических сетей для исключения ошибочных начислений за электрическую энергию». Пункт 119 Правил устанавливает, что в случае отсутствия счетчика оплата производится по среднесуточному расходу электрической энергии, и такой расчет не должен превышать одного месяца, в течение которого счетчик должен быть восстановлен.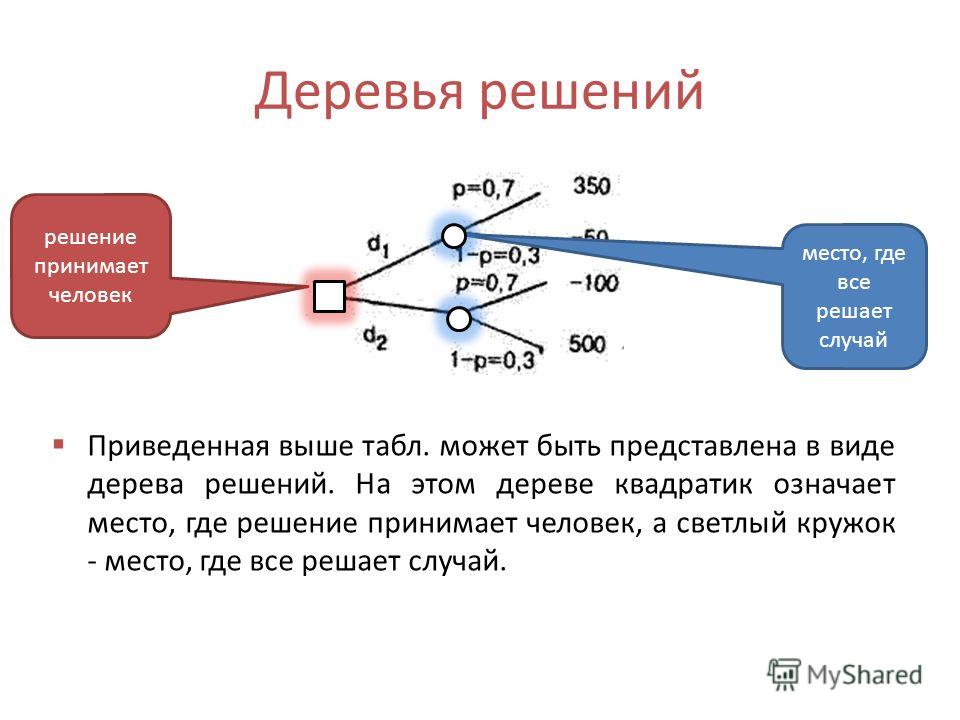
В Правилах оказания услуг теплоснабжения в многоквартирных домах и Правилах оказания услуг водоснабжения и водоотведения потребителям (прил. NN 1, 2 к ПКМ N 194 от 15.07.2014 г.) также есть решение вопроса. У тепловиков это пункт 110, а у водоснабженцев – пункт 114. Согласно этим нормам при проживании временных жителей (нанимателей) оплата производится полностью за количество фактически проживающих лиц. Потребитель обязан письменно информировать поставщика об увеличении или уменьшении числа граждан, проживающих (в том числе временно) в занимаемом им жилом помещении, не позднее 5 рабочих дней со дня произошедших изменений, – если жилое помещение не оборудовано прибором учета. При этом составляется трехсторонний акт между представителями поставщика, органа самоуправления граждан и владельцем.
Что дальше?
Несмотря на то что у электриков, тепловиков и водоснабженцев, в сравнении с газовиками, Правила более совершенны, они тоже требуют уточнения.
Отсутствие четко прописанных норм нередко приводит к недопониманию и конфликтным ситуациям. Хотя есть немало фактов, когда стороны при обоюдном согласии находят оптимальное решение вопроса.
По Закону «О защите прав потребителей» потребитель оплачивает исключительно те услуги, которые получил. Чтобы подтвердить временное непроживание, можно было бы представлять в райгаз или Бюро принудительного исполнения справку из махаллинского комитета о количестве фактически проживающих по данному адресу. Справка выдается на основе акта, подтверждающего, что прописанный по данному адресу гражданин здесь временно не проживает. Акт составляют домком и несколько соседей. Кстати, многие поставщики коммунальных услуг используют такой механизм за неимением регламента для непроживающих. Эти данные могут быть введены в биллинговую систему и приняты во внимание при взаиморасчетах. В качестве доказательства временного непроживания в спорных вопросах могут служить также копия документа о регистрации граждан, квитанции, подтверждающие оплату газа по месту их фактического проживания, проездные и прочие документы.
В спорных случаях может быть инициировано судебное разбирательство. В качестве доказательства своей правоты потребитель вправе представить любые документы, позволяющие достоверно установить фактическое число проживающих.
Еще один ракурс проблемы с непроживающими связан с установленной Указом Президента «О дополнительных мерах по повышению эффективности деятельности органов прокуратуры в обеспечении исполнения принимаемых нормативно-правовых актов» (N УП-5343 от 15.02.2018 г.) солидарной ответственностью жильцов. Как быть, например, когда не проживающий, но прописанный в данной квартире живет в другом месте (городе) и имеет там временную прописку? Если нет механизма, устанавливающего факт непроживания, могут ли его привлечь к солидарной ответственности по уплате задолженности в двух местах: по месту постоянной и временной прописки?
Думается, эти важные для потребителей вопросы требуют решения.
Олег Гаевой.
Системы линейных уравнений: построение графиков
ОпределенияОсобые случаиЗаменаИсключение/добавлениеИсключение по ГауссуБольше примеров
Purplemath
Когда вы решаете системы уравнений (линейные или другие), вы, с точки зрения графических линий, связанных с уравнениями, находите любые точки пересечения из тех строк.
Если система уравнений состоит только из пары линейных уравнений с двумя переменными, то уравнение этой системы можно изобразить графически; график будет содержать две прямые линии, а решением системы будет точка (точки) пересечения этих линий. Поскольку две прямые линии на плоскости могут быть построены только тремя способами, то для данной системы уравнений существует только три соответствующих формы решения.
Содержание продолжается ниже
MathHelp.com
Решение систем с помощью графиков
Две прямые линии (1) имеют разные наклоны и точки пересечения, поэтому они пересекаются ровно в одной точке, (2) параллельны с разными точками пересечения, поэтому они никогда не пересекаются в любых точках, или (3) они имеют одинаковый наклон и точки пересечения, так что они на самом деле являются одной и той же линией, поэтому они «пересекаются» везде (где «везде» означает «везде, где идет одна линия, идет и другая линия). ; у них есть все свои точки — бесконечно много точек — общих»).
Эти три случая для пар прямых показаны ниже:
На первом графике выше, обозначенном как «Случай 1» в левой колонке, показаны две отдельные непараллельные линии, которые пересекаются ровно в одной точке. Соответствующая система уравнений называется «независимой» системой, а решением является одна ( x , y ) точка.
На втором графике выше, обозначенном как «Случай 2» в средней колонке, показаны две отдельные параллельные линии. Поскольку параллельные прямые никогда не пересекаются, то и пересечения этих прямых быть не может; то есть для системы двух линейных уравнений, которая изображается в виде двух параллельных линий, не может быть решения. Это называется «несогласованной» системой уравнений.
На третьем графике выше, обозначенном как «Случай 3» в правой колонке, показана только одна линия. На самом деле, это одна и та же линия, проведенная дважды. Эти «две» линии, на самом деле являющиеся одной и той же линией, «пересекаются» (в техническом смысле) в каждой точке своей длины.
Это означает, что каждая точка на прямой(ых) является решением системы. Это называется «зависимой» системой, а «решением» является вся линия.
Это показывает, что система уравнений может иметь одно решение (конкретное x , y -точка), либо вообще нет решения, либо бесконечное решение (являющееся всеми решениями уравнения). У вас никогда не будет системы с двумя линейными уравнениями и двумя переменными с двумя или более решениями; он всегда будет один, ни один или бесконечно много.
Если это зависимая система, то почему «бесконечно» или «все точки» не является правильным ответом?
В то время как решение зависимой системы линейных уравнений представляет собой бесконечный набор точек, «бесконечность» не является числом, «бесконечность» недостаточно ясна, а точек off линия(и) системы не являются решениями. Только те точки, которые действительно лежат на прямой, являются решениями системы. Таким образом, ваш ответ для типа системы будет «зависимым», но решением на самом деле будет уравнение линии, поскольку это уравнение неявно перечисляет все точки, которые решают систему.
Например, если два уравнения в зависимой системе сводятся к y = − x + 3, то вы должны представить решение как линейное уравнение, или вы можете использовать парное обозначение координат; а именно, ( x , − x + 3).
Решение с помощью графика
Вероятно, первым методом решения систем уравнений, который вы увидите, будет «решение с помощью графика». Предупреждение: вы должны относиться к этим проблемам с недоверием. Единственный способ найти решение на графике: , ЕСЛИ , вы рисуете очень аккуратную систему координат, , ЕСЛИ , вы рисуете очень аккуратные линии, , ЕСЛИ , решение оказывается точкой с хорошими аккуратными целочисленными координатами, и IF линии не близки к параллельным.
Например, если линии пересекаются под небольшим углом, практически невозможно сказать, где они пересекаются.
И если точка пересечения не является аккуратной парой целых чисел, все ставки сняты.
Я имею в виду, можете ли вы сказать, просто взглянув на…
…что показанный выше перекресток имеет координаты (-4,3, -0,95)? Нет? Тогда вы понимаете мою точку зрения.
С положительной стороны, поскольку они будут вынуждены давать вам красивые и аккуратные решения для «решения с помощью графика», вы сможете получить правильные ответы , если вы рисуете очень аккуратно . Например:
2 x − 3 y = −2
4 x + y = 24
Я знаю, что мне нужен аккуратный график, поэтому я возьму линейку и начну. Сначала я решу каждое уравнение относительно « y =», чтобы легко построить график:
2 x − 3 y = −2
2 x + 2 = 3 y
( 2/3) х + (2/3) = у
4 х + y = 24
y = −4 x + 24
Вторую линию будет легко построить, используя только наклон и точку пересечения, но мне понадобится T-диаграмма для первой линии.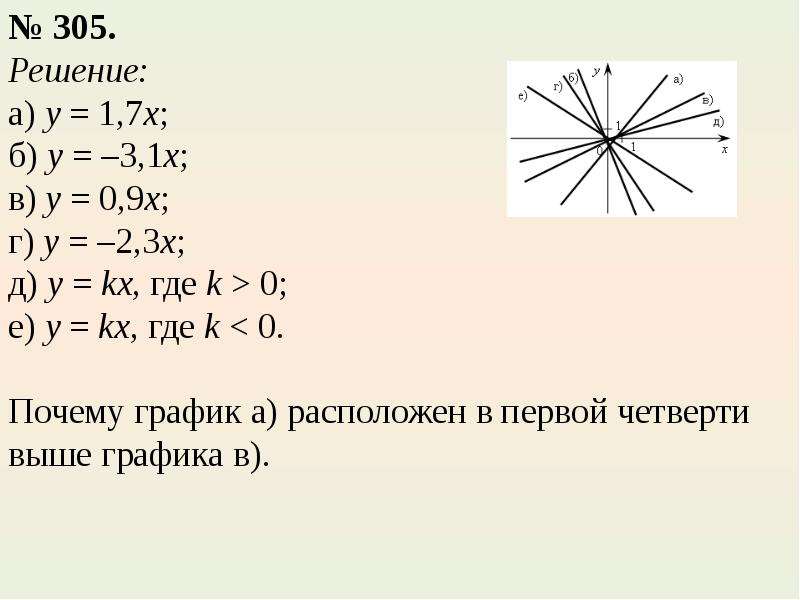
Иногда вы заметите пересечение прямо на Т-диаграмме. Вы видите точку, которая находится в обоих уравнениях выше? Проверьте заштрихованную серым строку выше.
Теперь, когда у меня есть несколько точек, я аккуратно возьму линейку и график и поищу пересечение:
Даже если бы я не заметил точку пересечения на Т-диаграмме, картина.
решение: ( x , y ) = (5, 4)
Если вы застряли в решении с помощью графика, пожалуйста, ради бога, нарисуйте линии так, чтобы они действительно пересекались в точке решения . Не будь неряшливым!
Вы можете использовать приведенный ниже виджет Mathway, чтобы попрактиковаться в решении с помощью графика (или пропустить виджет и перейти к следующей странице). Попробуйте введенное упражнение (щелкнув стрелку и выбрав «Решить с помощью графика» во всплывающем окне) или введите свое собственное упражнение. Затем сравните свой ответ с ответом Мэтуэя. (Или пропустите виджет и продолжите урок.)
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите здесь, чтобы перейти непосредственно на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)
URL: https://www.purplemath.com/modules/ systlin2.htm
Страница 1Страница 3Страница 4Страница 5Страница 6Страница 7
Наборы решений
Цели
- Понять взаимосвязь между набором решений Ax=0 и набором решений Ax=b.
- Поймите разницу между набором решений и диапазоном столбцов.
- Рецепты: параметрическая векторная форма, запишите множество решений однородной системы в виде промежутка.
- Картинки: набор решений однородной системы, набор решений неоднородной системы, отношения между ними.
- Словарный запас: однородный / неоднородный , тривиальное решение .
В этом разделе мы изучим геометрию множества решений любого матричного уравнения Ax=b.
Уравнение Ax=b легче решить, когда b=0, поэтому начнем с этого случая.
Определение
Система линейных уравнений вида Ах=0 называется однородной .
Система линейных уравнений вида Ax=b при bB=0 называется неоднородной .
Однородная система — это просто система линейных уравнений, в которой все константы справа от знака равенства равны нулю.
Однородная система всегда имеет решение x=0. Это называется тривиальным решением . Любое ненулевое решение называется нетривиальным .
Пример (нет нетривиальных решений)
Когда однородное уравнение Ax=0 действительно имеет нетривиальные решения, оказывается, что множество решений удобно выразить в виде интервала.
Форма параметрического вектора (гомогенный случай)
Рассмотрим следующую матрицу в сокращенной ступенчатой форме строк:
А=С10-8-701430000D.
Матричное уравнение Ax=0 соответствует системе уравнений
Tx1-8×3-7×4=0x2+4×3+3×4=0.
Мы можем записать параметрическую форму следующим образом:
GMKMIx1=8×3+7x4x2=-4×3-3x4x3=x3x4=x4.
Мы написали избыточные уравнения x3=x3 и x4=x4, чтобы превратить приведенную выше систему в векторное уравнение :
.x=EPNx1x2x3x4FQO=x3EPN8-410FQO+x4EPN7-301FQO.
Это векторное уравнение называется параметрический вектор формы набора решений. Поскольку x3 и x4 могут быть любыми, это говорит о том, что набор решений представляет собой набор всех линейных комбинаций EPN8-410FQO и EPN7-301FQO. Другими словами, набор решений равен
.SpanGMKMIEPN8-410FQO,EPN7-301FQOHMLMJ.
Вот общая процедура.
Рецепт: Параметрическая векторная форма (однородный случай)
Пусть A — матрица размера m × n. Предположим, что свободными переменными в однородном уравнении Ax=0 являются, например, x3,x6 и x8.
- Найдите сокращенную ступенчатую форму строки A.
- Напишите параметрическую форму набора решений, включая избыточные уравнения x3=x3,x6=x6,x8=x8.
Поставьте уравнения для всех xi по порядку. - Составьте одно векторное уравнение из этих уравнений, превратив коэффициенты x3,x6 и x8 в векторы v3,v6 и v8 соответственно.
Поставьте уравнения для всех xi по порядку.Решения для Ax=0 тогда будут выражены в форме
х=x3v3+x6v6+x8v8
для некоторых векторов v3,v6,v8 в Rn и любых скаляров x3,x6,x8. Это называется параметрический вектор формы решения.
В этом случае набор решений можно записать как Span{v3,v6,v8}.
Особо подчеркнем следующий факт.
Множество решений однородного уравнения Ax=0 является пролетом.
Пример (набор решений представляет собой строку)
Поскольку в приведенном выше примере было две переменные , набор решений является подмножеством R2. Так как одна из переменных была свободна, набор решений равен строка :
Чтобы на самом деле найти нетривиальное решение Ax=0 в приведенном выше примере, достаточно подставить любое ненулевое значение вместо свободной переменной x2.
Пример (множество решений представляет собой плоскость)
Поскольку в приведенном выше примере было трех переменных , набор решений является подмножеством R3. С два переменных были свободны, множество решений представляет собой плоскость .
Здесь возникает естественный вопрос: можно ли написать решение однородного матричного уравнения, используя меньше векторов, чем указано в приведенном выше рецепте? Мы увидим в примере в Разделе 2.5, что ответ нет : векторы из рецепта всегда линейно независимы, а это означает, что нет способа написать решение с меньшим количеством векторов.
Другой естественный вопрос: являются ли множества решений неоднородных уравнений также остовными? Как мы вскоре увидим, они никогда не являются интервалами, но они тесно связаны с интервалами.
Существует естественная связь между количеством свободных переменных и «размером» набора решений, как показано ниже.
Размер набора растворов
Приведенные выше примеры показывают нам следующую закономерность: когда в согласованном матричном уравнении есть одна свободная переменная, множество решений представляет собой прямую, а когда есть две свободные переменные, множество решений представляет собой плоскость и т. д. Количество свободных переменных называется измерением множества решений.
Мы разработаем строгое определение размерности в разделе 2.7, но пока размерность будет просто означать количество свободных переменных. Сравните с этим важным примечанием в Разделе 2.5.
Интуитивно понятно, что размерность набора решений — это количество параметров, необходимых для описания точки в наборе решений. Для линии нужен только один параметр, а для плоскости нужны два параметра. Это похоже на то, как расположение здания на Пичтри-стрит, похожее на линию, определяется одним числом, а угол улицы на Манхэттене, похожее на плоскость, определяется двумя числами.
Напомним, что матричное уравнение Ax=b называется неоднородным , когда bB=0.
Пример (набор решений представляет собой строку)
В приведенном выше примере набором решений были все векторы вида
х=Rx1x2S=x2R31S+R-30S
, где x2 — любой скаляр. Вектор p=A−30B также является решением Ax=b: возьмем x2=0. Мы называем p частным раствором .
В наборе решений x2 может быть любым, поэтому набор решений получается следующим образом: мы берем все скалярные числа, кратные A31B, и затем добавляем конкретное решение p=A−30B к каждому из этих скалярных множителей. Геометрически это достигается тем, что сначала рисуется отрезок A31B, который представляет собой линию, проходящую через начало координат (и, что не случайно, решение Ax=0), и мы переведите или протолкните эту строку вдоль p=A−30B. Переведенная строка содержит p и параллельна Span{A31B}: это перевод строки .
Ах=0Ах=бпПример (множество решений представляет собой плоскость)
В приведенном выше примере набором решений были все векторы вида
х=Cx1x2x3D=x2C110D+x3C−201D+C100D.
, где x2 и x3 — любые скаляры. В этом случае частным решением является p=C100D.
В предыдущем примере и в предыдущем примере параметрическая векторная форма набора решений Ax=b была точно такой же, как параметрическая векторная форма набора решений Ax=0 (из этого примера и этого примера соответственно) , плюс конкретное решение.
Ключевое замечание
Если Ax=b непротиворечиво, множество решений получается путем взятия одного частного решения p задачи Ax=b и сложения всех решений задачи Ax=0.
В частности, если Ax=b непротиворечиво, набор решений представляет собой преобразование диапазона .
Параметрическая векторная форма решений Ax=b — это просто параметрическая векторная форма решений Ax=0 плюс конкретное решение p.
Нетрудно понять, почему ключевое наблюдение верно. Если p — частное решение, то Ap=b, а если x — решение однородного уравнения Ax=0, то
А(х+р)=Ах+Ар=0+b=b,
, так что x+p является еще одним решением Ax=b.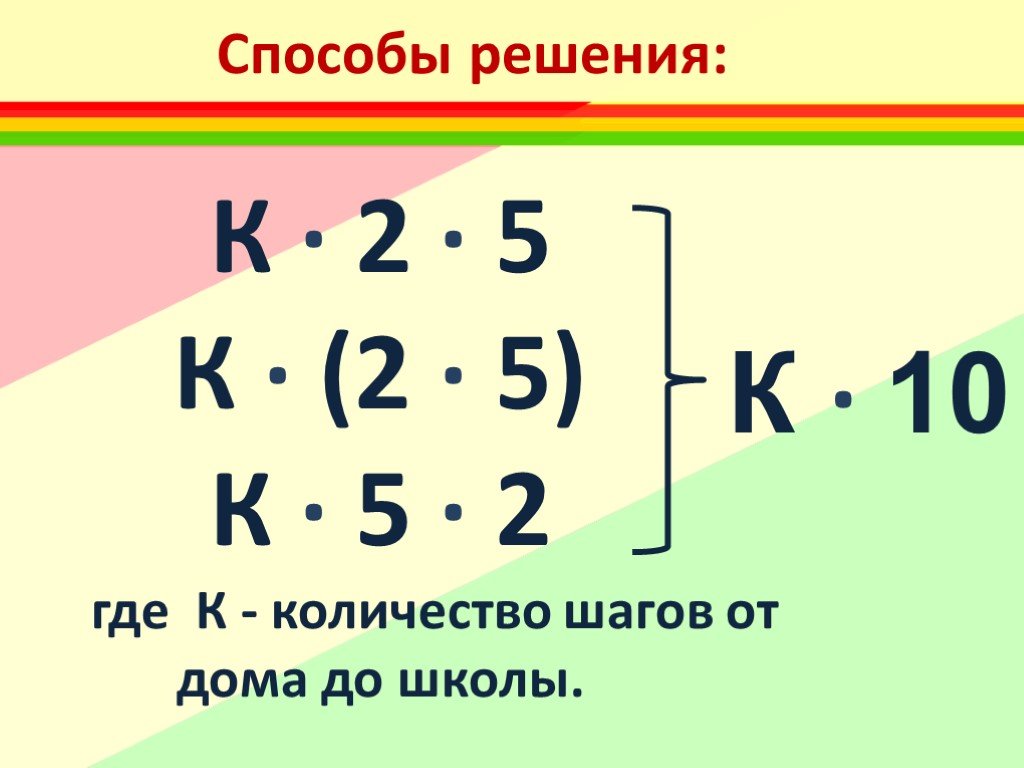
С другой стороны, если мы начнем с любого решения x для Ax=b, то x−p будет решением для Ax=0, поскольку
А(х-р)=Ах-Ар=b-b=0.
Пример (множество решений — точка)
См. интерактивные рисунки в следующем подразделе для визуализации ключевого наблюдения.
Размер набора растворов
Как и в этом важном примечании, когда в согласованном матричном уравнении есть одна свободная переменная, множество решений представляет собой линию — эта линия не проходит через начало координат, когда система неоднородна — когда есть две свободные переменные, множество решений является плоскостью (опять же не через начало координат, когда система неоднородна) и т. д.
Еще раз сравните с этим важным примечанием в Разделе 2.5.
Каждой матрице A размера m×n мы теперь связали два совершенно разных геометрических объекта, оба описываемых с помощью интервалов.
Не путайте эти две геометрические конструкции! В первом случае вопрос заключается в том, какие х работают для данного b, а во втором вопрос заключается в том, какие b работают для некоторого х.