Примеры решений задач по эконометрике. Эконометрика
Время на чтение: 83 минут
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Санкт- Петербургский Государственный Университет экономики и финансов
Заочный факультет, кафедра статистики и эконометрики
Контрольная работа
По эконометрике
Студента группа №351
Хмель Валентина Александровича
Вариант 3
1. Задача 1
2. Задача 2
3. Задача 3
4. Задача 4
5. Задача 5
Литература
Цена квартиры, тыс.долл. | Жилая площадь, кв. | ||
м1.Постройте поле корреляции, характеризующее зависимость цены квартиры от жилой площади.
2.Определите параметры уравнения парной линейной регрессии. Дайте интерпретацию коэффициента регрессии и знака при свободном члене уравнения.
3.Рассчитайте линейный коэффициент корреляции и поясните его смысл. Определите коэффициент детерминации и дайте его интерпретацию.
5.Рассчитайте стандартную ошибку регрессии.
7.С вероятностью 0,95 постройте доверительный интервал ожидаемого значения цены квартиры в предположении, что жилая площадь квартиры увеличится на 5% от своего среднего значения. Сделайте выводы.
Определим уравнение парной линейной регрессии методом наименьших квадратов.
Для линейной модели
Параметр a 1 =0,702 показывает среднее изменение результата y с изменением фактора x на единицу. Параметр a 0 =11,39=y, когда x=0. Так как а 0 >0, то относительное изменение результата происходит медленнее, чем изменение фактора, то есть вариация результата меньше вариации фактора.
3.Рассчитаем линейный коэффициент корреляции
Коэффициент корреляции величин x и y (r xy) — свидетельствует о наличии или отсутствии линейной связи между переменными:
Если: r xy = -1 , то наблюдается строгая отрицательная связь; r xy = 1, то наблюдается строгая положительная связь; r xy = 0, то линейная связь отсутствует.
Находим необходимые значения:
Определяем коэффициент детерминации
Коэффициент детерминации — квадрат коэффициента корреляции:
Чем выше показатель детерминации, тем лучше модель описывает исходные данные.
Следовательно, качество описания исходных данных в данной модели 69,8%
4.Находим среднюю ошибку аппроксимации
Средняя ошибка аппроксимации — среднее относительное отклонение расчетных значений от фактических:
Средняя ошибка аппроксимации:
5.Рассчитываем стандартную ошибку регрессии
Стандартная ошибка регрессии:
где n — число единиц совокупности; m — число параметров при переменных. Для линейной регрессии m = 1.
6. С вероятностью 0,95 оцениваем статистическую значимость уравнения регрессию в целом, а также его параметров
Для оценки статистической значимости коэффициентов линейной регрессии и линейного коэффициента парной корреляции r xy применяется t-критерий Стьюдента и рассчитываются доверительные интервалы каждого из показателей.
Согласно t-критерию выдвигается гипотеза Н 0 о случайной природе показателей, т. е. о незначимом их отличии от нуля. Далее рассчитываются фактические значения критерия t факт для оцениваемых коэффициентов регрессии и коэффициента корреляции r xy путем сопоставления их значений с величиной стандартной ошибки.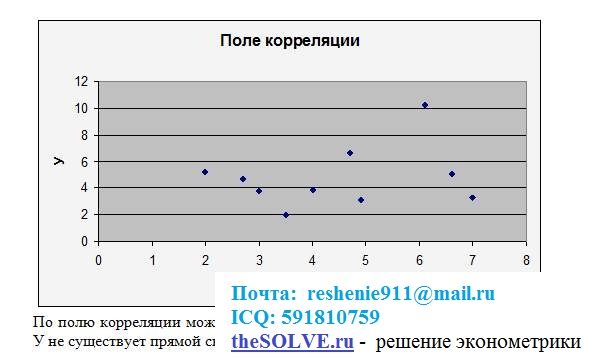
Составляем таблицу промежуточных вычислений:
Остаточная сумма квадратов равна: , а ее среднее квадратическое отклонение:
Находим стандартную ошибку коэффициента регрессии:
Находим стандартную ошибку параметра a 0:
Рассчитываем фактическое значение критерия Стьюдента для коэффициента регрессии:
Находим табличные значения t-критерия Стьюдента при уровне значимости?=0,05
Оценка значимости всего уравнения регрессии в целом осуществляется с помощью F-критерия Фишера.
F-критерий Фишера заключается в проверке гипотезы Н о о статистической незначимости уравнения регрессии. Для этого выполняется сравнение фактического F факт и критического (табличного) F табл значений F-критерия Фишера.
Находим фактическое значение F-критерия:
Находим табличное значение F-критерия, учитывая k 1 = m=1, k 2 = n — m — 1=8:
Так как F табл
7. С вероятностью 0,95 строим доверительный интервал ожидаемого значения цены квартиры в предположении, что жилая площадь квартиры увеличится на 5% от своего среднего значения
Строим таблицу промежуточных вычислений:
1.
Постройте линейное уравнение множественной регрессии
2.Найдите коэффициент множественной детерминации в том числе скорректированный. Сделайте выводы.
1.Линейное уравнение множественной регрессии
В данной задаче уравнение множественной регрессии имеет вид:
Множественная регрессия применяется в ситуациях, когда из множества факторов, влияющих на результативный признак, нельзя выделить один доминирующий фактор и необходимо учитывать влияние нескольких факторов.
Получаем систему уравнений:
Находим определитель матрицы коэффициентов:
Заменяем последовательно столбцы матрицы коэффициентов столбцом свободных членов и находим определители получившихся матриц:
Коэффициент множественной детерминации находится по формуле:
Скорректированный коэффициент множественной детерминации содержит поправку на число степеней свободы и рассчитывается следующим образом:
5.Определите частные коэффициенты корреляции и сделайте выводы.
Частные коэффициенты корреляции определяются по ф-ле:
6.
Определите частные и средние коэффициенты эластичности и сделайте выводы.
Тогда доверительный интервал равен
Решение задачи по эконометрике. Контрольные работы по эконометрике на заказ.
Решение задач по эконометрике – сколько времени потратить?
Немного цифр об эклнометрике:
- порядка 113 формул
- количество часов вычетки 50-150
- тысячи вариантов условий задач
- программы для расчета показателей на ПК – 5
- использование в реальной жизни – 0,2 часа
- среднее количесвто страницы методичек – 50
Давайте посчитаем.
Чтобы научиться решать задачи, потратим 50 часов личного времени.
Чтобы освоить программные комплексы которые устарели 10 лет назад – 20 часов.
Чтобы сделать контрольную – 10 часов.
Чтобы сдать экзамен – 45 минут.
Сумма этих цифр – время, которые вы бы могли потратить на занятие любимым делом, работу, семью. Хотя многие решают его тратить на предмет, знание которого никогда в жизни им не пригодится.
Что в этом случае делать?
Есть 2% людей которые профессионально занимаются решением задач и выполнением контрольных по эконометрике. Для них это – работа, хобби, хлеб.
Мы собрали этих людей у себя.
Оформите заказ на решение задач и через день они будут готовы к сдаче.
Как заказать контрольную работу по эконометрике?
Отличие в заказе контрольной работы только одно. Выполняться она будет на несколько дней дольше. Но это не время, которое придется тратить вам! Вы все так же отдыхаете!
А не проще ли посмотреть готовые решения задач?
Конечно, уже решенные примеры мы собрали в соответствующем разделе – Теория по эконометрике. Можете провести в нем все свободное время и решить все заданный задачи самостоятельно.
Кластерный анализ — это совокупность методов, позволяющих классифицировать многомерные наблюдения, каждое из которых описывается набором признаков (параметров) Х1, Х2, …, Хk. Целью кластерного анализа является образование групп схожих между собой объектов, которые принято называть кластерами (другие названия — класс, таксон, сгущение).
Методы кластерного анализа …
Для оценки параметров идентифицируемой системы может использоваться косвенный метод наименьших квадратов. Пусть строится система взаимозависимых уравнений регрессии: Эта система является структурной формой, а параметры a10, b12, a11, a20, b21 и a22 — структурными коэффициентами. Подставим правую часть второго уравнения в первое уравнение вместо ; после преобразований получим: …
Система одновременных уравнений может быть преобразована к приведенной форме, в каждом уравнении которой результативная переменная выражена только через факторные переменные. Первоначальная система в этом случае называется структурной формой. Для существования однозначного соответствия между параметрами структурной и приведенной форм необходимо, чтобы каждое уравнение системы …
Экономические показатели, часто оказываются взаимозависимыми.
Точечный прогноз результата Y представляет собой рассчитанное по уравнению регрессии значение Y в предположении того, что факторы X1, X2, …, Xp примут соответственно значения x01, x02, …, x0p: . Стандартная ошибка прогноза . Интервальный прогноз значения Y: , где tтаб — табличное значение t-критерия Стьюдента при и . Предполагается, что с вероятностью фактическое значение Y …
Для экономического анализа уравнения регрессии используют: 1. Средний коэффициент эластичности . Он показывает, на сколько процентов изменяется в среднем Y при увеличении только фактора Xj на один процент.
Автокорреляции остатков наблюдается тогда, когда значения предыдущих остатков завышают (положительная) или занижают (отрицательная) значения последующих. Положительная автокорреляция на графике остатков проявляется в чередовании зон положительных и отрицательных остатков: Отрицательная автокорреляция на графике выражается в том, что остатки «слишком часто» меняют знак: …
Гетероскедастичность остатков проявляется в том, что их дисперсия (разброс) зависит от значений факторов: и: Гетероскедастичность приводит к тому, что может быть ошибочно принято решение о статистической значимости коэффициентов регрессии, тогда как на самом деле это не так. Выполнение предпосылки 3 может проверяться методом Глейзера, для чего рассчитывается коэффициент .
..
Проверка предпосылки 1 может проводиться путем визуального анализа графиков остатков от значений факторов либо от предсказанных уравнением регрессии значений результата Y. Остатки считают случайными, если на графике они расположены в виде горизонтальной полосы: Выполнение предпосылки 5 может проверяться с помощью R/S‑критерия , где emax, emin — соответственно наибольший и …
Коэффициенты уравнения регрессии b0, b1, b2, …, bp являются случайными величинами. Если выполняются предпосылки 1 — 4 МНК, то они обладают следующими свойствами: 1. Несмещенности. Математическое ожидание коэффициента равно соответствующему истинному параметру регрессии: . 2. Эффективности. Они характеризуются наименьшей дисперсией: . 3. Состоятельности. При увеличении числа …
Для получения корректной модели следует проверить выполнение предпосылок МНК: 1.
Остатки регрессии (i=1, 2,…, n) являются случайными. 2. Средняя величина остатков равна нулю. Данная предпосылка всегда выполняется для линейных моделей со свободным коэффициентом. 3. Дисперсия остатков одинакова и не зависит от значений факторов. 4. Остатки независимы (отсутствие …
Для проверки значимости уравнения в целом используется F–статистика . Уравнение значимо, если , где Fтаб — табличное значение F‑критерия Фишера при принятом , и . В качестве меры точности используются стандартная ошибка регрессии и средняя относительная ошибка аппроксимации . Продолжение примера 3. В EXCEL также были получены F–статистика F=17,08 и стандартная ошибка …
Компьютерные программы рассчитывают для каждого из коэффициентов уравнения регрессии стандартную ошибку и t-статистику . Коэффициент bj признается статистически значимым, если , где tтаб — табличное значение t-критерия Стьюдента в соответствии с принятым и .
Обычно рассчитывается и наблюдаемый уровень значимости («P-Значение») — вероятность того, что bj сформировался …
Основным показателем качества модели множественной регрессии является множественный коэффициент детерминации . Он показывает, какая доля изменений результата Y учтена в модели и обусловлена влиянием включенных факторов. Чем ближе R2 к единице, тем выше качество модели. Заметим, что R2 всегда увеличивается при добавлении в модель новых факторов, даже не оказывающих …
Ситуация, когда два фактора связаны между собой тесной линейной связью (), называется коллинеарностью. Коллинеарные факторы математически дублируют друг друга, поэтому один из них целесообразно исключить из рассмотрения, исходя из желаемого вида модели. Если ни одному из факторов нельзя отдать предпочтение, то в модели оставляют тот из них, который имеет больший по модулю .
..
Перед построением модели вычисляются парные коэффициенты корреляции между всеми исследуемыми переменными, анализ которых позволяет выявить факторы наиболее сильно связанные с результатом Y, а также определить направление связей и факторы, тесно связанные друг с другом. Пример 2. Пусть получена матрица парных коэффициентов корреляции: Y X1 X2 X3 X4 Y …
Наиболее часто применяются два метод отбора факторов: 1. Метод исключения предполагает построение модели, включающей всю совокупность факторов, с последующим сокращением их числа до тех пор, пока все коэффициенты при факторах не будут иметь t-статистики, превышающие по модулю единицу. На каждом шаге исключается тот фактор, коэффициент при котором незначим и имеет наименьшую …
В модели регрессии можно учесть влияние на Y и качественного фактора, для чего его необходимо преобразовать в фиктивную переменную (ФП), в качестве которой используются двоичные переменные, принимающие значения (уровня): 0 или 1.
Модель регрессии с хотя бы одной фиктивной переменной называется моделью с переменной структурой. Значение фиктивной переменной, равное «1», обычно …
Чем больше факторов включено в модель, тем лучше она объясняет формирование результата Y. Однако при этом: каждый фактор должен быть теоретически обоснованным; в модель следует включать только существенно влияющие на Y факторы; факторы не должны находиться друг с другом в тесной связи; число наблюдений n должно как минимум в 4 раза превышать число факторов p: .
На практике изменение значения результата Y обычно зависит от одновременного изменения нескольких факторов. В этом случае строится модель множественной регрессии, простейшей из которых является линейная модель . Параметры 1, 2, …, p показывают, на сколько единиц в среднем изменяется Y при увеличении соответствующего фактора на одну единицу и неизменных значениях остальных .
..
Практические задачи по эконометрике: где их найти
ВведениеИзучая принципы эконометрики, очень важно, чтобы вы не только понимали основные понятия, но и практиковали достаточное количество вопросов, чтобы понять приложения и помочь при изучении эконометрики тесты. Хотя предыдущие контрольные работы по эконометрике могут быть доступны вместе с решениями экзамена по эконометрике, систематический подход к изучению вместе с практическими вопросами по каждой теме весьма полезен.
В этой статье рассказывается о некоторых ресурсах в Интернете и о некоторых профессорах различных университетов, которые тестируют вопросы эконометрики после практики вместе с решениями экзаменов по эконометрике. После этого в статье основное внимание уделяется тому, как эконометрика Albert.io является лучшим местом для отработки вопросов для теста по принципам эконометрики.
Практические задачи по эконометрике онлайн В Интернете нет недостатка в практических задачах по эконометрике.
Есть несколько задач по эконометрике разного уровня, которые учащийся может найти в Интернете. Просто чтобы дать вам представление:
Профессор СМУ Ю Цзюнь публикует лекции по эконометрике вместе с наборами задач и их решениями. Их можно найти здесь. Также публикуются различные задания, а также проекты и решения экзаменов по эконометрике.
Профессор Джозеф Херригес из известного Университета штата Айова также публикует наборы задач вместе с решениями по принципам эконометрики.
Профессор Виктор Лима из Чикагского университета также публикует на своей веб-странице несколько наборов задач вместе с экзаменационными вопросами. Некоторые наборы задач не имеют решений; тем не менее, они чрезвычайно полезны, поскольку представляют собой хороший сборник практических задач по эконометрике для студентов. Их можно найти здесь.
Практические задания, описанные выше, не всегда представляют собой вопросы с несколькими вариантами ответов. Это объемные задачи, но они обеспечивают превосходное применение принципов эконометрики.
Academia.edu имеет огромное хранилище вопросов с несколькими вариантами ответов, связанных с эконометрикой. Эти вопросы не являются длинными, и учащийся может решить их быстро. Как правило, вопрос не включает более одного понятия. Хотя это отличный сборник задач, у них нет подробных решений.
Несмотря на то, что в Интернете существует множество таких практических задач, факт заключается в том, что они не индивидуализированы и, короче говоря, доставляют неудобства при обучении. Часто студент, изучающий эконометрику, хотел бы решать задачи во время учебы. Практические задачи, доступные в Интернете и на веб-страницах разных профессоров, обычно основаны на более широкой теме, в которой есть несколько концепций. Для новичка, который впервые изучает концепции и не практиковался в достаточном количестве вопросов, легко отклониться от целевой концепции. Они, вероятно, в конечном итоге потратят много времени на выяснение того, какую концепцию использовать и, самое главное, почему.
Почему Albert.
io Econometrics? Эконометрика Albert.io обеспечивает беспроблемное обучение для всех, кто хочет освоить принципы эконометрики. Albert.io организует контент по различным темам, по несколько тем в каждой теме. Список вопросов достаточно обширен, и вопросы помечены как легкие, средние или сложные. Используя фильтры сложности, можно сначала решить простые вопросы, затем модерировать и, наконец, сложные вопросы.
Это вопросы с несколькими вариантами ответов, которые обеспечивают немедленную обратную связь, как только выбран ответ. В то время как многие практические наборы, циркулирующие в Интернете, предлагают различные вопросы с несколькими вариантами ответов по эконометрике вместе с ключом ответа, почти ни один из них не дает подробного объяснения того, как решать каждый вопрос.
Цель Albert.io Econometrics — убедиться, что вы понимаете то, что изучаете.
Таким образом, при ответе на вопрос также отображается подробное объяснение решения, которое поможет вам узнать, как решить проблему.
По каждой теме эконометрики есть набор практических задач. После того, как вы ответили на все вопросы, вы можете увидеть уровень точности. Это поможет вам определить, какие темы вы поняли правильно и смогли ответить на вопросы с высокой точностью. Эта встроенная обратная связь на Albert.io помогает учащимся определить те темы, которые им необходимо изучить снова, чтобы улучшить свои знания основных понятий принципов эконометрики.
Благодаря всему этому Albert.io превращает обучение в приятное занятие. Учащемуся не нужно часами сидеть в Интернете в поисках нужного набора вопросов. Даже после того, как они найдут вопросы, им не нужно тратить время на поиск решений, а также на то, какие концепции использовать и почему. В Albert.io существует систематический опыт обучения, и каждый может выбирать, какие темы изучать и практиковать в зависимости от своих требований.
Без сомнения, в Интернете есть огромная коллекция вопросов и, возможно, всевозможных вопросов, которые только можно себе представить, но нужен не только контент , но и организованный контент , и Albert.
io стремится достичь этого.
В заключение отметим, что эконометрика является чрезвычайно важной областью и, возможно, самой сложной, если ее не изучать должным образом. Как бы ни было важно содержание принципов эконометрики, отработка задач, прохождение экзаменационных решений по эконометрике, прохождение пробного теста по эконометрике и т. д. весьма важны.
Хотя профессора разных университетов размещают на своих веб-страницах несколько экзаменационных вопросов, они настраиваются в соответствии с требованиями соответствующих университетов и могут не подходить каждому учащемуся. Следовательно, студент, изучающий эконометрику, должен зарегистрироваться на Albert.io Econometrics, потому что он обещает быть подходящей, индивидуальной, простой в освоении и преуспеть, а также интерактивной платформой для изучения принципов эконометрики.
Рекомендуемый источник изображения
Давайте применим все на практике.
Попробуйте этот практический вопрос по эконометрике: Ищете больше практики эконометрики?
На Albert.io можно найти тысячи практических вопросов. Albert.io позволяет вам настроить учебный процесс так, чтобы он ориентировался на практику, в которой вам больше всего нужна помощь. Мы дадим вам сложные практические вопросы, которые помогут вам достичь мастерства в эконометрике.
Начните тренироваться здесь .
Вы учитель или администратор, заинтересованный в повышении успеваемости учащихся AP® Biology?
Узнайте больше о наших школьных лицензиях здесь .
Интерактивное решение проблем: онлайн-эконометрика, день 2
Я очень рад сообщить, что две самые большие проблемы, с которыми я столкнулся в понедельник, были решены. Тесты, которые мы составили для каждого из модулей класса, чтобы проверить взаимодействие с видео, теперь работают безупречно.
Я не знаю, почему мы не могли исправить ошибки раньше, но Instructure что-то сделала со своими серверами, чтобы решить проблему. Надеюсь, мы видели последний из них.
Во-вторых, очень приятный сотрудник службы поддержки Zoom указал мне место в настройках приложения, где я мог включить «Включить двойной поток для двух мониторов». Это позволяет мне видеть весь класс на одном дисплее и делиться слайдами на втором дисплее. Я также смог включить настройку, которая показывала имена всех под их видео. Я, как известно, плохо запоминаю имена, и у меня не должно быть ни единого неловкого «Как тебя звали?» момент этот термин.
Сегодняшнее занятие я начал с того, что ответил на единственный вопрос, с которым у них возникли проблемы в модульной викторине. Я разбил решение на части и попросил разных учеников объяснить каждый шаг. Оглядываясь назад, я хотел бы, чтобы ученик, который ошибся, объяснил, где он ошибся, поскольку смотреть, как кто-то другой решает проблему, неоптимально — всегда лучше немного перенаправить ученика и дать ему решить ее самому.
Большую часть класса мы решили еще три задачи. Я представлял проблему и давал им 5-10 минут, чтобы попытаться решить ее самостоятельно. Я не уверен, что это было оптимально, но это не казалось слишком коротким или слишком длинным. Затем мы прошлись по комнате, работая шаг за шагом, и все должны были участвовать. Я бы предпочел, чтобы они работали парами или группами по три человека, но у нас пока нет технологии, позволяющей сделать это гладко.
Последние 10 минут урока я преподал один из моих любимых уроков: Задача Монти Холла. Я начинаю с того, что излагаю проблему и смотрю, какова их интуиция. Вместо того, чтобы сразу переходить к ответу, мы пытаемся вместе выяснить, что не так с неправильными ответами. Это намного сложнее, чем понять правильный ответ. Задача Монти Холла имеет много общего с иллюзией Старухи/Молодой девушки в том смысле, что здесь легко выбрать правильный ответ. Я думаю, что, имея немного больше времени, было бы полезно поставить задачу в терминах условных и предельных вероятностей.