Макарычев 8 класс алгебра 13. Найдите область определения функции. – Рамблер/класс
Макарычев 8 класс алгебра 13. Найдите область определения функции. – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
ответы
находим это следующим образом
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Психология
ЕГЭ
10 класс
9 класс
похожие вопросы 5
150 Алгебра 9 класс Макарычев Помогите решить графически
Решите графически уравнение:
а) х3 = 2; б) х3 = 4; в) х3 = -5.
ЭкзаменыАлгебра9 классМакарычев Ю.Н.ГДЗ
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
сахара и расчёт его массовой доли в растворе.
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
ГДЗЕГЭРусский языкЦыбулько И.П.
8 класс. Алгебра. Никольский. Учебник. Ответы к стр. 25
Простейшие функции. Квадратные корниФункции и графики
Понятие функцииОтветы к стр. 25
53. Пусть дана функция у = f(x) (х ∈ М). Что называют:
а) независимой переменной или аргументом;
б) зависимой переменной или функцией;
в) областью определения функции?
Приведите три примера функций, заданных формулами. Назовите зависимую и независимую переменные, область определения этой функции.
а) х — независимая переменная или аргумент;
б) у — зависимая переменная или функция;
в) множество М — область определения функции.
у = 2х, у — зависимая переменная, х — независимая переменная, (-∞; +∞) — область определения этой функции,
у = 1/х, у — зависимая переменная, х — независимая переменная, (-∞; 0) ∪ (0; +∞) — область определения этой функции,
у = 1/1-х, у — зависимая переменная, х — независимая переменная, (-∞; 1) ∪ (1; +∞) — область определения этой функции.
54. а) Функция задана формулой у = 2х + 7. Назовите зависимую и независимую переменные, область определения этой функции. Вычислите: у(3), y(-2), у(0). Результаты запишите в таблицу. Например, если х = -5, то у = 2 • (-5) + 7 = -10 + 7 = -3.
| х | -5 | |||
| у | -3 |
б) Функция задана формулой у = х2. Вычислите: y(0), у(2), у(-2), y(-1), y(0,4), у(3/4). Решение оформите в виде таблицы.
а) у = 2х + 7, у — зависимая переменная, х — независимая переменная, (-∞; +∞) — область определения этой функции
у(3), если х = 3, то у = 2 • 3 + 7 = 6 + 7 = 13
y(-2), если х = -2, то у = 2 • (-2) + 7 = -4 + 7 = 3
у(0), если х = 0, то у = 2 • 0 + 7 = 0 + 7 = 7
| х | -5 | 3 | -2 | 0 |
| у | -3 | 13 | 3 | 7 |
б) у(0), если х = 0, то у = 02 = 0
y(2), если х = 2, то у = 22 = 4
у(-2), если х = -2, то у = (-2)2 = 4
у(-1), если х = -1, то у = (-1)2 = 1
y(0,4), если х = 0,4, то у = 0,42 = 0,16
у(3/4), если х = 3/4, то у = (3/4)2 = 9/16
| х | 0 | 2 | -2 | -1 | 0,4 | 3/4 |
| у | 0 | 4 | 4 | 1 | 0,16 | 9/16 |
55. Функция задана формулой у = 3x — 1. Верно ли равенство:
Функция задана формулой у = 3x — 1. Верно ли равенство:
а) у(2) = 3; б) y(5) = 17; в) у(1/3
а) у(2), если х = 2, то у = 3 • 2 — 1 = 6 — 1 = 5 — неверно;
б) у(5), если х = 5, то у = 3 • 5 — 1 = 15 — 1 = 14 — неверно;
в) у(1/3), если х = 1/3, то у = 3 • 1/3 — 1 = 1 — 1 = 0 — верно;
г) у(-1), если х = -1, то у = 3 • (-1) — 1 = -3 — 1 = -4 — неверно.
56. Функция задана формулой у = 1 — 4х.
а) Найдите: у(6), у(-7), у(0,5), y(2/3).
б) Верно ли равенство: у(5) = 19, у(-2) = 9, y(0) = 1, y(-0,5) = 2, y(- 3/4) = 4?
а) у(6), если х = 6, то у = 1 — 4 • 6 = 1 — 24 = -23,
у(-7), если х = -7, то у = 1 — 4 • (-7) = 1 + 28 = 29,
у(2/3), если х = 2/3, то у = 1 — 4 • 2/3 = 1 — 8/3 = — 5/3 = -1 2/3;
б) у(5), если х = 5, то у = 1 — 4 • 5 = 1 — 20 = -19 — неверно,
у(-2), если х = -2, то у = 1 — 4 • (-2) = 1 + 8 = 9 — верно,
у(0), если х = 0, то у = 1 — 4 • 0 = 1 — 0 = 1 — верно,
у(-0,5), если х = -0,5, то у = 1 — 4 • (-0,5) = 1 + 2 = 3 — неверно,
у(- 3/4), если х = — 3/4, то у = 1 — 4 • (- 3/4) = 1 + 3 = 4 — верно.
57. Задайте функцию формулой, если закон зависимости у от х для х > 0 заключается в том, что каждому х соответствует у:
а) в 2 раза больший; б) меньший на 2;
в) больший на 5; г) в 4 раза больший;
д) в 7 раз меньший; е) равный удвоенному квадрату х.
а) у = 2х;
б) у = х — 2;
в) у = х + 5;
г) у = 4х;
д) у = 1/7х;
е) у = 2х2.
58. Вычислите значения функции у = 3х, взяв значения х от -2 до 2 через 0,5. Решение оформите в виде таблицы.
у(-2), если х = 0, то у = 3 • (-2) = -6
y(-1,5), если х = -1,5, то у = 3 • (-1,5) = -4,5
у(-1), если х = -1, то у = 3 • (-1) = -3
у
y(0), если х = 0, то у = 3 • 0 = 0
у(0,5), если х = 0,5, то у = 3 • 0,5 = 1,5
y(1), если х = 1, то у = 3 • 1 = 3
у(1,5), если х = 1,5, то у = 3 • 1,5 = 4,5
у(2), если х = 2, то у = 3 • 2 = 6
| х | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 |
| у | -6 | -4,5 | -3 | -1,5 | 0 | 1,5 | 3 | 4,5 | 6 |
59. Вычислите значения функции у = х2, взяв значения х от -1 до 1 через 0,2. Решение оформите в виде таблицы.
Вычислите значения функции у = х2, взяв значения х от -1 до 1 через 0,2. Решение оформите в виде таблицы.
y(-0,8), если х = -0,8, то у = (-0,8)2 = 0,64
у(-0,6), если х = -0,6, то у = (-0,6)2 = 0,36
у(-0,4), если х = -0,4, то у = (-0,4)2 = 0,16
y(-0,2), если х = -0,2, то у = (-0,2)2 = 0,04
у(0), если х = 0, то у = 02 = 0
y(0,2), если х = 0,2, то у = 0,22 = 0,04
у(0,4), если х = 0,4, то у = 0,42 = 0,16
у(0,6), если х = 0,6, то у = 0,62 = 0,36
у(0,8), если х = 0,8, то у = 0,82 = 0,64
y(1), если х = 1, то у = 12 = 1
| х | -1 | -0,8 | -0,6 | -0,4 | -0,2 | 0 | 0,2 | 0,4 | 0,6 | 0,8 | 1 |
| у | 1 | 0,64 | 0,36 | 0,16 | 0,04 | 0 | 0,04 | 0,16 | 0,36 | 0,64 | 1 |
Ответы по алгебре. 8 класс. Учебник. Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В.
8 класс. Учебник. Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В.
Алгебра. 8 класс
Математика 8 класс | Функции
Учащиеся учатся представлять, интерпретировать и анализировать функции в различных формах, что приводит к пониманию таких характеристик, как скорость изменения, начальные значения и интервалы возрастания и убывания.
Раздел 4
8-й класс
Краткое содержание раздела
В Разделе 4 учащиеся восьмого класса знакомятся с концепцией функции, которая связывает входы и выходы. Они начинают с изучения всех типов взаимосвязей между множествами, такими как количество учеников и их братьев и сестер, количество монет и количество минут стоянки на метре, расстояние и время, потраченное на пробежку, и т. д. Они учатся представлять и интерпретировать функции в различных форм, включая таблицы, уравнения, графики и словесные описания (МП.2). По мере прохождения модуля учащиеся анализируют функции, чтобы лучше понять такие характеристики, как скорость изменения, начальные значения и интервалы увеличения или уменьшения, что, в свою очередь, позволяет учащимся сравнивать функции, даже если они не представлены в одном и том же формате. . Учащиеся анализируют реальные ситуации на предмет скорости изменения и начальных значений и используют эти признаки для построения уравнений для моделирования взаимосвязей функций (MP.4). Учащиеся также проводят время, сравнивая линейные функции с нелинейными функциями, формируя понимание базовой структуры функции, которая делает ее линейной (MP.7), настраивая их для модуля 5. Наконец, учащиеся устанавливают связи между историями и графиками, моделируя ситуации. как расстояние или скорость во времени.
. Учащиеся анализируют реальные ситуации на предмет скорости изменения и начальных значений и используют эти признаки для построения уравнений для моделирования взаимосвязей функций (MP.4). Учащиеся также проводят время, сравнивая линейные функции с нелинейными функциями, формируя понимание базовой структуры функции, которая делает ее линейной (MP.7), настраивая их для модуля 5. Наконец, учащиеся устанавливают связи между историями и графиками, моделируя ситуации. как расстояние или скорость во времени.
В шестом и седьмом классах ученики изучали коэффициент и константу пропорциональности в пропорциональных отношениях. Они разработали понимание того, как одна величина изменяется по отношению к другой. Учащиеся опираются на эти знания, когда исследуют взаимосвязь величин в таблицах, уравнениях и графиках, а также исследуют линейные и нелинейные отношения.
Сразу после этого раздела учащиеся восьмого класса приступают к изучению линейных отношений. В этом блоке они пересмотрят и расширят многие темы, представленные в этом блоке «Функции». Учащиеся будут интерпретировать скорость изменения как наклон, а начальное значение – как точку пересечения $$y-$$ линейного уравнения $$y=mx+b$$. В старших классах изучение функций распространяется на несколько тем и областей обучения, включая квадратичные, экспоненциальные и тригонометрические функции.
Учащиеся будут интерпретировать скорость изменения как наклон, а начальное значение – как точку пересечения $$y-$$ линейного уравнения $$y=mx+b$$. В старших классах изучение функций распространяется на несколько тем и областей обучения, включая квадратичные, экспоненциальные и тригонометрические функции.
Темп: 16 учебных дней (12 уроков, 3 дня гибкого графика, 1 день оценки)
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Узнать больше
Оценка
Следующие оценки сопровождают Раздел 4.
Предварительная часть
Предложите учащимся пройти Предварительную оценку и Предварительную самооценку учащихся перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Mid-Unit
Предложите учащимся пройти промежуточную оценку.
Post-Unit
Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0Самооценка студентов после окончания обучения
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.
Скачать образец
Подготовка блока
Интеллектуальная подготовка
Предложения по подготовке к обучению данного модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Запуск модуля
Подготовьтесь к преподаванию этого модуля, погрузившись в стандарты, большие идеи и связи с предыдущим и будущим содержанием. Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.
Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.
Обновление до Plus
Интернализация стандартов с помощью итоговой оценки
- Пройдите итоговую оценку. Аннотировать для:
- Стандарты, которым соответствует каждый вопрос
- Стратегии и представления, используемые на ежедневных уроках
- Связь с основными понятиями модуля
- Уроки, на которые Оценка указывает
Интернализация траектории отряда
- Прочитайте и аннотируйте сводку отряда.
- Обратите внимание на последовательность понятий в модуле с помощью карты урока.
- Выполнить все целевые задачи. Аннотируйте целевые задачи для:
- Основные понятия
- Связь с вопросами послемодульной оценки
- Определите ключевые возможности для вовлечения учащихся в академический дискурс. Прочтите наш Инструмент для учителя на
Академический дискурс и ссылайтесь на него на протяжении всего модуля.

Интеллектуальная подготовка для конкретного модуля
- Прочтите ход выполнения общих основных государственных стандартов по математике, 8 класс, старшая школа, функции для стандартов, относящихся к этому разделу.
- Также полезно ознакомиться с разделами Progressions для Common Core State Standards in Mathematics, 6–8, Expressions and Equations, в частности для 8.EE.5 и 8.EE.6, поскольку они тесно связаны со стандартами функций. .
- Прочтите следующую таблицу, в которой указаны модели, используемые во всем устройстве.
| Модель | Пример |
| Таблица функций ввода/вывода | |
| Уравнение функции | градусов по Фаренгейту является функцией градусов по Цельсию $$F=\frac{9}{5}C+32$$ |
| График функции | Температура является функцией времени. |
| Вербальное представление функции | Общее расстояние, пройденное бегуном, зависит от времени, потраченного на бег. |
Основные понятия
Основные математические концепции, которые учащиеся поймут в этом модуле. Функции могут быть представлены в виде таблиц, уравнений, графиков и словесных описаний.
Материалы
Материалы, иллюстрации и инструменты, которые потребуются преподавателям и учащимся для работы с данным модулем
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Дополнительно : Сухой стираемый маркер (1 на учащегося)
- Дополнительно : Белая доска (1 на учащегося)
Чтобы ознакомиться со всеми материалами, необходимыми для этого курса, ознакомьтесь с нашим Обзором материалов курса для 8-го класса.
Словарный запас
Термины и обозначения, которые учащиеся изучают или используют на уроке
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950функция
ввод/вывод
начальное значение
линейная функция
нелинейная функция
скорость изменения
3
3
3 Чтобы увидеть весь словарный запас для модуля 4, просмотрите наш глоссарий лексики для 8-го класса.
Карта урока
Тема A: Определение функций
Определение и идентификация функций.
8.Ф.А.1
Использовать функциональный язык для описания функций. Определите функциональные правила.
8.Ф.А.1
Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.
Уже есть учетная запись? Войти
Тема B: Представление и интерпретация функций
Определите свойства функций, представленных в таблицах, уравнениях и словесных описаниях. Оцените функции.
8.Ф.А.1
8.Ф.А.2
8. Ф.Б.4
Ф.Б.4
Представление функций уравнениями.
8.Ф.А.1 8.Ф.Б.4
Чтение входов и выходов в графиках функций. Определить, являются ли графики функциями.
8.Ф.А.1
Определите свойства функций, представленных на графиках.
8.Ф.А.1 8.Ф.Б.4
Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.
Уже есть учетная запись? Войти
Тема C: Сравнение функций
Определение линейных и нелинейных функций и построение графиков.
8.Ф.А.3
Определите, являются ли функции линейными или нелинейными, когда они представлены в виде таблиц, графиков и уравнений.
8.Ф.А.1 8.Ф.А.3
Сравните функции, представленные разными способами (Часть 1).
8.Ф.А.2
Сравните функции, представленные разными способами (Часть 2).
8.Ф.А.2
Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.
Уже есть учетная запись? Войти
Тема D: Описание и построение графиков функций
Описывать функции, анализируя графики. Определите интервалы возрастающей, убывающей, линейной или нелинейной активности.
Определите интервалы возрастающей, убывающей, линейной или нелинейной активности.
8.Ф.Б.5
Эскизные графики функций с качественными описаниями отношений.
8.Ф.Б.5
Создайте бесплатную учетную запись, чтобы получить доступ к тысячам планов уроков.
Уже есть учетная запись? Войти
Общие базовые стандарты
Ключ
Основной кластер
Вспомогательный кластер
Дополнительный кластер
Основные стандарты
Стандарты контента, рассматриваемые в этом разделе
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Функции
8.Ф.А.1 — Поймите, что функция — это правило, которое назначает каждому входу ровно один выход. График функции представляет собой набор упорядоченных пар, состоящих из входа и соответствующего выхода. Обозначение функции не требуется в 8 классе.
8.
 F.A.2 — Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями). Например, если задана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения.
F.A.2 — Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями). Например, если задана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения. 8.Ф.А.3 — интерпретировать уравнение y = mx + b как определяющее линейную функцию, график которой представляет собой прямую линию; приведите примеры функций, которые не являются линейными. Например, функция A = s², определяющая площадь квадрата как функцию длины его стороны, не является линейной, поскольку ее график содержит точки (1,1), (2,4) и (3,9), которые не лежат на прямой.
8.Ф.Б.4 — Создайте функцию для моделирования линейной зависимости между двумя величинами. Определить скорость изменения и начальное значение функции по описанию зависимости или по двум значениям (x, y), в том числе прочитать их из таблицы или из графика.
 Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.
Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений. 8.Ф.Б.5 — Качественно описать функциональную связь между двумя величинами, анализируя график (например, где функция возрастает или убывает, линейна или нелинейна). Нарисуйте график, демонстрирующий качественные характеристики функции, описанной словесно.
Основополагающие стандарты
Стандарты, изучаемые в предыдущих разделах или классах, которые являются важной основой для текущего раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Выражения и уравнения
6.EE.A.2.C
7.EE.B.4
Соотношения и отношения пропорциональности
6.
 РП.А.2
РП.А.27.РП.А.2
7.РП.А.2.Б
7.РП.А.2.С
7.РП.А.2.Д
Будущие стандарты
Стандарты будущих классов или разделов, которые связаны с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Функции здания
F.BF.A.1
Выражения и уравнения
8.EE.B.5
8.EE.B.6
Функции интерпретации
Ф.ИФ.А.1
Ф.И.Ф.А.2
Ф.
 И.Б.4
И.Б.4
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 — Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
Модуль 3
Преобразования и взаимосвязи углов
значок/стрелка/вправо/большойМодуль 5
Линейные отношения
CMP3 класс 8 — Connected Mathematics Project
8-1 Мышление математическими моделями
Понятия и пояснения | Примеры домашних заданий | Math Background
В Думая математическими моделями ваш ребенок будет моделировать отношения с помощью графиков и уравнений. Они будут использовать модели для анализа ситуаций и решения проблем. Исследования в этом разделе помогут им понять следующие идеи.
Они будут использовать модели для анализа ситуаций и решения проблем. Исследования в этом разделе помогут им понять следующие идеи.
- Представление данных с помощью графиков, таблиц, словесных описаний и алгебраических выражений.
- Распознавать линейные и нелинейные зависимости в таблицах и графиках.
- Использование уравнений линейной и обратной вариации для моделирования двумерных данных
- Используйте остаточный анализ для измерения соответствия моделей линейной и обратной вариации.
- Анализ, приближение и решение линейных уравнений.
- Используйте линейные и обратные вариационные уравнения для решения задач, прогнозирования и принятия решений
- Используйте диаграммы рассеяния, двусторонние таблицы и коэффициенты корреляции для описания закономерностей ассоциации в парах переменных.
- Используйте стандартное отклонение для измерения изменчивости распределения данных.
Когда ваш ребенок сталкивается с новой проблемой, рекомендуется задать такие вопросы, как:
- Каковы ключевые переменные в этой ситуации?
- Если существует закономерность, связывающая переменные, достаточно ли она сильна, чтобы я мог делать прогнозы?
- Какой шаблон связывает переменные?
- Какое уравнение будет выражать отношения?
- Как я могу использовать уравнение, чтобы ответить на вопросы об отношениях?
8-2 В поисках Pythagoras
Понятия и пояснения | Примеры домашних заданий | Math Background
В В поисках Пифагора ваш ребенок изучит важное соотношение между длинами сторон прямоугольного треугольника. Они узнают, как:
Они узнают, как:
- Разработать стратегии для нахождения расстояния между двумя точками на координатной сетке
- Объясните доказательство теоремы Пифагора
- Понимать и использовать теорему Пифагора для решения повседневных задач
- Записывайте дроби как повторяющиеся или заканчивающиеся десятичные дроби
- Запись десятичных дробей в виде дробей
- Распознавать рациональные и иррациональные числа
- Найдите иррациональные числа в числовой строке
- Соотнесите площадь квадрата с длиной его стороны, а объем куба с длиной его стороны
- Оценка квадратных и кубических корней
Когда ваш ученик сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Какие величины в этой задаче?
- Является ли Теорема Пифагора полезной и уместной в этой ситуации?
- Откуда мне знать?
- Нужно ли мне найти расстояние между двумя точками?
- Как связаны длина стороны и площадь квадрата?
- Как вычислить квадратный или кубический корень числа?
8-3 Рост, рост, рост
Понятия и пояснения | Примеры домашних заданий | Математический фон
В задании Растет, растет, растет ваш ребенок будет изучать экспоненциальные функции, один из наиболее важных типов нелинейных отношений. Исследования в этом разделе помогут им научиться:
Исследования в этом разделе помогут им научиться:
- Определять ситуации, в которых количество растет или уменьшается экспоненциально
- Распознавать связи между моделями роста в таблицах, графиках и уравнениях, которые представляют экспоненциальные функции
- Построение уравнений для выражения отношения между переменными в экспоненциальной функции в таблицах данных, графиках и проблемных ситуациях
- Сравнение экспоненциальной и линейной функций
- Разработать и использовать правила работы с показателями степени, включая экспоненциальное представление, для написания и интерпретации эквивалентных выражений
- Решайте задачи об экспоненциальном росте и спаде из различных областей, включая науку и бизнес
Пока ваш ребенок работает над задачами в этом разделе, задавайте вопросы о ситуациях, включающих нелинейные отношения, такие как:
- Как я могу определить, является ли отношение между переменными экспоненциальной функцией?
- Что такое фактор роста или распада?
- Какое уравнение моделирует данные таблицы, графика или проблемной ситуации?
- Что я могу узнать об этой ситуации, изучая таблицу или график экспоненциальной функции?
- Как я могу ответить на вопросы о проблемной ситуации, изучая таблицу, график или уравнение, представляющее показательную функцию?
8-4 Лягушки, блохи и окрашенные кубики
Понятия и пояснения | Примеры домашних заданий | Математический фон
В наборе «Лягушки, блохи и раскрашенные кубики» ваш ребенок изучит квадратичные функции, важный тип нелинейных функций. Они узнают, как
Они узнают, как
- распознавать закономерности изменения квадратичных отношений
- Напишите уравнения для квадратичных функций, представленных в виде таблиц, графиков и проблемных ситуаций
- Соедините квадратные уравнения с закономерностями в таблицах и графиках квадратичных функций
- Использование квадратного уравнения для определения максимального или минимального значения, точек пересечения по осям x и y, линии симметрии и других важных характеристик графика квадратичной функции
- Распознавать эквивалентные квадратные выражения
- Используйте Распределительное свойство для записи эквивалентных квадратных выражений в факторизованной и расширенной форме
- Использование таблиц, графиков и уравнений квадратичных функций для решения задач в различных ситуациях из геометрии, науки и бизнеса
- Сравните свойства квадратичных, линейных и экспоненциальных функций
Когда ваш ребенок сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Что такое независимые и зависимые переменные?
- Как узнать, являются ли отношения между переменными квадратичными?
- Какое уравнение моделирует квадратичную функцию, заданную в таблице, на графике или в контексте задачи?
- Как я могу ответить на вопросы о проблемной ситуации, изучая таблицу, график или уравнение, представляющее квадратичную функцию?
8-5 Бабочки, вертушки и обои
Понятия и пояснения | Примеры домашних заданий | Математический фон
В наборе «Бабочки, вертушки и обои» ваш ребенок научится:
- Находить фигуры с различными видами симметрии
- Описать типы симметрии, используя отражения, повороты и переносы
- Используйте преобразования симметрии, чтобы сравнить размер и форму фигур, чтобы увидеть, конгруэнтны они или похожи
- Эффективно определять конгруэнтные и подобные треугольники и четырехугольники
- Использование свойств равных и подобных треугольников для решения задач о формах и измерениях
Когда ваш учащийся сталкивается с новой задачей, полезно задать такие вопросы, как:
- Как я могу использовать симметрию для описания формы и свойств фигур в схеме или задаче?
- Какие фигуры в узоре конгруэнтны?
- Какие части конгруэнтных фигур будут сопоставлены преобразованием конгруэнтности?
- Какие фигуры в задаче подобны?
8-6 Произнеси это с помощью символов
Понятия и пояснения Примеры домашних заданий | Математический фон
Алгебра предоставляет идеи и символы для выражения информации о количественных переменных и отношениях. В Say It With Symbols ваш ребенок будет решать задачи, предназначенные для развития его понимания и навыков использования символических выражений и уравнений в алгебре. Они узнают, как:
В Say It With Symbols ваш ребенок будет решать задачи, предназначенные для развития его понимания и навыков использования символических выражений и уравнений в алгебре. Они узнают, как:
- Представлять шаблоны и отношения в символических формах
- Определить, когда различные символьные выражения математически эквивалентны
- Напишите алгебраические выражения в удобных эквивалентных формах
- Объединение символьных выражений с использованием алгебраических операций для формирования новых выражений
- Анализ выражений или уравнений для определения моделей изменений в таблицах и графиках, которые представляет выражение или уравнение
- Решите линейные и квадратные уравнения, используя символьные рассуждения
- Используйте алгебраические рассуждения для проверки обобщений и предположений
Когда ваш ребенок сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Какое выражение или уравнение представляет шаблон или связь в контексте?
- Можете ли вы написать эквивалентное выражение для данного выражения, чтобы предоставить новую информацию об отношении?
- Какие операции могут преобразовать данное уравнение или выражение в эквивалентную форму, которую можно использовать для ответа на вопрос?
- Как символическое рассуждение может помочь подтвердить гипотезу?
8-7 Это в системе
Понятия и пояснения | Примеры домашних заданий | Математический фон
В этом разделе ваш ребенок будет писать и решать системы линейных уравнений и неравенств, которые моделируют реальные ситуации. Методы решения этих алгебраических систем сочетают в себе графические и алгебраические рассуждения из более ранних модулей Connected Mathematics. Вы научитесь
Методы решения этих алгебраических систем сочетают в себе графические и алгебраические рассуждения из более ранних модулей Connected Mathematics. Вы научитесь
- Решать линейные уравнения и системы линейных уравнений с двумя переменными
- Решение линейных неравенств и систем неравенств с двумя переменными
- Использовать системы линейных уравнений и неравенств для решения задач
Когда ваш ребенок сталкивается с новой проблемой, полезно задать такие вопросы, как:
- Какие переменные в этой задаче?
- Требует ли задача решения системы уравнений или неравенств, связывающих эти переменные?
- Какая стратегия будет наиболее эффективной при решении системы?
8-8 Функциональное соединение
Понятия и пояснения | Примеры домашних заданий | Math Background
Функции были основной темой на протяжении всей работы вашего ребенка с алгеброй. В Function Junction ваш ребенок более подробно рассмотрит функции и изучит новые функции.



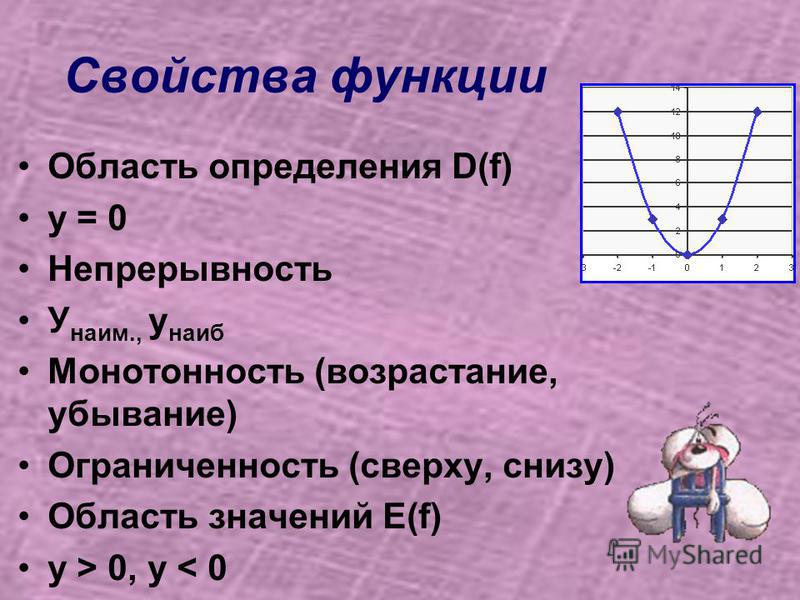 F.A.2 — Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями). Например, если задана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения.
F.A.2 — Сравните свойства двух функций, каждая из которых представлена по-разному (алгебраически, графически, численно в таблицах или словесными описаниями). Например, если задана линейная функция, представленная таблицей значений, и линейная функция, представленная алгебраическим выражением, определите, какая функция имеет большую скорость изменения.  Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.
Интерпретируйте скорость изменения и начальное значение линейной функции с точки зрения ситуации, которую она моделирует, и с точки зрения ее графика или таблицы значений.  РП.А.2
РП.А.2 И.Б.4
И.Б.4