Экспонента ряд тейлора: Разложение экспоненты в ряд — Лисья нора

{i\pi} + 1 = 0

5 мая, 2020

Содержание

Формула Эйлера, том II — aj tz’ihb — LiveJournal

Завершаем обсуждение формулы Эйлера

Продолжая рассуждения предыдущей части, в итоге получаем степенной ряд (он же ряд Маклорена, он же ряд Тейлора) для экспоненты

который прекрасно сходится и ничуть не страдает, если вещественную переменную х заменить в нем на комплексную z:

Вообще, по нынешним временам, именно этот ряд нередко берут как определение экспоненты, а ее остальные свойства из него выводятся. Например, то, что при дифференцировании этот ряд переходит сам в себя, достаточно очевидно, по-моему.

Обратите внимание, насколько простая идея стоит за кулисами ряда Тейлора. Если положить

То автоматически

благодаря тому, что слева от k-го члена слагаемые обнулятся дифференцированием, а справа за счет ненулевой степени разности. И вуаля:

Но да, нюанс. Это все конечно весело и приятно, но сходимость полученных рядов следует исследовать отдельно, тут целое поле граблей, по которым математики 18 века вдоволь находились.

И здесь как раз вступают в бой все те признаки и свойства сходимости, почленной дифференцируемости и т.п. из курса матанализа. Но мы этим здесь заниматься не будем, а будем верить мне на слово.

Еще одно замечание по дороге. Если мы определяем экспоненту в виде ряда, то совершенно необязательно в этот ряд подставлять числа. Если для некоторых сущностей определены операции сложения, умножения между собой и умножения на число, а так же осмысленно понятие предела, то есть задана банахова алгебра, то ряд для экспоненты имеет вполне себе внятный смысл. Например, можно взять экспоненту от квадратной матрицы. А то и еще чего почище учудить. Но это уже другая история.

Возвращаясь к формуле Эйлера, я уже без вывода, прямо запишу:

И, чтоб упростить вам восприятие:

Ряды у нас хорошие, складывать их можно как угодно. И на данном этапе формула

представляется совершенно очевидной. Видимо Эйлер именно так к ней и пришел: играясь с рядами Маклорена.

Если пойти еще немгого дальше, то вообще окажется, что синус и косинус удобнее определить следующим образом:

а дальнейшие нужные нам свойства тригонометрических функций доказать.

Кстати, обратите внимание, что выражение

имеет период два пи вдоль мнимой оси. Так что, помимо известных свойств, у экспоненты появились и некоторые новые. Представить заранее, что экспонента станет периодической функцией, было бы (наверное) довольно сложно.

Напоследок скажу, что хотя формула Муавра уже была известна к моменту открытия Эйлера, возможность представить любое комплексное число в виде открыла совершенно новые, невиданные возможности. В качестве простого и очень примитивного примера, чтобы не быть голословным, напомню, что именно на этом представлении базируются всем известные методы расчета линейных цепей переменного тока. Есть и куда более интересные применения, но о них как-нибудь в другой раз.

Tags: opus, математика

Интуиция для ряда Тейлора (аналогия ДНК) – BetterExplained

У вашего тела есть странное свойство: вы можете получить информацию о целом организме из одной клетки. Выберите клетку, погрузитесь в ядро и извлеките ДНК. Теперь вы можете заново вырастить все существо из этого крошечного образца.

Здесь математическая аналогия. Возьмите функцию, выберите конкретную точку и погрузитесь в нее. Вы можете извлечь достаточно данных из одной точки, чтобы перестроить всю функцию. Вау. Это как переделывать фильм из одного кадра. 92$, что мы можем обнаружить в одном месте?

Обычно мы рассчитываем одно значение, например $f(4) = 16$. Но под поверхностью скрыто гораздо больше:

$f(x)$ = значение функции в точке $x$
$f'(x)$ = первая производная или скорость изменения функции (скорость)

$f»(x)$ = Вторая производная, или скорость изменения (ускорение)
$f»'(x)$ = третья производная или скорость изменения в изменения меняются (ускорение ускорения)
И так далее

Исследование одной точки позволяет получить несколько, возможно бесконечных, битов информации о поведении. (Некоторые функции имеют бесконечное количество данных (производных) в одной точке).

Итак, учитывая всю эту информацию, что нам делать? Конечно, вырастить организм из одной клетки! ( Маниакальное кудахтанье здесь. )

Выращивание функции с точки

Наш план состоит в том, чтобы вырастить функцию из единой отправной точки. Но как мы можем описать любую функцию в общем виде?

Большой ага-момент: представьте, что любая функция по своей сути является полиномом (возможно, с бесконечными членами):

Чтобы перестроить нашу функцию, мы начинаем с фиксированной точки ($c_0$) и добавляем кучу других терминов на основе значения, которое мы ему передаем (например, $c_1x$). «ДНК» — это значения $c_0, c_1, c_2, c_3$, которые точно описывают нашу функцию.

Хорошо, у нас есть общий «формат функции». Но как нам найти коэффициенты для конкретной функции, такой как sin(x) (высота угла x на единичной окружности)? Как мы вытащим его ДНК?

Время магии 0.

Давайте начнем с подстановки значения функции в $x=0$. Делая это, мы получаем:

Все термы равны нулю, кроме $c_0$, что логично: отправной точкой нашего проекта должна быть $f(0)$. Для $f(x) = \sin(x)$ мы можем вычислить $c_0 = \sin(0) = 0$. У нас есть первая часть ДНК!

Получение большего количества ДНК

Теперь, когда мы знаем $c_0$, как нам выделить $c_1$ в этом уравнении?

Хрм. Несколько идей: 93) + \cdots$ . Хотя мы знаем $c_0$, остальные константы суммируются. Мы не можем вытащить $c_1$ самостоятельно.

Что если разделить на $x$? Это дает:

Тогда мы можем установить $x=0$, чтобы другие члены исчезли… верно? Это хорошая идея, за исключением того, что мы теперь делим на ноль.

грн. Этот подход действительно близок. Как мы можем почти разделить на ноль? Использование производной!

Если мы возьмем производную схемы $f(x)$, мы получим:

Каждая степень уменьшается на 1, а постоянное значение $c_0$ становится равным нулю. Это почти слишком удобно.

Теперь мы можем изолировать $c_1$, используя наш трюк с $x=0$:

В нашем примере $\sin'(x) = \cos(x)$, поэтому мы вычисляем: $f'(0) = \sin'(0) = \cos(0) = 1 = c_1$

Ура, еще один кусочек ДНК! В этом заключается магия ряда Тейлора: многократно применяя производную и устанавливая $x = 0$, мы можем вытащить полиномиальную ДНК.

Попробуем еще раз:

После взятия второй производной силы снова уменьшаются. Первые два члена ($c_0$ и $c_1x$) исчезают, и мы можем снова изолировать $c_2$, установив $x=0$:

Для нашего примера с синусоидой $\sin» = -\sin$ , поэтому:

или $c_2 = 0$.

Поскольку мы продолжаем брать производные, мы выполняем больше умножений и увеличиваем факториал перед каждым членом (1!, 2!, 3!).

Ряд Тейлора для функции вокруг точки x=0:

(Формально ряд Тейлора вокруг точки $x=0$ называется рядом Маклорена.)

Обобщенный ряд Тейлора, извлеченный из любой точки a: такой же. Вместо нашего обычного плана мы используем:

Поскольку мы растем из $f(a)$, мы видим, что $f(a) = c_0 + 0 + 0 + \dots = c_0$. Остальные коэффициенты можно получить, взяв производные и установив $x = a$ (вместо $x =0$). 92 + 3$) уже находятся в их «полиномиальном формате» и не имеют бесконечных производных, чтобы поддерживать работу ДНК.

2) Синус отсутствует в каждом втором члене
Если мы повторно возьмем производную синуса при x = 0, мы получим:
со значениями:
Игнорируя деление на факториал, мы получаем шаблон:
Итак, ДНК синуса повторяется примерно как [0, 1, 0, -1].
3) Различные стартовые позиции имеют разную ДНК
Ради интереса, вот ряд Тейлора $\sin(x)$, начинающийся с $x =\pi$ (ссылка):
Несколько заметок:
Теперь ДНК выглядит примерно так [0 , -1, 0, 1]. Цикл аналогичен, но начальное значение изменилось, так как мы начинаем с $x=\pi$.
Записанные как вычисляемые числа, знаменатели 1, 6, 120, 5040 выглядят странно. Но они просто любой другой факториал: 1! = 1, 3! = 6, 5! =120, 7! = 5040. В общем случае ряд Тейлора может иметь корявые знаменатели. 9{12}$ и выше. Поскольку $\sin(x)$ имеет бесконечные производные, у нас бесконечные члены, и компьютер должен где-то нас обрезать. ( Хватит с тебя Тейлоринга на сегодня, приятель. )
Применение: аппроксимация функций
Ряд Тейлора часто используется для получения быстрой аппроксимации функции. Если вы хотите головастика, вам нужна ДНК всей лягушки?
Ряд Тейлора состоит из набора терминов, обычно упорядоченных по важности: 92 $, квадратичный член, говорит нам, насколько нужно ускориться при удалении от нашей точки.
и так далее
Если нам нужен прогноз только на несколько мгновений вокруг нашей точки, начальное положение и скорость могут быть достаточно хорошими:
Если мы отслеживаем дольше, то ускорение становится важным:

Как мы получаем дальше от нашей начальной точки, нам нужно больше терминов, чтобы наш прогноз был точным. x$: 9x$ имеет положительные члены, а синус и косинус чередуют знаки. Как мы можем связать их вместе?
Эйлер понял, что мнимое число может поменять знак с положительного на отрицательный:
Ого. Использование воображаемой экспоненты и разделение на нечетные/четные степени показывает, что синус и косинус прячутся внутри экспоненциальной функции. Удивительный.
Хотя это доказательство формулы Эйлера не показывает , почему мнимое число имеет смысл, оно показывает папочку, прячущегося за кулисами.
Приложение: Ассорти Ага! Моменты
Связь с рядом Фурье
Ряд Тейлора извлекает «полиномиальную ДНК», а ряд/преобразование Фурье извлекает «циклическую ДНК» функции. Оба рассматривают функции как построенные из более мелких частей (многочленов или экспоненциальных путей).
Всегда ли работает серия Taylor?
Математический анализ мне не по плечу, но некоторые функции нелегко (или вообще невозможно) аппроксимировать полиномами.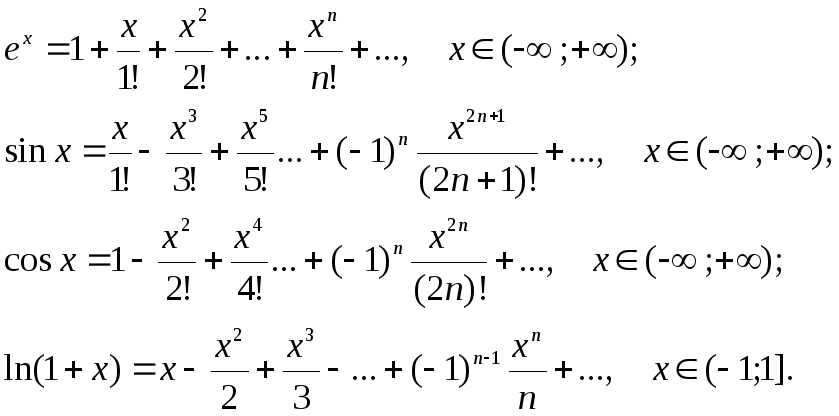 93$ взрываются по мере роста $x$. Чтобы иметь медленную, постепенную кривую, вам нужна армия полиномиальных членов, сражающихся за нее, и один победитель едва ли появится. Если вы остановите поезд слишком рано, приближение снова взорвется.
Например, вот ряд Тейлора для $\ln(1 + x)$. Черная линия — это та кривая, которую мы хотим, и добавление дополнительных членов, даже десятков, едва ли дает нам точность выше $x=1,0$. Просто слишком сложно поддерживать пологий склон с терминами, которые хотят разгуляться.
source
В этом случае у нас есть только радиус сходимости, при котором аппроксимация остается точной (например, около $|x| < 1$).
Превращение геометрических определений в алгебраические
Синус часто определяется геометрически: высота линии на круглой фигуре.
Превратить это в уравнение кажется очень сложным. Ряд Тейлора дает нам процесс: если мы знаем одно значение и то, как оно изменяется (производная), мы можем реконструировать ДНК. 93 + \точки $. Мы перешли от словесного описания к уравнению.
Фу! Несколько пунктов для размышления.
Счастливая математика.
Другие сообщения из этой серии
Нежное введение в изучение исчисления
Понимание исчисления с помощью метафоры банковского счета
Доисторическое исчисление: открытие Пи

Аналогия исчисления: интегралы как умножение
Исчисление: построение интуиции для производной
Как понимать деривативы: произведение, мощность и правила цепочки
Как понимать производные: правило частных, показатели степени и логарифмы
Интуитивно понятное знакомство с ограничениями
Интуиция для ряда Тейлора (аналогия ДНК)
Зачем нужны пределы и бесконечно малые числа?
Обучение исчислению: преодоление нашей искусственной потребности в точности
Дружеский разговор о том, 0,999… = 1
Аналогия: исчисление камеры
Практика абстракции: графы исчисления
Quick Insight: более простая арифметика с исчислением
Как прибавить от 1 до 100 с помощью исчисления
Интеграл Sin(x): Геометрическая интуиция
Формула серии Тейлора — Что такое формула серии Тейлора?
Ряд Тейлора функции – это бесконечная сумма членов, которая выражается через производные функции в любой точке, где каждый следующий член имеет больший показатель степени, например x, x
2 , x ³ и т. д. Таким образом, формула ряда Тейлора помогает в математическом представлении ряда Тейлора. Давайте изучим формулу ряда Тейлора, используя несколько решенных примеров в конце страницы. 9n \)
Здесь
f(x) = действительная или комплекснозначная функция, которая бесконечно дифференцируема при действительном или комплексном числе «a» — это степенной ряд
n = общее количество терминов в ряду

Доказательство формулы ряда Тейлора
Утверждение теоремы ряда Тейлора:
Предположим, что если $f(x)$ – действительная или составная функция, которая является дифференцируемой функцией числа окрестности, которая также является вещественной или составной. Тогда ряд Тейлора описывает следующий степенной ряд: 9{3}+\ldots\)
Следовательно, ряд Тейлора доказан.
Рассмотрим применение формулы ряда Тейлора в следующем разделе.

Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия. С Cuemath вы будете учиться визуально и будете удивлены результатами.
Забронировать бесплатный пробный урок
Пример 1: Найти разложение для функции, f(x) = 2x — 2x ² с центром в точке a = -3 с использованием формулы ряда Тейлора.
Решение:
Найти ряд Тейлора для заданной функции
Дано:

Функция, f(x) = 2x — 2x
$P_n\ )(x) = f(a) + f′(a)(x − a) + f′′(a)/2! × (x − a) ² + f′′′(a)/3! × (x − a) ³ + f ⁽⁴⁾ (a)/4! × (x − a) ⁴ + … + f ⁽ⁿ⁾ (a)/n! × (х — а) ⁿ
Функция и ее производные.
f(x) = 2x − 2x ²
f′(x) = 2− 4x
f′′(x) = −4
f′′′(x) = 0
9034 8 С a = −3 и n = 3, требуемое разложение:
f(x) = f(−3) + f′(−3)(x − (−3)) + f′′(−3)/ 2! × (x − (−3)) ² + f′′′(−3)/3! × (x − (−3)) ³
f(x) = f(−3) + f′(−3)(x + 3) + f′′(−3)/2! × (x + 3) ² + f′′′(−3)/3! × (x + 3) ³
Вычислим функцию и ее производные при x = a = −3:
f(−3) = 2(−3) − 2(−3)
2 = -24
f′(−3) = 2 — 4(-3) = 14
f′′ (−3) = −4
f′′′(−3) = 0, и все производные отсюда и далее равны нулю.
Разложение в ряд Тейлора для данной функции:
\(P_3$(x) = -24 + 14(x + 3) — 4/2! (х + 3) ² — 0/3! (x + 3) ³
$P_3$(x) = -24 + 14(x + 3) — 2(x + 3) ²
Ответ: Разложение в ряд Тейлора вокруг a = −3 для функции f(x) = 2x − 2x ² равно -24 + 14(x + 3) — 2(x + 3) ² .
Пример 2: Найти разложение в ряд Тейлора для функции f(x) = cos x с центром в точке x = 0.
Решение:
Функция , f(x) = Cos x
Используя формулу ряда Тейлора,
f(x) = f(a) + f′(a)(x − a) + f′′(a)/2! × (x − a) ² + f′′′(a)/3! × (x − a) ³ + f ⁽⁴⁾ (a)/4! × (х — а) ⁴ + … + f ^(н) (а)/н! × (x − a) ⁿ
Вычислим функцию и ее производные: ) = −cos(x)
f»'(x) = sin(x)
Таким образом,
cos(x) = cos(a) − sin(a)/1! (x — a) − cos(a)/2! (x — a) ² + sin(a)/3! (x — a) ³ + …
Теперь положим a = 0,
cos(x) = 1 − 0/1! (x — 0) − 1/2! (x — 0) ² + 0/3! (х — 0) ³ + 1/4! (x — 0) ⁴ + . ..
cos(x) = 1 − x ² /2! + х ⁴ /4! − …
Ответ: Разложение в ряд Тейлора для данной функции, cos(x) = 1 − x ² /2! + х ⁴ /4! − …
Пример 3. Найдите ряд Тейлора для f(x) = x ³ — 10x ² + 6 при x=3.
Решение: Сначала найдем производные данной функции.
f(x) = x ^{{3}
\end{aligned}\)}
Ответ: Разложение в ряд Тейлора для данной функции: = − 57 − 33(x−3) − (x−3) ² + (x−3) ³
Часто задаваемые вопросы о формуле серии Тейлора
Для чего используется формула серии Тейлора?
Ряд Тейлора полезен в информатике, исчислении, химии, физике и т. д. Ряд Тейлора используется для оценки того, как выглядит функция.
Что такое формула ряда Тейлора?
Формула ряда Тейлора помогает расширить функцию вокруг значения переменной, используя производные функции.
No related posts.