О вычислении матричной экспоненты / Хабр
При построении и анализе поведения решений систем обыкновенных дифференциальных уравнений иногда требуется определять матричную экспоненту [1]. Классический метод связан с тем, что приходится рассчитывать большие степени матриц. В данном топике рассматривается алгоритм приближенного вычисления матричной экспоненты, который за фиксированное число матричных операций дает результат с заданной точностью. Проведен вычислительный эксперимент с целью анализа эффективности алгоритма.
1. Вычисление матричной экспоненты
Вычисление экспоненты
где E — единичная матрица, t — время, связано с необходимостью расчета высоких степеней матрица A. Получим формулу, позволяющую определить матричную экспоненту с помощью n степеней матрицы A (n — ее порядок).
Пусть характеристическое уравнение матрицы A имеет вид
По теореме Гамильтона-Кэли [2] матрица A удовлетворяет матричному уравнению, аналогичному (2):
откуда
Следуя методу Д. К. Фаддеева [2], коэффициенты характеристического уравнения определяются по рекуррентному соотношению
К. Фаддеева [2], коэффициенты характеристического уравнения определяются по рекуррентному соотношению
где — след матрицы (сумма элементов, стоящих на главной диагонали),
Далее введем обозначение: если m=0, то ; иначе (при натуральном m)
Умножим обе части соотношения (3) на матрицу A с учетом введенных обозначений. Получим
Выражение (5) можно переписать как
Теперь умножим обе части равенства (6) на матрицу A, подставив при этом в полученное соотношение формулу (3):
Тогда из выражения (7) с помощью последовательного умножения на матрицу A обеих его частей следует, что
Теперь представим матричную экспоненту как
Откуда имеем
2. Описание алгоритма
Для реализации вычисления матричной экспоненты, согласно (8), был применен следующий алгоритм. Сначала нужно инициировать результат значением нулевой матрицы. Вычислить для k от 0 до n. Далее выполнить для k от 0 до n–1 следующую последовательность операций:
Вычислить для k от 0 до n. Далее выполнить для k от 0 до n–1 следующую последовательность операций:
1. Вычислить сумму . В качестве критерия прекращения суммирования использовать условие , где — положительное число, характеризующее точность вычисления суммы.
При вычислении матричной экспоненты с помощью данного алгоритма используется рекуррентное соотношение (4). При больших значениях m и k большинство значений q будут рассчитываться повторно много раз. Поскольку q(m,k) является чистой функцией (зависит только от входных аргументов), то будет разумно применить стратегию мемоизации.
Мемоизация — оптимизационная техника, заключающаяся в запоминании результатов вычисления функции для предотвращения множественного расчета значения функции от одних и тех же аргументов. Данная оптимизация позволяет улучшить временные характеристики алгоритма за счет увеличения затрат памяти.
3. Сравнение с классическим алгоритмом
Заметим, что классический алгоритм имеет потребление памяти . Описанный алгоритм, в виду необходимости хранить n-1 степень матрицы A, имеет потребление памяти .
Нами был проведен вычислительный эксперимент с целью сравнить быстродействие алгоритмов. Для этого была разработана KipDblK программа из комплекса [3] на языке C++, реализующая оба алгоритма. С помощью данной программы были произведены расчеты матричной экспоненты для матриц различного размера. Порядок матрицы изменялся от 2 до 132. Матрица инициализировалась случайными числами в диапазоне [0;1]. Экспонента вычислялась для t=1.
Рис. 1. Сравнение временных характеристик классического алгоритма (верхняя кривая) вычисления матричной экспоненты и алгоритма, описанного в данном топике (нижняя кривая).
P.S.
Данный топик был подготовлен по материалам нашей статьи [4].
Литература
1. Демидович Б.П. Лекции по математической теории устойчивости. — М.: Наука, 1967.
2. Гантмахер Ф.Р. Теория матриц. – М.: Наука, 1967.
3. KipDblKmaxima_comm.tar.gz.
4. Безгин С.В., Пчелинцев А.Н. Организация матричных и символьных вычислений для исследования поведения решений обыкновенных дифференциальных уравнений // Системы управления и информационные технологии, 2012. Т. 47, №1. — С. 4-7.
Калькулятор Экспоненты — Mathcracker.
 (1/3)’.
(1/3)’.
Все, что вам нужно сделать, это ввести правильное числовое выражение, включающее экспоненту, а затем нажать кнопку «Вычислить».
Как правило, выражения с экспонентами допускают некоторые упрощения при перемножении членов с экспонентами.
Как упростить или вычислить экспоненты?
Экспоненты часто встречаются в алгебре, и, естественно, во многих контекстах. С экспонентами легко работать при условии наличия определенных структур. Для того чтобы упрощения были простыми, необходимо иметь умножения и одинаковое основание, но это не единственный способ.
Каковы правила работы с экспонентами?
Мы могли бы сделать этот список более компактным, но это основные правила экспоненты, которые помогут вам упростить выражения
- Правило 1: \(a^m \cdot a^n = a^{m+n}
- Правило 2: \(\displaystyle \frac{a^m}{a^n} = \displaystyle a^{m-n}\)
- Правило 3: \({a^{m}}^n = a^{mn}\)
- Правило 4: \((ab)^m = a^m b^m\)
- Правило 5: \(\displaystyle \left(\frac{a}{b}\right)^m = \displaystyle \frac{a^m}{b^m}\)
- Правило 6: \(a^{-m} = \displaystyle \frac{1}{a^m} \)
- Правило 7: \(a^0 = 1\)
- Правило 8: \(a^{\frac{m}{n}} = \displaystyle \sqrt[n]{a^m} \)
Некоторые правила в этом списке избыточны, и мы могли бы вывести их из меньшего набора правил, но сейчас это не является нашей главной целью.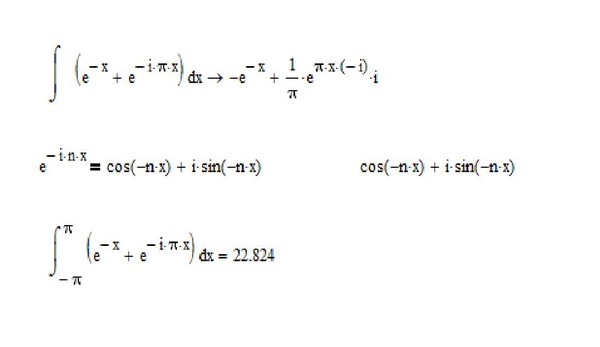
Как оперировать экспонентами?
Кажется, что я не даю ответа на этот вопрос, но ответ таков: используйте правила, представленные выше. Не существует единственно правильного способа работы с экспоненциальными выражениями, кроме соблюдения порядка операций, и начинать упрощать сначала легкие, простые термины.
Затем, основываясь на структуре того, что у вас есть, вы можете свернуть термины с экспонентами, в зависимости от того, имеют ли они одинаковое основание, или одинаковую экспоненту, или любую другую структуру, которая может использовать правила, представленные выше.
Почему важно вычислять экспоненты?
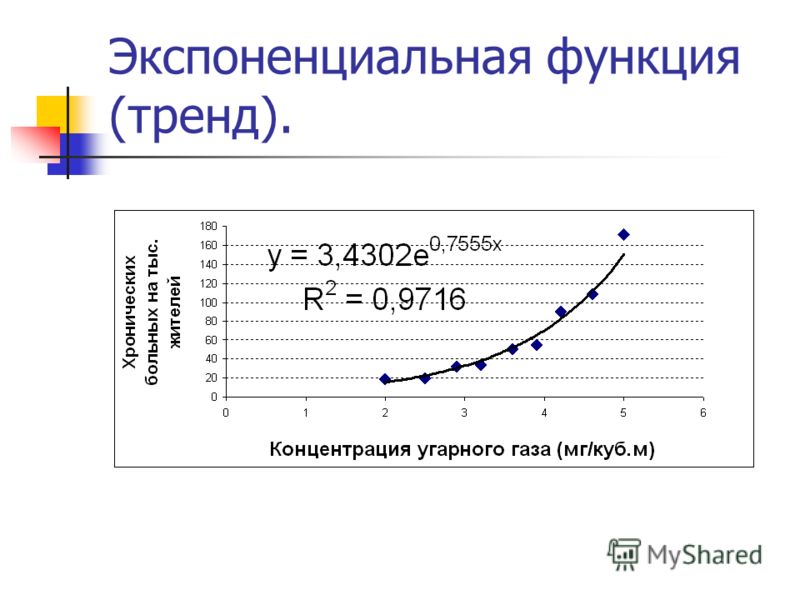
Экспоненты — естественное явление в алгебраических терминах, и умение обращаться с ними и, по возможности, уменьшать эти экспоненты может оказаться очень ценным навыком в вашем арсенале. 2 = \frac{4}{9} \times 36 = 16 \]
2 = \frac{4}{9} \times 36 = 16 \]
чем завершается расчет.
Больше калькуляторов по алгебре
Экспоненты — не единственные важные операции в алгебре. Дроби также важны, и вы можете использовать это
калькулятор сокращения дробей
, для уменьшения заданной дроби, или еще лучше использовать это
Калькулятор дробей
для обработки любых операций с дробями. Также в связи с дробями вы можете попробовать
перевести дробь в проценты
или же
дробь до десятичной
.
Как возвести экспоненту в степень в excel
Компьютеры admin 0 комментариев
Содержание
- 1 Функция EXP в Excel
- 2 Вычисление экспоненты в Эксель
- 2.1 Способ 1: вычисление экспоненты при помощи ручного ввода функции
- 2.2 Способ 2: использование Мастера функций
- 2.3 Способ 3: построение графика
- 3 Описание
- 4 Синтаксис
- 5 Замечания
- 6 Пример
Рассмотрим возможности возведения экспоненты в степень и в частности использования числа Е в Excel, также известного как число Эйлера.
Число Е — основание натурального логарифма, математическая константа равная приблизительно 2,71828.
Также данное число называют как число Эйлера или число Непера.
Экспонента — показательная функция f(x) = exp (x) = e x , где е — число Эйлера.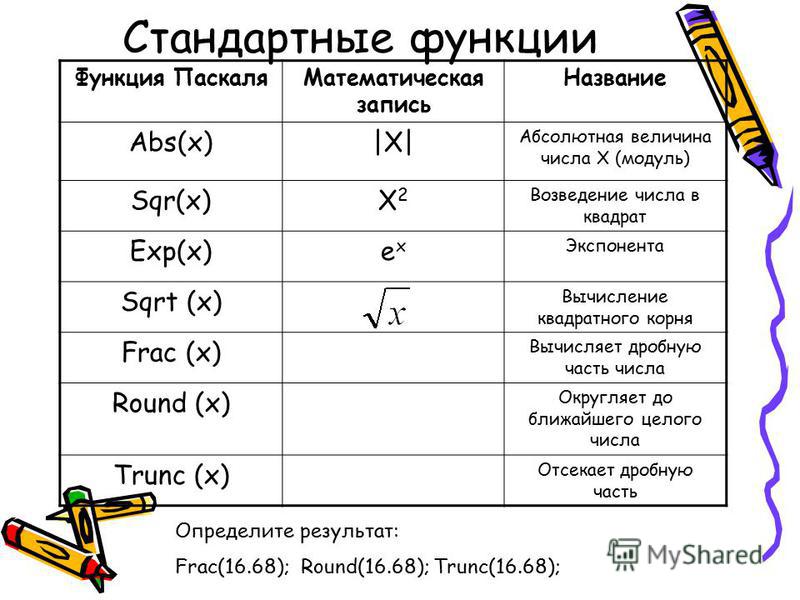
Также в Excel есть возможность использовать другую известную математическую константу — число Пи.
Функция EXP в Excel
Чтобы возвести экспоненту в степень в Excel можно воспользоваться стандартной функцией:
EXP(число)
Возвращает экспоненту заданного числа.
- Число(обязательный аргумент) — степень, в которую возводится число Е (приблизительное значение 2,71828182845904).
Для получения числа Е в Excel достаточно в качестве аргумента функции EXP взять значение 1:
Одной из самых известных показательных функций в математике является экспонента. Она представляет собой число Эйлера, возведенное в указанную степень. В Экселе существует отдельный оператор, позволяющий её вычислить. Давайте разберемся, как его можно использовать на практике.
Вычисление экспоненты в Эксель
Экспонента является числом Эйлера, возведенным в заданную степень.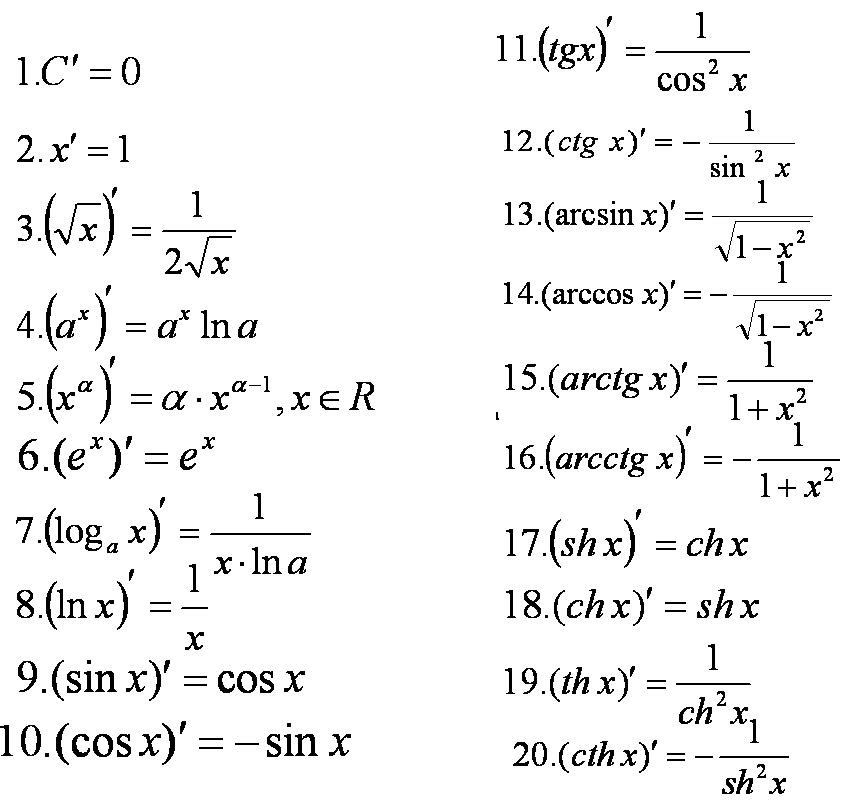 Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
Само число Эйлера приблизительно равно 2,718281828. Иногда его именуют также числом Непера. Функция экспоненты выглядит следующим образом:
где e – это число Эйлера, а n – степень возведения.
Для вычисления данного показателя в Экселе применяется отдельный оператор – EXP. Кроме того, эту функцию можно отобразить в виде графика. О работе с этими инструментами мы и поговорим далее.
Способ 1: вычисление экспоненты при помощи ручного ввода функции
Для того чтобы рассчитать в Экселе величину экспоненты для значения e в указанной степени, нужно воспользоваться специальным оператором EXP. Его синтаксис является следующим:
То есть, эта формула содержит только один аргумент. Он как раз и представляет собой степень, в которую нужно возвести число Эйлера. Этот аргумент может быть как в виде числового значения, так и принимать вид ссылки на ячейку, содержащую в себе указатель степени.
- Таким образом для того, чтобы рассчитать экспоненту для третьей степени, нам достаточно ввести в строку формул или в любую незаполненную ячейку на листе следующее выражение:
 Итог выводится в заранее указанную ячейку.
Итог выводится в заранее указанную ячейку.Способ 2: использование Мастера функций
Хотя синтаксис расчета экспоненты предельно прост, некоторые пользователи предпочитают применять Мастер функций. Рассмотрим, как это делается на примере.
- Устанавливаем курсор на ту ячейку, где должен будет выводиться итоговый результат расчета. Щелкаем по значку в виде пиктограммы «Вставить функцию» слева от строки формул.
Открывается окошко Мастера функций. В категории «Математические» или «Полный алфавитный перечень» производим поиск наименования «EXP». Выделяем это название и жмем на кнопку «OK».
Открывается окно аргументов. Оно имеет только одно поле – «Число». Вбиваем в него цифру, которая будет означать величину степени числа Эйлера. Жмем на кнопку «OK».

Если в качестве аргумента используется ссылка на ячейку, которая содержит показатель степени, то нужно поставить курсор в поле «Число» и просто выделить ту ячейку на листе. Её координаты тут же отобразятся в поле. После этого для расчета результата щелкаем по кнопке «OK».
Способ 3: построение графика
Кроме того, в Экселе существует возможность построить график, взяв за основу результаты, полученные вследствие вычисления экспоненты. Для построения графика на листе должны уже иметься рассчитанные значения экспоненты различных степеней. Произвести их вычисление можно одним из способов, которые описаны выше.
- Выделяем диапазон, в котором представлены экспоненты. Переходим во вкладку «Вставка». На ленте в группе настроек «Диаграммы» нажимаем на кнопку «График». Открывается список графиков. Выбирайте тот тип, который считаете более подходящим для выполнения конкретных задач.
 ).
).Функция EXP является обратной по отношению к функции LN, т. е. к натуральному логарифму числа.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
Приблизительное значение e
Основание натурального логарифма e, возведенное в квадрат
показателей — определение, примеры | Свойства показателей степени
Показатель степени числа показывает, сколько раз мы умножаем число само на себя. Например, 3 4 означает, что мы умножаем 3 четыре раза. Его расширенная форма 3×3×3×3. Экспонента также известна как степень числа. Это может быть целое число, дробь, отрицательное число или десятичные дроби. Давайте узнаем больше об экспонентах в этой статье.
1. | Что такое экспоненты? |
| 2. | Законы (свойства или правила) экспонентов |
| 3. | Отрицательные показатели |
| 4. | Экспоненты с дробями |
| 5. | Десятичные экспоненты |
| 6. | Научное обозначение с показателями |
| 7. | Часто задаваемые вопросы по экспонентам |
Что такое экспоненты?
Показатель степени числа показывает, сколько раз число умножается само на себя. Например, 2×2×2×2 можно записать как 2 4 , так как 2 умножается на себя 4 раза. Здесь 2 называется «базой», а 4 называется «показатель степени» или «степень». В общем, x n означает, что x умножается сам на себя n раз.
Здесь в члене x n ,
- x называется «базовым»
- n называется «показатель степени»
- x n читается как «x в степени n» (или) «x в степени n».

Ниже приведены некоторые примеры показателей степени:
- 3 × 3 × 3 × 3 × 3 = 3 5
- -2 × -2 × -2 = (-2) 3
- а × а × а × а × а × а = а 6
Показатель степени важен, потому что без него, когда число повторяется само по себе много раз, очень трудно написать произведение. Например, очень легко написать 5 7 вместо записи 5 × 5 × 5 × 5 × 5 × 5 × 5.
Свойства показателей степени
Свойства показателей или законы показателей используются для решения задач, связанных с показателями. Эти свойства также считаются основными правилами показателей степени, которым необходимо следовать при решении показателей степени. Свойства экспонент упоминаются ниже.
- Закон произведения: a m × a n = a m+n
- Закон частного: а м /а н = а м-н
- Закон нулевой степени: a 0 = 1
- Закон отрицательного показателя степени: a -m = 1/a m
- Закон Силы Силы: (a m ) n = a mn
- Закон мощности продукта: (ab) m = a m b m
- Закон степени частного: (a/b) m = a m /b m
Отрицательные показатели
Отрицательная экспонента говорит нам, сколько раз мы должны умножить обратную величину основания. Например, если известно, что a -n , его можно разложить как 1/a n . Это означает, что мы должны умножить обратную величину a, то есть 1/a ‘n’ раз. Отрицательные показатели степени используются при записи дробей с показателями степени. Некоторые примеры отрицательных показателей: 2 × 3 -9 , 7 -3 , 67 -5 и т. д. Мы можем преобразовать их в положительные показатели следующим образом:
Например, если известно, что a -n , его можно разложить как 1/a n . Это означает, что мы должны умножить обратную величину a, то есть 1/a ‘n’ раз. Отрицательные показатели степени используются при записи дробей с показателями степени. Некоторые примеры отрицательных показателей: 2 × 3 -9 , 7 -3 , 67 -5 и т. д. Мы можем преобразовать их в положительные показатели следующим образом:
- 2 × 3 -9 = 2 × (1/3 9 ) = 2 / 3 9
- 7 -3 = 1/7 3
- 67 -5 = 1/67 5
Экспоненты с дробями
Если показатель степени числа является дробью, он называется дробным показателем. Квадратные корни, кубические корни, корень n th являются частями дробных показателей. Число со степенью 1/2 называется квадратным корнем из основания. Точно так же число со степенью 1/3 называется кубическим корнем из основания. Некоторые примеры показателей степени с дробями: 5 2/3 , -8 1/3 , 10 5/6 и т. д. Мы можем записать их как:
Некоторые примеры показателей степени с дробями: 5 2/3 , -8 1/3 , 10 5/6 и т. д. Мы можем записать их как:
- 5 2/3 = (5 2 90 0 3 19030 = 25 1/3 = ∛25
- -8 1/3 = ((-2) 3 ) 1/3 = -2
- 10 5/6 = (10 5 ) 6 = 6 √10 5 = 6 √1000002
Десятичные экспоненты
Если показатель степени числа задан в десятичной форме, он называется десятичным показателем степени. Немного сложно оценить правильный ответ любого десятичного показателя степени, поэтому мы находим приблизительный ответ для таких случаев. Десятичные показатели степени можно решить, сначала преобразовав десятичную дробь в дробную форму. Например, 4 1.5 может быть записано как 4 3/2 , что может быть дополнительно упрощено, чтобы получить окончательный ответ 8. т.е. = 8.
т.е. = 8.
Научное обозначение с показателями
Научная нотация — это стандартная форма записи очень больших или очень маленьких чисел. При этом числа записываются с помощью десятичной дроби и степеней 10. Говорят, что число записывается в научной записи, когда число от 0 до 10 умножается на степень 10. В случае числа больше 1 , степень 10 будет положительной, а в случае чисел меньше 1 , степень 10 будет отрицательной. Давайте разберемся с этапами записи чисел в экспоненте с экспонентами:
- Шаг 1: Ставим десятичную точку после первой цифры числа слева. Если в числе только одна цифра без нулей, то десятичную дробь ставить не нужно.
- Шаг 2: Умножьте это число на степень 10 так, чтобы степень была равна количеству сдвигов десятичной точки.
Следуя этим двум простым шагам, мы можем записать любое число в стандартной форме с показателями, например, 560000 = 5,6 × 10 5 , 0,00736567 = 7,36567 × 10 -3 .
Чтобы узнать больше об использовании степеней в научной записи чисел, посетите следующие статьи:
- Как записать 2,5 миллиона в научной записи?
- Как записать 12 миллионов в экспоненциальном представлении?
- Как записать 0,0001 в экспоненциальном представлении?
- Какое научное обозначение для 8 миллионов?
- Как записать 13 миллионов в экспоненциальном представлении?
- Какое из следующих выражений записано в экспоненциальной записи
Советы и подсказки:
- Если у дроби отрицательный показатель степени, то мы берем обратную дробь, чтобы показатель степени был положительным. т. е. (а/б) -т = (б/а) м .
- Если показатели степени одинаковы в обеих частях уравнения, мы можем установить равные основания и наоборот. то есть м = а н ⇔ м = н.
☛ Связанные темы по показателям степени
Посмотрите еще несколько интересных статей, основанных на показателях степени в математике.
- Умножение показателей степени
- Экспоненциальные функции
- Экспоненциальные уравнения
- Иррациональные Показатели
Показатели Примеры
Пример 1: Размеры шкафа даны в таких показателях, как x 5 единицы, у 3 единицы и х 8 единицы. Найдите его объем.
Решение:
Данные размеры шкафа представлены в виде показателей, т. е. длина = х 5 ед., ширина = у 3 ед., высота = х 8 ед. Объем гардероба составляет, объем= двч. Итак, путем подстановки значений объем гардероба равен х 5 × у 3 × х 8 = х 13 у 3 (с использованием формулы показателей = a m × a n = a (m+n) ). Следовательно, объем гардероба равен х 13 у 3 кубических единиц.
Пример 2: В саду на каждом дереве около 5 7 листьев, а в саду около 5 3 деревьев.
 Найдите общее количество листьев в терминах показателей.
Найдите общее количество листьев в терминах показателей.Решение:
Количество деревьев в саду = 5 3 и количество листьев в каждом дереве = 5 7 . Общее количество листьев: 5 3 × 5 7 = 5 10 (с использованием формулы показателей степени = a m × a n = a (m+n) ). Следовательно, общее количество листьев равно 5 10 .
Пример 3: Упростите следующее выражение: p 12 ÷ p 4 q.
Решение:
Данное выражение равно p 12 ÷ стр 4 кв. Чтобы упростить это выражение, мы используем закон отношения показателей, который гласит: a m / a n = a m-n
⇒ P 12 /P 4 Q
⇒ P 12-4 /Q
⇒ P 8 /Q
Следовательно, P 12 ÷ P 4 Q = P 8 / кв.

перейти к слайдуперейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных эффектов.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по Exponents
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по экспонентам
Что такое экспоненты в математике?
Показатель степени — это число, которое помещается над числом в виде надстрочного индекса. Другими словами, это указывает на то, что основание возведено в определенную степень. Показатель степени также называют другими именами, такими как индекс и мощность. Если m — положительное число, а n — его показатель степени, то m n означает, что m умножается само на себя n раз.
Каковы свойства экспонент?
Законы экспоненты — это некоторые правила, которые мы используем для вычислений с экспонентами. Эти правила помогают нам быстро считать. Ниже перечислены законы показателей или несколько важных свойств показателей:
Эти правила помогают нам быстро считать. Ниже перечислены законы показателей или несколько важных свойств показателей:
Каковы примеры показателей степени?
Вот некоторые примеры показателей степени:
- 7 × 7 × 6 × 6 × 6 = 7 2 × 6 3
- -4 × -4 × -4 × -4 = (-4) 4
- р × р × р × р × р = р 5
Как экспоненты относятся к реальной жизни?
В реальной жизни мы используем понятие экспоненты для упрощенного и краткого написания чисел. Повторное умножение можно легко записать с помощью показателей степени. Кроме того, мы используем показатель степени для записи больших чисел, например, расстояния Луны от Земли, количества бактерий, присутствующих на поверхности, и т. д.
д.
Как добавить экспоненты?
Экспоненты не могут быть добавлены. Мы можем добавлять только одинаковые термины (термы, имеющие один и тот же показатель степени и одну и ту же переменную). Но, в случае умножения членов с одинаковыми переменными, мы прибавляем показатели степени переменной к умножению. Например, х 2 × х 4 = х (2+4) = х 6 . Попробуйте калькулятор сложения показателей степени от Cuemath и получите ответы быстро и легко.
Почему показатели степени важны?
Экспоненты важны для записи значений чисел в упрощенной форме. Мы знаем, что многократное сложение можно записать как умножение. Точно так же многократное умножение можно записать просто с помощью показателей степени.
Как рассчитать показатели степени с помощью калькулятора показателей степени?
«Калькулятор степени» — это онлайн-инструмент, который находит значение экспоненциального выражения. Проверьте теперь калькулятор экспоненты Cuemath и найдите значение экспоненциального выражения для заданного значения основания и экспоненты в течение нескольких секунд.
☛ Также проверьте:
- Калькулятор отрицательных показателей
- Калькулятор степени деления
- Калькулятор умножения показателей степени
- Калькулятор правил экспоненты
- Калькулятор дробей с показателями степени
Как умножать показатели степени?
Когда необходимо умножить показатели степени, мы сначала решаем числа в скобках, степень вне скобок умножается на каждую степень внутри скобок. Например, (3x 2 y 3 ) 2 = 3 2 × x 2×2 × y 3×2 = 9x 4 y 6.
Какая польза от свойств экспонент?
Свойства экспонент широко используются в математике, особенно в алгебре. С помощью свойств показателей степени мы можем легко упростить выражения, а также написать выражения за меньшее количество шагов. Давайте разберемся в этом на простом примере. С помощью свойств экспоненты 2 4 × 2 6 можно упростить двумя быстрыми шагами: 2 4 × 2 6 = 2 (4 + 6) = 2 10 .
Каково реальное применение экспонентов?
Экспоненты имеют различные применения. Ниже перечислены некоторые области применения экспонентов:
- Экспоненты широко используются в компьютерных играх, измерительных весах и т. д.
- Научные шкалы, такие как шкала рН или шкала Рихтера, основаны на показателях степени.
- Они используются при вычислении площади, объема и задач, связанных с измерением.
- Чаще всего они используются в соответствующих областях науки, техники, экономики, бухгалтерского учета и финансов.
- Они часто используются для представления памяти компьютера или ноутбука.
Как законы экспоненты используются в алгебре?
Законы экспоненты очень полезны в алгебре. Например, алгебраическая формула (a — b) 2 = a 2 + b 2 — 2ab можно легко записать и вычислить, применяя правила возведения в степень. Многие такие алгебраические формулы зависят только от законов показателей.
Как отрицательные показатели используются в реальной жизни?
Отрицательные показатели степени используются для записи очень маленьких чисел в реальной жизни, что означает числа со значениями от 0 до 1.
Что такое нулевая степень?
Нулевой показатель степени означает числа, у которых показатель степени равен 0. Значения этих чисел всегда равны 1. Любое число с 0 в качестве его показателя равно 1.
Численный расчет наибольшего показателя Ляпунова
Численный расчет наибольшего показателя Ляпунова15 октября 1997 г.
(пересмотрено 8 января 2015 г.)
Обычным тестом на хаос является расчет
наибольший показатель Ляпунова. Положительный крупнейший Ляпунов
экспонента указывает на хаос. Когда человек имеет доступ к
уравнения, порождающие хаос, это относительно легко
делать. Когда у человека есть доступ только к записи экспериментальных данных,
такой расчет трудно или невозможно, и в этом случае будет
здесь не рассматривать. Общая идея состоит в том, чтобы следовать двум
близлежащие орбиты и вычислить их среднюю логарифмическую скорость
разделение. Всякий раз, когда они отходят слишком далеко друг от друга, один из
орбиты должны быть перемещены обратно в окрестности другой вдоль
линия разделения. Консервативная процедура заключается в том, чтобы сделать это
на каждой итерации. Полная процедура выглядит следующим образом:
Когда у человека есть доступ только к записи экспериментальных данных,
такой расчет трудно или невозможно, и в этом случае будет
здесь не рассматривать. Общая идея состоит в том, чтобы следовать двум
близлежащие орбиты и вычислить их среднюю логарифмическую скорость
разделение. Всякий раз, когда они отходят слишком далеко друг от друга, один из
орбиты должны быть перемещены обратно в окрестности другой вдоль
линия разделения. Консервативная процедура заключается в том, чтобы сделать это
на каждой итерации. Полная процедура выглядит следующим образом:
- Начните с любого начального условия в бассейне Привлечение.
- Повторяйте, пока орбита не окажется на аттракторе.
- Выберите (почти любую) близлежащую точку (через d 0 ).
- Продвинуть обе орбиты на одну итерацию и вычислить новую
разделение d 1 .

- Журнал оценки | d 1 / d 0 | в любой удобной базе.
- Скорректировать одну орбиту так, чтобы расстояние между ней было d 0 и находится в том же направлении, что и d 1 .
- Повторите шаги 4-6 много раз и рассчитайте среднее значение шаг 5.
Еще лучше было бы начать с точки, о которой известно, что она находится на аттрактор, в этом случае шаг 2 можно пропустить.
Это требует некоторого суждения или предварительного знания системы.
 в стадии изучения. Для большинства систем безопасно просто повторять
несколько сотен раз и предположим, что этого достаточно. Обычно это
будет, и в любом случае ошибка, вызванная небольшим отклонением
аттрактор обычно невелик, если только вы не очень
близко к точке бифуркации.
в стадии изучения. Для большинства систем безопасно просто повторять
несколько сотен раз и предположим, что этого достаточно. Обычно это
будет, и в любом случае ошибка, вызванная небольшим отклонением
аттрактор обычно невелик, если только вы не очень
близко к точке бифуркации.Подходящим выбором d 0 является тот, который находится на порядок квадратного корня из точности плавающей номера точек, которые используются. Например, в (8-байт) двойная точность (минимум, рекомендуемый для таких вычислений), переменные имеют 52-битную мантисса, и точность, таким образом, равна 2 -52 = 2,22 х 10 -16 . Поэтому значение d 0 = 10 -8 обычно достаточно.
Разделение рассчитывается из суммы квадратов различия в каждой переменной. Итак, для двумерной системы с переменными x и y , разделение будет d = [( x a — x b ) 2 + ( y a — y b ) 2 ] 1/2 , где нижние индексы ( a и b ) обозначают две орбиты соответственно.
По соглашению, натуральный логарифм (основание- e ) обычно используется, но для карт показатель Ляпунова часто указывается битами за итерацию, и в этом случае вам нужно будет использовать base-2. (Обратите внимание, что log 2 x = 1,4427 log e x ). Вы можете получить ошибки времени выполнения при вычислении логарифма, если d 1 становится настолько малым, что становится неотличимым от нуля.
 В
в таком случае попробуйте использовать большее значение д 0 . Если этого недостаточно, вам, возможно, придется игнорировать значения, в которых это
бывает, но при этом ваш расчет ляпуновской
экспонента будет несколько ошибкой.
В
в таком случае попробуйте использовать большее значение д 0 . Если этого недостаточно, вам, возможно, придется игнорировать значения, в которых это
бывает, но при этом ваш расчет ляпуновской
экспонента будет несколько ошибкой.Это, пожалуй, самый сложный и подверженный ошибкам шаг. В качестве пример (в 2-х измерениях), предположим, орбита б тот самый для корректировки, и его значение после одной итерации равно ( x b1 , у b1 ). Затем он будет повторно инициализирован до x b0 . = x a1 + d 0 ( x b1 — x a1 ) / d 1 и y b0 = у а1 + д 0 ( у б1 — у а1 ) / д 1 .
Возможно, вы захотите отбросить первые несколько значений, которые вы получите. уверены, что орбиты сориентировались в направлении максимальное расширение. Также неплохо рассчитать скользящее среднее как показатель того, имеют ли значения установить уникальный номер и получить указание на достоверность расчета. Иногда в результате сходится довольно медленно, но несколько тысяч итераций карты обычно достаточно, чтобы получить оценку с точностью до двух значащие цифры. Это хорошая идея, чтобы убедиться, что ваш результат не зависит от начальных условий, значение д 0 , и количество итераций, включенных в среднее значение. Ты может также захотеть проверить неограниченные орбиты, так как вы вероятно получить числовые ошибки и показатель Ляпунова не будет иметь смысл в таком случае.

Если система состоит из обыкновенных дифференциальных уравнений (а
потока) вместо разностных уравнений (карты) процедура
то же самое, за исключением того, что полученный показатель степени делится на
размер шага итерации, чтобы он имел единицы обратных секунд
вместо обратных итераций. Обычно вам понадобится
миллионы итераций дифференциальных уравнений, чтобы получить
результат хороший или лучше, чем две значащие цифры. Ан
пример для аттрактора Лоренца доступен.
См. также код для расчета
весь спектр показателей Ляпунова.
Ан
пример для аттрактора Лоренца доступен.
См. также код для расчета
весь спектр показателей Ляпунова.
Иногда можно получить весь спектр показателей, используя
описанный выше метод, например, когда система представляет собой двумерную
хаотическая карта или трехмерный хаотический поток, если вы знаете
скорость сжатия пространства состояний, усредненная по орбите (
диссипация), представляющая собой сумму показателей Ляпунова (легко
вычисляется по следу матрицы Якоби, усредненному вдоль
орбиты для потока или от среднего определителя
матрица Якоби для карты) и используя тот факт, что один показатель степени
должен быть равен нулю для непрерывного потока.
Чтобы оценить неопределенность вычисленного показателя Ляпунова,
вы можете повторить расчет для многих различных начальных
условия (в пределах бассейна притяжения) и возмущение
направления. Для хаотической системы достаточно начального условия
изменяться незначительно, так как орбиты быстро становятся некоррелированными из-за
чувствительной зависимости от начальных условий. Затем вы можете
рассчитать среднее значение и стандартное отклонение рассчитанных значений
чтобы избежать слишком распространенной ошибки цитирования большего количества цифр
чем значительны.
Затем вы можете
рассчитать среднее значение и стандартное отклонение рассчитанных значений
чтобы избежать слишком распространенной ошибки цитирования большего количества цифр
чем значительны.
Ref: JC Sprott, Хаос и временные ряды Анализ (Oxford University Press, 2003), стр. 116-117.
Назад к техническим примечаниям Sprott
: расчет, значения и многое другое
Вибху Сингх, Варун Дивакар и Ашиш Гарг
В этом блоге мы обсудим важную концепцию анализа временных рядов: показатель Херста . Мы научимся его вычислять на примере.
Во-первых, давайте разберемся, что такое показатель Херста.
Определение показателя Херста
Показатель Херста используется в качестве меры долговременной памяти временных рядов. Это связано с автокорреляцией временных рядов и скоростью, с которой они уменьшаются по мере увеличения отставания между парами значений.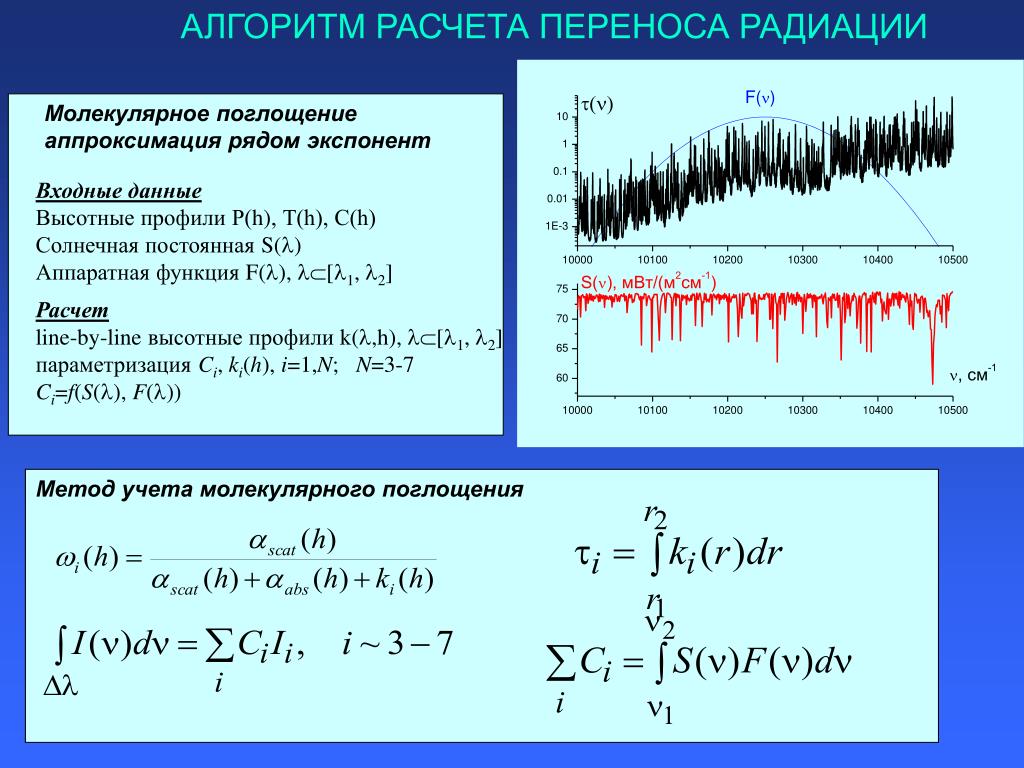
Значение Херста
Значение Херста больше 0,5
Если значение Hurst больше 0,5, то это будет указывать на устойчивый временной ряд (примерно соответствует трендовому рынку).
Значение Херста меньше 0,5
Если значение Херста меньше 0,5, то это можно рассматривать как антипостоянный временной ряд (грубо говоря, боковой рынок).
Значение Херста равно 0,5
Если значение Херста равно 0,5, то это указывает на случайное блуждание или на рынок, где предсказание будущего на основе прошлых данных невозможно.
Как вычислить показатель Херста
Чтобы вычислить показатель степени, нам нужно разделить данные на разные части. Например, если у вас есть данные возврата BTC/USD за последние 8 дней, вы делите их пополам следующим образом.
На примере 8 наблюдений только для иллюстрации 1 :
| Данные | Кусок 1 |
| 0,04 | |
| 0,02 | |
| 0,05 | |
| 0,08 | |
| 0,02 | |
| -0,17 | |
| 0,05 | |
| 0 |
1 Длина подряда в практических приложениях обычно намного больше и влияет на среднее значение и стандартное отклонение R/S-статистики.
Затем мы разделяем данные на 3 разных канала следующим образом:
- Раздел 1 — один блок из 8 наблюдений
- Раздел 2 — два блока из 4 наблюдений в каждом
- Раздел 3 — четыре блока из 2 наблюдений в каждом
| Данные | Кусок 1 |
| 0,04 | |
| 0,02 | |
| 0,05 | |
| 0,08 | |
| 0,02 | |
| -0,17 | |
| 0,05 | |
| 0 |
| Данные | Часть 2 | Часть 3 |
| 0,04 | 0,02 | |
| 0,02 | -0,17 | |
| 0,05 | 0,05 | |
| 0,08 | 0 |
| Данные | Кусок 4 | Кусок 5 | Кусок 6 | Кусок 7 |
| 0,04 | 0,05 | 0,02 | 0,05 | |
| 0,02 | 0,08 | -0,17 | 0 |
После разделения данных на фрагменты мы выполняем следующие вычисления для каждого фрагмента:
Шаг 1
Сначала мы вычисляем среднее значение фрагмента, скажем, с n наблюдениями,
M = (1/n) [h(1)+h(2)+...+h(n)]
| Данные | Кусок 1 |
| 0,04 | |
| 0,02 | |
| 0,05 | |
| 0,08 | |
| 0,02 | |
| -0,17 | |
| 0,05 | |
| 0 |
| Данные | Часть 2 | Часть 3 |
| 0,04 | 0,02 | |
| 0,02 | -0,17 | |
| 0,05 | 0,05 | |
| 0,08 | 0 |
| Данные | Кусок 4 | Кусок 5 | Кусок 6 | Кусок 7 |
| 0,04 | 0,05 | 0,02 | 0,05 | |
| 0,02 | 0,08 | -0,17 | 0 |
Шаг 2
Затем мы вычисляем стандартное отклонение (S) n наблюдений
s(n) = STD( h(1)+h(2)+...+h(n))
| Среднее | 0,011 |
| Стандартный | 0,072 |
| Среднее | 0,048 | -0,025 |
| Стандартный | 0,022 | 0,099 |
| Среднее | 0,030 | 0,065 | -0,075 | 0,025 |
| Стандартный | 0,0141 | 0,021 | 0,134 | 0,035 |
Шаг 3
Затем мы создаем среднецентрированный ряд, вычитая среднее значение из наблюдений,
x(1) = h(1) - M x(2) = h(2) - M ... x(n) = h(n) - M
| Кумулятивная сумма среднего серия | 0,029 |
| 0,038 | |
| 0,076 | |
| 0,145 | |
| 0,154 | |
| -0,028 | |
| 0,011 | |
| 0,000 |
| Суммарная сумма среднецентрированного ряда | -0,008 | 0,045 |
| -0,035 | -0,100 | |
| -0,033 | -0,025 | |
| 0,000 | 0,000 |
| Суммарная сумма среднецентрированного ряда | 0,010 | -0,015 | 0,095 | 0,025 |
| 0,000 | 0,000 | 0,000 | 0,000 |
Шаг 4
Затем мы вычисляем кумулятивное отклонение путем суммирования средних центрированных значений,
Y(1) = x(1) Y(2) = x(1) + x(2) ... Y(n) = x(1) + x(2) + ...+ x(n)
| Среднецентровый ряд (h(n)-M) | 0,029 |
| Стандартный | 0,009 |
| Среднецентровый ряд (h(n)-M) | -0,008 | 0,045 |
| Стандартный | -0,028 | -0,145 |
| Среднецентровый ряд (h(n)-M) | 0,010 | -0,015 | 0,095 | 0,025 |
| Стандартный | -0,010 | 0,015 | -0,095 | -0,025 |
Шаг 5
Далее мы вычисляем диапазон (R), который представляет собой разницу между максимальным значением кумулятивного отклонения и минимальным значением кумулятивного отклонения:
| Диапазон | 0,182 |
| Диапазон | 0,035 | 0,145 |
| Диапазон | 0,010 | 0,015 | 0,095 | 0,025 |
Шаг 6
И, наконец, мы вычисляем отношение диапазона R к стандартному отклонению S. Это также известно как масштабированный диапазон .
Это также известно как масштабированный диапазон .
| Диапазон | 0,182 |
| R/S (диапазон/станд.) | 2,528 |
| Средний R/S | 2,528 |
| Диапазон | 0,035 | 0,145 |
| R/S (диапазон/станд.) | 1,617 | 1,467 |
| Средний R/S | 1,542 |
| Диапазон | 0,010 | 0,015 | 0,095 | 0,025 |
| R/S (диапазон/станд.) | 0,707 | 0,707 | 0,707 | 0,707 |
| Средний R/S | 0,707 |
Этап 7
Как только у нас есть масштабированный диапазон для всех фрагментов, мы вычисляем среднее значение каждого подразделения и записываем его вместе с количеством выборок в каждом фрагменте этого подразделения, как показано.
| Диапазон | 0,182 |
| R/S (диапазон/станд.) | 2,528 |
| Средний R/S | 2,528 |
| Диапазон | 0,035 | 0,145 |
| R/S (диапазон/станд.) | 1,617 | 1,467 |
| Средний R/S | 1,542 |
| Диапазон | 0,010 | 0,015 | 0,095 | 0,025 |
| R/S (диапазон/станд.) | 0,707 | 0,707 | 0,707 | 0,707 |
| Средний R/S | 0,707 |
Шаг 8
Далее мы вычисляем логарифмические значения для размера каждой области и для масштабируемого диапазона каждой области.
| Сводка | |||
| Размер | Р/С | Журнал размера | Журнал Р/С |
| 8 | 2,528 | 2,079 | 0,927 |
| 4 | 1,542 | 1,386 | 0,433 |
| 2 | 0,707 | 0,693 | -0,347 |
Результат
Показатель Херста «H» представляет собой не что иное, как наклон графика логарифма (R/S) каждого диапазона по сравнению с логарифмом (размером) каждого диапазона.
Здесь log(R/S) — зависимая переменная или переменная y, а log(size) — независимая переменная или переменная x:
| Показатель Херста | 0,918 |
Заключение
Это значение показателя Херста указывает на то, что наши данные являются постоянными, но мы должны помнить, что наш набор данных слишком мал, чтобы сделать такой вывод.
Например, если вы хотите вычислить показатель Херста в Python с помощью библиотеки «hurst», вам потребуется указать не менее 100 точек данных.
Мы надеемся, что вы научились вычислять показатель Херста из этого блога. В нашем продвинутом курсе по криптовалютам мы продемонстрировали, как экспонента Херста вместе с другим техническим индикатором может давать оптимизированные торговые сигналы.
Отказ от ответственности: Все инвестиции и торговля на фондовом рынке сопряжены с риском. Любые решения о размещении сделок на финансовых рынках, включая торговлю акциями или опционами или другими финансовыми инструментами, являются личным решением, которое должно приниматься только после тщательного исследования, включая личный риск и финансовую оценку, а также привлечение профессиональной помощи в той степени, в которой вы считаю нужным. Торговые стратегии или связанная с ними информация, упомянутая в этой статье, предназначены только для информационных целей.


 Найдите общее количество листьев в терминах показателей.
Найдите общее количество листьев в терминах показателей.

 ..+h(n)]
..+h(n)]  ..+h(n))
..+h(n)) 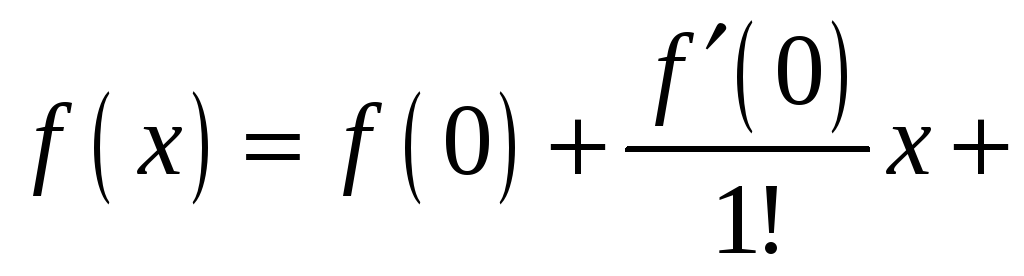 .. Y(n) = x(1) + x(2) + ...+ x(n)
.. Y(n) = x(1) + x(2) + ...+ x(n)