Экстремальная комбинаторика: [PDF] Continuous optimisation in extremal combinatorics

Содержание

Комбинаторика

Комбинаторика — это область математики, прежде всего связанная с подсчетом, как средство и цель получения результатов, так и с определением свойств конечных структур. Она тесно связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей и применяется в различных областях знаний (например, в генетике, информатике, статистической физике).

Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».

Полный охват комбинаторики не является общепризнанным. Согласно Х. Дж. Райзеру, определение предмета трудно, потому что она пересекает много математических разделов. Поскольку область может быть описана типами задач, которые она решает, комбинаторика связана с:

перечислением (подсчет) определенных структур, иногда упоминаемых аранжировками или конфигурациями в самом общем смысле, связанными с конечными системами;
существованием таких структур, которые удовлетворяют определенным заданным критериям;
построением таких структур; возможно, несколькими способами;
оптимизацией, поиском «наилучшей» структуры или решения из нескольких возможных, будь то «наибольшая», «наименьшая» или удовлетворяющая какому-либо другому критерию оптимальности.

Леон Мирский сказал: «Комбинаторика — это ряд взаимосвязанных исследований, которые имеют что-то общее и все же сильно расходятся в своих целях, методах и степени согласованности, которой они достигли». Одним из способов определения комбинаторики является, возможно, описание её разделов с их проблемами и методами. Именно такой подход используется ниже. Однако, существуют также чисто исторические причины включения или исключения некоторых тем в комбинаторику. Хотя в первую очередь речь идет о конечных системах, в некоторых комбинаторных вопросах и методах система может быть расширена до бесконечности (в частности, по счету), но дискретно установлена.

Комбинаторика хорошо известна широким охватом задач, которые она решает. Комбинаторные задачи возникают во многих областях фундаментальной математики, особенно в алгебре, теории вероятностей, топологии и геометрии, а также во многих областях ее приложений. Многие комбинаторные вопросы исторически рассматривались изолированно, давая специальное решение возникающей задачи в некотором математическом контексте. Однако, в конце ХХ века были разработаны мощные и общетеоретические методы, сделавшие комбинаторику самостоятельным разделом математики. Одной из старейших и наиболее изученной частью комбинаторики является теория графов, которая сама по себе имеет многочисленные естественные связи с другими областями. Комбинаторика часто используется в информатике для получения формул и оценок при анализе алгоритмов.

История

Основные комбинаторные понятия и перечислительные результаты появились в древнем мире. В VI веке до нашей эры древнеиндийский врач Сушрута утверждает в «Сушрута-самхите», что 63 комбинации могут быть составлены из 6 различных вкусов, взятых по одному, по два и т. д., таким образом вычисляя 26–1 всех возможных вариантов. Древнегреческий историк Плутарх обсуждает спор между Хрисиппом (III век до н. э.) и Гиппархом (II век до н. э.) относительно довольно деликатной проблемы перечисления, которая была продемонстрирована позже и связана с числами Шрёдера–Гиппарха. В Стомахионе Архимед (III век до н. э.) рассматривает мозаичные головоломки.

В Средние века комбинаторика продолжала изучаться, в основном за пределами европейской цивилизации. Индийский математик Махавира (около 850 г.) представил формулы для числа перестановок и комбинаций, и эти формулы, возможно, были знакомы индийским математикам еще в VI веке н. э. Философ и астроном Рабби Авраам ибн Эзра (ок. 1140) установил симметрию биномиальных коэффициентов, а замкнутая формула была получена позже талмудистом и математиком Леви Бен Гершом (более известным как Герсонид) в 1321 году. Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Хотя этот способ был уже известен на Востоке (примерно с X века) и он назывался арифметическим треугольником. Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Арифметический треугольник представляет собой графическую диаграмму, показывающую отношения между биномиальными коэффициентами. Позже, в средневековой Англии, кампанология предоставила примеры того, что теперь известно как Гамильтоновы циклы в графах Кэли на перестановках.

В эпоху Возрождения, наряду с остальной математикой и науками, комбинаторика пережила возрождение. Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей. В историю зарождавшейся теории вероятностей вошла переписка заядлого игрока Шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

Наряду с Лейбницем, он считается основоположником современной комбинаторики. Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.

В этот же период формируется терминология новой науки. Термин «сочетание» (combination) впервые встречается у Паскаля (1653, опубликован в 1665 году). Термин «перестановка» (permutation) употребил в указанной книге Якоб Бернулли (хотя эпизодически он встречался и раньше). Бернулли использовал и термин «размещение» (arrangement).

После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала.

Окончательно комбинаторика как самостоятельный раздел математики оформилась в трудах Эйлера. Он детально рассмотрел, например, следующие проблемы:

задача о ходе коня;
задача о семи мостах, с которой началась теория графов;
построение греко-латинских квадратов;
обобщённые перестановки.

Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями. Их работы (Паскаля, Ньютона, Якоба Бернулли и Эйлера) стали фундаментальными в развивающейся этой области. В наше время работы Дж. Дж. Сильвестра (конец XIX века) и Перси Макмэхона (начало XX века) помогли заложить основы перечислительной и алгебраической комбинаторики. Теория графов также пользовалась большим интересом в это время, особенно в связи с теоремой о четырех красках.

Во второй половине XX века комбинаторика пережила бурный рост, что привело к созданию десятков новых журналов и конференций по данной тематике. Частично этот рост был стимулирован новыми связями и приложениями в других областях, начиная от алгебры и заканчивая вероятностью, от функционального анализа до теории чисел и т. д. Эти связи стирают границы между комбинаторикой и частями математики, и теоретической информатикой, но в то же время приводят к частичной фрагментации этой области.

Примеры комбинаторных конфигураций и задач

Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:

Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
Перестановкой из n элементов (например чисел 1, 2, … n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.

Примеры комбинаторных задач:

Сколькими способами можно разместить n предметов по m ящикам, чтобы выполнялись заданные ограничения?

Сколько существует функций F {displaystyle F} из m-элементного множества в n-элементное, удовлетворяющих заданным ограничениям?

Сколько существует различных перестановок из 52 игральных карт? Ответ: 52! (52 факториал), то есть, 80 658 175 170 943 880 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 или примерно 8,0658 ⋅ 1067.

При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, в которых сумма очков на верхних гранях равна двенадцати? Решение: Каждый возможный исход соответствует функции F : { 1 , 2 } → { 1 , 2 , 3 , 4 , 5 , 6 } {displaystyle F:{1,2} o {1,2,3,4,5,6}} (аргумент функции — это номер кости, значение — очки на верхней грани). Очевидно, что лишь 6 + 6 даёт нам нужный результат 12. Таким образом, существует лишь одна функция, ставящая в соответствие 1 число 6, и 2 число 6. Или, другими словами, существует всего одна комбинация, при которой сумма очков на верхних гранях равна двенадцати.

Методы и разделы комбинаторики

Перечислительная комбинаторика

Перечислительная комбинаторика (или исчисляющая комбинаторика) рассматривает задачи о перечислении или подсчёте количества различных конфигураций (например, перестановок) образуемых элементами конечных множеств, на которые могут накладываться определённые ограничения, такие как: различимость или неразличимость элементов, возможность повторения одинаковых элементов и т. п.

Количество конфигураций, образованных несколькими манипуляциями над множеством, подсчитывается согласно правилам сложения и умножения.

Числа Фибоначчи являются типичным примером задачи в перечислительной комбинаторике, а также известная известная Задача о письмах. Двенадцатеричный путь обеспечивает единую структуру для подсчета перестановок, сочетаний и разбиений.

Аналитическая комбинаторика

Аналитическая комбинаторика относится к перечислению комбинаторных структур с использованием инструментов из комплексного анализа и теории вероятности. В отличие от перечислительной комбинаторики, которая использует явные комбинаторные формулы и производящие функции последовательности для описания результатов, аналитическая комбинаторика нацелена на получение асимптотических формул.

Теория разбиения

Теория разбиения изучает различные перечислительные и асимптотические задачи, связанные с разбиением натуральных чисел и тесно связана с q-рядами, специальными функциями и ортогональными многочленами. Первоначально она была частью теории чисел и анализа, а теперь рассматривается как часть комбинаторики или самостоятельная область. Она включает в себя биективный подход и различные инструменты анализа, и аналитической теории чисел и имеет связи со статистической механикой.

Теория графов

Графы являются фундаментальными объектами в комбинаторике. Теория графов рассматривает перечисления (например, число n вершин с k ребрами графа), существующие структуры (например, гамильтоновы циклы), алгебраические представления (например, возьмем граф G и два числа x и y, имеет ли Многочлен Татта TG(x,y) комбинаторное представление?). Хотя между теорией графов и комбинаторикой существуют очень сильные связи, они иногда рассматриваются как отдельные предметы. То же время комбинаторные методы применимы ко многим задачам теории графов, эти две дисциплины обычно используются для поиска решений различных типов задач.

Теория схем

Теория схем — это исследование комбинаторных схем, которые представляют собой наборы подмножеств с определенными свойствами пересечения. Блок схемы – это комбинаторные схемы особого типа. Эта область является одной из старейших частей комбинаторики, например, предложенная в 1850 году задача Киркмана о школьницах. Решение задачи является частным случаем системы Штейнера, системы которой играют важную роль в классификации простых конечных групп. Эта область имеет дальнейшие связи с теорией кодирования и геометрической комбинаторикой.

Конечная геометрия

Конечная геометрия — это изучение геометрических систем, имеющих только конечное число точек. Структуры аналогичны тем, которые встречаются в непрерывной геометрии (плоскость Евклидова, реальное проективное пространство и т. д.), но определены комбинаторно основные изучаемые элементы. Эта область предоставляет богатый источник примеров для теории схем. Её не следует путать с дискретной геометрией (комбинаторной геометрией).

Теория порядка

Теория порядка — это изучение частично упорядоченных множеств, как конечных, так и бесконечных. Различные примеры частичных порядков встречаются в алгебре, геометрии, теории чисел и во всей комбинаторике, и теории графов. Известные классы и примеры частичных порядков включают решетки и булевы алгебры.

Теория матроидов

Теория матроидов абстрагирует часть геометрии. Она изучает свойства множеств (обычно конечных множеств) векторов в векторном пространстве, которые не зависят от конкретных коэффициентов в линейно зависимом отношении. Не только структура, но и перечислительные свойства принадлежат теории матроидов. Теория матроидов была введена Хасслером Уитни и изучалась как часть теории порядка. В настоящее время это самостоятельная область исследований, имеющая ряд связей с другими разделами комбинаторики.

Экстремальная комбинаторика

Экстремальная комбинаторика изучает экстремальные вопросы о системах множеств. Типы вопросов, рассматриваемых в этом случае, относятся к самому большому возможному графу, который удовлетворяет определенным свойствам. Например, самый большой граф без треугольников на 2n вершинах – это полный двудольный граф Kn,n. Часто бывает слишком трудно даже точно найти экстремальный ответ f(n) и можно дать только асимптотическую оценку.

Теория Рамсея

Теория Рамсея — это еще одна часть экстремальной комбинаторики. Она утверждает, что любая достаточно большая конфигурация будет содержать некоторый порядок и изучает наличие регулярных структур в случайных конфигурациях элементов. Это расширенное обобщение принципа Дирихле («принцип голубей и ящиков»). Примером утверждения из теории Рамсея может служить следующее:

в группе из 6 человек всегда можно найти трёх человек, которые либо попарно знакомы друг с другом, либо попарно незнакомы.

В терминах структурной комбинаторики это же утверждение формулируется так:

в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3.

Вероятностная комбинаторика

Этот раздел отвечает на вопросы вида: какова вероятность присутствия определённого свойства для случайного дискретного объекта, такого как случайный граф? Например, каково среднее число треугольников в случайном графе? Вероятностные методы также используются для определения существования комбинаторных объектов с определенными заданными свойствами (для которых явные примеры может быть трудно найти), просто наблюдая, что вероятность случайного выбора объекта с этими свойствами больше 0. Этот подход (часто называемый вероятностным методом) доказал свою высокую эффективность в приложениях экстремальной комбинаторики и теории графов. Тесно связанной областью является изучение конечных цепей Маркова, особенно на комбинаторных объектах. Здесь снова используются вероятностные инструменты для оценки времени смешивания.

Часто ассоциируемая с Палом Эрдёшем, который сделал новаторскую работу по этому предмету, вероятностная комбинаторика традиционно рассматривалась как набор инструментов для изучения задач в других частях комбинаторики. Однако с ростом приложений для анализа алгоритмов в информатике, а также классической теории вероятностей, аддитивной теории чисел и вероятностной теории чисел, эта область в последнее время выросла и стала самостоятельной областью комбинаторики.

Алгебраическая комбинаторика

Алгебраическая комбинаторика — это область математики, которая использует методы абстрактной алгебры, в частности теорию групп и теорию представлений, в различных комбинаторных контекстах и, наоборот, применяет комбинаторные методы к задачам алгебры. Алгебраическая комбинаторика постоянно расширяет свой охват, как в тематических направлениях, так и в методах и может рассматриваться как область математики, где взаимодействие комбинаторных и алгебраических методов особенно сильно и существенно.

Комбинаторика слов

Комбинаторика слов имеет дело с формальными языками. Она возникла самостоятельно в нескольких областях математики, в том числе в теории чисел, теории групп и теории вероятности. Она имеет приложения в перечислительной комбинаторике, фрактальном анализе, теоретической информатике, теории автоматов и лингвистике. Хотя многие приложения являются новыми, классическая иерархия Хомского классов формальных грамматик является, пожалуй, самым известным результатом в этой области.

Комбинаторная геометрия

Геометрическая комбинаторика связана с выпуклой и дискретной геометрией, в частности с комбинаторикой многогранников. Например, она спрашивает, сколько граней каждого измерения может иметь выпуклый многогранник. Важную роль играют также метрические свойства многогранников, например, теорема Коши о жесткости выпуклых многогранников. Рассматриваются также особые многогранники, такие как перестановочные многогранники, ассоциаэдры и многогранники Биркгофа. Комбинаторная геометрия — это старомодное название дискретной геометрии.

Топологическая комбинаторика

Топологическая комбинаторика применяет идеи и методы комбинаторики в топологии, при изучении раскрасок графа, справедливого делёжа, разбиения, дерева принятия решений, частично упорядоченных множеств, задач “ожерелья” и дискретной теории Морсе. Её не следует путать с комбинаторной топологией, которая является более старым названием алгебраической топологии.

Арифметическая комбинаторика

Арифметическая комбинаторика возникла из взаимодействия между теорией чисел, комбинаторикой, эргодической теории и гармоническим анализом. Она о комбинаторных оценках, связанных с арифметическими операциями (сложение, вычитание, умножение и деление). Аддитивная теория чисел (иногда также называемая аддитивной комбинаторикой) относится к частному случаю, когда задействованы только операции сложения и вычитания. Одним из важных методов арифметической комбинаторики является эргодическая теория динамических систем.

Инфинитарная комбинаторика

Инфинитарная комбинаторика — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам. Это часть теории множеств, область математической логики, но использует инструменты и идеи как теории множеств, так и экстремальной комбинаторики.

Джан-Карло Рота использовал название непрерывной комбинаторики для описания геометрической вероятности, поскольку существует много аналогий между подсчетом и мерой.

Связанные области

Комбинаторная оптимизация

Комбинаторная оптимизация — это исследование оптимизации дискретных и комбинаторных объектов. Она начиналась как часть комбинаторики и теории графов, но теперь рассматривается как раздел прикладной математики и информатики, связанный с исследованием операций, теорией алгоритмов и теорией сложности вычислений.

Теория кодирования

Теория кодирования началась как часть теории схем с ранними комбинаторными конструкциями кодов, исправляющих ошибки. Основная идея предмета заключается в разработке эффективных и надежных методов передачи данных. Сейчас это большая область исследований, часть теории информации.

Дискретная и вычислительная геометрия

Дискретная геометрия (также называемая комбинаторной геометрией) также началась как часть комбинаторики, с ранними результатами выпуклых многогранников и контактных чисел. С появлением приложений дискретной геометрии в вычислительной геометрии, эти две области частично слились и стали отдельной областью изучения. Остается много связей с геометрической и топологической комбинаторикой, которые сами по себе можно рассматривать как порождения ранней дискретной геометрии.

Комбинаторика и динамические системы

Комбинаторные аспекты динамических систем — это еще одна развивающаяся область. Здесь динамические системы могут быть определены комбинаторными объектами. См., например, динамическая система графов.

Комбинаторика и физика

Между комбинаторикой и физикой, в частности статистической физикой, усиливается взаимосвязь. Примеры включают точное решение модели Изинга и связь между моделью Поттса с одной стороны, и хроматическими многочленами и многочленами Татте, с другой стороны.

Открытые проблемы

Комбинаторика, и в частности, теория Рамсея, содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем N в любой группе из N человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно).

А также есть и другие нерешённые задачи или не доказанные гипотезы:

Гипотеза Адамара (1893): Для каждого натурального n {displaystyle n} , делящегося на 4, существует вещественная матрица Адамара порядка n {displaystyle n} . Пояснение: Известно, что делимость на 4 является лишь необходимым условием существования матрицы Адамара. Существуют различные методы построения вещественных матриц Адамара порядка n = 4 k {displaystyle n=4k} для некоторых бесконечных серий натуральных чисел делящихся на 4, однако они не позволяют доказать гипотезу Адамара. Наименьшим порядком, кратным 4, для которого матрица Адамара неизвестна является n = 668 {displaystyle n=668} .
Существование конечной проективной плоскости натурального порядка, не являющегося степенью простого числа.
Гипотеза Эрдёша — Реньи. Если k {displaystyle k} — фиксированное целое число k ≥ 3 {displaystyle kgeq 3} , то lim inf ( p e r ( A ) ) 1 n > 1 {displaystyle lim ;inf(per(A))^{frac {1}{n}}>1} для A {displaystyle A} из Λ n k {displaystyle Lambda _{n}^{k}} . {k}} — множество всех ( 0 , 1 ) {displaystyle (0,1)} — матриц порядка n {displaystyle n} c k {displaystyle k} единицами в каждой строке и каждом столбце.
Числа Рамсея N ( q 1 , q 2 , . . . , q t ; r ) {displaystyle N(q_{1},q_{2},…,q_{t};r)} для случая t > 2 {displaystyle t>2} почти не изучены.
Задача нахождения минимума перманента дважды стохастической матрицы в общем случае не решена.
Не известны необходимые и достаточные условия, при которых существует общая трансверсаль для трёх семейств подмножеств.

Комбинаторика в языкознании

Комбинаторика (языкознание) — это свойство единиц языка и соответствующих им единиц речи вступать в синтагматические отношения, то есть в отношения сочетаемости.

Комбинаторика — Википедия — Study in China 2023

Комбинато́рика (иногда называемая комбинаторным анализом) — раздел математики, посвящённый решению задач, связанных с выбором и расположением элементов некоторого (чаще всего конечного) множества в соответствии с заданными правилами. Каждое такое правило определяет некоторую выборку из элементов исходного множества, которая называется комбинаторной конфигурацией. Простейшими примерами комбинаторных конфигураций^[1]^[2] являются перестановки, сочетания и размещения^[⇨].

Типичные задачи^[1] комбинаторики^[⇨]:

Определить количество комбинаторных конфигураций, соответствующих заданным правилам (в частности, доказать или опровергнуть их существование).
Найти практически пригодный алгоритм их полного построения.
Определить свойства заданного класса комбинаторных конфигураций.

Комбинаторика тесно связана со многими другими областями математики — алгеброй, геометрией, теорией вероятностей, теорией чисел и другими^[⇨]. Она применяется в самых различных областях знаний (например, в генетике, информатике, статистике, статистической физике, лингвистике).

Содержание

Show / Hide

Примеры комбинаторных конфигураций и задач

Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
Перестановкой из n элементов (например чисел 1, 2, … n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Композицией числа n называется всякое представление n в виде упорядоченной суммы целых положительных чисел.
Разбиением числа n называется всякое представление n в виде неупорядоченной суммы целых положительных чисел.

Примеры комбинаторных задач:

Сколько имеется способов разместить n предметов по m ящикам, чтобы выполнялись заданные ограничения?
Сколько существует функций F{\displaystyle F} из m-элементного множества в n-элементное, удовлетворяющих заданным ограничениям?
Сколько существует различных перестановок из 52 игральных карт?

или примерно 8,0658⋅1067.

{67}.}

При игре в кости бросаются две кости, и выпавшие очки складываются; сколько существует комбинаций, в которых сумма очков на верхних гранях равна двенадцати?

История

Основная статья: История комбинаторики

Древность и средние века

Основные комбинаторные понятия и вычислительные результаты появились в древнем мире. Классическая задача комбинаторики: «сколько есть способов извлечь m элементов из N возможных» упоминается ещё в сутрах древней Индии (начиная примерно с IV века до н. э.)^[3]. Индийские математики, видимо, первыми открыли биномиальные коэффициенты и их связь с биномом Ньютона^[3]. {n}} .

Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо^[4]. Историки отмечают также комбинаторные проблемы в руководствах по игре в Го и другие игры. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты.

Античные греки также рассматривали отдельные комбинаторные задачи, хотя систематическое изложение ими этих вопросов, если оно и существовало, до нас не дошло. Хрисипп (III век до н. э.) и Гиппарх (II век до н. э.) подсчитывали, сколько следствий можно получить из 10 аксиом; методика подсчёта нам неизвестна, но у Хрисиппа получилось более миллиона, а у Гиппарха — более 100000^[5]. Аристотель при изложении своей логики безошибочно перечислил все возможные типы трёхчленных силлогизмов. Аристоксен рассмотрел различные чередования длинных и коротких слогов в стихотворных размерах. ^[5] Какие-то комбинаторные правила пифагорейцы, вероятно, использовали при построении своей теории чисел и нумерологии (совершенные числа, фигурные числа, пифагоровы тройки и др.).

В Средние века комбинаторика также продолжала развиваться, в основном, за пределами европейской цивилизации. В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями. Другой индийский математик, Махавира^[en] (середина IX века), опубликовал формулы для числа перестановок и сочетаний, причём эти формулы, возможно, были знакомы индийским математикам еще в VI веке н. э. Философ и астроном рабби Авраам ибн Эзра (около 1140 года) подсчитал число размещений с перестановками в огласовках имени Бога^[6]. Он же установил симметрию биномиальных коэффициентов. Точную формулу для них обнародовал позже талмудист и математик Леви бен Гершом (более известный как Герсонид) в 1321 году.

Несколько комбинаторных задач содержит «Книга абака» (Фибоначчи, XIII век). Например, он поставил задачу найти наименьшее число гирь, достаточное для взвешивания любого товара весом от 1 до 40 фунтов.

Новое время

Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Позднее выяснилось, что этот способ был уже известен на Востоке (примерно с X века) и он назывался арифметическим треугольником. Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника. Арифметический треугольник представляет собой графическую диаграмму, показывающую отношения между биномиальными коэффициентами. Позже, в средневековой Англии, кампанология^[en] предоставила примеры того, что теперь известно как гамильтоновы циклы в графах Кэли на перестановках.

В эпоху Возрождения, наряду с прочими науками, комбинаторика начала стремительное развитие. Джероламо Кардано написал проницательное математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Никколо Тарталья и Галилео Галилей. История теории вероятностей началась с переписки заядлого игрока шевалье де Мерэ с Пьером Ферма и Блезом Паскалем, где были затронуты несколько тонких комбинаторных вопросов. Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.

Сам термин «комбинаторика» придумал Лейбниц, он считается основоположником современной комбинаторики. В 1666 году (ему было тогда 20 лет) опубликовал книгу «Рассуждения о комбинаторном искусстве». Правда, термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него всю конечную математику и даже логику^[7]. Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.

задача о ходе коня;
задача о семи мостах, с которой началась теория графов;
построение греко-латинских квадратов;
обобщённые перестановки.

Кроме перестановок и сочетаний, Эйлер изучал разбиения, а также сочетания и размещения с условиями.

Современное состояние

Работы Паскаля, Ньютона, Якоба Бернулли и Эйлера стали фундаментальными в развитии этой области. В наше время работы Дж. Дж. Сильвестра (конец XIX века) и Перси Макмэна^[en] (начало XX века) помогли заложить основы перечислительной и алгебраической комбинаторики. Теория графов также вызывала растущий интерес, особенно в связи с теоремой о четырёх красках и задачами экономики.

Во второй половине XX века комбинаторика пережила новый бурный рост, что было связано с быстрым развитием дискретной математики, информатики, кибернетики и планирования эксперимента. Частично этот рост был стимулирован обнаруженными связями и приложениями в других областях математики — в алгебре, теорией вероятностей, функциональном анализе, теории чисел и т. д. Эти связи стирают границы между комбинаторикой и другими областями математики, но в то же время приводят к определённой фрагментации комбинаторики.

В начале XX века началось развитие комбинаторной геометрии: были доказаны теоремы Радона, Хелли, Юнга, Бляшке, а также строго доказана изопериметрическая теорема. На стыке топологии, анализа и комбинаторики были доказаны теоремы Борсука — Улама и Люстерника — Шнирельмана^[en].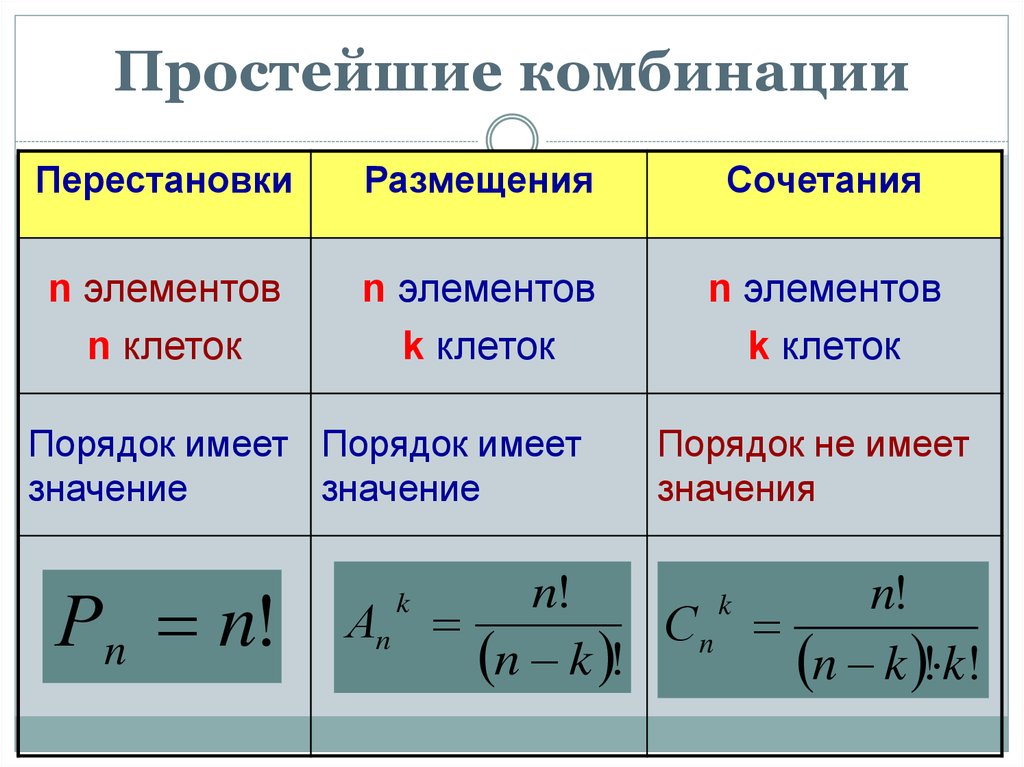 Во второй четверти XX века были поставлены проблема Борсука и проблема Нелсона — Эрдёша — Хадвигера. В 1940-х годах оформилась теория Рамсея. Отцом современной комбинаторики считается Пал Эрдёш, который ввёл в комбинаторику вероятностный анализ. Внимание к конечной математике и, в частности, к комбинаторике значительно повысилось со второй половины XX века, когда появились компьютеры. Сейчас это чрезвычайно содержательная и быстроразвивающаяся область математики.

Методы и разделы комбинаторики

Перечислительная комбинаторика

Основная статья: Перечислительная комбинаторика

Пять двоичных деревьев с тремя вершинами, пример чисел Каталана

Числа Фибоначчи являются типичным примером задачи в перечислительной комбинаторике, а также известная Задача о письмах. Двенадцатеричный путь обеспечивает единую структуру для подсчета перестановок, сочетаний и разбиений.

Аналитическая комбинаторика

Основная статья: Аналитическая комбинаторика^[en]

Плоское разбиение

Теория разбиения

Основная статья: Разбиение числа

Теория разбиения изучает различные перечислительные и асимптотические задачи, связанные с разбиением натуральных чисел, и тесно связана с q-рядами, специальными функциями и ортогональными многочленами. Первоначально она была частью теории чисел и анализа, а теперь рассматривается как часть комбинаторики или самостоятельная область. Она включает в себя биективный подход, различные инструменты анализа и аналитической теории чисел, имеет также связи со статистической механикой.

Граф Петерсена

Теория графов

Основная статья: Теория графов

Графы являются фундаментальными объектами в комбинаторике. Теория графов рассматривает перечисления (например, число n вершин с k ребрами графа), существующие структуры (например, гамильтоновы циклы), алгебраические представления (например, возьмем граф G и два числа x и y, имеет ли Многочлен Татта T_G(x, y) комбинаторное представление?). Хотя между теорией графов и комбинаторикой существуют очень сильные связи, они иногда рассматриваются как отдельные предметы. В то же время комбинаторные методы применимы ко многим задачам теории графов, эти две дисциплины обычно используются для поиска решений различных типов задач.

Теория схем

Основная статья: Комбинаторная схема

Теория схем — это исследование комбинаторных схем, которые представляют собой наборы подмножеств с определенными свойствами пересечения. Блок схемы — это комбинаторные схемы особого типа. Эта область является одной из старейших частей комбинаторики, например, предложенная в 1850 году задача Киркмана о школьницах. Решение задачи является частным случаем системы Штейнера, системы которой играют важную роль в классификации простых конечных групп. Эта область имеет дальнейшие связи с теорией кодирования и геометрической комбинаторикой.

Конечная геометрия

Основная статья: Конечная геометрия

Диаграмма Хассе, булеан — {x, y, z} упорядоченный по включению

Теория порядка

Основная статья: Отношение порядка

Теория матроидов

Основная статья: Матроид

Экстремальная комбинаторика

Основная статья: Экстремальная комбинаторика^[en]

Экстремальная комбинаторика изучает экстремальные вопросы о системах множеств. Типы вопросов, рассматриваемых в этом случае, относятся к самому большому возможному графу, который удовлетворяет определенным свойствам. Например, самый большой граф без треугольников на 2n вершинах — это полный двудольный граф K_{n, n}. Часто бывает слишком трудно даже точно найти экстремальный ответ f(n) и можно дать только асимптотическую оценку.

Теория Рамсея

Основная статья: Теория Рамсея

В терминах структурной комбинаторики это же утверждение формулируется так:

в любом графе с 6 вершинами найдётся либо клика, либо независимое множество размера 3.

Самоустраняющаяся прогулка по решетке

Вероятностная комбинаторика

Основная статья: Вероятностный метод

Диаграмма Юнга формы (5, 4, 1)

Алгебраическая комбинаторика

Основная статья: Алгебраическая комбинаторика

Демонстрация создания последовательности Морса — Туэ.

Комбинаторика слов

Основная статья: Комбинаторика слов^[en]

Комбинаторная геометрия

Основная статья: Комбинаторная геометрия

Пример ожерелья, разделённого на k = 2 (то есть между двумя участниками дележа) и t = 2 (то есть два типа бусин, имеется 8 красных и 6 зелёных). Показаны 2 разреза — один из участников получает большую секцию, а другой получает оставшиеся два куска.

Топологическая комбинаторика

Основная статья: Топологическая комбинаторика

Топологическая комбинаторика применяет идеи и методы комбинаторики в топологии, при изучении раскрасок графа, справедливого делёжа, разбиения, дерева принятия решений, частично упорядоченных множеств, задач «ожерелья» и дискретной теории Морсе. Её не следует путать с комбинаторной топологией, которая является более старым названием алгебраической топологии.

Арифметическая комбинаторика

Основная статья: Арифметическая комбинаторика

Инфинитарная комбинаторика

Основная статья: Инфинитарная комбинаторика^[en]

Инфинитарная комбинаторика (англ.) — применение идей и методов комбинаторики к бесконечным (в том числе, несчётным) множествам. Это часть теории множеств, область математической логики, но использует инструменты и идеи как теории множеств, так и экстремальной комбинаторики.

Связанные области

Комбинаторная оптимизация

Теория кодирования

Дискретная и вычислительная геометрия

Комбинаторика и динамические системы

Комбинаторика и физика

Открытые проблемы

Комбинаторика (в частности, теория Рамсея) содержит много известных открытых проблем, подчас с весьма несложной формулировкой. Например, неизвестно, при каком наименьшем N{\displaystyle N} в любой группе из N{\displaystyle N} человек найдутся 5 человек, либо попарно знакомых друг с другом, либо попарно незнакомых (хотя известно, что 49 человек достаточно)^[9].

Также есть и другие нерешённые задачи и недоказанные гипотезы:

Гипотеза Адамара (1893): для каждого натурального n{\displaystyle n} , делящегося на 4, существует вещественная матрица Адамара порядка n{\displaystyle n} . Пояснение: известно, что делимость на 4 является лишь необходимым условием существования матрицы Адамара. Существуют различные методы построения вещественных матриц Адамара порядка n=4k{\displaystyle n=4k} для некоторых бесконечных серий натуральных чисел, делящихся на 4, однако они не позволяют доказать гипотезу Адамара. Наименьшим порядком, кратным 4, для которого матрица Адамара неизвестна, является n=668{\displaystyle n=668} ^[10].
Существование конечной проективной плоскости натурального порядка, не являющегося степенью простого числа. {k}} — множество всех (0,1){\displaystyle (0,1)} — матриц порядка n{\displaystyle n} c k{\displaystyle k} единицами в каждой строке и каждом столбце^[11].
Числа Рамсея N(q1,q2,…,qt;r){\displaystyle N(q_{1},q_{2},…,q_{t};r)} для случая t>2{\displaystyle t>2} почти не изучены^[12].
Задача нахождения минимума перманента дважды стохастической матрицы в общем случае не решена^[13].
Не известны необходимые и достаточные условия, при которых существует общая трансверсаль для трёх семейств подмножеств^[14].

Комбинаторика в языкознании

Примечания

↑ ¹ ² Сачков В. Н. Комбинаторный анализ // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1979. — Т. 2. — С. 974—979. — 1104 с.
↑ БРЭ.
↑ ¹ ² Amulya Kumar Bag. Binomial theorem in ancient India. Архивная копия от 3 августа 2021 на Wayback Machine Indian J. History Sci., 1:68-74, 1966.
↑ Виленкин Н. Я., 1975, с. 7.
↑ ¹ ² Виленкин Н. Я., 1975, с. 9.
↑ Краткий комментарий к Исход, 3:13.
↑ Виленкин Н. Я., 1975, с. 19.
↑ O’Connor, John; Edmund Robertson. Abraham de Moivre (неопр.). The MacTutor History of Mathematics archive. Дата обращения: 31 мая 2010. Архивировано 27 апреля 2012 года.
↑ Weisstein, Eric W. Числа Рамсея (англ.) на сайте Wolfram MathWorld.
↑ МАТРИЦЫ АДАМАРА. Архивировано 21 января 2022 года.
↑ Минк X. Перманенты.. — Мир. — 1982. — 211 с.
↑ Рыбников, 1972, с. 96.
↑ Рыбников, 1972, с. 110.
↑ Капитонова Ю. В., Кривой С. Л., Летичевский А. А. Лекции по дискретной математике. — СПб.: БХВ-Петербург, 2004. — С. 530. — 624 с. — ISBN 5-94157-546-7.

Литература

Андерсон, Джеймс. Дискретная математика и комбинаторика = Discrete Mathematics with Combinatorics. — М.: «Вильямс», 2006. — 960 с. — ISBN 0-13-086998-8.
Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975.
Вялый М. Н. Линейные неравенства и комбинаторика. М.: МЦНМО, 2003. 32 с.
Ерош И. Л. Дискретная математика. Комбинаторика — СПб.: СПбГУАП, 2001. — 37 c.
Леонтьев В. К. Избранные задачи комбинаторного анализа. — М. : Изд-во МГТУ им. Н. Э. Баумана, 2001. — 179, [3] с.; 20 см; ISBN 5-7038-1862-1
Леонтьев В. К. Комбинаторика и информация : учеб. пос. … по направлению … «Прикладные математика и физика». — Москва : МФТИ, 2015. — 21 см; ISBN 978-5-7417-0518-6
Леонтьев В. К., Гордеев Э. Н. Комбинаторные аспекты теории информации. М.: МФТИ, 2019.
Липский В. Комбинаторика для программиста. — М.: Мир, 1988. — 213 с.
Райгородский А. М. Линейно-алгебраические и вероятностные методы в комбинаторике. — Летняя школа «Современная математика». — Дубна, 2006.
Райзер Г. Дж. Комбинаторная математика. — пер. с англ. — М., 1966.
Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. — М.: Мир, 1980. — 476 с.
Риордан Дж. Введение в комбинаторный анализ. — пер. с англ. — М., 1963.
Рыбников К. А. Введение в комбинаторный анализ. — М.: МГУ, 1972. — С. 96. — 308 с.
Стенли Р. Перечислительная комбинаторика = Enumerative Combinatorics. — М.: «Мир», 1990. — 440 с. — ISBN 5-03-001348-2.
Стенли Р. Перечислительная комбинаторика. Деревья, производящие функции и симметрические функции = Enumerative Combinatorics. Volume 2. — М.: «Мир», 2009. — 767 с. — ISBN 978-5-03-003476-8.

Ссылки

Белешко Д. Комбинаторика. 2004.
Комбинаторный анализ / Сачков В. Н. // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
Теория вероятностей. 3. Элементы комбинаторики

Хамовники — 9 класс | Подготовка школьников Москвы к олимпиадам по математике

Хамовники — 9 класс | Главная

Занятия кружка предназначены для школьников, обладающих статусом «кандидат в сборную Москвы».

Место занятий

ЦПМ, Хамовнический вал, 6.

Время занятий:

понедельник, 17:00–19:30
четверг, 17:00–19:30

Преподаватели:

Афризонов Денис Владимирович
Кушнир Андрей Юрьевич
Логинов Константин Валерьевич
Попов Леонид Андреевич
Рухович Алексей Дмитриевич
Соколов Артемий Алексеевич
Тихонов Юлий Васильевич
Трещев Виктор Дмитриевич
Юргин Григорий Алексеевич

Материалы занятий:

	«Догоняющие», ауд. 44	«Настигающие», ауд. 42	«Убегающие», ауд. 43
2018-09-10 (пн)	Отборочная олимпиада, решения
2018-09-17 (пн)	Подсчет двумя способами	Серия 1. Периодическая	Серия 1. Периодическая
2018-09-20 (чт)	Квадратный трехчлен	Серия 2. Двойной подсчёт и усреднение	Серия 2. Двойной подсчёт и усреднение
2018-09-24 (пн)	Задачи на подобие	Серия 3. Комбинаторные идеи в ТЧ	Серия 3. Комбинаторные идеи в ТЧ
2018-09-27 (чт)	Графы и антиграфы	Серия 4. Введение в теорию вероятностей	Серия 4. Введение в теорию вероятностей
2018-10-01 (пн)	Теоремы Чевы и Менелая	Серия 5.Несколько задач по ТЧ	Серия 5. Несколько задач по ТЧ
2018-10-04 (чт)	Классические неравенства + добавка	Дорешивание/разбор	Серия 6. Доп. комбинаторные задачи
2018-10-08 (пн)	Теория чисел	Серия 7. Экстремальные графы	Серия 7. Экстремальные графы
2018-10-11 (чт)	Полуинвариант	Серия 8. Простые неравенства	Серия 8. Простые неравенства
2018-10-15 (пн)	Тематический разнобой	Дорешивание	Дорешивание
2018-10-18 (чт)	Безу и Виет	Серия 9. Непростые неравенства	Серия 9. Непростые неравенства
2018-10-22 (пн)	Отборочная олимпиада, решения		Дорешивание
2018-10-25 (чт)	Оценка + пример	Серия 10. Однородные неравенства	Серия 10. Однородные неравенства
2018-10-29 (пн)	Отрезки касательных	Серия 11. Доски и таблицы	Серия 11. Добрая клетчатая комбинаторика
2018-11-01 (чт)	Неравенство КБШ		Большой разбор
2018-11-05 (пн)	Турниры		Московские сборы
2018-11-08 (чт)	Теория чисел
2018-11-12 (пн)	Индукция в графах
2018-11-15 (чт)	Игры и стратегии
2018-11-19 (пн)	Дорешивание	Серия 12. Комбинаторный разнобой	Серия 12. Комбинаторный разнобой
2018-11-22 (чт)	Про многочлены	Серия 13. Перестановки	Серия 13. Перестановки, ликбез
2018-11-26 (пн)	Степень точки	Серия 14. Многочлены	Серия 14. Многочлены
2018-11-29 (чт)	Опять неравенства	Серия 15. Перестановки, продолжение	Серия 15. Перестановки, продолжение
2018-12-03 (пн)	Уравнения в целых числах	Дорешивание	Дорешивание
2018-12-06 (чт)	Геометрический разнобой	Серия 16. Информация	Серия 16. Информация
2018-12-10 (пн)	Интерполяция	Серия 17. Интерполяция	Серия 17. Интерполяция
2018-12-13 (чт)	Радикальная ось	Серия 18. Информация, добавка	Серия 18. Информация, добавка
2018-12-17 (пн)	Дискретная непрерывность	Серия 19. Лемма об уточнении показателя	Серия 19. Лемма об уточнении показателя
2018-12-20 (чт)		Серия 20. Ориентированные графы	Серия 20. Ориентированные графы
		Новогодний листик по комбинаторике Новогодний листик по алгебре Новогодний листик по геометрии
2018-01-14 (пн)	Отборочная олимпиада, решения
2019-01-17 (чт)	Региональный геометрический разнобой	Серия 21. Разнобой-1	Серия 21. Разнобой-1
2019-01-21 (пн)	Региональный алгебраический разнобой	Серия 22. Разнобой-2	Серия 22. Разнобой-2
2019-01-24 (чт)	Региональный комбинаторный разнобой	Серия 23. Разнобой-3	Серия 23. Разнобой-3
2019-01-25 (пт)	Тренировочная олимпиада (16:00 — 21:00, аудитория 54).
2019-01-28 (пн)	Дорешивание/разбор	Дорешивание/разбор	Дорешивание/разбор
2019-01-31 (чт)	Нет занятия	Нет занятия	Нет занятия
2019-02-04 (пн)	Нет занятия	Нет занятия	Нет занятия
2019-02-07 (чт)	Нет занятия	Нет занятия	Нет занятия
2019-02-11 (пн)	Вектора и скалярное произведение	Вектора и скалярное произведение	Вектора и скалярное произведение
2019-02-14 (чт)	Комбинаторика в теории чисел	Серия 24. Алгоритмы без обратной связи Серия 24′. Алгоритмы без обратной связи, добавка	Серия 24. Алгоритмы без обратной связи Серия 24′. Алгоритмы без обратной связи, добавка
2019-02-18 (пн)	Комплексные числа	Серия 25. Системы линейных уравнений	Серия 25. Системы линейных уравнений
2019-02-21 (чт)	Ортоцентр	Серия 26. Алгоритмы с оценками	Серия 26. Алгоритмы с оценками
2019-02-25 (пн)	Обратные остатки	Дорешивание/разбор	Дорешивание/разбор
2019-02-28 (чт)	Тригонометрическая запись комплексного числа	Серия 27. Теорема Кронекера	Серия 27. Теорема Кронекера
2019-03-04 (пн)	Метрические соотношения в треугольнике	Серия 28. Разнобой «Существует ли»?	Серия 28. Разнобой «Существует ли?»
2019-03-07 (чт)	Комбинаторика на плоскости	Серия 29. k	Серия 30. Линейные рекурренты	Серия 30. Линейные рекурренты
2019-03-14 (чт)	Теорема Шаля	Серия 31. Неравенства доп.	Серия 31. Неравенства доп. задачи
2019-03-18 (пн)	Метод Штурма	Серия 32. Хардкорная комбинаторика	Серия 32. Хардкорная комбинаторика
2019-03-21 (чт)	Принцип Дирихле в геометрии	Серия 33. UVW-метод решения неравенств	Серия 33. UVW-метод решения неравенств
2019-03-25 (пн)	Корни из единицы	Серия 34. Конфигурации прямых	Серия 34. Конфигурации прямых
2019-03-28 (чт)	Движения плоскости	Дорешивание и разбор	Дорешивание и разбор
2019-04-01 (пн)	Дорешивание корней из единиц	Московские сборы
2019-04-04 (чт)	Слепые алгоритмы
2019-04-08 (пн)	Раскраски графов
2019-04-11 (чт)	Счет углов
2019-04-15 (пн)	Неравенства, суммы и последовательности	Тренировочная олимпиада 1 (16:00 — 21:00)
2019-04-18 (чт)	Дорешивание	Тренировочная олимпиада 2 (16:00 — 21:00)
2019-04-22 (пн)	Счет отрезков
2019-04-25 (чт)	Снова раскраски графов
2019-04-29 (пн)	Гомотетия
2019-05-13 (пн)	Композиция гомотетий	Серия 35. Раскраски графов	Серия 35. Раскраски графов
2019-05-16 (чт)	Оценка + пример	Серия 36. Метод касательных	Серия 36. Метод касательных
2019-05-20 (пн)	Отборочная олимпиада + решения	Серия 35′. Раскраски графов, доп. задачи	Серия 35′. Раскраски графов, доп. задачи
2019-05-23 (чт)	Разные последовательности	Серия 37. SOS-метод решения неравенств	Серия 37. SOS-метод решения неравенств
2019-05-27 (пн)	Разбор	Дорешивание/разбор	Дорешивание/разбор
2019-05-30 (чт)		Игра	Игра

[PDF] Непрерывная оптимизация в экстремальной комбинаторике

title={Непрерывная оптимизация в экстремальной комбинаторике}, автор={Мэттью Дженссен}, год = {2017} }
- Мэтью Дженсен
- Опубликовано 26 июля 2017 г.
- Математика
В этой диссертации мы исследуем примеры, в которых инструменты непрерывной оптимизации могут быть использованы для решения задач теории экстремальных графов и гиперграфов. Мы начнем с введения обобщенного понятия лагранжиана гиперграфа и используем инструменты теории нелинейной оптимизации для изучения некоторых его свойств. В качестве приложения мы находим туранскую плотность небольшого семейства гиперграфы. Мы определяем точное k-цветное число Рамсея нечетного цикла на n вершинах, когда n велико. Это…
View via Publisher
etheses.lse.ac.uk
A Note on the Lagrangian of Linear 3-Uniform Hypergraphs
- Sinan Hu, Biao Wu
- Mathematics
  Symmetry
- 2022
Lots симметричных свойств хорошо изучены и проанализированы в экстремальной теории графов, таких как хорошо известная операция симметризации в задаче Турана и высокая симметрия в экстремальной…
Лагранжевы плотности линейных лесов и числа Турана их расширений
Лагранжиан гиперграфа был полезным инструментом в экстремальных задачах гиперграфа. В последнее время активно изучаются лагранжевы плотности гиперграфов и числа Турана их расширений.…
Лагранжевы плотности некоторых разреженных гиперграфов и числа Турана их расширений . Дж. Комб.
2018

Лагранжевы плотности некоторых $3$-однородных гиперграфов

Зилонг Ян, Юецзянь Пэн
Математика
2022

Лагранжева плотность r-однородного гиперграфа H is r ! умножая супремум лагранжианов всех H -свободных r -однородных гиперграфов. Для r-однородного графа H с t вершинами ясно…

Иррациональная лагранжева плотность одиночного гиперграфа

Число Турана r-однородного графа F , обозначаемое ex(n, F ), является максимальным число ребер в F -свободном r-однородном графе на n вершинах. Плотность Турана F определяется как π(F ) = lim n→∞…

Неперескакивающие плотности Турана гиперграфов

Цзылун Ян, Юэцзянь Пэн
Математика
2021

Прыжок

Действительное число если существует c > 0 такое, что никакое число из (α, α + c) не может быть плотностью Турана семейства r-однородных графов. Классический результат Эрдёша…

Лагранжевы плотности циклов гиперграфа

Юэцзянь Пэн, Зилонг Ян
Математика
2018

Плотность лагранжиана $r$-однородного гиперграфа $F$ равна $r!$, умноженной на супремум лагранжианов всех $F$-свободных $r$-однородных гиперграфов. Для $r$-графа $H$ с $t$ вершинами это…

Лагранжевы плотности коротких 3-равномерных линейных путей и числа Турана их продолжений

Biao Wu, Yuejian Peng
Математика
Графики Гребень.
2021

Показано, что $P_3$ и $P-4$ совершенны, что подтверждает гипотезу inyanpeng о том, что все $3-однородные линейные гиперграфы совершенны.

с изображением 1-10 из 90 ссылок

Сорт Byrelevancemost, повлиявшие на документ,

Об подтверждениях асимптотических подходящих предположений

S. Friedland, E. Krop, P. H. Lundow, K. Markström 9004
, Mathematics, P. H. Lundow, K. Markström
11188.
2006

Описана общая конструкция бесконечных семейств r-регулярных торографов и даны алгоритмы вычисления мономер-димерной энтропии плотности p для любого p∈[0,1] для этих графов.

Паросочетания и независимые множества фиксированного размера в регулярных графах

Тина Кэрролл, Дэвид Дж. Галвин, П. Тетали
Математика
Дж. Комб. Теория, сер. A
2009

Трюк с двудольной перестановкой на гомоморфизмах графов

Мы даем верхнюю границу числа гомоморфизмов графов из G в H, где H — фиксированный граф с определенными свойствами, а G варьируется по всем N- вершинный, d-регулярный граф. Этот результат обобщает…

Экстремумы внутренней энергии модели Поттса на кубических графах

Эван Дэвис, Мэтью Дженсен, Уилл Перкинс, Барнаби Робертс
Математика
Случайная структура. Алгоритмы
2018

Переход к пределу нулевой температуры дает новые результаты в экстремальной комбинаторике: число $q-раскрасок $3-регулярного графа для любого $q \ge 2$ максимизируется объединением $K_{3,3}$, что доказывает случай d=3 гипотезы Гальвина и Тетали.

The triangle-free process

T. Bohman
Mathematics
2008

The triangle-free process and R(3,k)

Gonzalo Fiz Pontiveros, Simon Griffiths, J. Morris
Математика
2013

Области теории Рамсея и случайных графов были тесно связаны с тех пор, как в 1947 г. к. В начале 1990-е годы,…

Рэмзи-добро – и все остальное

Питер Аллен, Г. Брайтуэлл, Дж. Скокан
Математика
Комб.
2013

Грэм, Рёдл и Ручиньский показали, приняв G за подходящий расширяющий граф, что обязательно r∆ > 2c∆ для некоторой константы c>0, и показали, что сама гипотеза Берра неверна даже для Pnk, k-й степени пути Pn.

О МАКСИМАЛЬНЫХ ПУТЯХ И ЦЕПЯХ ГРАФОВ

П. Эрдгс
Математика
2002

В 1940 г. Турин поставил следующий вопрос: если число узлов n графа задано и если I является целым числом cs n, то каково число ребер, которые График должен содержать, чтобы…

Обобщенная теория Рэмси для нескольких цветов

P. Erdös, R. Faudre ЧИСЛА РАМСИ ДЛЯ ГРАФОВ
- С. Берр
- Математика
- 1973
Если G и H являются графами (что будет означать конечные, без петель или параллельных линий), определите число Рамсея r(G, H) как наименьшее число p такое, что если линии полного графа Kp окрашены…
Институт комбинаторики – математических наук
Исследования
Примите меры
Главная Математические науки Исследовательская работа Институт комбинаторики
Об Институте комбинаторики
Группа комбинаторики и теории графов в Университете Мемфиса была уникальной, высокопродуктивное и активное исследовательское подразделение с начала 1970-е годы, когда группа начала сотрудничество с Полом Эрдёшем. Это сотрудничество длилось два десятилетия и привело к тому, что основные участники стали некоторые из его наиболее частых соавторов. Импульс продолжился с созданием в 1995 г. на кафедре передового опыта Джаби Хардин в области теории графов и комбинаторики, вместе с чередующейся должностью старшего преподавателя. Это привело к чрезвычайно эффективная группа, как в исследованиях, так и в наставничестве следующего поколения студентов для академических и отраслевых исследовательских возможностей в этой динамичной области.
Институт комбинаторики объединяет преподавателей, посетителей, докторантов, студентов, и персонал, чтобы обеспечить исследовательскую группу мирового класса в области комбинаторики и теории графов.
Контактная информация
Триша Симмонс, Координатор проекта Белы Боллобас, профессор кафедры комбинаторики имени Джаби Хардин
Электронная почта: tdsimmns@memphis. edu
Телефон: 901.678.5610
Факс: 901.678.4481
Серия лекций Эрдёша
Серия лекций Эрдёша — это конференция, проводимая почти каждый год в университете. Мемфиса в честь давних отношений отдела с Полом Эрдёшем.
К сожалению, из-за трудностей с финансированием серия лекций Эрдёша 2015 года была отменена.
Ссылки на постеры и сайты предыдущих конференций:
- Веб-сайт серии лекций Эрдёша, 2019 г.
- Веб-сайт серии лекций Эрдёша, 2014 г.
- Плакат серии лекций Эрдёша, 2012 г.
- Плакат серии лекций Эрдёша, 2008 г.
- Плакат серии лекций Эрдёша, 2007 г.
- Плакат серии лекций Эрдёша 9, 2004 г. 0004
- Плакат серии лекций Эрдёша, 2003 г.
- Плакат серии лекций Эрдёша, 2002 г.
- Плакат серии лекций Эрдёша, 2001 г.
Фокус исследований
Основными направлениями деятельности являются экстремальная и вероятностная комбинаторика, общий граф теория, приложения линейной алгебры к теории графов и аддитивная теория чисел.
Семинары
Институт комбинаторики обычно проводит семинары по пятницам в 15:00.
участников
Пол Балистер, Бывший профессор
Научные интересы: Вероятностная комбинаторика, случайные геометрические графы
1. Пол Балистер, Бела Боллобас, Роберт Моррис. Острый порог для изготовления квадратов. Анналы математики. 188 (2018), вып. 1, 49–143.
2. Пол Балистер, Бела Боллобас, Роберт Моррис, Джулиан Сахасрабухе, Мариус Тиба. Задача Эрдеша–Селфриджа с бесквадратными модулями.
3. Пол Балистер, Бела Боллобас, Роберт Моррис, Джулиан Сахасрабухе, Мариус Тиба. Плоские многочлены Литтлвуда существуют.
Бела Боллобас, профессор; Джейби Хардин Кафедра передового опыта в области комбинаторики
Научные интересы: Вероятностная комбинаторика, теория графов, функциональный анализ

Давид Гринкевич, Ассоциированный профессор
Научные интересы: Аддитивная теория чисел, Экстремальная комбинаторика
1. Повторяемые наборы сумм и разделов наборов. Появится в Ramanujan J.
2. Повторяемые суммы сумм и подпоследовательностей. Дж. Комбин. Теория Сер. А 160 (2018), 136–167.
3. Планарные подмножества с небольшим удвоением. QJ Math. 68 (2017), вып. 1, 161–192.
Chao Liu, Faudree Postdoc
Научные интересы: комбинаторная теория чисел, аддитивная комбинаторика

Владимир Никифоров, Профессор
Научные интересы: Экстремальная теория графов, приложения линейной алгебры к теории графов

Эстафета вокруг света по комбинаторике, вторник, 8 июня 2021 г.
Эстафета вокруг света по комбинаторике, вторник, 8 июня 2021 г.
Эстафета вокруг света по комбинаторике, вторник, 8 июня 2021 г.
Международная «Эстафета вокруг света по комбинаторике». Вторник, 8 июня 2021 г. Проведено 22 семинара, организованных разными группами. во всем мире. День начался в Австралии в 2 часа ночи по всемирному координированному времени и закончился в Аляска в 23:00 UTC. Остановки по пути включают Бразилию, Канаду, Чили, Китай, Чехия, Франция, Венгрия, Новая Зеландия, Польша, Россия, Юг Корея, Великобритания и США.
Спасибо Balazs Keszegh за дизайн плаката справа. PDF-версию плаката можно найти здесь.
Мероприятие координировал Алекс Скотт (электронная почта: фамилия на maths.ox.ac.uk). Особая благодарность Яношу Паху (который внес большой вклад, в том числе предложил название), а также Андрею Купавскому и Санг-илу Оуму.
Расписание
Встреча прошла в Zoom. Выступления были записаны и доступны на youtube-канале. Удивительные вступительные части к видеороликам создала Юлия Рылова.
Время отображается в формате UTC и по местному времени вашего браузера; спасибо Sang-il Oum за javascript, который это делает.
2:00 (UTC) Семинар по дискретной математике Монаша, Мельбурн, Австралия (организуемый Яном Уэнлессом и Грэмом Фарром)
Докладчик: Дэвид Вуд (Университет Монаша)
Название: Универсальность в минорно-замкнутых классах графов
Абстрактный. Станислав Улам спросил, существует ли универсальная счетная планарный граф (то есть счетный планарный граф, содержащий все счетный планарный граф в качестве подграфа). Янош Пах (1981) ответил на это вопрос в минусе. Усилим этот результат, показав, что каждое счетный граф, содержащий все счетные планарные графы, должен содержать бесконечный полный граф в качестве минора. С другой стороны, мы строим счетный граф, содержащий все счетные планарные графы и имеющий несколько ключевые свойства, такие как линейные числа раскраски, линейное расширение и все конечный n-вершинный подграф имеет ширину O(\sqrt{n}) (что подразумевает Теорема Липтона-Тарьяна о разделителе). В более общем случае для каждого фиксированного положительного целое число t построим счетный граф, содержащий все счетные К _t — второстепенный граф и обладает указанными выше ключевыми свойствами. Совместная работа с Тони Хьюн, Боян Мохар, Роберт Самал и Карстен Томассен.
3:00 (UTC) Семинар по комбинаторике SCMS, Шанхайский центр математических наук, Китай (организуют Пин Ху, Хэхуэй Ву и Цицинь Се)
Докладчик: Баоган Сюй (Нанкинский педагогический университет, Китай)
Название: О раскраске графов обхвата 2l+1 без более длинных нечетных отверстий
Аннотация: Дыра — это индуцированный цикл длины не менее 4. Пусть l≥2 — натуральное число, пусть Ĝ _l обозначим семейство графов, имеющих обхват 2l+1 и не имеющих отверстий нечетной длины не менее 2l+3, и пусть G ∈ Ĝ _л . Для вершины u ∈ V(G) и непустого множества S ⊆ V(G) пусть d(u,S) = min{d(u,v) : v∈S}, и пусть L _i (S )={u∈V(G) и d(u,S)=i} для любого целого числа i≥0. Покажем, что если G[S] связна и G[L _i (S)] двудольна для каждого i∈{1…,l-1}, то G[L _i (S)] двудольна для каждого i>0 и, следовательно, χ(G)≤4, где G [S] обозначает подграф, индуцированный S. Для графа G∈ Ĝ ₂ , покажем, что χ(G)≤3, если G не индуцирует двух циклов длины 5, имеющих общие ребра. Пусть θ+ — граф, полученный из графа Петерсена удалением двух соседних вершин. Покажем, что если G ∈ Ĝ ₂ 3-связен и не имеет неустойчивых 3-разрезов, то G не индуцирует θ+. Как следствие, минимальные нераскрашиваемые в 3 графы Ĝ ₂ не индуцируют θ+. Это совместная работа с Ди Ву и Ян Сюй.
4:00 (UTC) Семинар по алгебре и комбинаторике, Окленд, Новая Зеландия (организовано Лукасом Зобернигом и Мэтью Кондером)
Докладчик: Йерун Шиллеварт (Оклендский университет)
Название: Построение высокорегулярных расширителей из гиперболических групп Кокстера
Аннотация: Для струнной системы Кокстера (W,S) мы строим высокорегулярные частные 1-скелета его универсального многогранника P, образующие бесконечное семейство графов-расширителей, когда (W,S) не определено, а P имеет конечное вершинные связи. Регулярность графиков в этом семействе зависит от Диаграмма Кокстера (W, S). Расширение связано с суперприближением применяется к (W, S). Эта конструкция также распространяется на покрытие Витоффиана. многогранники. В качестве прямого приложения мы получаем несколько примечательных семейств графы-расширители с высоким уровнем регулярности, отвечающие, в частности, вопрос, поставленный Чепменом, Линиалом и Пеледом, положительно.
(Совместная работа с Марстоном Кондером, Александром Любоцким и Франсуа Тильмани)
5:00 (UTC) Семинар CMSA, Австралия (организаторы Нина Камцев и Анита Либенау)
Докладчик: Гордон Ройл (Университет Западной Австралии (UWA))
Название: Вещественные хроматические корни планарных графов
Абстрактный: Хроматический многочлен P(G,q) графа G — это функция, которая для положительного целого числа q подсчитывает количество правильных q-раскрасок графа. Результирующая функция является многочленом, поэтому независимо от того, имеет ли она какой-либо комбинаторный смысл, мы можем вычислить ее при любом комплексном числе и, следовательно, найти ее корни, которые могут быть целыми, действительными или комплексными. Общая цель этой тщательно изученной темы — понять взаимосвязь между свойствами графика и расположением его хроматических корней.
В этом докладе я сосредоточусь на действительных корнях хроматических многочленов планарных графов. Я начну с рассказа об истории, предыстории и основных результатах, а затем сосредоточусь на попытках (моих и других) показать, что плоские хроматические корни плотны в реальном интервале (3,4).
Разговор в основном на общем уровне, и любой, кто знаком с основными понятиями графов, правильной раскраской графов и полиномами, сможет понять его суть.
6:00 (UTC) Семинар по дискретной математике в IBS Discrete Mathematics Group, Южная Корея (организован Санг-ил Оум)
Докладчик: О-Джон Квон (Инчхонский национальный университет и группа дискретной математики IBS)
Название: Классы орграфов пересечений с хорошими алгоритмическими свойствами
Аннотация: Орграф пересечений — это орграф, в котором каждая вершина v представлена упорядоченной парой (S _v , T _v ) множеств таких, что существует ребро из v в w тогда и только тогда, когда S _v и T _w пересекаются. Орграф пересечения рефлексивен, если S _v ∩ T _v ≠ ∅ для каждой вершины v. По сравнению с хорошо известными неориентированными графами пересечений, такими как графы интервалов и графы перестановок, разработано не так много алгоритмических приложений для орграфов пересечений.
Вдохновленные успешной историей алгоритмических приложений графов пересечений с использованием параметра ширины графа, называемого mim-width, мы вводим его направленный аналог, называемый `bi-mim-width’, и доказываем, что различные классы рефлексивных орграфов пересечений имеют ограниченную bi-mim-ширину. . В частности, мы показываем, что рефлексивные H-орграфы как естественное расширение H-графов имеют линейную бимим-ширину не более 12|E(H)|, что расширяет границу линейной mim-ширины H-графов [О разрешимости задач оптимизации на H-графах. Алгоритмика 2020].
Для приложений мы вводим новую структуру направленных версий локально проверяемых задач, которая упрощает определение и изучение многих проблем в литературе и облегчает их общую алгоритмическую обработку. Получены унифицированные полиномиальные алгоритмы для этих задач на орграфах ограниченной бимим-ширины, когда задано разложение по ветвям. Локально проверяемые задачи включают ядро, доминирующее множество и направленный H-гомоморфизм.
Это совместная работа с Ларсом Яффке и Яном Арне Телле.
7:00 (UTC) Семинар TCS в Jagiellonian, Польша (организованный Павел Идзяк и Петр Мичек)
Спикер: Бартош Вальчак (ягеллонский)
Название: Раскрашивание графов видимости полигонов и их обобщения
Аннотация: Граф видимости многоугольника P образован такими парами вершин u и v многоугольника P, что отрезок uv не пересекается с внешностью P. Покажем, что класс графов видимости многоугольника χ-ограничен, тем самым отвечая на вопрос Кара, Пор и Вуд, 2005 г. В частности, мы доказываем оценку χ≤3·4 ^ω-1 . Мы получаем такую же оценку для обобщений графов видимости многоугольников, в которых многоугольник заменяется кривой, а прямолинейные отрезки заменяются отрезками в псевдолинейном расположении. Доказательство проводится в постановке упорядоченных графов. В частности, мы показываем χ-ограниченность нескольких классов упорядоченных графов с исключенными упорядоченными подструктурами. Совместная работа с Джеймсом Дэвисом, Томашем Кравчиком и Роуз Маккарти.
8:00 (UTC) Мини-онлайн-встреча по шотландской комбинаторике, Университет Глазго, Великобритания (организовано Китти Микс)
Докладчик: Хэн Го (Эдинбургский университет)
Название: Цепной подход Маркова к выборке Локальная лемма Ловаша
Аннотация: Локальная лемма Ловаша является мощным инструментом для установления существования комбинаторных объектов при определенных условиях зависимости. Алгоритмическая локальная лемма Мозера и Тардоса дает эффективный способ нахождения таких объектов. Нас интересует локальная лемма выборки, цель которой — равномерно и эффективно генерировать эти объекты, потенциально при более жестких условиях, чем условия локальной леммы. В последние годы эта проблема выборки быстро развивалась, и в этом докладе я проиллюстрирую подход к этой задаче с помощью цепи Маркова. Текущим примером будет выборка решений для формул k-CNF, где каждая переменная не появляется в слишком большом количестве предложений. Основная трудность при построении цепи Маркова здесь заключается в том, что пространство решений не связано локальными перемещениями. Эта проблема будет обойдена идеей проекции.
9:00 (UTC) Лондонская фондовая биржа, Великобритания (организуют Ахмад Абди и Йозеф Скокан)
Спикер: Анника Хекель (LMU)
Название: Как меняется хроматическое число случайного графа?
Аннотация: Насколько сильно хроматическое число случайного графа G(n, 1/2) отличаться? Шамир и Спенсер доказали, что оно содержится в некоторой последовательности интервалы длиной около n ^1/2 . Алон улучшил это слегка n ^1/2 / log n. Однако до недавнего времени не нижние оценки флуктуаций хроматического числа G(n, 1/2) были известны, хотя этот вопрос поднимался Боллобасом многими много лет назад. Я расскажу об основных идеях, необходимых для доказательства того, что хотя бы для бесконечно многих n хроматическое число G (n, 1/2) равно не сконцентрировано менее чем на n ^1/2-o(1) последовательных ценности.
Я также рассмотрю гипотезу о зигзаге, выдвинутую недавно Боллобасом. Хекель, Моррис, Панагиоту, Риордан и Смит: это предполагает, что правильная длина интервала концентрации «зигзаги» между п ^1/4+o(1)) и n ^1/2+o(1) , в зависимости от н.
Совместная работа с Оливером Риорданом.
10:00 (UTC) Большой семинар МФТИ по комбинаторике и геометрии, Москва, Россия (организаторы А. Купавский, Я. Пах, А. Полянский, И. Шкредов, М. Жуковский)
Докладчик: Нога Алон (Принстон и Тель-Авив)
Название: Разделение случайных ожерелий
Абстрактный: Пусть N — случайное ожерелье из км бусин каждого из t типов. Каково типичное минимальное количество точек, в которых можно разрезать N так, чтобы можно было разбить полученные интервалы бусинок на k коллекций, каждая из которых содержит ровно m бусин каждого типа? Известно, что это число не превосходит (k-1)t с вероятностью 1, обычно он значительно меньше? Расскажу о недавней совместной работе с Дор Эльбойм, Яношем Паком и Габором. Тардос обращается к этой проблеме и показывает, что она связана с несколько, казалось бы, не связанных между собой тем, в том числе совпадения в почти регулярные гиперграфы и случайные блуждания в евклидовых пространствах.
11:00 (UTC) Семинар в Будапеште (BBC+G), Венгрия (организаторы Янош Пах, Дёмётёр Палвёльи, Геза Тот)
Докладчик: Ласло Ловаш (Университет Этвош, Будапешт)
Название: Ортогональные представления и пределы графа
Аннотация: Ортогональные представления сыграли важную роль в теории информации, комбинаторная оптимизация, теория жесткости и квантовая физика. Мы начинаем с обзором этих соединений.
Недавний интерес к этой конструкции мотивирован теорией пределов графов. Предельные объекты последовательностей сходящихся графов были определены в двух крайние случаи: графоны (пределы плотных последовательностей графов) и графики. (пределы последовательностей графов ограниченной степени). В средних диапазонах Марков цепи играют важную роль. Интересный пример из этого точки зрения — это цепь Маркова на сфере в фиксированной размерности, где шаг это ход на 90 градусов в любом направлении.
Основной вопрос: является ли этот объект пределом конечных графов (и в каком смысл)? Чтобы получить утвердительный ответ, нам нужно определить плотность данный простой граф в графе ортогональности. Это приводит к проблеме определение и вычисление случайного ортогонального представления этого графа, что само по себе интересно и нетривиально.
12:00 (UTC) Семинар в Бордо, Франция (организуют Джонатан Нарбони и Марта Бонами)
Докладчик: Карла Гроенланд (Утрехтский университет)
Название: Универсальные графики и схемы разметки
Аннотация: Индуцированный универсальный граф для класса графов содержит все графы этого класса в качестве индуцированного подграфа. Мы строим индуцированные универсальные графы для всех классов наследственных графов и выводим из этого схемы маркировки достижимости для орграфов и схемы маркировки сравнимости для po-множеств. Все эти результаты являются асимптотически оптимальными. Этот доклад призван дать некоторое представление об этих концепциях и наших методах (включая лемму регулярности Семереди и эффективные словари). Мы также обсудим новое место исследования: что, если мы усилим индуцированное до изометрического? Несколько интересных вопросов остаются открытыми.
Это основано на совместной работе с Мартой Бонами, Луи Эспере, Сирилом Гавуалем и Алексом Скоттом.
13:00 (UTC) Семинар по комбинаторике в Нью-Йорке, США (организованный Кира Адаричева, Дипак Бал, Надя Бенакли, Джонатан Катлер, Эзра Халлек, Сандра Кинган, Иосиф Малкевич, Керри Окаджан, Эрик Роуленд и Минсянь Чжун.)
Докладчик: Дипак Бал (Государственный университет Монклера)
Название: Размер Рамсея числа путей и циклов
Абстрактный: Пусть ℱ ₁ и ℱ ₂ две семьи графики. Размер числа Рамсея R̂(ℱ ₁ , ℱ ₂ ) — наименьшее число m такое, что существует граф G с m ребрами, в которых каждая красно-синяя раскраска E(G) содержит либо красный график из ℱ ₁ или синий график из ℱ ₂ . Пусть P _n представляет путь на n вершинах и пусть 𝒞 представлять семейство всех циклов. Мы обсуждаем некоторые недавние успехи в области размера Рэмси. числа в случаях, когда ℱ ₁ = ℱ ₂ = P _n (улучшение нижней границы) и где ℱ ₁ = P _n , ℱ ₂ = 𝒞 (улучшение нижней и верхней границы). Мы также обсудим некоторые недавние результаты, касающиеся размера Рамсея. количество путей гиперграфа. Это основано на совместных работах с DeBiasio и Шудрих.
14:00 (UTC) Вебинар по экстремальной и вероятностной комбинаторике (организаторы Ян Гладкий, Диана Пиге, Ян Волец и Лиана Епремян)
Докладчик: Друв Мубайи (Иллинойсский университет в Чикаго)
Название: Допустимая область гиперграфов
Абстрактный: Многие экстремальные задачи гиперграфа стремятся максимизировать количество ребер с учетом некоторых локальных ограничений. Мы стремимся получить более подробную понимание таких проблем путем изучения максимального предмета дополнительное глобальное ограничение, а именно размер тени. Помещать иначе мы ищем пары (x, y) в единичном квадрате такие, что существуют Гиперграфы без F, плотность теней которых приближается к x, а плотность ребер подходит к ю. Я дам некоторые общие результаты о форме этого «возможный район», а также расширить и улучшить некоторые классические Туранские результаты для конкретных вариантов F. Это совместная работа с Xizhi Liu.
15:00 (UTC) Совместный семинар DIMEA и FORMELA, Масариков университет, Чешская Республика (организуют Даниэль Крал и Самуэль Мор)
Спикер: Джеймс Дэвис (Ватерлоо)
Название: Графы-раскраски и их обобщения
Аннотация: Круговой граф — это граф пересечений набора хорд на окружности; вершины смежны, когда их соответствующие хорды пересекаются. А классический результат раскраски графа из-за того, что Дьярфас утверждает, что круговые графы являются χ-ограниченными, т. 3) треугольников можно сделать без треугольников, удалив о (n ² ) края. В этом докладе я рассмотрю последние расширения и варианты, количественные аспекты, приложения и открытые проблемы.
17:00 (UTC) Семинар по комбинаторике и теории вероятностей Университета штата Огайо, США (организован Мэтью Кале, Хой Нгуен, Дэвид Сивакофф и Кэролайн Терри (англ.
Докладчик: Аллан Слай (Принстон)
Название: Распространение инфекций случайными ходоками
Аннотация: Рассматривается класс взаимодействующих систем частиц, где частицы совершают независимые случайные прогулки по Z ^d и распространяют инфекцию в соответствии с моделью Susceptible-Infectious-Recovered или SIR. Мы показываем, что если скорость выздоровления достаточно низкая, инфекция распространяется линейно. Я буду описать новые методы для понимания процессов роста в таких моделях.
Совместная работа с Дунканом Довернем
18:00 (UTC) Семинар в Рио, Бразилия (организовано Робом Моррисом)
Спикер: Марсело Кампос (IMPA)
Название: Название: Вероятность сингулярности случайной симметричной матрицы экспоненциально мала
Аннотация: Пусть A равномерно случайным образом выбирается из набора всех симметричных матриц размера n x n с элементами в {-1,1}. Я опишу некоторые недавние работы, в которых мы показываем, что Pr(det(A) = 0) -cn для некоторой абсолютной константы c > 0.
Совместная работа с Мэтью Йенссеном, Маркусом Мишленом и Джулианом Сахасрабудхе.
19:00 (UTC) Технический семинар Джорджии, США (организаторы Антон Бернштейн, Чжию Ван и Синсин Юй)
Докладчик: Джим Гилен (Университет Ватерлоо)
Название: Гомоморфизмы и раскраска графов и бинарных матроидов
Аннотация: Разговор начинается с теоремы Рёдля о том, что графы с огромным хроматическим числом содержат подграфы без треугольников с большим хроматическим числом. Мы рассмотрим различные связанные результаты и гипотезы с заметной матроидной предвзятостью; новые результаты — совместная работа с Питером Нельсоном и Рафаэлем Штайнером.
20:00 (UTC) Семинар АГКО, Чили (организатор Майя Штайн)
Докладчик: Дэвид Конлон (Калифорнийский технологический институт)
Название: Случайные полилинейные отображения и проблема ящика Эрдёша
Абстрактный: Используя случайные полилинейные карты, мы обеспечиваем новые нижние границы для Эрдёша. задача о ящике, задача об оценке экстремального числа полных d-дольный d-однородный гиперграф с двумя вершинами в каждой части, тем самым улучшение работы Гундерсона, Рёдля и Сидоренко. Совместная работа с Cosmin Похоата и Дмитрий Захаров.
21:00 (UTC) Семинар по дискретной математике ЮФУ, Университет Саймона Фрейзера, Канада (организуют Шусин Ли и Александра Весолек)
Докладчик: Фан Чанг (UCSD)
Название: Деревья и леса в функциях Грина графа
Абстрактный: Функции Грина графика являются псевдообратными лапласианам и поэтому полезны для решения многих типов уравнений Лапласа в дискретных условиях.
В этом докладе мы дадим комбинаторные интерпретации функций Грина в терминах Подсчет деревьев и лесов на графике. Мы также упомянем несколько приложений, касающихся алгоритмов рейтинга страниц и времени попадания для случайных блужданий.
22:00 (UTC) Семинар по дискретной математике Университета Виктории, Канада (организатор Наташа Моррисон и Джонатан Ноэль)
Спикер: Эндрю Сук (UCSD)
Название: Задачи типа Турана для точечных инцидентов
Аннотация: В этом докладе я обсужу несколько результатов типа Турана для инцидентов точка-линия. Он будет основан на совместных работах с Иштваном Томоном и Можганом Мирзаеи.
23:00 (UTC) Университет Аляски Фэрбенкс, США (организатор Джилл Фодри)
Спикер: Рон Гулд (Эмори)
Название: Аккордовые циклы
Хорда цикла — это ребро между двумя вершинами цикла, не край цикла. Цикл в графе G называется хордовым, если его вершины индуцируют хотя бы одну хорду, и она называется двухордовой, если ее вершины индуцируют два и более аккорда. В последнее десятилетие резко возросло количество исследований аккордовых циклов.
В этом докладе я рассмотрю множество результатов, касающихся аккордовых циклов. я рассмотрим несколько типов вопросов, касающихся аккордовых циклов и Рассмотрим основные известные результаты в каждой из этих областей. Это включает минимум результаты степени и суммы степеней, результаты запрещенного подграфа и плотность ребер полученные результаты. Мы будем задавать вопросы типа: Когда ребро может быть хордой цикла? и когда ребро может быть ребром цикла хордового цикла? Много раз я буду попробуйте сопоставить эти результаты аккордового цикла с известными результатами на циклах и показать, что результаты хордового цикла на самом деле являются естественными расширениями известные результаты цикла.
No related posts.