круги Эйлера — Основы логики и логические основы компьютера
Леонард Эйлер – величайший из математиков,написал более 850 научных работ. В одной из них и появились эти круги. Учёный писал, что «они очень подходят для того, чтобы облегчить наши размышления». Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью. Задача 1 Из 90 туристов, отправляющихся в путешествие, немецким языком владеют 30 человек, английским – 28 чел, французским – 42 чел. Английским и немецким одновременно владеют 8 человек, английским и французским -10 чел, немецким и французским – 5 чел, всеми тремя языками – 3 чел. Решение: Покажем условие задачи графически – с помощью трёх кругов Ответ: 10 человек. Задача 2 Многие ребята нашего класса любят футбол, баскетбол и волейбол. А некоторые — даже два или три из этих видов спорта. Известно, что 6 человек из класса играют только в волейбол, 2 – только в футбол, 5 – только в баскетбол. Только в волейбол и футбол умеют играть 3 человека, в футбол и баскетбол – 4, в волейбол и баскетбол – 2. Один человек из класса умеет играть во все игры, 7 не умеют играть ни в одну игру. Требуется найти: Сколько всего человек в классе? Сколько человек умеют играть в футбол? Сколько человек умеют играть в волейбол? Задача 3 В детском лагере отдыхало 70 ребят. Из них 20 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов, а 3 спортсмена посещают и драмкружок, и хор. Задача 4 Из сотрудников фирмы 16 побывали во Франции, 10 – в Италии, 6 – в Англии. В Англии и Италии – пятеро, в Англии и Франции – 6, во всех трёх странах – 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работает 19 человек, и каждый их них побывал хотя бы в одной из названных стран? Задача 5 Шестиклассники заполняли анкету с вопросами об их любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем трем среди них нравятся еще и «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма. У «Волка и теленка» 13 фанатов, пятеро из которых назвали в анкете два мультфильма. Надо определить, скольким же шестиклассникам нравится «Губка Боб Квадратные Штаны». Задачи для решения учащимися 1. В классе 35 учеников. Все они являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 — в районной. Сколько из них: а) не являются читателями школьной библиотеки; б) не являются читателями районной библиотеки; в) являются читателями только школьной библиотеки; г) являются читателями только районной библиотеки; д) являются читателями обеих библиотек? 2.Каждый ученик в классе изучает английский или немецкий язык, или оба этих языка. Английский язык изучают 25 человек, немецкий — 27 человек, а тот и другой — 18 человек. Сколько всего учеников в классе? 3.На листе бумаги начертили круг площадью 78 см2 и квадрат площадью 55 см2. Площадь пересечения круга и квадрата равна 30 см2. Не занятая кругом и квадратом часть листа имеет площадь 150 см2. Найдите площадь листа. 4. В группе туристов 25 человек. 5. В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое, или то и другое. Половина детей любит пирожное, а 20 человек — пирожное и мороженое. Сколько детей любит мороженое? 6. В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек —.и математический, и физический, 5 — и математический, и химический, 3 — и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки? 7. После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Решение задач ЕГЭ с помощью кругов Эйлера Задача 1 В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение: При помощи кругов Эйлера изобразим условия задачи. Опираясь на условия задачи, составим уравнения:
Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что: 4800 + 3 = 7000, откуда получаем 3 = 2200. Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что: 2 + 2200 = 4500, откуда 2 = 2300. Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор. Задача 2 В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах) будет найдено по запросу Торты? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов. Решение Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера. Обозначим каждый сектор отдельной буквой (А, Б, В). Из условия задачи следует: Торты │Пироги = А+Б+В = 12000 Торты & Пироги = Б = 6500 Пироги = Б+В = 7700 Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги. Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300 Сектор А равен 4300, следовательно Торты = А+Б = 4300+6500 = 10800 Задача 3 В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах) будет найдено по запросуВыпечка? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов. Решение Для решения задачи отобразим множестваПироженых и Выпечек в виде кругов Эйлера. Обозначим каждый сектор отдельной буквой (А, Б, В). Из условия задачи следует: Пироженое & Выпечка = Б = 5100 Пироженое = А+Б = 9700 Пироженое │ Выпечка = А+Б+В = 14200 Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти секторВ, для этого из общего множества (Пироженое │ Выпечка ) отнимем множество Пироженое. Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500 Сектор В равен 4500, следовательно Выпечка = Б + В = 4500+5100 =9600 Задача 4
Решение Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г). Преобразим условие задачи в виде суммы секторов: спаниели │(терьеры & овчарки) = Г + Б спаниели│овчарки = Г + Б + В спаниели│терьеры│овчарки = А + Б + В + Г терьеры & овчарки = Б Из сумм секторов мы видим какой запрос выдал больше количества страниц. Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4 Задача 5 В таблице приведены запросы к поисковому серверу.
Решение Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г). Преобразим условие задачи в виде суммы секторов: барокко│ классицизм │ампир = А + Б + В + Г Из сумм секторов мы видим какой запрос выдал больше количества страниц. Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1 Задача 6
Решение Для решения задачи представим запросы в виде кругов Эйлера. K — канарейки, Щ – щеглы, С – содержание, Р – разведение. Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький. В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1 Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса. Только при таких условиях мы можем быть уверены, что правильно решили задачу.
Задача 7 (ЕГЭ 2013) В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Какое количество страниц (в тысячах) будет найдено по запросу Эсминец? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.  Ответ: 2200 Решение: Запрос «Фрегат» обозначим символом «Ф», «Эсминец» — символом «Э». Э=(Ф|Э)-Ф+(Ф&Э)=3400-2100+900=2200. Разбор задачи B12 (демо ЕГЭ 2012)Время выполнения-2 мин, уровень сложности-повышенный В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
Какое количество страниц (в тысячах) будет найдено по запросу Шахматы? Ответ: 3270 Решение: Изобразим запросы в виде диаграмм Эйлера-Венна. Запрос «Шахматы» обозначим символом «Ш», «Теннис» — символом «Т». Ш=(Ш|Т)-Т+(Ш&Т)=7770-5500+1000=3270. Задачи для самостоятельного решения Задача 1 В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Задача 2 В таблице приведены запросы к поисковому серверу.
Ответы к задачам для самостоятельного решения
|
1.
 6. Круговые схемы Эйлера. Логика. Учебное пособие
6. Круговые схемы Эйлера. Логика. Учебное пособие1.6. Круговые схемы Эйлера
Как мы уже знаем, в логике выделяется шесть вариантов отношений между понятиями. Два любых сравнимых понятия обязательно находятся в одном из этих отношений. Например, понятия писатель и россиянин находятся в отношении пересечения, писатель и человек – подчинения, Москва и столица России – равнозначности, Москва и Петербург – соподчинения, мокрая дорога и сухая дорога – противоположности, Антарктида и материк – подчинения, Антарктида и Африка – соподчинения и т. д. и т. п.
Надо обратить внимание на то, что если два понятия обозначают часть и целое, например месяц и год, то они находятся в отношении соподчинения, хотя может показаться, что между ними отношение подчинения, ведь месяц входит в год. Однако, если бы понятия месяц и год были подчиненными, то тогда надо было бы утверждать, что месяц – это обязательно год, а год – это не обязательно месяц (вспомним отношение подчинения на примере понятий 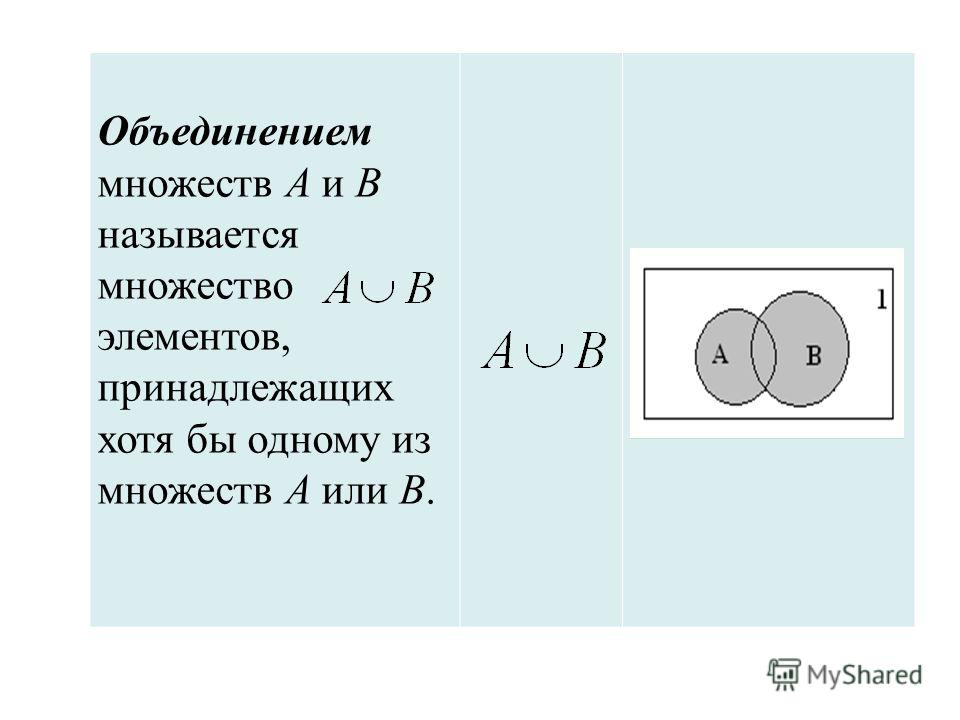 Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия месяц и год, так же, как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом и т. п., находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.
Месяц – это не год, а год – это не месяц, но и то, и другое – отрезок времени, следовательно, понятия месяц и год, так же, как и понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом и т. п., находятся в отношении соподчинения, т. к. часть и целое – не то же самое, что вид и род.
В начале говорилось о том, что понятия бывают сравнимыми и несравнимыми. Считается, что рассмотренные шесть вариантов отношений применимы только к сравнимым понятиям. Однако возможно утверждать, что все несравнимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин
и небесное тело возможно рассматривать как соподчиненные, ведь пингвин – это не небесное тело и наоборот, но в то же время объемы понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающего мира или форма материи (ведь и пингвин и небесное тело – это различные объекты окружающего мира или различные формы материи). Если же одно понятие обозначает что-то материальное, а другое – нематериальное (например, дерево и мысль), то родовым для этих (как возможно утверждать) соподчиненных понятий является понятие форма бытия, т. к. и дерево, и мысль, и что угодно еще – это различные формы бытия.
Если же одно понятие обозначает что-то материальное, а другое – нематериальное (например, дерево и мысль), то родовым для этих (как возможно утверждать) соподчиненных понятий является понятие форма бытия, т. к. и дерево, и мысль, и что угодно еще – это различные формы бытия.Как нам уже известно, отношения между понятиями изображаются круговыми схемами Эйлера. Причем до сих пор мы изображали схематично отношения между двумя понятиями, а это можно сделать и с большим количеством понятий. Например, отношения между понятиями
Взаимное расположение кругов показывает, что понятия боксер и негр находятся в отношении пересечения (боксер может быть негром и может им не быть, а также негр может быть боксером и может им не быть), а понятия боксер и человек, так же как и понятия негр и человек находятся в отношении подчинения (ведь любой боксер и любой негр – это обязательно человек, но человек может не быть ни боксером, ни негром).
Рассмотрим отношения между понятиями дедушка, отец, мужчина, человек с помощью круговой схемы:
Как видим, указанные четыре понятия находятся в отношении последовательного подчинения: дедушка – это обязательно отец, а отец – не обязательно дедушка; любой отец – это обязательно мужчина, однако не всякий мужчина является отцом; и, наконец, мужчина – это обязательно человек, но человеком может быть не только мужчина. Отношения между понятиями хищник, рыба, акула, пиранья, щука, живое существо изображаются следующей схемой:
Попробуйте самостоятельно прокомментировать эту схему, установив все имеющиеся на ней виды отношений между понятиями.
Подытоживая сказанное, отметим, что отношения между понятиями – это отношения между их объемами. Значит, для того, чтобы было возможно установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными. Что касается неопределенных понятий, о которых шла речь выше, то установить точные отношения между ними достаточно сложно, фактически невозможно, ведь из-за неясности их содержания и нерезкости объема два каких-нибудь неопределенных понятия можно будет характеризовать как равнозначные или как пересекающиеся, или как подчиняющиеся и т.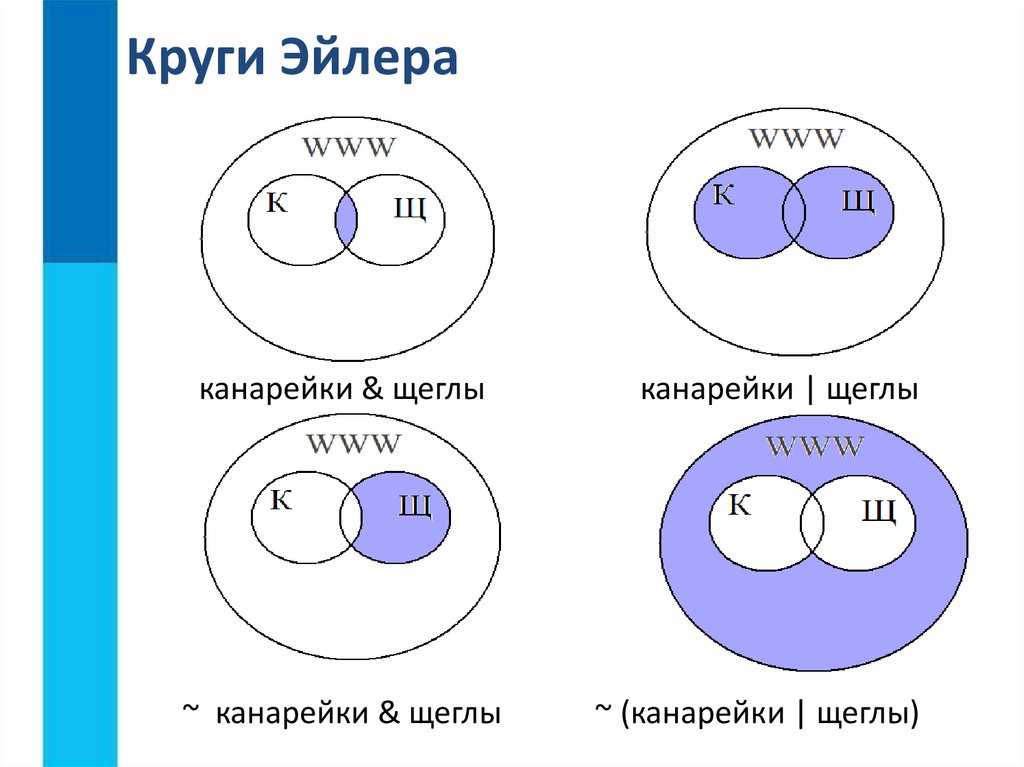
Данный текст является ознакомительным фрагментом.
9.1. Графические схемы структуры аргументации
9.1. Графические схемы структуры аргументации Всякая аргументация начинается с установления и обсуждения некоторых фактов, которые в дальнейшем будут называться данными, и с помощью которых выдвигается и обосновывается некоторое заключение. Кроме того, для перехода от
Кроме того, для перехода отКомментарии и схемы
Комментарии и схемы Учение, в основе которого лежит внутренняя работа личности, не могло бы пережить саму эту личность без приливов новой внутренней работы новых личностей. Тех, кто увидел для себя особый смысл в этом учении. Меняются условия существования, приходит
Нравственная философия Толстого и Достоевского в рамках ницшеанской схемы нигилизма
Нравственная философия Толстого и Достоевского в рамках ницшеанской схемы нигилизма Начиная с последней четверти прошлого века проблема нигилизма выходит на одно из первых мест в числе важнейших проблем западноевропейской философии. Своим «статусом» она прежде всего
СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ
СХЕМЫ ПРАВИЛЬНЫХ РАССУЖДЕНИЙ
Вот два примера дедуктивных выводов из рассказа русского юмориста начала века В. Билибина. «Если бы на свете не существовало солнца, то пришлось бы постоянно жечь свечи и керосин. Если бы пришлось постоянно жечь свечи и керосин, то чиновникам
Билибина. «Если бы на свете не существовало солнца, то пришлось бы постоянно жечь свечи и керосин. Если бы пришлось постоянно жечь свечи и керосин, то чиновникам
Теоретические схемы и абстрактные объекты технической теории
Теоретические схемы и абстрактные объекты технической теории Теоретические схемыпредставляют собой совокупность абстрактных объектов, ориентированных, с одной стороны, на применение соответствующего математического аппарата, а с другой, – на мысленный эксперимент,
2. Диалектика схемы, аллегории и символа
2. Диалектика схемы, аллегории и символа Какие же возможны вообще виды этого взаимоотношения? Их очень много. Но, следуя Шеллингу, можно указать три основных таких вида. При этом будем иметь в виду, что наши термины «внутреннее» и «внешнее» – очень общие термины и их можноИконография как система методов: схемы и угрозы
Иконография как система методов: схемы и угрозы
Сама практика иконографического анализа сформировала «проверенную схему» последовательных исследовательских действий. Схема подразумевает:– уяснение исторического значения мотива – с точки зрения времени (момент
Схема подразумевает:– уяснение исторического значения мотива – с точки зрения времени (момент
2.1.1. Нормы-схемы речевого общения: речевой этикет
2.1.1. Нормы-схемы речевого общения: речевой этикет Выбор первой проблемной области – речевого этикета – обусловлен следующим. При определении сущностных характеристик нормы мы начали движение от социальных норм, при этом заметили, что их существование в полной мере
2.1.2. Семиотически закрепленные нормы-схемы: жанры
2.1.2. Семиотически закрепленные нормы-схемы: жанры Основой противопоставления социально и семиотически закрепленных норм, как было сказано в главе I, является способ их закрепления в социокультурной практике. Первые – неписаные законы – становятся программами, схемами
Как совершенствовать логику и перестать заблуждаться
Почему мы верим во всякую чушь? Откуда у людей столько предрассудков? Что такое мистическое мышление? Ответы на эти и другие вопросы дает Никита Непряхин, книга которого описывает самые популярные мифы и заблуждения в истории человечества — от астрологии и гомеопатии до экстрасенсов и призраков — и дает умные, подробные, понятные инструменты для их разоблачения и развития критического мышления.
 Здесь и понимание своих и чужих когнитивных искажений, и основы формальной и неформальной логики, и теория аргументации, и технологии фактчекинга, и много чего еще. Публикуем отрывок из книги «Анатомия заблуждений», посвященный развитию такой важной части мышления, как логика.
Здесь и понимание своих и чужих когнитивных искажений, и основы формальной и неформальной логики, и теория аргументации, и технологии фактчекинга, и много чего еще. Публикуем отрывок из книги «Анатомия заблуждений», посвященный развитию такой важной части мышления, как логика.Никита Непряхин
Издательство Альпина Паблишер, 2020
Чтобы погрузиться в науку логику, для начала определим основополагающие понятия. Вот с самого «понятия» и «определения» и начнем. Без грамотного понимания и определения явления или события невозможно разобраться с логикой рассуждений и уяснить их смысл.
Что подразумевает человек, когда произносит какие-либо слова? Что он имеет в виду? Можно ли понять смысл предложения, если в нем есть неизвестное нам слово? Что конкретно имеет в виду человек, когда произносит, например, слово «право»? Имеет ли он в виду общепринятое широкое значение или узкое юридическое? Без понятий и определений мы не смогли бы понимать друг друга. Мы все прекрасно понимаем значение таких слов, как «окно», «компьютер», «собака», «карандаш», «стол».
Итак, об этих базовых элементах мышления, фундаменте логики мы и поговорим. Начнем с термина «понятие», а потом перейдем к термину «определение». Мы все мыслим с помощью понятий.
Понятием называется форма мышления, которая обозначает какой-либо объект или его свойство
Вокруг нас бесчисленное множество разных объектов, и каждый из них отражается в нашем сознании как какое-либо понятие. Просто оглянитесь вокруг. Вы видите горы, реки, облака, светящее солнце? А может быть, стол, лампу, календарь и ручку с блокнотом? Каждому объекту или явлению в этом мире мы задаем свои имена. Вот такие имена в логике и называют «понятие». Мы анализируем разные предметы, сравниваем их с другими, выявляем их различные свойства и характеристики, объединяем разные предметы в группы на основании сходных принципов, для того чтобы сформировать их мысленные образы: это все «фрукты», а это «цитрусовые», из них вот это «мандарины», это «грейпфруты», а это «апельсины».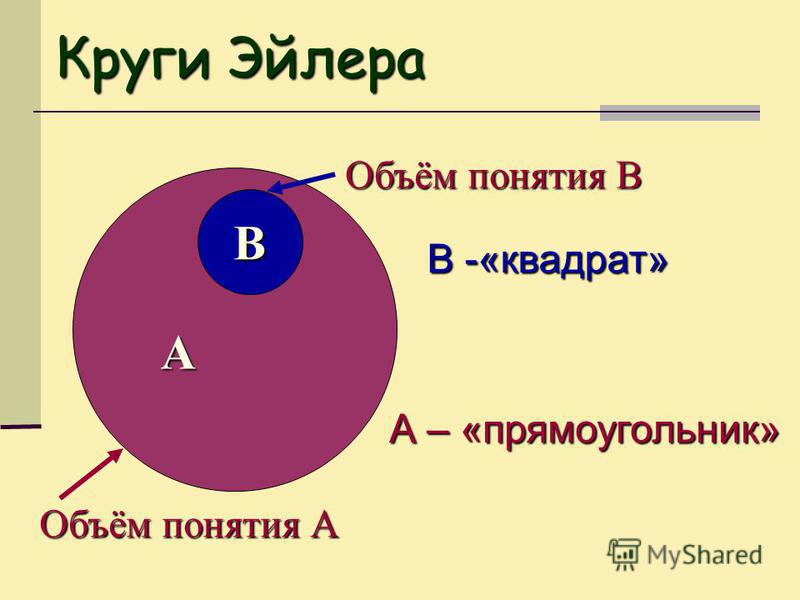
Только подумайте: в объективной реальности никаких понятий нет. Это все плод человеческого разума и воображения, так люди договорились между собой. Все, что мы называем, существует лишь в нашей голове. Нет в объективном мире никаких «прав» и «свобод», нет «демократии» и «денег», нет «юристов» и «учителей», «бакалавров» и «специалистов», не существует «хордовых» и «одноклеточных». Есть понятия, к которым мы обращаемся, чтобы не только общаться и понимать друг друга, но и чтобы наш мозг составил правильную картину окружающего мира.
Не стоит путать «слово» и «понятие»: это все-таки разные вещи. Понятия выражаются словами. Иногда одним словом могут выражаться разные понятия.
Чтобы проиллюстрировать это наглядно, предлагаю обратиться к так называемым кругам (или диаграммам) Эйлера.❓Также используется название «диаграмма Эйлера‒Венна». Если вы думаете, что ничего не знаете о кругах Эйлера, то глубоко ошибаетесь, потому что каждый хоть раз в жизни видел их в виде интернет-мемов.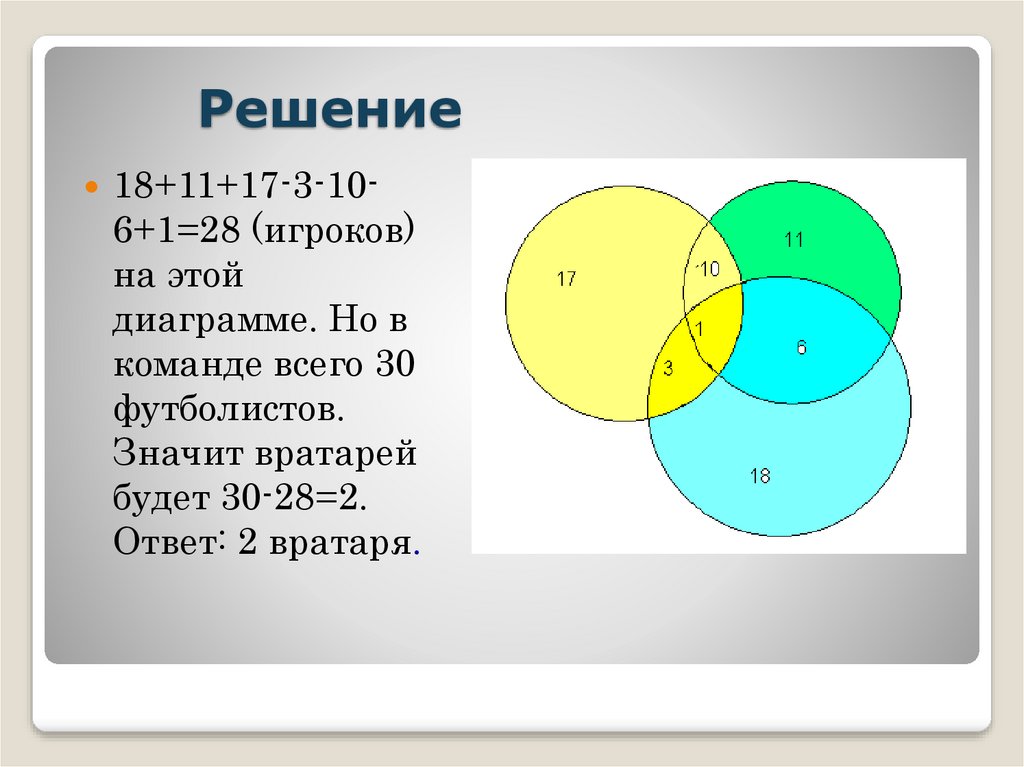
Научиться контролировать эмоции вам поможет курс «Критическое мышление».
Леонард Эйлер (1707–1783) — известный швейцарский, немецкий и российский математик, член Петербургской академии наук. Он придумал использовать простую визуализацию для обозначения объема понятий и множеств элементов. Круги Эйлера просты и наглядны, они очень упрощают рассуждения и именно поэтому так часто используются в логике, математике, статистике и менеджменте. Они отлично показывают, в каких логических взаимоотношениях могут быть те или иные понятия. Давайте посмотрим, какие возможны варианты таких взаимоотношений понятий.
Тождество — в данном случае понятия подразумевают один и тот же предмет. Например, А = квадрат, В = равносторонний прямоугольник; А = Москва, В = столица России; А = лучший тренер по технологиям убеждения, В = Никита Непряхин. Ладно, шучу.
Пересечение — в таких случаях объем одного понятия частично входит в объем другого понятия. Например, А = студент, В = спортсмен. Действительно, часть студентов могут быть спортсменами, а часть — нет. И наоборот, кто-то из спортсменов может учиться в вузе, а кто-то нет. Или: А = мужчина, В = врач. Кто-то из мужчин действительно работает врачом, но какая-то часть врачей — явно женщины. Может быть, и большая.
Действительно, часть студентов могут быть спортсменами, а часть — нет. И наоборот, кто-то из спортсменов может учиться в вузе, а кто-то нет. Или: А = мужчина, В = врач. Кто-то из мужчин действительно работает врачом, но какая-то часть врачей — явно женщины. Может быть, и большая.
Подчинение — в этих случаях одно понятие включает в себя другое. Например, А = верующий, В = православный. Все православные — верующие. Но среди верующих есть еще и католики, и протестанты, и буддисты, и мусульмане. Или: А = цитрусовые, В = апельсин; А = растение, В = береза.
Противоречие понятий представляет собой отрицание одним понятием другого. Например, А = низкий, В = высокий; А = работающий, В = безработный; А = черный, В = белый и т.д.
Давайте рассмотрим несколько примеров использования кругов Эйлера, но уже более сложные варианты.
Что мы видим из схемы, в которой продемонстрировано последовательное подчинение? Каждый мужчина — человек. Но не каждый человек — мужчина. Любой отец — мужского пола. Но не каждый мужчина успел обзавестись потомством. Не каждый отец является дедушкой. При этом любой дедушка всегда является также отцом.
Но не каждый мужчина успел обзавестись потомством. Не каждый отец является дедушкой. При этом любой дедушка всегда является также отцом.
Как читать эту схему? Не все явления природы являются стихийными бедствиями. Например, им не является северное сияние или молния. Равным образом не все стихийные бедствия — это явления природы, некоторые могут возникать в результате деятельности человека. Землетрясение — это всегда явление природы, но не каждое землетрясение признается стихийным бедствием. Наводнение и пожар могут быть как явлением природы, так и следствием человеческой халатности или злого умысла, как, например, в случае прорыва плотины или поджога здания. И не все наводнения и пожары при этом признаются стихийными бедствиями.
Научиться контролировать эмоции вам поможет курс «Критическое мышление».
Немного практики
Представьте отношения между следующими понятиями с помощью кругов Эйлера.
15.1 Ученый, психолог, кандидат психологических наук.
15.2 Автобус, такси, трамвай, городской транспорт, общественный транспорт.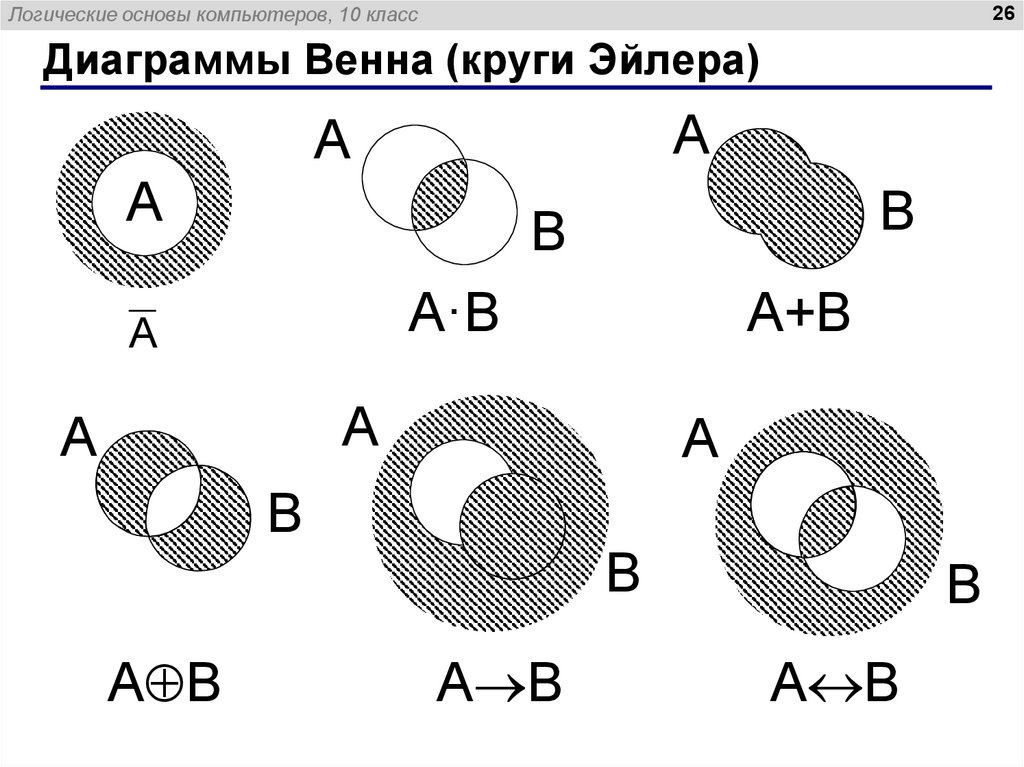
15.3 Русский писатель, дореволюционный писатель, советский писатель, Достоевский, Пушкин, Шолохов, Булгаков.
15.4 Искусственный спутник, Луна, планета, небесное тело, Земля, планета Солнечной системы, Марс, спутник.
15.5 Человек, имеющий одного ребенка; человек, имеющий двоих детей; человек, имеющий детей; мать.
15.6 Синий свитер; свитер любого цвета, кроме синего.
15.7 Автор романа «Преступление и наказание», автор романа «Братья Карамазовы».
15.8 Диван-кровать, мебель, диван, кровать, табурет.
15.9 Человек, владеющий иностранным языком; человек, владеющий английским языком; человек с высшим образованием; профессиональный переводчик.
15.10 Врач, пациент, мужчина, женщина.
В рубрике «Открытое чтение» мы публикуем отрывки из книг в том виде, в котором их предоставляют издатели. Незначительные сокращения обозначены многоточием в квадратных скобках.
Мнение автора может не совпадать с мнением редакции.
сек. 3.6 – Математика колледжа для начального образования
Глава 3, Раздел 6
Математические темы – Диаграммы Эйлера и логические аргументы, «Если… то» (условные) утверждения
Тема обучения – Какие типы представлений подходят?
youtube.com/embed/Di1F-wT05h8?version=3&rel=1&showsearch=0&showinfo=1&iv_load_policy=1&fs=1&hl=en&autohide=2&wmode=transparent» allowfullscreen=»true» sandbox=»allow-scripts allow-same-origin allow-popups allow-presentation»>Логические аргументы
В предыдущем разделе у нас был пример
Все кошки — животные. Флаффи — кот.
Если вы посмотрите на диаграмму (не привнося свои знания), на диаграмме также видно, что Пушистик должен быть животным.
Мы можем записать это как заключение логического аргумента:
Первые две строки аргумента — это предпосылки, то, что мы считаем истинным.
Последняя строка — заключение.
Чтобы быть действительным аргументом, заключение должно следовать из двух посылок. То есть, если мы за исключением того, что посылки верны, вывод должен быть истинным на основе посылок . Приведенный выше аргумент действителен.
Что делает аргумент не действительным? Попробуем несколько изменить набор предпосылок и выводов:
Все кошки — животные.
Дэн — животное.
Значит, Дэн - кот.
Чтобы проверить, является ли это аргументом действительным, нарисуйте рисунок только помещения.
Даже не смотрите на вывод, когда рисуете!
Глядя на нашу картинку, мы видим, что вывод, Дан — это кот, недействителен. Дэн может быть котом, или Дэн может быть другим видом животных. На диаграмме показано, что D может находиться в двух возможных местах.
Это означает, что аргумент недействителен (недействителен).
Чтобы аргумент был действительным, мы должны быть на 100% уверены в том, что вывод верен на основе предпосылок.
Пример 1 Какой вывод верный?
Чтобы решить, постройте диаграмму Эйлера, используя каждый набор предпосылок.
Помните, что для построения диаграммы используйте только помещения, не вывод.
Помещения:
Обратите внимание, что М может стоять в двух возможных местах. М должно быть в четырехстороннем круге вещей, потому что это первая предпосылка. M также может быть в круге квадратов, потому что это еще одно возможное место внутри четырехстороннего круга вещей.
Для X есть только одно возможное место внутри квадратного круга, так как это первая предпосылка этого аргумента. X не может быть вне этого круга, так как это означало бы, что X не был квадратом. Помните, мы берем каждый из предпосылки быть абсолютно правдой.
Теперь смотрим на выводы, чтобы увидеть, следуют ли они из посылок.
Верен ли вывод Следовательно, M является квадратом ?
№
Глядя на нашу диаграмму, мы видим, что M может быть квадратом, а может и не быть. M может быть за пределами круга квадратов и иметь только 4 стороны. Например, M может выглядеть так:
M — 4-сторонний.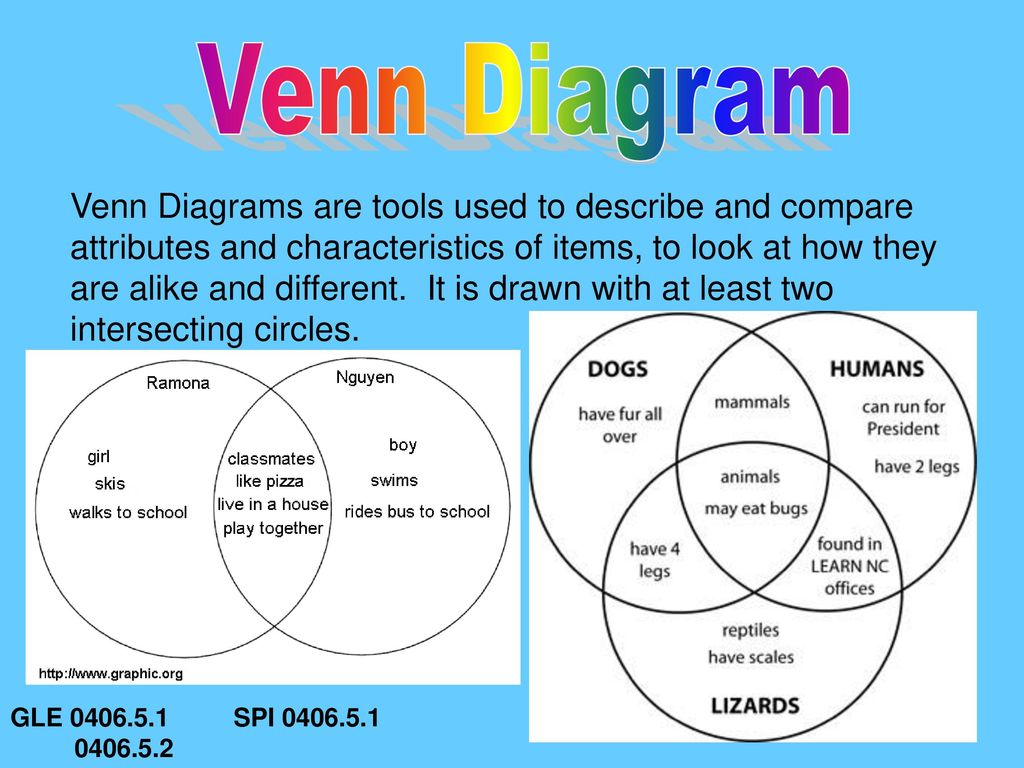
Вывод, Следовательно, X четырехсторонний , верно?
Да, потому что X находится внутри четырехстороннего круга вещей. Все квадраты четырехсторонние.
Но когда вы указываете причину, по которой аргумент действителен, используйте первую часть причины, указанную выше: «Да, потому что X находится внутри четырехстороннего круга вещей». Вторая часть, « Все квадрата четырехсторонние», просто повторяет предпосылку. Переформулировка посылки (даже курсивом или подтекстом!) не является достаточной причиной для поддержки вашего аргумента. Вместо этого обратитесь к своей диаграмме и объясните, используя диаграмму.
Итог
НЕВЕРНЫЙ Аргумент и причина
Все квадраты четырехсторонние.
М четырехсторонний.
Следовательно, M — квадрат.
Недействительно, так как M может находиться в части круга вне квадратов
(см. схему).
ДЕЙСТВИТЕЛЬНО Аргумент и причина
Все квадраты четырехсторонние.
X — квадрат.
Следовательно, X четырехсторонний.
Действителен, потому что X должен быть в круге квадратных вещей,
, который находится внутри четырехсторонних вещей, так что это автоматически делает X
также четырехсторонним (см. схему).
Условное
Другой способ показать логический аргумент — использовать символы вместо диаграмм Эйлера или в дополнение к ним.
Все кошки — животные — это то же самое, что сказать: Если — это кошка, , то — это животное.
Утверждение «if…then» известно как условное .
Мы используем стрелку для обозначения условного выражения: c → a, где c означает «это кошка, а a — это животное». Мы используем три точки, ∴, чтобы представить слово поэтому.
Действительный аргумент
Обратите внимание, что когда мы используем условную стрелку, мы больше не называем кота Пушистиком. Это делается для того, чтобы вторая посылка могла точно соответствовать первой части условного предложения.
В действительный ( не действительно) аргумент
Посмотрите внимательно на порядок двух аргументов выше. Следуя этому шаблону, для оператора if-then типа A → B, какая вторая строка и вывод будут давать действительный аргумент?
Официальное название действительной формы аргумента — modus ponens , но можно просто сказать «правильный порядок».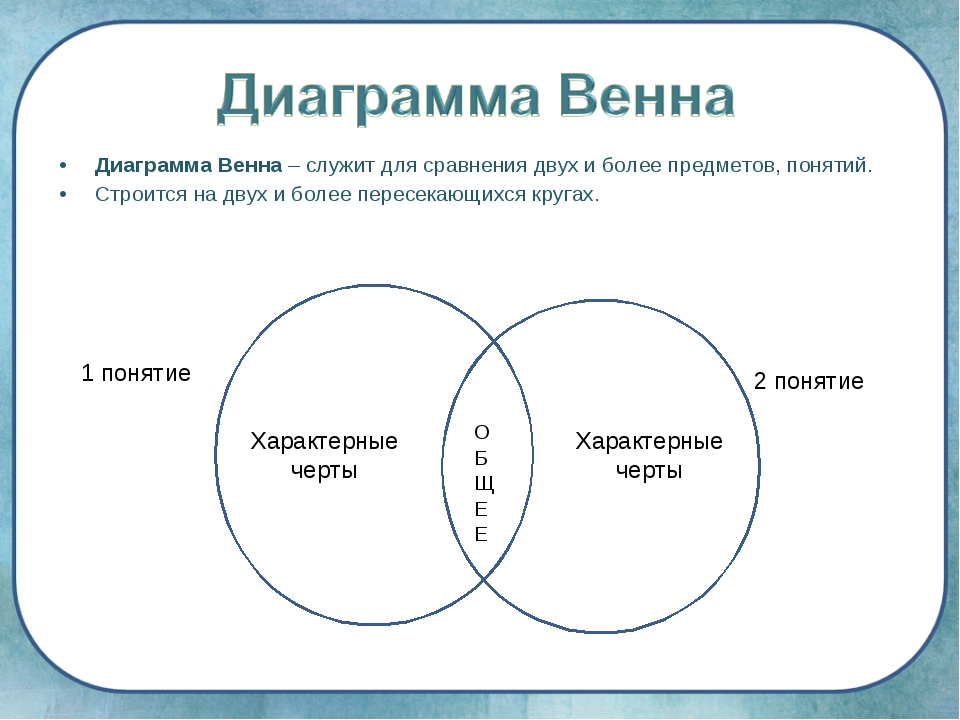 В правильном аргументе вторая посылка и вывод следуют в том же порядке, что и в условном выражении. Студент в моем классе указал, что это происходит потому, что условная стрелка не является коммутативной. То есть сказать A → B не то же самое, что сказать B → A. Или, вернемся к нашему предыдущему примеру, , если это кошка, то это животное; не то же самое, что сказать , если это животное, то это животное. кот .
В правильном аргументе вторая посылка и вывод следуют в том же порядке, что и в условном выражении. Студент в моем классе указал, что это происходит потому, что условная стрелка не является коммутативной. То есть сказать A → B не то же самое, что сказать B → A. Или, вернемся к нашему предыдущему примеру, , если это кошка, то это животное; не то же самое, что сказать , если это животное, то это животное. кот .
Мы можем использовать как диаграмму Эйлера , так и символическую логику , чтобы решить, является ли аргумент допустимым. Некоторым учащимся визуальное представление проще всего; для других студентов символическое представление является самым простым. Вот почему мы хотим всегда стараться дать нашим ученикам множество способов представления математики!
Пример 2 Верен или недействителен следующий аргумент? Для принятия решения используйте диаграмму Эйлера и символическую логику с условным символом.
Все собаки дружелюбны.
Бонзо — собака.
Поэтому Бонзо дружелюбен.
Чтобы принять решение, сначала перепишите аргумент в виде условного оператора («Если… то»). Посмотрите, к какому из приведенных выше шаблонов он подходит. Наконец, проверьте, нарисовав диаграмму Эйлера, чтобы визуально увидеть, действительна ли она.
Этот аргумент действителен – думайте о собаке как об А, а о дружелюбии как о Б; вы можете видеть, что порядка аргумента верны. У вас есть
A → B
A
∴ B
Диаграмма Эйлера приводит нас к тому же выводу. вещи», а это значит, что Бонзо находится внутри круга «дружеских вещей».
Пример 3 Верен или недействителен следующий аргумент?
Все собаки дружелюбны.
Рекс дружелюбный.
Следовательно, Рекс — собака.
Чтобы принять решение, мы перепишем аргумент как условное выражение, чтобы увидеть закономерность.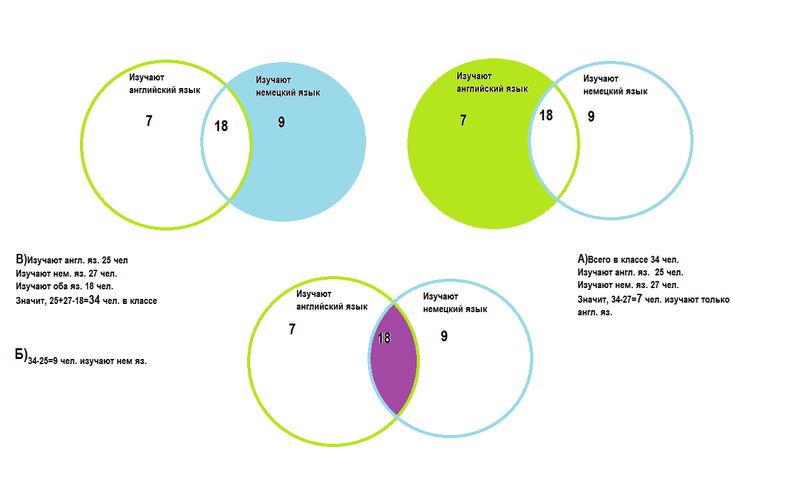 Затем мы рисуем диаграмму Эйлера, чтобы визуально увидеть, верна ли она.
Затем мы рисуем диаграмму Эйлера, чтобы визуально увидеть, верна ли она.
Этот аргумент недействителен – думайте о собаке как A и дружелюбной как B; вы можете видеть, что порядок аргумента неверен. У вас есть
A → B
B
∴ A
Если у нас есть A → B , правильный порядок будет иметь A в качестве первой посылки, за которой следует B. Но в этом аргументе сначала B, а затем A.
Диаграмма Эйлера приводит нас к тот же вывод — аргумент недействителен , потому что Рекс может быть в любом месте. Не факт, что Рекс находится внутри круга «Собаки». Чтобы быть действительным аргументом, вывод должен быть на 100% уверен.
Символ «не» в логических аргументах
В логических рассуждениях, если мы хотим сказать: «Это , а не собака», мы должны использовать букву d, чтобы обозначить «это собака», и поставить символ «не», ~, перед ним: ~d означает «не собака».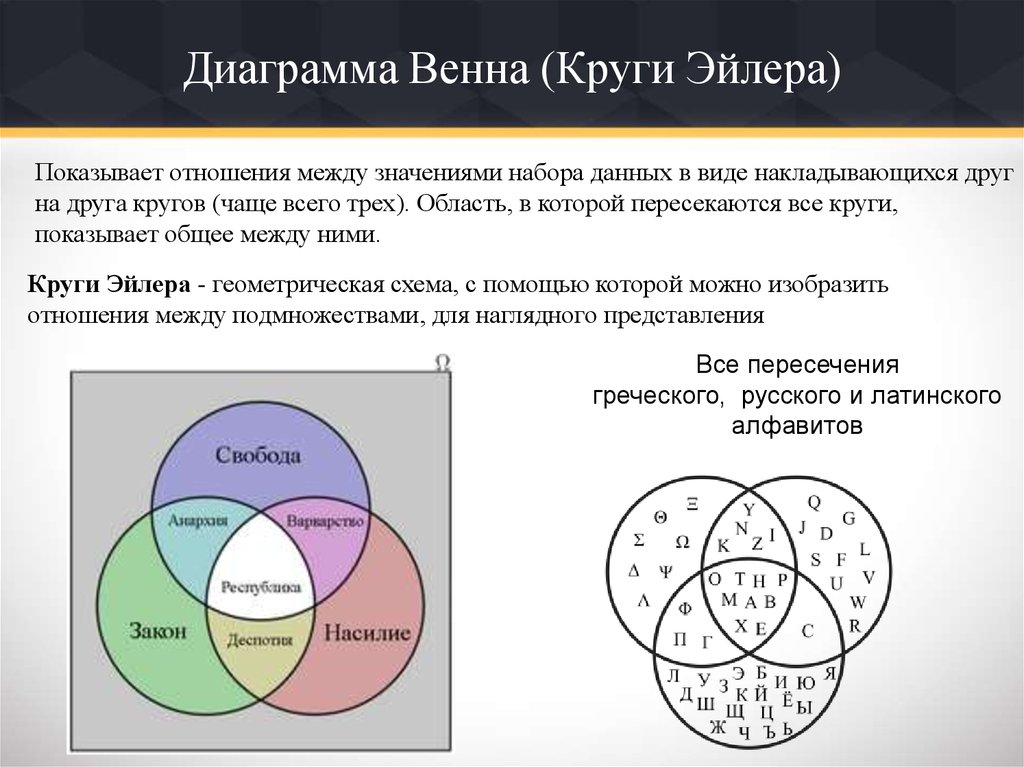 Этот символ подобен символу дополнения в наборах.
Этот символ подобен символу дополнения в наборах.
Пример 4 Верен или неверен следующий аргумент?
Если зеленый, то это не собака.
Зеленый.
Следовательно, это не собака.
Чтобы решить, пишем аргумент символами, чтобы увидеть закономерность. Мы также переписываем утверждение, чтобы мы могли нарисовать диаграмму Эйлера, чтобы визуально увидеть, верно ли оно.
Этот аргумент действителен: вторая посылка и вывод следуют в том же порядке, что и в условном (если… то). То есть в первой строке g → ~d, g стоит первой, а ~d — второй. Следующая посылка g и заключение ~d следуют в том же порядке.
С диаграммой Эйлера, Если он зеленый, значит это не собака переводил бы на два отдельных круга. Это то же самое, что и , собаки не зеленые .
Используя диаграмму Эйлера, мы видим, что аргумент действителен , так как Гарри находится в круге зеленых вещей, поэтому он не может быть в круге собак, так как они не пересекаются.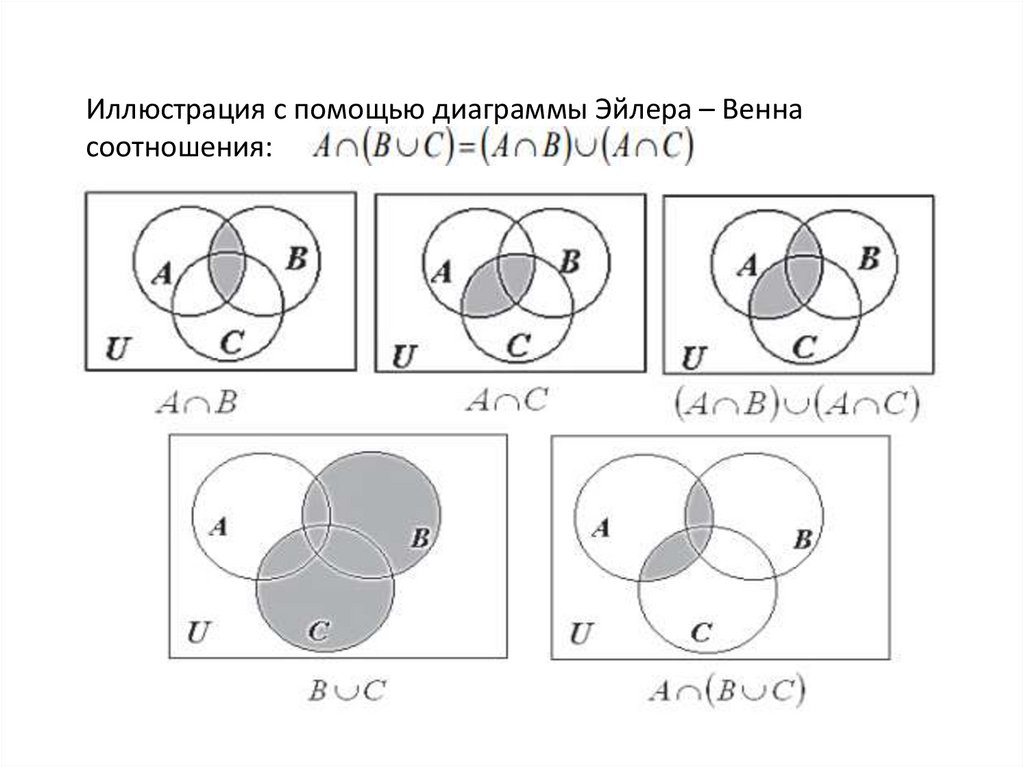
Логические аргументы с использованием «Некоторые» и «Нет»
Пример 5 Является ли следующий аргумент допустимым или недействительным?
Некоторые кошки являются домашними животными.
Пушистый кот.
Следовательно, Пушистик — домашнее животное.
Из предыдущего раздела мы знаем, что F можно поставить в двух местах: Пушистик может быть котом, который является домашним животным (в центре), или котом, который не является домашним животным (слева). Поскольку мы не знаем наверняка, что Пушистик находится в кошачьем круге, аргумент недействителен. Помните, что для того, чтобы аргумент был недействительным, вывод должен следовать без сомнения из посылок.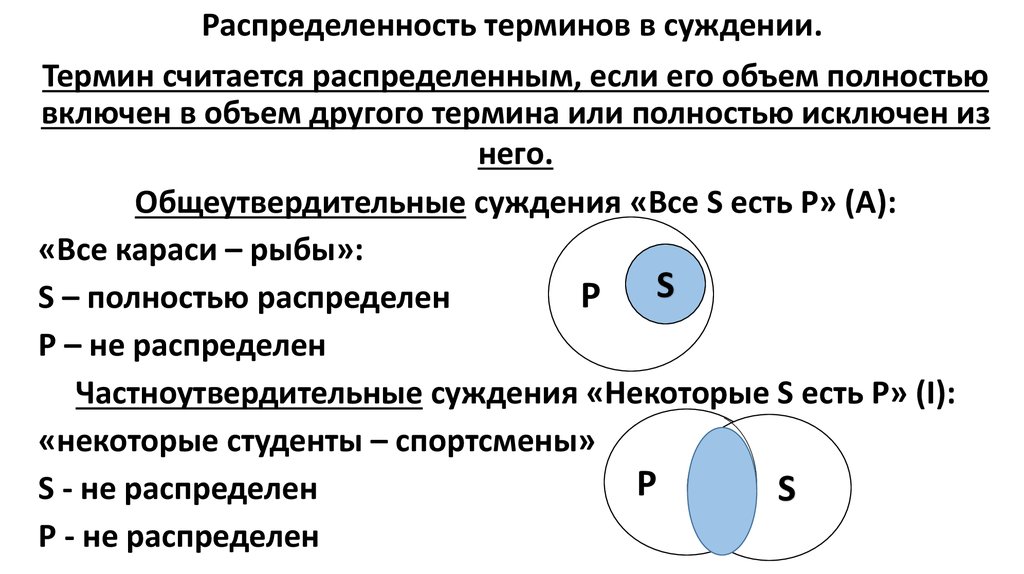
В этом примере мы делаем , а не , превращаем аргумент в символы, потому что оператор some переводит , а не в условное выражение.
Некоторые кошки являются домашними животными не эквивалентно c → p, это будет все кошки являются домашними животными.
Важно уметь выбирать, какой тип представления — визуальный или символический — лучше всего использовать в данной ситуации.
Пример 6 Верен или недействителен следующий аргумент? Используйте диаграмму Эйлера или символы, в зависимости от того, что лучше, чтобы решить.
Некоторые телешоу смешные.
Вебстер не смешной.
Следовательно, Вебстер — это не телешоу.
Для любого аргумента с «some» мы не можем использовать условное выражение , поэтому рисуем диаграмму Эйлера.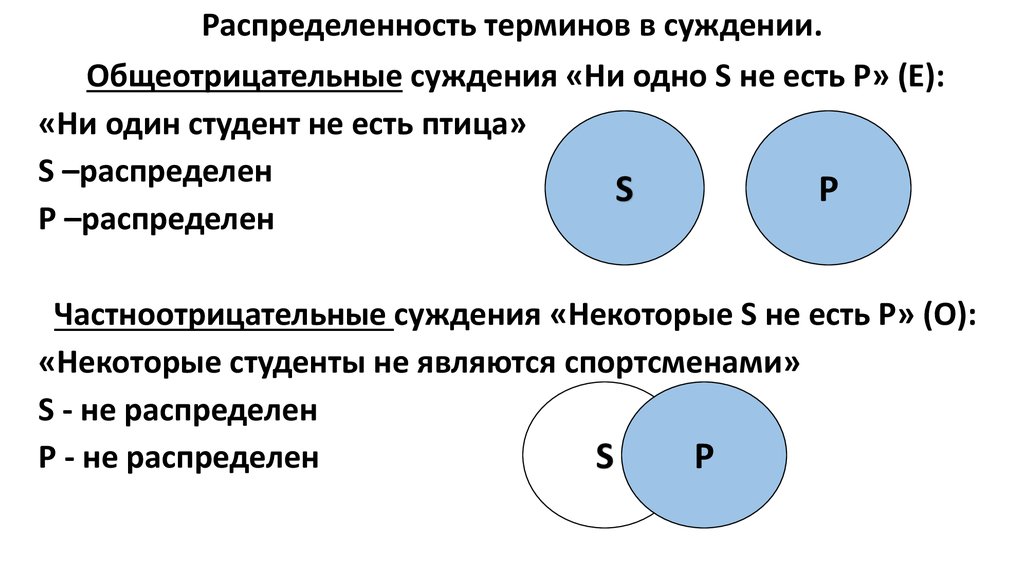 Здесь у нас есть «Некоторые телешоу смешные».
Здесь у нас есть «Некоторые телешоу смешные».
Поскольку Вебстер не смешной, есть два возможных места, где можно поместить Вебстера, кроме «Забавных вещей». Одно из этих возможных мест находится внутри телешоу, поэтому вывод «Вебстер — это не телешоу» будет 9.0003 неверный .
Все отношения и Транзитивность
Какой вывод правильный, чтобы сказать нам о том, как связаны квадраты и четырехугольники?
Все квадрата являются прямоугольниками.
Все прямоугольники являются четырехугольниками (имеют четыре стороны).
Следовательно, все ____ являются _______.
Правильный вывод создаст действительный аргумент.
Используйте диаграмму, чтобы увидеть, какой набор будет подмножеством другого.
действительный вывод равен Следовательно, все квадраты четырехугольники (имеют четыре стороны).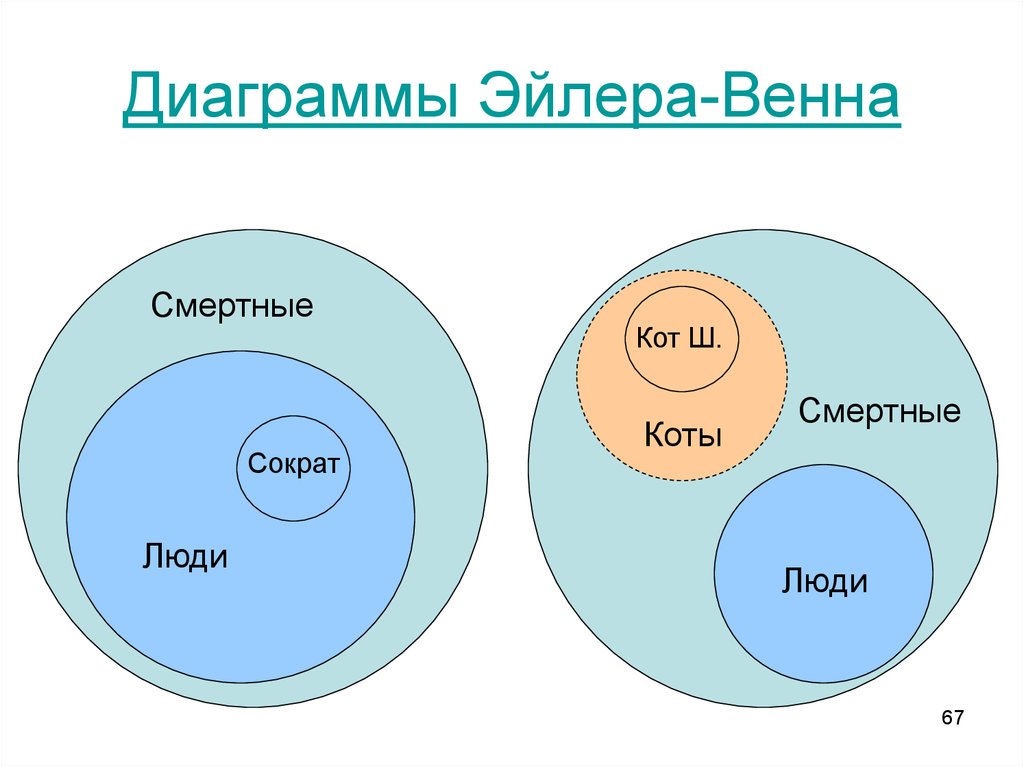
Мы знаем, что это так, потому что на нашей диаграмме набор квадратов равен внутри набора четырехугольников.
Мы также можем использовать условное выражение и символы, чтобы понять, почему.
Условный Символы
Если это квадрат, то это прямоугольник. с → р
Если это прямоугольник, то это четырехугольник r → q
Следовательно, если это квадрат, то это четырехугольник. ∴ s → q
Символы по порядку: s → r, r → q. То есть s → r → q
Это образует непрерывную цепочку от s, хотя и r, до q. Таким образом, вывод s → q верен.
Этот тип аргумента
A → B
B → C
∴ A → C
называется действительным аргументом на транзитивность .
Он показывает цепочку, идущую от А к В, затем от В к С, следовательно, А идет к С. Если одно число на меньше другого на , мы пишем a < b .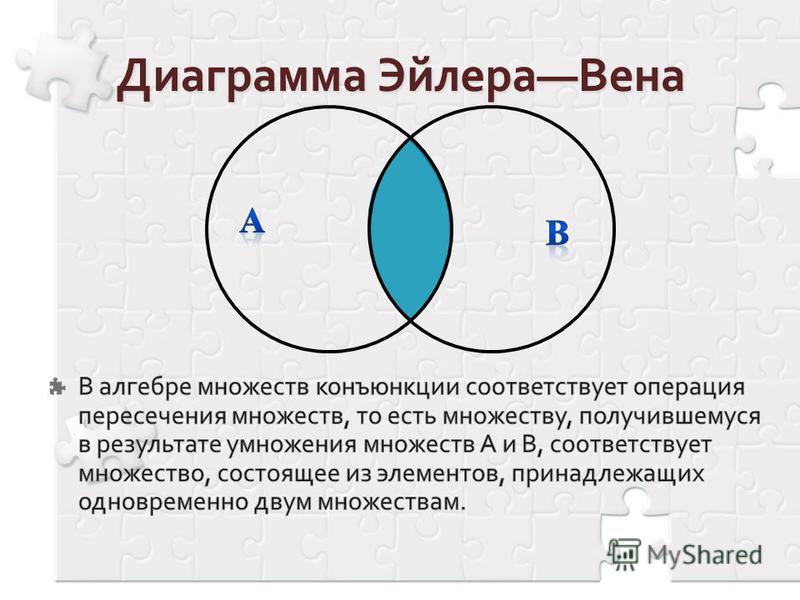 Например, 3 < 4.
Например, 3 < 4.
Теперь предположим, что мы знаем, что a < b и мы знаем, что b < c. Мы можем записать это как одно неравенство: a < b < c ( a меньше b меньше c ).
Мы можем заключить, что a должно быть на меньше, чем c , то есть a < c.
Написанное числами, это все равно, что сказать, что если 3 < 4 и 4 < 5, мы знаем, что 3 < 5. .
А → В
С → В
∴ А → С
— это , а не — допустимый аргумент по транзитивности.
, а не показывает цепочку, идущую от A к B, затем от B к C. Вместо этого и A, и C ведут к B, поэтому ничего не связывает A с C.
Пример 7 Используйте ваше знание наборов чисел для создания действительного аргумента по транзитивности.
Все натуральные числа являются целыми числами.N → W
Все целые числа являются целыми числами W → I
Следовательно, все натуральные числа ____? ∴ N → ____?
Можно было бы правильно заключить, что N → I. Это следует из построения цепочки из посылок: N → W, W → I, значит имеем N → W → I
Пример 8 аргумент в силе?
Все целые числа являются целыми числами. W → I
Все натуральные числа целые N → I
Следовательно, все целые числа являются натуральными числами ∴ W → N
Мы можем видеть, что этот аргумент недействителен , глядя на ту же диаграмму – множество целых чисел не входит в множество натуральных чисел,
Мы также можем видеть, что этот аргумент недействителен , взглянув на символы:
W → I, N → I
Цепочки от W до N нет, каждая стрелка указывает на I, ничто не указывает от до N.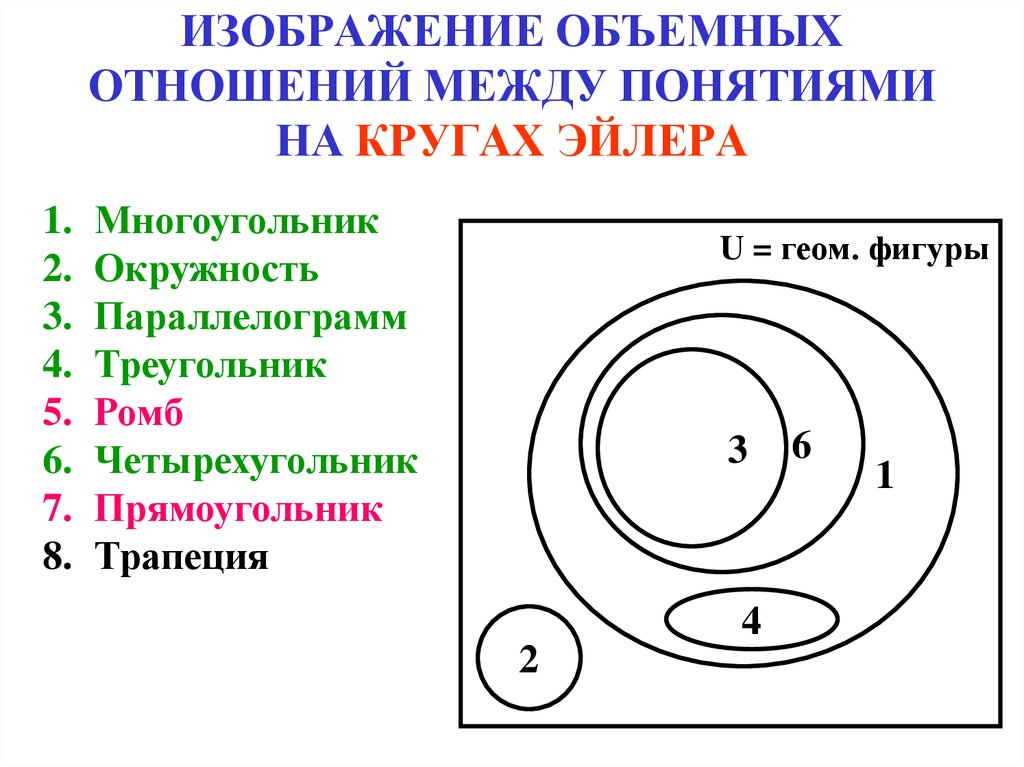
Пример 9 Какие из следующих аргументов, показанных только символами, верны транзитивностью? Что недействительно? Совет: посмотрите, сможете ли вы найти цепочку, ведущую от одной буквы в заключении к другой.
Аргумент 1 Аргумент 2 Аргумент 3 Аргумент 4
P → Q M → Z x → ~ Y A → B
A → B M → R ~ Y → Q C → B
Q → R A → T Q → M ∴ A → C
∴ P → R ∴ M → T ∴ x → Q
Первый аргумент может быть указан в одной длинной строке, чтобы увидеть, что связано с чем. Имеем p → q, a → b, q → r. Мы можем избавиться от a → b, так как эта посылка не имеет ничего общего с остальными. Теперь у нас есть p → q, q → r, что дает нам цепочку: p → q → r, что означает, что p действительно приводит к r , p → r. Аргумент равен действительный .
Можно удалить из посылок аргумент, который не влияет на ваш вывод! Предположим, кто-то сказал вам: «Все свиньи быстрые» (p → q), все аллигаторы большие (a → b) и все быстрые существа быстрые (q → r).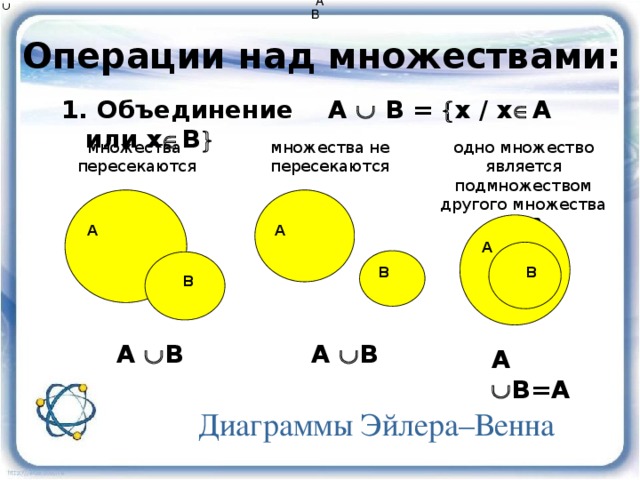 Вы определенно можете проигнорировать эту часть об аллигаторах и сделать вывод, что все свиньи быстрые (p → r).
Вы определенно можете проигнорировать эту часть об аллигаторах и сделать вывод, что все свиньи быстрые (p → r).
Для аргумента 2 имеем m → z, m → r, a → t. Поскольку в заключении m → t, мы ищем в посылках цепочку, связывающую m с t, например: m → ___ → ___ …→ t. Цепь, идущая от m к t, отсутствует. Вместо этого m переходит в z и в r, но ни z, ни r не ведут ни к чему другому. Аргумент неверный .
Для аргумента 3 имеем x → ~ y, ~ y → q и q → m в посылках. Поскольку вывод x → q, мы ищем в посылках цепочку, которая связывает x с q. У нас есть эта цепочка: у нас есть x → ~ y, ~ y → q, что становится x → ~ y → q, так что мы имеем x → q. Аргумент допустим .
Наконец, аргумент 4 равен недействителен , так как у нас нет цепочки, идущей от а к с в помещении. У нас есть a, идущий к b, и у нас также есть c, идущий к b. Нет ничего, что привело бы к c. Проблема в том, что вторая посылка — это наоборот . Если бы мы вместо этого имели a → b и b → c, то мы могли бы заключить, что ∴ a → c.
Если бы мы вместо этого имели a → b и b → c, то мы могли бы заключить, что ∴ a → c.
сек-3.6-домашнее заданиеСкачать
сек-3.6-домашнее задание-ответыСкачать
Нравится:
Нравится Загрузка…
Эйлеровы круги на примере решения задач. Логические задачи и круги Эйлера Круги Эйлера с тремя множествами
Текст работы размещается без изображений и формул.
Полная версия работы доступна во вкладке «Работа» в формате PDF
В наше время вокруг нас накопилось огромное количество информации, разобраться в которой бывает непросто. Поэтому многие не знают, что за названием «Круги Эйлера» скрывается практичный и удобный метод решения различных задач. Все о них слышали, но мало кто может объяснить, что они из себя представляют. Однако я считаю, что круги Эйлера полезны как в повседневной жизни, так и в науке, поэтому каждый должен уметь их использовать. В этой работе я собрал всю необходимую информацию, чтобы понять, что такое круги Эйлера и где их удобно применять.
Окружности Эйлера — это геометрическая диаграмма, которую можно использовать для визуализации отношений между различными множествами и подмножествами. Такая схема помогает находить логические связи между явлениями и понятиями; он был изобретен Леонардом Эйлером и используется в математике и других научных дисциплинах. Использование кругов Эйлера упрощает рассуждения и помогает быстрее и проще получить ответ. (1),(2)
Окружности Эйлера неразрывно связаны с понятием множества. Поэтому, чтобы лучше понять, что изображено на окружностях Эйлера, нужно знать, что такое множество и какие множества бывают.
Под множеством можно понимать совокупность любых объектов, называемых элементами множества. Наборы могут объединять любые предметы с общим признаком. Например, набор учащихся гимназии 11, учащихся 7 «Б» классов составляют отдельный набор. Наборы могут быть неодушевленными объектами. Например, много книг, написанных каким-то автором. С помощью кругов Эйлера множество обозначается как пустой круг, а его элементы обозначаются точками.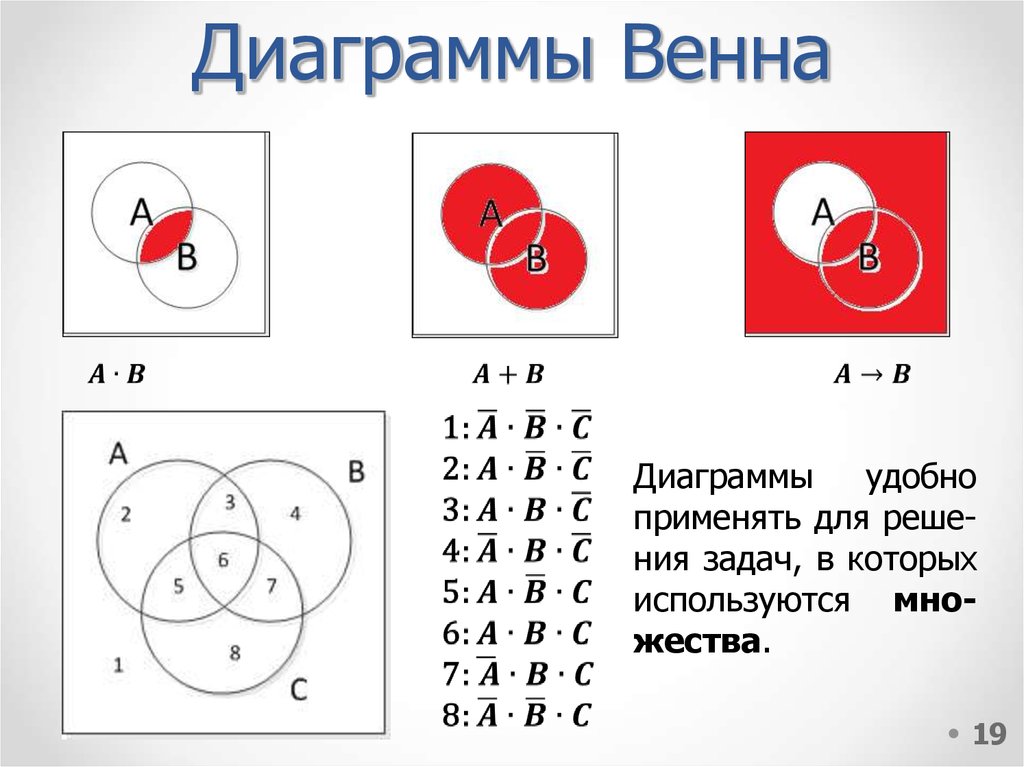 (5)
(5)
Нарисуем много цифр. На рисунке контуром обозначено множество, а точками — элементы этого множества.
Наборы бывают трех видов:
окончательные (например — набор чисел)
Бесконечные (например — набор чисел)
Пустые (множество натуральных чисел
меньше нуля). (5)
Группа объектов, образующих набор, являющийся частью большего набора, изображается в виде меньшего круга, начерченного внутри большего круга, и называется подмножеством. Такая связь формируется между большим набором животных и его подмножеством плоских червей. (5)
В тех случаях, когда два понятия совпадают лишь частично, связь между такими множествами изображается с помощью двух пересекающихся окружностей. Такое отношение формируется между многими учащимися 7 «Б» классов и многими троечниками. Некоторые элементы множества учащихся 7-го «Б» класса также относятся к множеству троечников. (5)
Когда ни один предмет из одного множества не может одновременно принадлежать ко второму множеству, то отношение между ними изображается с помощью двух окружностей, проведенных одна вне другой.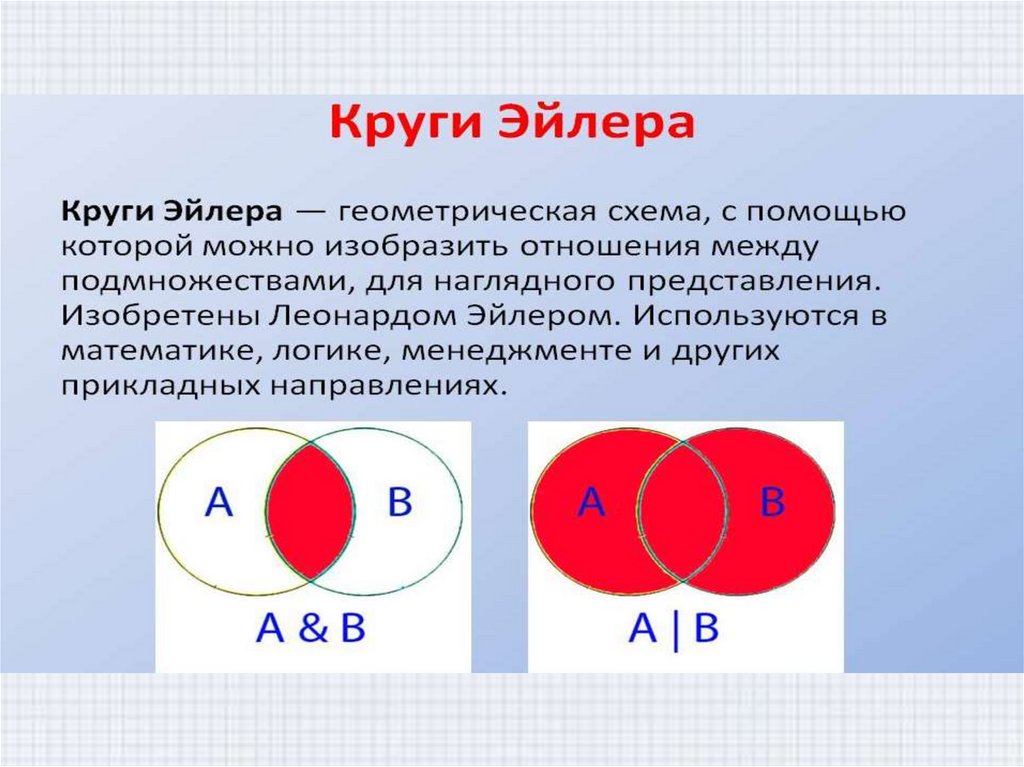 Такими множествами являются множество отрицательных и множество положительных чисел. (5)
Такими множествами являются множество отрицательных и множество положительных чисел. (5)
Круги Эйлера были изобретены и названы в честь Леонарда Эйлера (портрет слева). Он был швейцарским математиком, внесшим значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук. Эйлер родился в Швейцарии, учился в Германии, но работал и умер в России. Этот ученый является автором 800 работ. Леонард Эйлер родился в 1707 году в семье пастора. Его отец был другом семьи Бернулли. Эйлер рано проявил математические способности. Учась в гимназии, мальчик увлеченно занимался математикой, а позже стал посещать университетские лекции Иоганна Бернулли. 20 октября 1720 года Леонард Эйлер стал студентом художественного факультета Базельского университета. Одаренный юноша привлек внимание профессора Иоганна Бернулли. Он дал студенту математические статьи для изучения, а также пригласил его прийти к себе домой для совместного анализа непонятного. В доме своего учителя Эйлер познакомился и начал общаться с сыновьями Бернулли, Даниилом (портрет слева) и Николаем (портрет справа), которые также занимались математикой. (6)
(6)
Молодой Эйлер написал несколько научных работ. «Диссертация по физике звука» получила положительный отзыв. В то время количество научных вакансий в Швейцарии было небольшим. Поэтому братья Даниил и Николай Бернулли уехали в Россию, где начала создаваться Российская академия наук; они обещали работать там и на должность Эйлера. В начале зимы 1726 года Эйлер получил письмо из Петербурга: по рекомендации братьев Бернулли он приглашен на должность адъюнкта по физиологии с окладом в 200 рублей. Эйлер много времени провел в России, где внес значительный вклад в русскую науку. С 1731 г. он был избран академиком Петербургской академии. Он хорошо знал русский язык, издавал сочинения и учебники на русском языке. (6)
Затем Эйлер подробно описывает свой метод решения некоторых задач с использованием кругов Эйлера. В 1741 г. Эйлер написал «Письма по разным физическим и философским вопросам, к некой немецкой принцессе..», где упоминаются «круги Эйлера». Эйлер писал, что «круги очень подходят для облегчения наших размышлений». (3)
(3)
Метод Эйлера получил заслуженное признание и популярность. А после него многие ученые использовали его в своей работе, а также модифицировали на свой лад. Бернар Больцано использовал тот же метод, но с прямоугольными узорами. Благодаря вкладу Венна этот метод даже называют диаграммами Венна или даже диаграммами Эйлера-Венна. Эйлеровы круги имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, управлении и прочем. (один)
Вот несколько задач, для решения которых удобно использовать круги Эйлера:
Задача 1.
У ребят из одной школы спросили про их питомцев. 100 из них ответили, что у них дома есть собака и/или кошка. У 87 детей была одна собака и у 63 детей была одна кошка. У скольких детей есть и собака, и кошка?
Решение:
Чтобы решить эту задачу без использования кругов Эйлера, нужно посчитать, сколько собак и кошек было у учеников. Для этого складываем 87 и 63. 87+63=150 питомцев. Учеников было всего 100, а дробное количество питомцев получить нельзя. Таким образом, если у каждого ученика есть 1 домашнее животное, остается еще 50 дополнительных. Следовательно, у 50 студентов есть 2 домашних животных. А так как в задаче сказано, что ни у кого из учеников нет 2 кошек и 2 собак, то это означает, что у 50 учеников есть и кошка, и собака.
Для этого складываем 87 и 63. 87+63=150 питомцев. Учеников было всего 100, а дробное количество питомцев получить нельзя. Таким образом, если у каждого ученика есть 1 домашнее животное, остается еще 50 дополнительных. Следовательно, у 50 студентов есть 2 домашних животных. А так как в задаче сказано, что ни у кого из учеников нет 2 кошек и 2 собак, то это означает, что у 50 учеников есть и кошка, и собака.
Но этот способ долгий и подходит только для простых задач. Гораздо удобнее решать такую задачу в терминах окружностей Эйлера.
Красный кружок будет обозначать множество владельцев собак, а синий круг — множество владельцев кошек. Всего было 100 студентов. Тех, у кого есть и кошка, и собака X. Чтобы найти количество учеников, у которых есть только собака, нужно из 87 вычесть X. Так как всего учеников 100, получаем:
X=50 учеников
Ответ: у 50 учеников есть и кошка, и собака
Задание 2.
Однажды у школьников спросили, кто из них любит математику, кто русский язык, а кто физику.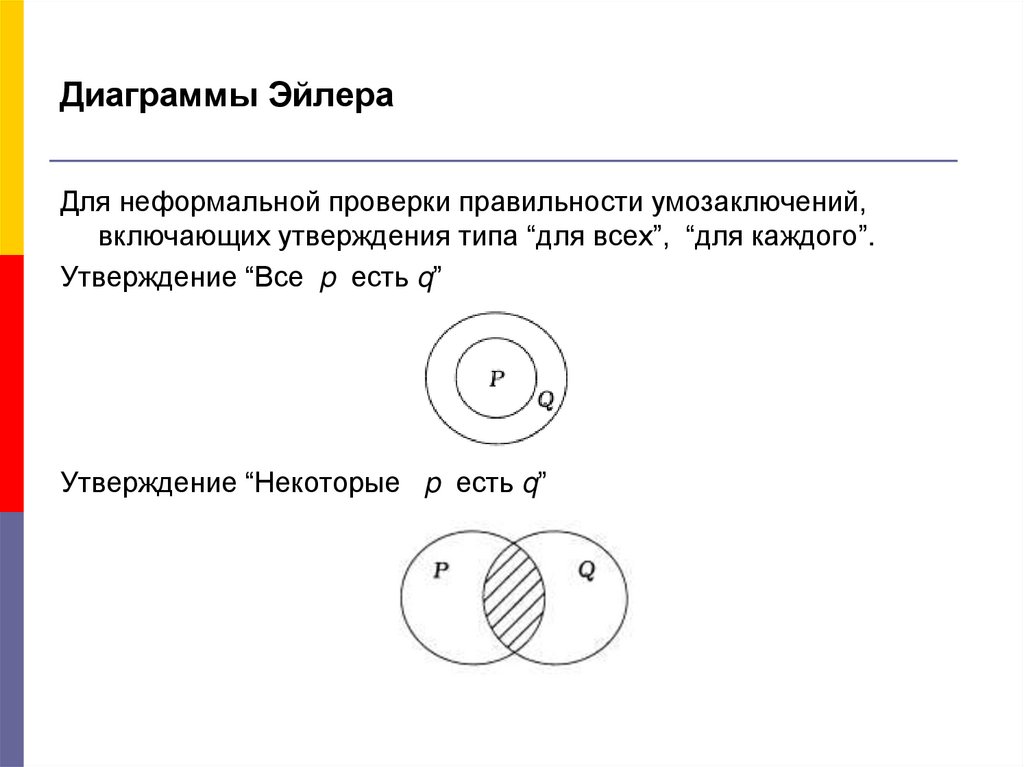 Выяснилось, что из 36 учеников 2 не любят ни математику, ни русский язык, ни физику. 25 студентов любят математику, 11 студентов любят русский язык, 17 студентов любят физику; и математика, и русский язык — 6; и математика, и физика — 10; Русский язык и физика — 4.
Выяснилось, что из 36 учеников 2 не любят ни математику, ни русский язык, ни физику. 25 студентов любят математику, 11 студентов любят русский язык, 17 студентов любят физику; и математика, и русский язык — 6; и математика, и физика — 10; Русский язык и физика — 4.
Скольким людям нравятся все три предмета?
Решение:
Нарисуем 3 комплекта. Красный набор — те, кто любит математику, синие — те, кто любит русский язык, зеленый — физику.
Теперь запишем количество элементов в наборе. 6 человек любят и русский язык, и математику. Из них X люди также любят физику. Итак, только математику и русский язык любят 6 человек. Только математика и физика 10-х, только русский язык и физика 4 человека. 25 человек любят математику. Но люди X, 6-X, 10-X любят и другие вещи. Итак, 25-(6-Х)-(10-Х)-Х = 25-6+Х-10+Х -Х=5+Х люди любят только математику. Только русский язык любят 11-(6-Х)-(4-Х)-Х= 11-10+2Х-Х=1+Х школьники, только физику 17-(10-Х)-(4-Х)- Х= 17-14+2Х-Х= 3+Х.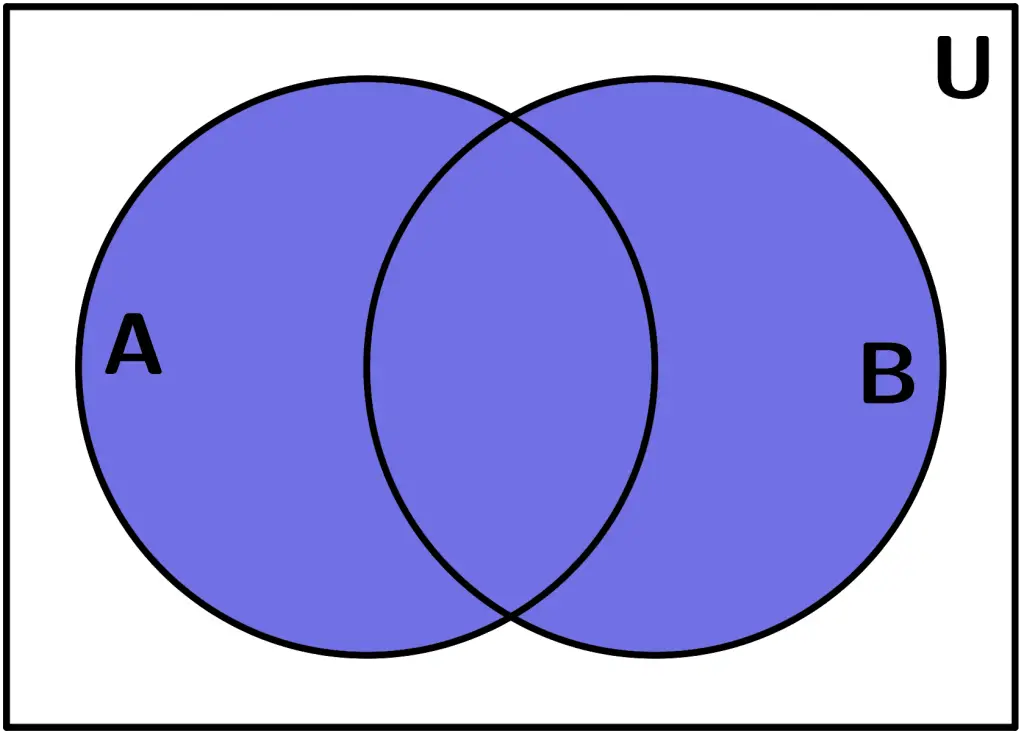
Так как 2 человека не любят ни один из этих предметов, то:
3+X+9+X+1+X+6-X+10-X+4-X+X=36-2
Ответ: 1 человек любит все три предмета
Задача 3.
В таблице представлены запросы и количество найденных ими страниц для определенного сегмента Интернета.
Сколько страниц (в тысячах) будет найдено по характеру запроса? (четыре)
Решение :
По человеческому запросу найдено 2 100 000 страниц. 900 из них тоже о природе. Это значит, что только о человеке 2100-900=200 тысяч страниц, а о природе только X-900 тысяч. Получаем, что:
2100-900+X-900+900=3400
2100-900+X=3400
X=2200 тыс. страниц
Ответ: по запросу будет найдено 2 200 000 страниц.
Как видите, круги Эйлера — полезное и важное открытие для математики вообще и для каждого из нас в частности. Круги Эйлера встречаются не только на экзаменах, они нужны нам и в повседневной жизни. Это интересная и нужная вещь, о которой нельзя забывать.
Это интересная и нужная вещь, о которой нельзя забывать.
Литература:
https://www.tutoronline.ru/blog/krugi-jejlera
https://en.wikipedia.org/wiki/%D0%9A%D1%80%D1%83%D0%B3%D0%B8_%D0%AD%D0%B9%D0%BB%D0%B5% Д1 %80%Д0%В0
http://sibac.info/shcoolconf/science/xvii/42485
http://www.jwy.narod.ru/logic/_04_eiler.html
https://ru.wikipedia.org/wiki/%D0%AD%D0%B9%D0%BB%D0%B5%D1%80,_%D0%9B%D0%B5%D0%BE%D0% БД %D0%B0%D1%80%D0%B4
Если вы думаете, что ничего не знаете о кругах Эйлера, вы ошибаетесь. На самом деле, вы наверняка не раз сталкивались с ними, просто не знали, как это называется. Где именно? Круговые диаграммы Эйлера легли в основу многих популярных интернет-мемов (изображений, тиражируемых на определенную тему в Сети).
Давайте вместе разберемся, что это за круги, почему они так называются и почему их так удобно использовать для решения многих задач.
Происхождение термина
— геометрическая схема, помогающая найти и/или сделать более наглядными логические связи между явлениями и понятиями. Это также помогает изобразить отношения между любым набором и его частью.
Это также помогает изобразить отношения между любым набором и его частью.
Пока не очень понятно, да? Посмотрите на эту картинку:
На рисунке изображен набор — все возможные игрушки. Часть игрушек — конструкторы — они выделены отдельным овалом. Это часть большого набора «игрушек» и одновременно отдельный набор (ведь конструктором может быть Лего и примитивные блоки для малышей). Какая-то часть из большого количества «игрушек» может быть заводной. Они не конструкторы, поэтому рисуем для них отдельный овал. Желтый овал «заводная машина» принадлежит как к набору «игрушки», так и к меньшему набору «заводная игрушка». Поэтому он изображен внутри обоих овалов сразу.
Ну что, стало понятнее? Именно поэтому круги Эйлера — это метод, наглядно демонстрирующий, что лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и легче получить ответ.
Автор метода — ученый Леонард Эйлер (1707-1783). Вот что он сказал о схемах, названных его именем: «кружки годятся для облегчения наших размышлений». Эйлера считают немецким, швейцарским и даже русским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской Академии наук и внес значительный вклад в развитие отечественной науки.
Эйлера считают немецким, швейцарским и даже русским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской Академии наук и внес значительный вклад в развитие отечественной науки.
До него аналогичным принципом в построении своих выводов руководствовался немецкий математик и философ Готфрид Лейбниц.
Метод Эйлера получил заслуженное признание и популярность. А после него многие ученые использовали его в своей работе, а также модифицировали на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами.
Немецкий математик Эрнест Шредер также внес свой вклад. Но главные заслуги принадлежат англичанину Джону Венну. Он был специалистом по логике и опубликовал книгу «Символическая логика», в которой подробно изложил свой вариант метода (использовал в основном образы пересечений множеств).
Благодаря вкладу Венна этот метод даже называют диаграммами Венна или даже диаграммами Эйлера-Венна.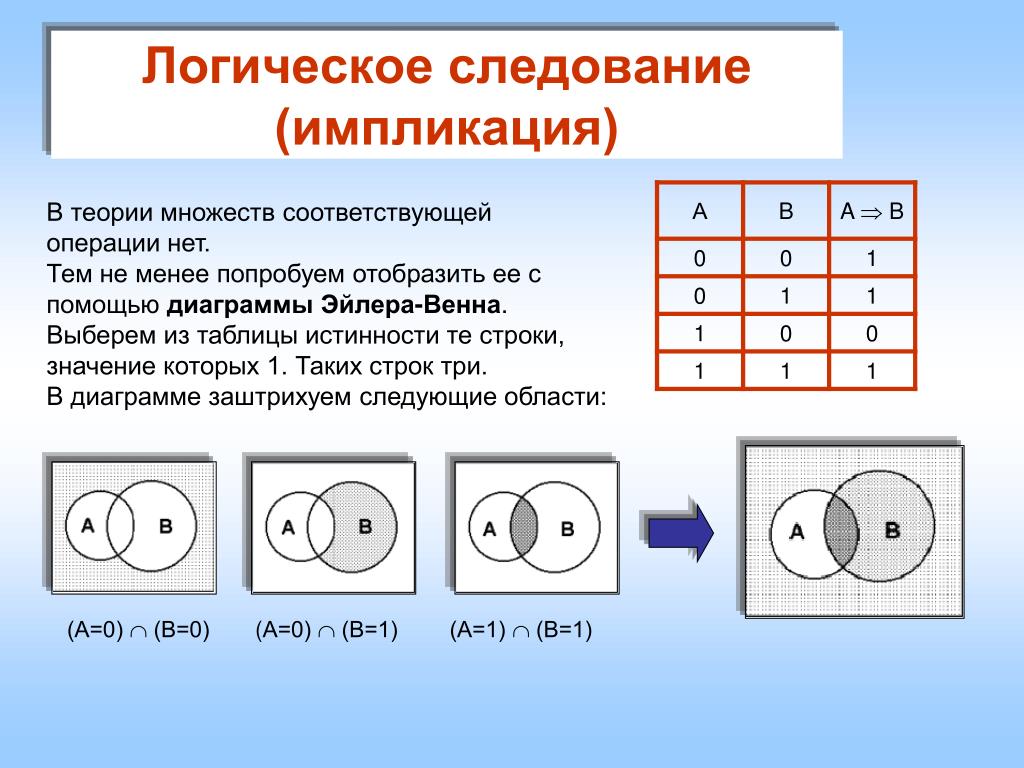
Зачем нужны круги Эйлера?
Окружности Эйлера имеют прикладное назначение, то есть с их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике, управлении и прочем.
Если говорить о типах окружностей Эйлера, то их можно разделить на те, которые описывают объединение некоторых понятий (например, соотношение рода и вида) — мы рассмотрели их на примере в начале статьи .
А также те, которые описывают пересечение множеств по какому-либо признаку. Этим принципом руководствовался Джон Венн в своих схемах. И именно он лежит в основе многих популярных мемов в Интернете. Вот один из примеров таких кругов Эйлера:
Забавно, правда? И самое главное, все сразу становится понятно. Можно потратить много слов, объясняя свою точку зрения, а можно просто нарисовать простую схему, которая сразу все расставит по своим местам.
Кстати, если вы не можете решить, какую профессию выбрать, попробуйте нарисовать диаграмму в виде окружностей Эйлера. Возможно, вам поможет определиться вот такой рисунок:
Возможно, вам поможет определиться вот такой рисунок:
Те варианты, которые будут на пересечении всех трех кругов, и есть профессия, которая не только сможет вас прокормить, но и понравится вам.
Решение задач с помощью окружностей Эйлера
Рассмотрим несколько примеров задач, которые можно решить с помощью окружностей Эйлера.
Вот на этом сайте — http://logika.vobrazovanie.ru/index.php?link=kr_e.html Елена Сергеевна Саженина предлагает интересные и простые задачи, для решения которых потребуется метод Эйлера. С помощью логики и математики разберем один из них.
Задание о любимых мультфильмах
Шестиклассники заполнили анкету с вопросами о любимых мультфильмах. Оказалось, что большинству из них нравятся «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны» и «Волк и теленок». В классе 38 учеников. «Белоснежка и семь гномов» нравится 21 ученику. Причем троим из них тоже нравится «Волк и теленок», шестерым — «Губка Боб Квадратные Штаны», а один ребенок одинаково любит все три мультфильма.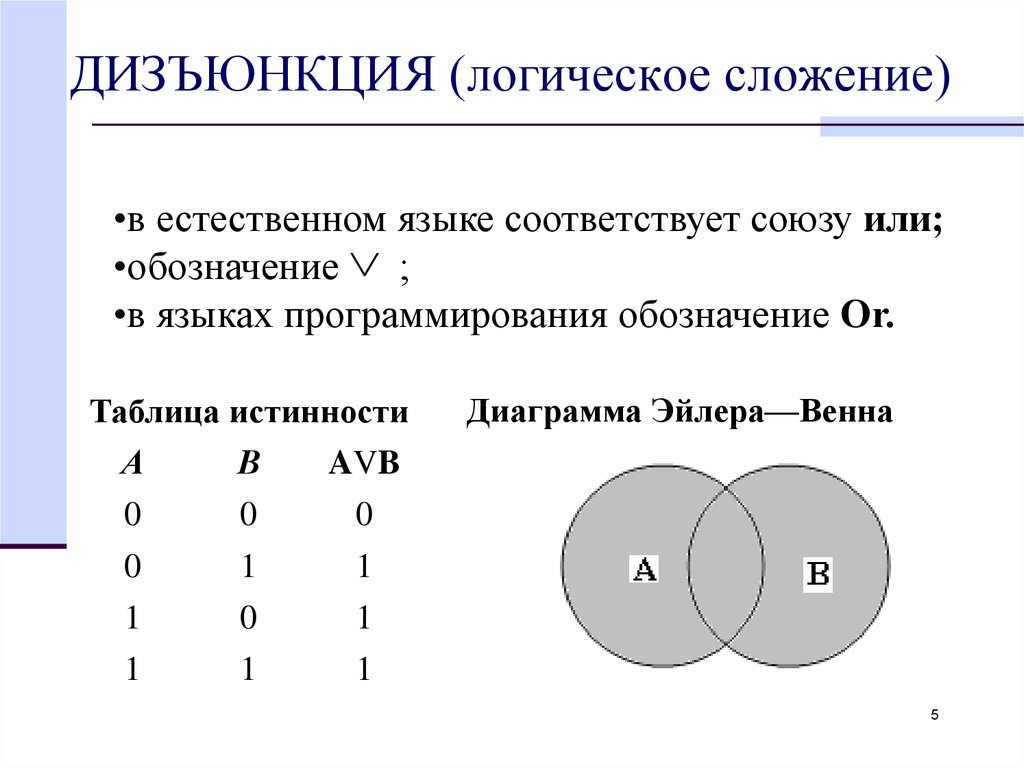 У «Волка и теленка» 13 поклонников, пятеро из которых назвали в анкете два мультфильма. Нам нужно определить, скольким шестиклассникам нравится Губка Боб Квадратные Штаны.
У «Волка и теленка» 13 поклонников, пятеро из которых назвали в анкете два мультфильма. Нам нужно определить, скольким шестиклассникам нравится Губка Боб Квадратные Штаны.
Решение:
Так как по условиям задачи нам дано три множества, то рисуем три окружности. А так как по ответам ребят получается, что множества пересекаются друг с другом, то рисунок будет выглядеть так:
Мы помним, что по условиям задания, среди любителей мультфильма «The Волк и теленок», пятеро ребят выбрали сразу два мультфильма:
Получается, что:
21 — 3 — 6 — 1 = 11 — ребята выбрали только «Белоснежку и семь гномов».
13 — 3 — 1 — 2 = 7 — ребята смотрят только «Волка и теленка».
Осталось только выяснить, сколько шестиклассников предпочитают мультфильм «Губка Боб Квадратные Штаны» двум другим вариантам. Из общего числа учеников вычитаем всех, кто любит два других мультфильма или выбрал несколько вариантов:
38 — (11 + 3 + 1 + 6 + 2 + 7) = 8 — Люди смотрят только Губку Боба Квадратные Штаны.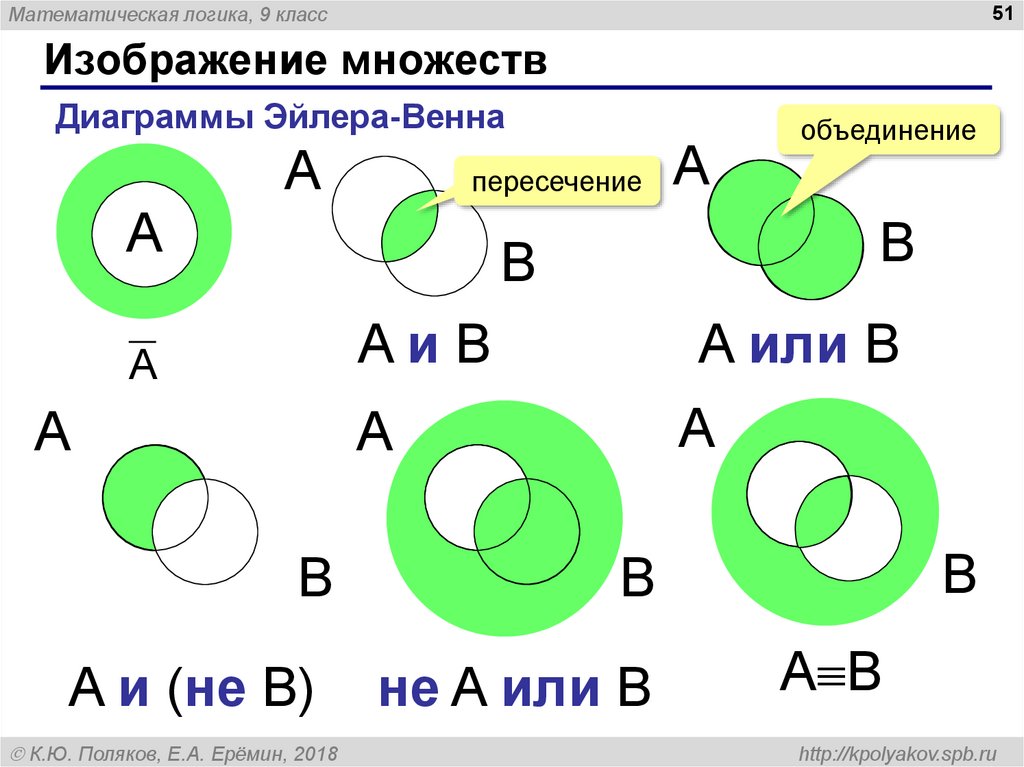
Теперь смело можно сложить все полученные числа и узнать, что:
мультфильм «Губка Боб Квадратные Штаны» выбрали 8+2+1+6=17 человек. Это ответ на поставленный в задаче вопрос.
Также рассмотрим задание , которое в 2011 году было сдано на демонстрационный тест ЕГЭ по информатике и ИКТ (источник — http://eileracrugi.narod.ru/index/0-6).
Условия задачи:
В языке запросов поисковика символ «|» используется для обозначения логической операции «ИЛИ», а символ «&» используется для логической операции «И».
В таблице представлены запросы и количество найденных по ним страниц для определенного сегмента Интернета.
| Запрос | Найдено страниц (в тысячах) |
| Крейсер | Линкор | 7000 |
| Крейсер | 4800 |
| Линкор | 4500 |
Сколько страниц (в тысячах) будет найдено по запросу Cruiser & Battleship ?
Предполагается, что все вопросы выполняются практически одновременно, чтобы набор страниц, содержащих все поисковые слова, не менялся в процессе выполнения запросов.
Решение:
С помощью окружностей Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используются для обозначения получившихся площадей.
Исходя из условий задачи, составим уравнения:
- Крейсер | Линкор: 1 + 2 + 3 = 7000
- Крейсер: 1 + 2 = 4800
- Линкор: 2 + 3 = 4500
Чтобы найти Cruiser & Battleship (обозначены на чертеже как область 2), подставляем уравнение (2) в уравнение (1) и узнаем, что:
4800 + 3 = 7000, откуда получаем 3 = 2200
Теперь мы можем подставить этот результат в уравнение (3) и узнать, что:
2 + 2200 = 4500, следовательно, 2 = 2300.
Ответ: 2300 — количество страниц, найденных по запросу Крейсер и линкор.
Как видите, круги Эйлера помогают быстро и легко решать даже достаточно сложные или просто запутанные на первый взгляд задачи.
Заключение
Думаю, нам удалось убедить вас в том, что круги Эйлера — это не просто занимательная и интересная вещь, но и очень полезный метод решения задач. И не только абстрактные задачи на школьных уроках, но и вполне бытовые задачи. Выбор будущей профессии, например.
И не только абстрактные задачи на школьных уроках, но и вполне бытовые задачи. Выбор будущей профессии, например.
Вам, наверное, еще будет любопытно узнать, что в современной массовой культуре круги Эйлера находят свое отражение не только в виде мемов, но и в популярных сериалах. Как Теория большого взрыва и 4isla.
Используйте этот полезный и наглядный метод для решения проблем. И обязательно расскажите об этом своим друзьям и одноклассникам. Для этого под статьей есть специальные кнопки.
блог.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Секции: Информатика
1. Введение
В курсе информатики и ИКТ начальной и старшей школы изучаются такие важные темы, как «Основы логики» и «Поиск информации в Интернете». При решении определенного типа задач удобно использовать окружности Эйлера (диаграммы Эйлера-Венна).
Математическая помощь. Диаграммы Эйлера-Венна используются в основном в теории множеств как схематическое представление всех возможных пересечений нескольких множеств. Как правило, они изображают все 2n комбинаций n свойств. Например, при n=3 диаграмму Эйлера-Венна обычно изображают в виде трех окружностей с центрами в вершинах равностороннего треугольника и с одинаковым радиусом, примерно равным длине стороны треугольника.
Как правило, они изображают все 2n комбинаций n свойств. Например, при n=3 диаграмму Эйлера-Венна обычно изображают в виде трех окружностей с центрами в вершинах равностороннего треугольника и с одинаковым радиусом, примерно равным длине стороны треугольника.
2. Представление логических связок в поисковых запросах
При изучении темы «Поиск информации в Интернете» приведены примеры поисковых запросов с использованием логических связок, близких по смыслу к союзам «и», «или» русского языка язык, считаются. Смысл логических связок становится понятнее, если проиллюстрировать их с помощью графической схемы — окружностей Эйлера (диаграмм Эйлера-Венна).
| логический канал | Пример запроса | Пояснение | Окружности Эйлера |
| и — «И» | Париж и университет | Будут выбраны все страницы, где упоминаются оба слова: Париж и университет | Рис.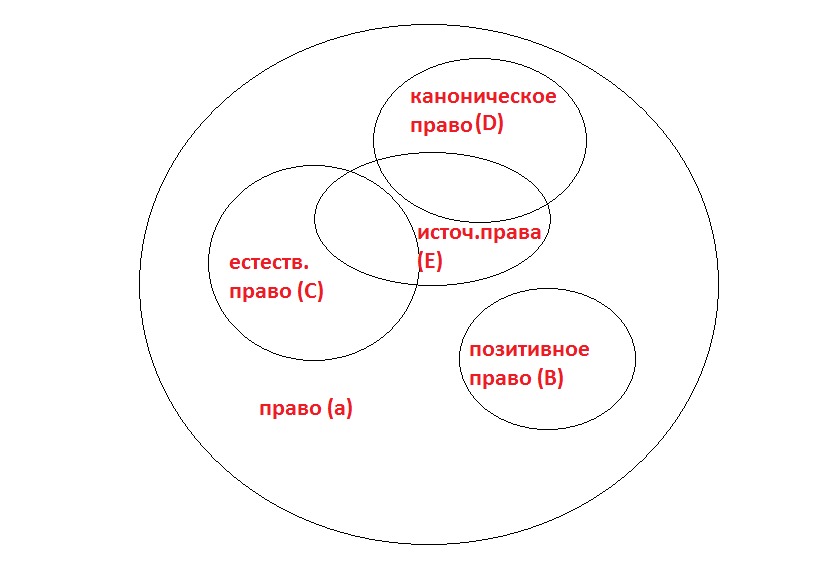 1 1 |
| | — «ИЛИ» | Париж | университет | Будут выбраны все страницы, содержащие слова Париж и/или университет | Рис.2 |
3. Связь логических операций с теорией множеств
С помощью диаграмм Эйлера-Венна можно визуализировать связь между логическими операциями и теорией множеств. Вы можете использовать слайды для демонстрации Приложение 1.
Логические операции определяются их собственными таблицами истинности. В AT Приложение 2 подробно рассмотрены графические иллюстрации логических операций вместе с их таблицами истинности. Поясним принцип построения диаграммы в общем случае. На диаграмме площадь кружка с именем А отображает истинность утверждения А (в теории множеств кружок А — это обозначение всех элементов, входящих в это множество). Соответственно, область вне круга отображает значение «ложь» соответствующего утверждения. Для того чтобы понять, какая область диаграммы будет отображением логической операции, необходимо заштриховать только те области, в которых значения логической операции на множествах А и В равны «истине».
Для того чтобы понять, какая область диаграммы будет отображением логической операции, необходимо заштриховать только те области, в которых значения логической операции на множествах А и В равны «истине».
Например, значение импликации «истинно» в трех случаях (00, 01 и 11). Закрашиваем последовательно: 1) область вне двух пересекающихся окружностей, что соответствует значениям А=0, В=0; 2) площадь, относящаяся только к окружности B (полумесяцу), что соответствует значениям A=0, B=1; 3) площадь, относящаяся как к окружности А, так и к окружности В (пересечение) — соответствует значениям А=1, В=1. Объединение этих трех областей будет графическим представлением операции логического следования.
4. Использование окружностей Эйлера при доказательстве логических равенств (законов)
Для доказательства логических равенств может быть применен метод диаграмм Эйлера-Венна. Докажем следующее равенство ¬(AvB) = ¬A&¬B (закон де Моргана).
Для наглядности левой части уравнения выполним последовательно: заштрихуем обе окружности (применим дизъюнкцию) серым цветом, затем для отображения инверсии закрасим область вне окружностей цветом черный:
Рис. 3 Рис.4
3 Рис.4
Для наглядного представления правой части уравнения выполняем последовательно: закрашиваем область отображения инверсии (¬A) серым цветом и аналогично область ¬B также в сером цвете; то для отображения конъюнкции нужно взять пересечение этих серых областей (результат наложения показан черным цветом):
рис.5 рис.6 рис.7
Мы видим, что области для отображения левая и правая части равны. КЭД
5. Задания в формате ГИА и ЕГЭ на тему: «Поиск информации в Интернете»
Задача №18 из демо-версии ГИА 2013.
В таблице представлены запросы к поисковому серверу. Для каждого запроса указан его код — соответствующая буква от A до D. Расположите коды запросов слева направо в порядке по убыванию количество страниц, которые поисковик найдет по каждому запросу.
| Код | Запрос |
| НО | (Летайте и деньги) | Самовар |
| Б | Летать и деньги и базар и самовар |
| В | Летать | Деньги | Самовар |
| Г | Муха, деньги и самовар |
Для каждого запроса построим диаграмму Эйлера-Венна:
| Запрос A | Запрос Б | Запрос B | Запрос D |
Ответ: ВАГБ.
Задание Б12 из демо-версии ЕГЭ-2013.
В таблице представлены запросы и количество найденных ими страниц для определенного сегмента Интернета.
| Запрос | Найдено страниц (в тысячах) |
| Фрегат | Эсминец | 3400 |
| Фрегат и Эсминец | 900 |
| Фрегат | 2100 |
Сколько страниц (в тысячах) будет найдено по запросу Destroyer ?
Предполагается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не менялся в процессе выполнения запросов.
F — количество страниц (в тысячах) по запросу Фрегат ;
E — количество страниц (в тысячах) по запросу Destroyer ;
X — количество страниц (в тысячах) для запроса, в котором упоминается фрегат и без упоминания эсминца ;
Y — количество страниц (в тысячах) для запроса, в котором упоминается Эсминец и , а не упоминается Фрегат.
Построим диаграммы Эйлера-Венна для каждого запроса:
| Запрос | Диаграмма Эйлера-Венна | Количество страниц |
| Фрегат | Эсминец | Рис.12 | 3400 |
| Фрегат и Эсминец | Рис.13 | 900 |
| Фрегат | Рис.14 | 2100 |
| Эсминец | Рис.15 | ? |
По диаграммам имеем:
- X + 900 + Y = F + Y = 2100 + Y = 3400.
 Отсюда находим Y = 3400-2100 = 1300.
Отсюда находим Y = 3400-2100 = 1300. - Е = 900 + U = 900 + 1300 = 2200.
Ответ: 2200.
6. Решение логических содержательных задач методом диаграмм Эйлера-Венна
В классе 36 человек. Учащиеся этого класса посещают математический, физико-химический кружки, причем математический кружок посещают 18 человек, физический — 14 человек, химический — 10 человек. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек посещают и математический, и математический, и химический, 3 – и физический, и химический.
Сколько учеников в классе не посещают кружки?
Для решения этой задачи очень удобно и наглядно использовать окружности Эйлера.
Самый большой круг — это множество всех учеников класса. Внутри круга три пересекающихся множества: члены математического ( M ), физического ( F ), химического ( X ) кругов.
Пусть МФХ — много ребят, каждый из которых посещает все три кружка.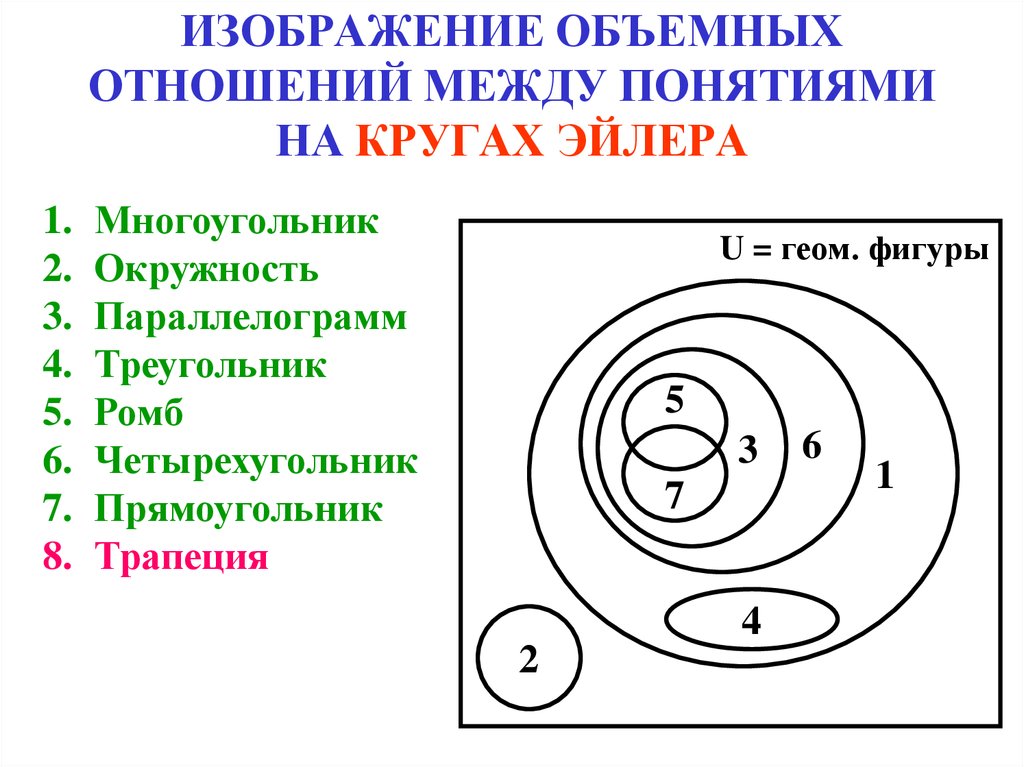 МФ-Н — много ребят, каждый из которых посещает математический и физический кружки, а не посещает химический ¬M¬PH — много ребят, каждый из которых посещает химический кружок и не посещает физико-математический кружок.
МФ-Н — много ребят, каждый из которых посещает математический и физический кружки, а не посещает химический ¬M¬PH — много ребят, каждый из которых посещает химический кружок и не посещает физико-математический кружок.
Аналогично вводим множества: ¬MFH, M¬PH, M¬F-H, ¬MF-H, ¬M-F-H.
Известно, что все три кружка посещают 2 человека, поэтому в регионе МФХ пишем цифру 2. И математический, и физический кружки посещают 8 человек, и среди них уже 2 человека посещают все три кружка , то в область MF-H пишем 6 человек (8-2). Аналогично определяем количество учеников в остальных наборах:
Суммируем количество людей во всех регионах: 7+6+3+2+4+1+5=28. Следовательно, кружки посещают 28 человек из класса.
Значит 36-28=8 учеников кружки не посещают.
После зимних каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Выяснилось, что из 36 учеников класса двое никогда не были в кино.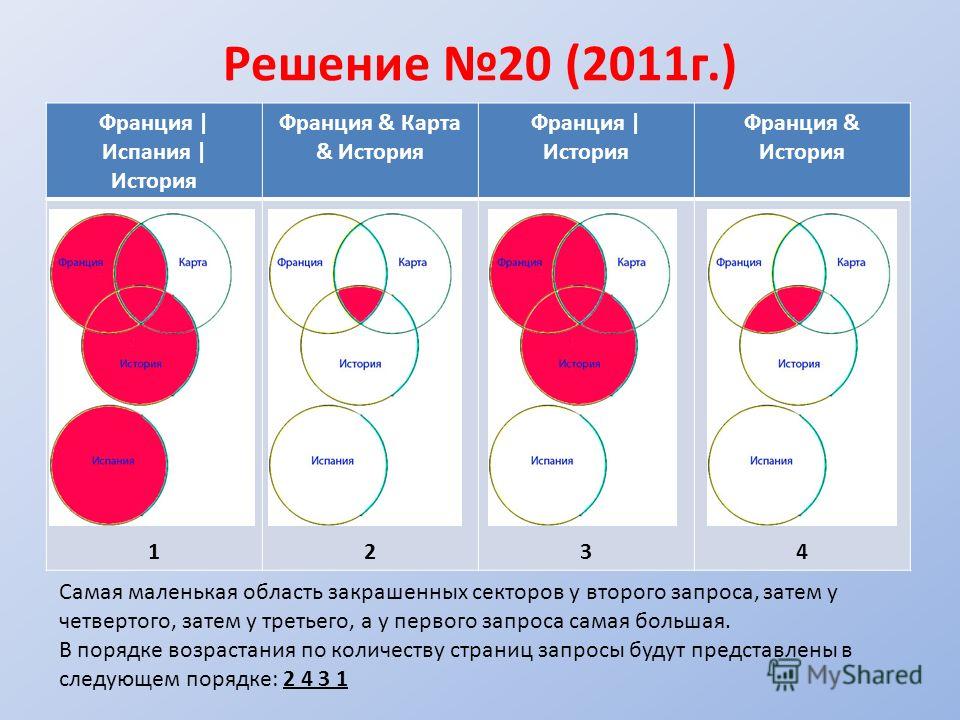 не в театре, не в цирке. в кинотеатре побывало 25 человек, в театре – 11 человек, в цирке – 17 человек; и в кино, и в театре — 6; и в кино и в цирке — 10; и в театре, и в цирке — 4.
не в театре, не в цирке. в кинотеатре побывало 25 человек, в театре – 11 человек, в цирке – 17 человек; и в кино, и в театре — 6; и в кино и в цирке — 10; и в театре, и в цирке — 4.
Сколько человек побывало в кино, театре и цирке?
Пусть x — количество детей, побывавших в кино, театре и цирке.
Затем можно построить следующую диаграмму и подсчитать количество парней в каждом районе:
| Кино и театр посетили 6 человек, значит, кино и театр посетили только 6 человек. Аналогично, только в кино и в цирке (10-е) человек. Только в театре и цирке (4) чел. В кино ходили 25 человек, значит, в кино ходили только 25 из них — (10-е) — (6-е) — х = (9 + х). Аналогично, только в театре было (1+x) человек. Только в цирке было (3+x) человек. Не были в театре, кино и цирке — 2 человека. Итак, 36-2=34 человека. С другой стороны, мы можем суммировать количество людей, которые были в театре, кино и цирке: (9+х)+(1+х)+(3+х)+(10-х)+(6-х)+(4-х)+х = 34 Отсюда следует, что только один человек посетил все три мероприятия. |
Таким образом, окружности Эйлера (диаграммы Эйлера-Венна) находят практическое применение при решении задач формата ЕГЭ и ГИА и при решении содержательных логических задач.
Литература
- В.Ю. Лыскова, Е.А. Ракитин. Логика в информатике. М.: Информатика и образование, 2006. 155 с.
- Л.Л. Босова. Арифметико-логические основы ЭВМ. М.: Информатика и образование, 2000. 207 с.
- Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ за 8 класс: БИНОМ. Лаборатория знаний, 2012. 220 с.
- Л.Л. Босова, А.Ю. Босова. Учебник. Информатика и ИКТ для 9 класса: БИНОМ. Лаборатория знаний, 2012. 244 с.
- Сайт ФИПИ: http://www.fipi.ru/
Эйлеровы круги — одна из самых простых тем, которая нужна для поступления в 5 класс физико-математических лицеев . На самом деле Эйлеровых кругов — это не что иное, как графическое представление наборов. Предметы, обладающие определенным свойством, находятся внутри круга Эйлера-Венна, те, у кого нет — находятся снаружи. Конечно, обычно на схеме не один круг, а несколько, каждый из которых объединяет объекты каким-то своим свойством. Любая задача из этого блока сводится к тому, что необходимо посчитать количество элементов в какой-либо области. Разберем на примерах что делать:
На самом деле Эйлеровых кругов — это не что иное, как графическое представление наборов. Предметы, обладающие определенным свойством, находятся внутри круга Эйлера-Венна, те, у кого нет — находятся снаружи. Конечно, обычно на схеме не один круг, а несколько, каждый из которых объединяет объекты каким-то своим свойством. Любая задача из этого блока сводится к тому, что необходимо посчитать количество элементов в какой-либо области. Разберем на примерах что делать:
Задачи для многих
Ученики учатся в классе. выучить английский, немецкий и французский языки. Никто не знает ни одного языка. Также известно, что из всех детей только один мальчик изучает языки: английский и французский. Сколько человек изучает язык?
Для решения задачи обозначим количество искомых учеников для (тех, кто изучает язык). Количество учащихся, изучающих другое количество языков, выражается через и условия в задаче. Диаграмма Эйлера-Венна в этом случае будет выглядеть так: Например, ребята, знающие только английский язык, отмечены красным и их номер.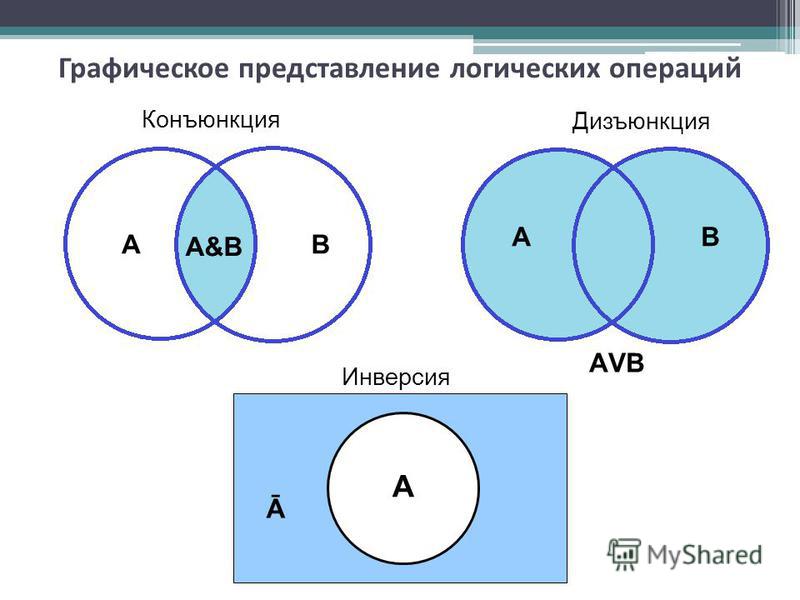
Обратите внимание, что мы никак не использовали общее количество студентов — это условие порождает то самое уравнение, с помощью которого будет решаться задача:
Получается, что все языки изучают люди (Теперь, зная, можно самостоятельно восстановить, сколько учеников было в классе и проверить ответ)
Задачи на делимость (комплексную делимость)
Это задачи повышенной сложности. Советуем сначала изучить тему. Обязательна к прочтению только тем, кто собирается выиграть призы.
Для скольких чисел между и верно следующее утверждение: число делится или не делится на ?
Такое ужасное и непонятное состояние становится простым, если использовать эйлеровых окружностей . Понятно, что в этой задаче числа считаются таковыми — нас интересуют те, которые находятся внутри соответствующего круга. Также есть номера, которые вдоц 12 — нас интересуют номера, которые вышли. Но как насчет чисел, принадлежащих обоим наборам? Во-первых, что у них общего, а во-вторых, интересны ли они нам?
Давайте сначала ответим на первый вопрос. Получается, что если число делится на два других числа одновременно, то оно делится на наименьшее общее кратное из этих двух чисел, то есть на минимальное число, которое делится без остатка на оба из них . Для чисел и НОК нет ничего, кроме числа, так как и , и нет меньшего числа с такими свойствами. В сумме пересечение наших множеств содержит числа, которые .
Получается, что если число делится на два других числа одновременно, то оно делится на наименьшее общее кратное из этих двух чисел, то есть на минимальное число, которое делится без остатка на оба из них . Для чисел и НОК нет ничего, кроме числа, так как и , и нет меньшего числа с такими свойствами. В сумме пересечение наших множеств содержит числа, которые .
Далее следует отметить, что в условии используется слово «ИЛИ» . Это означает, что для искомых чисел МИНИМУМ ОДНО из предложенных утверждений должно быть верным (возможно, оба). То есть числа, находящиеся внутри подходящего нам круга чисел, а также все числа, находящиеся вне круга.
Итак, диаграмма Эйлера-Венна выглядит так: Штриховкой обозначены числа, которые необходимо найти. Теперь, надеюсь, очевидно, что нам нужно найти, сколько чисел в рассматриваемой задаче, отнять от этого числа количество чисел и прибавить количество чисел, которые равны .
Итак приступим:
Получается, что нужные цифры
Итак, подведем итоги.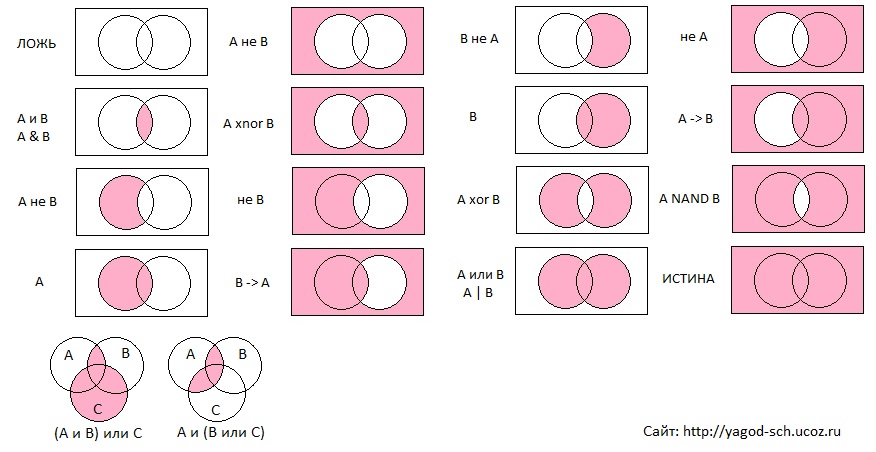 Если вы собираетесь поступать в 5 класс физико-математического лицея , то общие знания по кругам Эйлера-Венна Вам необходимы. Основная область применения — задачи, где есть наборы объектов, обладающих определенными свойствами, и необходимо найти количество объектов, обладающих (или не имеющих) набором заданных свойств.
Если вы собираетесь поступать в 5 класс физико-математического лицея , то общие знания по кругам Эйлера-Венна Вам необходимы. Основная область применения — задачи, где есть наборы объектов, обладающих определенными свойствами, и необходимо найти количество объектов, обладающих (или не имеющих) набором заданных свойств.
Логика. Учебник Гусев Дмитрий Алексеевич
1.6. Круговые диаграммы Эйлера
Как мы уже знаем, существует шесть вариантов отношений между понятиями в логике. Любые два сопоставимых понятия обязательно находятся в одном из этих отношений. Например, понятия писатель и русский относятся к пересечению, писатель и человек — подчинению Москва и столица России — эквивалентность Moscow and Petersburg — subordination, wet road and dry road — opposites Antarctica and mainland — subordination Antarctica and Africa — subordination, etc. , etc.
, etc.
It should be заметил, что если два понятия обозначают часть и целое, например месяц и год , то они находятся в отношениях подчинения, хотя может показаться, что между ними есть отношение подчинения, потому что месяц включен в год. Однако если понятия месяц и год были подчиненными, то нужно было бы утверждать, что месяц обязательно год, а год не обязательно месяц (вспомним отношение подчинения на примере понятий карась и рыба : карась это обязательно рыба, но рыба это не обязательно карась). Месяц не год, и год не месяц, но оба являются периодом времени, поэтому понятия месяц и год, а также понятия книга и страница книги, автомобиль и колесо автомобиля, молекула и атом и т. д., находятся в отношениях подчинения, так как часть и целое не тождественны виду и роду.
В начале было сказано, что понятия сравнимы и несравнимы. Считается, что рассмотренные шесть вариантов отношений применимы только к сопоставимым понятиям. Однако можно утверждать, что все несопоставимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело можно рассматривать как подчиненные, так как пингвин не является небесным телом и наоборот, но в то же время объем понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающей среды или форма материи (ведь и пингвин, и небесное тело являются разными объектами окружающего мира или разными формами материи) . Если одно понятие обозначает нечто материальное, а другое — нематериальное (например, дерево и мысль ), то родовым понятием для этих (как можно утверждать) подчиненных понятий является понятие форма бытия , ибо и дерево, и мысль, и что угодно другое — это разные формы быть.
Однако можно утверждать, что все несопоставимые понятия находятся между собой в отношении соподчинения. Например, такие несравнимые понятия, как пингвин и небесное тело можно рассматривать как подчиненные, так как пингвин не является небесным телом и наоборот, но в то же время объем понятий пингвин и небесное тело входят в более широкий объем третьего понятия, родового по отношению к ним: это может быть понятие объект окружающей среды или форма материи (ведь и пингвин, и небесное тело являются разными объектами окружающего мира или разными формами материи) . Если одно понятие обозначает нечто материальное, а другое — нематериальное (например, дерево и мысль ), то родовым понятием для этих (как можно утверждать) подчиненных понятий является понятие форма бытия , ибо и дерево, и мысль, и что угодно другое — это разные формы быть.
Как мы уже знаем, отношения между понятиями представлены круговыми диаграммами Эйлера. И до сих пор мы схематически изображали отношения между двумя понятиями, а это можно сделать с большим количеством понятий. Например, связь между понятиями Боксер, негр и человек
И до сих пор мы схематически изображали отношения между двумя понятиями, а это можно сделать с большим количеством понятий. Например, связь между понятиями Боксер, негр и человек
Взаимное расположение кружков показывает, что концепты боксер и черный человек находятся в отношении пересечения (боксер может быть или не быть негром, а негр может или может и не быть боксером), но понятия боксер и человек, а также понятия черный человек и человек находятся в отношении подчинения (ведь любой боксер и любой негр обязательно человек, но человек не может быть ни боксером, ни негром).
Рассмотрим связь между понятиями дед, отец, мужчина, человек с помощью круговой диаграммы:
Как видите, эти четыре понятия находятся в отношении последовательной соподчиненности: дед обязательно является отцом, а отец нет обязательно дедушка; всякий отец обязательно мужчина, но не всякий мужчина отец; и, наконец, человек обязательно мужчина, но не только человек может быть человеком.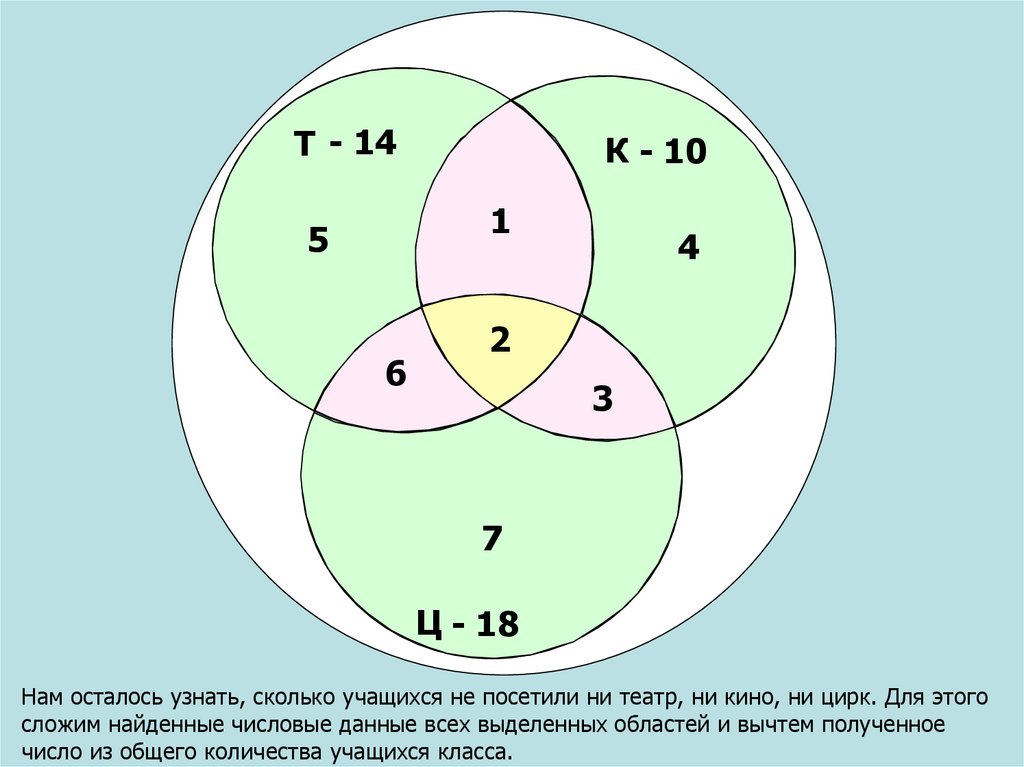 Соотношение понятий хищник, рыба, акула, пиранья, щука, живое существо показаны на следующей диаграмме:
Соотношение понятий хищник, рыба, акула, пиранья, щука, живое существо показаны на следующей диаграмме:
Попробуйте сами прокомментировать эту диаграмму, установив все имеющиеся на ней типы отношений между понятиями.
Подводя итог сказанному, отметим, что отношение между понятиями есть отношение между их объемами. Это значит, что для того, чтобы можно было установить отношения между понятиями, их объем должен быть резким, а содержание, соответственно, ясным, т. е. эти понятия должны быть определенными. Что же касается рассмотренных выше неопределённых понятий, то установить точное соотношение между ними довольно сложно, практически невозможно, так как в силу неоднозначности их содержания и размытости объёма любые два неопределённых понятия могут быть охарактеризованы как равнозначные или как пересекающиеся, или как подчиненные и т. д. Например, можно ли устанавливать отношения между неопределенными понятиями небрежность и небрежность ? Будет ли это эквивалентность, или субординация — точно сказать нельзя. Таким образом, отношения между неопределенными понятиями также являются неопределенными. Понятно поэтому, что в тех ситуациях интеллектуальной речевой практики, где требуются точность и однозначность в определении соотношения между понятиями, употребление неопределенных понятий нежелательно.
Таким образом, отношения между неопределенными понятиями также являются неопределенными. Понятно поэтому, что в тех ситуациях интеллектуальной речевой практики, где требуются точность и однозначность в определении соотношения между понятиями, употребление неопределенных понятий нежелательно.
Из книги Проницательность автора Ефимов Виктор Алексеевич
Из книги Философия науки и техники автора Степин Вячеслав Семенович
Теоретические схемы и абстрактные объекты технической теории Теоретические схемы — совокупность абстрактных объектов, ориентированных, с одной стороны, на применение соответствующих математических
Из книги Диалектика мифа автора Лосев Алексей Федорович
2. Диалектика схемы, аллегории и символа Какие типы этих отношений вообще возможны? Их очень много. Но, вслед за Шеллингом, можно указать три основных таких типа. В то же время мы будем иметь в виду, что наши термины «внутренний» и «внешний» являются очень общими терминами, и их можно
Из книги Курс Эпохи Водолея. Апокалипсис или возрождение автора Ефимов Виктор Алексеевич
Апокалипсис или возрождение автора Ефимов Виктор Алексеевич
Из книги Избранные произведения автора Щедровицкий Георгий Петрович
Из книги Человек среди учений автора Кротов Виктор Гаврилович
Комментарии и схемы Учение, основанное на внутренней работе личности, не могло бы пережить эту самую личность без приливов новой внутренней работы новых личностей. Тем, кто увидел для себя особый смысл в этом учении. Условия существования меняются,
Из книги Искусство правильно мыслить автора Ивин Александр Архипович
СХЕМЫ ПРАВИЛЬНЫХ РАССМОТРЕНИЙ Вот два примера дедуктивных умозаключений из рассказа русского юмориста начала века В. Билибина. «Если бы на свете не существовало солнца, то нам приходилось бы постоянно жечь свечи и керосин. Если приходилось постоянно жечь свечи и керосин, то чиновники
Из книги Этика любви и метафизика своеволия: проблемы нравственной философии.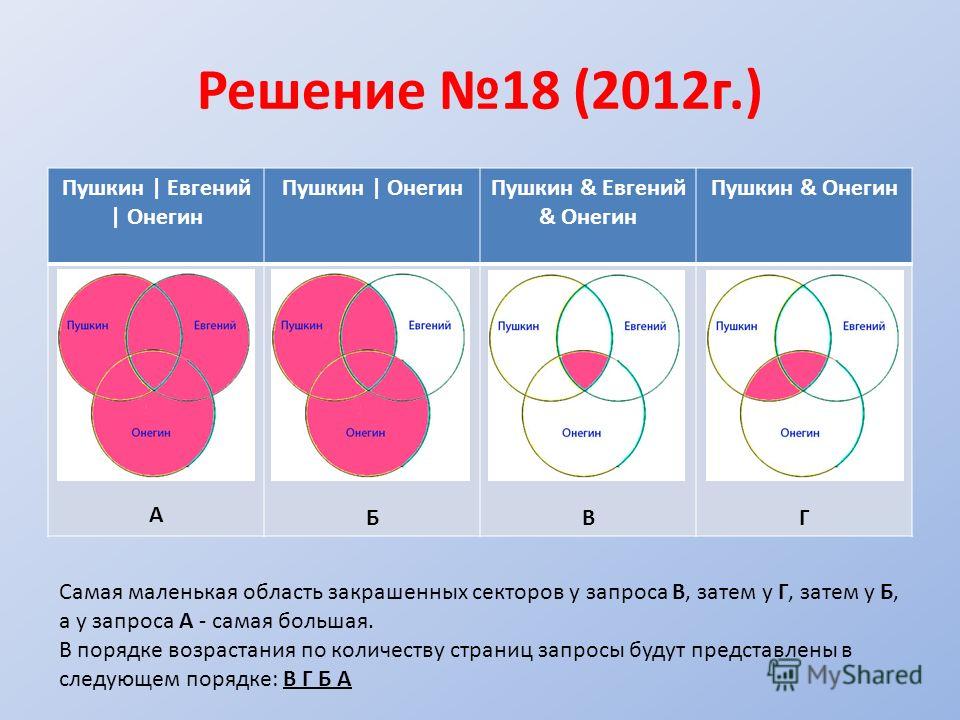 автора Давыдов Юрий Николаевич
автора Давыдов Юрий Николаевич
Нравственная философия Толстого и Достоевского в рамках ницшеанской схемы нигилизма С последней четверти прошлого века проблема нигилизма вышла на одно из первых мест среди важнейших проблем западноевропейской философии. Со своим «статусом» она прежде всего
Из книги Нормы в пространстве языка автора Федяева Наталья Дмитриевна
2.1.1. Нормы-схемы речевого общения: речевой этикет Выбор первой проблемной области — речевого этикета — обусловлен следующим. При определении сущностных признаков нормы мы стали отходить от социальных норм, заметив при этом, что их существование вполне
Из книги Спиральная динамика [Управление ценностями, лидерством и изменениями в 21 веке] автора Бек Дон
2.1.2. Семиотически закрепленные нормы-схемы: жанры Основанием для противопоставления социально и семиотически закрепленных норм, как было сказано в главе I, является способ их закрепления в социокультурной практике.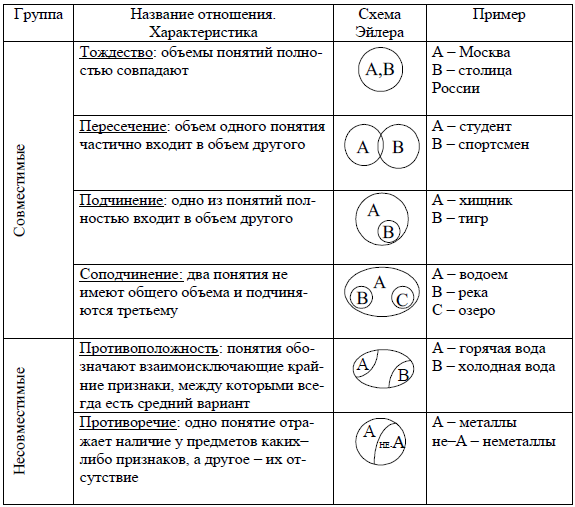 Первыми — неписаными законами — становятся программы, схемы
Первыми — неписаными законами — становятся программы, схемы
Из книги Логика и аргументация: Учебник. пособие для вузов. автора Рузавин Георгий Иванович
Из книги Архитектура и иконопись. «Тело символа» в зеркале классической методологии автора Ванеян Степан Сергеевич.
9.1. Структура аргументации Графические диаграммы Любая аргументация начинается с установления и обсуждения некоторых фактов, которые в дальнейшем будут называться данными, и с помощью которых выдвигается и обосновывается некий вывод. Кроме того, перейти от
Из книги автора
Иконография как система методов: схемы и угрозы Сама практика иконографического анализа сформировала «отработанную схему» последовательной исследовательской деятельности. Схема предполагает: — осмысление исторического смысла мотива — с точки зрения времени (момент
Диаграммы и концепция логической системы | Логические рассуждения с диаграммами
Фильтр поиска панели навигации Oxford AcademicЛогические рассуждения с диаграммамиАрхитектура компьютера и логическое проектированиеКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicЛогические рассуждения с диаграммамиАрхитектура компьютера и логическое проектированиеКнигиЖурналы Термин поиска на микросайте
Расширенный поиск
Иконка Цитировать Цитировать
Разрешения
- Делиться
- Твиттер
- Подробнее
CITE
BARWISE, JON и ERIC HAMMER,
‘Диаграммы и концепция логической системы’
,
Логические рассуждения с диаграммами
(
,
1996;
онлайн, онлайн, онлайн, онлайн, онлайн, онлайн, онлайн, онлайн, онлайн, онлайн, онлайн,
,
1996;
.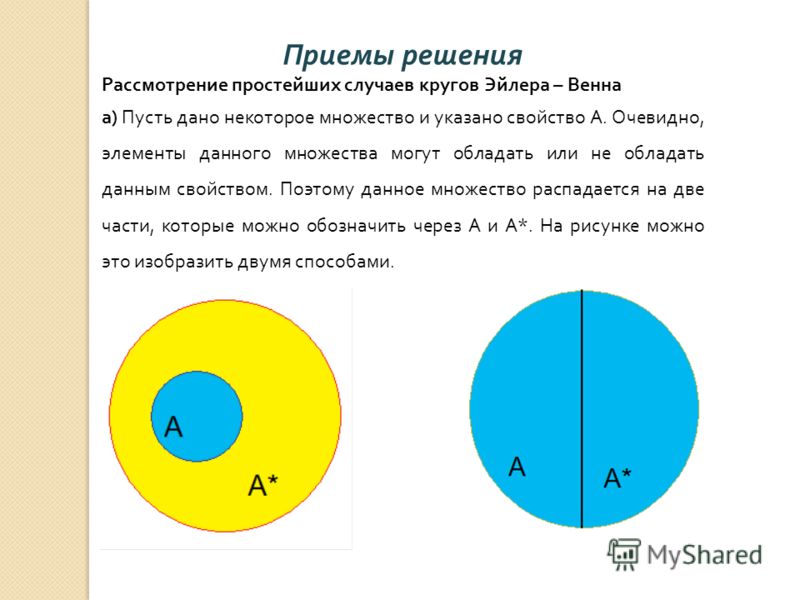
Oxford Academic
, 12 ноября 2020 г.
), https://doi.org/10.1093/9780195104271.003.0007,
по состоянию на 11 октября 2022 г.
Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)
Закрыть
Фильтр поиска панели навигации Oxford AcademicЛогические рассуждения с диаграммамиАрхитектура компьютера и логическое проектированиеКнигиЖурналы Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Oxford AcademicЛогические рассуждения с диаграммамиАрхитектура компьютера и логическое проектированиеКнигиЖурналы Термин поиска на микросайте
Advanced Search
Abstract
При попытке проанализировать понятие логической системы можно использовать различные подходы.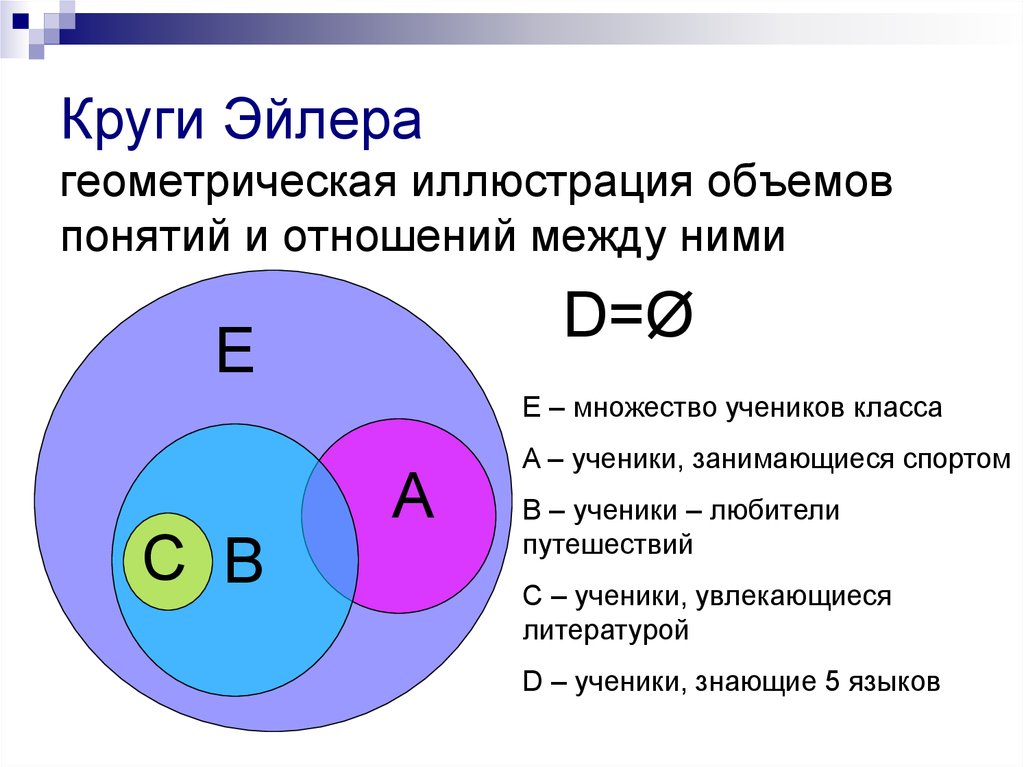 Можно было бы взглянуть на то, что люди называют логическими системами, и попытаться разработать естественную структуру, которая охватывала бы большинство или многие из них, а затем исследовать последствия этой структуры, видя, что еще подпадает под эту структуру и каковы последствия общее представление так и есть. В основном такой подход применялся, например, у Барвайза [19].74], одна из первых попыток разработать такую структуру. У этого подхода есть много достоинств, но он также имеет как минимум два серьезных недостатка. Она слишком зависит от исторических случайностей, т. е. от того, какие именно логические системы выработались у людей. Существует по крайней мере теоретическая возможность того, что предубеждения прецедента и моды сыграли значительную роль в том, как все пошло. Если это так, то абстрагирование от практики чревато опасностью систематизации этих исторически обусловленных предубеждений, превращая их в необходимые черты логической системы. Оборотной стороной этой проблемы является то, что вполне могут существовать некоторые неестественные логические системы, которые искажают структуру.
Можно было бы взглянуть на то, что люди называют логическими системами, и попытаться разработать естественную структуру, которая охватывала бы большинство или многие из них, а затем исследовать последствия этой структуры, видя, что еще подпадает под эту структуру и каковы последствия общее представление так и есть. В основном такой подход применялся, например, у Барвайза [19].74], одна из первых попыток разработать такую структуру. У этого подхода есть много достоинств, но он также имеет как минимум два серьезных недостатка. Она слишком зависит от исторических случайностей, т. е. от того, какие именно логические системы выработались у людей. Существует по крайней мере теоретическая возможность того, что предубеждения прецедента и моды сыграли значительную роль в том, как все пошло. Если это так, то абстрагирование от практики чревато опасностью систематизации этих исторически обусловленных предубеждений, превращая их в необходимые черты логической системы. Оборотной стороной этой проблемы является то, что вполне могут существовать некоторые неестественные логические системы, которые искажают структуру.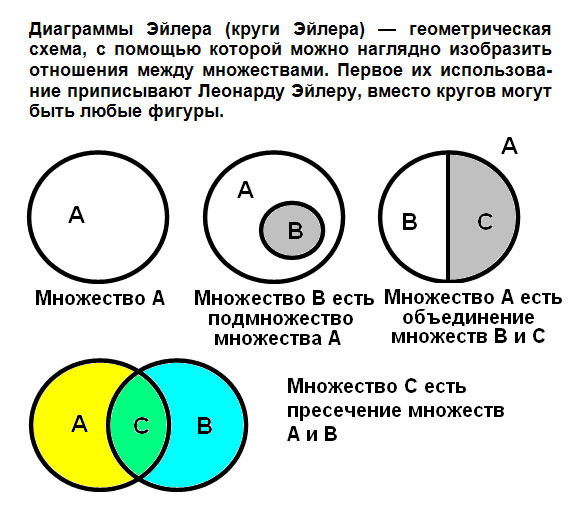 Но как еще можно было бы поступить в попытке получить принципиальное понятие логической системы? Другой подход, который мы используем здесь, состоит в том, чтобы взглянуть на существующие логические системы, разработанные людьми, и попытаться понять, чем они занимались в более общих чертах. Мы надеемся найти какое-нибудь интересное природное явление, скрывающееся за этими системами, «природного типа», если хотите. Если бы такое природное явление существовало, его можно было бы использовать для формулировки абстрактного понятия логической системы. Если бы с помощью этого подхода можно было найти характеристику логических систем, он потенциально имел бы два существенных преимущества по сравнению с более ортодоксальным подходом. Во-первых, это обеспечило бы основу, на основе которой можно было бы дать принципиальную критику существующих систем, заявленных как логические системы. Во-вторых, это указывало бы на пробелы, то есть на логические системы, которые еще предстоит разработать.
Но как еще можно было бы поступить в попытке получить принципиальное понятие логической системы? Другой подход, который мы используем здесь, состоит в том, чтобы взглянуть на существующие логические системы, разработанные людьми, и попытаться понять, чем они занимались в более общих чертах. Мы надеемся найти какое-нибудь интересное природное явление, скрывающееся за этими системами, «природного типа», если хотите. Если бы такое природное явление существовало, его можно было бы использовать для формулировки абстрактного понятия логической системы. Если бы с помощью этого подхода можно было найти характеристику логических систем, он потенциально имел бы два существенных преимущества по сравнению с более ортодоксальным подходом. Во-первых, это обеспечило бы основу, на основе которой можно было бы дать принципиальную критику существующих систем, заявленных как логические системы. Во-вторых, это указывало бы на пробелы, то есть на логические системы, которые еще предстоит разработать.
Ключевые слова: Теория АТС, Интенсивность полосы, Диаметр столкновения, Димеры, Электрическое поле, Резонанс Ферми, Зона основного состояния, Оператор Гамильтона, Тензор инерции
Тема
Компьютерная архитектура и логическое проектирование
В настоящее время у вас нет доступа к этой главе.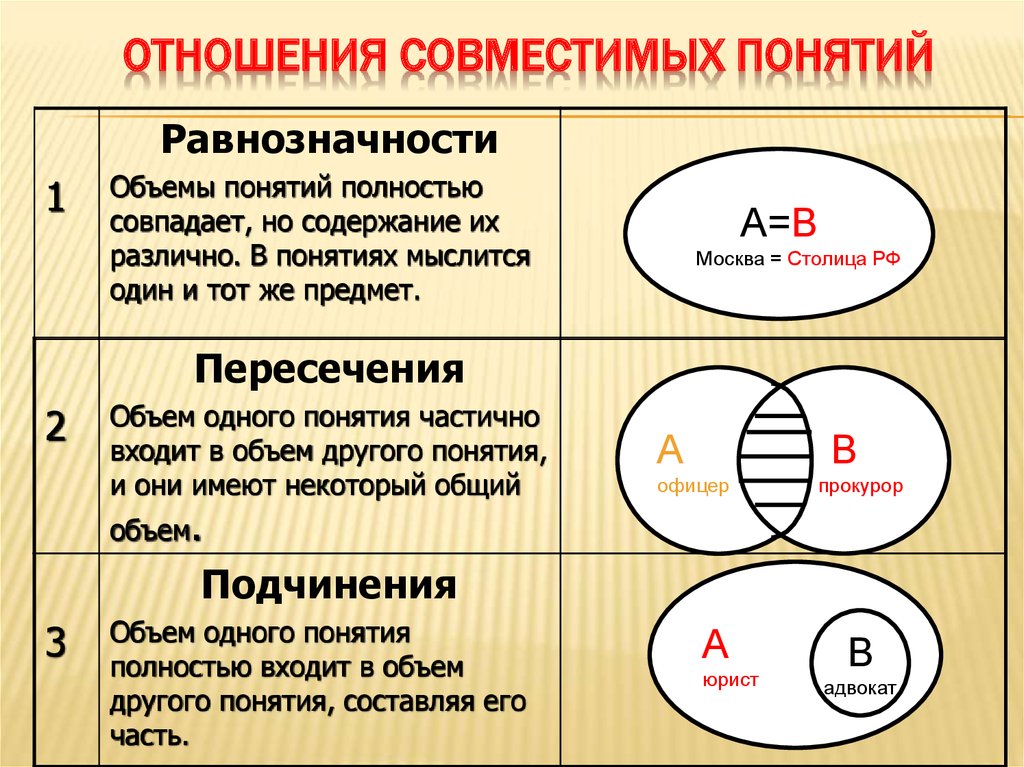
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.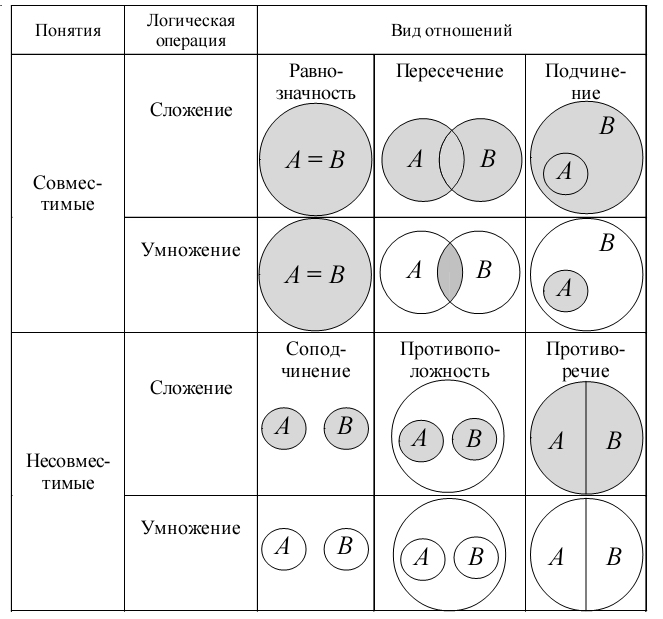
- Щелкните Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic.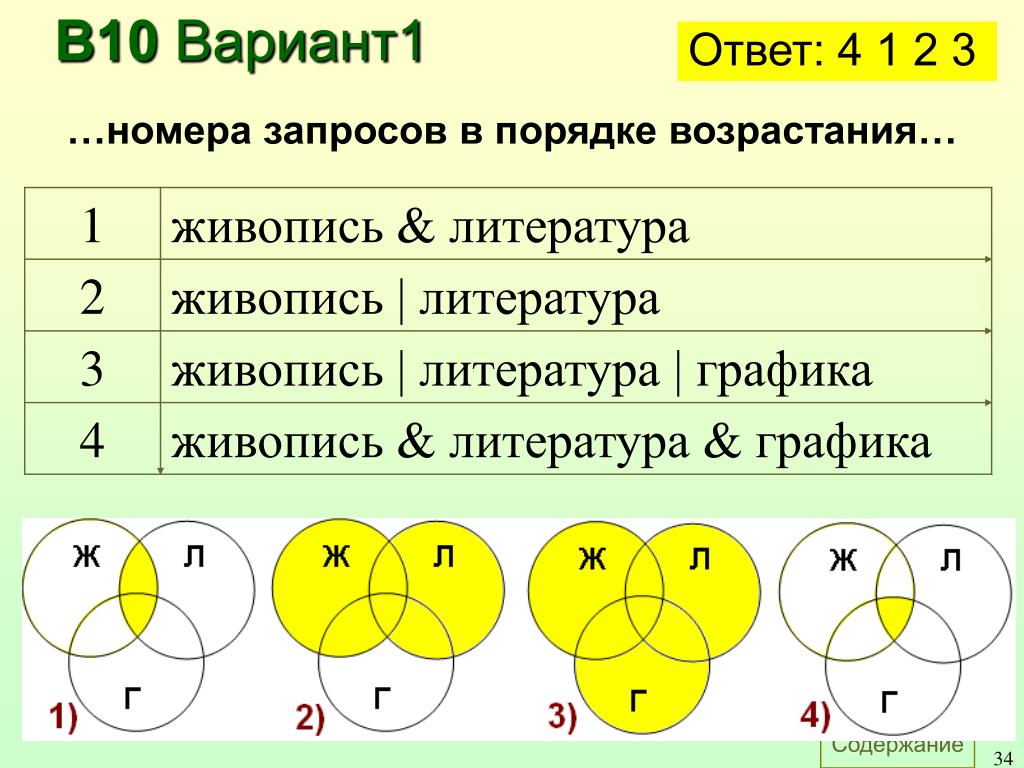 Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
- После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Вход через личный кабинет
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.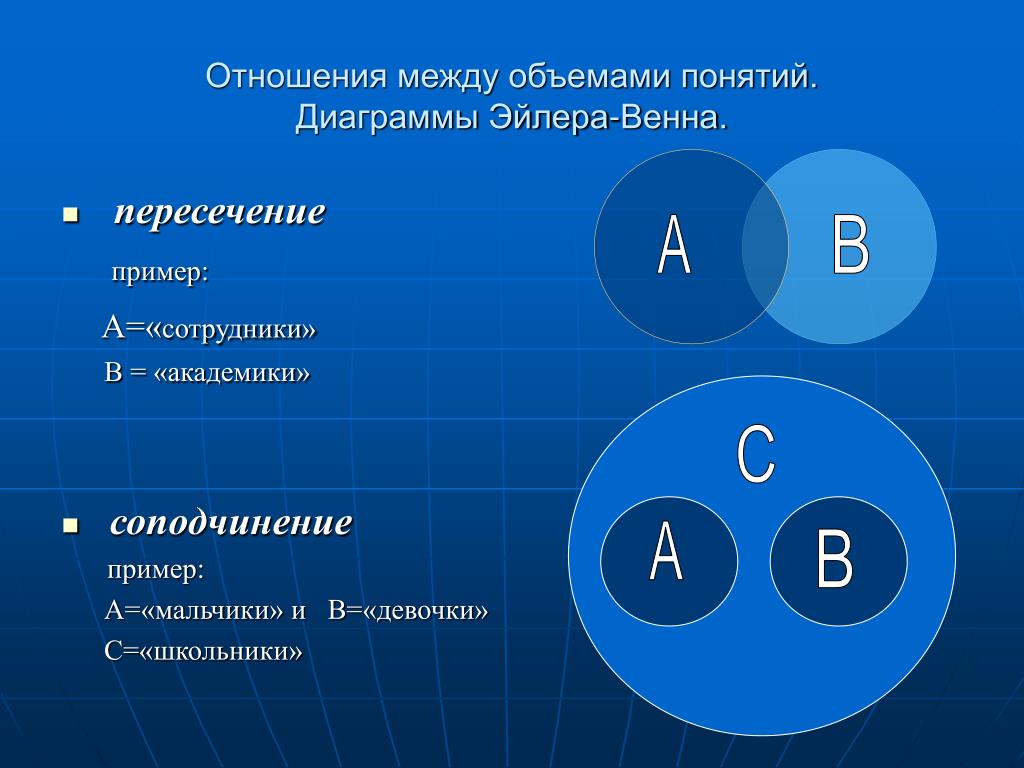
Просмотр учетных записей, вошедших в систему
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.
- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т.

 Сколько туристов не владеют ни одним языком?
Сколько туристов не владеют ни одним языком?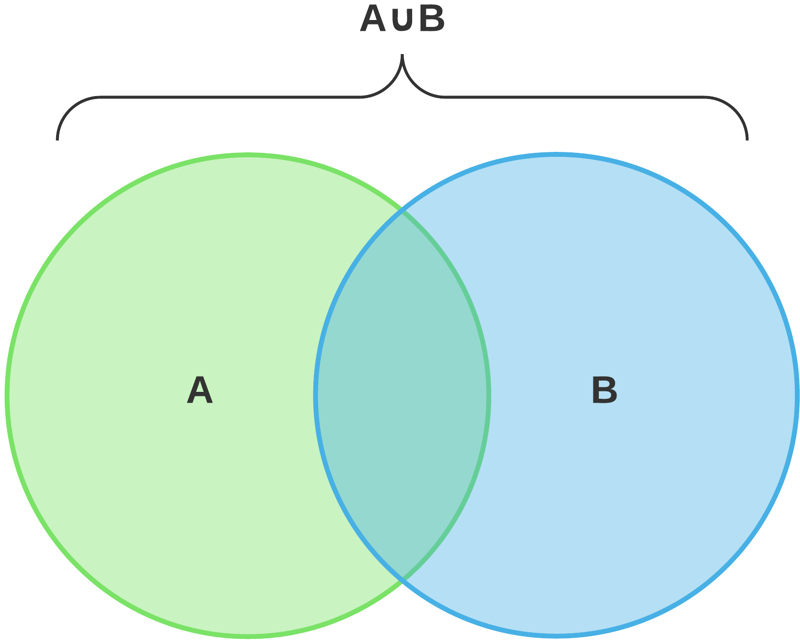 Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
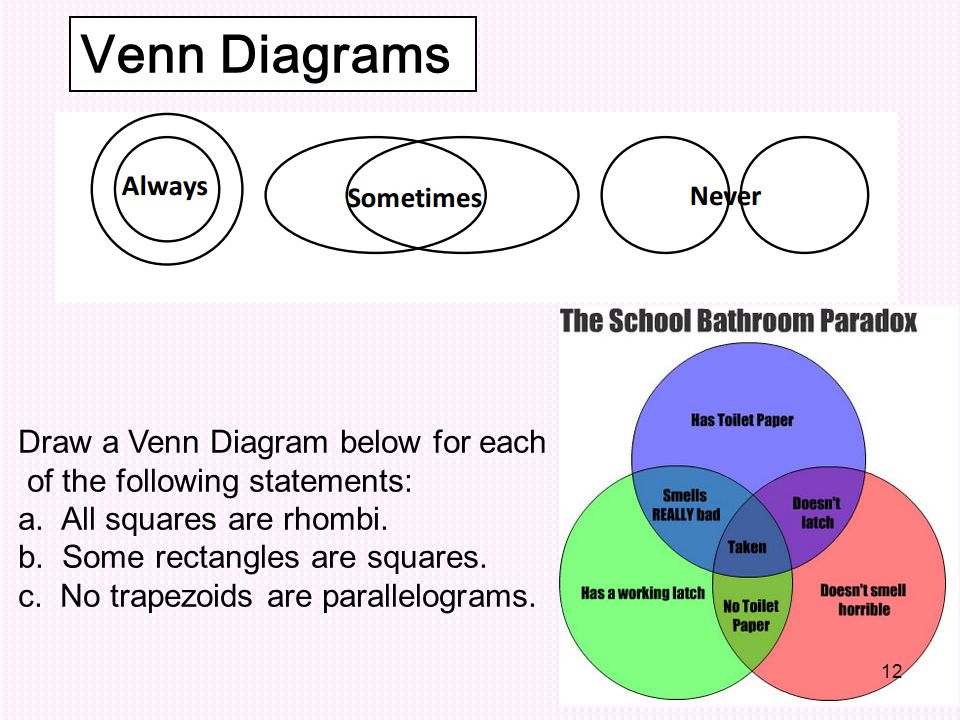 Среди них 20 человек моложе 30 лет и 15 человек старше 20 лет. Может ли так быть? Если может, то в каком случае?
Среди них 20 человек моложе 30 лет и 15 человек старше 20 лет. Может ли так быть? Если может, то в каком случае?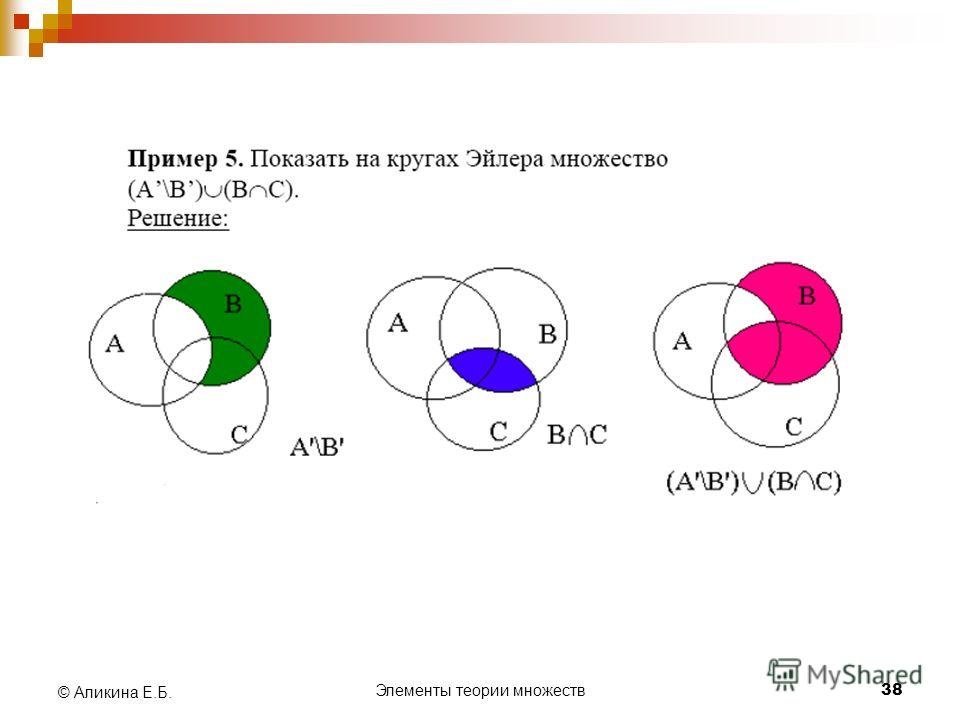 Сколько человек побывали в театре, кино и цирке одновременно?
Сколько человек побывали в театре, кино и цирке одновременно?  При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.
При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.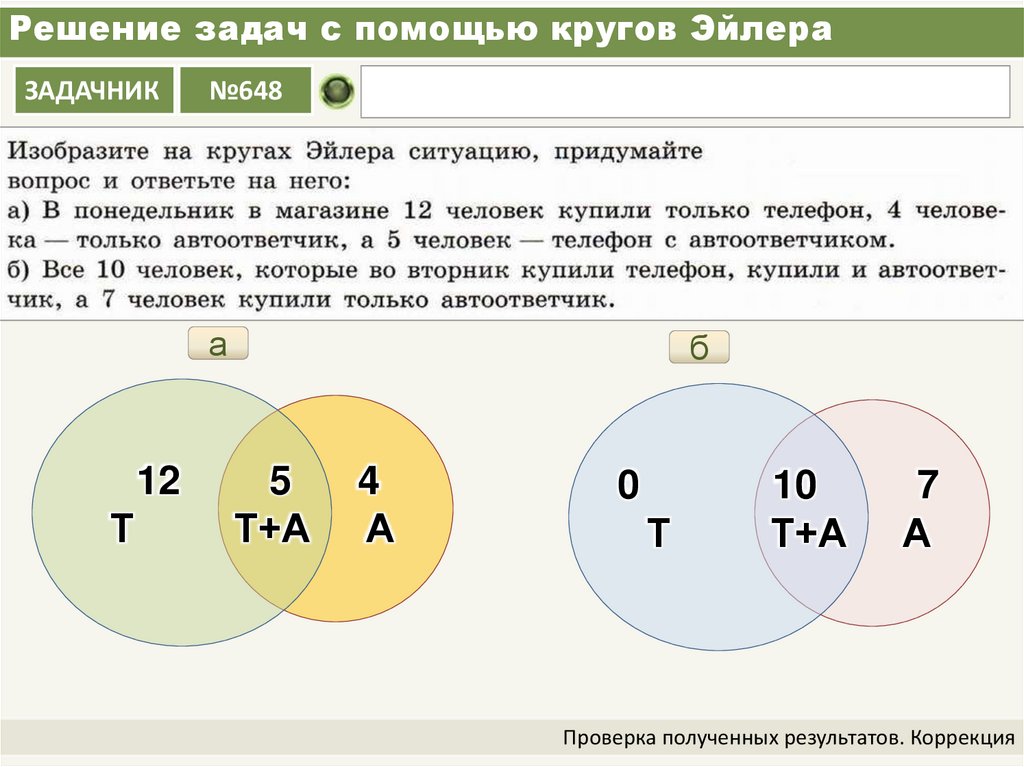
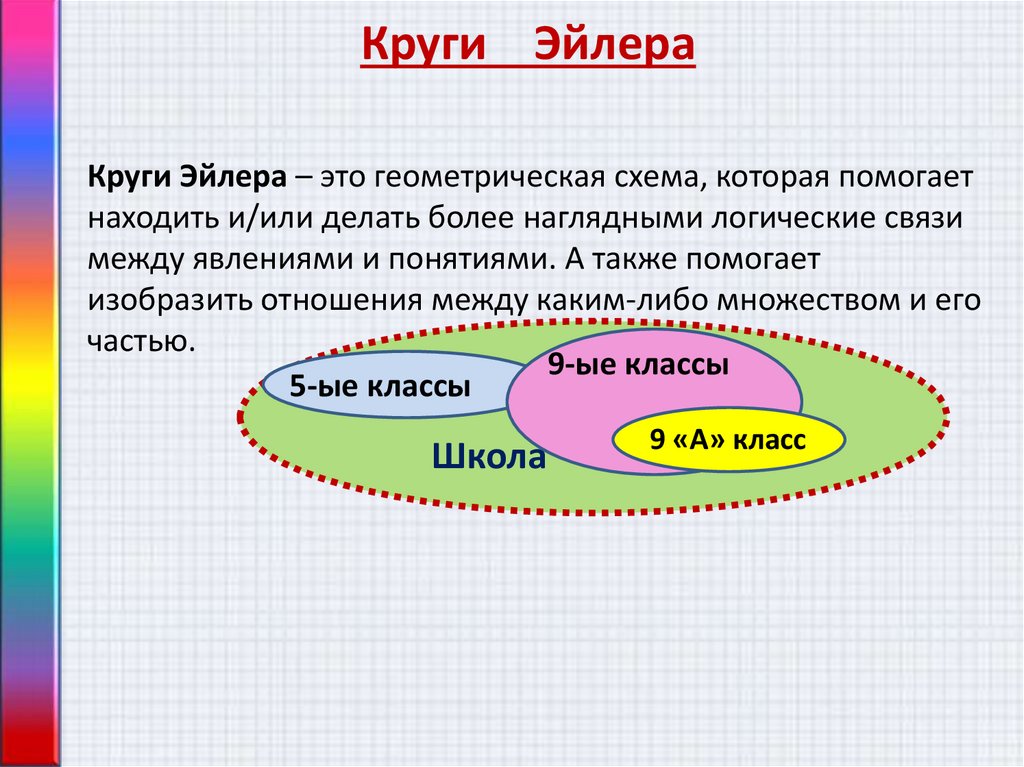

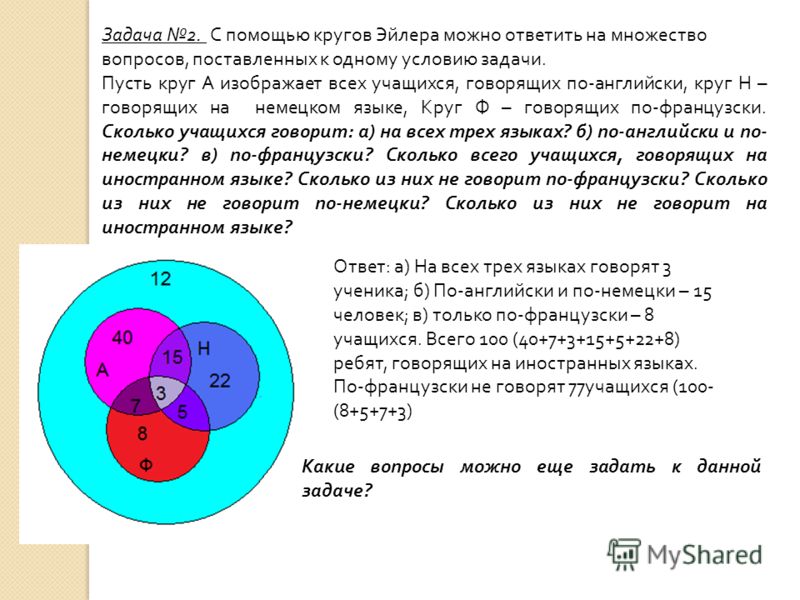
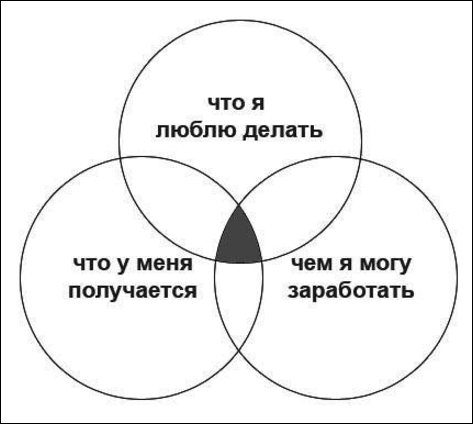 Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
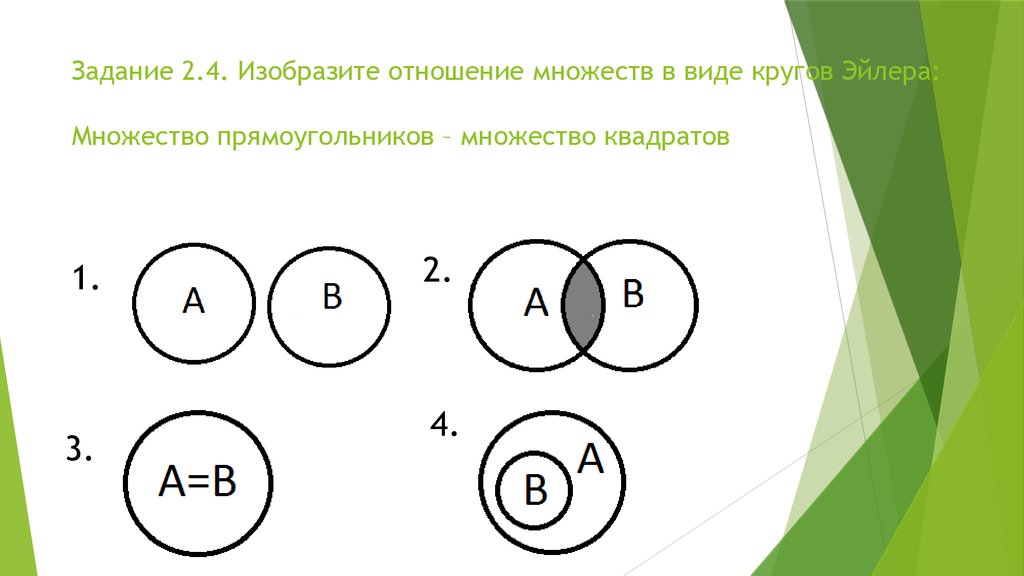
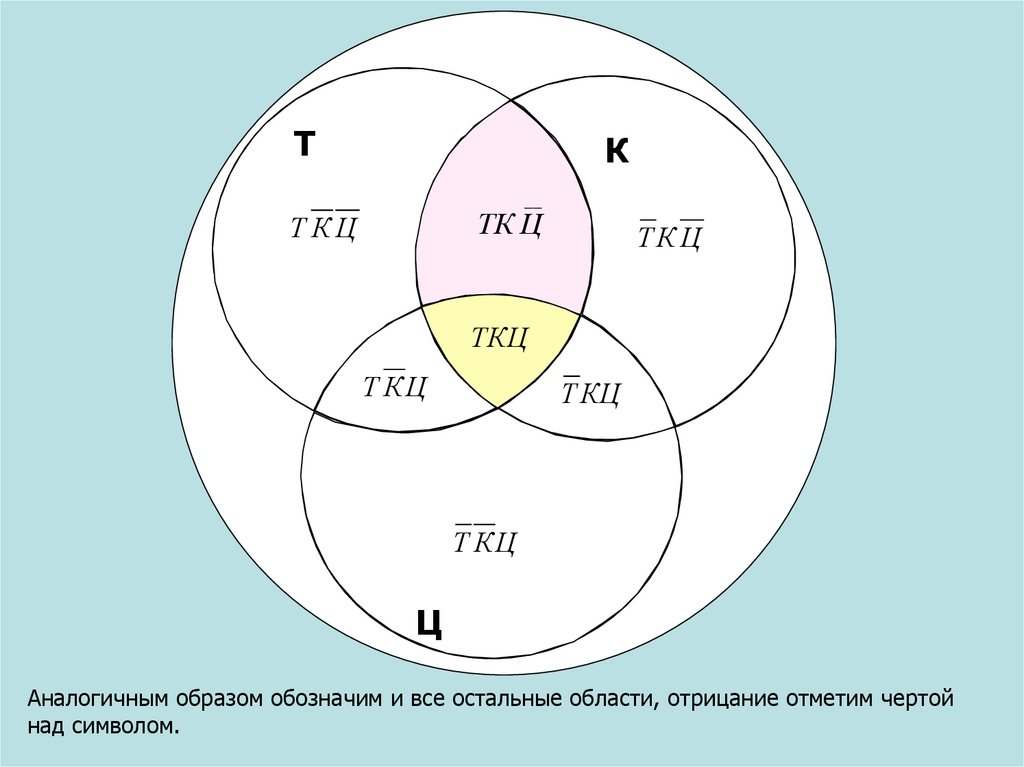
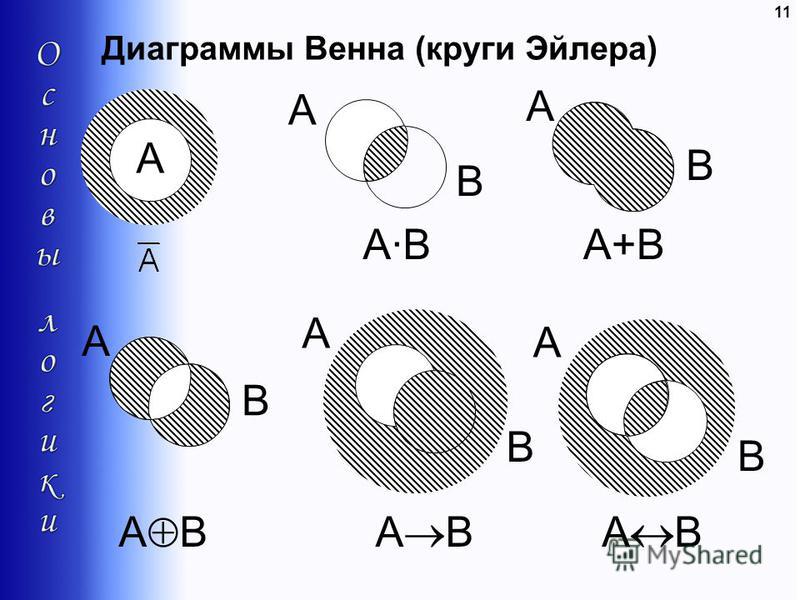
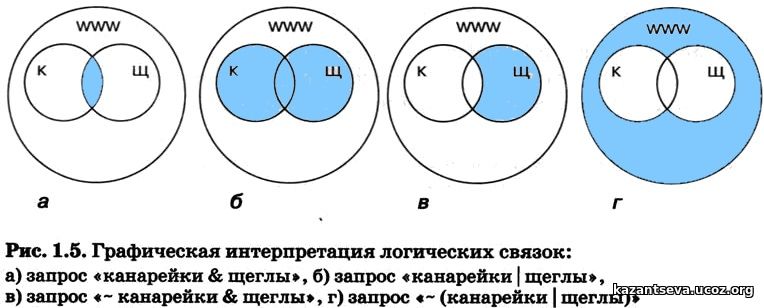 Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.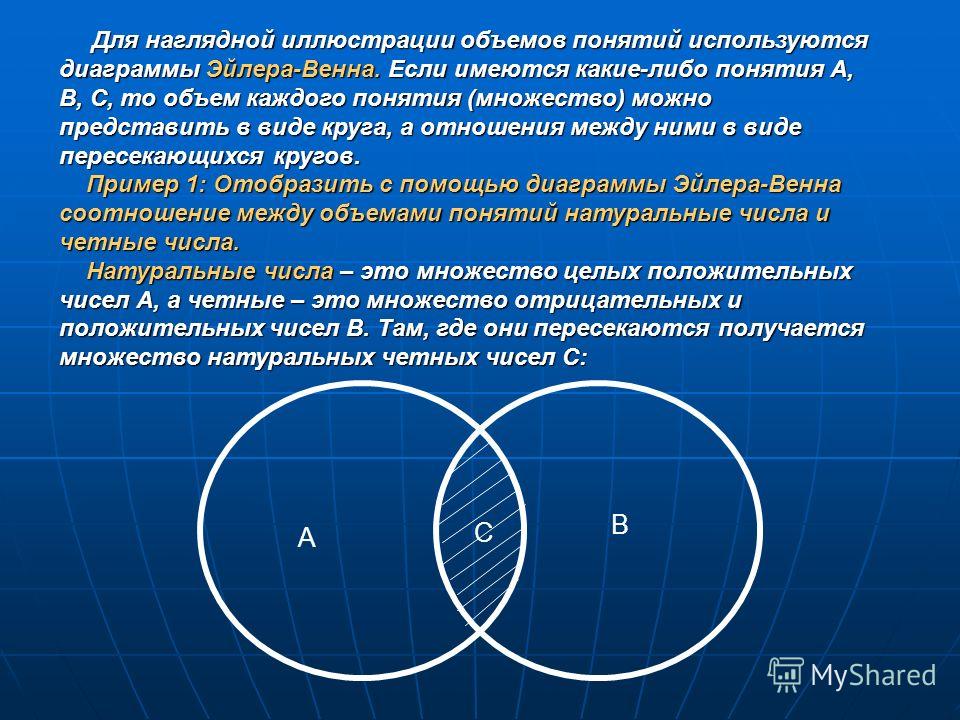
 N → W
N → W 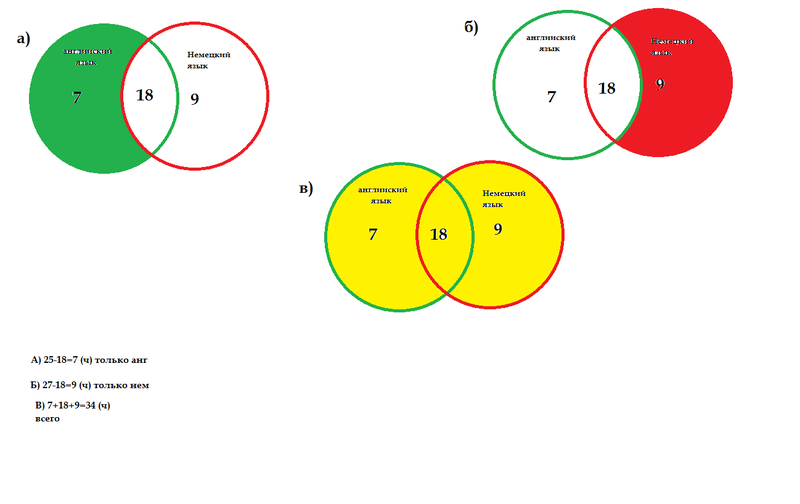 Отсюда находим Y = 3400-2100 = 1300.
Отсюда находим Y = 3400-2100 = 1300.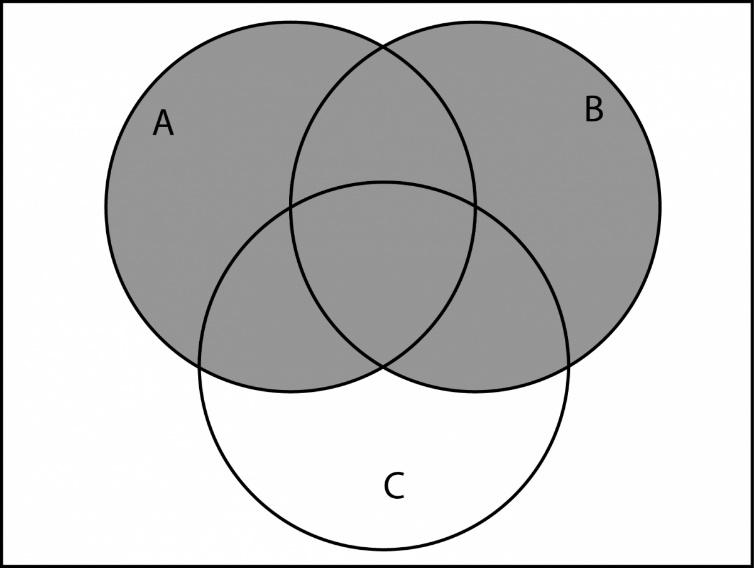 посещал мероприятия.
посещал мероприятия.