Синус суммы углов формула. Основные тригонометрические тождества, их формулировки и вывод
Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.
В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.
Навигация по странице.
Основные тригонометрические тождества
Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.
Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .
Формулы приведения
Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.
Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .
Формулы сложения
Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов.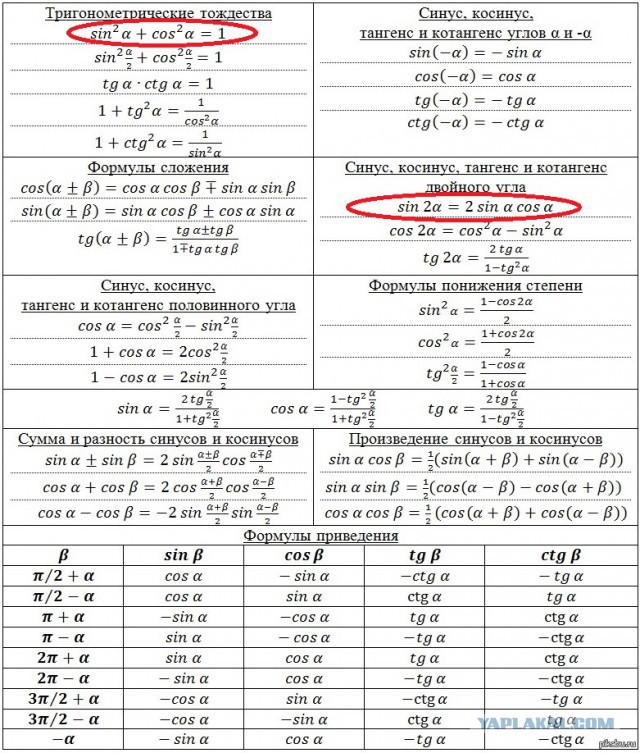
Формулы двойного, тройного и т.д. угла
Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.
Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .
Формулы половинного угла
Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.
Их вывод и примеры применения можно посмотреть в статье .
Формулы понижения степени
Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Иными словами, они позволяют понижать степени тригонометрических функций до первой.
Формулы суммы и разности тригонометрических функций
Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.
Формулы произведения синусов, косинусов и синуса на косинус
Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .
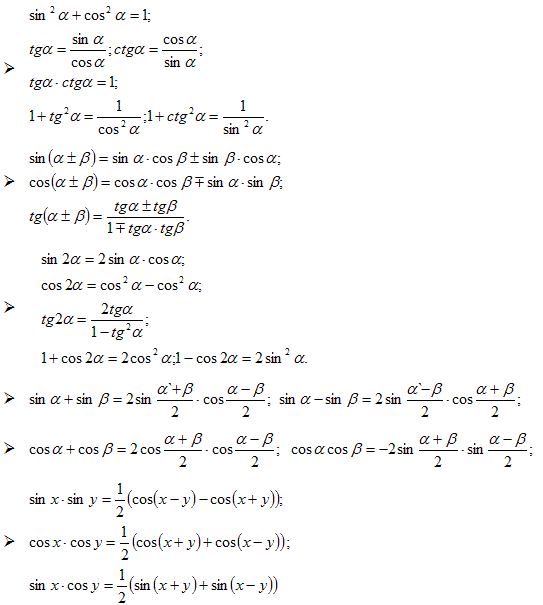 учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
В этой статье мы всесторонне рассмотрим . Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую.
Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Навигация по странице.
Связь между синусом и косинусом одного угла
Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида . Объяснение этому факту достаточно простое: равенства получаются из основного тригонометрического тождества после деления обеих его частей на и соответственно, а равенства и следуют из определений синуса, косинуса, тангенса и котангенса . Подробнее об этом поговорим в следующих пунктах.
То есть, особый интерес представляет именно равенство , которому и дали название основного тригонометрического тождества.
Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его.
Основное тригонометрическое тождество очень часто используется при преобразовании тригонометрических выражений . Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей.
Тангенс и котангенс через синус и косинус
Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида и сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть, , а котангенс есть отношение абсциссы к ординате, то есть, .
Благодаря такой очевидности тождеств и часто определения тангенса и котангенса дают не через отношение абсциссы и ординаты, а через отношение синуса и косинуса. Так тангенсом угла называют отношение синуса к косинусу этого угла, а котангенсом – отношение косинуса к синусу.
В заключение этого пункта следует отметить, что тождества и имеют место для всех таких углов , при которых входящие в них тригонометрические функции имеют смысл.
Связь между тангенсом и котангенсом
Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида . Понятно, что оно имеет место для любых углов , отличных от , в противном случае либо тангенс, либо котангенс не определены.
Доказательство формулы очень просто. По определению и , откуда . Можно было доказательство провести и немного иначе. Так как и , то .
Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть .
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Yandex.RTB R-A-339285-1
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Я не буду убеждать вас не писать шпаргалки. Пишите! В том числе, и шпаргалки по тригонометрии. Позже я планирую объяснить, зачем нужны шпаргалки и чем шпаргалки полезны. А здесь — информация, как не учить, но запомнить некоторые тригонометрические формулы. Итак — тригонометрия без шпаргалки!Используем ассоциации для запоминания.
1. Формулы сложения:
косинусы всегда «ходят парами»: косинус-косинус, синус-синус. И еще: косинусы — «неадекватны». Им «все не так», поэтому они знаки меняют: «-» на «+», и наоборот.
Синусы — «смешиваются» : синус-косинус, косинус-синус.
2. Формулы суммы и разности:
косинусы всегда «ходят парами». Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
Синусы — «смешиваются» :
3. Формулы преобразования произведения в сумму и разность.
Когда мы получаем пару косинусов? Когда складываем косинусы. Поэтому
Когда мы получаем пару синусов? При вычитании косинусов. Отсюда:
«Смешение» получаем как при сложении, так и при вычитании синусов. Что приятнее: складывать или вычитать? Правильно, складывать. И для формулы берут сложение:
В первой и в третьей формуле в скобках — сумма. От перестановки мест слагаемых сумма не меняется. Принципиален порядок только для второй формулы. Но, чтобы не путаться, для простоты запоминания мы во всех трех формулах в первых скобках берем разность
а во вторых — сумму
Шпаргалки в кармане дают спокойствие: если забыл формулу, можно списать. А дают уверенность: если воспользоваться шпаргалкой не удастся, формулы можно легко вспомнить.
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей.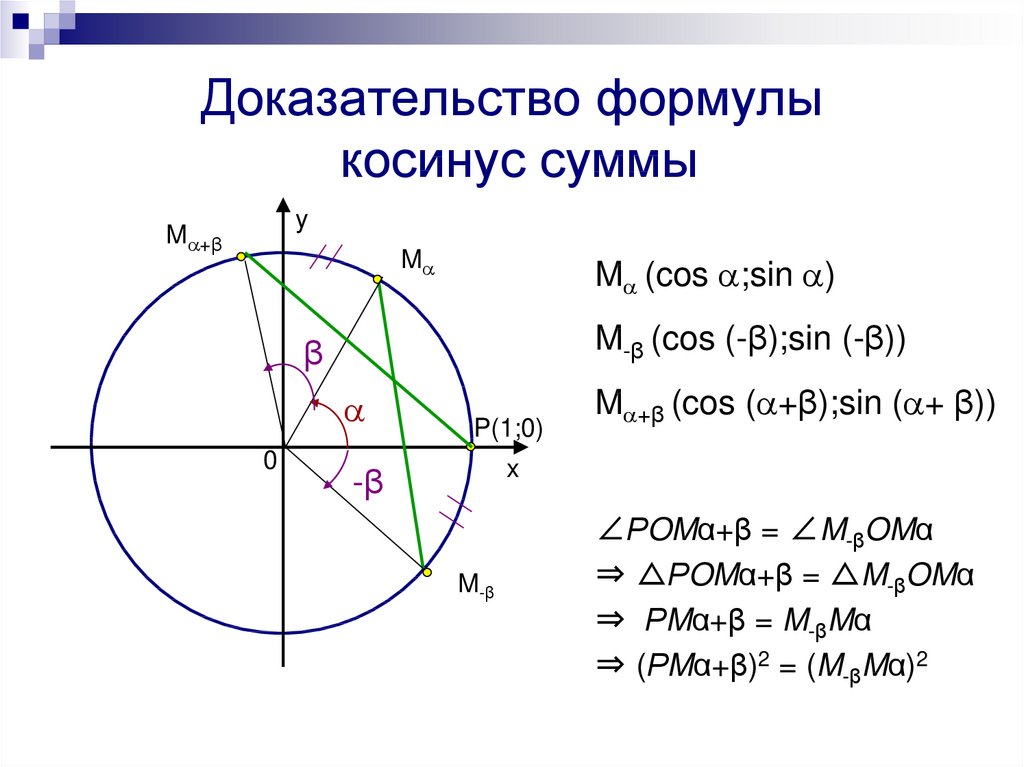 Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу. То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.
Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Тригонометрические функции, формулы и графики. sin, cos, tg, ctg….Значения тригонометрических функций. Формулы приведения тригонометрических функций. Тригонометрические тождества. / / Основные тригонометрические формулы. Формулы приведения тригонометрических функций. Тригонометрические тождества. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.ru Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator Free xml sitemap generator | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
что такое? Как найти синус, косинус и тангенс
Косинус суммы и разности двух углов
В этом параграфе будут доказаны следующие две формулы:
cos (α + β) = cos α cos β — sin α sin β, (1)
cos (α — β) = cos α cos β + sin α sin β. (2)
Косинус суммы (разности) двух углов равен произведению косинусов этих углов минус (плюс) произведение синусов этих углов.
Нам удобнее будет начать с доказательства формулы (2). Для простоты изложения предположим сначала, что углы α и β удовлетворяют следующим условиям:
1) каждый из этих углов неотрицателен и меньше 2π :
0 α 2π, 0 β
2) α > β .
Пусть положительная часть оси 0х является общей начальной стороной углов α и β .
Конечные стороны этих углов обозначим соответственно через 0А и 0В. Очевидно, что угол α — β можно рассматривать как такой угол, на который нужно повернуть луч 0В вокруг точки 0 против часовой стрелки, чтобы его направление совпало с направлением луча 0А.
На лучах 0А и 0В отметим точки М и N, отстоящие от начала координат 0 на расстоянии 1, так что 0М = 0N = 1.
В системе координат х0у точка М имеет координаты (cos α, sin α ), а точка N — координаты (cos β , sin β ). Поэтому квадрат расстояния между ними равен:
d 1 2 = (cos α — cos β) 2 + (sin α — sin β) 2 = cos 2 α — 2 cos α cos β +
+ cos 2 β + sin 2 α — 2sin α sin β + sin 2 β = .
При вычислениях мы воспользовались тождеством
sin 2 φ + cos 2 φ = 1 .
Теперь рассмотрим другую систему координат В0С, которая получается путем поворота осей 0х и 0у вокруг точки 0 против часовой стрелки на угол β .
В этой системе координат точка М имеет координаты (cos (α — β ), sin (α — β )), а точка N -координаты (1,0). Поэтому квадрат расстояния между ними равен:
d 2 2 = 2 + 2 = cos 2 (α — β) — 2 cos (α — β) + 1 +
+ sin 2 (α — β) = 2 .
Но расстояние между точками М и N не зависит от того, относительно какой системы координат мы рассматриваем эти точки. Поэтому
Поэтому
d 1 2 = d 2 2
2 (1 — cos α cos β — sin α sin β) = 2 .
Отсюда и вытекает формула (2).
Теперь следует вспомнить о тех двух ограничениях, которые мы наложили для простоты изложения на углы α и β .
Требование, чтобы каждый из углов α и β был неотрицательным, на самом деле не существенно. Ведь к любому из этих углов можно прибавить угол, кратный 2я, что никак не отразится на справедливости формулы (2). Точно так же от каждого из данных углов можно вычесть угол, кратный 2π . Поэтому можно считать, что 0 α 2π , 0 β 2π .
Не существенным оказывается и условие α > β . Действительно, если α β , то β >α ; поэтому, учитывая четность функции cos х , получаем:
cos (α — β) = cos (β — α) = cos β cos α + sin β sin α,
что по существу совпадает с формулой (2). Таким образом, формула
cos (α — β) = cos α cos β + sin α sin β
верна для любых углов α и β . В частности, заменяя в ней β на —β и учитывая, что функция cos х является четной, а функция sin х нечетной, получаем:
В частности, заменяя в ней β на —β и учитывая, что функция cos х является четной, а функция sin х нечетной, получаем:
cos (α + β) = cos [α — (- β)] =cos α cos (-β) + sin α sin (-β) =
= cos α cos β — sin α sin β,
что доказывает формулу (1).
Итак, формулы (1) и (2) доказаны.
Примеры.
1) cos 75° = cos (30° + 45°) = cos 30° cos 45°-sin 30°-sin 45° =
2) cos 15° = cos (45° — 30°) = cos 45° cos 30° + sin 45° sin 30° =
Упражнения
1 . Вычислить, не пользуясь тригонометрическими таблицами:
a) cos 17° cos 43° — sin 17° sin 43°;
б) sin 3° sin 42° — cos 39° cos 42°;
в) cos 29° cos 74° + sin 29° sin 74°;
г) sin 97° sin 37° + cos 37° cos 97°;
д) cos 3π / 8 cos π / 8 + sin 3π / 8 sin π / 8 ;
e) sin 3π / 5 sin 7π / 5 — cos 3π / 5 cos 7π / 5 .
2.Упростить выражения:
a). cos (α + π / 3 ) + cos (π / 3 — α ) .
cos (α + π / 3 ) + cos (π / 3 — α ) .
б). cos (36° + α ) cos (24° — α ) + sin (36° + α ) sin (α — 24°).
в). sin (π / 4 — α ) sin (π / 4 + α ) — cos (π / 4 + α ) cos (π / 4 — α )
г) cos 2α + tg α sin 2α .
3 . Вычислить :
a) cos (α — β) , если
cos α = — 2 / 5 , sin β = — 5 / 13 ;
90° α β
б) cos (α + π / 6), если cos α = 0,6;
3π / 2 α
4 . Найти cos (α + β) и cos (α — β) ,если известно, что sin α = 7 / 25 , cos β = — 5 / 13 и оба угла (α и β ) оканчиваются в одной и той же четверти.
5 .Вычислить:
а). cos [ arcsin 1 / 3 + arccos 2 / 3 ]
б). cos [ arcsin 1 / 3 — arccos (- 2 / 3)] .
в). cos [ arctg 1 / 2 + arccos (- 2) ]
Формулы суммы и разности синусов и косинусов для двух углов α и β позволяют перейти от суммы указанных углов к произведению углов α + β 2 и α — β 2 . Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Сразу отметим, что не стоит путать формулы суммы и разности синусов и косинусов с формулами синусов и косинусов суммы и разности. Ниже мы перечислим эти формулы, приведем их вывод и покажем примеры применения для конкретных задач.
Yandex.RTB R-A-339285-1
Формулы суммы и разности синусов и косинусов
Запишем, как выглядят формулы суммы и разности для синусов и для косинусов
Формулы суммы и разности для синусов
sin α + sin β = 2 sin α + β 2 cos α — β 2 sin α — sin β = 2 sin α — β 2 cos α + β 2
Формулы суммы и разности для косинусов
cos α + cos β = 2 cos α + β 2 cos α — β 2 cos α — cos β = — 2 sin α + β 2 cos α — β 2 , cos α — cos β = 2 sin α + β 2 · β — α 2
Данные формулы справедливы для любых углов α и β . Углы α + β 2 и α — β 2 называются соответственно полусуммой и полуразностью углов альфа и бета. Дадим формулировку для каждой формулы.
Определения формул сумм и разности синусов и косинусов
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус полуразности.
Разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус полусуммы.
Сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы и косинуса полуразности этих углов.
Разность косинусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразности этих углов, взятому с отрицательным знаком.
Вывод формул суммы и разности синусов и косинусов
Для вывода формул суммы и разности синуса и косинуса двух углов используются формулы сложения. Приведем их ниже
sin (α + β) = sin α · cos β + cos α · sin β sin (α — β) = sin α · cos β — cos α · sin β cos (α + β) = cos α · cos β — sin α · sin β cos (α — β) = cos α · cos β + sin α · sin β
Также представим сами углы в виде суммы полусумм и полуразностей.
α = α + β 2 + α — β 2 = α 2 + β 2 + α 2 — β 2 β = α + β 2 — α — β 2 = α 2 + β 2 — α 2 + β 2
Переходим непосредственно к выводу формул суммы и разности для sin и cos.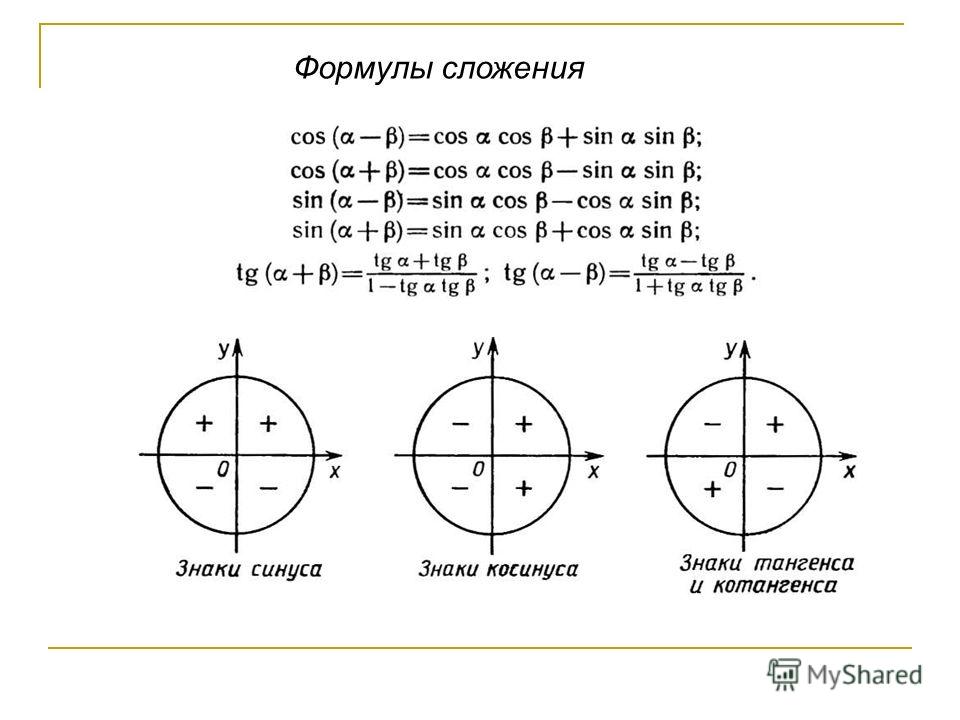
Вывод формулы суммы синусов
В сумме sin α + sin β заменим α и β на выражения для этих углов, приведенные выше. Получим
sin α + sin β = sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2
Теперь к первому выражению применяем формулу сложения, а ко второму — формулу синуса разностей углов (см. формулы выше)
sin α + β 2 + α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 sin α + β 2 + α — β 2 + sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 Раскроем скобки, приведем подобные слагаемые и получим искомую формулу
sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 + sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α + β 2 cos α — β 2
Действия по выводу остальных формул аналогичны.
Вывод формулы разности синусов
sin α — sin β = sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 sin α + β 2 + α — β 2 — sin α + β 2 — α — β 2 = sin α + β 2 cos α — β 2 + cos α + β 2 sin α — β 2 — sin α + β 2 cos α — β 2 — cos α + β 2 sin α — β 2 = = 2 sin α — β 2 cos α + β 2
Вывод формулы суммы косинусов
cos α + cos β = cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 + cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 + cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = 2 cos α + β 2 cos α — β 2
Вывод формулы разности косинусов
cos α — cos β = cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 cos α + β 2 + α — β 2 — cos α + β 2 — α — β 2 = cos α + β 2 cos α — β 2 — sin α + β 2 sin α — β 2 — cos α + β 2 cos α — β 2 + sin α + β 2 sin α — β 2 = = — 2 sin α + β 2 sin α — β 2
Примеры решения практических задач
Для начала, сделаем проверку одной из формул, подставив в нее конкретные значения углов. Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пусть α = π 2 , β = π 6 . Вычислим значение суммы синусов этих углов. Сначала воспользуемся таблицей основных значений тригонометрических функций, а затем применим формулу для суммы синусов.
Пример 1. Проверка формулы суммы синусов двух углов
α = π 2 , β = π 6 sin π 2 + sin π 6 = 1 + 1 2 = 3 2 sin π 2 + sin π 6 = 2 sin π 2 + π 6 2 cos π 2 — π 6 2 = 2 sin π 3 cos π 6 = 2 · 3 2 · 3 2 = 3 2
Рассмотрим теперь случай, когда значения углов отличаются от основных значений, представленных в таблице. Пусть α = 165 ° , β = 75 ° . Вычислим значение разности синусов этих углов.
Пример 2. Применение формулы разности синусов
α = 165 ° , β = 75 ° sin α — sin β = sin 165 ° — sin 75 ° sin 165 — sin 75 = 2 · sin 165 ° — sin 75 ° 2 cos 165 ° + sin 75 ° 2 = = 2 · sin 45 ° · cos 120 ° = 2 · 2 2 · — 1 2 = 2 2
С помощью формул суммы и разности синусов и косинусов можно перейти от суммы или разности к произведению тригонометрических функций. Часто эти формулы называют формулами перехода от суммы к произведению. Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Формулы суммы и разности синусов и косинусов широко используются при решении тригонометрических уравнений и при преобразовании тригонометрических выражений.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Одним из разделов математики, с которыми школьники справляются с наибольшими трудностями, является тригонометрия. Неудивительно: для того чтобы свободно овладеть этой областью знаний, требуется наличие пространственного мышления, умение находить синусы, косинусы, тангенсы, котангенсы по формулам, упрощать выражения, уметь применять в вычислениях число пи. Помимо этого, нужно уметь применять тригонометрию при доказательстве теорем, а это требует либо развитой математической памяти, либо умения выводить непростые логические цепочки.
Истоки тригонометрии
Знакомство с данной наукой следует начать с определения синуса, косинуса и тангенса угла, однако прежде необходимо разобраться, чем вообще занимается тригонометрия.
Исторически главным объектом исследования данного раздела математической науки были прямоугольные треугольники. Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Начальный этап
Первоначально люди рассуждали о взаимоотношении углов и сторон исключительно на примере прямоугольных треугольников. Затем были открыты особые формулы, позволившие расширить границы употребления в повседневной жизни данного раздела математики.
Изучение тригонометрии в школе сегодня начинается с прямоугольных треугольников, после чего полученные знания используются учениками в физике и решении абстрактных тригонометрических уравнений, работа с которыми начинается в старших классах.
Сферическая тригонометрия
Позже, когда наука вышла на следующий уровень развития, формулы с синусом, косинусом, тангенсом, котангенсом стали использоваться в сферической геометрии, где действуют иные правила, а сумма углов в треугольнике всегда больше 180 градусов. Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Возьмите глобус и нитку. Приложите нитку к двум любым точкам на глобусе, чтобы она оказалась натянутой. Обратите внимание — она обрела форму дуги. С такими формами и имеет дело сферическая геометрия, применяющаяся в геодезии, астрономии и других теоретических и прикладных областях.
Прямоугольный треугольник
Немного узнав про способы применения тригонометрии, вернемся к базовой тригонометрии, чтобы в дальнейшем разобраться, что такое синус, косинус, тангенс, какие расчёты можно с их помощью выполнять и какие формулы при этом использовать.
Первым делом необходимо уяснить понятия, относящиеся к прямоугольному треугольнику. Во-первых, гипотенуза — это сторона, лежащая напротив угла в 90 градусов. Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Например, если две стороны равны 3 и 4 сантиметрам соответственно, длина гипотенузы составит 5 сантиметров. Кстати, об этом знали ещё древние египтяне около четырех с половиной тысяч лет назад.
Две оставшиеся стороны, которые образуют прямой угол, носят название катетов. Кроме того, надо помнить, что сумма углов в треугольнике в прямоугольной системе координат равняется 180 градусам.
Определение
Наконец, твердо понимая геометрическую базу, можно обратиться к определению синуса, косинуса и тангенса угла.
Синусом угла называется отношение противолежащего катета (т. е. стороны, располагающейся напротив нужного угла) к гипотенузе. Косинусом угла называется отношение прилежащего катета к гипотенузе.
Запомните, что ни синус, ни косинус не может быть больше единицы! Почему? Потому что гипотенуза — это по умолчанию самая длинная Каким бы длинным ни был катет, он будет короче гипотенузы, а значит, их отношение всегда будет меньше единицы. Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Наконец, тангенсом угла называется отношение противолежащей стороны к прилежащей. Тот же самый результат даст деление синуса на косинус. Посмотрите: в соответствии с формулой мы делим длину стороны на гипотенузу, после чего делим на длину второй стороны и умножаем на гипотенузу. Таким образом, мы получаем то же самое соотношение, что и в определении тангенса.
Котангенс, соответственно, представляет собой отношение прилежащей к углу стороны к противолежащей. Тот же результат мы получим, разделив единицу на тангенс.
Итак, мы рассмотрели определения, что такое синус, косинус, тангенс и котангенс, и можем заняться формулами.
Простейшие формулы
В тригонометрии не обойтись без формул — как найти синус, косинус, тангенс, котангенс без них? А ведь именно это требуется при решении задач.
Первая формула, которую необходимо знать, начиная изучать тригонометрию, говорит о том, что сумма квадратов синуса и косинуса угла равна единице. Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Многие учащиеся не могут запомнить вторую формулу, также очень популярную при решении школьных задач: сумма единицы и квадрата тангенса угла равна единице, деленной на квадрат косинуса угла. Присмотритесь: ведь это то же самое утверждение, что и в первой формуле, только обе стороны тождества были поделены на квадрат косинуса. Выходит, простая математическая операция делает тригонометрическую формулу совершенно неузнаваемой. Помните: зная, что такое синус, косинус, тангенс и котангенс, правила преобразования и несколько базовых формул вы в любой момент сможете сами вывести требуемые более сложные формулы на листе бумаги.
Формулы двойного угла и сложения аргументов
Ещё две формулы, которые требуется выучить, связаны со значениями синуса и косинуса при сумме и разности углов. Они представлены на рисунке ниже. Обратите внимание, что в первом случае оба раза перемножается синус и косинус, а во втором складывается попарное произведение синуса и косинуса.
Также существуют формулы, связанные с аргументами в виде двойного угла. Они полностью выводятся из предыдущих — в качестве тренировки попробуйте получить их самостоятельно, приняв угол альфа равным углу бета.
Наконец, обратите внимание, что формулы двойного угла можно преобразовать так, чтобы понизить степень синуса, косинуса, тангенса альфа.
Теоремы
Двумя основными теоремами в базовой тригонометрии являются теорема синусов и теорема косинусов. С помощью этих теорем вы легко сможете понять, как найти синус, косинус и тангенс, а значит, и площадь фигуры, и величину каждой стороны и т. д.
Теорема синусов утверждает, что в результате деления длины каждой из сторон треугольника на величину противолежащего угла мы получим одинаковое число. Более того, это число будет равно двум радиусам описанной окружности, т. е. окружности, содержащей все точки данного треугольника.
Теорема косинусов обобщает теорему Пифагора, проецируя её на любые треугольники. Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Ошибки по невнимательности
Даже зная, что такое синус, косинус и тангенс, легко совершить ошибку из-за рассеянности внимания или ошибки в простейших расчётах. Чтобы избежать таких ошибок, ознакомимся с наиболее популярными из них.
Во-первых, не следует преобразовывать обыкновенные дроби в десятичные до получения окончательного результата — можно и ответ оставить в виде обыкновенной дроби, если в условии не оговорено обратное. Такое преобразование нельзя назвать ошибкой, однако следует помнить, что на каждом этапе задачи могут появиться новые корни, которые по задумке автора должны сократиться. В этом случае вы напрасно потратите время на излишние математические операции. Особенно это актуально для таких значений, как корень из трёх или из двух, ведь они встречаются в задачах на каждом шагу.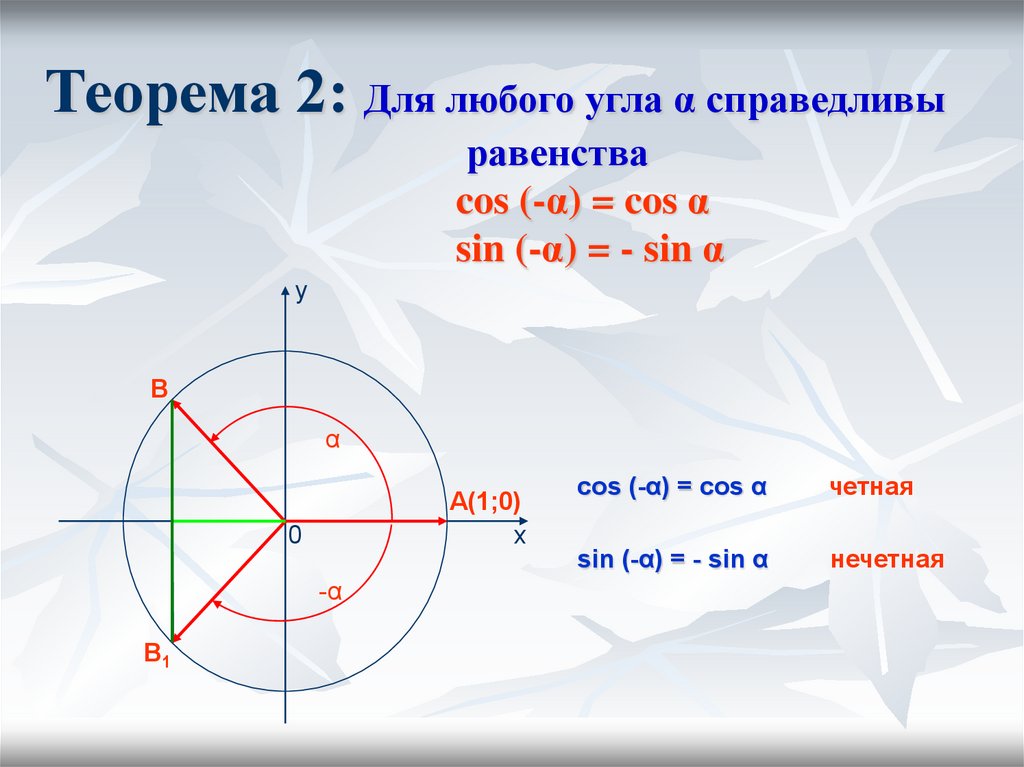 То же касается округлений «некрасивых» чисел.
То же касается округлений «некрасивых» чисел.
Далее, обратите внимание, что к любому треугольнику применима теорема косинусов, но не теорема Пифагора! Если вы по ошибке забудете вычесть удвоенное произведение сторон, умноженное на косинус угла между ними, вы не только получите совершенно неверный результат, но и продемонстрируете полное непонимание предмета. Это хуже, чем ошибка по невнимательности.
В-третьих, не путайте значения для углов в 30 и 60 градусов для синусов, косинусов, тангенсов, котангенсов. Запомните эти значения, ведь синус 30 градусов равен косинусу 60, и наоборот. Их легко перепутать, вследствие чего вы неизбежно получите ошибочный результат.
Применение
Многие ученики не спешат приступать к изучению тригонометрии, поскольку не понимают её прикладного смысла. Что такое синус, косинус, тангенс для инженера или астронома? Это понятия, благодаря которым можно вычислить расстояние до далёких звёзд, предсказать падение метеорита, отправить исследовательский зонд на другую планету.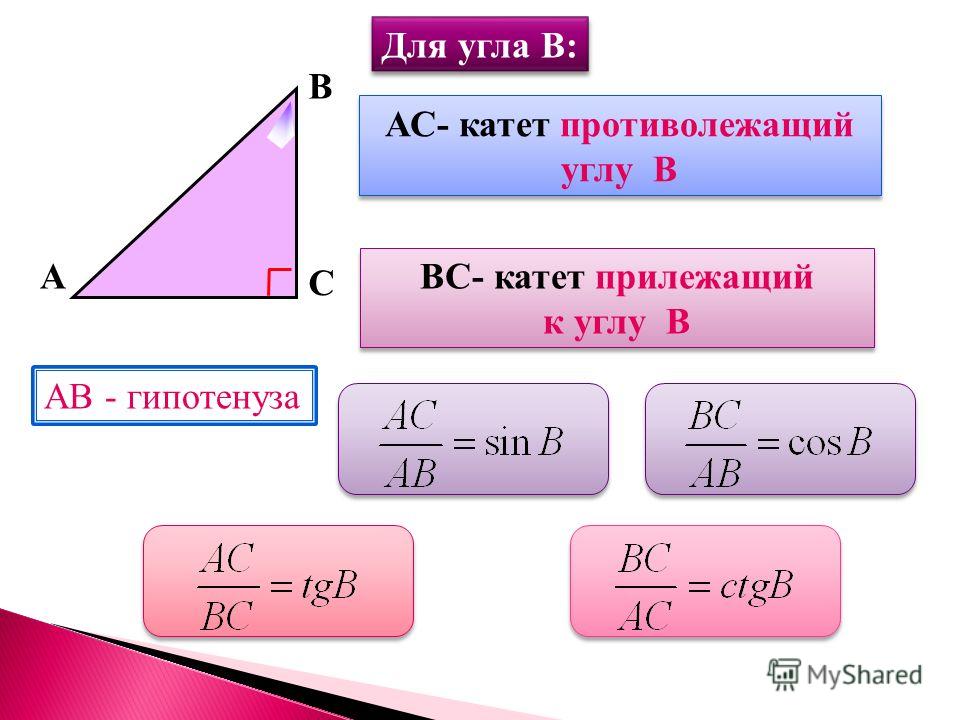 Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
В заключение
Итак, вы синус, косинус, тангенс. Вы можете использовать их в расчётах и успешно решать школьные задачи.
Вся суть тригонометрии сводится к тому, что по известным параметрам треугольника нужно вычислить неизвестные. Всего этих параметров шесть: длины трёх сторон и величины трёх углов. Всё различие в задачах заключается в том, что даются неодинаковые входные данные.
Как найти синус, косинус, тангенс исходя из известных длин катетов или гипотенузы, вы теперь знаете. Поскольку эти термины обозначают не что иное, как отношение, а отношение — это дробь, главной целью тригонометрической задачи становится нахождение корней обычного уравнения либо же системы уравнений. И здесь вам поможет обычная школьная математика.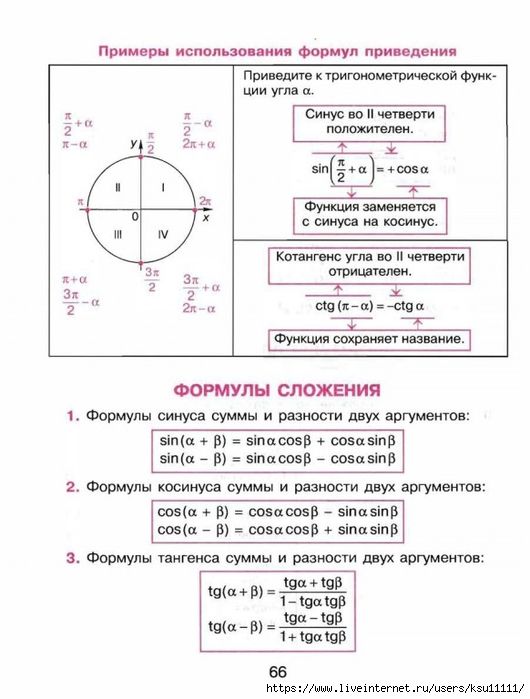
Варенье из бузины: польза и вред
Узнать встретимся ли мы. Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания
Определение, формула, примеры и доказательство
Позвольте мне нарисовать вам сценарий. Скажем, вы запускаете воздушного змея, который находится ровно в 9 футах от земли. Между тем, вы стоите в 12 футах от того места, где летит воздушный змей. Вам интересно узнать, под каким углом поднимается воздушный змей, которым вы управляете. Нарисовав это на бумаге, вы обнаружите, что эта задача создает треугольник, как показано ниже.
Реальная задача, Айша Амри — StudySmarter Originals
Итак, как бы вы определили этот угол? Вот тут-то и вступает в игру закон синусов! Мы действительно можем использовать эту концепцию, чтобы найти этот угол. Мало того, мы могли бы даже найти расстояние по диагонали между вами и воздушным змеем. Разве это не довольно изящно? В этой теме мы будем изучать закон синусов и наблюдать за его применением при решении треугольников.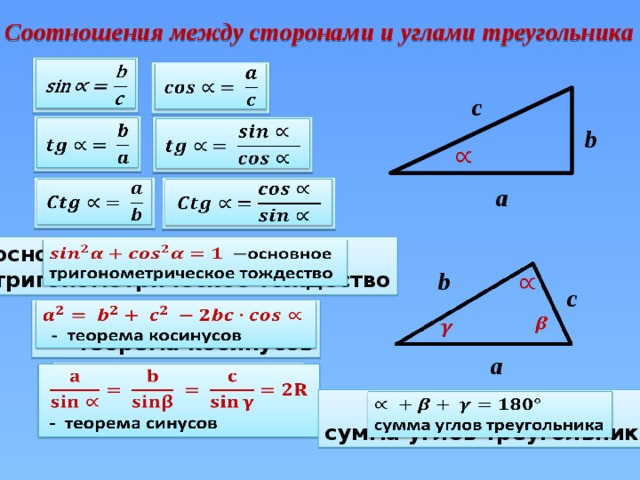
Закон синусов
Прежде чем обратиться к основной теме этой статьи, давайте сначала посмотрим на площадь треугольника в новом свете. Следуя этому, мы стремимся соединить идею закона синусов вместе с площадью треугольника и отношением синусов. Вы увидите, что эти концепции идеально сочетаются друг с другом! Начнем с того, что вспомним коэффициент синуса.
Резюме: коэффициент синусоиды
Ниже показан прямоугольный треугольник с углом θ .
Прямоугольный треугольник, Айша Амри — StudySmarter Originals
Напомним, что синус угла находится путем деления противоположного угла на гипотенузу. Это коэффициент синуса.
sinθ=противоположная гипотенуза
Нахождение площади треугольника
Кроме того, напомним, что площадь треугольника определяется формулой ниже.
Площадь△=12×высота×основание
Теперь, когда мы установили коэффициент синуса и площадь треугольника, давайте посмотрим на их соотношение. Рассмотрим треугольник ниже.
Рассмотрим треугольник ниже.
Площадь треугольника, Айша Амри — StudySmarter Originals
Мы можем найти площадь этого треугольника, зная его основание и высоту. Используя формулу, площадь треугольника выше определяется как:
Площадь△ABC=12ch.
Предположим, что высота здесь неизвестна. Однако нам все еще говорят найти площадь этого треугольника. Фактически, мы можем сделать это, зная угол A и длину стороны b. Чтобы определить высоту, мы будем использовать коэффициент синуса для угла A.
sinA=hb
Следовательно, h=bsinA.
Теперь, когда у нас есть выражение для h, подставим его в исходную формулу площади этого треугольника.
Area△ABC=12bcsinA
Точно так же мы можем найти площадь этого треугольника, используя другие варианты этой формулы. Теперь, почему могут быть разные способы выражения приведенной выше формулы? Обратите внимание, что предыдущая формула записана через угол A и стороны b и c. Скажем, у нас другой треугольник и нам не дают информацию о тех мерах. Вместо этого нам даны меры других сторон или углов. В этом случае нам нужно решить их по сопутствующей паре сторон и соответствующим углам. Эти два других варианта показаны ниже.
Скажем, у нас другой треугольник и нам не дают информацию о тех мерах. Вместо этого нам даны меры других сторон или углов. В этом случае нам нужно решить их по сопутствующей паре сторон и соответствующим углам. Эти два других варианта показаны ниже.
Area△ABC=12acsinBArea△ABC=12absinC
Давайте рассмотрим пример.
Найдите площадь треугольника, если A = 31 o , b = 22 см и c = 18 см.
Решение
Начнем с рисования этого треугольника.
Пример 1, Айша Амри — StudySmarter Originals
По данной формуле площадь этого треугольника определяется как: ⇒Площадь△ABC≈101,98 см2 (исправить до двух знаков после запятой)
Таким образом, площадь этого треугольника приблизительно равна 101,98 см 2 .
Закон синусов
Так откуда взялся закон синусов? Учитывая наши идеи выше, мы, по сути, создали основу для вывода закона синусов. Прежде всего, обратите внимание, что все приведенные выше формулы площади треугольника ABC описывают площадь одного и того же треугольника.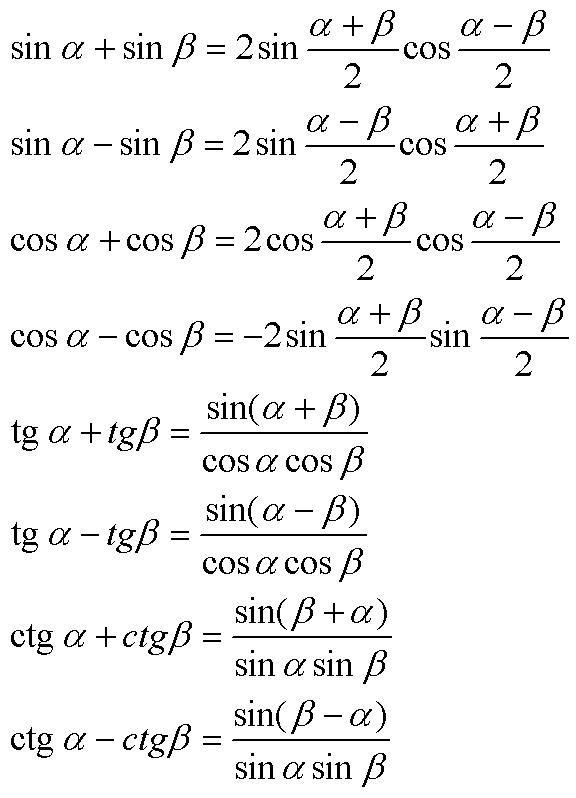
Вывод закона синусов, Айша Амри — StudySmarter Originals
Это означает, что правая часть всех трех выражений равна одному и тому же значению. Имея это в виду, давайте установим эти области равными друг другу.
12bcsinA=12acsinB=12absinC
Теперь, разделив все это выражение на 12abc и упростив его, мы получим закон синусов.
⇒ 12bcsinA12abc=12acsinB12abc=12absinC12abc⇒sinAa=sinBb=sinCc
Закон синусов: Для любого треугольника ABC sinAa=sinBb=sinCc.
Закон синусов можно записать в виде трех отдельных уравнений, как показано ниже.
sinAa=sinBbsinBb=sinCcsinAa=sinCc
Применение закона синусов
Мы можем применить закон синусов к любому треугольнику, учитывая меры двух случаев:
Величина двух углов и любой стороны
Величина двух сторон и угла, противолежащего одной из них
Давайте посмотрим на некоторые рабочие примеры, которые применяют закон синусов.
Решение треугольника с двумя углами и стороной
Учитывая приведенный ниже треугольник, найдите угол A и длины a и c.
Пример 2, Айша Амри — StudySmarter Originals
Решение
Даны углы B = 80 o и C = 40 o и сторона b = 14 см.
Здесь у нас есть значение двух углов и стороны.
Начнем с нахождения угла A. Напомним, что сумма внутренних углов любого треугольника равна 180 o .
A+B+C=180o⇒A=180o-B-C⇒A=180o-80o-40o⇒A=60o
Таким образом, угол A равен 60 o . Теперь воспользуемся законом синусов, чтобы найти длины а и с.
sinAa=sinBb⇒sin(60)a=sin(80)14⇒a=14sin(60)sin(80)⇒a≈12,31 см (исправить до двух знаков после запятой)sinCc=sinBb⇒sin(40)c=sin(80) 14⇒c=14sin(40)sin(80)⇒c≈90,14 см (исправить до двух знаков после запятой)
Таким образом, a и c приблизительно равны 12,31 см и 9,14 см соответственно.
Решение треугольника по двум сторонам и углу
Учитывая приведенный ниже треугольник, найдите углы B и C и длину b.
Пример 3, Айша Амри — StudySmarter Originals
Решение
Даны угол A = 27 o и стороны a = 10 см и c = 12 см.
Здесь у нас есть значение двух сторон и угла, противолежащего одной из них.
Начнем с вычисления угла C, используя приведенный ниже закон синусов.
sinAa=sinCc⇒sin(27)10=sinC12⇒sinC=12sin(27)10⇒C=sin-112sin(27)10⇒C≈33,01o(исправить до двух знаков после запятой)
Таким образом, угол C приблизительно равен 33,01 o . Чтобы найти угол B, вычтем значение углов A и C из 180 o .
A+B+C=180o⇒B=180o-A-C⇒B≈180o-27o-33,01o⇒B≈119,99oисправить до двух знаков после запятой)
Таким образом, угол B приблизительно равен 119,99 o . Наконец, мы можем найти длину b, используя закон синусов.
sinAa=sinBb⇒sin(27)10=sin(119,99)b⇒b=10sin(119,99)sin(27)⇒b≈19,08 см (исправить до двух знаков после запятой)
Таким образом, b равно приблизительно 19,08 см.
Решения треугольника
Треугольник может иметь или не иметь единственное решение, учитывая значение двух сторон и угла, противолежащего одной из них. Чтобы определить количество решений, которые может иметь треугольник, важно проанализировать предоставленный угол и длины заданных сторон треугольника, прежде чем применять закон синусов. Что касается данного угла, мы должны определить, является ли он прямым, острым или тупым углом. Для треугольника с заданными значениями двух сторон и угла, противолежащего одной из них, следует рассмотреть три случая:
Нет решений = Треугольник не существует
Одно решение = Существует ровно один треугольник
Два решения = Два треугольника существуют .
Предположим, у нас есть значения угла A и сторон a и b для данного треугольника.
 В таблице ниже приведены критерии для каждого случая данного треугольника.
В таблице ниже приведены критерии для каждого случая данного треугольника.Количество растворов
A Островая
A <90 O
A IS RIGHT или DUEPUS
A ≥
249249292929292929292928 492492492492492492492492492492492492492492929292929292929292929292929292929н0292929нте.
O 6928Glencoe McGraw-Hill, Algebra 2 (2008)
A
Glencoe McGraw-Hill, алгебра 2 (2008)
A ≤
A ≤
A ≤ AbOne Solution
Glencoe McGraw-Hill, Algebra 2 (2008)
a = b sin A
Glencoe McGraw-Hill, Algebra 2 (2008 )
a > b
Glencoe McGraw-Hill, Algebra 2 (2008)
a ≥ b
Two Solutions
Glencoe McGraw-Hill, Algebra 2 (2008)
B> A> B SIN A
Один раствор
для TRIANGLE ABC, где B = 9596666, , , , , , , , , , , , , , , , , , , , , , , , , , , ,
.
 19 и c = 12, определите, имеет ли ABC одно решение или два решения.
19 и c = 12, определите, имеет ли ABC одно решение или два решения.Решение
Поскольку угол B тупой и b > c, у нас должно быть одно решение. Треугольник ABC нарисован ниже.
Пример 4, Айша Амри — StudySmarter Originals
Теперь воспользуемся этим, чтобы найти углы A и C и сторону a. Используя закон синусов
sinBb=sinCc⇒sin(95)19=sinC12⇒sinC=12sin(95)19⇒C=sin-112sin(95)19⇒C≈38,99°(исправить до двух знаков после запятой)
Таким образом, угол C составляет примерно 38,99 o . Таким образом, мы можем найти угол A как
A=180o-B-C⇒A≈180o-95o-38,99o⇒A≈46,01o (исправить до двух знаков после запятой)
Угол A приблизительно равен 46,01 o . Опять же, применяя закон синусов
sinAa=sinBb⇒sin(46,01)a=sin(95)19⇒a=19sin(46,01)sin(95)⇒a≈13,72(исправить до двух знаков после запятой)
Таким образом, длина a составляет приблизительно 13,72 единицы.

Нет решений
Для треугольника ABC, где B = 95 o , b = 10 и c = 12, определите, имеет ли ABC одно решение или два решения.
Решение
Поскольку угол B тупой и b < c, решений нет. Точнее, для данных размерностей такого треугольника не существует.
Два решения
Для треугольника ABC, где A = 44°, b = 19 и a = 14, укажите, имеет ли ABC одно решение или два решения.
Решение
Здесь угол А острый. Кроме того, оценивая b sin A, мы получаем:
bsinA=19sin(44)⇒bsinA≈13,2(исправить на один десятичный знак)
Теперь сравним это с заданными значениями a и b. Обратите внимание, что b > a > b sin A, поэтому у нас должно быть два решения. Эскиз этого треугольника показан ниже.
Пример 5, Айша Амри — StudySmarter Originals
Теперь воспользуемся этим, чтобы найти неизвестные углы и стороны. Здесь следует рассмотреть два случая.

Случай 1: B является острым, B 1
Использование закона синусов 44)14⇒B1≈70,52o(исправить до двух знаков после запятой)
Таким образом, угол B 1 приблизительно равен 70,52 o . Таким образом, мы можем найти угол C 1 как
C1=180o-A-B1⇒C1≈180o-44o-70,52o⇒C1≈65,48o(исправить до двух знаков после запятой)
Опять же, применяя закон синусов
sinAa1=sinC1 =sin(65,48)c1⇒c1=14sin(65,48)sin(44)⇒c1≈18,34(исправить до двух знаков после запятой)
Таким образом, длина c 1 составляет приблизительно 18,34 единицы.
Случай 2: B — Тупоугольный, B 2
Обратите внимание, что треугольник B 1 C 3 B 3 — равнобедренный треугольник. Напомним, что углы при основании равнобедренного треугольника всегда равны. Следовательно, углы B 1 и B 3 примерно равны 70,52 o .

Кроме того, треугольники B 1 C 1 B 3 и A B 2 C 2 являются дополнительными. Таким образом, B 2 можно найти как 180 o — 70,52 o ≈ 109,48 o .
Другой способ найти B 2 состоит в том, чтобы определить тупой угол, синус которого также равен
19sin(44)14≈0,94 Мы делаем это, вычитая угол B 1 = 70,52 o найдено в случае 1 из 180 o .
Таким образом, B 2 приблизительно равно 180 o — 70,52 o ≈ 109,48 o , как и раньше. Таким образом, мы можем найти угол C 2 как
C2=180o-A-B2⇒C1≈180o-44o-109,48o⇒C1≈26,52o(исправить до двух знаков после запятой)
Используя закон синусов еще раз
sinC2a2cinC⇒sin(44)14=sin(26,52)c2⇒c2=14sin(26,52)sin(44)⇒c2≈9,0(исправить до двух знаков после запятой)
Таким образом, длина c 2 составляет примерно 9,0 единиц.

Реальный пример с использованием закона синусов
Свет от маяка на судне вращается по часовой стрелке с постоянной скоростью один оборот в минуту. Луч попадает в точку на берегу, которая находится в 1200 футах от судна. Четыре секунды спустя свет падает на точку в 575 футах дальше по берегу. На каком расстоянии судно от берега?
Решение
Давайте начнем с наброска этой задачи.
Пример лодки, Айша Амри — StudySmarter Originals
Маяк делает один оборот каждые 60 секунд. Таким образом, угол, под которым свет проходит за 4 секунды, равен
460(360°)=24°
. Чтобы найти угол X, применим закон синусов.
sinX1200=sin(24)575⇒sinX=1200sin(24)575⇒X=sin-11200sin(24)575⇒X≈58,09o(исправить до двух знаков после запятой)
Теперь, когда у нас есть угол X, мы можем использовать это, чтобы найти угол Y.
X+A=90°(углы X и Aдополнительны)⇒58,09o+(Y+24o)≈90o(так как A=Y+24o)⇒Y≈90o-58,09o-24o⇒Y≈7,91o
Наконец, мы можем определить расстояние от маяка до берега, вычислив d.
 Здесь мы будем использовать отношение косинуса.
Здесь мы будем использовать отношение косинуса.cosY=adjacenthypotenuse=ABAD⇒cos(7,91)≈d1200⇒d≈1200cos(7,91)⇒d≈1188,58(исправить до двух знаков после запятой)
Таким образом, расстояние от маяка до берега составляет примерно 1188,58 футов.
Закон синусов – основные выводы
- Площадь треугольника можно найти с помощью
Area△ABC=12bcsinAArea△ABC=12acsinBArea△ABC=12absinC
- The Law of Sines states that
sinAa=sinBbsinBb=sinCcsinAa=sinCc
Law of Sines — Math Images
From Math Images
( Перенаправлено с закона синусов)
Перейти к: навигация, поиск
закон синусов Область: Геометрия Изображение создано: Ричард Скотт Закон синусов
- Закон синусов — это инструмент, обычно используемый для решения произвольных треугольников.
 Это формула, которая связывает синус данного угла с длиной его противоположной стороны.
Это формула, которая связывает синус данного угла с длиной его противоположной стороны.
Содержимое
- 1 Основное описание
- 2 Более математическое объяснение
- 2.1 Две производные
- 2.1.1 Использование области
- 2.1.2 Использование определения синуса
- 2.2 Геометрическое удлинение
- 2.2.1 Доказательство
- 2.3 Пример проблемы
- 2.3.1 Решение
- 2.1 Две производные
- 3 Учебные материалы
- 4 Каталожные номера
В любом треугольнике существует взаимосвязь между мерами углов и длинами сторон: против наибольшей стороны лежит наибольший угол, против второй наибольшей стороны лежит второй по величине угол, а против наименьшего угла лежит напротив самой короткой стороны.
Закон синусов — это уравнение, которое более точно выражает отношение между углами треугольника и длинами их противоположных сторон. Закон синусов гласит, что отношение между длиной одной стороны треугольника и синусом противоположного ему угла одинаково для всех трех сторон.
 Конкретно:
Конкретно:Дан треугольник с длинами сторон и противоположными углами ,
Закон синусов используется для нахождения всех длин сторон и мер углов для произвольного треугольника, имея только часть этой информации. Этот процесс называется решением треугольника. Чтобы использовать закон синусов при решении треугольников, необходимо знать не менее трех элементов треугольника. Всякий раз, когда даны длина стороны и два угла, закон синусов можно использовать для решения треугольника.В некоторых случаях закон синусов может дать несколько решений для треугольника. Если две длины соседних сторон даны с одним из противоположных углов, закон синусов не может окончательно определить треугольник, но вместо этого предлагает ноль, одно или два возможных решения в так называемом неоднозначном случае.
Закон синусов не помогает в решении треугольника в некоторых случаях. С двумя известными длинами сторон и мерой угла между ними невозможно использовать закон синусов для решения треугольника, потому что не существует пары противоположных меры угла и длины стороны.
 Закон синусов сам по себе также не может дать решения, когда даны три длины сторон. Вместо этого для решения треугольников в этих случаях часто используется закон косинусов.
Закон синусов сам по себе также не может дать решения, когда даны три длины сторон. Вместо этого для решения треугольников в этих случаях часто используется закон косинусов. [Щелкните для просмотра более математического объяснения] Две производные
Есть по крайней мере два различных способа вывести закон синусов: используя площадь […]по крайней мере, два разных способа вывести закон синусов: используя формулу площади и используя определение синуса. Использование площади
Формула площади треугольника использует длины основания и высоты. Используя эти длины и меры углов треугольника, мы можем вывести закон синусов.
Треугольник можно сориентировать так, что любая сторона может быть использована в качестве основания. В зависимости от того, какая сторона выбрана в качестве основания треугольника, высота может быть разной.
 Позвольте быть высотой, когда сторона длины является основанием. Когда — основание, — это расстояние от вершины до противоположной стороны, перпендикулярной стороне. Когда ориентируется как основание треугольника, проходит перпендикулярно стороне и является расстоянием от стороны до вершины.
Позвольте быть высотой, когда сторона длины является основанием. Когда — основание, — это расстояние от вершины до противоположной стороны, перпендикулярной стороне. Когда ориентируется как основание треугольника, проходит перпендикулярно стороне и является расстоянием от стороны до вершины.Сначала мы должны определить высоту треугольника для каждой ориентации основания.
При ориентации в качестве основания,
Когда ориентируется как основание,
В любом треугольнике
Поскольку площадь треугольника одинакова независимо от того, как треугольник ориентирован, площадь треугольника с основанием равна площади треугольника с основанием.Подставляя формулу площади треугольника,
И то, и другое может быть записано в терминах длин сторон и углов, как показано в разделе «Подробнее о высоте». Следовательно, мы можем заменить и вместо , что дает нам
Следовательно, мы можем заменить и вместо , что дает нам
Умножение обеих частей на и деление на дает нам
Тогда, переставляя еще раз, мы получаем наше уравнение в его наиболее распространенной форме,
Так как мы можем ориентировать базу по-разному и выполнять тот же процесс с другими переменными, мы знаем, что , поэтомуэто закон синусов.
Используя определение синуса
Мы знаем, что в прямоугольном треугольнике
Пусть обозначают высоту и представляют длины противоположных сторон соответственно, подключают соответствующие меры для решения для .
Очистка дробей,
Очистка дробей,Приравняйте оба уравнения друг к другу, чтобы получить
Разделите обе части на for
Поскольку мы можем проделать тот же процесс, используя другой угол и другие переменные, мы знаем, что , поэтомуГеометрическое расширение
Для каждого треугольника существует окружность, вершины которой лежат на окружности.
 Этот треугольник известен как вписанный треугольник, а окружность известна как описанная окружность или описанная окружность.
Этот треугольник известен как вписанный треугольник, а окружность известна как описанная окружность или описанная окружность.По расширенному закону синусов,
где радиус описанной окружностиДоказательство
Пусть есть два вписанных треугольника на окружности радиуса . Позвольте быть треугольником, у которого есть гипотенуза, которая проходит через центр круга. Позвольте быть косой треугольник, который разделяет с .
Для ,
Угол равен углу, потому что они оба являются вписанными углами, которые пересекают одну и ту же дугу. По свойствам вписанных углов два вписанных угла, пересекающих одну и ту же дугу в окружностях приходящего радиуса, равны. Так как и одинаковы, то и .Замена дает нам
Решение для дает нам
Поскольку диаметр,- .
 Добавьте учебные материалы.
Добавьте учебные материалы.- Убедитесь, что у вас есть диаграмма, на которой четко обозначены все известные стороны и углы.
- Найдите на рисунке противоположные пары сторон и углов.

- Подставить известные стороны и углы в закон синусов, в идеале использовать версию, в которой есть неизвестное, что вам нужно вычислить в числителе.
- Перестройте уравнение, чтобы найти неизвестное.
т. к. это длина противоположной стороны .
к. это длина противоположной стороны .По закону синусов мы знаем, что
и, следовательно, переходным свойством,
Пример задачи
Решите треугольник. Найдите все его части, , заданные , ,.
Решение
[показать больше] [скрыть]
Так как сумма всех углов треугольника составляет
Перемножение дает нам
Так как и ,
Cross-multiplying gives us
Так как и ,
Подставляя значения для ,
С ,Все изображения сделаны автором страницы в программах Adobe Photoshop и Cinderella2.
Если у вас есть возможность, рассмотрите возможность добавления или редактирования этой страницы! Есть вопросы по изображению или пояснениям на этой странице?
Оставьте сообщение на странице обсуждения , щелкнув вкладку «обсуждение» в верхней части этой страницы изображения.[[Описание::Закон синусов — это инструмент, обычно используемый для решения произвольных треугольников. Это формула, которая связывает синус данного угла с длиной его противоположной стороны.|]]
Объяснение урока: закон синусов
В этом объяснении мы узнаем, как применять закон синусов. синусов, чтобы найти длины и меры углов в непрямоугольных треугольниках.
Мы уже должны быть знакомы с тем, как применять соотношения синуса, косинуса и тангенса в прямоугольных треугольниках.
 Закон синусов
расширение этих тригонометрических методов для включения более широкого класса треугольников.
Закон синусов
расширение этих тригонометрических методов для включения более широкого класса треугольников.Определение: Закон синусов
Рассмотрим треугольник 𝐴𝐵𝐶, с соответствующими сторонами длин 𝑎, 𝑏 и 𝑐. При обозначении таких треугольников принято, что каждая сторона обозначается строчной буквой, соответствующей противоположному углу.
Закон синусов гласит, что 𝑎𝐴=𝑏𝐵=𝑐𝐶.sinsinsin
Верно и обратное: sinsinsin𝐴𝑎=𝐵𝑏=𝐶𝑐.
Другими словами, закон синусов говорит нам, что отношение между любой длиной стороны и синус противолежащего ему угла одинаков для всех трех пар сторон и углов внутри любого треугольника. На практике мы обычно используем только две части отношения в нашем вычисления, а не все три. Первая версия закона синусов, где стороны появляются в числителе, наиболее полезен при вычислении длины стороны, в то время как обратная версия, где синусы углов появляются в числителе, наиболее полезен при вычислении угла просто потому, что менее алгебраическая перестановка требуется для достижения ответа.

Поскольку закон синусов описывает отношение сторон и синусов их противоположностей углов, мы можем признать необходимость закона синусов, установив, что информация, данная в вопросе, состоит из пар сторон и противоположных углов в непрямоугольном треугольнике.
Давайте теперь продемонстрируем, как применить закон синусов для вычисления неизвестной длины в треугольнике.
Пример 1: Использование закона синусов для вычисления неизвестной длины
Для данной цифры 𝐴𝐵=3 и 𝐵𝐶=𝑎. Используйте закон синусов, чтобы вычислить 𝑎. Дайте ответ с точностью до двух знаков после запятой.
Ответ
Нам будет полезно добавить к диаграмме заданные длины сторон.
Теперь мы можем видеть, что длина стороны в 3 единицы противоположна углу 31∘, и длину стороны, которую мы хотим рассчитать, 𝑎, лежит против угла 64∘. Таким образом, мы можем применить закон синусов: 𝑎𝐴=𝑐𝐶.sinsin
Подстановка значений из диаграммы и решение для 𝑎 дает 𝑎64=331𝑎=36431.
 sinsinsinsin∘∘∘∘
sinsinsinsin∘∘∘∘Вычисление, а затем округление нашего ответа до двух знаков после запятой, как того требует вопрос, дает 𝑎=5,235…≈5,24.
Длина 𝑎 с точностью до двух знаков после запятой составляет 5,24 единицы.
В нашем предыдущем примере мы продемонстрировали, как рассчитать длину недостающую сторону по закону синусов. Теперь мы рассмотрим, как применить аналогичный процесс вычислить величину неизвестного угла.
Пример 2. Использование закона синусов для вычисления неизвестного угла в треугольнике
𝐴𝐵𝐶 — треугольник, где 𝑎=9, 𝑏=6, и 𝑚∠𝐴=58,1∘. Найдите 𝑚∠𝐵 с точностью до десятых степень.
Ответ
Приступая к решению этого типа задач, мы должны начать с наброска треугольника используя известную информацию, как показано ниже (не в масштабе).
Мы видим, что сторона длины 9 единиц противоположна углу 58,1∘, а сторона длины 6 единиц противоположна углу, который нам нужно вычислить.
 Поскольку мы работаем с противоположными парами сторон и углов, мы можем применить
закон синусов. так как мы вычисляем угол, мы будем использовать версию, которая
имеет синусы углов в числителе:
грех𝐵𝑏=𝐴𝑎.
Поскольку мы работаем с противоположными парами сторон и углов, мы можем применить
закон синусов. так как мы вычисляем угол, мы будем использовать версию, которая
имеет синусы углов в числителе:
грех𝐵𝑏=𝐴𝑎.Подставить значения из нашей диаграммы в закон синусов и переставить мы получаем sinsinsinsin𝐵6=58,19𝐵=658,19.∘∘
Мы решаем это уравнение для 𝐵, применяя обратное синусоидальная функция: 𝐵=658,19=(0,565…)=34,470…≈34,5.sinsinsin∘∘∘
Мерой угла 𝐵 с точностью до десятых долей градуса является 34,5∘.
Итак, мы рассмотрели примеры того, как вычислить длину стороны и величину угла по закону синусов. Мы можем обобщить этот процесс в следующих шагах.
Как вычислить неизвестную длину или угол с помощью закона синусов
При работе с треугольниками важно помнить, что самая длинная сторона треугольника треугольник всегда противоположен углу с наибольшей мерой, а кратчайшая сторона равна всегда против угла с наименьшей мерой. Теперь мы рассмотрим пример, в котором это знание полезно.
Пример 3: Использование закона синусов для вычисления наименьшей стороны в треугольнике
𝐴𝐵𝐶 — треугольник, где 𝑚∠𝐴=4611′17∘, 𝑚∠𝐵=274′46∘, и длина 𝑎=21,4см. Найдите длину самой короткой стороны 𝐴𝐵𝐶 дающей ответ до одного десятичного знака.
Ответ
Начнем с рисования треугольника 𝐴𝐵𝐶, как показано ниже (не в масштабе).
Вопрос касается длины самой короткой стороны этого треугольника.
 Нам не нужно вычислять длины обеих недостающих сторон, а затем отвечать
что короче. Вместо этого следует вспомнить, что самая короткая сторона в
любой треугольник противоположен своему наименьшему углу.
Нам не нужно вычислять длины обеих недостающих сторон, а затем отвечать
что короче. Вместо этого следует вспомнить, что самая короткая сторона в
любой треугольник противоположен своему наименьшему углу.Мы знаем меры углов 𝐴 и 𝐵, и мы можем вычислить меру угла 𝐶, используя сумму углов треугольник: 𝑚∠𝐶=180−4611′17′−274′46′=10643′57′′.∘∘∘∘
Возможно, это уже было ясно, но теперь мы ясно видим, что наименьший угол в треугольнике равен углу 𝐵, а значит, длина стороны 𝑏 которые мы хотим рассчитать. Информация, которую мы получаем, состоит из сторона, 𝑎, и ее противоположный угол, 𝐴, вместе с углом, противоположным стороне, которую мы хотите посчитать. Таким образом, мы можем применить закон синусов: 𝑎𝐴=𝑏𝐵.sinsin
Подставляя два известных угла и одну известную сторону, мы имеем 21,4(4611′17′′)=𝑏(274′46′′).sinsin∘∘
Решение для 𝑏 дает 𝑏=21,4(274′46′′)(4611′17′′)=13,500…≈13,5.
 sinsin∘∘
sinsin∘∘До одного десятичного знака длина самой короткой стороны треугольника 𝐴𝐵𝐶 13,5 см.
В некоторых задачах нам может понадобиться объединить закон синусов с другими геометрическими свойства, такие как правила углов или тригонометрия прямого угла. Давайте рассмотрим пример, в котором мы применяем все эти методы вместе.
Пример 4. Использование закона синусов для вычисления длины стороны в композите Рис.
На данном рисунке 𝐵𝐶𝐷𝑌 — прямоугольник, а 𝐵 — точка на прямой 𝐴𝐶. 𝐵𝐶=405м, 𝑚∠𝐷𝐴𝐶=21∘, и 𝑚∠𝑌𝐴𝐶=59∘. Найдите длину 𝐷𝐶 дать ответ ближайшему метр.
Ответ
Давайте начнем с добавления информации, указанной в вопросе, к диаграмме. Мы можем разделить угол 59∘ в 21∘, который является мерой угла 𝐷𝐴𝐶, и остальные 38∘.
Поскольку 𝐵𝐶𝐷𝑌 — прямоугольник, все его внутренние углы равны 90∘.
 Длина, которую мы хотим
вычислить, 𝐷𝐶, является частью прямоугольного треугольника
𝐷𝐴𝐶, ни одна из полных сторон которого
мы знаем. Нам нужна хотя бы одна длина, чтобы иметь возможность вычислить 𝐷𝐶, поэтому
вместо этого рассмотрим другой треугольник на рисунке, треугольник 𝐴𝑌𝐷. Этот треугольник имеет общую сторону 𝐴𝐷 с нашим прямоугольным треугольником,
поэтому мы можем использовать его для
выработать эту общую длину.
Длина, которую мы хотим
вычислить, 𝐷𝐶, является частью прямоугольного треугольника
𝐷𝐴𝐶, ни одна из полных сторон которого
мы знаем. Нам нужна хотя бы одна длина, чтобы иметь возможность вычислить 𝐷𝐶, поэтому
вместо этого рассмотрим другой треугольник на рисунке, треугольник 𝐴𝑌𝐷. Этот треугольник имеет общую сторону 𝐴𝐷 с нашим прямоугольным треугольником,
поэтому мы можем использовать его для
выработать эту общую длину.Мы знаем или можем вычислить дополнительную информацию о треугольнике 𝐴𝑌𝐷. Во-первых, используя чередующиеся углы в параллельных прямых, мы видим, что мера угла 𝑌𝐷𝐴 совпадает с мерой угла 𝐷𝐴𝐶, так что это 21∘. Затем мы можем рассчитать мера угла 𝐴𝑌𝐷 с использованием суммы углов треугольника: 𝑚∠𝐴𝑌𝐷=180−38−21=121.∘∘∘∘
Поскольку 𝐵𝐶𝐷𝑌 — прямоугольник, его противоположные стороны равны. Так, 𝑌𝐷=𝐵𝐶=405м.
Теперь мы можем использовать закон синусов для вычисления длины стороны 𝐴𝐷.
 𝐴𝐷 находится напротив измерения угла
121∘,
а у нас длина 405 м
напротив угла 38∘. Применение закона синусов дает
𝐴𝐷121=40538.sinsin∘∘
𝐴𝐷 находится напротив измерения угла
121∘,
а у нас длина 405 м
напротив угла 38∘. Применение закона синусов дает
𝐴𝐷121=40538.sinsin∘∘Затем мы можем найти 𝐴𝐷, умножив на sin121∘ и оценивая: 𝐴𝐷=40512138=563,869….sinsin∘∘
Теперь мы вычислили длину общей стороны 𝐴𝐷, которая является гипотенузой прямоугольный треугольник 𝐴𝐶𝐷. По отношению к углу 21∘, 𝐷𝐶 это противоположная сторона и поэтому мы можем применить тригонометрию прямоугольного треугольника, используя соотношение синусов: sin21=𝐷𝐶𝐴𝐷=𝐷𝐶563,869….∘
Преобразование этого уравнения для 𝐷𝐶 и округление до ближайшего метр, получаем 𝐷𝐶=563,869…21=202,072…≈202.sin∘
Длина 𝐷𝐶 с точностью до метра равна 202 м.
Важно понимать, что при применении закона синусов мы работаем с соотношение. Значения, которые мы используем для длин сторон, не обязательно должны быть сторонами.
 сами длины, но они должны быть в том же соотношении, что и длины сторон. Позволь нам
рассмотрим пример, в котором мы не можем вычислить длины сторон явно, но можем
рассчитать их соотношение.
сами длины, но они должны быть в том же соотношении, что и длины сторон. Позволь нам
рассмотрим пример, в котором мы не можем вычислить длины сторон явно, но можем
рассчитать их соотношение.Пример 5. Использование закона синусов для нахождения отношения длин сторон треугольника
𝐴𝐵𝐶 — треугольник, в котором 8𝐴=11𝐵=16𝐶грех грех. Найдите отношение 𝑎∶𝑏∶𝑐.
Ответ
Напомним, что закон синусов говорит нам, что отношение между длинами каждого Сторона и синус противолежащего ей угла в любом треугольнике одинаковы: sinsinsin𝐴𝑎=𝐵𝑏=𝐶𝑐.
Это немного похоже на уравнение, которое мы получили для треугольника 𝐴𝐵𝐶, но наше уравнение имеет коэффициенты для каждого из членов синуса и не имеет знаменателей. Поэтому нам нужно манипулировать уравнением, которое нам дали, чтобы записать его в формат, имитирующий закон синусов. Для этого мы можем разделить уравнение на наименьшее общее кратное 8, 11 и 16.
 Поскольку 8 является делителем 16, 11 и 16
взаимно просты, наименьшее общее кратное равно 11×16 (т. е. 176). Разделение через
на 11×16 дает
8𝐴11×16=11𝐵11×16=16𝐶11×16.sinsinsin
Поскольку 8 является делителем 16, 11 и 16
взаимно просты, наименьшее общее кратное равно 11×16 (т. е. 176). Разделение через
на 11×16 дает
8𝐴11×16=11𝐵11×16=16𝐶11×16.sinsinsinЗатем мы можем упростить каждую часть соотношения, убрав общие множители, чтобы получить sinsinsin𝐴22=𝐵16=𝐶11.
Сравнивая это с общей формой закона синусов, в котором знаменатели представляют собой длины сторон, мы видим, что отношение 𝑎∶𝑏∶𝑐 равно 22∶16∶11.
Обратите внимание, что это соотношение между длинами сторон, а не обязательно сами длины сторон. Если длины сторон были 44, 32 и 22 единицы, соответственно, то отношение будет грехсинсин𝐴44=𝐵32=𝐶22, которое можно упростить, умножив каждую часть отношения на 2 в дайте то же уравнение sinsin𝐴22=𝐵16=𝐶11, как мы видели ранее.
Мы видели несколько примеров того, как мы можем применить закон синусов для вычисления как длины сторон и меры углов в непрямоугольных треугольниках.
 На самом деле закон синусов
верно и для прямоугольных треугольников. Рассмотрим треугольник 𝐴𝐵𝐶 с
прямой угол в 𝐴.
На самом деле закон синусов
верно и для прямоугольных треугольников. Рассмотрим треугольник 𝐴𝐵𝐶 с
прямой угол в 𝐴.Тогда, рассматривая только две пары угол-сторона, мы имеем 𝑎90=𝑏𝐵.sinsin∘
Учитывая, что sin90=1∘, это упрощается до 𝑎=𝑏𝐵.sin
Затем мы переставляем, сначала умножая на sin𝐵, а затем деля от 𝑎 дать 𝑎𝐵=𝑏𝐵=𝑏𝑎.sinsin
Возвращаясь к исходному треугольнику, мы видим, что сторона 𝑎 является гипотенузой и, по отношению к углу 𝐵 сторона 𝑏 противоположна. Итак, имеем, что синус угла 𝐵 равна длине противоположной стороны, деленной на длину гипотенузы. Следовательно, закон синусов сводится к отношению синусов в прямоугольном треугольнике. Тогда вполне возможно применить закон синусов к прямоугольным треугольникам, но это излишне сложно, так как наши уравнения упростятся до уравнений мы могли бы получить, используя тригонометрию прямоугольного треугольника.
Давайте закончим, повторив некоторые ключевые моменты.




 В таблице ниже приведены критерии для каждого случая данного треугольника.
В таблице ниже приведены критерии для каждого случая данного треугольника. 19 и c = 12, определите, имеет ли ABC одно решение или два решения.
19 и c = 12, определите, имеет ли ABC одно решение или два решения.


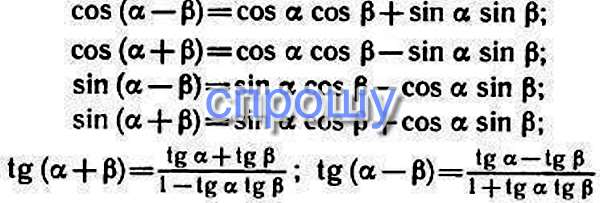
 Здесь мы будем использовать отношение косинуса.
Здесь мы будем использовать отношение косинуса. Это формула, которая связывает синус данного угла с длиной его противоположной стороны.
Это формула, которая связывает синус данного угла с длиной его противоположной стороны.  Конкретно:
Конкретно: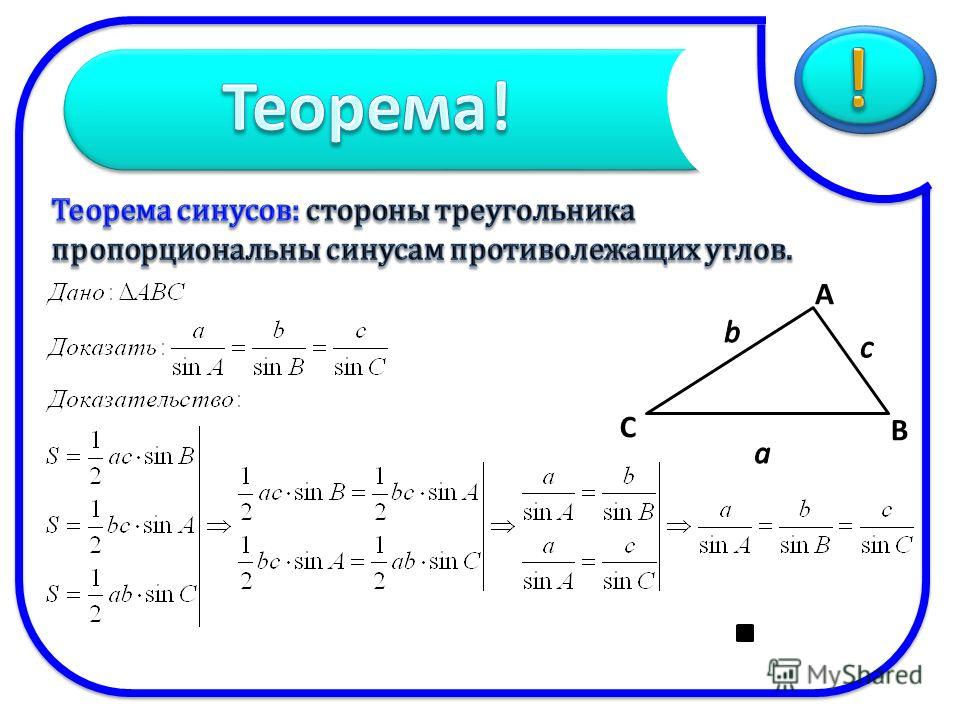 Закон синусов сам по себе также не может дать решения, когда даны три длины сторон. Вместо этого для решения треугольников в этих случаях часто используется закон косинусов.
Закон синусов сам по себе также не может дать решения, когда даны три длины сторон. Вместо этого для решения треугольников в этих случаях часто используется закон косинусов.  Позвольте быть высотой, когда сторона длины является основанием. Когда — основание, — это расстояние от вершины до противоположной стороны, перпендикулярной стороне. Когда ориентируется как основание треугольника, проходит перпендикулярно стороне и является расстоянием от стороны до вершины.
Позвольте быть высотой, когда сторона длины является основанием. Когда — основание, — это расстояние от вершины до противоположной стороны, перпендикулярной стороне. Когда ориентируется как основание треугольника, проходит перпендикулярно стороне и является расстоянием от стороны до вершины. Следовательно, мы можем заменить и вместо , что дает нам
Следовательно, мы можем заменить и вместо , что дает нам Этот треугольник известен как вписанный треугольник, а окружность известна как описанная окружность или описанная окружность.
Этот треугольник известен как вписанный треугольник, а окружность известна как описанная окружность или описанная окружность. к. это длина противоположной стороны .
к. это длина противоположной стороны . Добавьте учебные материалы.
Добавьте учебные материалы.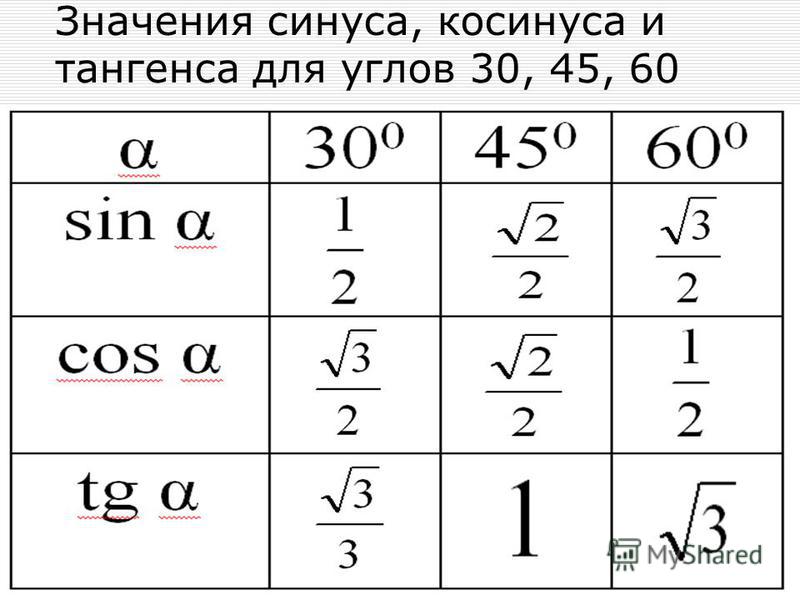 Закон синусов
расширение этих тригонометрических методов для включения более широкого класса треугольников.
Закон синусов
расширение этих тригонометрических методов для включения более широкого класса треугольников.
 sinsinsinsin∘∘∘∘
sinsinsinsin∘∘∘∘ Поскольку мы работаем с противоположными парами сторон и углов, мы можем применить
закон синусов. так как мы вычисляем угол, мы будем использовать версию, которая
имеет синусы углов в числителе:
грех𝐵𝑏=𝐴𝑎.
Поскольку мы работаем с противоположными парами сторон и углов, мы можем применить
закон синусов. так как мы вычисляем угол, мы будем использовать версию, которая
имеет синусы углов в числителе:
грех𝐵𝑏=𝐴𝑎.
 Нам не нужно вычислять длины обеих недостающих сторон, а затем отвечать
что короче. Вместо этого следует вспомнить, что самая короткая сторона в
любой треугольник противоположен своему наименьшему углу.
Нам не нужно вычислять длины обеих недостающих сторон, а затем отвечать
что короче. Вместо этого следует вспомнить, что самая короткая сторона в
любой треугольник противоположен своему наименьшему углу.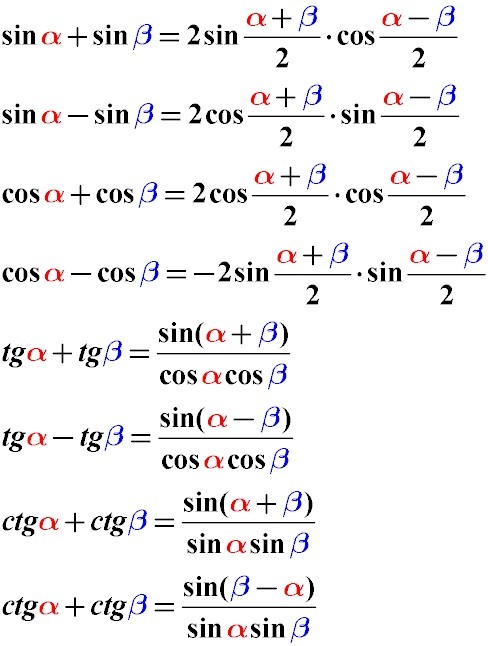 sinsin∘∘
sinsin∘∘ Длина, которую мы хотим
вычислить, 𝐷𝐶, является частью прямоугольного треугольника
𝐷𝐴𝐶, ни одна из полных сторон которого
мы знаем. Нам нужна хотя бы одна длина, чтобы иметь возможность вычислить 𝐷𝐶, поэтому
вместо этого рассмотрим другой треугольник на рисунке, треугольник 𝐴𝑌𝐷. Этот треугольник имеет общую сторону 𝐴𝐷 с нашим прямоугольным треугольником,
поэтому мы можем использовать его для
выработать эту общую длину.
Длина, которую мы хотим
вычислить, 𝐷𝐶, является частью прямоугольного треугольника
𝐷𝐴𝐶, ни одна из полных сторон которого
мы знаем. Нам нужна хотя бы одна длина, чтобы иметь возможность вычислить 𝐷𝐶, поэтому
вместо этого рассмотрим другой треугольник на рисунке, треугольник 𝐴𝑌𝐷. Этот треугольник имеет общую сторону 𝐴𝐷 с нашим прямоугольным треугольником,
поэтому мы можем использовать его для
выработать эту общую длину. 𝐴𝐷 находится напротив измерения угла
121∘,
а у нас длина 405 м
напротив угла 38∘. Применение закона синусов дает
𝐴𝐷121=40538.sinsin∘∘
𝐴𝐷 находится напротив измерения угла
121∘,
а у нас длина 405 м
напротив угла 38∘. Применение закона синусов дает
𝐴𝐷121=40538.sinsin∘∘ сами длины, но они должны быть в том же соотношении, что и длины сторон. Позволь нам
рассмотрим пример, в котором мы не можем вычислить длины сторон явно, но можем
рассчитать их соотношение.
сами длины, но они должны быть в том же соотношении, что и длины сторон. Позволь нам
рассмотрим пример, в котором мы не можем вычислить длины сторон явно, но можем
рассчитать их соотношение. Поскольку 8 является делителем 16, 11 и 16
взаимно просты, наименьшее общее кратное равно 11×16 (т. е. 176). Разделение через
на 11×16 дает
8𝐴11×16=11𝐵11×16=16𝐶11×16.sinsinsin
Поскольку 8 является делителем 16, 11 и 16
взаимно просты, наименьшее общее кратное равно 11×16 (т. е. 176). Разделение через
на 11×16 дает
8𝐴11×16=11𝐵11×16=16𝐶11×16.sinsinsin На самом деле закон синусов
верно и для прямоугольных треугольников. Рассмотрим треугольник 𝐴𝐵𝐶 с
прямой угол в 𝐴.
На самом деле закон синусов
верно и для прямоугольных треугольников. Рассмотрим треугольник 𝐴𝐵𝐶 с
прямой угол в 𝐴.