Эквивалентные пределы функции: 6.3.1. Примеры

6.3.1. Примеры

Ниже приведены примеры неопределённостей, для раскрытия которых удобно пользоваться таблицами эквивалентных бесконечно малых, полученных в качестве следствий 1 и 2 замечательных пределов, или непосредственно самими этими пределами.

При использовании эквивалентных бесконечно малых следует помнить, что Разность двух бесконечно малых – бесконечно малая более высокого порядка малости, чем каждая из них: , то . Заменять эквивалентными в такой разности непосредственно нельзя. Такое выражение должно быть предварительно преобразовано.

Пример 1.

.

Пример 2.

Решение. Обратите внимание, что . Замена и на привела бы к неправильному результату. Разность должна быть предварительно преобразована:

Тогда .

Пример 3.

.

Пример 4.

.

Пример 5.

Пример 6.

Пример 7.

Решение. При раскрытии неопределенностей вида следует воспользоваться вторым замечательным пределом .

Анализ выражения, стоящего под знаком 2 замечательного предела, показывает, что его конструкция такова: к единице прибавляется бесконечно малая величина и эта сумма возводиться в степень, равную обратной величине для прибавляемой бесконечно малой, т. е. х или . Если в данном примере к основанию степени мы прибавим и отнимем единицу, то выражение не изменится, но мы сможем определить вид прибавляемой бесконечно малой величины. Т. е.

.

Таким образом, роль бесконечно малой играет слагаемое , которое стремится к 0 при . Обратная величина будет . Выполним тождественное преобразование.

.

Предел основания в полученном выражении равен числу Е, т. е.

(по 2 замечательному пределу).

Тогда данный предел сводиться к вычислению предела показателя, т. е.

.

В результате проведенного анализа можно сделать вывод, что если – бесконечно малая, а Бесконечно большая в расматривамом процессе (Или ), то

Пример 8.

Решение. Выполним преобразование с основанием и показателем степени (См. пример 7.)

Тогда

Замечание. Если воспользоваться выводом из примера 7, то можно сразу записать, что

.

Пример 9.

Решение.

.

Следует заметить, что если бесконечно малые и эквивалентны и бесконечно большие и Эквивалентны, то

Этот факт существенно упрощает вычисление пределов при раскрытии неопределенностей вида

Так, если учесть, что , то последний пример можно было решать следующим образом

.

Пример 10.

.

Решение. 1 способ:

2 способ:

Так как , а , то

.

Ниже рассмотрены пределы при условии, что , тогда . В этих случаях удобна замена переменной , т. е. получение возможности непосредственного использования таблицы эквивалентных бесконечно малых величин для выделения «главных частей».

Пример 1.

Пример 2.

Решение. 1 способ.

.

2 способ. Следует заметить, что замену переменной можно было бы не делать. Так как при величина , т. е. является бесконечно малой, то .

Преобразуем числитель

при .

Тогда .

Пример 3.

Решение.

.

Пример 4.

Решение.

.

Пример 5.

Решение.

Пример 6.

Решение.

Пример 7.

Решение.

=.

Пример 8.

Решение.

.

< Предыдущая		Следующая >

14. Применение эквивалентных бесконечно малых к вычислению пределов

Пусть и — бесконечно малые функции, при , т.е. и , причем a может быть как числом, так и одним из символов , — .

Бесконечно малые функции и называются бесконечно малыми одного порядка, если предел их отношения , . Если же число А=0, то бесконечно малая называется бесконечно малой более высокого порядка малости по сравнению с . Если и , то бесконечно малая функция называется бесконечно малой порядка p по сравнению с бесконечно малой функцией . Бесконечно малые функции и называются эквивалентными, если . В этом случае пишут: ~ .

Теорема (о замене бесконечно малых функций им эквивалентными ). Предел отношения двух бесконечно малых функций не изменяется, если каждую из них или какую-либо одну заменить им эквивалентными функциями.

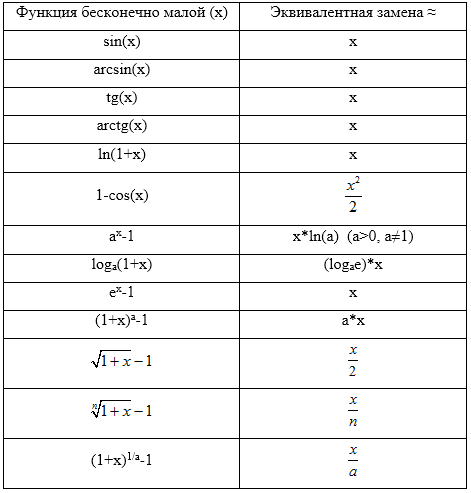
Если при некотором предельном переходе функция есть бесконечно малая, то Sin( )~ , tg( )~ ;

arcsin( )~ , arctg( )~ ; ln(1+ )~ , ln(1+k )~k , ~ , ~ ln a

Первый замечательный предел

Во многих случаях используется первый замечательный предел (х— длина дуг или угол, выраженный в радианах) и предполагается известным, что . Иногда при отыскании предела полезно сделать замену переменной с тем, чтобы упростить вычисление предела и использовать известные пределы. Если пол знаком предела делается замена переменной, то все величины, находящиеся под знаком, должны быть выражены через эту новую переменную. Из равенства, выражающего зависимость между старой переменной и новой, надо определить предельное значение новой переменной. Например, при нахождении предела обозначаем

t=kx , где при новая переменная , x=t/k.

Тогда

(т.к.cos (0)=1). Полезно помнить, что , где k -постоянная величина. Например, при функция sin(x) и tg(x) эквивалентные бесконечно малые, т.е. sin(x)~tg(x); т.к. .

Пример 1. Найти

Решение.

Применим сначала формулу тригонометрии

1-cos(t)=2sin²(t/2). У нас 1-cos(kx)=2sin²(kx/2), при ; sin²()~()². По теореме “замены эквивалентной” получим

. Заметим, что можно было воспользоваться первым замечательным пределом.

Ответ: k²/2.

Пример 2. Вычислить

Решение. По формуле тригонометрии sin(5(x+π))=sin(5x+5π)=- sin(5x).

Тогда

Поскольку при , sin(5x)~5x, e

3^x-1~ 3x

Ответ:-5/3.

Вычисление предела показательно-степенной функции

При нахождении пределов вида =C

Следует иметь ввиду, что:

1) если существуют конечные пределы

и , то C=A^B, т.е.

имеет место формула

Заметим, что предельное значение а может обозначать и число, и один из символов ;

2) если и , то вопрос о нахождении затруднений обычно не вызывает. В том случае полезны иногда формулы:

;

3) если и , т.е. имеем неопределенность вида { }, то полагают , где при и, следовательно,

Проиллюстрируем общий прием вычисления пределов на следующем примере ( раскрытие неопределенности вида { }).

Пример 3. Найти

Решение. Здесь основание степени при , а показатель степени , т.е. имеется неопределенность вида .

Тогда

(Получили в качестве при )

Замечание 1. При вычислении пределов выражений вида , где , при , удобно иногда пользоваться формулой

.

Замечание 2. При вычислении пределов полезно знать, что

а) если существует и положителен , то

; б) ;

в) .

1.5: оценка пределов с использованием подстановки

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

5676

Нахождение пределов для подавляющего большинства точек заданной функции так же просто, как подстановка числа, к которому x приближается, в функцию. Поскольку это превращает оценку пределов в подстановку на уровне алгебры, большинство вопросов, связанных с пределами, сосредоточены на случаях, когда подстановка не работает. Как вы можете решить, является ли замена подходящим аналитическим инструментом для нахождения 9?0024 ограничение ?

Использование подстановки для нахождения пределов

Нахождение предела аналитически означает нахождение предела алгебраическими средствами. Чтобы оценить множество пределов, вы можете подставить значение, к которому x приближается, в функцию и оценить результат. Это отлично работает, когда нет дыр или асимптот для этого конкретного значения x. Вы можете быть уверены, что этот метод работает, если вы не делите на ноль при подстановке.

Если функция f(x) не имеет дырок или асимптот в точке x=a, то:

Иногда в точке x=a будет дырка . Предел в этом случае — это высота функции, если бы дыры не было. Другими словами, если функция является рациональным выражением с коэффициентами, которые можно сократить, сократите член алгебраически, а затем подставьте в результирующее выражение.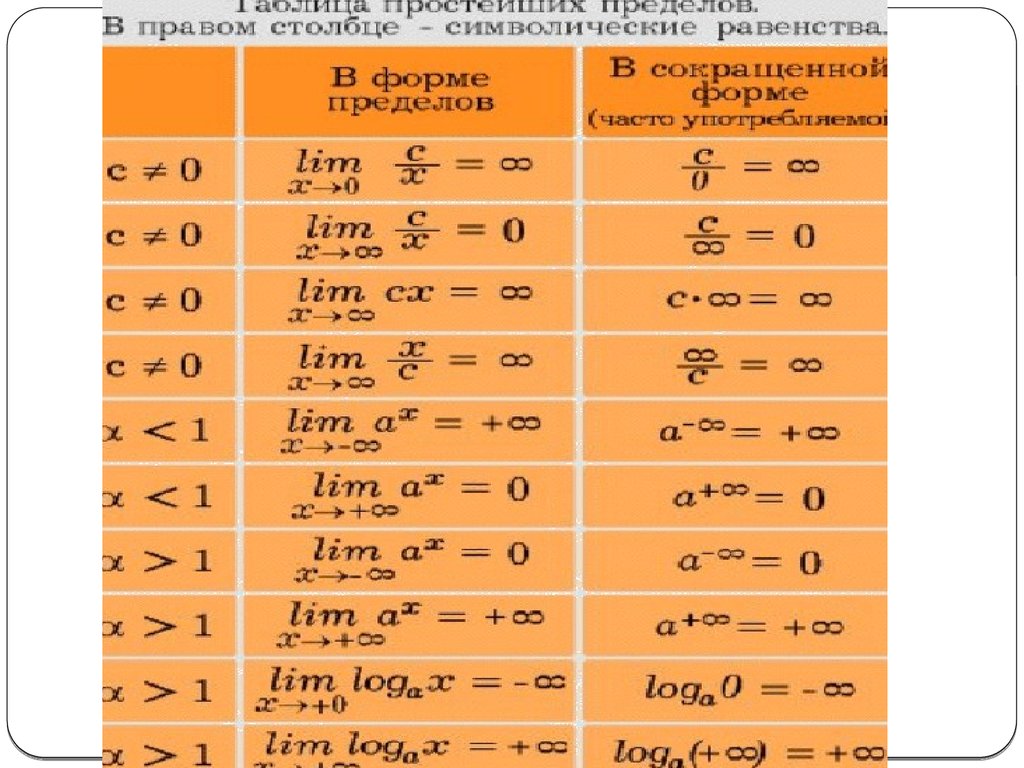 Если никакие факторы нельзя отменить, возможно, предела в этой точке не существует из-за асимптот.

Посмотрите на следующие два предела:

Предел слева не может быть вычислен прямой подстановкой, потому что если подставить 2, то получится деление на ноль. Предел справа можно вычислить с помощью прямой подстановки. потому что дыра существует при x=2, а не при x=3. Таким образом, предел равен:

---

Примеры

Пример 1

Ранее вас спрашивали, как определить, следует ли использовать подстановку для решения ограничения. Чтобы решить, является ли замена подходящим первым шагом, вы всегда можете просто попробовать ее. Вы поймете, что это не сработает, если в конечном итоге попытаетесь вычислить выражение со знаменателем, равным нулю. Если это произойдет, вернитесь назад и попытайтесь учесть и отменить, а затем попробуйте заменить снова.

Пример 2

Оцените следующий предел, сначала отменив, а затем используя замену.

Пример 3

Оцените следующий предел аналитически:

Пример 4

Оцените следующий предел аналитически.

Пример 5

Оцените следующий предел аналитически.

---

Обзор

Аналитически оцените следующие пределы.

---

Обзор (ответы)

Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 14.4.

---

Словарь

Срок	Определение
аналитически	Одним из способов аналитической оценки предела является подстановка. Подстановка — это метод определения пределов, при котором значение, к которому приближается х, подставляется в функцию и оценивается результат.
Асимптоты	Асимптота — это линия на графике функции, представляющая значение, к которому функция может приближаться, но не достигает (за некоторыми исключениями).
Отверстие	На графике рациональной функции существует дыра при любом входном значении, при котором и числитель, и знаменатель функции равны нулю.
предел	Предел — это значение, к которому приближается выход функции, когда вход функции приближается к заданному значению.

---

Дополнительные ресурсы

Практика: оценка пределов с помощью замены

Реальный мир: пределы допуска

---

Эта страница под названием 1.5: Оценить ограничения с помощью замещения распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с использованием исходного контента, отредактированного в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

ПОД ЛИЦЕНЗИЕЙ

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   СК12

   Лицензия

   СК-12

   Программа OER или Publisher

   СК-12

   Показать оглавление

   нет

2. Теги

   1. аналитически
   2. асимптоты
   3. отверстие
   4. предел
   5. источник@https://www. ck12.org/c/calculus

Раздел 9.2: Нахождение пределов: свойства пределов

Результаты обучения

• Найдите предел суммы, разности и произведения.
• Найдите предел многочлена.
• Найдите предел силы или корня.
• Найдите предел частного.

Нахождение предела суммы, разности и произведения

Построение графика функции или изучение таблицы значений для определения предела может быть обременительным и занимать много времени. Когда это возможно, более эффективно использовать свойства пределов , который представляет собой сборник теорем для нахождения пределов.

Знание свойств пределов позволяет нам напрямую вычислять пределы. Мы можем складывать, вычитать, умножать и делить пределы функций, как если бы мы выполняли операции над самими функциями, чтобы найти предел результата. Точно так же мы можем найти предел функции, возведенной в степень, возведя предел в эту степень. Мы также можем найти предел корня функции, взяв корень предела. Используя эти операции над пределами, мы можем найти пределы более сложных функций, найдя пределы их более простых составляющих функций.

A Общее примечание: свойства пределов

Пусть [латекс]а,к,А[/латекс] и [латекс]В[/латекс] представляют действительные числа, а [латекс]f[/латекс] и [латекс ]g[/latex] — функции, такие, что [latex]\underset{x\to a}{\mathrm{lim}}f\left(x\right)=A[/latex] и [latex]\underset{ x\to a}{\mathrm{lim}}g\left(x\right)=B[/latex]. Для пределов, которые существуют и являются конечными, свойства пределов суммированы в таблице ниже.

.

Константа, к	[латекс]\underset{x\to a}{\mathrm{lim}}k=k[/latex]
Постоянное время функции	[латекс]\underset{x\to a}{\mathrm{lim}}\left[k\cdot f\left(x\right)\right]=k\underset{x\to a}{\mathrm{ lim}}f\left(x\right)=kA[/latex]
Сумма функций	[латекс]\underset{x\to a}{\mathrm{lim}}\left[f\left(x\right)+g\left(x\right)\right]=\underset{x\to a }{\mathrm{lim}}f\left(x\right)+\underset{x\to a}{\mathrm{lim}}g\left(x\right)=A+B[/latex]
Различие функций	[латекс]\underset{x\to a}{\mathrm{lim}}\left[f\left(x\right)-g\left(x\right)\right]=\underset{x\to a }{\mathrm{lim}}f\left(x\right)-\underset{x\to a}{\mathrm{lim}}g\left(x\right)=AB[/latex]
Произведение функций	[латекс]\underset{x\to a}{\mathrm{lim}}\left[f\left(x\right)\cdot g\left(x\right)\right]=\underset{x\to a}{\mathrm{lim}}f\left(x\right)\cdot \underset{x\to a}{\mathrm{lim}}g\left(x\right)=A\cdot B[/latex ]
Коэффициент функций 9{n}[/latex], где [latex]n[/latex] — целое положительное число
n -й корень функции, где n — натуральное число	[латекс] \ underset {x \ to a} {\ mathrm {lim}} \ sqrt [n] {f \ left (x \ right)} = \ sqrt [n] {\ underset {x \ to a} { \mathrm{lim}}\left[f\left(x\right)\right]}=\sqrt[n]{A}[/latex]
Полиномиальная функция	[латекс]\underset{x\to a}{\mathrm{lim}}p\left(x\right)=p\left(a\right)[/latex]

Пример 1. Алгебраическое вычисление предела функции

Вычислить [латекс]\занижено{х\до 3}{\mathrm{lim}}\влево(2x+5\вправо)[/латекс].

Показать решение

Попробуйте

Оцените следующий предел: [latex]\underset{x\to -12}{\mathrm{lim}}\left(-2x+2\right)[/latex].

Показать решение

Попробуйте

Нахождение предела многочлена

Не все функции или их пределы предполагают простое сложение, вычитание или умножение. Некоторые могут включать полиномы. Напомним, что многочлен — это выражение, состоящее из суммы двух или более слагаемых, каждое из которых состоит из константы и переменной, возведенных в неотрицательную целую степень. Чтобы найти предел полиномиальной функции, мы можем найти пределы отдельных членов функции, а затем сложить их вместе. Кроме того, предел полиномиальной функции при приближении [latex]x[/latex] к [latex]a[/latex] эквивалентен простому вычислению функции для [latex]a[/latex] .

Как: Для заданной функции, содержащей многочлен, найти ее предел.

1. Используйте свойства пределов, чтобы разбить многочлен на отдельные члены.
2. Найдите пределы отдельных терминов.
3. Сложите ограничения вместе.
4. В качестве альтернативы оцените функцию для [latex]a[/latex] . 9{3}+5\вправо)[/латекс].

   Показать решение

   Попробуйте

   Нахождение предела степени или корня

   Когда предел включает в себя степень или корень, нам нужно другое свойство, которое поможет нам оценить его. Квадрат предела функции равен пределу квадрата функции; то же самое относится и к высшим силам. Точно так же квадратный корень из предела функции равен пределу квадратного корня функции; то же верно и для высших корней. 9{2}+6x+8}{x — 2}\right)[/latex] , можем ли мы определить предел функции, когда [latex]x[/latex] приближается к [latex]a[/latex] ?

   Да. Некоторые функции можно алгебраически переставить, чтобы можно было оценить предел упрощенной эквивалентной формы функции.

   Нахождение предела частного

   Нахождение предела функции, выраженной в виде частного, может оказаться более сложной задачей. Нам часто нужно переписать функцию алгебраически, прежде чем применять свойства предела. Если знаменатель равен 0, когда мы применяем свойства предела напрямую, мы должны переписать частное в другой форме. Один из подходов состоит в том, чтобы записать частное в факторизованной форме и упростить. 9{2}-11x+28}{7-x}\справа)[/латекс].

   Показать решение

   Попробуйте

   Пример 6.

   Оценка предела частного путем поиска ЖК-дисплея }{x}-\frac{1}{5}}{x — 5}\right)[/latex].

   Показать решение

   Попробуйте

   Оцените [латекс]\underset{x\to -5}{\mathrm{lim}}\left(\dfrac{\frac{1}{5}+\frac{1}{x}} {10+2x}\справа)[/латекс].

   Показать решение

   Как сделать: Учитывая предел функции, содержащей корень, используйте сопряжение для оценки.

   1. Если приведенное частное не находится в неопределенной форме [латекс]\левый(\фрак{0}{0}\правый)[/латекс], оценить напрямую.
   2. В противном случае перепишите сумму (или разность) двух частных как одно частное, используя наименьший общий знаменатель (LCD) .
   3. Если в числителе есть корень, рационализируйте числитель; умножьте числитель и знаменатель на сопряженное числителя. Напомним, что [latex]a\pm \sqrt{b}[/latex] являются сопряженными.
   4. Упростить.
   5. Оцените полученный лимит.

   Пример 7. Вычисление предела, содержащего корень, с использованием сопряжения {x}\right)[/latex].

   Показать решение

   Попробуйте

   Оцените следующий предел: [латекс]\underset{h\to 0}{\mathrm{lim}}\left(\dfrac{\sqrt{16-h}-4}{h}\right )[/латекс].

   Показать решение

   Попробуйте

   Пример 8. Оценка предела частного функции с помощью факторизации

   Оценить [латекс]\underset{x\to 4}{\mathrm{lim}}\left(\dfrac{4-x}{\sqrt{x}-2}\right)[/latex].

   Показать решение

   Попробуйте

   Оцените следующий предел: [латекс]\underset{x\to 3}{\mathrm{lim}}\left(\dfrac{x — 3}{\sqrt{x}-\sqrt{3) }}\справа)[/латекс].

   Показать решение

   Как: Имея частное с абсолютными значениями, оценить его предел.

   1. Попробуйте разложить или найти ЖК-дисплей.
   2. Если предел не может быть найден, выберите несколько значений рядом и по обе стороны от входа, где функция не определена. 9{+}}{\mathrm{lim}}\dfrac{6-x}{|x — 6|}[/latex].

      Показать решение

      Основные понятия

      • Свойства пределов можно использовать для выполнения операций над пределами функций, а не над самими функциями.
      • Предел полиномиальной функции можно найти, найдя сумму пределов отдельных членов.
      • Предел функции, возведенной в степень, равен той же степени предела функции. Другой метод — прямая замена.
      • Предел корня функции равен соответствующему корню предела функции.
      • Один из способов найти предел функции, выраженной в виде частного, состоит в том, чтобы записать частное в факторизованной форме и упростить.
      • Еще один метод нахождения предела сложной дроби — найти ЖК.
      • Предел, содержащий функцию, содержащую корень, может быть оценен с помощью сопряжения.
      • Пределы некоторых функций, выраженных в виде частных, можно найти с помощью факторизации.
      • Одним из способов оценки предела частного, содержащего абсолютные значения, является использование числовых данных. Настройка его по частям также может быть полезной.

      Глоссарий

      свойства пределов

      сборник теорем для нахождения пределов функций путем выполнения математических операций над пределами

       

      Раздел 9.2. Домашнее задание. Упражнения

      1. Приведите пример функции [latex]f[/latex], предел которой, когда [latex]x[/latex] приближается к [latex]a[/latex], это [латекс]f\влево(а\вправо)[/латекс].

      2. Когда для оценки предела рациональной функции используется прямая подстановка, когда [латекс]x[/латекс] приближается к [латекс]а[/латекс], и результат равен [латекс]f\left(a\right) =\frac{0}{0}[/latex], значит ли это, что предел [latex]f[/latex] не существует?

      3. Что значит сказать, что предел [латекс]f\левый(х\правый)[/латекс], когда [латекс]х[/латекс] приближается к [латекс]с[/латекс], не определен ?

      Для следующих упражнений оцените пределы алгебраически.

      9{2}}{x — 2}\right)[/latex]

      В следующем упражнении используйте данную информацию для оценки пределов: [latex]\underset{x\to c}{\mathrm{lim}} f\left(x\right)=3[/latex], [latex]\underset{x\to c}{\mathrm{lim}}g\left(x\right)=5[/latex]

      31 , [латекс]\underset{x\to c}{\mathrm{lim}}\left[2f\left(x\right)+\sqrt{g\left(x\right)}\right][/latex]

      32.

      No related posts.