Элемент множества множество: Множества — Теория — Основные понятия и обозначения

Множества — Теория — Основные понятия и обозначения

Множества Основные понятия и обозначения

Множество является настолько общим и одновременно изначальным понятием, что его строгое определение через более простые понятия дать затруднительно. Поэтому вслед за Г. Кантором, мы принимаем интуитивное представление о множестве, как о совокупности некоторых элементов, вполне определенных в случае каждого конкретного множества.      Определение. Элементы множества — это объекты, которые образуют данное множество, и могут обладать некоторыми свойствами и находиться в некоторых отношениях между собой или с элементами других множеств.      Пример. Множеством может быть школа, состоящая из элементов множества — учеников и работников школы. Воздух в комнате есть множество газовых молекул и взвешенных пылинок — твердых частиц. В то же время, множество молекул может быть твердым телом.      Обозначения. Множества обозначают заглавными, а элементы множеств — строчными латинскими буквами или строчными латинскими буквами с индексами. Элементы множеств обычно заключаются в фигурные скобки. Например, запись А={a,b,d,h} означает, что множество А состоит из четырех элементов a,b,d,h. В общем виде утверждение, что конечное множество A состоит из n элементов, записывается так:      Принадлежность элемента множеству обозначается символом ∈: (читают: элемент а принадлежит множеству А). В противном случае обозначают (читают: элемент а не принадлежит множеству А).      В дальнейшем изложении используются следующие общепринятые обозначения основных числовых множеств:      N — множество натуральных чисел, N={1,2,3,…};      Z — множество целых чисел, Z={…,-3,-2,-1,0,1,2,3,…};      Q — множество рациональных чисел. Всякое рациональное число можно представить в виде дроби: a/b, где ;      R — множество действительных чисел. Всякое действительное число можно представить в виде бесконечной десятичной дроби , с целой частью и . Множеству действительных чисел соответствует множество точек на числовой прямой.      Элементами множеств могут быть другие множества, тогда эти элементы могут обозначаться заглавными буквами.      Пример.      A = {D,C}, D={a, b}, C={c, d, e}. При этом , , но и .      A = {{x,y},z}. Эта запись означает, что множество A содержит два элемента: множество {x,y} и элемент z.      B= {{v}}. Это означает, что единственным элементом множества B является множество {v}.      Одна книга из множества книг в шкафу может рассматриваться как множество страниц.

§ 1. Понятие множества.

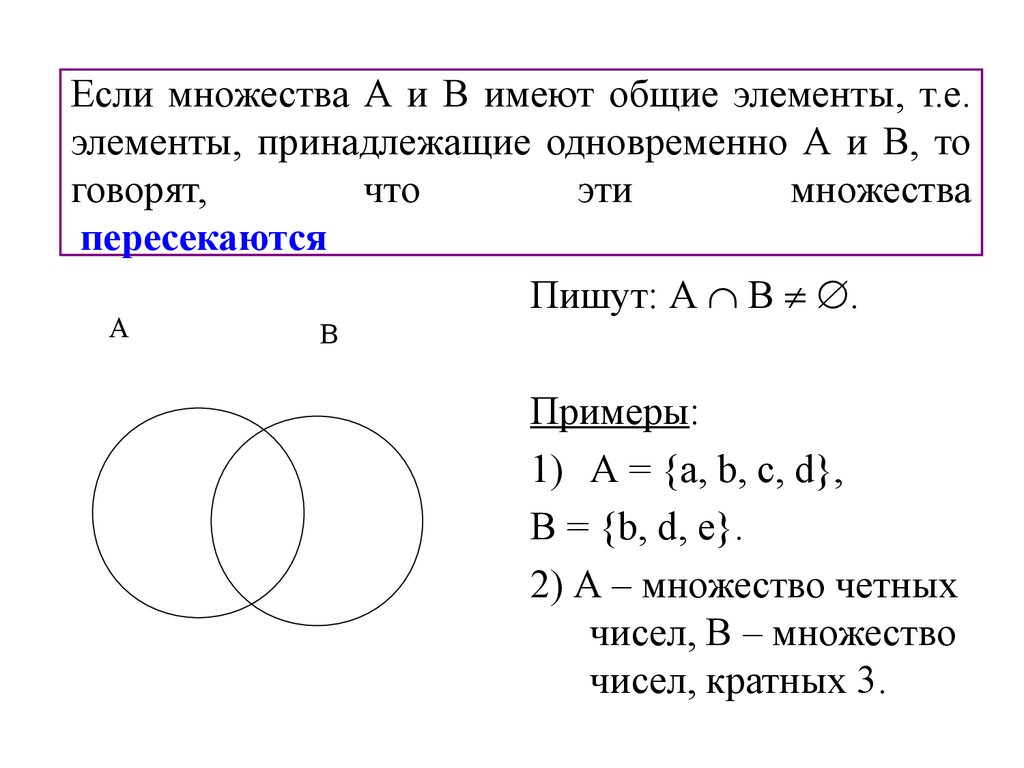Элемент множества. Пустое множество

Множество – основное понятие математики и поэтому не определяется через другие.

Обычно под множеством понимают совокупность предметов, объединенных по общему признаку. Так, можно говорить о множестве студентов в группе, множестве букв русского алфавита и т.д. В повседневной жизни вместо слова «множество» употребляют слова «набор», «коллекция», «группа» и т.д. Множества принято обозначать прописными буквами латинского алфавита: А, В, С, …, Z.

Для числовых множеств в математике приняты специальные обозначения:

N – множество натуральных чисел;

N₀ – множество целых неотрицательных чисел;

Z – множество целых чисел;

Q – множество рациональных чисел;

R – множество действительных чисел.

Объекты, из которых образовано множество, называют его элементами. Например, сентябрь является элементом множества месяцев в году, число 5 – элемент множества натуральных чисел. Элементы множества принято обозначать строчными буквами латинского алфавита. Элементами множества могут быть множества. Так можно говорить о множестве групп института. Элементы этого множества – группы, являющиеся в свою очередь множествами студентов.

Связь между множеством и его элементом выражают при помощи слова «принадлежит». Высказывание «Элемент а принадлежит множеству А» записывают так: а  А, причем эта запись может быть прочитана иначе: «а – элемент множества А», «множество А содержит элемент а». Высказывание «Элемент а не принадлежит множеству А» записывают так: а  А (иначе: «а не является элементом множества

А», «множество А не содержит элемент а»).

Если в обыденной речи слово «множество» связывают с большим числом предметов, то в математике этого не требуется. Множество может содержать один элемент, не содержать ни одного элемента.

Множество, не содержащее ни одного элемента, называют пустым и обозначают символом . Существует лишь одно пустое множество. Примерами пустого множества могут служить множество людей на Солнце, множество натуральных корней уравнения х + 8 = 0.

Множества могут быть конечными и бесконечными.

Множество называется конечным, если существует натуральное число п, такое, что все элементы множества можно перенумеровать числами от 1 до п. в противном случае множество называют бесконечным. Примером конечного множества является множество цифр, бесконечного – множество натуральных чисел.

Множество считают заданным, если о любом объекте можно сказать, принадлежит он этому множеству или не принадлежит.

Множество можно задать, перечислив все его элементы. Запись С = {а, б, в, г} обозначает, что множество С содержит элементы а, б, в, г.

Каждый элемент входит в множество только один раз. Например, множество различных букв в слове «математика» запишется так: {м, а, т, е, и, к}.

Данный способ применим для конечных множеств, которые содержат небольшое число элементов.

Иногда, используя данный способ, можно задать и бесконечное множество. Например, множество натуральных чисел может быть представлено в виде: N = {1, 2, 3, 4, …}. Такой способ записи возможен лишь тогда, когда из записанной части множества видно, что скрывается под многоточием.

Другой способ задания множеств состоит в следующем: указывают характеристическое свойство его элементов. Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.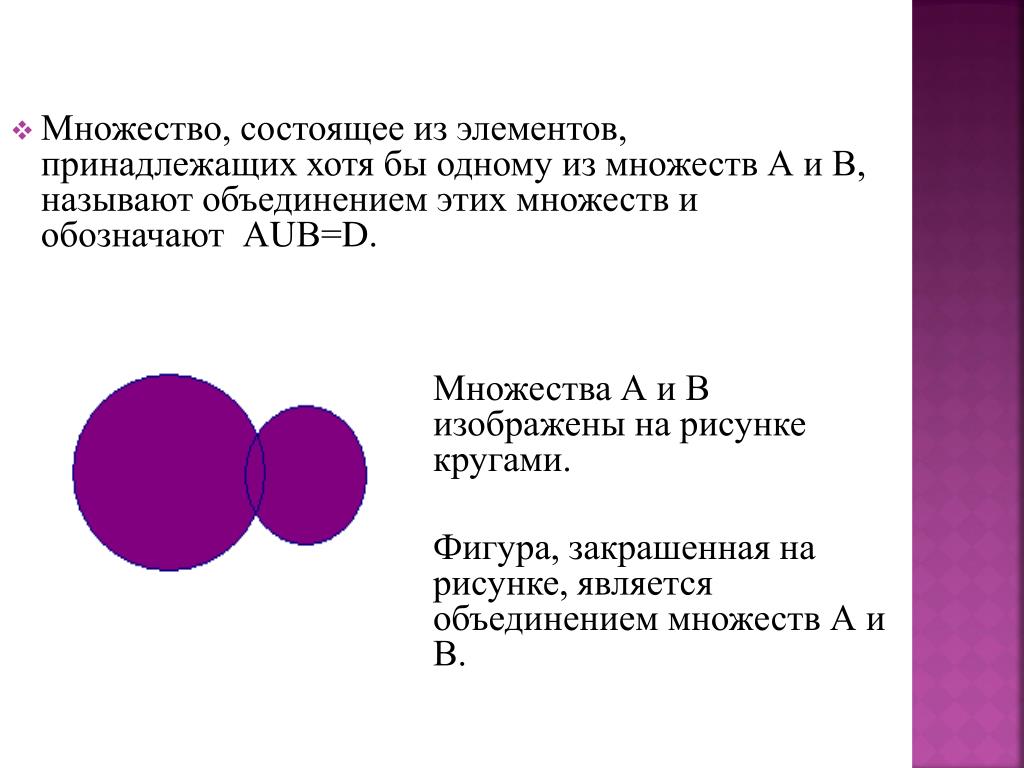

Случается, что одно и то же множество можно задать, указав различные характеристические свойства его элементов. Например, множество двузначных чисел, делящихся на 11 и множество натуральных чисел первой сотни, записанных двумя одинаковыми цифрами, содержат одни и те же элементы.

При данном способе задания множество может быть записано так: в фигурных скобках пишут сначала обозначение элемента, затем проводят вертикальную черту, после которой записывают свойство, которым обладают элементы данного множества. Например, множество

А натуральных чисел, меньших 5, запишется так: А = {ххN, х < 5}.

Диаграмма Венна — примеры, определение, формула, символы, типы

Диаграмма Венна используется для визуального представления различий и сходств между двумя понятиями. Диаграммы Венна также называются логическими или диаграммами множеств и широко используются в теории множеств, логике, математике, бизнесе, обучении, информатике и статистике.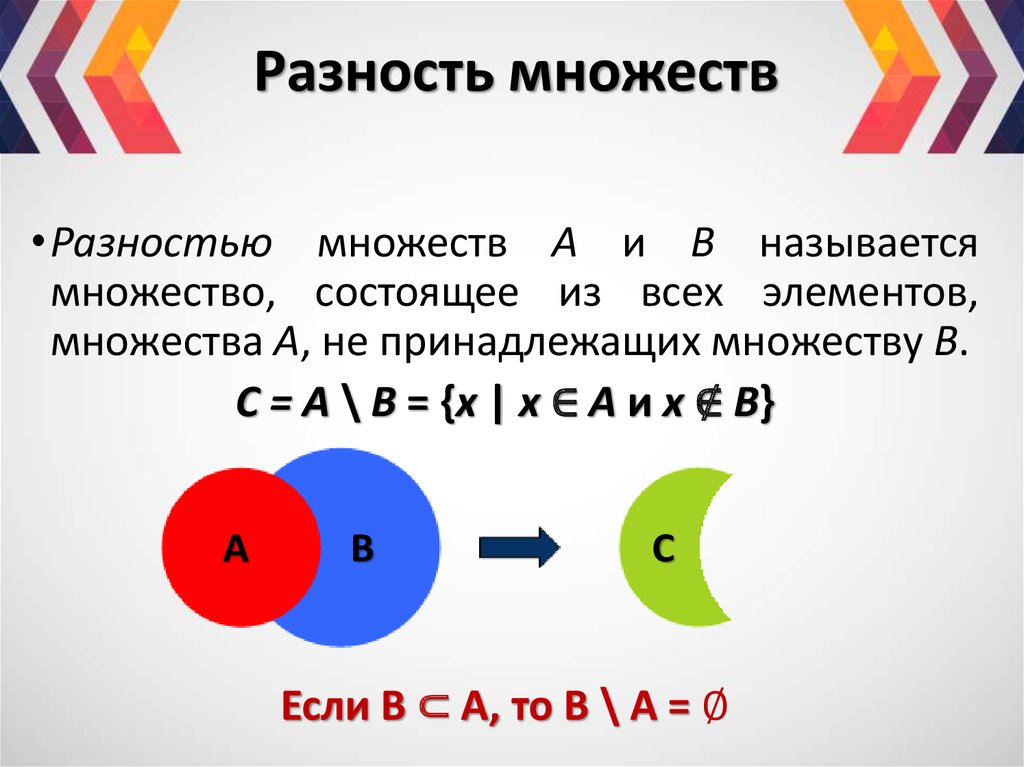

Давайте узнаем о диаграммах Венна, их определении, символах и типах с решенными примерами.

1.	Что такое диаграмма Венна?
2.	Символы диаграммы Венна
3.	Диаграмма Венна для операций набора
4.	Диаграмма Венна для трех наборов
5.	Как нарисовать диаграмму Венна?
6.	Диаграмма Венна Формула
7.	Применение диаграмм Венна
8.	Часто задаваемые вопросы о диаграмме Венна

Что такое диаграмма Венна?

Диаграмма Венна — это диаграмма, которая помогает нам визуализировать логическую связь между наборами и их элементами и помогает нам решать примеры на основе этих наборов. Диаграмма Венна обычно использует пересекающиеся и непересекающиеся круги (хотя могут использоваться и другие замкнутые фигуры, такие как квадраты) для обозначения отношений между множествами.

Пример диаграммы Венна

Рассмотрим пример диаграммы Венна. Вот диаграмма Венна, которая показывает корреляцию между следующим набором чисел.

• Один набор содержит четные числа от 1 до 25, а другой набор содержит числа из таблицы 5x от 1 до 25.
• Пересекающаяся часть показывает, что 10 и 20 являются четными числами, а также кратными 5 от 1 до 25.

Термины, относящиеся к диаграмме Венна

Давайте разберемся со следующими терминами и понятиями, связанными с диаграммой Венна, чтобы лучше понять ее.

Универсальный набор

Всякий раз, когда мы используем набор, проще сначала рассмотреть более крупный набор, называемый универсальным набором, который содержит все элементы во всех рассматриваемых наборах. Всякий раз, когда мы рисуем диаграмму Венна:

• Большой прямоугольник используется для представления универсального множества и обычно обозначается символом E или иногда U.
• Все остальные наборы представлены кружками или замкнутыми фигурами внутри этого большего прямоугольника.
• Каждое множество является подмножеством универсального множества U.

Рассмотрим приведенное выше изображение:

• U — универсальный набор со всеми числами от 1 до 10, заключенными в прямоугольник.
• A — множество четных чисел от 1 до 10, являющееся подмножеством универсального множества U и помещенное внутри прямоугольника.
• : Все нечетные числа от 1 до 10 будут помещены за пределы круга и внутри прямоугольника, как показано выше.

Подмножество

Диаграммы Венна используются для отображения подмножеств. Подмножество на самом деле является набором, который содержится в другом наборе. Рассмотрим примеры двух множеств A и B на приведенном ниже рисунке. Здесь A является подмножеством B. Окружность A полностью содержится внутри окружности B. Кроме того, все элементы A являются элементами множества B.

Это отношение символически представлено как A ⊆ B. Оно читается как A является подмножеством B или A подмножеством B. Каждое множество является подмножеством самого себя. то есть A ⊆ A. Вот еще один пример подмножеств:

• N = множество натуральных чисел
• I = набор целых чисел
• Здесь N ⊂ I, потому что все натуральные числа целые.

Символы диаграммы Венна

Имеется более 30 символов диаграммы Венна. В этом разделе мы узнаем о трех наиболее часто используемых символах. Они перечислены ниже как:

Символы диаграммы Венна	Пояснение
Символ союза — ∪	A ∪ B читается как объединение A B. Элементы, принадлежащие либо к набору A, либо к набору B, либо к обоим наборам. У — универсальный набор.
Символ пересечения — ∩	A ∩ B читается как A пересечение B. Элементы, принадлежащие обоим наборам А и В. У — универсальный набор.
Символ дополнения — A c или A’	А’ читается как дополнение. Элементы, не принадлежащие множеству А. У — универсальный набор.

Давайте разберемся в концепции и использовании трех основных символов диаграммы Венна, используя изображение, приведенное ниже.

Символ	Относится к	Всего элементов (количество студентов)
А ∪ С	Количество студентов, предпочитающих либо гамбургер, либо пиццу, либо и то, и другое.	1 + 10 + 2 + 2 + 6 + 9 = 30
А ∩ С	Количество студентов, предпочитающих и гамбургер, и пиццу.	2 + 2 = 4
А ∩ В ∩ С	Количество студентов, предпочитающих гамбургер, пиццу, а также хот-дог.	2
А с или А’	Количество студентов, которые не предпочитают гамбургер.	10 + 6 + 9 = 25

Диаграмма Венна для операций над множествами

В теории множеств мы можем выполнять определенные операции над заданными множествами. Эти операции следующие:

• Союз Сет
• Пересечение набора
• Дополнение к набору
• Отличие комплекта

Объединение множеств Диаграмма Венна

Объединение двух множеств A и B может быть задано следующим образом: A ∪ B = {x | x ∈ A или x ∈ B}. Эту операцию над элементами множества A и B можно представить с помощью диаграммы Венна с двумя окружностями. Суммарная область обеих окружностей вместе обозначает объединение множеств A и B.

Пересечение множества Диаграмма Венна

Пересечение множеств A и B определяется формулой: A ∩ B = {x : x ∈ A и x ∈ B}. Эту операцию над множествами A и B можно представить с помощью диаграммы Венна с двумя пересекающимися окружностями. Область, общая для обеих окружностей, обозначает пересечение множества A и множества B.

Дополнение множества Диаграмма Венна

Дополнение любого множества A может быть задано как A’. Это представляет элементы, которых нет в наборе A, и может быть представлено с помощью диаграммы Венна с кругом. Область, покрываемая универсальным набором, исключая область, покрываемую множеством A, дает дополнение A.

Разность наборов Диаграмма Венна

Разность наборов может быть представлена ​​как A — B. Это также называется «относительным дополнением». Эту операцию над множествами можно представить с помощью диаграммы Венна с двумя окружностями. Область, покрываемая множеством A, исключая область, общую для множества B, дает разницу множеств A и B.

Мы можем наблюдать вышеописанные операции с множествами, используя цифры, приведенные ниже:

Диаграмма Венна для трех наборов

Три набора Диаграмма Венна состоит из трех перекрывающихся кругов, и эти три круга показывают, как связаны элементы трех наборов. Когда диаграмма Венна состоит из трех наборов, ее также называют диаграммой Венна с тремя кругами. На диаграмме Венна, когда все эти три круга перекрываются, перекрывающиеся части содержат элементы, которые либо являются общими для любых двух кругов, либо они являются общими для всех трех кругов. Давайте рассмотрим приведенный ниже пример:

Вот некоторые важные наблюдения из приведенного выше изображения:

• Элементы в P и Q = только элементы в P и Q плюс элементы в P, Q и R.
• Элементы в Q и R = только элементы в Q и R плюс элементы в P, Q и R.
• Элементы в P и R = только элементы в P и R плюс элементы в P, Q и R.

Как нарисовать диаграмму Венна?

Диаграммы Венна можно рисовать с неограниченным количеством кругов. Поскольку число больше трех становится очень сложным, мы обычно будем рассматривать только два или три круга на диаграмме Венна. Вот 4 простых шага, чтобы нарисовать диаграмму Венна:

• Шаг 1: Разделите все предметы на наборы.
• Шаг 2: Нарисуйте прямоугольник и назовите его в соответствии с соотношением между множествами.
• Шаг 3: Нарисуйте круги в соответствии с количеством имеющихся у вас категорий.
• Шаг 4: Поместите все предметы в соответствующие круги.

Пример: Давайте нарисуем диаграмму Венна, чтобы показать категории уличных и домашних животных для следующих домашних животных: попугаи, хомяки, кошки, кролики, рыбы, козы, черепахи, лошади.

• Шаг 1: Разделите все предметы на наборы (Здесь, его питомцы): Домашние питомцы: Кошки, Хомяки и Попугаи. Домашние животные на открытом воздухе: лошади, черепахи и козы. Обе категории (открытая и закрытая): Кролики и Рыбы.
• Шаг 2: Нарисуйте прямоугольник и назовите его в соответствии с соотношением между двумя наборами. Здесь давайте назовем прямоугольник домашними животными.
• Шаг 3: Нарисуйте круги в соответствии с количеством имеющихся у вас категорий. В вопросе-образце есть две категории: домашние животные и домашние животные. Итак, давайте нарисуем два круга и убедимся, что круги перекрываются.

• Шаг 4: Поместите всех питомцев в соответствующие круги. Если есть определенные питомцы, подходящие под обе категории, разместите их на пересечении наборов, где круги перекрываются. Кроликов и рыбок можно содержать в качестве комнатных и уличных питомцев, поэтому они располагаются на пересечении обоих кругов.

• Шаг 5: Если есть питомец, который не подходит ни для дома, ни для улицы, поместите его внутри прямоугольника, но вне кругов.

Диаграмма Венна Формула

Для любых двух заданных множеств A и B формула диаграммы Венна используется для нахождения одного из следующих значений: количество элементов A, B, A U B или A ⋂ B, когда заданы остальные 3. Формула гласит:

• n(A U B) = n(A) + n(B) – n (A ⋂ B)

Здесь n(A) и n(B) представляют количество элементов в A и B соответственно. n(A UB) и n(A ⋂ B) представляют количество элементов в AU B и A ⋂ B соответственно. Эта формула также расширена до 3 сетов и говорит:

• n (A U B U C) = n(A) + n(B) + n(C) — n(A ⋂ B) — n(B ⋂ C) — n(C ⋂ A) + n(A ⋂ Б ⋂ В)

Вот пример формулы диаграммы Венна.

Пример: В крикетной школе 12 игроков любят боулинг, 15 любят играть ватин, а 5 любят и то, и другое. Тогда сколько игроков любят либо боулинг, либо ватин.

Решение:

Пусть A и B — наборы игроков, которые любят играть в боулинг и ватин соответственно. Тогда

n(A) = 12

n(B) = 15

n(A ⋂ B) = 5 

Нам нужно найти n(A UB). Используя формулу диаграммы Венна, получаем

Применение диаграммы Венна

Использование диаграмм Венна имеет несколько преимуществ. Диаграмма Венна используется для иллюстрации понятий и групп во многих областях, включая статистику, лингвистику, логику, образование, информатику и бизнес.

• Мы можем визуально организовать информацию, чтобы увидеть отношения между наборами элементов, такие как общие черты и различия, и изобразить отношения для визуальной коммуникации.
• Мы можем сравнить два или более предмета и четко увидеть, что у них общего, а что отличает их. Это может быть сделано для выбора важного продукта или услуги для покупки.
• Математики также используют диаграммы Венна в математике для решения сложных уравнений.
• Мы можем использовать диаграммы Венна для сравнения наборов данных и поиска корреляций.
• Диаграммы Венна можно использовать для объяснения логики утверждений или уравнений.

☛ Статьи по теме:

Ознакомьтесь со следующими страницами, посвященными диаграммам Венна:

• Операции над множествами
• Обозначение реестра
• Набор нотаций конструктора
• Статистика
• Вероятность

Важные примечания к диаграммам Венна:

Вот несколько моментов, которые следует помнить при изучении диаграмм Венна:

• Каждое множество является подмножеством самого себя, т. е. A ⊆ A.
• Универсальный набор вмещает все рассматриваемые наборы.
• Если A ⊆ B и B ⊆ A, то A = B
• Дополнением дополнения является само заданное множество.

 

Примеры диаграммы Венна

1. Пример 1: Возьмем в качестве примера набор с различными видами фруктов, A = {гуава, апельсин, манго, заварное яблоко, папайя, арбуз, вишня}. Представьте эти подмножества, используя обозначения множеств: а) плоды с одним семенем б) плоды с более чем одним семенем

   Решение: Среди различных фруктов только манго и вишня имеют одно семя.

   Таким образом,

   Ответ: а) Плод с одним семенем = {манго, вишня} b) Плод с более чем одним семенем = {гуава, апельсин, заварное яблоко, папайя, арбуз}

   Примечание: Если мы представляем эти два набора на диаграмме Венна, часть пересечения пуста.

2. Пример 2: Возьмем в качестве примера два множества A и B, где A = {3, 7, 9} и B = {4, 8}. Эти два множества являются подмножествами универсального множества U = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Найдите A ∪ B.

   Решение: Диаграмму Венна для приведенных выше соотношений можно изобразить следующим образом:

   Ответ: A ∪ B означает, что все элементы принадлежат либо множеству A, либо множеству B, либо обоим наборы = {3, 4, 7, 8, 9}

3. Пример 3: Используя диаграмму Венна, найдите X ∩ Y, учитывая, что X = {1, 3, 5}, Y = {2, 4, 6}.

   Решение:

   Дано: X = {1, 3, 5}, Y = {2, 4, 6}

   Диаграмма Венна для приведенного выше примера может быть представлена ​​как

   3

   3 Ответ: Из заштрихованной синей частью диаграммы Венна видно, что X ∩ Y = ∅ (нулевое множество).

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами

Записаться на бесплатный пробный урок

Практические вопросы по диаграмме Венна

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о диаграммах Венна

Что такое диаграмма Венна в математике?

В математике диаграмма Венна используется для визуализации логической связи между множествами и их элементами и помогает нам решать примеры на основе этих множеств.

Как читать диаграмму Венна?

Следующие шаги необходимо выполнить при чтении диаграммы Венна:

• Во-первых, обратите внимание на все круги, которые присутствуют на всей диаграмме.
• Каждый элемент, присутствующий в круге, является отдельным элементом или набором данных.
• Пересекающиеся или перекрывающиеся части кругов содержат элементы, общие для разных кругов.
• Части, которые не перекрываются и не пересекаются, показывают элементы, уникальные для другой окружности.

В чем важность диаграммы Венна?

Диаграммы Венна используются в различных областях, включая бизнес, статистику, лингвистику и т. д. Диаграммы Венна можно использовать для визуальной организации информации, чтобы увидеть взаимосвязь между наборами элементов, таких как общие черты и различия, и изобразить отношения для визуальной коммуникации .

Как называется середина диаграммы Венна?

Когда два или более набора пересекаются, перекрываются в середине диаграммы Венна, это называется пересечением диаграммы Венна. Это пересечение содержит все элементы, общие для всех перекрывающихся наборов.

Как представить универсальное множество с помощью диаграммы Венна?

Большой прямоугольник используется для представления универсального набора и обычно обозначается символом E или иногда U. Все остальные наборы представлены кружками или замкнутыми фигурами внутри этого большего прямоугольника, представляющего универсальный набор.

Какие существуют типы диаграмм Венна?

Различные типы диаграмм Венна:

• Двухмножественная диаграмма Венна: Простейшая из диаграмм Венна, состоящая из двух кругов или овалов из разных наборов, чтобы показать их перекрывающиеся свойства.
• Диаграмма Венна с тремя наборами: Их также называют диаграммой Венна с тремя кругами, так как они состоят из трех кругов.
• Диаграмма Венна с четырьмя наборами: они состоят из четырех перекрывающихся кругов или овалов.
• Диаграмма Венна с пятью наборами: они состоят из пяти кругов, овалов или кривых. Чтобы построить диаграмму Венна с пятью наборами, вы также можете соединить диаграмму с тремя наборами с повторяющимися кривыми или кругами.

Каковы различные области применения диаграмм Венна?

Существуют различные случаи применения диаграмм Венна: теория множеств, логика, математика, бизнес, преподавание, информатика и статистика.

Может ли диаграмма Венна иметь 2 непересекающихся окружности?

Да, биграмма Венна может иметь две непересекающиеся окружности, где нет данных, общих для категорий, принадлежащих обеим окружностям.

Что такое формула диаграммы Венна?

Формула, которая очень помогает найти неизвестную информацию о диаграмме Венна: n(AU B) = n(A) + n(B) – n (A ⋂ B), где

• A и B — два набора.
• n(AU B) — количество элементов в A U B.
• n (A ⋂ B) — количество элементов в A ⋂ B.

Может ли диаграмма Венна иметь 3 круга?

Да, на диаграмме Венна может быть 3 круга, и она называется диаграммой Венна с тремя множествами, чтобы показать перекрывающиеся свойства трех кругов.

Что такое союз на диаграмме Венна?

Объединение — это один из основных символов, используемых на диаграмме Венна для отображения отношений между множествами. Объединение двух множеств C и D можно изобразить как C ∪ D и прочитать как C union D. Это означает, что элементы принадлежат либо множеству C, либо множеству D, либо обоим множествам.

Что такое диаграмма Венна A∩B?

A ∩ B (что означает пересечение A B) на диаграмме Венна представляет часть, общую для обеих окружностей, связанных с A и B. A ∩ B также может быть нулевым множеством, и в этом случае две окружности будет либо непересекающимся, либо может быть представлен пересекающимися кругами, не имеющими данных в части пересечения.

комплектов

комплектов

Грубо говоря, набор — это набор объекты. Объекты называются членов или элементов набора.

Теория множеств является основой математики, и существует ряд системы аксиом для теории множеств; фон Нейман-Годель-Бернайс (NBG) и Zermelo-Fraenkel-Choice (ZFC) являются наиболее известными. я дам неформальное изложение здесь, без обращения к системе аксиом.

Вы конструируете или определяете набор, говоря, каковы его элементы.

Вы можете определить набор с помощью листинга его элементы между фигурными скобки:

Я некоторое время использовал обозначение «элемент».

Определение. означает, что x является элементом комплект Х.

означает, что x не является элементом S.

порядка элементов в списке элементов набора не имеет значения. Таким образом,

Определение. Пусть X и Y — множества. Тогда, если и только если X и Y имеют одни и те же элементы.

Понятно, когда вы перечисляете элементы множества, которые не дубликаты разрешены: вы не пишете такие вещи, как » «.

Вы также можете определить набор, используя нотацию конструктора набора . Вот пример:

Конструктор множества состоит из двух операторов, разделенных символом » «, содержащихся в фигурных скобках. Два утверждения вместе дают свойства, которым должна удовлетворять элемент множества. (Таким образом, » » действует как логическое «и».)

Некоторые люди предпочитают следовать правилу, использованному выше: слева от » » указано, какое большое множество построено множество является подмножеством, а оператор справа от » » дает критерии принадлежности для подмножества.

Однако обычно предыдущее множество записывается как

Это проще написать и избежать введения ненужная переменная n в первом определении. Я обычно использую вторая версия везде, где это возможно.

Этот набор состоит из всех целых чисел, являющихся полными квадратами. Я мог бы напишите это более явно (но менее точно) как

Это менее точно, потому что «…» предполагает, что это понятно что за узор. Однако, увидев ряд Элементы «образца» могут сделать более очевидным, какие члены набор похож. В этом нет ничего плохого, пока есть нет возможности запутаться.

Вот пример использования двух переменных:

Я мог бы также написать это как

Этот набор состоит из пар действительных чисел, таких, что второе квадрат первого. (Кстати, последнее предложение дает словесное описание комплекта. Полезно говорить словами когда символы путаются.) Вот некоторые элементы набора:

Рассматриваемый набор на самом деле является графом .

В этом случае я не могу перечислить элементы набора — когда Я обсуждаю мощность , объясню почему — и таким образом, это особенно важно иметь определение конструктора набора доступный.

Вы также можете иметь наборы, элементы которых являются наборами. Например:

Это множество из трех элементов, два из которых являются множествами из двух элементы.

Определение. Пусть X — множество. Мощность X обозначается . Для конечного множества это количество элементов в X.

Оставим на время в стороне, что означает кардинальность для бесконечности. наборы. Однако отмечу, что существуют разные виды «бесконечный»!

Таким образом,

Определение. Набор без элементов называется пустой набор и обозначается или же .

Обратите внимание, что: пустой набор — это единственный набор с нулем элементы.

Примечание. Вы должны быть осторожны при строительстве множеств, чтобы избежать теоретико-множественных парадоксов. Например, вот Парадокс Рассела . Рассмотрим «множество S все множества, которые не являются членами самих себя». Является ли S элементом из С?

Если S является элементом S, то по определению S не является членом сам по себе — что противоречит моему предположению, что S является элементом S.

Если S не является элементом S, то S является элементом S, поскольку S состоит из множеств, которые не являются членами самих себя. Это тоже противоречие.

По закону исключенного третьего либо S является элементом S, либо не — но обе альтернативы приводят к противоречиям.

Парадоксов такого рода можно избежать, установив аксиомы для множества теории, которые не позволяют строить множества, подобные этому.

Мы использовали некоторые стандартные обозначения для определенных наборов, которые встречаются часто в математике. Вот краткий обзор:

представляет собой набор из целых чисел .

это множество рациональных номера .

это набор из действительных чисел .

это набор из комплексные номера .

Если вам просто нужны положительные целые числа (также известные как натуральных чисел , используйте или ; если вам нужны неотрицательные целые числа (иногда называемые целыми числами ), используйте . Примечание что некоторые люди включают 0 в (поэтому под «естественным цифры» они означают). Во избежание путаницы, это вероятно, лучше обратиться к «положительным целым числам» или «целые неотрицательные числа».

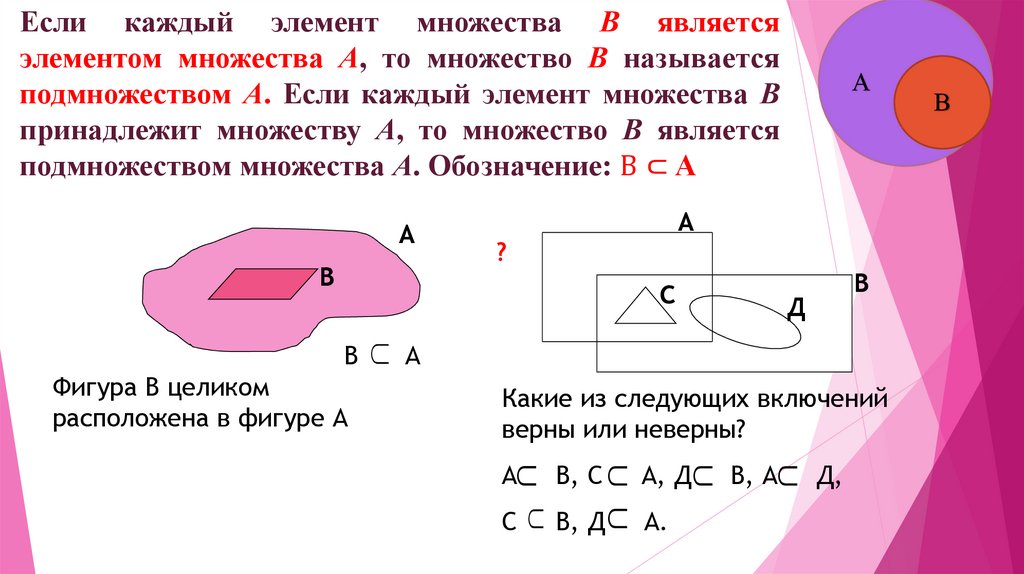
Определение. Пусть S и T — множества. Т это подмножество S тогда и только тогда, когда подразумевается . означает, что T является подмножеством S, и означает, что T не является подмножеством S.

Эта картинка иллюстрирует:

Изображение выше называется диаграммой Венна . Диаграммы Венна часто полезны для изображения множеств и отношений. среди наборов. Будьте осторожны, не заменяйте диаграммы доказательствами, Однако!

Замечания. (a) Некоторые люди используют » » для обозначения того, что T является подмножеством S, но не является равно S. Подмножество S, отличное от самого S, называется правильное подмножество S. С этим соглашением вы написать, чтобы означать, что T является подмножеством S, возможно, само S.

Я предпочитаю писать, чтобы означать, что T равно любому подмножеству S из . Если я хотите, чтобы T было правильным подмножеством S, я напишу . Причина: Чаще всего вы хотите включить возможность того, что , и вы должны использовать более простую запись ( а не ) для случая, который встречается чаще.

С другой стороны, некоторые люди предпочитают, потому что это аналогично записи, когда x и y являются числами.

б) тогда и только тогда, когда и .

Чтобы убедиться в этом, заметьте, что отношения и означают, что каждый элемент S является элементом T, и каждый элемент T является элементом S — то есть S и T имеют одни и те же элементы.

Мы будем часто доказывать равенство двух множеств, показывая, что каждое из них подмножество другого.

(c) Если (т. е. X — множество из n элементов) и S — подмножество X, то каждый элемент X может быть либо элементом S, либо нет. Таким образом, есть 2 варианта для каждого элемента. Отсюда следует, что Х имеет подмножества. (Помните, что это включает в себя как пустой set и сам X.)

---

Пример. Перечислите подмножества:

(а) .

(б) .

(a) Множество состоит из 3 элементов, поэтому оно имеет подмножества:

Обратите внимание, что вы должны писать » «, а не «а». это устанавливает с одним элементом a, тогда как a сам по себе является не набор.

(b) В наборе 2 элемента, а именно a и . Обратите внимание, что вы не «распаковывать».

Думайте о наборе как о сумке. В набор входит один элемент a и другой мешок (который содержит два элемента f и г). Количество вещей во «внешнем уровень» 2.

Отсюда следует, что множество имеет подмножества:

Обратите внимание, что » » получил «двойную упаковку: это набор содержащий набор.

---

Пример. Пусть

Докажи это .

Чтобы доказать это, я должен показать, что если , то . Часто можно доказать включение или равенство множеств, рассмотрев элементы.

Позволять . По определению B у меня есть для некоторого . В настоящее время

Так как m является целым числом, то и . Следовательно, n имеет вид , поэтому по определению .

Следовательно, .

---

Лемма. Пусть S и T — множества.

(а) .

(б) .

Доказательство. (a) Чтобы доказать, что , я надо доказать, что если , то . Но ложно для всех x, поэтому условное утверждение должно будь настоящим. (В этой ситуации вы часто говорите, что утверждение беспричинно верно — условие выполнено потому что дел нет!)

(b) Чтобы доказать, что , я должен показать, что если , то . Это тривиально верно — есть тавтология — так что .

Когда кто-то обсуждает наборы, обычно имеется в виду «большой набор». который содержит все рассматриваемые множества. Это большое множество» обычно называют вселенной ; обычно из контекста понятно, что это такое. Например, если я обсуждаю наборы целых чисел, вселенная — это набор целые числа . Если я обсуждаю наборы действительных чисел, Вселенная представляет собой набор действительных чисел.

Определение. (a) Пусть S и T — множества в вселенной X. 90 607 дополнений 90 608 к S — это множество элементы вселенной, не содержащиеся в S; это обозначено или же . Таким образом,

(b) (Относительное) дополнение S в T является множество элементов T, не являющихся элементами S; это обозначено. Таким образом,

Вот картинка; заштрихованная область.

Функция набора дополнений любит логические отрицания; аналогия даже распространяется на законы ДеМоргана, как я покажу ниже.

Определение. Пусть S и T — множества. Объединение S и T — это множество, элементами которого являются элементы S или элементы T; это обозначено. То есть,

Картина:

Определение. Пусть S и T — множества. Пересечение S и T — это множество, элементы которого являются элементами и S и T; это обозначено . То есть,

Картина:

Обратите внимание, что «или» и «и» в последних двух определения являются логическими «или» и «и».

---

Пример. Предположим, что вселенная представляет собой множество положительные целые числа:

Предполагать

Найдите элементы следующих множеств:

(а) .

(б) .

(с) .

(г) .

(е) .

(а) . Это набор, состоящий из 5, 7 и всех целых чисел, больших или равных 9.

(б) .

(с) .

(г) .

(е) .

---

Вы, вероятно, видели интервальных обозначений в другие курсы (например, по написанию решений неравенств). Предположим, что a и b — действительные числа, где .

У нас также есть полубесконечные интервалы:

В некоторых случаях нам нужно «разобрать» соединение неравенство типа » «, чтобы сделать доказательство. А составное неравенство — это союз («и») двух неравенства:

Аналогичные замечания остаются в силе, когда » » заменяется на » «.

Прежде чем я перейду к следующим примерам, вот предложения для чтение таких доказательств. Лучше всего было бы взять постановку задачи в примере и посмотреть, сможете ли вы написать доказательство самостоятельно — возможно, подсмотрите решение, когда вы застряли.

Если вы хотите просто прочитать эти решения, отметьте каждое заявление, выписывая дополнительные примечания или детали самостоятельно, если что-то не ясно. Вы должны работать — читать корректуру не похоже на чтение комикса! Когда вы читаете доказательства, которые длиннее и сложнее, вы должны ожидать, что вам придется работать усерднее — заниматься математикой, как делать упражнения. Возможно, вы не сможете уловить большая картина доказательства с первого раза, но по крайней мере попытаться понимать отдельные шаги.

Пример. Докажите, что .

Чтобы показать, что два набора равны, вы можете показать, что каждый из них содержится в Другой.

Это доказательство можно записать, используя множество логических обозначений, но я думаю, что это делает его несколько запрещающим читать. Следовательно, я буду напишите доказательство, используя комбинацию символов и слов.

Сначала я это докажу.

Позволять . По определению пересечение, это означает, что и . Эти утверждения эквивалентны составным неравенствам

Как я уже отмечал выше, каждое из этих составных неравенств может быть нарушено. разложить на два простых неравенства. При этом я получаю

В частности, у меня есть и . Эти простые неравенства такой же как . Но это подразумевает, что .

Я показал, что если , то . Это доказывает, что .

Далее я покажу это.

Позволять . Это означает, что или

Во-первых, , так что вместе с я получаю .

Далее , так что вместе с я получаю . Следовательно, .

(Интересно посмотреть, как последнее «Следовательно» следует из Наши правила логики. По правилу построения дизъюнкция , «» дает» или «. Но» или «это одно и то же в качестве » «. Вы, возможно, не понимали до этого «» содержит логическое «или»!)

Продолжая свое доказательство, у меня есть и , поэтому . Следовательно, .

Аналогично, у меня есть и , поэтому . Следовательно, .

Так как и , у меня есть по определению перекрестка. Это доказывает, что .

Наконец, так как и , я доказал, что .

---

Пример. Докажите, что .

Я покажу, что каждое из множеств и содержится в другом.

Предполагать . По определению союза или . Есть два случая.

Если , то . Но так . Следовательно, .

Если , то . Но так . Следовательно, .

Таким образом, выполняется в обоих случаях. Это показывает, что .

Теперь предположим. Затем .

Идея состоит в том, что четыре числа, составляющие конечные точки интервалы расположены так:

Я возьму два случая, выбрав число от 1 до 6. Я выбираю 3.

Теперь так или или. Рассмотрим два случая.

Во-первых, предположим. Но так . Следовательно, . Следовательно, .

(Если подумать, это построение дизъюнкции: дает или , которая, в свою очередь, подразумевает.)

Во-вторых, предположим. Но так . Следовательно, . Следовательно, .

Таким образом, выполняется в обоих случаях. Это показывает .

Это завершает доказательство того, что .

---

Пример. Пусть

Докажи это .

Я докажу результат, показав то и это.

Чтобы доказать это, я начинаю взяв элемент — но единственным элементом является 0. Так что я должен показать, что .

Во-первых, потому что . Следующий, потому что . Так как и , это Следовательно . Следовательно, .

Теперь я должен это показать. Позволять . По определение пересечения, это означает, что и .

Так как у меня есть. Так как я имеют . Это значит, что так. Следовательно, .

Это доказывает, что .

---

При доказательстве алгебры множеств мы увидим, что диаграммы Венна полезны в проверка того, что заданное отношение истинно. Однако они становятся слишком сложно, когда есть более 3 наборов.