Элементарная алгебра: Книга: «Современная элементарная алгебра в задачах и упражнениях» — Сергей Гашков. Купить книгу, читать рецензии | ISBN 978-5-4439-1196-0

Math.ru

Генрих Вебер, Иосиф Вельштейн

Одесса, Mathesis, 1906. 624 с.

Загрузить (Mb) djvu (8.44) pdf (-) ps (-) html (-) tex (-)

Содержание

Предисловие к русскому изданию.
Предисловие автора.
Предисловие ко второму изданию.

Книга I.
Основания арифметики.

Глава I. Натуральные числа.
§ 1.Единицы, комплексы.
§ 2.Сопряжение, мощность.
§ 3.Числа и счет.
§ 4.Теорема о совершенной индукции.
§ 5.Расположение чисел натурального ряда по величине.
§ 6.Кардинальные числа. Системы счисления.

Глава II. Арифметические действия.
§ 7.Сложение.
§ 8.Умножение.
§ 9.Произведения сумм.
§ 10.Возвышение в степень.
§ 11.Вычитание. Отрицательные числа.
§ 12.Действия над целыми числами.
§ 13.Умножение.

Глава III. Деление и введение дробей.
§ 14.Деление и делимость чисел.
§ 15.Общий наибольший делитель. Числа, первые между собой. Наименьшее кратное.
§ 16.Простые и составные числа.
§ 17.Дроби.
§ 18.Действия над дробями.
§ 19.Десятичные дроби.
§ 20.Приближенные значения десятичных дробей.

Глава IV. Иррациональные числа.
§ 21.Извлечение квадратных корней.
§ 22.Иррациональные числа.
§ 23.Верхняя и нижняя граница.

§ 24.Действия над иррациональными числами.
§ 25.Беcконечные десятичные дроби.
§ 26.Превращение обыкновенных дробей в десятичные.

Глава V. Отношения
§ 27.Измеримость.
§ 28.Отношения.
§ 29.Физические меры.
§ 30.Несоизмеримые величины.
§ 31.Пропорции.

Глава VI. Степени и логарифмы.
§ 32.Корни.
§ 33.Общая теория степеней.
§ 34.Логарифмы.
§ 35.Неперовы логарифмы.
§ 36.Бригговы логарифмы.
§ 37.Интерполяция.
§ 38.Примеры.

Глава VII. Уравнения первой степени.
§ 39.Уравнения первой степени с одним и двумя неизвестными.
§ 40.Уравнения первой степени с тремя неизвестными.

§ 41.Однородные уравнения.
§ 42.Приложения.

Глава VIII. Квадратные уравнения и мнимые числа.
§ 43.Квадратные уравнения.
§ 44.Мнимые числа.
§ 45.Извлечение квадратного корня из мнимых чисел.
§ 46.Функции второй степени.
§ 47.Геометрическое изображение комплексных чисел.

Глава IX. Перестановки и сочетания.
§ 48.Перестановки.
§ 49.Четные и нечетные перестановки.
§ 50.Составление перестановок.
§ 51.Изображение перестановок в циклах.
§ 52.Группы перестановок.
§ 53.Сочетания без повторений.
§ 54.Сочетания с повторениями.

Глава X. Различные приложения.

§ 55.Бином Ньютона.
§ 56.Арифметические ряды.
§ 57.Арифметические ряды высшего порядка.
§ 58.Геометрические ряды.
§ 59.Вычисление процентов и ренты.

Книга II.
Алгебра.

Глава XI. Алгебраические уравнения.
§ 60.Целые функции и их корни.
§ 61.Деление целых функций.
§ 62.Общий наибольший делитель.
§ 63.Приводимые и неприводимые функции.

Глава XII. Основные теоремы алгебры.
§ 64.Симметрические функции.
§ 65.Суммы одинаковых степеней.
§ 66.Основная теорема о существовании корня алгебраического уравнения.

Глава XIII. Неопределенные уравнения первой степени.

§ 67.Сравнения.
§ 68.Степенные вычеты.
§ 69.Периодические десятичные дроби.
§ 70.Уравнения Диофанта.

Глава XIV. Неопределенные уравнения второй степени.
§ 71.Теорема Вильсона.
§ 72.Квадратичные вычеты.
§ 73.Пифагоровы треугольники.
§ 74.Знаменитая теорема Фермата.
§ 75. Разложение числа на сумму двух квадратов.
§ 76.Разложение больших чисел на простых множителей.
§ 77.Совершенные числа.

Глава XV. Непрерывные дроби.
§ 78.Обращение иррацональных чисел в непрерывные дроби.
§ 79.Приближенное выражение иррациональных чисел при помощи рациональных дробей.
§ 80.Обращение квадратных корней в непрерывные дроби.

§ 81.Уравнение Пелля.

Глава XVI. Алгебраическое решение уравнений 3-ей и 4-ой степени.
§ 82.Трисекция угла.
§ 83.Формула Кардана.
§ 84.Мнимые корни.
§ 85.Дискриминант кубического уравнения.
§ 86.Тригонометрическое решение кубического уравнения.
§ 87.Решение уравнений четвертой степени.
§ 88.Дискриминант уравнения четвертой степени.
§ 89.Группа уравнения четвертой степени.
§ 90.Система двух уравнений второй степени с двумя неизвестными.

Глава XVII. Приближенное вычисление корней численных уравнений.
§ 91.Декартово правило знаков.
§ 92.Теорема Штурма.
§ 93.Regula Falsi.

§ 94.Пример.
§ 95.Разложение вещественного корня в непрерывную дробь.

Глава XVIII. Деление окружности на равные части.
§ 96.Корни из единицы.
§ 97.Алгебраическое определение корней из единицы.
§ 98.Правильный семнадцатиугольник.

Глава XX. Доказательства невозможности.
§ 99.Построение с помощью циркуля и линейки.
§ 100.Кубическое уравнение не разрешается с помощью квадратных корней.
§ 101.Разложение функции с помощью приобщения радикала.
§ 102.Неприводимый случай при решении кубического уравнения.
§ 103.Выражение корней из единицы при помощи радикалов.
§ 104.Уравнение пятой степени в общем виде не разрешается в радикалах.

Глава XXI. Из истории алгебры.
§ 105.Основные моменты в истории учения об алгебраическом решениии уравнений.

Книга III.
Анализ.

Глава XXII. Бесконечные ряды.
§ 106.Ряды с положительными членами.
§ 107.Бесконечные геометрические ряды.
§ 108.Дальнейшие примеры сходящихся и расходящихся рядов.
§ 109.Признаки сходимости.
§ 110.Основание системы натуральных логарифмов.

Глава XXIII. Бесконечные ряды с положительными и отрицательными членами.
§ 111.Общее определение суммы бесконечного ряда.
§ 112.Абсолютная и неабсолютная сходимость.
§ 113.Абелева теорема о непрерывности степенного ряда.
§ 114.Ряды с комплексными членами.

§ 115.Степенные ряды. Круг сходимости.
§ 116.Действия над бесконечными рядами.

Глава XXIV. Бесконечные сходящиеся ряды для показательной и для тригонометрических функций.
§ 117.Ряд для показательной функции.
§ 118.Тригонометрические функции как суммы рядов.

Глава XXV. Биномиальный ряд.
§ 119.Биномиальный ряд для целых отрицательных показателей.
§ 120.Непрерывность биномиальнаго ряда.
§ 121.Сумма биномиальнаго ряда.
§ 122.Биномиальный ряд на границе сходимости.

Глава XXVI. Логарифмические ряды.
§ 123.Логарифмические ряды.
§ 124.Циклометрические ряды.
§ 125.Функция arctg x.
§ 126.Тригонометрические ряды.

Глава XXVII. Бесконечные произведения.

§ 127.Сходимость беcконечного произведения.
§ 128.Преобразование синуса в бесконечное произведение.
§ 129.Бесконечное произведение для косинуса.
§ 130.Бернуллиевы числа.
§ 131.Эйлерово доказательство неограниченности комплекса простых чисел.

Глава XXVIII. Трансцендентность чисел е и π.
§ 132.Производные целой функции.
§ 133.Свойства показательной функции.
§ 134.Трансцендентность числа е.
§ 135.Трансцендентность числа π.

Глава XXIX. Функции, дифференциалы и интегралы.
§ 136.Геометрическое представление функций.
§ 137.Дифференциал и производная.
§ 138.Дифференциалы простых функций.
§ 139.Дифференциалы сложных функций.
§ 140.Теоремы Тейлора и Маклорена.
§ 141.Пoнятие об интеграле.
§ 142.Приближенное вычисление интегралов.

Дополнения.
I. § 144.Из истории числа и счисления.
II. § 144.Работы Евклида, Диофанта и Фермата по теории чисел.
III. § 145.Исторические сведения об иррациональных числах.
IV. § 146.Исторические сведения о логарифмах.
V. § 147.Определители.
VI. § 148.Распространение формулы Ньютона на полиномы.
VII. § 149.Разложение целых алгебраических функций на множителей.
VIII. § 150.Сравнения высших степеней.
IX. § 151.Сушествование первообразных корней по простому модулю.
X. § 152.Квадратичные вычеты простых чисел.

---

Загрузить (Mb) djvu (8.44) pdf (-) ps (-) html (-) tex (-)

Постоянный адрес этой страницы: http://math. ru/lib/62

Соминский И.С. Элементарная алгебра. Дополнительный курс

• формат pdf
• размер 4,23 МБ
• добавлен 02 августа 2015 г.

М.: ГИФМЛ, 1967. — 200 с.

Книга содержит, с одной стороны, более углубленное изложение изучаемых в школе разделов элементарной алгебры, с другой стороны, в ней излагаются и такие вопросы элементарной алгебры, которые совсем не входят в школьный курс, но бывают необходимы при дальнейшем изучении математики. Может быть использована поступающими в вузы, преподавателями математики и студентами педвузов, а также для самообразования. Содержит богатый материал для использования в школьных математических кружках.

Элементарные методы решения алгебраических уравнений с одним неизвестным
Решение алгебраического уравнения
Равносильные преобразования уравнений
Появление посторонних корней в процессе решения уравнения
Двучленные уравнения степени n
Трехчленные уравнения
Понижение степени возвратных и симметрических уравнений
Некоторые примеры решения уравнений высших степеней
Графическое решение уравнений четвертой степени пересечением окружности и фиксированной параболы Решение дробно-рациональных уравнений
Задачи к главе 1
Теория соединений
Размещения с повторениями
Перестановки с повторениями
Сочетания с повторениями
Задачи по комбинаторике
Приложение комбинаторики к вычислению вероятностей
Задачи к главе 2
Бином Ньютона и полиномиальная теорема
Бином Ньютона и биномиальные коэффициенты
Треугольник Паскаля
Полиномиальная теорема
Полиномиальные коэффициенты
Методы вычисления сумм степеней m первых n натуральных чисел
Задачи к главе 3
Многочлены от нескольких переменных
Однородные многочлены
Определение числа членов однородных многочленов данной степени
Тождество Лагранжа
Тождественность двух многочленов
Применение метода неопределенных коэффициентов к тождественным преобразованиям многочленов
Задачи к главе 4
Нелинейные системы алгебраических уравнений
Равносильность двух систем уравнений и теоремы о равносильных системах
Уравиения. являющиеся следствием данной системы уравнений
Элементариые методы решения нелинейных систем уравнений
Графические приемы решения системы с двумя неизвестными
Задачи к главе 5
Неравенства
Неравенство Коши
Средние величины
Примеры других тождественных неравенств
Приложение неравенств к элементарному определению экстремумов
Об экстремальных значениях квадратного трехчлена
Решение алгебраических неравенств с одним неизвестным первой и второй степени
Решение алгебраических неравенств с одним неизвестным степени выше второй
Задание областей на плоскости системами неравенств
Решение систем алгебраических неравенств с двумя неизвестными первой степени
Задачи к главе 6
Иррациональные алгебраические уравнения в действительной области
Тождественные преобразования явных алгебраических иррациональных функций в действительной области Способы решений иррациональных алгебраических уравнений и соответствующих систем уравнений
Задачи к глaвe 7
Показательные и логарифмические уравнения в действительной области
Основные тождества, применяемые при решении показательных и логарифмических уравнений
Способы решений показательных и логарифмических уравнений и соответствующих систем уравнений Графические приемы решения уравнений и систем
Задачи к главе 8
Указания, решения и ответы

Похожие разделы

1. Академическая и специальная литература
2. Математика
3. Линейная алгебра и аналитическая геометрия
4. Линейная алгебра

Элементарная алгебра — Открытая библиотека учебников

Доступные форматы

• ПДФ
• электронная книга
• Онлайн

Условия использования

Атрибуция
СС ПО

отзывов

Узнайте больше об отзывах.

Отзыв Ян Ван, инструктора Rogue Community College от 13.01.21

В книге подробно освещены все темы традиционной элементарной алгебры. читать далее

Отзыв Ян Ван, инструктора Rogue Community College от 13.01.21

Полнота рейтинг: 5 видеть меньше

В книге подробно освещены все темы традиционной элементарной алгебры.

Точность содержания рейтинг: 5

Ошибок не нашел.

Актуальность/долговечность рейтинг: 5

Примеры очень традиционные и типичные, прослужат долго.

Ясность рейтинг: 5

Текст написан ясным и простым языком, понятным учащимся.

Последовательность рейтинг: 5

Текст согласован с точки зрения терминологии и структуры.

Модульность рейтинг: 5

Текст можно легко реорганизовать и перестроить на протяжении всего курса.

Организация/Структура/Поток рейтинг: 5

Хорошо организовано!

Интерфейс рейтинг: 5

Интерфейс четкий, без искажений и не запутывает читателей.

Грамматические ошибки рейтинг: 5

Я не заметил ошибок в грамматике.

Культурная значимость рейтинг: 5

Язык книги совсем не оскорбительный.

Комментарии

1. Начертание шрифта затрудняет чтение учебника, возможно, поможет другой шрифт.
Вопросы в разделах «ПОПРОБУЙТЕ», которые находятся после каждого примера, выделены светло-серым цветом, что также затрудняет чтение текста.
3. Я думаю, что добавление цветов может сделать книгу более визуально привлекательной.

Отзыв Майка Дойла, адъюнкт-профессора муниципального колледжа Северного берега, от 03.06.20

Все охваченные области, где первый раздел каждой главы содержит соответствующий предметный указатель для каждой темы. читать далее

Отзыв Майка Дойла, адъюнкт-профессора муниципального колледжа Северного берега, от 03.06.20

Полнота рейтинг: 4 видеть меньше

Все охваченные области, где первый раздел каждой главы содержит соответствующий предметный указатель для каждой темы.

Точность содержания рейтинг: 5

Ошибок не заметил

Актуальность/долговечность рейтинг: 5

Не так много изменений в математике. Я чувствую, что обновления будет легко реализовать.

Ясность рейтинг: 3

Разделы слишком короткие. Хотелось бы видеть больше и разнообразных примеров. Одним из примеров является введение объединения подобных (похожих) терминов. Мне также нравится использование распределительного свойства, используемого для введения концепции, ab+ac=a(b+c)

. Последовательность рейтинг: 5

Никаких сюрпризов, я думал, что каждая концепция раскрыта.

Модульность рейтинг: 5

Каждый раздел достаточно мал, чтобы талантливые учителя могли расширить каждую тему.

Организация/Структура/Поток рейтинг: 4

Я бы предпочел, чтобы перед главой о факторинге многочленов была отдельная глава об операциях над полиномами. Кроме того, последнюю главу об одновременных уравнениях я хотел бы видеть после главы о построении графиков уравнений с двумя неизвестными.

Интерфейс рейтинг: 5

Диаграммы и графики выглядят хорошо, и использование редактора формул хорошо используется.

Грамматические ошибки рейтинг: 5

Я не нашел ошибок в грамматике. Большинство разделов состояло только из примеров, где каждый шаг также был показан без ошибок.

Культурная значимость рейтинг: 5

Ничего оскорбительного.

Комментарии

Текст бесплатный, поэтому не стоит ожидать глянцевых красочных страниц. Я хотел бы, чтобы каждый раздел состоял из множества примеров с более чем одним подходом к решению проблемы. Многие учащиеся на этом уровне должны увидеть множество текстовых задач, приложений каждой концепции, чтобы подготовить их к будущим занятиям по математике.
Формат упражнений не должен состоять из длинного бесконечного списка, где навигация к решениям занимает так много времени. Может ли быть лучший способ справиться с этим?

Отзыв Ирины Родерик, доцента Колледжа Марин, 19.03.19

Текст охватывает все традиционные положения курса элементарной алгебры. читать далее

Отзыв Ирины Родерик, доцента Колледжа Марин, 19.03.19

Полнота рейтинг: 4 видеть меньше

Текст охватывает все традиционные элементы курса элементарной алгебры.

Точность содержания рейтинг: 4

Текст излагает материал точно.

Актуальность/долговечность рейтинг: 4

Текст актуален и не устареет в ближайшее время.

Ясность рейтинг: 4

Материал изложен лаконично и ясно.

Последовательность рейтинг: 4

Текст согласован с точки зрения способа изложения и терминологии.

Модульность рейтинг: 4

Текст можно легко разделить на небольшие разделы и использовать на протяжении всего курса.

Организация/Структура/Поток рейтинг: 4

Текст структурирован и понятен.

Интерфейс рейтинг: 4

У текста нет проблем с интерфейсом.

Грамматические ошибки рейтинг: 5

Мне не удалось обнаружить ни одной грамматической ошибки.

Культурная значимость рейтинг: 4

Текст не выглядит нечувствительным к культурным особенностям. Он представляет материал таким образом, чтобы его могли понять учащиеся, принадлежащие к разным этническим и культурным группам.

Комментарии

Этот текст можно использовать для ознакомления с темами элементарной алгебры перед изучением средней алгебры или в качестве текста для курса элементарной алгебры.

Отзыв Эмаана Абдул-Маджида, доцента муниципального колледжа LaGuardia/CUNY от 01.02.18

Текст охватывает все области и идеи базового курса алгебры. В нем есть подробные примеры проблем с решениями и пошаговые инструкции по поиску решения. читать далее

Отзыв Эмаана Абдул-Маджида, доцента муниципального колледжа LaGuardia/CUNY от 01.02.18

Полнота рейтинг: 5 видеть меньше

Текст охватывает все области и идеи базового курса алгебры. В нем есть подробные примеры проблем с решениями и пошаговые инструкции по поиску решения.

Точность содержания рейтинг: 5

Содержание кажется беспристрастным и точным.

Актуальность/долговечность рейтинг: 5

Эта книга содержит информацию, которая не устареет. Он учит основам решения задач по алгебре, которые использовались в течение десятилетий и будут использоваться в течение десятилетий.

Ясность рейтинг: 5

Книга написана ясно и понятно.

Последовательность рейтинг: 5

Текст книги последовательно написан.

Модульность рейтинг: 5

Текст легко реорганизуется и выравнивается. Таким образом, вы можете удобно назначать различные разделы книги в другом порядке, чем хронологический порядок, в котором книга установлена ​​авторами.

Организация/Структура/Поток рейтинг: 5

Темы текста представлены логически.

Интерфейс рейтинг: 5

Интерфейс понятен и не отвлекает читателя.

Грамматические ошибки рейтинг: 5

Текст написан без грамматических ошибок.

Культурная значимость рейтинг: 3

Текст никоим образом не является культурно оскорбительным. Он не обсуждает расы или национальности.

Содержание

• 1 Обзор арифметики
• 2 Основные свойства действительных чисел
• 3 Основные операции с вещественными числами
• 4 Алгебраические выражения и уравнения
• 5 Решение линейных уравнений и неравенств
• 6 Факторные полиномы
• 7 Графики линейных уравнений и неравенств с одной и двумя переменными
• 8 рациональных выражений
• 9 Уравнения корней, радикалов и квадратных корней
• 10 Квадратные уравнения
• 11 Системы линейных уравнений
• 12 Приложение

Вспомогательный материал

• Отправить вспомогательный ресурс

О книге

Элементарная алгебра — это рабочий текст, который охватывает традиционные темы, изучаемые в современном курсе элементарной алгебры. Использование этой книги поможет учащемуся развить понимание и интуицию, необходимые для овладения алгебраическими методами и манипулятивными навыками. «Элементарная алгебра» — это рабочий текст, который охватывает традиционные темы, изучаемые в современном курсе начальной алгебры. Он предназначен для учащихся, которые (1) не знакомы с элементарной алгеброй, (2) ранее имели неприятный опыт изучения элементарной алгебры или (3) нуждаются в повторении алгебраических понятий и методов.

Об участниках

Авторы

Уэйд Эллис-младший , 20 лет работал преподавателем математики в Общественном колледже Вест-Вэлли в Саратоге, Калифорния. Уэйд в настоящее время является вторым вице-президентом Математической ассоциации Америки. В прошлом он был президентом Калифорнийского математического совета, Общественного колледжа и членом Совета по образованию в области математических наук. Он является соавтором многочисленных книг по использованию компьютеров в преподавании и изучении математики. Среди его многочисленных наград — премия AMATYC за выдающиеся достижения в области математики, медаль за выдающиеся заслуги перед гражданской службой в армии США, премия Хейворда за выдающиеся достижения в области образования от Академического сената Калифорнии и награда за выдающиеся заслуги от Калифорнийского совета по математике, Общественный колледж.

Денни Бурзински — профессор математики в Колледже Южной Невады, расположенном в Лас-Вегасе, штат Невада.

Добавить эту страницу

Предложить изменение этой записи книги

Элементарная алгебра | Британика

точка на комплексной плоскости

См. все СМИ

Связанные темы:

алгебра

Просмотреть весь связанный контент →

элементарная алгебра , раздел математики, изучающий общие свойства чисел и отношения между ними. Алгебра является фундаментальной не только для всей дальнейшей математики и статистики, но и для естественных наук, информатики, экономики и бизнеса. Наряду с письменностью она является краеугольным камнем современной научной и технической цивилизации. Более ранние цивилизации — вавилонская, греческая, индийская, китайская и исламская — все внесли важный вклад в развитие элементарной алгебры. Однако Европе эпохи Возрождения оставалось разработать эффективную систему представления всех действительных чисел и символику для представления неизвестных, отношений между ними и операций.

Элементарная алгебра связана со следующими темами:

Викторина «Британника»

Числа и математика

1. Вещественные и комплексные числа, константы и переменные — все вместе они называются алгебраическими величинами.

2. Правила эксплуатации для таких количеств.

3. Геометрические представления таких величин.

4. Составление выражений с использованием алгебраических величин.

5. Правила работы с такими выражениями.

6. Составление предложений, также называемых уравнениями, с использованием алгебраических выражений.

7. Решение уравнений и систем уравнений.

Алгебраические величины

Основной отличительной чертой алгебры является использование простых символов для представления числовых величин и математических операций. Согласно системе, созданной французским мыслителем XVII века Рене Декартом, буквы в начале алфавита ( a , b , c ,…) обычно представляют известные, но произвольные числа в задаче, в то время как буквы в конце алфавита, особенно x , y и z , представляют неизвестные величины или переменные. Знаки + и — обозначают сложение и вычитание этих величин, а умножение просто обозначается соседними буквами. Таким образом, a x представляет собой произведение a на x . Это простое выражение можно интерпретировать, например, как проценты, полученные за один год на сумму долларов вложено по годовой ставке х . Его также можно интерпретировать как расстояние, пройденное за 90 258 90 259 часов автомобилем, движущимся со скоростью 90 258 x 90 259 миль в час. Именно такая гибкость представления придает алгебре большую полезность.

Еще одна особенность, значительно расширившая круг алгебраических приложений, — геометрическое представление алгебраических величин. Например, для представления действительных чисел воображается прямая линия, бесконечная в обоих направлениях. Произвольная точка O можно выбрать в качестве начала отсчета, представляющего число 0, и другую произвольную точку U , выбранную справа от O . Отрезок O U (или точка U ) затем представляет единицу длины или число 1. Остальные положительные числа соответствуют кратным этой единицы длины, так что, например, 2 представлено отрезком O V вдвое длиннее O U и вытянутым в том же направлении. Точно так же отрицательные действительные числа простираются слева от 9.0258 О . Прямая линия, точки которой таким образом отождествляются с действительными числами, называется числовой линией. Многие более ранние математики понимали, что существует связь между всеми точками на прямой и всеми действительными числами, но именно немецкий математик Рихард Дедекинд сформулировал это в виде постулата в своей работе «Непрерывность и иррациональные числа » (1872 г.).

В декартовой системе координат (названной в честь Декарта) аналитической геометрии одна горизонтальная числовая линия (обычно называемая 9-й0258 x -ось) и одна вертикальная числовая линия ( y -ось) пересекаются под прямым углом в их общем начале координат, чтобы обеспечить координаты для каждой точки на плоскости. Например, точка на вертикальной линии, проходящей через некоторые 90 258 х 90 259 по оси 90 258 х 90 259, и на горизонтальной линии, проходящей через некоторые 90 258 y 90 259 по оси 90 258 y 90 259, представлена ​​парой действительных чисел ( 90 258 x , и ). Аналогичное геометрическое представление ( см. рисунок) существует для комплексных чисел, где горизонтальная ось соответствует действительным числам, а вертикальная ось соответствует мнимым числам (где мнимая единица i равна квадратному корню из -1). Алгебраическая форма комплексных чисел: x + i y , где x представляет действительную часть, а i y — мнимую часть.

Это сочетание пространства и числа дает возможность соединить алгебраические выражения или функции в одной переменной с геометрическими объектами на плоскости, такими как прямые линии и окружности. Результат этого спаривания можно рассматривать как граф ( см. рисунок) выражения для разных значений переменной.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

Любая из упомянутых выше величин может быть объединена в выражения в соответствии с обычными арифметическими операциями сложения, вычитания и умножения. Таким образом, a x  +  b y и a x x  +  b x  +  c — распространенные алгебраические выражения. Однако экспоненциальное представление обычно используется, чтобы избежать повторения одного и того же члена в произведении, поэтому вместо x x и y ³ вместо y y y y 90 пишется x ² . . (По соглашению x ⁰  = 1.) Выражения, построенные таким образом из действительных и комплексных чисел, алгебраические величины a ,  b , c , …, x , y , z , а три приведенные выше операции называются многочленами — слово, введенное в конце 16 века французским математиком Франсуа Виетом от греческого polys ( polys «многие») и латинское nominem («имя» или «термин»). Один из способов характеристики многочлена — число различных неизвестных или переменных величин в нем. Другой способ характеристики полинома — его степень. Степенью многочлена от одного неизвестного называется наибольшая степень входящего в него неизвестного. Выражения a x  +  b , a x ²  +  b x  +  c , and a x ³  +  b x ²  +  c x  +  d — общие многочлены от одного неизвестного ( x ) степеней 1, 2 и 3 соответственно. Когда задействовано только одно неизвестное, не имеет значения, какая буква используется для него. Вышеупомянутые многочлены с таким же успехом можно было бы записать в виде a y  +  b , a z ²  +  b z  +  c , and a t ³  +  b t ²  +  c t  +  d .

Поскольку некоторое представление о сложных функциях можно получить, аппроксимируя их более простыми функциями, полиномы первой степени были исследованы на раннем этапе. В частности, а x + B Y = C , которая представляет собой прямую линию и A x + B y +8. 1595915995995959959959159591259. ++ B y + B ++ B ++ B ++ B ++ B . плоскость в трехмерном пространстве, были одними из первых изученных алгебраических уравнений.

Посмотрите, как решить большую математическую задачу, применяя метод FOIL

Посмотрите все видео к этой статье

Многочлены можно комбинировать в соответствии с тремя арифметическими операциями сложения, вычитания и умножения, и в результате снова получится многочлен. Для упрощения выражений, полученных при объединении полиномов таким способом, используют распределительный закон, а также коммутативный и ассоциативный законы сложения и умножения ( см. Нажмите здесь, чтобы увидеть полноразмерный планшет). До недавнего времени основным недостатком алгебры была крайне утомительная рутинная работа с многочленами, но теперь ряд программ символической алгебры делают эту работу такой же простой, как ввод выражений в компьютер.

Расширив операции над многочленами, включив в них деление или отношения многочленов, можно получить рациональные функции. Примерами таких рациональных функций являются 2/3 x и ( a + B x ² )/( C + D x ² + E x ).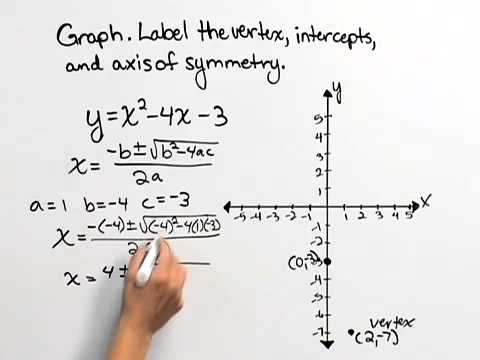 Работа с рациональными функциями позволяет ввести выражение 1/ х и его степени, 1/ х ² , 1/ х ³ , … (часто пишут х ⁻¹ 8, x ⁻² , x ⁻³ , …). Когда степень числителя рациональной функции не меньше степени ее знаменателя, можно разделить числитель на знаменатель так же, как одно целое число делится на другое. Таким образом, любую рациональную функцию можно записать в виде суммы многочлена и рациональной функции, в которой степень числителя меньше степени знаменателя. Например, ( x ⁸ — x ⁵ +3 x ³ +2)/( x ³ — 1) = x ³ — 1) = x ³ — 1). ³  − 1). Поскольку этот процесс уменьшает степени вовлеченных членов, он особенно полезен для вычисления значений рациональных функций и для работы с ними, когда они возникают в исчислении.

Для теоретических работ и приложений часто требуется найти числа, которые при замене неизвестных делают некоторый многочлен равным нулю. Такое число называется корнем многочлена. Например, многочлен −16 т ²  + 88 т  + 48 представляет собой высоту над Землей в t секунд снаряда, брошенного прямо вверх со скоростью 88 футов в секунду с вершины башни высотой 48 футов. (Число 16 в формуле получается из половины ускорения свободного падения, 32 фута в секунду за секунду.) Приравняв уравнение к нулю и разложив его на множители как (4 t  — 24)(−4 t  — 2) = 0, один положительный корень уравнения равен 6, а это означает, что объект упадет на землю примерно через 6 секунд после того, как будет брошен. (Эта задача также иллюстрирует важную алгебраическую концепцию свойства нулевого фактора: если a b  = 0, тогда либо a  = 0, либо b  = 0.)

Теорема о том, что у каждого полинома столько комплексных корней, сколько его степени, известна как основная теорема алгебры и впервые была доказана в 1799 году немецким математиком Карлом Фридрихом Гауссом. Существуют простые формулы для нахождения корней общих многочленов первой и второй степеней ( см. Щелкните здесь, чтобы увидеть полноразмерную таблицу), и гораздо менее простые формулы существуют для многочленов третьей и четвертой степеней. Незадолго до своей смерти в 1832 году французский математик Эварист Галуа обнаружил, что для общего многочлена степени выше четвертой такой формулы не существует. Однако существует много способов аппроксимации корней этих многочленов.

Решение систем алгебраических уравнений

Расширение изучения отдельных уравнений включает несколько уравнений, которые решаются одновременно — так называемые системы уравнений. For example, the intersection of two straight lines, a x  +  b y  =  c and A x  +  B y  =  C , can be found algebraically обнаружив значения x и и , которые одновременно решают каждое уравнение. Наиболее раннее систематическое развитие методов решения систем уравнений произошло в Древнем Китае. Адаптация задачи из классической китайской книги 1-го века нашей эры «Девять глав математических процедур » иллюстрирует, как возникают такие системы. Представьте, что есть два сорта пшеницы, четыре снопа первого сорта и пять снопов второго сорта. Хотя ни того, ни другого недостаточно для производства бушеля пшеницы, вы можете получить бушель, добавив три снопа первого типа к пяти снопам второго типа, или вы можете получить бушель, добавив четыре снопа первого типа к двум снопам второго типа. второй тип. Какую часть бушеля пшеницы содержит сноп каждого вида пшеницы?

Используя современные обозначения, предположим, что у нас есть два типа пшеницы соответственно, и х и y представляют собой количество бушелей, полученных на сноп первого и второго типа соответственно. Тогда задача приводит к системе уравнений: 3 x  + 5 y  = 1 (бушель) 4 x  + 2 y  = 1 (бушель)

Простой метод решения такой системы состоит в том, чтобы сначала решить любое уравнение для одной из переменных. Например, решив второе уравнение на y дает y  = 1/2 − 2 x . Затем правая часть этого уравнения может быть заменена на y в первом уравнении (3 x  + 5 y  = 1), а затем первое уравнение может быть решено, чтобы получить x (= 3/14). ). Наконец, это значение x можно подставить в одно из предыдущих уравнений, чтобы получить y (= 1/14). Таким образом, первый тип дает 3/14 бушелей на сноп, а второй тип дает 1/14. Обратите внимание, что решение (3/14, 1/14) было бы трудно различить с помощью графических методов. На самом деле любое точное значение, основанное на графическом решении, может быть только приблизительным; например, точка (0,0000001, 0) может выглядеть как (0, 0) на графике, но даже такая небольшая разница может иметь серьезные последствия в реальном мире.

Вместо индивидуального решения каждой возможной системы из двух уравнений с двумя неизвестными можно решить общую систему. Чтобы вернуться к общим уравнениям, приведенным выше: a x  +  b y  =  c A x  +  B y  =  C

Решения представлены как x  = ( B c  −  b C )/( a B — A B ) и Y = ( C A — C A )/( A B . Обратите внимание, что знаменатель каждого решения ( a B  —  A b ) одинаков. Он называется определителем системы, а системы, в которых знаменатель равен нулю, не имеют решения (в этом случае уравнения представляют собой параллельные прямые) или имеют бесконечно много решений (в этом случае уравнения представляют одну и ту же прямую).

Можно обобщить одновременные системы, чтобы рассмотреть m уравнений с n неизвестными. В этом случае один обычно использует подписку на буквы x ₁ , x ₂ ,…, x _N для Неизвестных и A 1, , , , , , , , , , , , , , , , , , 31.

No related posts.