Метод Гаусса
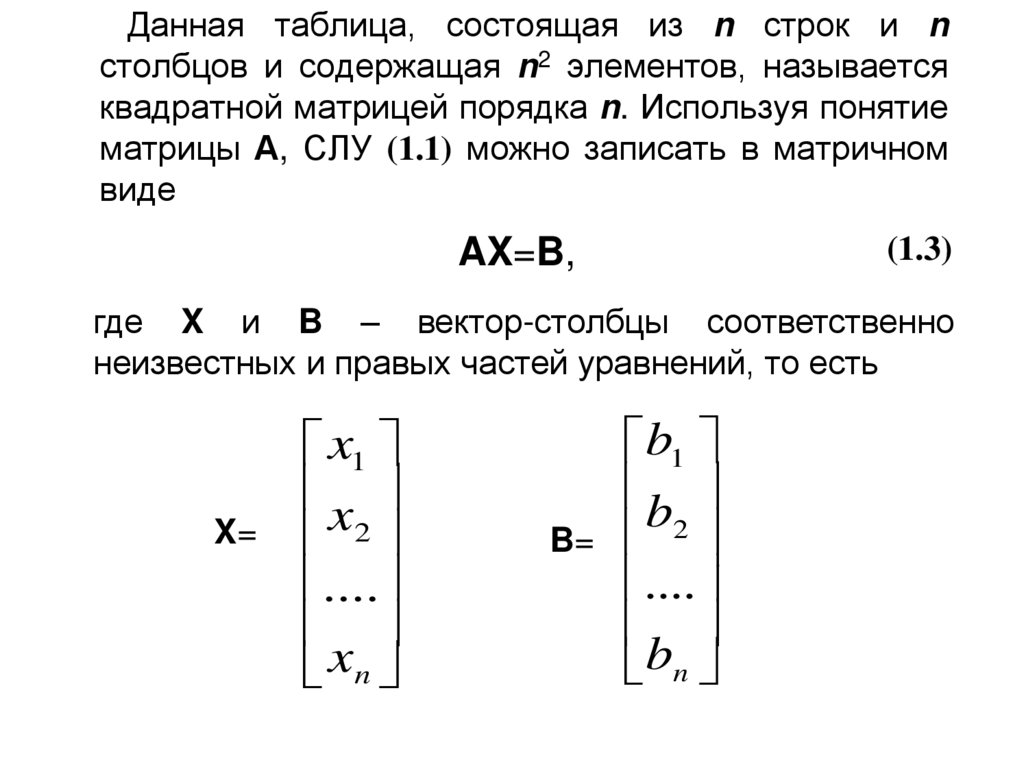
Пусть задана система линейных алгебраических уравнений, которую необходимо решить (найти такие значения неизвестных хi, что обращают каждое уравнение системы в равенство).
Мы знаем, что система линейных алгебраических уравнений может:
1) Не иметь решений (быть несовместной).
2) Иметь бесконечно много решений.
3) Иметь единственное решение.
Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений, который в каждом случае приведет нас к ответу! Сам алгоритм метода во всех трёх случаях работает одинаково. Если в методах Крамера и матричном необходимы знания определителей, то для применения метода Гаусса необходимо знание только арифметических действий, что делает его доступным даже для школьников начальных классов.
Преобразования расширенной матрицы (это матрица системы — матрица, составленная только из коэффициентов при неизвестных, плюс столбец свободных членов) системы линейных алгебраических уравнений в методе Гаусса:
1) строки матрицы можно переставлять местами.
2) если в матрице появились (или есть) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной.
3) если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить.
4) строку матрицы можно умножить (разделить) на любое число, отличное от нуля.
5) к строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля.
В методе Гаусса элементарные преобразования не меняют решение системы уравнений.
Метод Гаусса состоит из двух этапов:
- «Прямой ход» — с помощью элементарных преобразований привести расширенную матрицу системы линейных алгебраических уравнений к «треугольному» ступенчатому виду: элементы расширенной матрицы, расположенные ниже главной диагонали, равны нулю (ход «сверху-вниз»). Например, к такому виду:
Для этого выполним следующие действия:
1) Пусть мы рассматриваем первое уравнение системы линейных алгебраических уравнений и коэффициент при х1 равен К. Второе, третье и т.д. уравнения преобразуем следующим образом: каждое уравнение (коэффициенты при неизвестных, включая свободные члены) делим на коэффициент при неизвестном х Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0.
Из третьего преобразованного уравнения вычитаем первое уравнение, так до тех пор, пока все уравнения, кроме первого, при неизвестном х1 не будут иметь коэффициент 0.
2) Переходим к следующему уравнению. Пусть это будет второе уравнение и коэффициент при х2 равен М. Со всеми «нижестоящими» уравнениями поступаем так, как описано выше. Таким образом, «под» неизвестной х2 во всех уравнениях будут нули.
3) Переходим к следующему уравнению и так до тех пора, пока не останется одна последняя неизвестная и преобразованный свободный член.
- «Обратный ход» метода Гаусса – получение решения системы линейных алгебраических уравнений (ход «снизу-вверх»). Из последнего «нижнего» уравнения получаем одно первое решение – неизвестную хn. Для этого решаем элементарное уравнение А*хn = В. В примере, приведенном выше, х3 = 4. Подставляем найденное значение в «верхнее» следующее уравнение и решаем его относительно следующей неизвестной.
 Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Пример.
Решим систему линейных уравнений методом Гаусса, как советуют некоторые авторы:
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Поступим так:
Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное действие: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по апробированной методике:
2 шаг. Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
3 шаг. Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
4 шаг. К третьей строке прибавили вторую строку, умноженную на 2.
5 шаг. Третью строку разделили на 3.
Признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде (0 0 11 |23), и, соответственно, 11x3 = 23, x3 = 23/11, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Выполняем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
Обратный ход, напоминаю, работает «снизу вверх». В данном примере получился подарок:
x3 = 1
x2 = 3
x1 + x2 – x3 = 1, следовательно x1 + 3 – 1 = 1, x1 = –1
Ответ: x1 = –1, x2 = 3, x3 = 1.
Решим эту же систему по предложенному алгоритму. Получаем
4 2 –1 1
5 3 –2 2
3 2 –3 0
Разделим второе уравнение на 5, а третье – на 3. Получим:
4 2 –1 1
1 0.6 –0.4 0.4
1 0.66 –1 0
Умножим второе и третье уравнения на 4, получим:
4 2 –1 1
4 2,4 –1.6 1.6
4 2.64 –4 0
Вычтем из второго и третьего уравнений первое уравнение, имеем:
4 2 –1 1
0 0.4 –0.6 0.6
0 0.64 –3 –1
Разделим третье уравнение на 0,64:
4 2 –1 1
0 0.4 –0.6 0.6
0 1 –4.
Умножим третье уравнение на 0,4
4 2 –1 1
0 0.4 –0.6 0.6
0 0.4 –1.875 –0.625
Вычтем из третьего уравнения второе, получим «ступенчатую» расширенную матрицу:
4 2 –1 1
0 0.4 –0.6 0.6
0 0 –1.275 –1.225
Таким образом, так как в процессе вычислений накапливалась погрешность, получаем х3 = 0,96 или приблизительно 1.
х2 = 3 и х1 = –1.
Решая таким образом, Вы никогда не запутаетесь в вычислениях и не смотря на погрешности вычислений, получите результат.
Такой способ решения системы линейных алгебраических уравнений легко программируем и не учитывает специфические особенности коэффициентов при неизвестных, ведь на практике (в экономических и технических расчетах) приходиться иметь дело именно с нецелыми коэффициентами.
Желаю успехов! До встречи на занятиях! Репетитор Дмитрий Айстраханов.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Свойства определителей. Обратная матрица (Лекция №13)
- Если квадратная матрица AT является транспонированной матрицей A, то их определители
совпадают |AT | = |A|, т.е. определитель не
меняется, если заменить его строки столбцами и обратно, например, для
определителя третьего порядка .
Доказательство проводится проверкой, т.е. сравнением обеих частей записанного равенства. Вычислим определители, стоящие слева и справа:
- При перестановке 2-х строк или столбцов определитель изменит знак на противоположный, сохраняя абсолютную
величину, т.е., например,
Доказательство проводится аналогично доказательству свойства 1 сравнением обеих частей.
Проведём его для определителя второго порядка.
.
Для определителя третьего порядка проверьте самостоятельно.
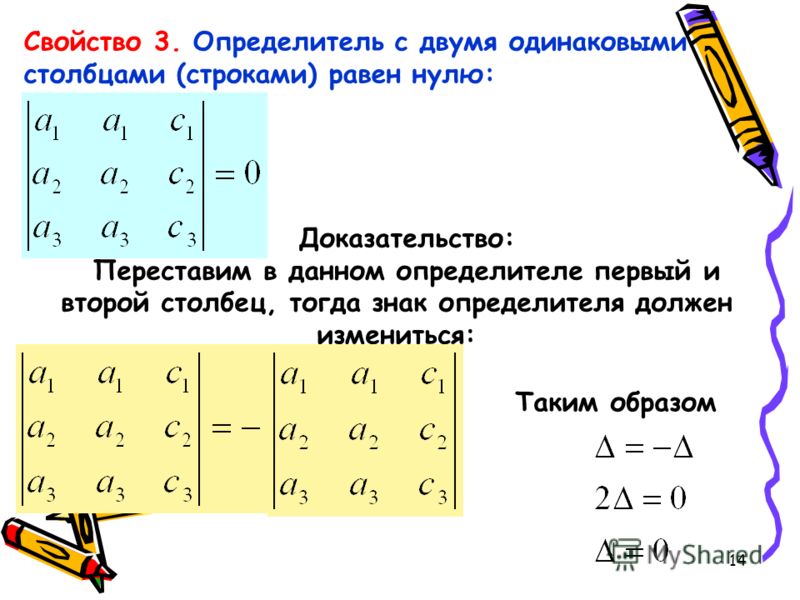
- Если определитель имеет две одинаковые строки или столбца, то он равен нулю. Например, .
Действительно, если переставить здесь 2-ю и 3-ю строки, то по свойству 2 этот определитель должен изменить знак, но сам определитель в данном случае не меняется, т.е. получаем |A| = –|A| или |A| = 0.
- Общий множитель строки или столбца можно выносить за
знак определителя. Например, .
Доказательство проводится проверкой, как и свойство 1. (Самостоятельно)
- Если все элементы какой–либо строки или столбца определителя равны нулю, то сам определитель равен нулю. (Доказательство – проверкой).
- Если все элементы какой–либо строки или столбца
определителя представлены в виде суммы 2-х слагаемых, то определитель можно
представить в виде суммы 2-х определителей по формуле, например,
.

Доказательство — проверкой, аналогично свойству 1.
- Если к какой–либо строке (или столбцу) определителя
прибавить соответствующие элементы другой строки (или столбца), умноженные на
одно и тоже число, то определитель не изменит своей величины. Например,
.
Докажем это равенство, используя предыдущие свойства определителя.
Эти свойства определителей довольно часто используются при вычислении определителей и в различных задачах.
АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ
Пусть имеем определитель третьего порядка: .
Минором, соответствующим данному элементу aij определителя третьего порядка,
называется определитель второго порядка, полученный из данного вычёркиванием
строки и столбца, на пересечении которых стоит данный элемент, т.е. i-ой строки и j-го столбца. Миноры
соответствующие данному элементу aij будем обозначать Mij.
Например, минором M12, соответствующим элементу a12, будет определитель , который получается вычёркиванием из данного определителя 1-ой строки и 2-го столбца.
Таким образом, формула, определяющая определитель третьего порядка, показывает, что этот определитель равен сумме произведений элементов 1-ой строки на соответствующие им миноры; при этом минор, соответствующий элементу a12, берётся со знаком “–”, т.е. можно записать, что
| . | (1) |
Аналогично можно ввести определения миноров для определителей второго порядка и высших порядков.
Введём ещё одно понятие.
Алгебраическим дополнениемэлемента aij определителя называется его минор Mij, умноженный на (–1)i+j.
Алгебраическое
дополнение элемента aij обозначается Aij.
Из определения получаем, что связь между алгебраическим дополнением элемента и его минором выражается равенством Aij = (–1)i+jMij.
Например,
Пример. Дан определитель . Найти A13, A21, A32.
Легко видеть, что используя алгебраические дополнения элементов, формулу (1) можно записать в виде:
.
Аналогично этой формуле можно получить разложение определителя по элементам любой строки или столбца.
Например, разложение определителя по элементам 2-ой строки можно получить следующим образом. Согласно свойству 2 определителя имеем:
Разложим полученный определитель по элементам 1-ой строки.
| . | (2) |
Отсюда т.к. определители
второго порядка в формуле (2) есть миноры элементов a21, a22, a23. Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой
строки.
Таким образом, , т.е. мы получили разложение определителя по элементам 2-ой
строки.
Аналогично можно получить разложение определителя по элементам третьей строки. Используя свойство 1 определителей (о транспонировании), можно показать, что аналогичные разложения справедливы и при разложении по элементам столбцов.
Таким образом, справедлива следующая теорема.
Теорема (о разложении определителя по заданной строке или столбцу). Определитель равен сумме произведений элементов какой–либо его строки (или столбца) на их алгебраические дополнения.
Всё вышесказанное справедливо и для определителей любого более высокого порядка.
Примеры.
- Вычислить определитель , раскладывая его по элементам 2-го столбца.
- Вычислить определитель, используя его свойства.
Прежде чем раскладывать определитель по элементам какой–либо строки, сводя к
определителям третьего порядка, преобразуем его, используя свойство 7, сделав в
какой–либо строке или столбце все элементы, кроме одного, равными нулю.
 В
данном случае удобно рассмотреть 4-й столбец или 4-ю строку:
В
данном случае удобно рассмотреть 4-й столбец или 4-ю строку:
ОБРАТНАЯ МАТРИЦА
Понятие обратной матрицы вводится только для квадратных матриц.
Если A – квадратная матрица, то обратной для неё матрицей называется матрица, обозначаемая A-1 и удовлетворяющая условию . (Это определение вводится по аналогии с умножением чисел)
Справедлива следующая теорема:
Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.
Доказательство:
- Необходимость.
Пусть для матрицы A
существует обратная матрица A-1. Покажем, что |A| ≠ 0.
Прежде всего заметим, что можно доказать следующее свойство определителей .
Предположим, что |A| = 0. Тогда . Но с другой стороны . Полученное противоречие и доказывает, что |A| ≠ 0.

- Достаточность.
Для простоты доказательство проведём для случая матрицы третьего порядка. Пусть
и |A| ≠ 0.
Покажем, что в этом случае обратной матрицей будет матрица
, где Aij алгебраическое дополнение элемента aij.
Найдём AB=C.
Заметим, что все диагональные элементы матрицы C будут равны 1. Действительно, например,
Аналогично по теореме о разложении определителя по элементам строки можно доказать, что c22 = c33 = 1.
Кроме того, все недиагональные элементы матрицы C равны нулю. Например,
Следовательно, AB=E. Аналогично можно показать, что BA=E. Поэтому B = A-1.
Таким образом, теорема содержит способ нахождения обратной матрицы.
Если условия теоремы выполнены, то матрица обратная к матрице находится следующим образом
,
где Aij — алгебраические дополнения
элементов aij данной матрицы A.
Итак, чтобы найти обратную матрицу нужно:
- Найти определитель матрицы A.
- Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу , элементами которой являются числа Aij.
- Найти
матрицу, транспонированную полученной матрице , и умножить её на – это и будет .
Аналогично для матриц второго порядка, обратной будет следующая матрица .
Примеры.
- Найти
матрицу, обратную данной . Сделать проверку.
|A| = 2. Найдем алгебраические дополнения элементов матрицы A.
Проверка:
.
Аналогично A∙A-1 = E.
- Найти элементы и матрицы A-1 обратной данной
.
Вычислим |A| = 4. Тогда .
.
- . Найдем обратную матрицу.
python — я хочу проверить, есть ли в матрице одинаковые строки
.
 Вы можете использовать
Вы можете использовать np.uniqueпо оси = 0 для получения уникальных строк.return_counts=Trueвернет количество повторений каждой строки.Помещение условия
c>1и проверка соответствия какой-либо строки этому условию с помощью.any()даст вам то, что вы хотите.
по определению is_dup_simple (обр):
u, c = np.unique (обр, ось = 0, return_counts = True)
возврат (c>1).любой()
печать (is_dup_simple (A))
печать (is_dup_simple (B))
Верно ЛОЖЬ
Вот как это можно сделать с помощью широковещательных операций. Это немного более длинный путь, но давайте будем очень гибкими в подходе (например, поиск дубликатов между разными массивами)
def is_dup(arr):
маска = ~np.eye(arr.shape[0], dtype=bool)
out = ((arr[None,:,:] == arr[:,None,:]).all(-1)&mask).any()
вернуться
печать (is_dup (A))
печать (is_dup (B))
Правда ЛОЖЬ
Таблица пошаговой трансляции —
обр[Нет,:,:] -> 1 , 10, 7 (добавление новой первой оси)
arr[:,None,:] -> 10, 1 , 7 (добавление новой второй оси)
--------------------------
== -> 10, 10, 7 (сравните элементы построчно)
все (-1) -> 10, 10 (сравните строки x строки)
& маска -> 10, 10 (диагонали ложные)
any() -> 1 (уменьшить до одного логического значения)
--------------------------
ОБЪЯСНЕНИЕ
Из массива 10,7 (10 строк, 7 столбцов) вы хотите сопоставить элементы так, чтобы в итоге вы получили матрицу (10,10) с логическими значениями, которые показывают, все ли элементы в массиве 7 строк соответствуют ЛЮБЫМ элементам в любых других строках.

Маска
= ~np.eye(arr.shape[0], dtype=bool)представляет собой матрицу формы 10,10 с ложными значениями по диагонали. Причина этого в том, что вы хотите игнорировать сравнение строки с самой собой. Подробнее об этом позже.Начиная с широковещательной булевой операции —
(arr[None,:,:] == arr[:,None,:]). Это приводит к логическому массиву 10,10,7, который сравнивает элементы каждой строки со всеми другими строками (10 x 10 сравнений, 7 совпадающих значений).Теперь, с
.all(-1), вы уменьшаете последнюю ось и получаете матрицу 10,10, которая содержит True, если все 7 элементов соответствуют любой другой строке, иначе false, даже если один элемент отличается.Затем, как вы понимаете, строка 0 всегда будет соответствовать строке 0, поэтому строка 1 будет соответствовать строке 1. Следовательно, диагональ в этой матрице всегда будет истинной. Чтобы сделать вывод о наличии повторяющихся строк, мы должны игнорировать истинные значения диагонали.
 Это можно сделать, выполнив операцию
Это можно сделать, выполнив операцию и(и) между маской (обсуждаемой выше) и логическим массивом 10,10. Единственное изменение, которое происходит из-за этого, заключается в том, что диагональные элементы становятся False вместо True.Наконец, вы можете уменьшить массив до одного логического значения, используя
.any(), которое будет иметь значение True, если хотя бы один элемент в новой матрице 10,10 имеет значение True (что указывает на наличие строки x, которая соответствует строка y точно И строка x отличается от строки y благодаря маске)
3.2: Свойства определителей — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14511
- Кен Каттлер
- Университет Бригама Янга via Lyryx 9010 6
- Переключение двух строк.
- Умножить строку на ненулевое число.
- Заменить строку числом, кратным другой строке, добавленной к самой себе.
- Доказательство
Мы докажем эту лемму с помощью математической индукции.
Если \(n=2\) это просто (проверьте!).
Пусть \(n\geq 3\) таково, что каждая матрица размера \(n-1\times n-1\) со строкой, состоящей из нулей, имеет определитель, равный нулю. Пусть \(i\) таково, что \(i\)-я строка \(A\) состоит из нулей. Тогда мы имеем \(a_{ij}=0\) для \(1\leq j\leq n\).
Исправьте \(j\in \{1,2, \dots ,n\}\) так, чтобы \(j\neq i\). Тогда матрица \(A(j)\), используемая при вычислении \(\mathrm{cof}(A)_{1,j}\), имеет строку, состоящую из нулей, и по нашему индуктивному предположению \(\mathrm{cof }(A)_{1,j}=0\). 9n a_{1,j} \mathrm{cof}(A)_{1,j}=0\nonumber \], так как каждое из слагаемых равно 0,
- \(j\)-е строки всех трех матриц одинаковы, для \(j\neq i\).
- Каждая запись в \(j\)-й строке \(A\) является суммой соответствующих записей в \(j\)-х строках \(B\) и \(C\).
- Доказательство
Проверить на \(n=2\) несложно (проверьте!).
Теперь предположим, что утверждение леммы верно для \(n-1\times n-1\) матриц, и зафиксируем \(A,B\) и \(C\), как в утверждении. Предположения утверждают, что мы имеем \(a_{l,j}=b_{l,j}=c_{l,j}\) для \(j\neq i\) и для \(1\leq l\leq n \) и \(a_{l,i}=b_{l,i}+c_{l,i}\) для всех \(1\leq l\leq n\). Поэтому \(A(i)=B(i)=C(i)\), а \(A(j)\) обладает тем свойством, что его \(i\)-я строка является суммой \(i\) строки \(B(j)\) и \(C(j)\) для \(j\neq i\), а остальные строки всех трех матриц идентичны. Следовательно, согласно нашему индуктивному предположению, мы имеем \(\mathrm{cof}(A)_{1j}=\mathrm{cof}(B)_{1j}+\mathrm{cof}(C)_{1j}\) для \(j\neq i\).
 9n a_{1,l} \mathrm{cof}(A)_{1,l}\\ &=\sum_{l\neq i} a_{1,l}(\mathrm{cof}(B)_{ 1,l}+\mathrm{cof}(C)_{1,l})+ (b_{1,i}+c_{1,i})\mathrm{cof}(A)_{1,i} \\ &= \det B+\det C\end{aligned}\] Это доказывает, что утверждение верно для всех \(n\), и завершает доказательство.
9n a_{1,l} \mathrm{cof}(A)_{1,l}\\ &=\sum_{l\neq i} a_{1,l}(\mathrm{cof}(B)_{ 1,l}+\mathrm{cof}(C)_{1,l})+ (b_{1,i}+c_{1,i})\mathrm{cof}(A)_{1,i} \\ &= \det B+\det C\end{aligned}\] Это доказывает, что утверждение верно для всех \(n\), и завершает доказательство.- Если \(A\) получается перестановкой \(i\)-й и \(j\)-й строк \(B\) (с \(i\neq j\)), то \(\det А=-\det В\).
- Если \(A\) получается умножением \(i\)-й строки \(B\) на \(k\), то \(\det A=k\det B\).
- Если две строки \(A\) идентичны, то \(\det A=0\).
- Если \(A\) получается умножением \(i\)-й строки \(B\) на \(k\) и прибавлением его к \(j\)-й строке \(B\) (\( i\neq j\)) затем \(\det A=\det B\).
- Доказательство
Все утверждения доказываем по индукции. Случай \(n=2\) легко проверить напрямую (и настоятельно рекомендуется проверить его).
 n b_{1l} B_{1l} =\det B.\nonumber \]
n b_{1l} B_{1l} =\det B.\nonumber \]Итак, мы доказали случай (1), когда \(j=i+1\). Для доказательства общего случая понадобится следующий факт. Если \(i
(2) Это как (1)… но гораздо проще. Предположим, что (2) верно для всех \(n-1\times n-1\) матриц. У нас есть это \(a_{ji}=k b_{ji}\) для \(1\leq j\leq n\). В частности \(a_{1i}=kb_{1i}\), а при \(l\neq i\) матрица \(A(l)\) получается из \(B(l)\) умножением одного из его строки на \(k\).
 Поэтому \(\mathrm{cof}(A)_{1l}=k\mathrm{cof}(B)_{1l}\) для \(l\neq i\), и для всех \(l\) мы имеют \(a_{1l} \mathrm{cof}(A)_{1l}=k b_{1l}\mathrm{cof}(B)_{1l}\). По \(\eqref{E1}\) имеем \(\det A=k\det B\).
Поэтому \(\mathrm{cof}(A)_{1l}=k\mathrm{cof}(B)_{1l}\) для \(l\neq i\), и для всех \(l\) мы имеют \(a_{1l} \mathrm{cof}(A)_{1l}=k b_{1l}\mathrm{cof}(B)_{1l}\). По \(\eqref{E1}\) имеем \(\det A=k\det B\).(3) Это следствие (1). Если две строки \(A\) идентичны, то \(A\) равна матрице, полученной путем перестановки этих двух строк и, следовательно, согласно (1) \(\det A=-\det A\). Отсюда следует \(\det A=0\).
(4) Предположим, что (4) верно для всех \(n-1\times n-1\) матриц, и зафиксируем \(A\) и \(B\) так, что \(A\) получается умножением \ (i\)-я строка \(B\) на \(k\) и добавление ее к \(j\)-й строке \(B\) (\(i\neq j\)) затем \(\det А=\дет В\). Если \(k=0\), то \(A=B\) и доказывать нечего, поэтому можно считать \(k\neq 0\).
Пусть \(C\) — матрица, полученная заменой \(j\)-й строки \(B\) на \(i\)-ю строку \(B\), умноженной на \(k\). По лемме \(\PageIndex{2}\) мы имеем, что \[\det A=\det B+\det C\nonumber \], и нам «всего лишь» нужно показать, что \(\det C=0\).
 Но \(i\)-я и \(j\)-я строки \(C\) пропорциональны. Если \(D\) получается умножением \(j\)-й строки \(C\) на \(\frac 1k\), то по (2) имеем \(\det C=\frac 1k\det D\) (напомним, что \(k\neq 0\)!). Но \(i\)-я и \(j\)-я строки \(D\) идентичны, поэтому по (3) мы имеем \(\det D=0\) и, следовательно, \(\det C=0\ ).
Но \(i\)-я и \(j\)-я строки \(C\) пропорциональны. Если \(D\) получается умножением \(j\)-й строки \(C\) на \(\frac 1k\), то по (2) имеем \(\det C=\frac 1k\det D\) (напомним, что \(k\neq 0\)!). Но \(i\)-я и \(j\)-я строки \(D\) идентичны, поэтому по (3) мы имеем \(\det D=0\) и, следовательно, \(\det C=0\ ).- Proof
Если \(A\) является элементарной матрицей любого типа, то умножение на \(A\) слева имеет тот же эффект, что и выполнение соответствующей операции с элементарной строкой. Поэтому равенство \(\det (AB) =\det A\det B\) в этом случае следует из примера \(\PageIndex{8}\) и теоремы \(\PageIndex{8}\).
Если \(C\) является редуцированной ступенчатой формой \(A\), то мы можем написать \(A=E_1\cdot E_2\cdot\dots\cdot E_m\cdot C\) для некоторых элементарных матриц \( E_1,\точки, E_m\).

Теперь рассмотрим два случая.
Предположим сначала, что \(C=I\). Затем \(A=E_1\cdot E_2\cdot \dots\cdot E_m\) и \(AB= E_1\cdot E_2\cdot \dots\cdot E_m B\). Применяя приведенное выше равенство \(m\) раз, а затем \(m-1\) раз, мы получаем, что \[\begin{aligned} \det AB&=\det E_1\det E_2\cdot \det E_m\cdot \det B\\ &=\det (E_1\cdot E_2\cdot\dots\cdot E_m) \det B\\ &=\det A\det B. \end{aligned}\]
Теперь предположим \(C\neq I\). Поскольку он находится в редуцированной строчно-эшелонной форме, его последняя строка состоит из нулей, а по (4) примера \(\PageIndex{8}\) последняя строка \(CB\) состоит из нулей. По лемме \(\PageIndex{1}\) имеем \(\det C=\det (CB)=0\) и, следовательно, \[\det A=\det (E_1\cdot E_2\cdot E_m)\cdot \ det (C) = \det (E_1\cdot E_2\cdot E_m)\cdot 0=0\nonumber \], а также \[\det AB=\det (E_1\cdot E_2\cdot E_m)\cdot \det (C B ) =\det (E_1\cdot E_2\cdot\dots\cdot E_m) 0 =0\nonnumber \] следовательно \(\det AB=0=\det A \det B\). 9Т\).
Свойства определителей I: примеры
У определителей много важных свойств. Поскольку многие из этих свойств связаны с операциями со строками, которые обсуждались в главе 1, мы сейчас вспомним это определение.
Поскольку многие из этих свойств связаны с операциями со строками, которые обсуждались в главе 1, мы сейчас вспомним это определение.
Определение \(\PageIndex{1}\): Операции со строками
Операции со строками состоят из следующих
Теперь рассмотрим влияние операций над строками на определитель матрицы. В следующих разделах мы увидим, что использование следующих свойств может сильно помочь в поиске определителей. В этом разделе теоремы будут использоваться в качестве мотивации для предоставления различных примеров полезности свойств.
Первая теорема объясняет влияние на определитель матрицы перестановки двух строк.
Теорема \(\PageIndex{1}\): переключение строк
Пусть \(A\) будет матрицей \(n\times n\), а \(B\) будет матрицей, полученной в результате перестановки двух строк из \(A. \) Тогда \(\det \left( B\right) = — \det \left( A\right).\)
\) Тогда \(\det \left( B\right) = — \det \left( A\right).\)
Когда мы переставляем две строки матрицы, определитель умножается на \ (-1\). Рассмотрим следующий пример.
Пример \(\PageIndex{1}\): переключение двух строк
Пусть \(A=\left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \right]\) и пусть \(B=\left[ \begin{array} {rr} 3 и 4 \\ 1 и 2 \end{массив} \right]\). Зная, что \(\det \left( A \right) = -2\), найдите \(\det \left( B \right)\).
Решение
По определению 3.1.1, \(\det \left(A\right) = 1 \times 4 — 3 \times 2 = -2\). Обратите внимание, что строки \(B\) являются строками \(A\), но перепутаны. По теореме \(\PageIndex{1}\), так как две строки \(A\) были переставлены местами, \(\det \left(B\right) = — \det \left(A\right) = — \left (-2\справа) = 2\). Вы можете убедиться в этом, используя Определение 3.1.1.
Следующая теорема демонстрирует влияние на определитель матрицы, когда мы умножаем строку на скаляр.
Теорема \(\PageIndex{2}\): умножение строки на скаляр
Пусть \(A\) — матрица \(n\x n\), а \(B\) — матрица, которая дает от умножения некоторой строки \(A\) на скаляр \(k\). Тогда \(\det \left( B\right) = k \det \left( A\right)\).
Тогда \(\det \left( B\right) = k \det \left( A\right)\).
Обратите внимание, что эта теорема верна, когда мы умножаем одну строку матрицы на \(k\). Если бы мы умножили 9п \дет(А)\).
Рассмотрим следующий пример.
Пример \(\PageIndex{2}\): умножение строки на 5
Пусть \(A=\left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \ right] ,\ B=\left[ \begin{array}{rr} 5 & 10 \\ 3 & 4 \end{array} \right].\) Зная, что \(\det \left( A \right) = -2\), найти \(\det \left( B \right)\).
Решение
По определению 3.1.1, \(\det \left( A\right) = -2.\) Мы также можем вычислить \(\det \left(B\right)\), используя определение 3.1.1 , и мы видим, что \(\det \left(B\right) = -10\).
Теперь давайте вычислим \(\det \left(B\right)\), используя теорему \(\PageIndex{2}\), и посмотрим, получим ли мы тот же ответ. Обратите внимание, что первая строка \(B\) в \(5\) раз больше первой строки \(A\), а вторая строка \(B\) равна второй строке \(A\) . По теореме \(\PageIndex{2}\), \(\det \left( B \right) = 5 \times \det \left( A \right) = 5 \times -2 = -10. \)
\)
Вы можете видеть, что это соответствует нашему ответу выше.
Наконец, рассмотрим следующую теорему для последней операции со строками — прибавления числа, кратного одной строке, к другой строке.
Теорема \(\PageIndex{4}\): добавление кратного строки к другой строке
Пусть \(A\) — матрица \(n\x n\), матрица, которая получается в результате прибавления числа, кратного одной строке, к другой строке. Тогда \(\det \left( A\right) =\det \left( B \right)\).
Следовательно, когда мы прибавляем кратное одной строки к другой строке, определитель матрицы не меняется. Обратите внимание, что если матрица \(A\) содержит строку, кратную другой строке, \(\det \left(A\right)\) будет равно \(0\). Чтобы убедиться в этом, предположим, что первая строка \(A\) равна \(-1\), умноженной на вторую строку. По теореме \(\PageIndex{4}\) мы можем добавить первую строку ко второй строке, и определитель не изменится. Однако эта операция строки приведет к строке нулей. Используя разложение Лапласа по ряду нулей, мы находим, что определитель равен \(0\).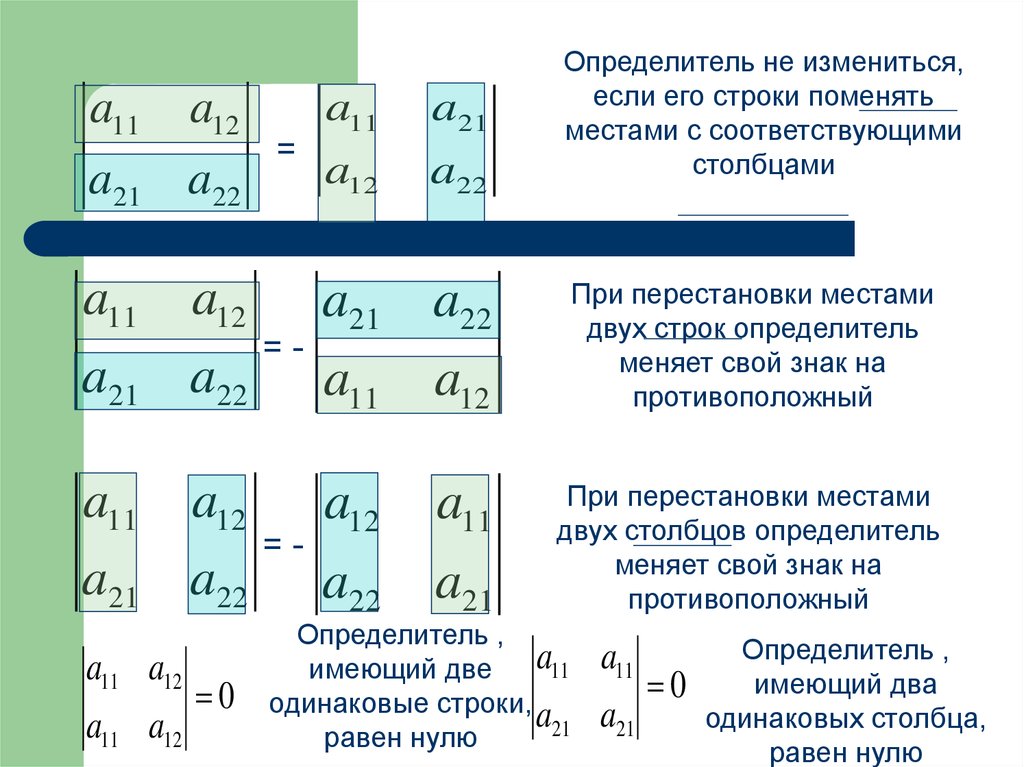
Рассмотрим следующий пример.
Пример \(\PageIndex{3}\): добавление строки к другой строке
Пусть \(A=\left[ \begin{array}{rr} 1 & 2 \\ 3 & 4 \end{array} \right]\) и пусть \(B=\left[ \begin{array}{rr} 1 & 2 \\ 5 & 8 \end{array} \right] .\) Найти \(\det \left(B \верно)\).
Решение
По определению 3.1.1, \(\det \left(A\right) = -2\). Обратите внимание, что вторая строка \(B\) в два раза больше первой строки \(A\), добавленной ко второй строке. По теореме \(\PageIndex{1}\), \(\det \left( B\right) = \det \left( A \right) = -2\). Как обычно, вы можете проверить этот ответ, используя Определение 3.1.1.
Пример \(\PageIndex{4}\): Несколько строк
Пусть \(A = \left[ \begin{array}{rr} 1 & 2 \\ 2 & 4 \end{array} \right ]\). Покажите, что \(\det \left( A \right) = 0\).
Решение
Используя определение 3.1.1, определитель задается как \[\det \left( A \right) = 1 \times 4 — 2 \times 2 = 0\nonumber \]
Однако обратите внимание, что второй строка равна \(2\), умноженной на первую строку. Тогда по приведенному выше обсуждению в соответствии с теоремой \(\PageIndex{4}\) определитель будет равен \(0\).
Тогда по приведенному выше обсуждению в соответствии с теоремой \(\PageIndex{4}\) определитель будет равен \(0\).
До сих пор основное внимание уделялось операциям со строками. Однако мы можем выполнять те же операции со столбцами, а не со строками. Три операции, описанные в определении \(\PageIndex{1}\), можно выполнять со столбцами, а не со строками. В этом случае в теоремах \(\PageIndex{1}\), \(\PageIndex{2}\) и \(\PageIndex{4}\) слово «строка» можно заменить словом «столбец». «.
Есть несколько других важных свойств определителей, которые не включают операции со строками (или столбцами). Первым является определитель произведения матриц.
Теорема \(\PageIndex{5}\): определитель произведения
Пусть \(A\) и \(B\) — две матрицы \(n\times n\). Тогда \[\det \left( AB\right) =\det \left( A\right) \det \left( B\right)\nonumber \]
Чтобы найти определитель произведения матриц, мы можно просто взять произведение определителей.
Рассмотрим следующий пример.
Пример \(\PageIndex{5}\): определитель произведения
Сравните \(\det \left( AB\right)\) и \(\det \left( A\right) \det \left ( B\right)\) для \[A=\left[ \begin{array}{rr} 1 & 2 \\ -3 & 2 \end{array} \right], B=\left[ \begin{array }{rr} 3 и 2 \\ 4 и 1 \end{массив} \right]\nonumber \]
Решение
Первое вычисление \(AB\), которое задается \[AB=\left[ \begin{array}{rr} 1 & 2 \\ -3 & 2 \end{array} \right] \ left[ \begin{array}{rr} 3 & 2 \\ 4 & 1 \end{array} \right] = \left[ \begin{array}{rr} 11 & 4 \\ -1 & -4 \end {array} \right]\nonumber \] и, следовательно, по определению 3.1.1 \[\det \left( AB\right) =\det \left[ \begin{array}{rr} 11 & 4 \\ -1 & -4 \end{array} \right] = -40\nonumber \]
Теперь \[\det \left( A\right) =\det \left[ \begin{array}{rr} 1 & 2 \\ -3 & 2 \end{массив} \right] = 8\nonumber \] и \[\det \left( B\right) =\det \left[ \begin{array}{rr} 3 & 2 \\ 4 & 1 \end{массив} \right] = -5\nonumber \] 9{-1}) = \frac{1}{\det(A)}\nonumber \]
Рассмотрим следующий пример.
Пример \(\PageIndex{7}\): Определитель обратимой матрицы
Пусть \(A = \left[ \begin{array}{rr} 3 & 6 \\ 2 & 4 \end{array} \ справа], B = \left[ \begin{array}{rr} 2 & 3 \\ 5 & 1 \end{array} \right]\). Для каждой матрицы определите, является ли она обратимой. Если да, то найти определитель обратного.
Решение
Сначала рассмотрим матрицу \(A\). Используя определение 3.1.1, мы можем найти определитель следующим образом: \[\det \left( A \right) = 3 \times 4 — 2 \times 6 = 12 — 12 = 0\nonnumber \] {7}\) \(А\) необратима. 9n a_{1,i} \mathrm{cof}(A)_{1,i}.\] Если \(n=1\), то \(\det A=a_{1,1}\).
Следующий пример является простым и настоятельно рекомендуется в качестве средства для привыкания к определениям.
Пример \(\PageIndex{8}\):
(1) Пусть \(E_{ij}\) — элементарная матрица, полученная перестановкой \(i\)-й и \(j\)-й строк матрицы \ (Я\). Тогда \(\det E_{ij}=-1\).
(2) Пусть \(E_{ik}\) — элементарная матрица, полученная умножением \(i\)-й строки \(I\) на \(k\). Тогда \(\det E_{ik}=k\). 9Т\).
Тогда \(\det E_{ik}=k\). 9Т\).
Многие доказательства в этом разделе используют принцип математической индукции. Эта концепция обсуждается в Приложении A.2 и для удобства рассмотрена здесь. Сначала проверим, что утверждение верно для \(n=2\) (случай \(n=1\) либо совсем тривиален, либо бессмыслен).
Далее предположим, что утверждение верно для \(n-1\) (где \(n\geq 3\)) и докажем его для \(n\). Как только это будет выполнено, по принципу математической индукции мы можем заключить, что утверждение верно для всех матриц \(n\times n\) для каждого \(n\geq 2\).
Если \(A\) является \(n\times n\) матрицей и \(1\leq j \leq n\), то матрица, полученная удалением \(1\)st столбца и \(j\ )-я строка из \(A\) является матрицей \(n-1\times n-1\) (ниже мы будем обозначать эту матрицу через \(A(j)\)). Поскольку эти матрицы используются при вычислении кофакторов \(\mathrm{cof}(A)_{1,i}\), для \(1\leq i\neq n\), к этим матрицам применимо предположение индукции.
Рассмотрим следующую лемму.
Лемма \(\PageIndex{1}\):
Если \(A\) — матрица \(n\times n\) такая, что одна из ее строк состоит из нулей, то \(\det A=0 \).
Лемма \(\PageIndex{2}\):
Предположим, что \(A\), \(B\) и \(C\) являются \(n\×n\) матрицами, которые для некоторого \(1\ leq i\leq n\) удовлетворяют следующему.
Тогда \(\det A=\det B+\det C\).
Теорема \(\PageIndex{8}\):
Пусть \(A\) и \(B\) — матрицы \(n\times n\).
Теорема \(\PageIndex{9}\):
Пусть \(A\) и \(B\) две матрицы \(n\times n\). Тогда \[\det \left( AB\right) =\det \left( A\right) \det \left( B\right)\nonumber \]
Приведенные выше рассуждения позволяют нам теперь доказать теорему 3.

 Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
Например, х2 – 4 = 1, т.е. х2 = 5. И так до тех пор, пока не найдем все неизвестные.
 В
данном случае удобно рассмотреть 4-й столбец или 4-ю строку:
В
данном случае удобно рассмотреть 4-й столбец или 4-ю строку:
 Вы можете использовать
Вы можете использовать 
 Это можно сделать, выполнив операцию
Это можно сделать, выполнив операцию  9n a_{1,l} \mathrm{cof}(A)_{1,l}\\ &=\sum_{l\neq i} a_{1,l}(\mathrm{cof}(B)_{ 1,l}+\mathrm{cof}(C)_{1,l})+ (b_{1,i}+c_{1,i})\mathrm{cof}(A)_{1,i} \\ &= \det B+\det C\end{aligned}\] Это доказывает, что утверждение верно для всех \(n\), и завершает доказательство.
9n a_{1,l} \mathrm{cof}(A)_{1,l}\\ &=\sum_{l\neq i} a_{1,l}(\mathrm{cof}(B)_{ 1,l}+\mathrm{cof}(C)_{1,l})+ (b_{1,i}+c_{1,i})\mathrm{cof}(A)_{1,i} \\ &= \det B+\det C\end{aligned}\] Это доказывает, что утверждение верно для всех \(n\), и завершает доказательство. n b_{1l} B_{1l} =\det B.\nonumber \]
n b_{1l} B_{1l} =\det B.\nonumber \]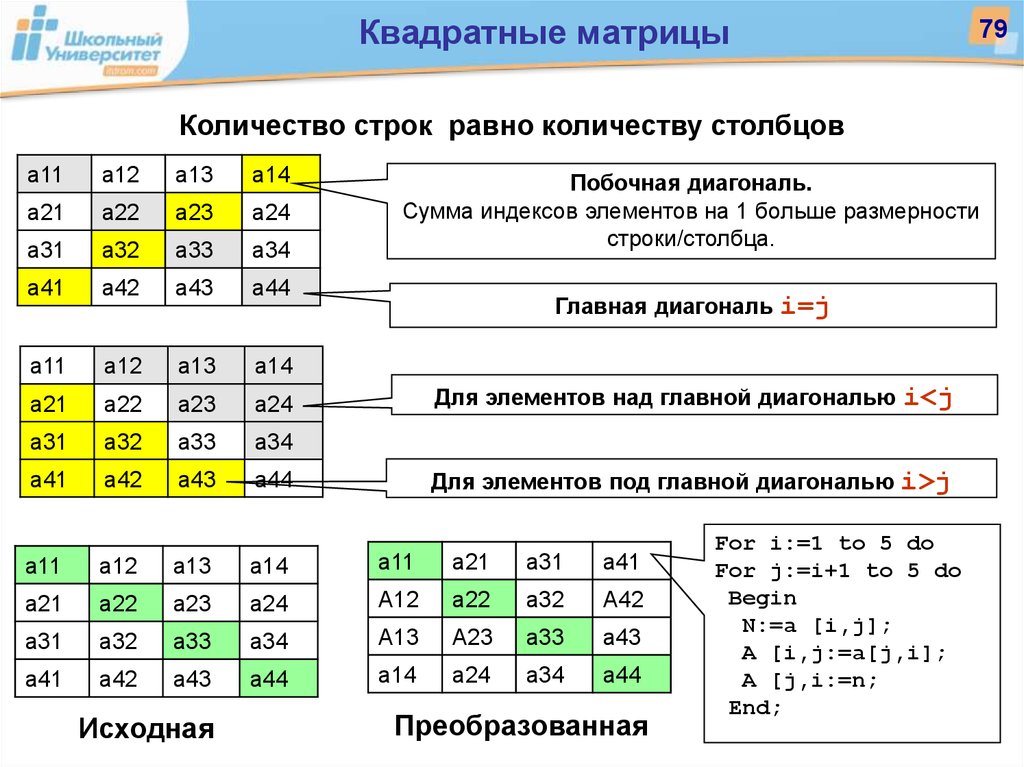 Поэтому \(\mathrm{cof}(A)_{1l}=k\mathrm{cof}(B)_{1l}\) для \(l\neq i\), и для всех \(l\) мы имеют \(a_{1l} \mathrm{cof}(A)_{1l}=k b_{1l}\mathrm{cof}(B)_{1l}\). По \(\eqref{E1}\) имеем \(\det A=k\det B\).
Поэтому \(\mathrm{cof}(A)_{1l}=k\mathrm{cof}(B)_{1l}\) для \(l\neq i\), и для всех \(l\) мы имеют \(a_{1l} \mathrm{cof}(A)_{1l}=k b_{1l}\mathrm{cof}(B)_{1l}\). По \(\eqref{E1}\) имеем \(\det A=k\det B\). Но \(i\)-я и \(j\)-я строки \(C\) пропорциональны. Если \(D\) получается умножением \(j\)-й строки \(C\) на \(\frac 1k\), то по (2) имеем \(\det C=\frac 1k\det D\) (напомним, что \(k\neq 0\)!). Но \(i\)-я и \(j\)-я строки \(D\) идентичны, поэтому по (3) мы имеем \(\det D=0\) и, следовательно, \(\det C=0\ ).
Но \(i\)-я и \(j\)-я строки \(C\) пропорциональны. Если \(D\) получается умножением \(j\)-й строки \(C\) на \(\frac 1k\), то по (2) имеем \(\det C=\frac 1k\det D\) (напомним, что \(k\neq 0\)!). Но \(i\)-я и \(j\)-я строки \(D\) идентичны, поэтому по (3) мы имеем \(\det D=0\) и, следовательно, \(\det C=0\ ).