Вектор задается: Вектор в системе координат — урок. Геометрия, 9 класс.

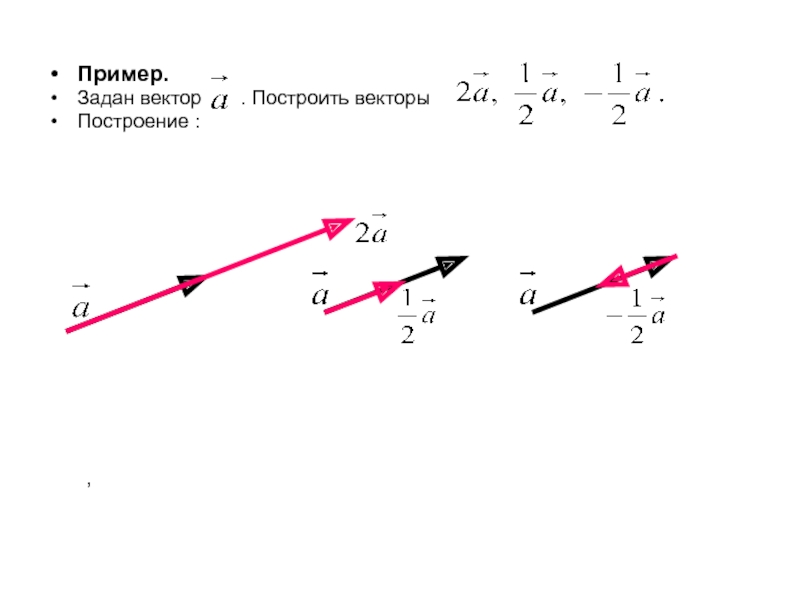
Векторы на плоскости и в пространстве: основные определения

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Определение 1

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a→. Если известны граничные точки вектора – его начало и конец, к примеру A и B, то вектор обозначается так AB→.

Нулевой вектор

Определение 2

Под нулевым вектором 0→ будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Определение 3

Под длиной вектора AB→ понимается число, большее либо равное 0, и равное длине отрезка АВ.

Длину вектораAB→ принято обозначать так AB→.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Определение 4

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Определение 5

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Определение 6

Сонаправленными векторами называют два коллинеарных вектора a→ и b→, у которых направления совпадают, такие векторы обозначаются так a→↑↑b→.

Определение 7

Противоположно направленными векторами называются два коллинеарных вектора a→ и b→, у которых направления не совпадают, т.е. являются противоположными, такие векторы обозначаются следующим образом a→↑↓b→.

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Определение 8

Равными называются сонаправленные вектора, у которых длины равны.

Определение 9

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Пусть заданы два произвольных вектора на плоскости или в пространстве a→ и b→. Отложим от некоторой точки O плоскости или пространства векторы OA→=a→ и OB→=b→. Лучи OA и OB образуют угол ∠AOB=φ.

Углы между векторами

Определение 9

Угол φ=∠AOB называется углом между векторами a→=OA→ и b→=OB→.

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Определение 10

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π2 радиан).

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Навигация по статьям

Предыдущая статья

Координаты вектора в ДСК

Следующая статья

Длина вектора

• Векторное произведение
• Векторное пространство
• Геометрическая фигура угол
• Деление отрезка в заданном соотношении
• Длина вектора
• Все темы по математике

• Дипломные работы
• Курсовые работы
• Рефераты
• Контрольные работы
• Отчет по практике
• Все предметы

Узнать подробнее

электрические аппараты

• Вид работы:

  Контрольная работа

• Выполнена:

  5 марта 2023 г.

• Стоимость:

  1 700 руб

Заказать такую же работу

Математические фокусы

• Вид работы:

  Школьный проект

• Выполнена:

  24 февраля 2023 г.

• Стоимость:

  1 000 руб

Заказать такую же работу

Создание сайта предмет основы разработки интернет систем

• Вид работы:

  Контрольная работа

• Выполнена:

  10 февраля 2023 г.

• Стоимость:

  3 600 руб

Заказать такую же работу

сдать онлайн экзамен на системного администратора Windows

Заказать такую же работу

Математические предметы

Заказать такую же работу

Приветствую Тема любой сервисный центр Интерфейс

• Вид работы:

  Лабораторная работа

• Выполнена:

  14 октября 2022 г.

• Стоимость:

  8 000 руб

Заказать такую же работу

Смотреть все работы по электронике

Векторы в пространстве — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

Направленный
отрезок АВ
А – начало вектора
В – конец вектора
a
А
В
Обозначения:
AB a

2. ВЕКТОР ЗАДАЕТСЯ КООРДИНАТАМИ

a
В
А
А a1 , a 2 , a3
В b1 , b2 , b3
Вычисление координат вектора:
a AB b1 a1 ; b2 a2 ; b3 a3
x
y
z

3. МОДУЛЬ ВЕКТОРА

Известны координаты вектора
a AB x; y; z
Длина вектора (модуль)
2
2
2
| a | x y z
Нулевой вектор:
Равные векторы:
AB 0 0
a b 1) a b;
2)
a b

4. ДЕЙСТВИЯ НАД ВЕКТОРАМИ

1. Сложение
a
b
( x1, y1, z1 )
x2 , y 2 , z 2
Правило
треугольника
b
a
c
параллелограмма
a
c
b
c a b ( x1 x 2 ; y1 y 2 ; z1 z 2 )

5. СЛОЖЕНИЕ ВЕКТОРОВ

Правило
многоугольника
a1
a2
c
an
c a1 a 2 . .. a n

6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ

2. Вычитание
a
a
b
( x1( x,1,yy11,,zz11) )
d
a
b
x2 , y 2 , z 2
d a b x1 x 2 ; y1 y 2 ; z1 z 2

7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ

3. Умножение вектора на число ( )
a AB x; y; z
0
a
a b
a b
Векторы сонаправленые
(одинаково направленные)
a x; y; z
0
a
a b
a b
Векторы противоположно
направленные

8. ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ СООТНОШЕНИИ НА ПЛОСКОСТИ

Отрезок АВ разделен точкой С в отношении
А
С
Если
AC : CB ,
В
то координаты точки С находятся по
формулам:
y
y
x
A xB
A
B
;
y
xC 1
C
1
1, то отрезок АВ разделен точкой С пополам.
Координаты середины находят по формулам:
y
x
y
z
x
z
x 2 ; y 2 ;z 2
A
C
B
A
C
B
A
C
B
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
ВЕКТОРОВ
a
b
a
b
Скалярным
произведением двух
векторов называется
произведение их длин на
косинус угла между ними:
a b a b cos

10.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВСкалярное произведение векторов
a x1; y1; z1 ; b x2 ; y2 ; z2
выражается формулой:
a b x1 x2 y1 y2 z1 z2
Косинус угла между ненулевыми
векторами:
cos
a b
a b
x1 x2 y1 y2 z1 z2
x12 y12 z12 x22 y22 z22

11. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ

13. Свойства скалярного произведения

14. КОЛЛИНЕАРНОСТЬ ВЕКТОРОВ

Векторы лежат на одной прямой
или параллельных прямых
a
c
b
d
Обозначают:
a || b

15. КОМЛАНАРНОСТЬ ВЕКТОРОВ

Векторы называются компланарными,
если отложены из одной точки и
лежат в одной плоскости
b
a
c
O
a, b, c
— компланарны
c xa yb
, где x и y – некоторые
числа.

16. ПРАВИЛО ПАРАЛЛЕЛЕПИПЕДА

Любой вектор можно разложить по трем
данным некомпланарным векторам:
d a b c
d
b
a
c

English     Русский Правила

компонентов вектора

Горячая математика

В двумерной системе координат любой вектор можно разбить на Икс -компонент и у -компонент.

в → «=» 〈 в Икс , в у 〉

Например, на рисунке ниже вектор в → распадается на две составляющие, в Икс и в у . Пусть угол между вектором и его Икс -компонент быть θ .

Вектор и его компоненты образуют прямоугольный треугольник, как показано ниже.

На приведенном выше рисунке компоненты можно быстро прочитать. Вектор в компонентной форме равен в → «=» 〈 4 , 5 〉 .

тригонометрические отношения дать отношение между величина вектора и компоненты вектора.

потому что θ «=» Соседняя сторона Гипотенуза «=» в Икс в

грех θ «=» Обратная сторона Гипотенуза «=» в у в

в Икс «=» в потому что θ

в у «=» в грех θ

Используя Теорема Пифагора в прямоугольном треугольнике с длинами в Икс и в у :

| в | «=» в Икс 2 + в у 2

Здесь показанные числа являются величинами векторов.

Дело 1: По данным компонентам вектора найдите модуль и направление вектора.

В этом случае используйте следующие формулы.

Величина вектора | в | «=» в Икс 2 + в у 2 .

Чтобы найти направление вектора, решите загар θ «=» в у в Икс для θ .

Случай 2: Зная величину и направление вектора, найдите компоненты вектора.

В этом случае используйте следующие формулы.

в Икс «=» в потому что θ

в у «=» в грех θ

Пример:

Величина вектора Ф → является 10 единицы, а направление вектора равно 60 ° с горизонталью. Найдите компоненты вектора.

Ф Икс «=» Ф потому что 60 ° «=» 10 ⋅ 1 2 «=» 5

Ф у «=» Ф грех 60 ° «=» 10 ⋅ 3 2 «=» 5 3

Итак, вектор Ф → является 〈 5 , 5 3 〉 .

Перекрестное произведение двух векторов

Перекрестное произведение двух векторов — это метод умножения двух векторов. Перекрестное произведение обозначается знаком умножения (x) между двумя векторами. Это бинарная векторная операция, определенная в трехмерной системе. Перекрестное произведение двух векторов — это третий вектор, перпендикулярный двум исходным векторам. Его величина определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. Перекрестное произведение двух векторов также известно как векторное произведение, поскольку результирующая перекрестного произведения векторов является векторной величиной. Здесь мы узнаем больше о векторном произведении двух векторов.

1.	Перекрестное произведение двух векторов
2.	Формула перекрестного произведения
3.	Правило правой руки перекрестного произведения
4.	Свойства перекрестного произведения
5.	Продукт тройного креста
6.	Пример перекрестного произведения
7.	Часто задаваемые вопросы о векторном произведении двух векторов

Перекрестное произведение двух векторов

Перекрестное произведение — это форма умножения векторов, выполняемая между двумя векторами разной природы или вида. Вектор имеет как величину, так и направление. Мы можем умножать два или более векторов на перекрестное произведение и скалярное произведение. Когда два вектора перемножаются друг с другом и произведение векторов также является векторной величиной, то результирующий вектор называется перекрестным произведением двух векторов или векторным произведением. Результирующий вектор перпендикулярен плоскости, содержащей два заданных вектора.

Определение векторного произведения

Если A и B — два независимых вектора, то результат векторного произведения этих двух векторов (Ax B) перпендикулярен обоим векторам и нормален к плоскости, содержащей оба вектора. Он представлен:
А х В = |А| |Б| sin θ

Мы можем понять это на примере, что если у нас есть два вектора, лежащих в плоскости X-Y, то их векторное произведение даст результирующий вектор в направлении оси Z, которая перпендикулярна плоскости XY . Символ × используется между исходными векторами. Векторное произведение или перекрестное произведение двух векторов показано как:

\(\overrightarrow{a} \times \overrightarrow{b} = \overrightarrow{c}\)

Где

• \(\overrightarrow{a}\) и \(\overrightarrow{b}\) два вектора.
• \(\overrightarrow{c}\) — результирующий вектор.

Перекрестное произведение двух векторов Значение

Используйте изображение, показанное ниже, и обратите внимание на углы между векторами \(\overrightarrow{a}\) и \(\overrightarrow{c}\) и углы между векторами \(\ overrightarrow{b}\) и \(\overrightarrow{c}\). 9\circ\).т. е. \(\overrightarrow{b}\) и \(\overrightarrow{c}\) являются ортогональными векторами.

Мы можем расположить \(\overrightarrow{a}\) и \(\overrightarrow{b}\) параллельно друг другу или под углом 0°, сделав результирующий вектор нулевым вектором.

Чтобы получить наибольшую величину, исходные векторы должны быть перпендикулярны (угол 90°), чтобы векторное произведение двух векторов было максимальным.

Формула перекрестного произведения

Формула перекрестного произведения между любыми двумя векторами дает площадь между этими векторами. Формула векторного произведения дает величину результирующего вектора, который представляет собой площадь параллелограмма, натянутого на два вектора.

Формула перекрестного произведения

Рассмотрим два вектора \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \шляпа i+b_2 \шляпа j+b_3 \шляпа k\). Пусть θ — угол, образованный между \(\overrightarrow{a}\) и \(\overrightarrow{b}\), а \(\hat n\) — единичный вектор, перпендикулярный плоскости, содержащей обе \(\overrightarrow{a }\) и \(\overrightarrow{b}\).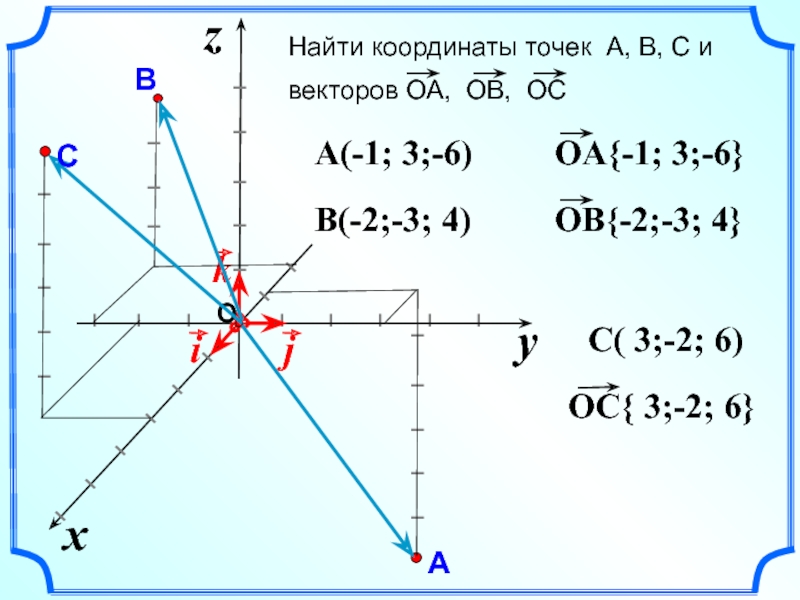 Перекрестное произведение двух векторов определяется формулой:

\(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)

Где

• \(\mid \overrightarrow a \mid\ ) — величина вектора a или длина \(\overrightarrow{a}\), 90 141
• \(\mid \overrightarrow b \mid\) — величина вектора b или длина \(\overrightarrow{b}\).

Предположим, что \(\overrightarrow{a}\) и \(\overrightarrow{b}\) — два вектора, такие что \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \ hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то с помощью определителей мы могли бы найти векторное произведение и запишите результат в виде формулы перекрестного произведения, используя матричную запись.

Перекрестное произведение двух векторов также представляется с помощью формулы перекрестного произведения как: j (a_1b_3-a_3b_1)\\+ \hat k (a_1b_2-a_2b_1)\)

Примечание: \( \hat i, \hat j, \text{ и } \hat k \) — единичные векторы в направлении оси x, оси y и оси z соответственно.

Правило правой руки — векторное произведение двух векторов

Мы можем узнать направление вектора, который получается при перекрестном произведении двух векторов по правилу правой руки. Мы следуем следующей процедуре, чтобы узнать направление результата перекрестного произведения двух векторов:

• Направьте указательный палец в направлении первого вектора (\(\overrightarrow{A}\)).
• Выровняйте средний палец в направлении второго вектора \(\overrightarrow{B}\).
• Теперь большой палец указывает в направлении векторного произведения двух векторов.

Посмотрите на изображение ниже, чтобы лучше понять это.

Свойства перекрестного произведения двух векторов

Свойства перекрестного произведения помогают ясно понять умножение векторов и помогают легко решать все проблемы векторных вычислений. Свойства векторного произведения двух векторов следующие:

1. Длина векторного произведения двух векторов \(= \overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta)\).
2. Антикоммутативное свойство: \(\overrightarrow{a} \times \overrightarrow{b} = — \overrightarrow{b} \times \overrightarrow{a}\)
3. Распределительное свойство: \(\overrightarrow{a} \times (\overrightarrow{b} + \overrightarrow{c}) = (\overrightarrow{a}\times \overrightarrow{b} )+ (\overrightarrow{a}\times \overrightarrow{с})\)
4. Перемножение нулевого вектора: \(\overrightarrow{a}\times \overrightarrow{0} = \overrightarrow{0}\)
5. Перемножение вектора с самим собой: \(\overrightarrow{a}\times \overrightarrow{a} = \overrightarrow{0}\)
6. Умножить на скалярную величину: \(\overrightarrow{c}(\overrightarrow{a}\times \overrightarrow{b}) = c\overrightarrow{a}\times \overrightarrow{b} = \overrightarrow{a}\times c\overrightarrow{b}\)
7. Перекрестное произведение единичных векторов: \(\overrightarrow{i}\times \overrightarrow{i} =\overrightarrow{j}\times \overrightarrow{j} = \overrightarrow{k}\times \overrightarrow{k} = 0\)
   
8. \(\overrightarrow{i}\times \overrightarrow{j} = \overrightarrow{k}\\ \overrightarrow{j}\times \overrightarrow{k}= \overrightarrow{i}\\\overrightarrow{k}\times \overrightarrow{i} = \overrightarrow{j}\)
9. \(\overrightarrow{j}\times \overrightarrow{i} = \overrightarrow{-k}\\ \overrightarrow{k}\times \overrightarrow{j}= \overrightarrow{-i}\\ \overrightarrow{i} \times \overrightarrow{k} = \overrightarrow{-j}\)

Тройное перекрестное произведение

Перекрестное произведение вектора на перекрестное произведение двух других векторов представляет собой тройное перекрестное произведение векторов. Результатом тройного перекрестного произведения является вектор. Равнодействующий вектора тройного пересечения лежит в плоскости данных трех векторов. Если a, b и c — векторы, то векторное тройное произведение этих векторов будет иметь вид:

\((\overrightarrow{a}\times \overrightarrow{b}) \times \overrightarrow{c} = (\overrightarrow{a}\cdot \overrightarrow{c})\overrightarrow{b} -(\overrightarrow{b}\cdot \overrightarrow{c}) \overrightarrow{a}\)

Перекрестное произведение двух векторов Пример

Перекрестное произведение играет решающую роль в нескольких областях науки и техники. Два очень простых примера показаны ниже.

Пример 1: Открытие крана: Мы прикладываем равные и противоположные силы к двум диаметрально противоположным концам крана. В этом случае применяется крутящий момент. В векторной форме крутящий момент представляет собой векторное произведение радиус-вектора (от оси вращения до точки приложения силы) и вектора силы.

т. е. \(\overrightarrow{T} = \overrightarrow{r} \times \overrightarrow{F}\)

Пример 2: Скручивание болта гаечным ключом: длина гаечного ключа равна одному вектору. Здесь направление, в котором мы прикладываем усилие к гаечному ключу (чтобы затянуть или ослабить болт), является другим вектором. Результирующее направление закручивания перпендикулярно обоим векторам.

Важные примечания

• В результате перекрестного произведения двух векторов получается вектор, ортогональный двум заданным векторам.
• Направление векторного произведения двух векторов определяется правилом большого пальца правой руки, а величина определяется площадью параллелограмма, образованного исходными двумя векторами \(\overrightarrow{a}\) и \(\overrightarrow {б}\).
• Перекрестное произведение двух линейных векторов или параллельных векторов является нулевым вектором.

☛ Также проверьте:

• Типы векторов
• Векторные формулы
• Компоненты вектора
• Калькулятор перекрестного произведения
• Добавление векторов

 

Примеры перекрестного произведения двух векторов

1. Пример 1: Два вектора имеют скалярную величину как ∣a∣=2√3 и ∣b∣ = 4, а угол между двумя векторами равен 60 ^∘ .

   Вычислить векторное произведение двух векторов.

   Решение:

   Мы знаем, что sin60° = √3/2

   Перекрестное произведение двух векторов определяется выражением \(\overrightarrow{a} \times \overrightarrow{b} \) = |a ||b|sin(θ)\( \шляпа n \) = 2√3×4×√3/2 = 12\( \шляпа n \)

   Ответ: перекрестное произведение равно 12n.

2. Вопрос 2: Найдите векторное произведение двух векторов \(\overrightarrow{a}\) = (3,4,5) и \(\overrightarrow{b}\) = (7,8,9)

   Решение:

   Перекрестное произведение задается как

   \(\begin{align}a \times b &=\begin{matrix} \hat i & \hat j & \hat k\\ 3 & 4 & 5\\ 7 & 8 & 9 \end{matrix}\end{align}\)

   = [(4×9)−(5×8)] \( \шляпа {i}\) −[(3×9)−(5×7)]\( \шляпа {j} \)+[(3×8)−(4 ×7)] \( \hat {k}\)

   = (36−40)\( \hat i\) − (27−35)\( \hat j\) +(24−28) \( \ шляпа k\) = −4\( \hat i\) + 8\( \hat j\) −4\( \hat k\)

   Ответ: ∴ \(\overrightarrow{a} \times \overrightarrow{ b} \) = −4\( \hat i\) + 8\( \hat j\) −4\( \hat k\)

3. Пример 3: Если \(\overrightarrow{a}\) = (2, -4, 4) и \(\overrightarrow{b}\) = (4, 0,3), найдите угол между ними.

   Решение

   \(\overrightarrow{a}\) = 2i — 4j + 4k

   \(\overrightarrow{b}\) = 4i + 0j +3k

   Величина \(\overrightarrow{a }\) равно

   ∣a∣=√(2 ² +4 ² +4 ² ) = √36 = 6

   Величина \(\overrightarrow{b}\) равна

   ∣ b∣=√(4 ² +0 ² +3 ² ) = √25 = 5
   Согласно формуле перекрестного произведения, мы имеем

   \(\begin{align}\overrightarrow{a}\times \overrightarrow{b} &= \begin{matrix} \hat i & \hat j & \hat k\\ 2 & -4 & 4\\ 4 & 0 & 3 \end{matrix}\\\\&=[(-4\times3) — (4\times0)]\hat i \\ — &[(3\times 2) — (4\times 4)] \hat j \\\\ + &[(2\times 0) -(-4\times 4)]\hat k \\\\&= -12\hat i + 10 \hat j +16 \hat k \\ \overrightarrow{a}\times \overrightarrow{b} &= (-12, 10, 16) \end{align}\)

   Длина \(\overrightarrow{c}\) равна

   ∣c∣=√(−(12) ² +10 ² +16 ² )

   = √(144+100 +256)

   =√500

   =10√5

   \(\begin{align}\overrightarrow{a}\times \overrightarrow{b} &= \mid a \mid \mid b \mid \sin\ тета\\\sin\theta &= \dfrac{\overrightarrow{a}\times \overrightarrow{b}}{\mid a \mid \mid b \mid}\end{align}\)

   sinθ = 10√ 5/(5×6)

   sinθ = √5/3

   θ = sin ⁻¹ (√5/3)

   θ = sin ⁻¹ (0,74)

   θ = 48 ^∘

   Ответ: Угол между векторами равен 4 8 ^∘ .

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по векторному произведению двух векторов

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о перекрестном произведении двух векторов

Что такое векторное произведение двух векторов?

В результате перекрестного произведения двух векторов при умножении третий вектор перпендикулярен двум исходным векторам. Величина результирующего вектора определяется площадью параллелограмма между ними, а его направление можно определить по правилу большого пальца правой руки. a × b = c, где c — векторное произведение двух векторов a и b.

Каков результат векторного перекрестного произведения?

Когда мы находим векторное произведение двух векторов, мы получаем другой вектор, выровненный перпендикулярно плоскости, содержащей два вектора. Величина результирующего вектора является произведением греха угла между векторами и величиной двух векторов. а × б = | а | |б| грех θ.

Что такое скалярное произведение и векторное произведение двух векторов?

Векторы можно умножать двумя разными способами, т. е. скалярным произведением и перекрестным произведением. Результаты обоих этих умножений векторов различны. В результате скалярное произведение дает скалярную величину, тогда как векторное произведение дает векторную величину. Скалярное произведение — это скалярное произведение двух векторов, а перекрестное произведение двух векторов — это векторное произведение двух векторов. Скалярное произведение также известно как скалярное произведение, а перекрестное произведение также известно как векторное произведение. Векторное произведение двух векторов задается как: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\) и формула скалярного произведения двух векторов задается как: \(\overrightarrow{a}. \overrightarrow{b} = |a| |b| \cos(\theta)\)

Как найти векторное произведение двух векторов?

Перекрестное произведение двух векторов определяется по формуле: \(\overrightarrow{a} \times \overrightarrow{b} = |a| |b| \sin(\theta) \hat n\)

Где

• |\(\overrightarrow a\)| величина или длина \(\overrightarrow{a}\),
• |\(\overrightarrow b\)| является величиной или длиной \(\overrightarrow{b}\)

Почему перекрестное произведение является синусоидальным?

Поскольку θ — это угол между двумя исходными векторами, используется sin θ, поскольку площадь параллелограмма получается путем перекрестного произведения двух векторов.

Всегда ли положительное произведение двух векторов?

Когда угол между двумя исходными векторами изменяется от 180° до 360°, векторное произведение становится отрицательным. Это связано с тем, что sin θ отрицателен для 180°< θ <360°.

В чем разница между скалярным произведением и перекрестным произведением двух векторов?

При умножении векторов скалярное произведение исходных векторов дает скалярную величину, тогда как перекрестное произведение двух векторов дает векторную величину. Скалярное произведение — это произведение величины векторов и cos угла между ними. а . б = |а| |б| cosθ. Векторное произведение — это произведение величины векторов на синус угла между ними. а × б = | а | |б| грех θ.

Что такое формула векторного произведения для двух векторов?

Формула векторного произведения определяет векторное произведение для любых двух заданных векторов, задавая площадь между этими векторами. Формула перекрестного произведения имеет вид \(\overrightarrow{A} × \overrightarrow{B} =|A||B| sin⁡θ\), где |A| = величина вектора A, |B| = величина вектора B, а θ = угол между векторами A и B.

Как найти величину векторного произведения двух векторов?

Перекрестное произведение двух векторов — это еще один вектор, величина которого определяется выражением \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3-a_3b_1) \\+ \шляпа k (a_1b_2-a_2b_1)\)

Что такое формула перекрестного произведения с использованием матричной записи?

Для двух заданных векторов \(\overrightarrow{a}\) и \(\overrightarrow{b}\) мы можем найти векторное произведение, используя определители. Например, \(\overrightarrow{a}\)= \(a_1\hat i+a_2 \hat j+a_3 \hat k\) и \(\overrightarrow{b}\) = \(b_1 \hat i+b_2 \hat j+b_3 \hat k\), то мы можем записать результат как \(\overrightarrow{a} \times \overrightarrow{b} = \hat i (a_2b_3-a_3b_2) \\- \hat j (a_1b_3- a_3b_1)\\+ \шляпа k (a_1b_2-a_2b_1)\)

Как использовать формулу перекрестного произведения?

Рассмотрим заданные векторы.

• Шаг 1: Проверьте компоненты векторов |A| = величина вектора A, |B| = модуль вектора B и θ = угол между векторами A и B.
• Шаг 2: Подставьте значения в формулу векторного произведения: \ ((\vec {A × B})=|A||B|\text{Sin⁡}\vec{θ_n}\)

Например, если \(\vec {A}=a\hat{i} + b\hat{j}+c\hat{k}\) и \( \vec{B}=d\hat{i } + e\hat{j}+f\hat{k}\), затем \({\vec{A × B}} = \begin{matrix} \hat{i} & \hat{j} & \hat{ k} \\ a & b & c \\ d & e & f \end{matrix}\)

\({\vec{A × B}} = \шляпа{i}(bf-ce) — \шляпа{j}(af-cd) + \шляпа{k}(ae-bd)\)

Что такое правило большого пальца правой руки для перекрестного произведения двух векторов?

Правило правой руки для векторного произведения двух векторов помогает определить направление результирующего вектора.