Есть 9 кубиков 8 кубиков имеют одинаковую массу: Ответы | 9. Есть 9 кубиков. Восемь кубиков имеют одинаковую массу, а девятый кубик — меньшую массу. Алесь говорит: Можно найти более лёгкий кубик двумя взвешиваниями на рычажных весах. Прав ли Алесь? — Математика, 4 класс

Содержание

Вопросы-головоломки на собеседованиях с ответами. Часть 2 — Work.ua

Work.ua продолжает публиковать ответы на самые сложные и неожиданные вопросы на собеседованиях, в которых кандидат должен проявить свою смекалку, логическое мышление и фантазию.

В предыдущей статье мы писали, что вопросы-головоломки порой могут не иметь единственного правильного ответа, а предназначены для того, чтобы проверить поведение кандидата в нестандартных ситуациях, узнать как он размышляет, и как справляется со сложными ситуациями.

Work.ua подготовил еще 5 головоломок, которые могут встретиться на вашем пути.

Бильярдные шары

Этот вопрос чаще всего задают IT-специалистам, чтобы проверить способность логически мыслить.

Вопрос: Есть 8 бильярдных шаров. Один из них немного тяжелее других. За какое минимальное количество взвешиваний на рычажных весах без гирь можно найти этот шар?

Ответ: 2 взвешивания. Нужно разделить все шары на три части: по 3 шара в двух частях, и 2 шара в третьей части. Сначала взвешиваете первые две части по 3 шара. Если одна из частей оказалась тяжелее, то взвешиваем между собой любые 2 шара из нее. Или один из них будет искомым шаром, или не взвешенный, если они оказались равны. В случае равного веса частей при первом взвешивании, более тяжелый шар окажется в третьей части из двух шаров.

Дом

Вопрос: Нарисуйте дом.

Ответ: Казалось бы, что может быть проще. Рисуем квадрат, пару прямоугольников и треугольник наверху. А вот и нет. Этот тест рассчитан для должностей, которые требуют от сотрудника нестандартных решений и индивидуального подхода к каждой задаче (дизайнеров, менеджеров по рекламе). Во-первых, нужно проявить креативность, а не рисовать шаблонный дом. Во-вторых, нужно сперва уточнить для кого этот дом: кто в нем будет жить, и сколько будет этих жильцов. Не стоит приступать к работе, не узнав всех нюансов.

Вас могут попросить нарисовать не только дом, а все что угодно. Но всегда нужно узнавать все подробности, чтобы итоговый результат был правильным. А сам процесс будет значить намного больше, чем этот итоговый результат.

Слон

Вопрос: Как узнать вес слона без весов?

Ответ: Вариантов может быть очень много, вы ограничены лишь своей находчивостью и фантазией. Например, слона можно поставить на баржу и отметить ее осадку. Затем убрать слона и ставить на баржу предметы, вес которых вам известен — пятилитровые бутылки с водой, допустим. А когда осадка баржи будет такого же уровня как и со слоном, умножаем количество предметов на их вес. Тут главное — ваша изобретательность.

Драже M&M’s

Вопрос: Почему глазурь на известных драже M&M’s идеально гладкая? Как их делают, они что летают в воздухе?

Ответ: Еще один вопрос, правильный ответ на который не настолько важен, как варианты, предложенные кандидатом. Как бы вы решили эту задачу, если бы внезапно попали на производство? Держали бы драже на воздушном потоке? Приклеивали бы на нитку, где расположен логотип? На самом деле их опрыскивают глазурью во вращающемся барабане. Таким образом их поверхность остается гладкой, а глазурь наносится равномерно. Но ваш индивидуальный подход к решению этой задачи будет значить намного больше.

Русская рулетка

Решение этой задачи зависит от специфики вашей профессии. Ответ можно найти как с помощью точных вычислений, так и просто используя логику.

Вопрос: Есть шестизарядный револьвер. В нем 2 пули, обе расположены рядом друг с другом. Ваш оппонент раскручивает барабан, приставляет дуло к виску и нажимает на курок. Выстрела не произошло. Как поступите вы: сразу нажмете на курок или сперва снова раскрутите барабан?

Ответ: Правильный ответ один — сразу нажать на курок. Если произвести точные вычисления, то вероятность остаться в живых в этом случае составляет 75%, а если сперва раскрутить барабан — снижается до 66,7%. Так как пули расположены рядом друг с другом, можно логически определить, что лучше жать на курок сразу.

Читайте также: Вопросы-головоломки на собеседованиях с ответами. Часть 1

Читайте нас в Telegram

Чтобы оставить комментарий, нужно войти.

Мерзляк 5 класс — § 23. Объём прямоугольного параллелепипеда

Ответы к учебнику для 5 класса. А. Г. Мерзляк
Переход на главную страницу сайта

Вопросы к параграфу

1. Какими свойствами обладает объём фигуры?

Равные фигуры имеют равные объёмы.
Объём фигуры равен сумме объёмов фигур, из которых она состоит.

2. Какой куб называют единичным?

Единичным называют куб, ребро которого равно единичному отрезку.

3. Приведите примеры единиц измерения объёма.

1 мм³ — один кубический миллиметр
1 см³ — один кубический сантиметр
1 дц³ — один кубический дециметр
1 м³ — один кубический метр
1 л — один литр (при измерении жидкостей, 1 л = 1 дм³)

Что означает измерить объём фигуры?

Измерить объем фигуры — значит подсчитать, сколько единичных кубов в ней помещается.

5. Чему равен объём прямоугольного параллелепипеда с измерениями а, b, с?

V = abc

6. По какой формуле вычисляют объём куба?

V= a³

7. Как вычислить объём прямоугольного параллелепипеда, зная его площадь основания и высоту?

V = Sh

Решаем устно

1. Заполните пропуски в цепочке вычислений:

2. Сколько необходимо использовать кубиков с ребром 1 см, чтобы сложить кубик с ребром 2 см?

Чтобы сложить кубик с ребром 2 см, надо использовать 8 кубиков с ребром 1 см.

3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?

3 • 4 + 5 • 4 + 6 • 4 = 12 + 20 + 24 = 56 (см) — проволоки.

Ответ: 56 см.

4. Расставьте вместо звёздочек знаки «+» и «—» так, чтобы запись 20 * 30 * 10 * 80 * 70 = 50 стала верным равенством.

20 + 30 — 10 + 80 — 70 = (20 + 30) + (80 — 10 — 70) = 50 + 0 = 50

Упражнения

617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?

1 дм = 10 см
1 дм² = 10 см • 10 см = 100 см²
1 дм³ = 10 см • 10 см • 10 см = 1 000 см³

2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?

1 м = 100 см
1 м² = 100 см • 100 см = 10 000 см²
1 м³ = 100 см • 100 см • 100 см = 1 000 000 см³

618. Фигуры, изображённые на рисунке 179, сложены из кубиков, рёбра которых равны 1 см. Найдите объём каждой фигуры.

Для того, чтобы найти объём фигуры, надо посчитать количество единичных кубов, из которых она состоит.

1 фигура (на рисунке слева):

V = 5 • 2 + 3 + 3 + 2 = 10 + 8 = 18 см³

2 фигура (на рисунке справа):

V = 6 • 3 + 2 +2 + 3 • 2 + 5 + 2 = 18 + 4 + 6 + 7 = 18 + 17 = 35 см³

Ответ: 18 см³ и 35 см³.

619. Вычислите объём прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.

Дано:

a = 12 м
b = 15 м
c = 6 м
V = ? м³

Решение:

V = abc = 12 • 15 • 6 = 12 • 90 = 1 080 м³

Ответ: 1 080 м³.

620. Чему равен объём куба, ребро которого равно 6 см?

Дано:

a = 12 см
V = ? см³

Решение:

V= a³ = 6³ = 36 • 6 = 216 см³

Ответ: 216 см³.

621. Чему равен объём прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?

Дано:

a = 10 дм
b = 8 дм
c = 4 дм
V = ? дм³

Решение:

V = abc = 10 • 8 • 4 = 10 • 32 = 320 дм³

Ответ: 320 дм³.

622. Выразите:

1) в кубических миллиметрах:

7 см³ = 7 000 мм³

38 см³ = 38 000 мм³

12 см³ 243 мм³ = 12 000 мм³ + 243 мм³ = 12 243 мм³

42 см³ 68 мм³ = 42 000 мм³ + 68 мм³ = 42 068 мм³

54 см³ 4 мм³; = 54 000 мм³ + 4 мм³ = 54 004 мм³

1 дм³ 20 мм³ = 1 000 000 мм³ + 20 мм³ = 1 000 020 мм³

18 дм³ 172 см³ = 18 000 000 мм³ + 172 000 мм³ = 18 172 000 мм³

35 дм³ 67 см³ 96 мм³ = 35 000 000 мм³ + 67 000 мм³ + 96 мм³ = 35 067 096 мм³

2) в кубических дециметрах:

4 м³ = 4 000 дм³

264 м³ = 264 000 дм³

10 м³ 857 дм³ = 10 000 дм³ + 857 дм³ = 10 857 дм³

28 м³ 2 дм³ = 28 000 дм³ + 2 дм³ = 28 002 дм³

44 000 см³ = 44 дм³

5 430 000 см³ = 5 430 дм³

623. Выразите в кубических сантиметрах:

8 дм³ = 8 000 см³

62 дм³ = 62 000 см³

378 000 мм³ = 378 см³

520 000 мм³ = 520 см³

78 дм³ 325 см³ = 78 000 см³ + 325 см³ = 78 325 см³

56 дм³ 14 см³ = 56 000 см³ + 14 см³ = 56 014 см³

8 м³ 4 дм³ 6 см³ = 8 000 000 см³ + 4 000 см³ + 6 см³ = 8 004 006 см³

624.

Ширина прямоугольного параллелепипеда равна 15 дм, длина — на 3 дм больше ширины, а высота — в 3 раза меньше длины. Найдите объём данного параллелепипеда.

Дано:

a = ? см, на 3 дм больше, чем ребро b
b = 15 дм
c = ? см, в 3 раза меньше, чем ребро a
V = ? см³

Решение:

1) 15 + 3 = 18 (дм) — длина прямоугольного параллелепипеда.

2) 18 : 3 = 6 (дм) — высота прямоугольного параллелепипеда.

V = abc

3) 18 • 15 • 6 = 18 • 90 = 1 620 (дм³) — объем V прямоугольного параллелепипеда.

Ответ: V= 1 620 дм³.

625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объём данного параллелепипеда.

Дано:

a = ? см, на 4 см больше, чем ребро с
b = ? см, в 5 раз меньше, чем ребро c
c = 20 см
V = ? см³

Решение:

1) 20 + 4 = 24 (см) — длина прямоугольного параллелепипеда.

2) 20 : 5 = 4 (см) — ширина прямоугольного параллелепипеда.

V = abc

3) 24 • 5 • 20 = 24 • 80 = 1 920 (дм³) — объем V прямоугольного параллелепипеда.

Ответ: V= 1 920 дм³.

626. Объём прямоугольного параллелепипеда равен 560 см³, длина — 14 см, ширина — 8 см. Найдите высоту данного параллелепипеда.

Дано:

a = 14 см
b = 8 см
V = 560 см³
h = ? см

Решение:

V = Sh, значит h = V : S

1) 14 • 8 = 122 (см²) — площадь основания S прямоугольного параллелепипеда.

2) 560 : 120 = 5 (см) — высота h прямоугольного параллелепипеда.

Ответ: 5 см.

627. Длина прямоугольного параллелепипеда равна 18 см, высота — 15 см, а объём — 3 240 см³. Найдите ширину данного параллелепипеда.

Дано:

a = 18 см
h = 15 см
V = 3 240 см³
b = ? см

Решение:

V = Sh, значит S = V : h

1) 3 240 : 15 = 216 (см²) — площадь основания S прямоугольного параллелепипеда.

S = a • b, значит b = S : a

2) 216 : 18 = 12 (см) — ширина b прямоугольного параллелепипеда.

Ответ: 12 см.

628. Объём комнаты, имеющей форму прямоугольного параллелепипеда, равен 144 м³, а высота — 4 м. Найдите площадь пола комнаты.

Дано:

h = 4 м
V = 144 м³
S = ? м²

Решение:

V = Sh, значит S = V : h

1) 144 : 4 = 36 (м²) — площадь пола комнаты.

Ответ: 36 м².

629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объём равен 960 м³, а площадь пола равна 192 м². Найдите высоту спортивного зала.

Дано:

S = 192 м²
V = 960 м³
h= ? м

Решение:

V = Sh, значит h = V : S

1) 960 : 192 = 5 (м) — высота спортивного зала.

Ответ: 5 м.

630. Найдите объём фигуры, изображённой на рисунке 180 (размеры даны в сантиметрах).

Выполним дополнительное построение: проведём линии, соединяющие выступающие части исходной фигуры. Теперь можно сказать, что V = V_А— V_В, где:

V — объем искомой фигуры.
V_А— объем большого прямоугольного параллелепипеда, измерения которого равны 30 см, 20 см и 25 см.
V_В— объем малого прямоугольного параллелепипеда (красный), который вырезали из большого параллелепипеда для получения искомой фигуры. Его измерения: 15 см, 5 см и 20 см.

V = abc

V_А= 30 • 20 • 25 = 600 • 25 = 15 000 (cм³)

V_А= 15 • 5 • 20 = 15 • 100 = 1 500 (cм³)

V = V_А— V_В = 15 000 — 1 500 = 13 500 (cм³)

Ответ: V= 13 500 cм³

631. Найдите объём фигуры, изображённой на рисунке 181 (размеры даны в сантиметрах).

Фигуру, изображенную на рисунке 181, можно разделить на три прямоугольных параллелепипеда:

жёлтый
зелёный
красный

Рассмотрим прямоугольный параллелепипед № 3 (красный):

длина равна 15 см
ширина равна 8 + 8 = 16 см
высота равна 14 см

V = abc

V₃= 15 • 16 • 14 = 240 • 14 = 3 360 (cм³)

Рассмотрим прямоугольный параллелепипед № 2 (зелёный):

длина равна 8 см
ширина равна 8 см
высота равна 14 + 8 = 22 см

V = abc

V₂= 8 • 8 • 22 = 64 • 22 = 1 408 (cм³)

Рассмотрим прямоугольный параллелепипед № 1 (жёлтый):

длина равна 12 см
ширина равна 8 + 8 = 16 см
высота равна 14 см

V = abc

V₁= 12 • 16 • 14 = 192 • 14 = 2 688 (cм³)

Объем фигуры равен сумме объемов фигур, из которых она состоит.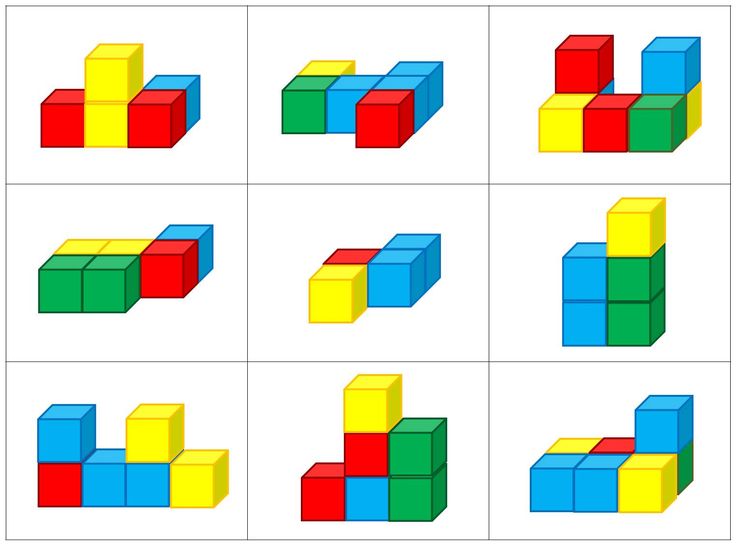

V = V₁+ V₂+ V₃= 2 688 + 1 408 + 3 360 = 7 456 (cм³)

Ответ: V = 7 456 cм³.

632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если масса 1 см³ цинка составляет 7 г.

Дано:

a = 4 cм²
Масса 1 cм³ = 7 г
Масса куба = ? г

Решение:

V = a³

V = 4 • 4 • 4 = 16 • 4 = 64 (см³)

Масса 1 см³ куба равна 7 г, значит масса 64 см³ равна:

64 • 7 = 448 (г)

Ответ: 448 г.

633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм³ земли?

150 м = 15 000 см

1) 15 000 • 80 • 60 = 1 200 000 • 60 = 72 000 000 (см³) — объем выкопанной машиной траншеи.

72 000 000 см³ = 72 м³

2) 72 : 8 = 9 (м³) — выкапывает машина за 1 час.

72 м³ = 72 000 дм³

3) 72 000 : 240 = 300 (человек) — коротышек могут заменить 1 машину.

Ответ: 9 м³, 300 коротышек.

634. Куб и прямоугольный параллелепипед имеют равные объёмы. Найдите площадь поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.

1) 12 • 2 = 6 (см) — сторона b прямоугольного параллелепипеда.

2) 12 • 4 = 3 (см) — сторона с прямоугольного параллелепипеда.

3) V = a • b • c = 12 • 6 • 3 = 72 • 3 = 216 (см³) — объём прямоугольного параллелепипеда.

V (прямоугольного параллелепипеда) = V (куба) = a³ = 216 (см³)

Значит сторона куба равна такому числу, которое при возведении в третью степень равно 216. Методом подбора можем определить что это число 6, то есть сторона квадрата а = 6 см.

У куба 6 одинаковых граней, площадь каждой из которых равна а².

4) а² = 6 • 6 = 36 (см²) — площадь поверхности одной грани куба.

5) 36 • 6 = 216 (см²) — площадь поверхности куба.

Ответ: Площадь поверхности куба равна 216 см².

635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объём первого куба больше объёма второго?

Пусть длина ребра второго куба равна х единиц, тогда длина ребра первого куба будет равна 4х единиц.

S = 6a²

S₂ = 6a² = 6x² (ед²) — площадь поверхности второго куба.

S₁ = 6a² = 6(4x)² = 6 • (4 • 4 • x • x) = 6 • 16 x² = 96 x² (ед²) — площадь поверхности первого куба.

S₂ : S₁=96 x² : 6x² = 96 : 6 = 16 (раз) — площадь поверхности первого куба больше площади поверхности второго куба.

V = a³

V₂ = a³ = х³ (ед³) — объём второго куба.

V₁ = a³ = (4х)³ = 4 • 4 • 4 • x • x • x = 16 • 4 • х³ = 64 х³ (ед³) — объём второго куба.

V₁ : V₂= 64 х³ : х³ = 64 (раза) — объём первого куба больше объёма второго куба.

Ответ: Площадь поверхности больше в 16 раз, объём больше в 64 раза.

636. Как изменится объём прямоугольного параллелепипеда, если:

1) длину увеличить в 4 раза, ширину — в 2 раза, высоту — в 5 раз

V = abc

V₁ = (4 • a) • (2 • b) • (5 • c) = (4 • 2 • 5) abc = 40 abc

V₁ : V = 40 abc : abc = 40 (раз)

Ответ: объём увеличится в 40 раз.

2) ширину уменьшить в 4 раза, высоту — в 2 раза, а длину увеличить в 16 раз

V = abc

V₁ = (16 • a) • (b : 4) • (c : 2) = (16 : 4 : 2) abc = (4 : 2) abc = 2 abc

V₁ : V = 2 abc : abc = 2 (раза)

Ответ: объём увеличится в 2 раза.

637. Как изменится объём прямоугольного параллелепипеда, если:

1) каждое измерение увеличить в 2 раза

V = abc

V₁ = (2 • a) • (2 • b) • (2• c) = (2 • 2 • 2) abc = 8 abc

V₁ : V = 8 abc : abc = 8 (раз)

Ответ: объём увеличится в 8 раз.

2) длину уменьшить в 3 раза, высоту — в 5 раз, а ширину увеличить в 15 раз

V = abc

V₁ = (a : 3) • (b • 15) • (c : 5) = (15 : 3 : 5) abc = (5 : 5) abc = abc

V₁ : V = abc : abc = 1 (раз)

Ответ: объём не изменится.

638. В бассейн, площадь дна которого равна 1 га, налили 1 000 000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?

S = 1 га = 10 000 м² = 1 000 000 дм²

V = 1 000 000 л = 1 000 000 дм³

V = S • h, значит h = V : S

h = V : S = 1 000 000 дм³ : 1 000 000 дм² = 1 дм = 10 см — высота налитой в басейн воды.

Это значит, что плавать в этом бассейне невозможно.

Ответ: Нет, соревнования по плаванию провести нельзя.

639. В кубе с ребром 3 см проделали три сквозных квадратных отверстия со стороной 1 см (рис. 182). Найдите объём оставшейся части.

1) V (куба) = a³ = 3³ = 9 • 3 = 27 (см³) — объём куба с ребром 3 см.

2) V (одного отверстия) = abc = 1 • 1 • 3 = 3 (см³) — объем одного сквозного отверстия со стороной 1 см.

Так как все три отверстия пересекаются в центре куба, то объём вырезанной части:

3) V (вырезанной части) = 3 см³ • 3 ( размер трёх сквозных отверстий) — 1 см³ (размер пересечения второго отверстия в первым и третьим) — 1 см³ размер пересечения третьего отверстия с первым и вторым) = 9 — 1 — 1 = 7 (см³) — объём вырезанной части.

4) V (оставшейся части) = V (куба) — V (вырезанной части) = 27 — 7 = 20 (см³) — объём оставшейся части.

Ответ: 20 см³.

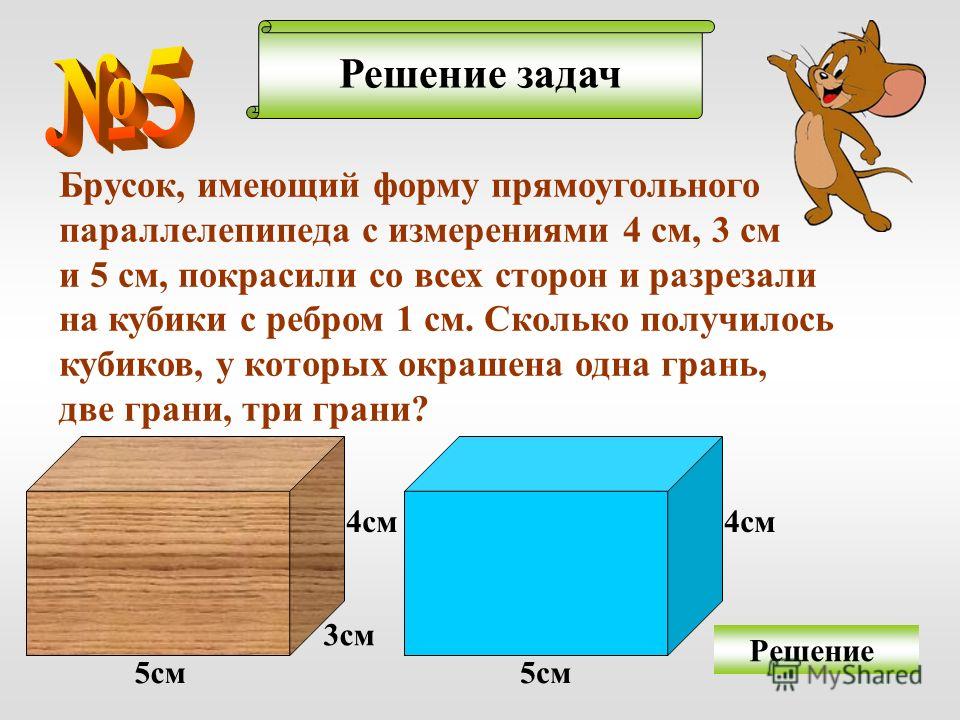
640. Размеры куска мыла, имеющего форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?

1) 12 • 6 • 4 = 72 • 4 = 288 (см³) — объём нового куска мыла.

2) (12 : 2) • (6 : 2) • (4 : 2) = 6 • 3 • 2 = 18 • 2 = 36 (см³) — объём мыла через 14 дней использования.

3) 288 — 36 = 252 (см³) — мыла было использовано за 14 дней.

4) 252 : 14 = 18 (см³) — мыла используется за 1 день.

5) 36 : 18 = 2 (дня) — хватит оставшегося мыла.

Ответ: на 2 дня.

Упражнения для повторения

641. В школьном коридоре, длина которого равна 30 м, ширина — 35 дм, надо заменить линолеум. Какое наименьшее количество рулонов линолеума для этого нужно, если длина рулона линолеума равна 12 м, а ширина — 160 см?

35 дм = 350 см

1) 350 = 2 • 160 + 30 (см)

Значит, для того, чтобы покрыть линолеумом в один ряд пол по ширине коридора необходимо использовать 2 рулона материала и ещё полосу шириной в 30 см.

2) 30 = 12 • 2 + 6 (м)

Значит, для того, чтобы покрыть линолеумом в один ряд пол по длине коридора необходимо использовать 2 целых рулона и ещё одну половину рулона (6 = 12 : 2).

Сделаем раскладку:

1 ряд по длине — 2 рулона + полоса 12 м х 30 см
2 ряд по длине — 2 рулона + полоса 12 м х 30 см
3 ряд по длине — (половина рулона + половина рулона) + полоса 6 м х 30 см.

Половина рулона + половина рулона = 1 целый рулон.

Полосы 12 м х 30 см, 12 м х 30 см и 6 м х 30 см можно выкроить из 1 целого рулона.

Значит нам потребуется:

3) 2 + 2 + 1 + 1 = 6 (шт) — рулонов линолеума потребуется для замены линолеума в школьном коридоре.

Ответ: 6 рулонов.

642. Из двух населённых пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу два велосипедиста и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?

1) 12 • 2 = 24 (км) — проехал первый велосипедист до места встречи.

2) 54 — 24 = 30 (км) — проехал второй велосипедист до места встречи.

3) 30 : 2 = 15 (км/ч) — скорость второго велосипедиста.

Ответ: 15 км/ч.

643. Найдите значение выражения:

1) 7a + 7b, если a + b = 14

7a + 7b = 7 (a + b) = 7 • 14 = 98

2) m • 17 + n • 17, если m + n = 1 000

m • 17 + n • 17 = 17 (m + n) = 17 • 1 000 = 17 000

3) k • 9 + 9l, если k + l = 12

k • 9 + 9l = 9 (k + l) = 9 • 12 = 108

4) 4c — 4d, если с — d = 125

4c — 4d = 4 (c — d) = 4 • 125 = 500

5) x • 23 — 23y, если x — у = 4

x • 23 — 23y = 23 (x — y) = 23 • 4 = 92

6) 56p — r • 56, если р — r = 11

56p — r • 56 = 56 (p — r) = 56 • 11 = 616

Задача от мудрой совы

644. В записи первого трёхзначного числа используются только цифры 2 и 3, а в записи второго — только цифры 3 и 4. Может ли произведение этих чисел записываться только цифрами 2 и 4?

Если в записи первого трёхзначного числа используются только цифры 2 и 3, то таким трёхзначным числом могут быть числа:

222, 223, 232, 322, 233, 323, 332, 333.

Если в записи второго трёхзначного числа используются только цифры 3 и 4, то таким трёхзначным числом могут быть числа:

333, 334, 343, 433, 344, 434, 443, 444.

Расположим их в виде таблицы:

в первом столбце напишем все возможные варианты первого числа;
в верхней строке — все возможные варианты второго числа;
на пересечении — произведение соответствующего варианта первого и второго числа (можно их посчитать при помощи калькулятора).

	333	334	343	433	344	434	443	444
222	73926	74148	76146	96126	76368	96348	98346	98568
223	74259	74482	76489	96559	76712	96782	98789	99012
232	77256	77488	79576	100456	79808	100688	102776	103008
322	107226	107548	110446	139426	110768	139748	142646	142968
233	77589	77822	79919	100889	80152	101122	103219	103452
323	107559	107882	110789	139859	111112	140182	143089	143412
332	110556	110888	113876	143756	114208	144088	147076	147408
333	110889	111222	114219	144189	114552	144522	147519	147852

Мы видим, что ни одно произведение не удовлетворяет условию. Значит записать такое произведения только цифрами 2 и 4 невозможно.

Ответ: Нет, нельзя.

Ответы к учебнику для 5 класса. А. Г. Мерзляк
Переход на главную страницу сайта

Калькулятор кубической плотности

Создано Александрой Зайонц, доктором медицины

Отзыв от Krishna Nelaturu

Последнее обновление: 12 октября 2022 г.

Содержание:

Как пользоваться калькулятором кубической плотности?
Что такое плотность? Какова формула плотности куба?
Как рассчитать объем куба по плотности?
Другие калькуляторы плотности
Как рассчитать плотность бетонного куба?
Часто задаваемые вопросы

Калькулятор кубической плотности — это простой инструмент с большими возможностями. ‘Как найти плотность куба?’ больше никогда не будет для вас проблемой! Читайте дальше, чтобы узнать:

Какова формула плотности куба;
Как пошагово рассчитать плотность куба; и
Как рассчитать плотность бетонного куба.

Как пользоваться калькулятором кубической плотности?

Пользоваться калькулятором кубической плотности просто и интуитивно понятно, но в случае сомнений проверьте эти шаги.

См. панель калькулятора в левой части страницы.
Первое, что вы сделаете, это изображение куба с выделенными размерами. Благодаря ему вы можете видеть, о каких измерениях идет речь.
Введите массу (вес) вашего куба в калькулятор плотности куба. Помните, что вы всегда можете изменить единицу измерения так, как вам удобно.
Введите объем вашего куба в удобных единицах измерения. Если вы не знаете объем, выполните следующий шаг. В противном случае вы можете пропустить его.
Введите известные вам размеры куба: длина стороны, диагонали куба или диагонали грани. Калькулятор рассчитает объем автоматически.
Вы сразу видите результат в поле Density !
Если вы хотите узнать, как найти плотность куба шаг за шагом , продолжайте читать текст.

Что такое плотность? Какова формула плотности куба?

Плотность — термин, используемый в физике для описания масса на единицу объема пространства .

Формула плотности:

ρ=mV\rho = \frac{m}{V}ρ=Vm

где:

ρ\rhoρ — плотность,
ммм — масса, а
ВВВ — объем.

Если два объекта одинакового размера, но один из них тяжелее, мы можем сказать , что он имеет большую плотность.

Куб представляет собой правильную квадратную призму в трех ориентациях. У него шесть квадратных граней с тремя гранями, сходящимися в каждой вершине. 93}ρ=a3m

где:

ρ\rhoρ — плотность,
ммм — масса, а
ааа — длина ребра куба.

Как рассчитать объем куба по плотности?

Вот три способа расчета объема куба в зависимости от того, какое измерение у вас есть. Буквы в скобках относятся к изображению над калькулятором.

Вы знаете сторону (а) куба
- Рассчитать объем (VVV) как: 93V=(2
  f)3
  Еще калькуляторы плотности
  У нас на сайте есть еще крутые калькуляторы плотности:
  - Калькулятор плотности;
  - Калькулятор плотности газа;
  - Калькулятор массы в плотность;
  - Калькулятор объем-плотность;
  - Калькулятор плотности к массе;
  - Калькулятор соотношения плотности к весу;
  - Калькулятор плотности масса-объем;
  - Калькулятор плотности цилиндра;
  - Калькулятор плотности сфер.
  Как рассчитать плотность бетонного куба?
  Хотя плотность бетона уже определена (2400 кг/м ³ ), иногда ее необходимо рассчитать самостоятельно.
  1. Найдите массу (вес) вашего бетонного куба.
  2. Затем измерьте сторону куба.
  3. Как рассчитать объем куба по плотности? Используйте формулу: объем = сторона ³ .
  4. Теперь разделите массу на объем. плотность = масса/объем
  5. Расчет кубической плотности готов!
  Часто задаваемые вопросы
  Как определить плотность кусочка сахара?
  Чтобы найти плотность кусочка сахара:
  1. Возьмите линейку или другой измерительный инструмент и измерьте сторону кусочка сахара. Назовем его .
  2. Рассчитайте объем куба: объем = a ³
  3. Теперь взвесьте кубик сахара на кухонных весах.
  4. Чтобы найти плотность, нужно решить уравнение:
  плотность = масса/объем
  Как рассчитать плотность куба дерева?
  Древесина не является однородным материалом, поэтому, если вы хотите быть точным в отношении плотности деревянного куба, лучше посчитайте ее самостоятельно:
  1. Взвесьте свой деревянный куб.
  2. Измерьте куб. Самый простой способ — измерить его сторону.
  3. Рассчитайте объем вашей деревянной вещи. объем = (длина стороны) ³ .
  4. Теперь посчитайте плотность куба. Плотность = масса (вес)/объем .
  Как найти плотность куба со стороной 2 фута и весом 5 фунтов?
  Плотность этого куба составляет 0,625 фунт/фут ³ . Чтобы вычислить плотность этого куба:
  1. Вычислите объем куба по формуле объем = сторона ³ .
  2. Наш случай, объем = 2 фута ³ = 8 футов ³ .
  3. Чтобы вычислить плотность, решите уравнение плотность = масса/объем .
  4. В нашем случае плотность = 5 фунтов/8 футов ³ = 0,625 фунтов/фут ³ .
  5. Ответ: кубическая плотность = 0,625 фунт/фут ³ .
  Aleksandra Zając, MD
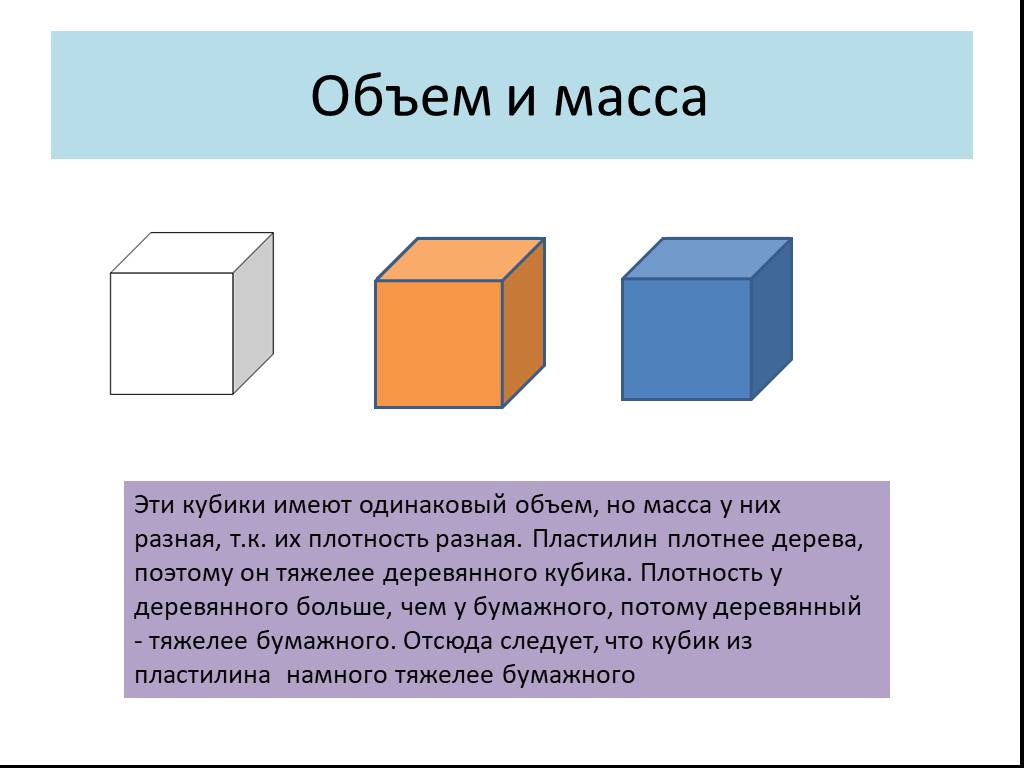
  Плотность
  Вес/масса
  Том
  Сторона (A)
  Диагональный (D)
  Diagonal (F)
  Проверьте 86 Classical Classical. 0003
  УскорениеУгол поворотаУгол крена… Еще 83
  Найдите фальшивый мяч в 3 гирях
  Найдите фальшивый мяч среди 9 шаров в 3 гирях. Все шары похожи. У вас есть чашечные весы без весов. Время решения 30 минут.
  Попробуйте, прежде чем продолжить.
  Бонусная головоломка
  Сможете ли вы найти все возможные способы решения головоломки?
  Нет ограничения по времени для этого и никакого решения от нас. Это только для вас, если вам интересно.
  Решение головоломки с 9 шарами 1 разного веса: Найдите фальшивый мяч за 3 взвешивания
  Каким должен быть лучший план для первого взвешивания? Мы не можем разделить 9 на две равные части; так что очевидно, что
  должно быть три части: два набора шаров одинакового размера, взвешенных друг против друга, и третий набор шаров, оставленный в стороне.
  Сразу возникает следующий вопрос,
  как лучше 9 разделить на 3 части?
  Мысленно исследуйте, что произойдет, если вы оставите только 1 мяч в стороне и взвесите 4 мяча против 4 других. В лучшем случае весы будут идеально сбалансированы, доказывая, что все 8 взвешенных мячей являются хорошими мячами, а 1 мяч, оставленный в стороне, является фальшивым. один. Просто взвесьте поддельный мяч с 1 из 8 хороших мячей, и вы узнаете, легче или тяжелее поддельный мяч, чем хорошие мячи.
  Но если вам не улыбнется такая удача, то у вас будет 8 подозрительных шаров, либо фальшивый среди 4-х более легких, либо среди 4-х более тяжелых.
  Этот путь совсем не перспективен и мы будем следовать общему принципу решения проблем исходя из опыта о как лучше разделять и властвовать,
  Разделить врага на мельчайшие группы с группой размеры максимально совпадают друг с другом.
  Все три группы должны быть наименьшими и одинаковыми, 9 должны быть разделены на три группы по 3 мяча в каждой,
  9 = 3 + 3 + 3.
  Эта стратегия также следует принцип симметрии,
  Если вы увеличите симметрию в задаче действием, это будет вашим САМЫМ ПЕРСПЕКТИВНЫМ ДЕЙСТВИЕМ.
  Мы тут же решаем взвешивать первыми,
  3 мяча против 3 других —6 мячей с 3 мячами в стороне.
  На рисунке показана первая комбинация взвешивания .
  Возможны три исхода взвешивания:
  1. Первый результат 1-го взвешивания – опускается правая чаша.
  Заключение: Все шесть шаров подозрительны. В частности,
  1.1. Либо левые три шара, идущие вверх, содержат фальшивый более легкий шар, либо
  1.2. На правом опускающемся поддоне установлен более тяжелый шар.
  На рисунке ниже показана ситуация.
  2. Второй вариант — левая чаша опускается:
  Вывод: Все шесть шаров подозрительны. В частности,
  2.1. Либо левая сторона нисходящих трех шаров содержит фальшивый более тяжелый шар, либо
  2. 2. Поддон с правой стороны имеет фальшивый шар для зажигалок. По сути, эти два результата потребуют точно таких же действий, как и результаты 1.1 и 1.2.
  Мы не будем анализировать эти два результата дальше. Анализ результатов 1.1 и 1.2 должен быть достаточным для достижения решения.
  3. Третий вариант — чаши одинаково сбалансированы:
  Вывод:
  три шара слева должны содержать поддельный шар и,
  Все шесть взвешенных мячей хорошие.
  Сначала рассмотрим третий результат .
  Изучение третьего результата 1-го взвешивания: Нахождение фальшивого мяча среди 3-х подозрительных шаров, оставленных в стороне во 2-х взвешиваниях и взвешиваем 2 против 2. Из 6 хороших мячей пять не используются.
  Следующая схема показывает эту комбинацию взвешивания. Подозрительные шары заштрихованы.
  Одна сторона должна идти вниз.
  Результат 3.1. Когда чаши были одинаково уравновешены при 1-м взвешивании И чаша с 1 исправным шаром опустилась при 2-м взвешивании:
  3.1.1. Либо единственный подозрительный шар с хорошим мячом (заштрихован и отмечен буквой L) тяжелее,
  3.1.2. Или два правых шара (заштрихованные и отмеченные R) имеют фальшивый более легкий.
  Ты еще не совсем уверен, но одно взвешивание у тебя еще осталось.
  Третья схема взвешивания для результата 3.1:
  Взвесьте два сомнительных шара в правой чаше против друг друга — заштрихованный R против другого заштрихованного R. Один из них может быть фальшивым более легким шаром.
  Это показано на следующей схеме.
  Окончательные выводы 3-го взвешивания для результата 3.1
  Только два возможных вывода,
  1. Поднимающаяся чаша имеет фальшивый шар для зажигалок , , если две чаши не уравновешивают друг друга.
  2. Единственный подозрительный шар, пропущенный при 3-м взвешивании, это фальшивый более тяжелый шар , , если две чаши уравновешены.
  Первый на рисунке слева, второй на рисунке справа.
  Результат 3.2: Когда чаши одинаково уравновешены при 1-м взвешивании И чаша с 1 хорошим шариком поднимается при 2-м взвешивании
  Здесь также вы предпримите точно такое же действие, взвешивая два шара в правой кастрюле друг против друга. Только результаты и выводы будут обратны результатам, которые мы только что получили.
  Время до анализа первого результата 1-го взвешивания.
  Головоломка «Найди поддельный шар в 9 шарах с помощью 3 взвешиваний»: изучение первого результата первого веса, когда левая чаша с 3 шарами поднялась
  Для удобства показана схема результата 1 первого взвешивания.
  И вывод : Все шесть шаров подозрительны . В частности,
  1.1. Либо три шара с левой стороны, идущие вверх, содержат фальшивый более легкий шар,
  1.2. Или, правая опускающаяся чаша имеет фальшивый более тяжелый шар.
  Все шесть предполагаемых фальшивых шаров заштрихованы восходящими левыми шарами панорамирования, помеченными буквой L, и опускающимися правыми шарами панорамы, помеченными буквой R, для удобства дальнейшего использования.
  Анализ и решение по взвешиванию для второго взвешивания двух групп по 3 подозрительных шара в каждой
  Мы должны мыслить нестандартно. Количество подозрительных шаров равно 6. Очки в нашу пользу:
  1. Левый фальшивый шар должен быть легче, а правый фальшивый шар должен быть тяжелее и,
  2. Три неучтенных мяча — это хорошие мячи.
  Первое решение принято для частичного баланса восходящей и нисходящей ситуации is,
  Обменять 1 мяч между двумя чашами.
  Вариант часто используемого метод выравнивания базы , используемый при решении математических задач на высокой скорости. Это действие уравновешивает асимметрию природы весов мячей и повышает общую симметрию.
  Второе решение принять к уменьшить количество возможных результатов второго и третьего взвешивания есть,
  ОСТАВИТЬ В СТОРОНЕ по 1 шару из каждой чаши.
  Разделение 6 подозрительных шаров на три группы по 2 шара в каждой в соответствии с нашей предыдущей стратегией,
  Это уменьшает размер трех частей 6 до 2, 2 и 2, и это наименьший размер групп деталей.
  Показана вторая комбинация взвешивания .
  При этом втором взвешивании каждая чаша имеет точно такую же комбинацию типов шариков,
  В каждой чашке есть один шар с маркировкой L, который может быть только более легким, если он окажется подделкой, и один шар с маркировкой R, который может быть только более тяжелым один, если нашли подделку.
  Результаты 2-го взвешивания за 1-й результат 1-го взвешивания: левая чаша поднялась и все 6 шаров оказались подозрительными
  Возможны три варианта,
  1. Левая чаша снова поднимается вверх— Вывод: Либо левая чашка L — более легкая подделка, либо правая чашка R — более тяжелая подделка,
  2. На этот раз левая чаша опускается— Вывод: Либо шар L правой чаши — более легкая подделка, либо шар R левой чаши — более тяжелая подделка, и
  3. Две кастрюли идеально сбалансированы— Вывод: Либо отложенный шар L — более легкая подделка, либо отложенный шар R — более тяжелая подделка.
  Выводы указывают на один и тот же результат во всех трех случаях — один из двух L-R пар шаров является подделкой.
  Окончательное 3-е взвешивание и решение головоломки с 9 шарами для 1-го результата 1-го взвешивания: левая чаша поднялась и все 6 шаров оказались подозрительными пара из двух мячей.
  
  Показана комбинация взвешивания,
  L-шар снова помещается на левую чашу, а исправный шар — на правую чашу, и последнее взвешивание выполнено.
  Может быть только два результата и следующих выводов:
  Если левая чаша поднимется, L-шар в ней будет поддельным шаром, и,
  Если две кастрюли идеально сбалансированы, отложенный в сторону R-шар является фальшивым более тяжелым шаром.
  Прощальный вопрос: Можно ли решить головоломку по-другому?
  Если вы исследуете, чтобы найти ответ, вы можете обнаружить новые способы решения этой не такой уж простой головоломки, а также вы поймете, почему мы предприняли сложное действие одновременного обмена и откладывания мячей в сторону.
  Знайте, как легко решать сложные задачи, не тратя время на случайные попытки
  Наша электронная книга о решении головоломок инновационными методами покажет вам именно это.
  Головоломки для взрослых: 50 головоломок с пошаговыми решениями: улучшите свои навыки решения задач , PayHip и другие)
  
  BUY the eBook Amazon Kindle version here , from Google Play here and Paperback here .
  Вторая книга об инновационных решениях головоломок из спичек от Suresolv
  КУПИТЬ Creative Matchstick Puzzles eBook Innovative Solutions Amazon Kindle version
  КУПИТЬ в мягкой обложке здесь.
  
  Головоломки, которые могут вам понравиться
  Головоломки от простых до сложных с систематическими решениями
  Сложные головоломки с решениями: длинный список.
  No related posts.