F x 1 x график: Свойства функции y = k/x и её график — урок. Алгебра, 8 класс.

Исследование функций

	1.Возрастание и убывание функции. 2.Экстремум функции. 3.Выпуклость графика функции. 4.Точки перегиба. 5.Асимптоты графика функции.
	10 11 12 13 14 15 16 17 18
	1. Возрастание и убывание функции
	Пусть задана функция f(x). Возьмем две точки на промежутке [a,b] х1 и х2 при условии, что х2 > x1. Тогда функция называется возрастающей на промежутке [a,b], если f(x2) > f(x1). Функция называется убывающей на промежутке [a,b], если f(x2) < f(x1).
	Если функция дифференцируема на определенном промежутке и производная функции в точке х = с положительна, то на этом промежутке она возрастает.    Действительно, согласно теореме Лагранжа, если х2 > x1 и f ‘(c) > 0, то функция возрастает.    т.е. если левая часть равенства положительна, где х1 <c< x2 и f ‘(c)>0, то f(x2)>f(x1)		Возрастающая функция.
	При убывании функции можно сделать аналогичный вывод.    Если функция дифференцируема на определенном промежутке и производная функции в точке х = с отрицательна, то на этом промежутке она убывает.    Опять же, согласно теореме Лагранжа, если х1 <c< x2 и f ‘(c) < 0, то функция убывает.		Убывающая функция.
	2.Экстремум функции.
	Если функция f(x) определена на определенном промежутке и существует такая точка А на этом промежутке, что f(x) < f(A) во всех точках окрестности точки А, то данная точка называется точкой максимума.    Если функция f(x) определена на определенном промежутке и существует такая точка В на этом промежутке, что f(x) > f(В) во всех точках окрестности точки B, то данная точка называется точкой минимума.    Точки максимума и минимума называются критическими точками и производная функции в этих точках или не существует, или равна нулю f ‘(A) = 0 f ‘(B) = 0.    Касательная к графику функции в данных точках параллельна оси ОХ.    Здесь нужно отметить, что не во всех критических точках функция имеет экстремум. Например функция y = x3 не имеет экстремума, т.к. не выполняется условие f(x) <(>) f(x0), т.е. в окрестности точки х0 значение функции должно быть больше (меньше) значения функции в точке х0. Таким образом, функция y = x3 имеет критическую точку при х=0 (т.к. f ‘(0)=0), но экстремума в этой точке нет.		Экстремум функции.
	3.Выпуклость графика функции.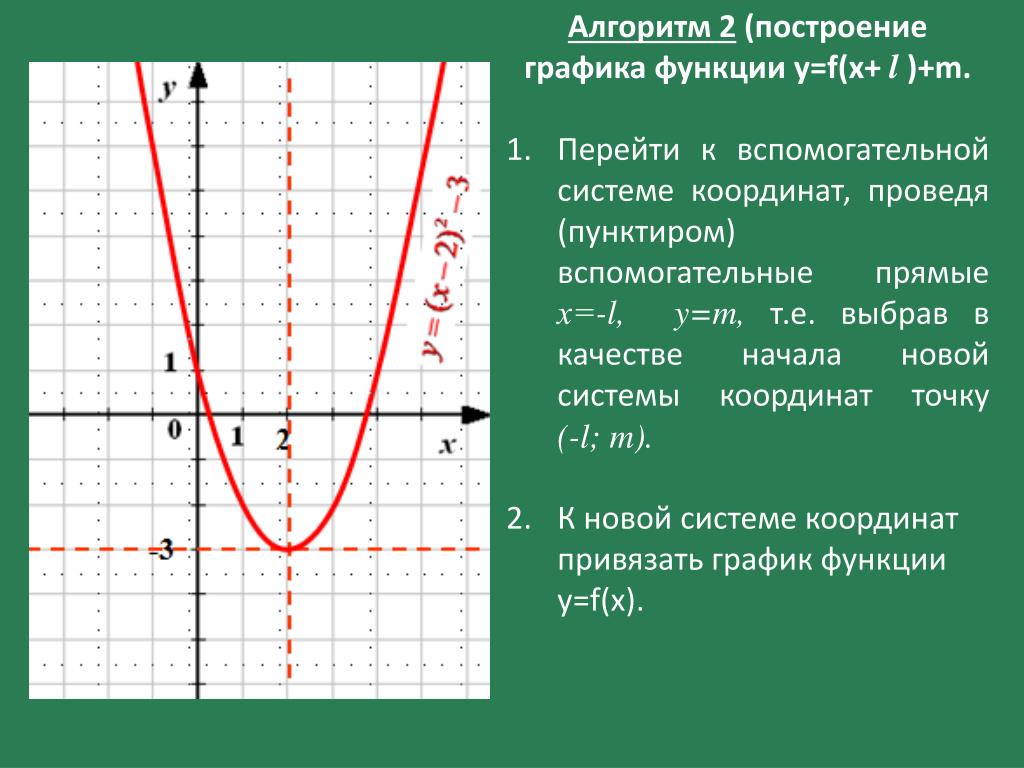
	Пусть задана функция y = f(x). Предположим, что функция f(x) дифференцируема на определенном промежутке [x1;x3].    Возьмем промежуток [x1;x2]. Тогда, если при любом значении х таком, что x1<x<x2, значение функции меньше значения касательной в точке х, т.е. fф(x) ≤ fк(x), то функция выпукла вверх.    Возьмем промежуток [x2;x3]. Тогда, если при любом значении х таком, что x2<x<x3, значение функции больше значения касательной в точке х, т.е. fф(x) ≥ f к(x), то функция выпукла вниз.    Если функция выпукла вверх, то вторая производная функции меньше нуля, т.е. f »(x) < 0.    Если функция выпукла вниз, то вторая производная функции больше нуля, т.е. f »(x) > 0.		Выпуклость графика функции.
	4.Точки перегиба.
	Если график функции слева и справа от точки А имеет разную выпуклость, то эта точка называется точкой перегиба.    В точке перегиба вторая производная функции f»(x)=0. Если второй производной в точке А не существует, тогда вторая производная для функции f(x) слева и справа от точки А будет иметь разные знаки.		Точка перегиба.
	Репетитор: Васильев Алексей Александрович       Предметы: математика, физика, информатика, экономика, программирование.   2000 руб / 120 мин — подготовка к ЕГЭ и ГИА для школьников. 3000 руб / 120 мин — индивидуально (базовый уровень). 2000 руб / 120 мин — студенты.
	5. Асимптоты графика функции.
	Асимптотой графика функции f(x) называется прямая, расстояние до которой от графика функции стремится к нулю при стремлении х к бесконечности. Т.е. fпр(х) — f(x) → 0 или fпр(x) → f(x)    Допустим функция определена в окрестности точки x0. Тогда если хотя бы один из пределов функции справа или слева равен бесконечности при стремлении x→x0, то пряма x=x0 называется вертикальной асимптотой.		Вертикальная асимптота.
	Если существует конечный предел функции равный b при стремлении х→∞, то прямая y = b есть горизонтальная асимптота.    Если существует только один конечный предел при стремлении х→∞       справа или слева, то функция имеет левостороннюю или правостороннюю асимптоту.		Горизонтальная асимптота.
	Если существуют конечные пределы такие, что то прямая y = kx + b называется наклонной асимптотой.    Бавают правосторонние и левосторонние наклонные асимптоты.		Наклонная асимптота.
	Пример.
	Получим:    точка х = -2,791 минимум,    точка х = 0 максимум,    в точке х = 1 функция не определена,    точка х = 1,791 минимум.
	6. Интервалы выпуклости и точки перегиба.
	10 11 12 13 14 15 16 17 18

Открытая Математика.

Функции и Графики. Монотонность функций

Монотонность функций

Функция f (x) называется возрастающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) < f (x₂).

Функция f (x) называется убывающей на промежутке D, если для любых чисел x₁ и x₂ из промежутка D таких, что x₁ < x₂, выполняется неравенство f (x₁) > f (x₂).

Промежутки возрастания и убывания функции На показанном на рисунке графике функция y = f (x), x∈[a;  b], возрастает на каждом из промежутков [a; x₁) и (x₂; b] и убывает на промежутке (x₁; x₂). Обратите внимание, что функция возрастает на каждом из промежутков [a; x₁) и (x₂; b], но не на объединении промежутков [a;  x1)∪(x2;  b].

Если функция возрастает или убывает на некотором промежутке, то она называется монотонной на этом промежутке.

Заметим, что если f – монотонная функция на промежутке D (f (x)), то уравнение f (x) = const не может иметь более одного корня на этом промежутке.

Действительно, если x₁ < x₂ – корни этого уравнения на промежутке D (f(x)), то f (x₁) = f (x₂) = 0, что противоречит условию монотонности.

Перечислим свойства монотонных функций (предполагается, что все функции определены на некотором промежутке D).

• Сумма нескольких возрастающих функций является возрастающей функцией.
• Произведение неотрицательных возрастающих функций есть возрастающая функция.
• Если функция f возрастает, то функции cf  (c > 0) и f + c также возрастают, а функция cf (c < 0) убывает. Здесь c – некоторая константа.
• Если функция f возрастает и сохраняет знак, то функция 1/f убывает.
• Если функция f возрастает и неотрицательна, то fn,  где n∈ℕ, также возрастает.
• Если функция f возрастает и n – нечетное число, то f ⁿ также возрастает.
• Композиция g (f (x)) возрастающих функций f и g также возрастает.

Аналогичные утверждения можно сформулировать и для убывающей функции.

Свойства функции

Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).

Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).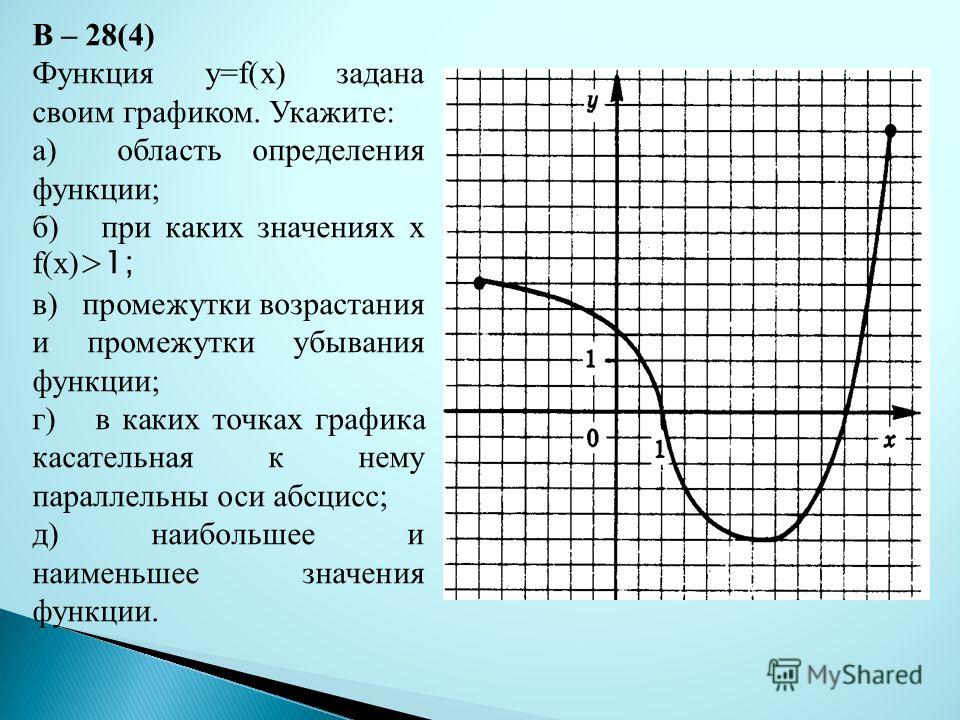

Точки, в которых достигается максимум или минимум функции, называются точками экстремума.

В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.

Если для любого x∈D   (x ≠ a) выполняется неравенство f (x) ≤ f (a) (a∈D),  то точка a называется точкой наибольшего значения функции на множестве D: maxx∈Dfx=fa.

Если для любого x∈D   (x ≠ b) выполняется неравенство f (x) > f (b)  (b∈D),  то точка b называется точкой наименьшего значения функции на множестве D. minx∈Dfx=fb.

Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.

Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.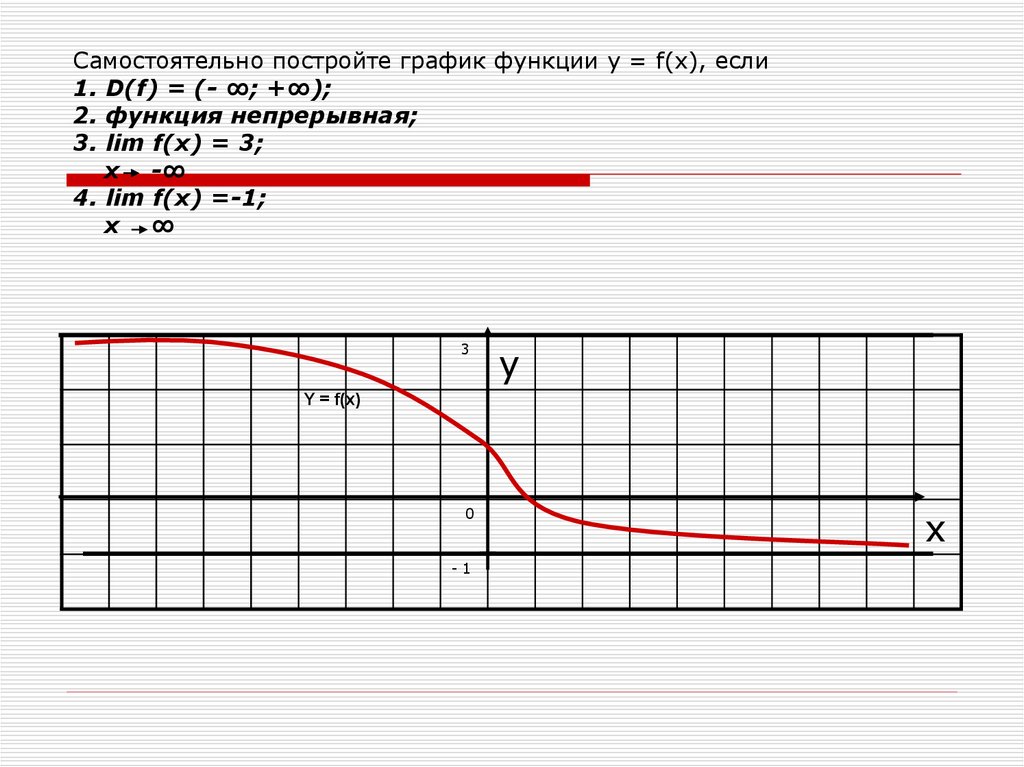

Функция, ограниченная сверху Функция, ограниченная снизу Функция, ограниченная на множестве D

Если существует число C такое, что для любого x∈D выполняется неравенство f (x) ≤ C, то функция f называется ограниченной сверху на множестве D.

Если существует число c такое, что для любого x∈D выполняется неравенство f (x) ≥ c, то функция f называется ограниченной снизу на множестве D.

Функция, ограниченная и сверху, и снизу, называется ограниченной на множестве D. Геометрически ограниченность функции f на множестве D означает, что график функции y = f (x), x∈D, лежит в полосе c ≤ y ≤ C.

Если функция не является ограниченной на множестве, то говорят, что она не ограничена.

Примером функции, ограниченной снизу на всей числовой оси, является функция y = x².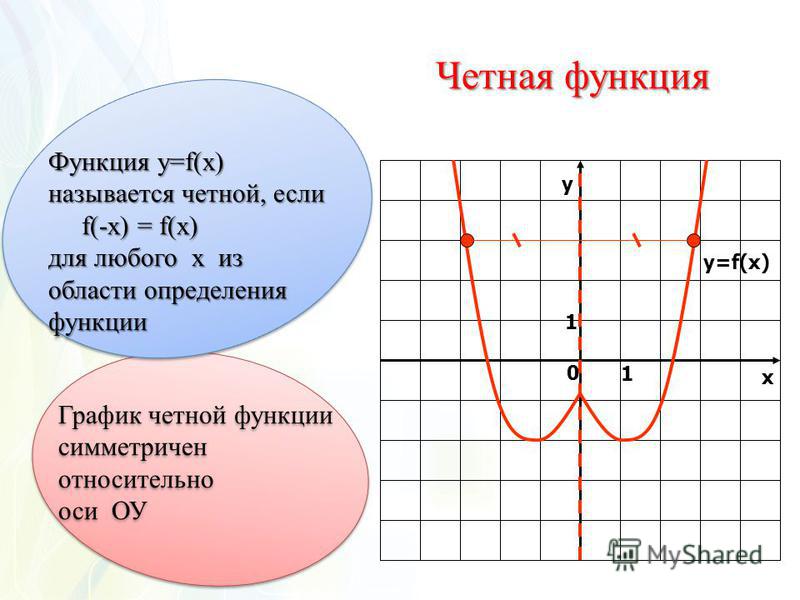 Примером функции, ограниченной сверху на множестве (–∞; 0) является функция y = 1/x. Примером функции, ограниченной на всей числовой оси, является функция y = sin x.





Риэлторские услуги это b2c

Находите клиентов в новом сервисе поиска услуг и специалистов

azbuka.ru

 

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».

{2}},x\neq 0

\left\{\begin{matrix}x=\frac{\sqrt{4f+1}-1}{2f}\text{; }x=-\frac{\sqrt{4f+1}+1}{2f}\text{,}&f\neq 0\text{и}f\geq -\frac{1}{4}\\x= 1\текст{, }&f=0\конец{матрица}\справа.

Викторина

Линейное уравнение

5 задач, похожих на:

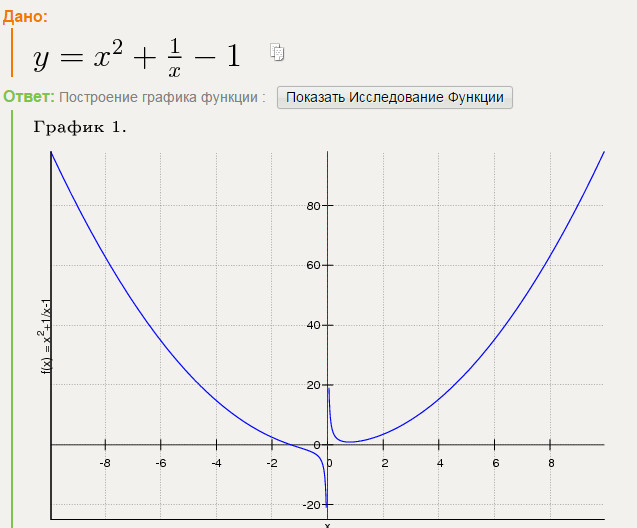
fx = \frac{ 1 }{ x } -1

Похожие задачи из поиска в Интернете

Поделиться

2 \left(-1\right)

Умножьте обе части уравнения на x. 9{2}-4ac}}{2a}.

x=\frac{-1±\sqrt{1-4f\left(-1\right)}}{2f}

Квадрат 1.

x=\frac{-1±\sqrt{1+\ влево(-4f\вправо)\влево(-1\вправо)}}{2f}

Умножить -4 раза f.

x=\frac{-1±\sqrt{1+4f}}{2f}

Умножить -4f на -1.

x=\frac{-1±\sqrt{4f+1}}{2f}

Добавьте 1 к 4f.

x=\frac{\sqrt{4f+1}-1}{2f}

Теперь решите уравнение x=\frac{-1±\sqrt{4f+1}}{2f}, когда ± плюс. Добавьте -1 к \sqrt{1+4f}.

х=\frac{-\sqrt{4f+1}-1}{2f}

Теперь решите уравнение x=\frac{-1±\sqrt{4f+1}}{2f}, когда ± минус. Вычтите \sqrt{1+4f} из -1.

x=-\frac{\sqrt{4f+1}+1}{2f}

Разделить -1-\sqrt{1+4f} на 2f.

x=\frac{\sqrt{4f+1}-1}{2f} x=-\frac{\sqrt{4f+1}+1}{2f}

Теперь уравнение решено.

x=-\frac{\sqrt{4f+1}+1}{2f}\text{, }x\neq 0 x=\frac{\sqrt{4f+1}-1}{2f}\text {, }x\neq 0

Переменная x не может быть равна 0.

fxx=1+x\left(-1\right)

Переменная x не может быть равна 0, так как деление на ноль не определено.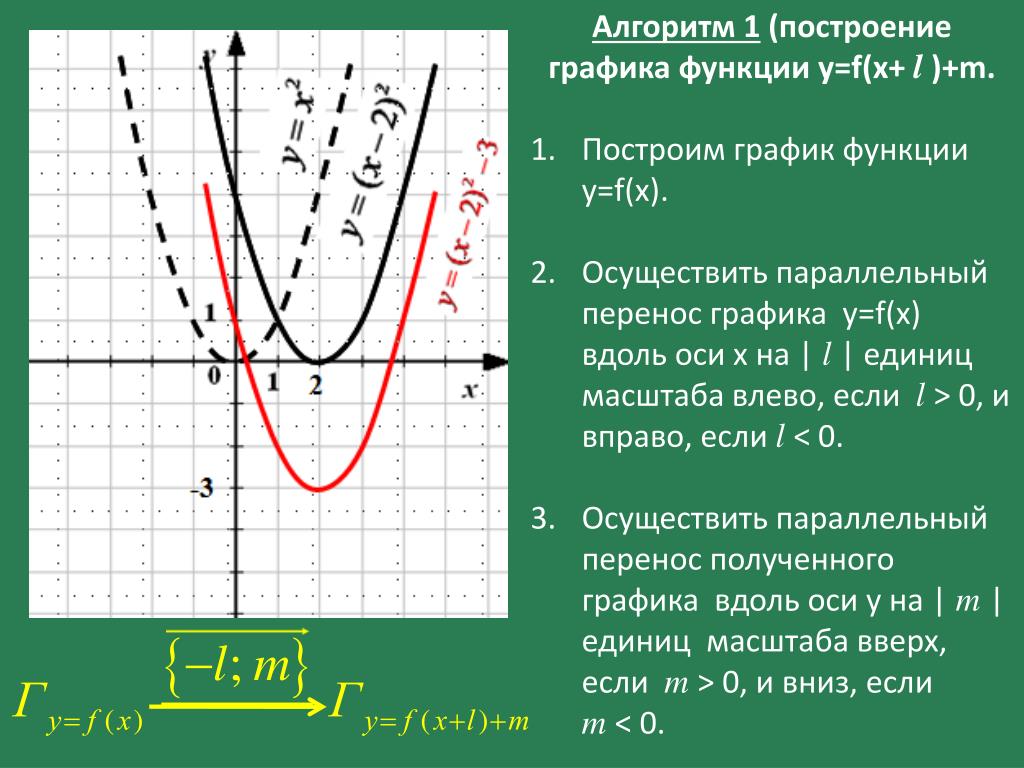 Умножьте обе части уравнения на х. 9{2}}}

Извлеките квадратный корень из обеих частей уравнения.

x+\frac{1}{2f}=\frac{\sqrt{4f+1}}{2|f|} x+\frac{1}{2f}=-\frac{\sqrt{4f+1} }{2|f|}

Упрощение.

x=\frac{\sqrt{4f+1}}{2|f|}-\frac{1}{2f} x=-\frac{\sqrt{4f+1}}{2|f|} -\frac{1}{2f}

Вычтите \frac{1}{2f} из обеих частей уравнения.

x=-\frac{\sqrt{4f+1}}{2|f|}-\frac{1}{2f}\text{, }x\neq 0 x=\frac{\sqrt{4f+ 1}}{2|f|}-\frac{1}{2f}\text{, }x\neq 0

Переменная x не может быть равна 0,9{ 2 } — 4 x — 5 = 0

Тригонометрия

4 \sin \theta \cos \theta = 2 \sin \theta

Линейное уравнение

y = 3x + 4

Арифметика 3 0 3 0 9

90

Матрица

\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{массив} \right]

Одновременное уравнение

\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right.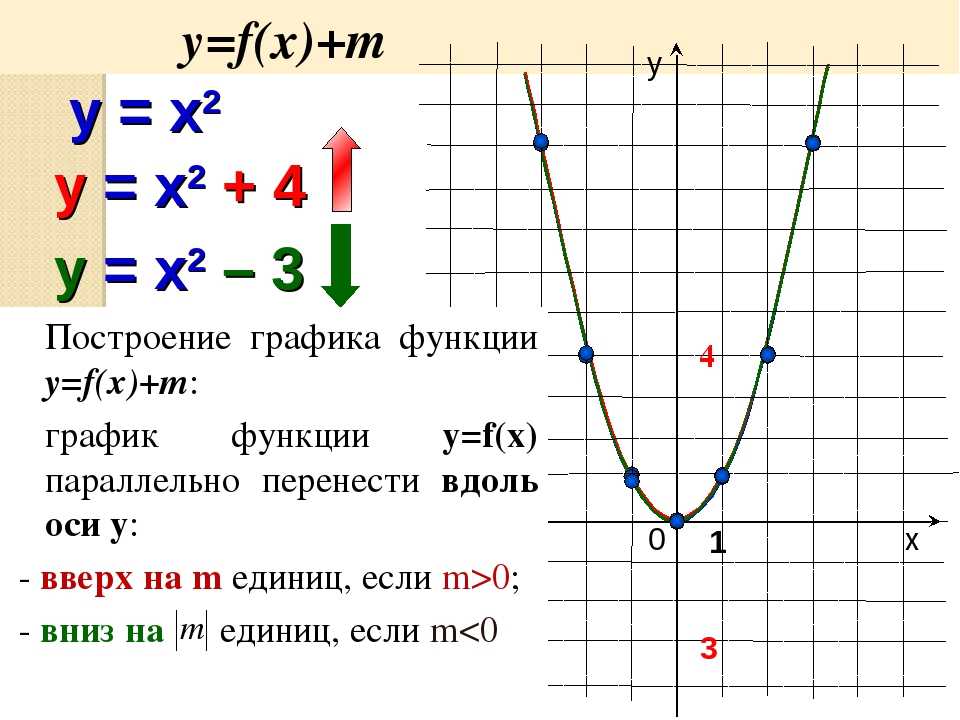 92 Найдите площадь A области между графиками f и g на интервале [1/2, 16].

Математическое исчисление Интегральное исчисление

Делена М.

спросил 01.12.20

Я сложил два уравнения вместе и получил x=1, а затем я установил интеграл от 1/2 до 16 и решил, и я получил 1,528… но я ошибаюсь. Как бы я решил это уравнение?

Подписаться І 1

Подробнее

Отчет

3 ответа от опытных наставников

Лучший Новейшие Самый старый

Автор: Лучшие новыеСамые старые

Алекс С. ответил 01.12.20

Репетитор

5 (35)

Репетиторство по математике, физике и языкам для студентов Стэнфордского университета

См. таких репетиторов

Посмотреть таких репетиторов

Сложность этой задачи в том, что на интервале [0,5,1] график g(x) = 1/x ² находится выше графика f(x) = 1/x, тогда как на интервале [1,16], наоборот, f(x) выше g(x). (подключите функции к графическому калькулятору, и их будет легче увидеть).

Это означает, что вы не можете просто вычислить интеграл одной функции минус другую от 0,5 до 16, чтобы получить площадь. Вам нужно разбить интеграл на две части. Первый интеграл будет интегралом от 0,5 до 1 от g(x) — f(x) dx (поскольку g(x) — верхняя функция на этом интервале), а второй интеграл — это интеграл от 1 до 16. функции f(x) — g(x) dx (поскольку f(x) — верхняя функция на этом интервале).

Оценив это с помощью данных функций, я полагаю, что ответ должен быть таким: площадь между двумя кривыми равна 2,142.

Голосовать за 1 Понизить

Подробнее

Отчет

Люк Г. ответил 01.12.20

Репетитор

5 (1) 92 dx из [1,16]

= — (1/x + ln(x)) из [1/2,1] + (ln(x) + 1/x) из [1,16]

= -1 — ln(1) + 2 + ln(1/2) + ln(16) +1/16 — ln(1) — 1

= 1/16 — ln(2) + 4ln(2)

= 3ln(2) + 1/16 ~ 2,14

Много хитростей со знаками и т. д., поэтому я, возможно, сделал некоторые ошибки при упрощении, но идея разбить его на два интеграла верна.

Голосовать за 0 Понизить

Подробнее

Отчет

Гарольд Т. ответил 01.12.20

Репетитор

5,0 (674)

Работа над кандидатской диссертацией по прикладной математике с 25-летним стажем репетиторства

См.