Физика как найти диаметр: Как найти диаметр окружности — ответ на Uchi.ru

Способы определения размеров молекул | Обучонок

Определение размеров молекул

1 способ. Основан на том, что молекулы вещества, когда оно находится в твердом или жидком состоянии, можно считать плотно прилегающими друг к другу. В таком случае для грубой оценки можно считать, что объем V некоторой массы m вещества просто равен сумме объемов содержащихся в нем молекул. Тогда объем одной молекулы мы получим, разделив объем V на число молекул N.

Число молекул в теле массой m равно, как известно,
,
где М — молярная масса вещества NA — число Авогадро.

Отсюда объем V0 одной молекулы определяется из равенства

В это выражение входит отношение объема вещества к его массе.

Обратное же отношение

есть плотность вещества,

так что

Плотность практически любого вещества можно найти в доступных всем таблицах. Молярную массу легко определить, если известна химическая формула вещества.

Объем одной молекулы, если считать ее шариком, равен
,
где r — радиус шарика.

Поэтому
,
откуда мы и получаем выражение для радиуса молекулы:

Первый из этих двух корней — постоянная величина, равная ≈ 7,4 · 10-9 моль 1/3, поэтому формула для r принимает вид .

Например, радиус молекулы воды, вычисленный по этой формуле, равен rВ ≈ 1,9 · 10-10 м.

Описанный способ определения радиусов молекул не может быть точным уже потому, что шарики нельзя уложить так, чтобы между ними не было промежутков, даже если они соприкасаются друг с другом. Кроме того, при такой «упаковке» молекул – шариков были бы невозможны молекулярные движения. Тем не менее, вычисления размеров молекул по формуле, приведенной выше, дают результаты, почти совпадающие с результатами других методов, несравненно более точных.

2 способ. Метод Ленгмюра и Дево. В данном методе исследуемая жидкость должна растворяться в спирте (эфире) и быть легче воды, не растворяясь в ней. При попадании капли раствора на поверхность воды спирт растворяется в воде, а исследуемая жидкость образует пятно площадью S и толщиной d (порядка диаметра молекул).

Если допустить, что молекула имеет форму шара, то объем одной молекулы равен:

где d – молекулы.

Необходимо определить диаметр молекулы d. В микропипетку набрать 0,5 мл раствора и, расположив ее над сосудом, отсчитать число капель n, содержащихся в этом объеме. Проделав опыт несколько раз, найти среднее значение числа капель в объеме 0,5 мл, а затем подсчитать объём исследуемой жидкости в капле: , где n – число капель в объеме 0,5 мл, 1:400 – концентрация раствора.

В ванну налить воду толщиной 1 – 2 см. Насыпать тальк тонким слоем на лист бумаги, ударяя слегка пальцем по коробочке. Расположив лист бумаги выше и сбоку от ванны на расстоянии 10 – 20 см, тальк сдуть с бумаги.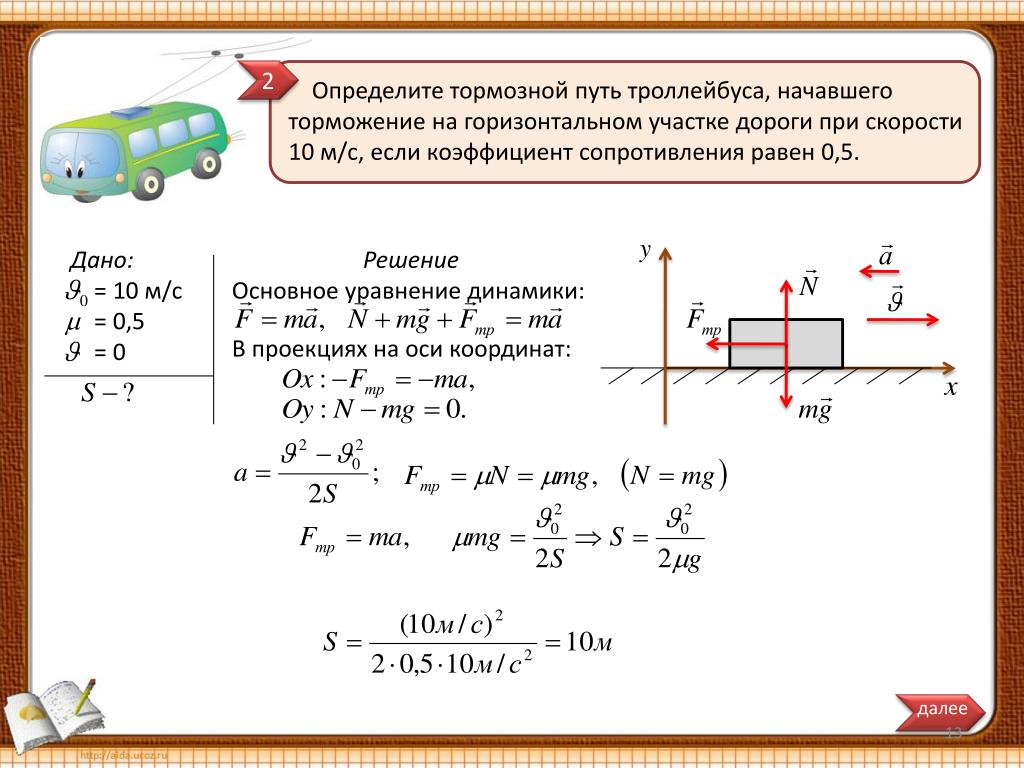 На поверхность воды в ванне из пипетки капнуть одну каплю раствора. Линейкой измерить, средний диаметр образовавшегося пятна D и подсчитываю его площадь. Опыт повторить 2- 3 раза, а затем подсчитать диаметр молекул d.

3 способ. Определение диаметра молекулы. Будем считать, что капля масла растекается по воде до тех пор, пока толщина масляной плёнки не станет равной одной молекуле, тогда диаметр одной молекулы можно определить по формуле: d=V/S, где V – объём капли масла, S — площадь масленого пятна.

Объём капли масла можно определить следующим образом: накапать 100 капель из капилляра в сосуд и измерить массу масла в нём. После этого массу, выраженную в килограммах, поделить на плотность масла, которую можно взять из таблицы плотности некоторых веществ (плотность масла растительного 800 кг/м3).

Затем полученный результат поделить на количество капель. Объём капли можно определить также с помощью мерного цилиндра: накапать масло в цилиндр, измерить его объём в см3 и перевести в м3, для чего поделить на 1000000, затем на количество капель масла. После того, как объём капли стал известен нужно капнуть одну каплю масла на поверхность воды, которая налита в широкий сосуд.

Для ускорения реакции предварительно немного нужно нагреть воду – приблизительно до 400С. Масло начнёт растекаться, и в результате получится круглое пятно. После того, как пятно перестанет расширяться, с помощью линейки измерить его диаметр и рассчитать площадь пятна по формуле:

Практическое получение наночастиц

В современном мире в связи с общей тенденцией к миниатюризации большими темпами стала развиваться такая наука, как нанотехнология. Методы нанотехнологии позволяют получить принципиально новые устройства и материалы с характеристиками, значительно превосходящими их современный уровень, что весьма важно для интенсивного развития многих областей техники, биотехнологии, медицины, охраны окружающей среды и др.

Ход работы:

1) Определение объёма капли

=14,13 мм3;

2) Определение объёма капли путём взвешивания.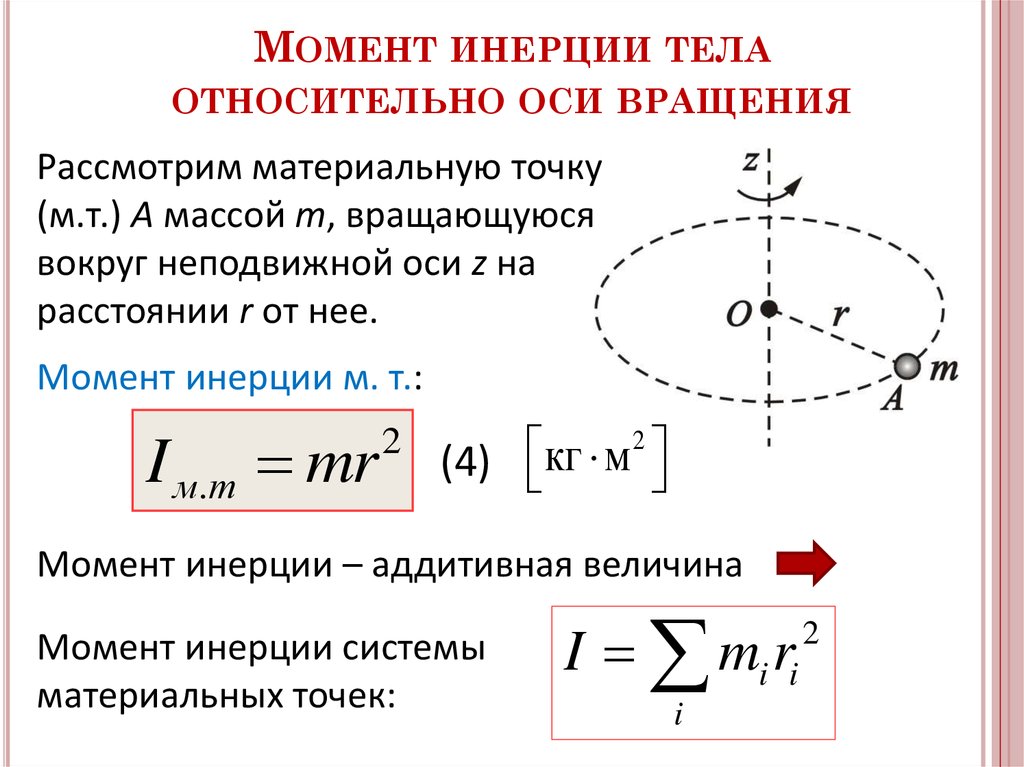

1. На весы накапали 10 капель растительного масла, измерили массу

mk=0,2 г

• Масса 1 капли m1=0,2 г/10=0,02 г
• Определение объёма капли V=m1/q=0,01г/0,8 г/см3=13 мм3

3) Определяем площадь пятна Sмасла=ПR2=11304 мм2

(Приложение 1,2,3,4,5)

4) Площадь пятна нефти Sнефти=20*16=32000 мм2

(Приложение 6,7,8,9)

5) Определяем толщину плёнки h=V/S

Для масла h=13/11304=1,2*10-7=120 нм

Для нефтиh=13/32000=4*10-8 м=40 нм

Вывод: В лабораторных условиях можно получать нанопленки

Заключение

Мы измерили толщину наноплёнок масла и нефти, изучили физические свойства плёнок и методы их получения, также ознакомились с физическими методами исследования микро- и наномасшатабных объектов.

К сожалению, из таких жидкостей как кислоты(уксусная, ортофосфорная, борная), моющие средства и мыло у нас не получилось сделать наноплёнки, потому что все эти жидкости гидрофобные(боятся воды). Мы пытались получить пленки с помощью скотча, но электронные весы позволяют измерять массу с точностью до десятых долей грамма

Список использованной литературы

1. Анциферов Л.И. Самодельные приборы для физического практикума в средней школе. М.: Просвещение, 1985.
2. Блудов М.И. Беседы по физике. М.: Просвещение, 1984.
3. Буров В.А. Практикум по физике в средней школе. М.: Просвещение, 1973.

Приложения

Перейти к содержанию
Исследовательской работы «Наночастицы и наноплёнки»

Диаметр молекулы подсолнечного масла | Образовательная социальная сеть

                                      МБОУ СОШ №3

               

  Проект:  Диаметр молекулы подсолнечного масла

 Направление проекта: Определение размера молекулы      

                              подсолнечного масла

        

Автор:

ученица 10 «А» класса

Зелепукина Виктория

Руководитель:

Ивакина Елена Васильевна

учитель  физики

                                                 Усмань, 2012 г.

---

Оглавление:

1. Введение

1.1Из истории вопроса

1.2Актуальность темы исследования

1.3Цель и задачи исследования

1.4Гипотеза исследования

1.5Методы и объект исследования

2. Основная часть

               2.1 Определение диаметра молекулы

3. Вывод
4. Список литературы

---

1. Введение

1. Из теории вопроса

Молекула в современном понимании – это наименьшая частица вещества, обладающая всеми его химическими свойствами. Молекула способна к самостоятельному существованию. Мысль о том, что вещество состоит из мельчайших частиц, первыми высказали еще в 5 –м веке до нашей эры древнегреческие философы Левкипп и Демокрит, которые утверждали, что в мире есть только атомы и пустота.

В качестве довода они привели, например, такой: вода, высыхая, дробится на такие мельчайшие части, которые совершенно недоступны для глаз.

Однако только через две с половиной тысячи лет после рождения атомной гипотезы – в  конце 20 –го  века – наука достигла уровня, когда ученые смогли увидеть атомы.

Самая маленькая молекула – одноатомная молекула гелия, имеет размер около 0,2 нм. Размер молекулы воды, состоящей из двух атомов водорода и одного атома кислорода, — около 0,3нм.

В одной чайной ложке воды содержится примерно столько же молекул воды, сколько чайных ложек воды содержится в мировом океане. Значит, чтобы пересчитать молекулы воды в чайной ложке, понадобилось бы столько же времени, сколько нужно для того, чтобы вычерпать чайной ложкой мировой океан!

В окружающем нас воздухе молекулы носятся со скоростями артиллерийских снарядов – сотни метров в секунду. Мы не ощущаем своей кожей отдельных ударов молекул потому, что массы молекул чрезвычайно малы, а дробь их ударов – очень частая. «Барабанная дробь» быстрых ударов крошечных молекул воспринимается как постоянное давления газа.

В начале 19 века английский ботаник Броун наблюдая в микроскоп крошечные частицы пыльцы растений, взвешенные в воде, обнаружил, что они пребывают в «вечной пляске», совершая непрестанное хаотическое движение. Ученый предположил, что наблюдаемое им движение – это движение живых существ, и повторил опыт с растолченными в мельчайшую пыль кусочками камня. Но и частички камня «плясали без умолку». Это «броуновское движение», как его называли, оставалось загадкой для ученых целых 50 лет.

Экспериментальное доказательство существования молекул первым наиболее убедительно дал французский физик Ж. Перрен в 1906 г. при изучении броуновского движения. Оно, как показал Перрен, является результатом теплового движения молекул – и ничем иным. Броуновское движение явилось первым опытным подтверждением молекулярного строение вещества: оно сыграло роль «мостика» между макро- и микромирами.

Атомы в молекулах соединены друг с другом в определенной последовательности и определённым образом распределены в пространстве. Связи между атомами имеют различную прочность; она оценивается величиной энергии, которую необходимо затратить для разрыва межатомных связей.

Молекула как система, состоящая из взаимодействующих электронов и ядер, может находиться в различных состояниях и переходить из одного состояния в другое вынужденно (под влиянием внешних воздействий) или самопроизвольно. Для всех молекул данного вида характерна некоторая совокупность состояний, которая может служить для идентификации молекул. Как самостоятельное образование молекула обладает в каждом состоянии определенным набором физических свойств, эти свойства в той или иной степени сохраняются при переходе от молекул к состоящему из них веществу и определяют свойства этого вещества.

Обычно молекулой называют электрически нейтральную частицу. В веществе положительные ионы всегда сосуществуют вместе с отрицательными.

    По числу входящих в молекулу атомных ядер различают молекулы двухатомные, трехатомные и т.д. Если число атомов в молекуле превосходит сотни и тысячи, молекула называется макромолекулой. Сумма масс всех атомов, входящих в состав молекулы, рассматривается как молекулярная масса. По величине молекулярной массы все вещества условно делят на низко- и высокомолекулярные.

2. Актуальность темы исследования:

В этом учебном году я начала более подробно изучать молекулярную физику.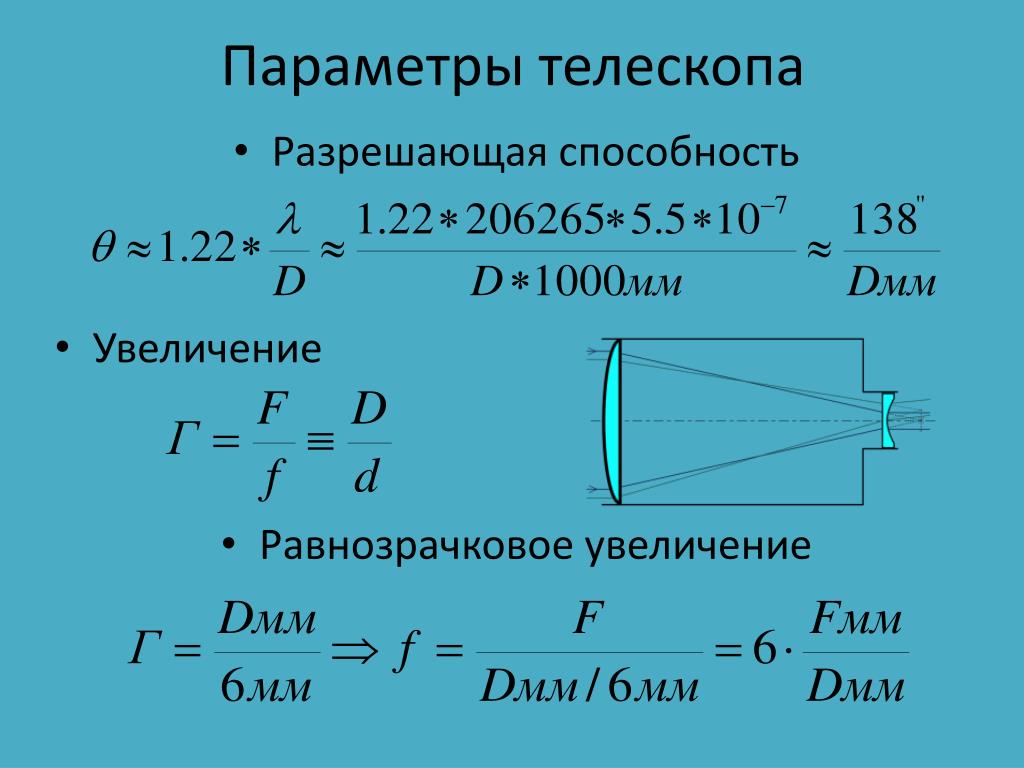 Я узнала, что тела, которые нас окружают, состоят из мельчайших частиц – молекул. Меня заинтересовало, каковы размеры молекул. Из-за очень малых размеров молекулы нельзя увидеть невооруженным глазом или с помощью обыкновенного микроскопа. Мне захотелось на практике измерить диаметр молекулы подсолнечного масла.

3. Цель и задачи исследования:

Цель проекта: измерить диаметр молекулы подсолнечного масла.

Задачи проекта:

1) изучение теории вопроса;

2) измерить объем одной капли;

3) измерить диаметр молекулы;

4. Гипотеза исследования:

Гипотеза: Если капля масла перестала растекаться по поверхности, то толщина образовавшегося пятна равна диаметру молекулы.

5. Методы и объект исследования:

Объект исследования: капля подсолнечного масла

Методы исследования: лабораторный метод.

---

2. Основная часть

            Определение диаметра молекулы

Я нашла объем капли подсолнечного масла. Для этого я накапала 100 капель  масла в мерный цилиндр, измерила его объем, затем  поделила на количество капель масла, то есть на 100. Таким образом объем капли получился равным  2*10-8м3.

После того как объем капли стал известен, из того же капилляра капнула одну каплю на поверхность воды, которая налита в широкий сосуд.

Для ускорения процесса предварительно немного нагрела воду приблизительно до 40 градусов Цельсия. Масло растеклось по поверхности, и в результате получилось круглое пятно. После того как пятно перестало расширяться, с помощью линейки я измерила его диаметр и перевела его в метры. Диаметр пятна получился равным 12*10-3м.

После этого рассчитала площадь пятна по формуле  S=D2 π/4. Площадь пятна получилась равной 2,8*10-3м2.  Затем объем капли поделила на площадь пятна, на которое она растеклась d =V/S. Диаметр получился равным 7*10-6 м  — это и будет диаметр одной молекулы масла, поскольку считается, что оно растекается по воде до тех пор, пока толщина масляной пленки не станет равной одной молекуле.

Я предположила, что диаметр молекулы зависит от температуры. Я провела тот же опыт с нагретым до 60 градусов Цельсия маслом. Диаметр молекулы  оказался ,что соответствует диаметру первого опыта. Значит, диаметр молекулы не зависит от температуры.

---

3. Вывод

      Я провела опыт, в результате которого  нашла размер молекулы подсолнечного масла, он оказался 7*10-6м, а также доказала, что диаметр молекулы не зависит от температуры.

      Я сравнила полученный результат с диаметром молекулы оливкового масла из ученика по физике Г.Я. Мякишева, где диаметр молекулы равен 1,7*10-7 см. Я пришла к выводу, что выбрала не совсем подходящий  метод, так как в нем капля масла растеклась по поверхности жидкости слоем неравномерной толщины, то есть приняла форму линзы, у которой толщина в середине больше чем по краям. Я предполагаю, это можно объяснить явлением натяжения жидкости, а оно в данном методе не учитывалось. К сожалению, данный метод не позволил мне получить точный результат.

---

4. Список литературы:

1. Г.Я.Мякишев, Б.Б. Буховцев. Физика, — М., Просвещение 2005.

2. Перышкин А.В. Факультатвный курс физики, М.,1980.

3. Перышкин А.В., Гутник, Физика, 2006.

4. Генденштейн Л.Э., Физика,2005.

5. Дик Ю.И., Физика, 2003.

Видео с вопросами: Определение диаметра сферы по ее массе и плотности

Стенограмма видео

Стальной шарикоподшипник имеет массу 0,034 грамма. Найдите диаметр шарикоподшипника в миллиметрах, округлив до ближайшего миллиметра. Используйте значение 8000 килограммов на кубический метр для плотности стали.

Итак, этот вопрос касается стального шарикоподшипника. Мы знаем, что он будет иметь сферическую форму, и нас просят найти его диаметр. Обозначим этот неизвестный диаметр как 𝑑. Мы также обозначим массу мяча как 𝑚, и нам сказали, что она равна 0,034 грамма. Еще одна вещь, о которой нам говорят, — это плотность стали, материала, из которого сделан шарикоподшипник. Мы обычно обозначаем плотность символом 𝜌, и нам говорят, что в этом случае плотность имеет значение 8000 килограммов на кубический метр. Мы можем вспомнить, что плотность 𝜌 объекта равна массе объекта 𝑚, деленной на его объем 𝑉. Мы также можем вспомнить, что объем 𝑉 сферы равен четырем третям, умноженным на 𝜋, умноженному на куб радиуса сферы 𝑟.

В этом вопросе мы на самом деле пытаемся вычислить не значение радиуса, а диаметр сферы, которую мы обозначили как 𝑑. Радиус 𝑟 — это расстояние от центра сферы до края, а диаметр 𝑑 — это расстояние по всей сфере от одной стороны до другой, проходящей через центр сферы. Значит, диаметр 𝑑 равен радиусу 𝑟, умноженному на два. Или, если мы разделим обе части этого уравнения на два, то в правой части двойки сокращаются, и мы получим, что радиус 𝑟 равен диаметру 𝑑, деленному на два.

Мы можем использовать эту связь между радиусом и диаметром, чтобы заменить радиус 𝑟 в этом уравнении для объема сферы. Заменив 𝑟 на 𝑑 на два, мы получим, что 𝑉 равно четырем третям, умноженным на 𝜋, умноженному на куб 𝑑 на два. Мы также можем записать это как четыре трети, умноженные на 𝜋, умноженные на 𝑑 в кубе на восемь. Или, если мы умножим вместе три и восемь в знаменателе, это даст нам 24. Итак, у нас есть дробь от четырех, деленная на 24, что упрощается до единицы, деленной на шесть. Итак, мы имеем, что объем 𝑉 сферы равен одной шестой, умноженной на 𝜋, умноженной на куб диаметра сферы. Мы можем использовать это уравнение вместе с этим здесь для плотности 𝜌, чтобы решить нашу проблему.

Если мы изменим это уравнение плотности, чтобы сделать 𝑉 предметом, то мы можем использовать наши значения массы 𝑚 и плотности 𝜌 шарикоподшипника, чтобы вычислить его объем. Затем, как только мы рассчитали этот объем, мы можем изменить это другое уравнение для объема сферы, чтобы сделать диаметр 𝑑 предметом. Затем, подставив в наше расчетное значение объем 𝑉, мы сможем определить диаметр 𝑑, что и требуется в вопросе. Одна трудность, с которой мы здесь столкнемся, связана с единицами величин. Нас просят найти диаметр в миллиметрах, нам дают массу в граммах и плотность в килограммах на кубический метр.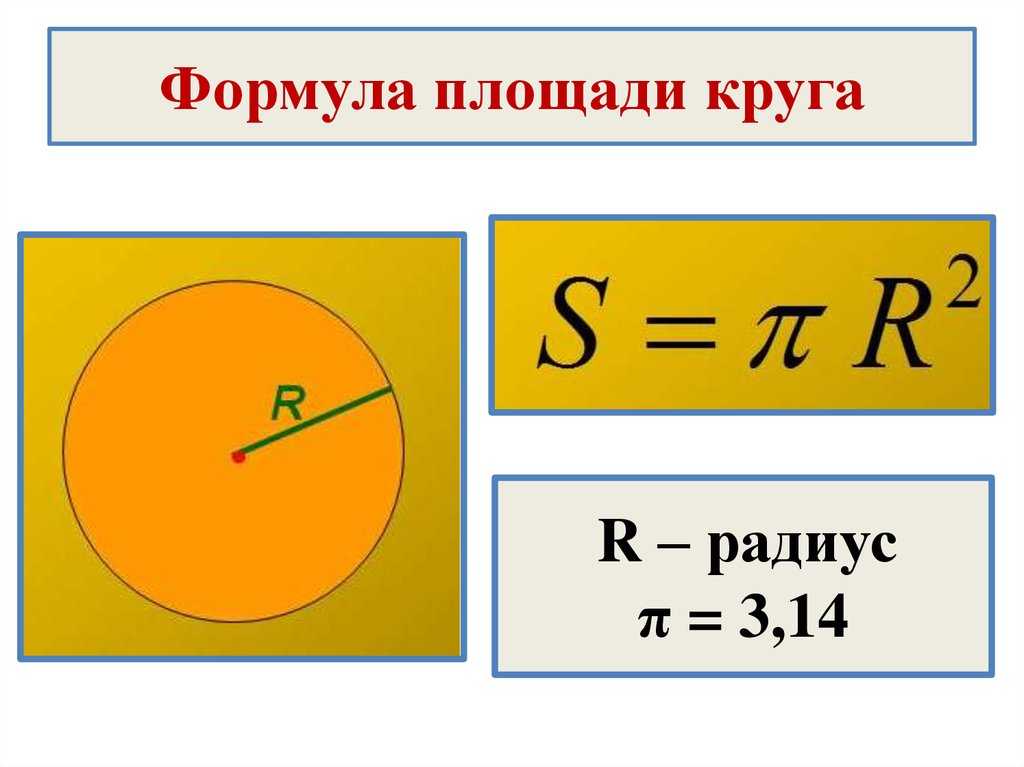

Давайте начнем с преобразования массы 𝑚 в единицы килограммов, чтобы она соответствовала единицам плотности 𝜌. Напомним, что один килограмм равен 1000 граммов. Разделив обе части на 1000 и сократив 1000 в правой части, мы получим, что один грамм равен одной тысячной килограмма. Итак, чтобы перевести из граммов в килограммы, нам нужно разделить значение на 1000. Когда мы делим значение массы шарикоподшипника в граммах на 1000, мы получаем результат 0,000034 килограмма. Мы могли бы также записать это значение в экспоненциальной записи как 3,4 умножить на 10 с минус пятью килограммами, где у нас есть степень минус пять, потому что нам пришлось переместить десятичную точку на пять знаков, чтобы превратить это значение в 3,4.

Теперь, когда у нас есть масса 𝑚 в килограммах, соответствующая нашей плотности в килограммах на кубический метр, мы можем использовать эти значения в этом уравнении для вычисления объема сферы 𝑉. Однако сначала нам нужно сделать 𝑉 предметом уравнения. Для этого мы сначала умножим обе части уравнения на 𝑉. В правой части 𝑉 в числителе сокращается с 𝑉 в знаменателе. Итак, мы получили объем 𝑉, умноженный на плотность 𝜌, что равно массе 𝑚. Теперь разделим обе части уравнения на плотность 𝜌. Два 𝜌 с левой стороны компенсируют друг друга. И мы приходим к уравнению, которое говорит, что объем 𝑉 равен массе 𝑚, деленной на плотность 𝜌.

Если мы подставим наши значения 𝑚 и 𝜌 для стального шарикоподшипника в правую часть этого уравнения, то получим, что объем сферы 𝑉 равен 3,4 умножить на 10 минус пять килограммов, деленных на 8000 килограммов на кубический метр. Что касается единиц измерения, то килограммы в числителе и знаменателе компенсируют друг друга. И это оставляет единицу, деленную на единицу, на метры в кубе или просто единицы метров в кубе. Когда мы оцениваем выражение, мы вычисляем результат 4,25 умножить на 10 с отрицательными девятью метрами в кубе. И это значение является объемом стального шарикоподшипника.

Теперь, когда у нас есть значение объема 𝑉, мы хотим использовать это значение в этом уравнении для расчета диаметра шарикоподшипника. Итак, давайте изменим уравнение, чтобы диаметр 𝑑 стал предметом. Мы начнем с умножения обеих частей уравнения на шесть, разделенных на 𝜋. В правой части шестерки и 𝜋 в числителе и знаменателе компенсируют друг друга. И у нас есть шесть умноженных на 𝑉, деленное на 𝜋, равно 𝑑 в кубе. Если мы затем возьмем кубический корень с обеих сторон, то справа кубический корень из 𝑑 в кубе будет просто равен 𝑑. Наконец, переписав уравнение наоборот, мы получим, что диаметр 𝑑 равен кубическому корню из шестикратного объема 𝑉, деленному на 𝜋.

Теперь мы готовы подставить наше значение объема 𝑉 шарикоподшипника в это уравнение. Когда мы это сделаем, мы получим вот это выражение для его диаметра 𝑑. Вычисление выражения внутри кубического корня дает результат 8,1169 умножить на 10 с отрицательными девятью метрами в кубе, где эллипсы показывают, что есть дополнительные десятичные знаки. Затем, оценивая кубический корень, мы получаем диаметр 𝑑 2,0097 и так далее, умноженный на 10 с точностью до минус трех метров. Обратите внимание, что поскольку объем 𝑉 был выражен в кубических метрах, у нас есть диаметр 𝑑 в метрах.

Однако нас просят дать ответ в миллиметрах. Напомним, что один метр равен 1000 миллиметрам, или, что эквивалентно, один метр равен 10 в трех миллиметрах. Итак, чтобы перевести метры в миллиметры, мы просто умножаем на 10 в степени 3. Если мы возьмем наше значение диаметра 𝑑 в метрах и умножим его на 10 в степени три, то мы получим 10 в отрицательной тройке, умноженное на 10 в тройке, и это просто равно единице. Тогда в миллиметрах диаметр шарикоподшипника равен 2,009.7 и так далее миллиметров.

Последнее, что осталось сделать, это округлить результат до ближайшего миллиметра. Это дает нам окончательный ответ для диаметра шарикоподшипника в два миллиметра.

18.3: Диаметры звезд — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

3730

• OpenStax
• OpenStax

Цели обучения

К концу этого раздела вы сможете:

• Описать методы, используемые для определения диаметра звезд
• Определите части кривой блеска затменной двойной звезды, которые соответствуют диаметрам отдельных компонентов

Диаметр Солнца легко измерить. Его угловой диаметр, то есть его видимый размер на небе, составляет около 1/2°. Если мы знаем угол, под которым Солнце находится в небе, и как далеко оно находится, мы можем рассчитать его истинный (линейный) диаметр, который составляет 1,39 миллиона километров, или примерно в 109 раз больше диаметра Земли.

К сожалению, Солнце — единственная звезда, угловой диаметр которой легко измерить. Все остальные звезды находятся так далеко, что даже через самые большие наземные телескопы кажутся светящимися точками. (Они часто кажутся больше, но это просто искажение, вызванное турбулентностью в атмосфере Земли.) К счастью, есть несколько методов, которые астрономы могут использовать для оценки размеров звезд.

Звезды, заблокированные Луной

Один из методов, который дает очень точные диаметры, но может быть использован только для нескольких звезд, заключается в наблюдении затемнения света, которое происходит, когда Луна проходит перед звездой. Что астрономы измеряют (с большой точностью), так это время, необходимое для того, чтобы яркость звезды упала до нуля, когда край Луны движется по диску звезды. Поскольку мы знаем, как быстро Луна движется по своей орбите вокруг Земли, можно вычислить угловой диаметр звезды. Если известно и расстояние до звезды, мы можем вычислить ее диаметр в километрах. Этот метод работает только для довольно ярких звезд, которые расположены вдоль зодиака, где Луна (или, что гораздо реже, планета) может проходить перед ними, если смотреть с Земли.

Затменные двойные звезды

Точные размеры большого количества звезд получены из измерений затменных двойных звездных систем, поэтому мы должны сделать небольшое отступление от нашей основной истории, чтобы исследовать этот тип звездных систем. Некоторые двойные звезды выстроены таким образом, что при наблюдении с Земли каждая звезда проходит впереди другой во время каждого оборота (рис. \(\PageIndex{1}\)). Когда одна звезда блокирует свет другой, не давая ему достичь Земли, светимость системы уменьшается, и астрономы говорят, что произошло затмение.

Рисунок \(\PageIndex{1}\) Кривая блеска затменно-двойной звезды. Кривая блеска затменной двойной звездной системы показывает, как суммарный свет от обеих звезд меняется из-за затмений на протяжении орбиты. Эта кривая блеска показывает поведение гипотетической затменной двойной звезды с полными затмениями (одна звезда проходит непосредственно впереди и позади другой). Цифрами обозначены участки кривой блеска, соответствующие различным положениям меньшей звезды на ее орбите. На этой диаграмме мы предположили, что меньшая звезда также является более горячей, поэтому она излучает больший поток (энергии в секунду на квадратный метр), чем большая. Когда меньшая и более горячая звезда идет за большей, ее свет полностью блокируется, поэтому на кривой блеска наблюдается сильный провал. Когда меньшая звезда проходит перед большей, небольшое количество света от большей звезды блокируется, поэтому на кривой блеска наблюдается меньший провал.

Открытие первой затменной двойной звезды помогло решить давнюю загадку астрономии. Звезда Алголь в созвездии Персея меняет свою яркость странным, но регулярным образом. Обычно Алголь — довольно яркая звезда, но с интервалом в 2 дня 20 часов 49 минут она тускнеет до одной трети своей обычной яркости. Через несколько часов цвет снова становится нормальным. Этот эффект легко увидеть даже без телескопа, если знать, что искать.

В 1783 году молодой английский астроном по имени Джон Гудрик (1764–1786) тщательно изучил Алгол (см. статью о Джоне Гудрике в разделе 19)..3 для обсуждения его жизни и творчества). Хотя Гудрик не мог ни слышать, ни говорить, за 21 год своей короткой жизни он сделал ряд важных открытий. Он предположил, что необычные изменения яркости Алгола могут быть связаны с невидимым компаньоном, который регулярно проходит перед более яркой звездой и блокирует ее свет. К сожалению, у Гудрик не было возможности проверить эту идею, так как лишь столетие спустя оборудование стало достаточно хорошим для измерения спектра Алгола.

В 1889 году немецкий астроном Герман Фогель (1841–1907) продемонстрировал, что, как и Мицар, Алголь является спектрально-двойной системой. Спектральные линии Алголя не были замечены двойными, потому что более слабая звезда из пары испускает слишком мало света по сравнению с более яркой звездой, чтобы ее линии были заметны в составном спектре. Тем не менее периодическое смещение линий более яркой звезды вперед и назад указывало на то, что она вращалась вокруг невидимого компаньона. (Линии обоих компонентов не обязательно должны быть видны, чтобы звезда была признана спектрально-двойной.)

Открытие того, что Алгол представляет собой спектрально-двойную систему, подтвердило гипотезу Гудрика. Плоскость, в которой вращаются звезды, обращена почти ребром к нашему лучу зрения, и каждая звезда проходит впереди другой во время каждого оборота. (Затмение более слабой звезды в системе Алголя не очень заметно, потому что ее закрытая часть дает небольшой вклад в общий свет системы. Однако это второе затмение можно обнаружить с помощью тщательных измерений.)

Любой двойная звезда производит затмения, если смотреть с правильного направления, вблизи плоскости ее орбиты, так что одна звезда проходит впереди другой (см. рисунок \(\PageIndex{1}\)). Но с нашей точки зрения на Земле только несколько двойных звездных систем ориентированы таким образом.

АСТРОНОМИЯ И МИФОЛОГИЯ: АЛГОЛ, ДЕМОН-ЗВЕЗДА И ПЕРСЕЙ-ГЕРОЙ

Имя Алгол происходит от арабского Рас-аль-Гул , что означает «голова демона». ¹ Слово «упырь» в английском языке имеет такое же происхождение. Как обсуждалось в книге «Наблюдение за небом: рождение астрономии», многие яркие звезды имеют арабские имена, потому что в течение долгих темных веков в средневековой Европе именно арабские астрономы сохранили и расширили греческие и римские знания о небе. Упоминание демона является частью древнегреческой легенды о герое Персее, память которого отмечена созвездием, в котором мы находим Алголя, и в чьих приключениях участвуют многие персонажи, связанные с северными созвездиями.

Персей был одним из многих героев-полубогов, рожденных от Зевса (Юпитера в римской версии), царя богов в греческой мифологии.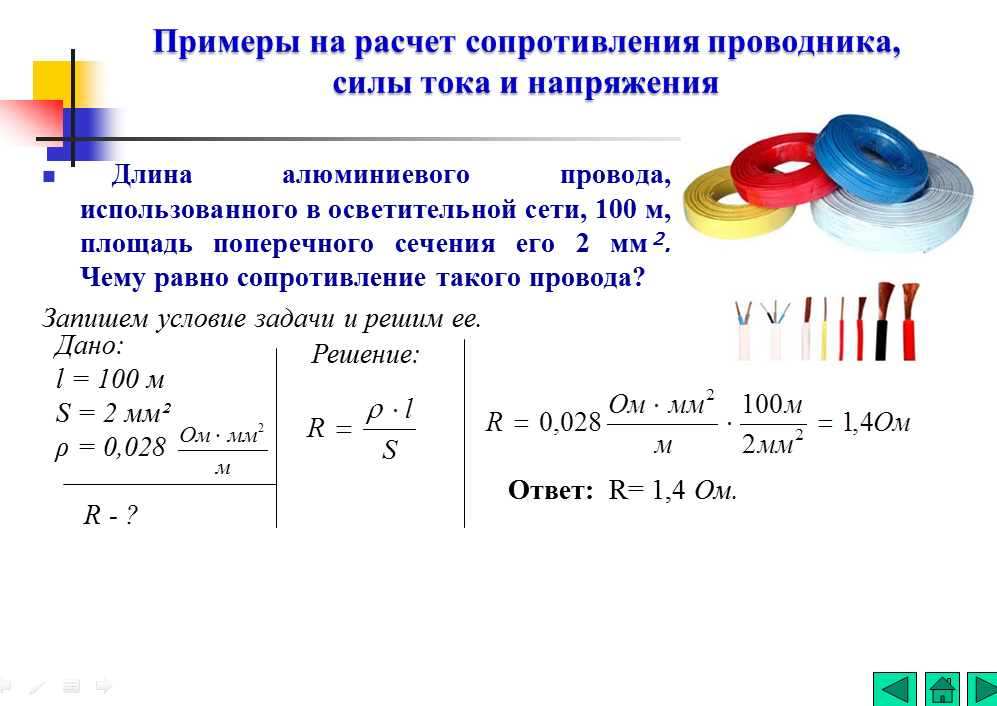 У Зевса был, мягко говоря, блуждающий взгляд, и он всегда зачинал кого-нибудь от человеческой девушки, которая привлекала его внимание. (Персей происходит от

Per Zeus , что означает «отец Зевса».) Брошенный по течению со своей матерью (по вполне понятным причинам) расстроенным отчимом, Персей вырос на острове в Эгейском море. Тамошний царь, заинтересовавшись матерью Персея, попытался избавиться от юноши, поручив ему чрезвычайно трудную задачу.

В момент всепоглощающей гордости красивая молодая женщина по имени Медуза сравнила свои золотые волосы с волосами богини Афины (Минервы у римлян). Греческие боги не любили, когда их сравнивали с простыми смертными, и Афина превратила Медузу в горгону: отвратительное злое существо с извивающимися змеями вместо волос и лицом, которое превращало любого, кто смотрел на него, в камень. Персею было дано задание убить этого демона, что казалось довольно верным способом навсегда убрать его с дороги.

Но поскольку отцом Персея был бог, другие боги дали ему инструменты для работы, в том числе отражающий щит Афины и крылатые сандалии Гермеса (Меркурия в римской истории).

Пролетев над ней и глядя только на ее отражение, Персей смог отрубить Медузе голову, ни разу не взглянув на нее прямо. Взяв с собой ее голову (которая, кстати, могла обращать зрителей в камень, даже не будучи прикрепленной к ее телу), Персей отправился в другие приключения.

Затем он пришел к скалистому морскому берегу, где из-за хвастовства еще одна семья попала в серьезные неприятности с богами. Царица Кассиопея осмелилась сравнить свою красоту с нереидами, морскими нимфами, дочерьми Посейдона (Нептуна в римской мифологии), бога моря. Посейдон был так оскорблен, что создал морского чудовища по имени Цетус, чтобы опустошить королевство. Царь Цефей, осажденный муж Кассиопеи, посоветовался с оракулом, который сказал ему, что он должен принести в жертву чудовищу свою прекрасную дочь Андромеду.

Когда Персей пришел и нашел Андромеду, прикованную к скале у моря, ожидающую своей участи, он спас ее, превратив чудовище в камень. (Исследователи мифологии на самом деле прослеживают суть этой истории до гораздо более древних легенд древней Месопотамии, в которых бог-герой Мардук побеждает чудовище по имени Тиамат.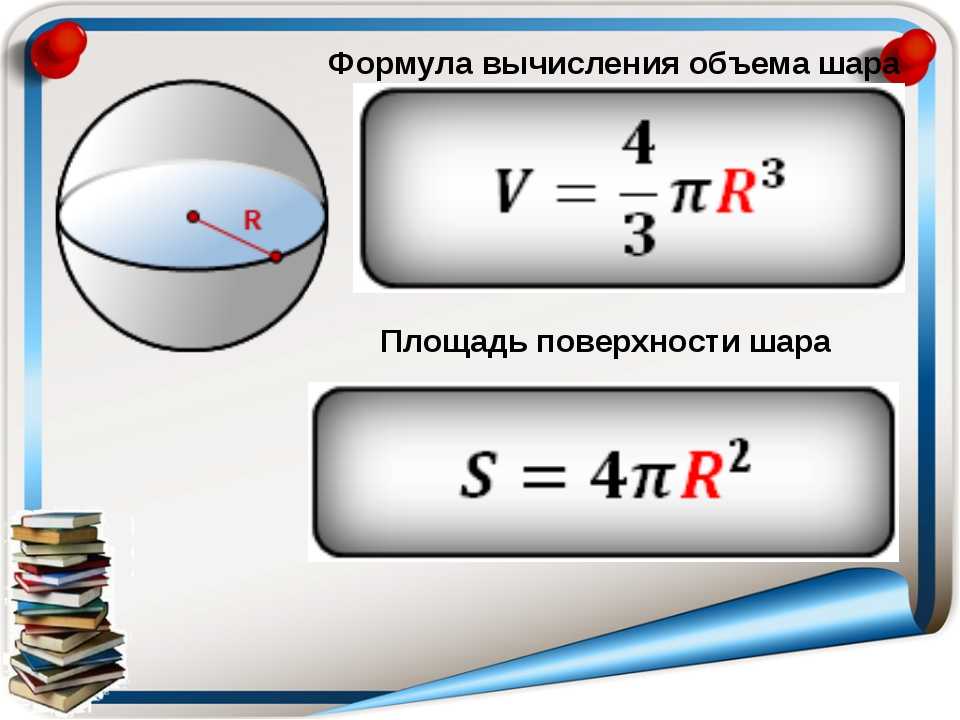 Символически герой, подобный Персею или Мардуку, обычно ассоциируется с Солнцем, чудовище с силой ночи, и прекрасная дева с хрупкой красотой зари, которую выпускает Солнце после своей ночной борьбы с тьмой.)

Многие персонажи этих греческих легенд можно найти в виде созвездий на небе, не обязательно напоминающих своих тезок, но служащих напоминанием об истории. Например, тщеславная Кассиопея обречена находиться очень близко к небесному полюсу, вечно вращаться по небу и каждую зиму висеть вниз головой. Древние представляли себе Андромеду все еще прикованной к своей скале (гораздо проще увидеть цепочку звезд, чем узнать прекрасную деву в этой звездной группе). Рядом с ней Персей с головой Медузы, свисающей с его пояса. Алгол представляет эту голову горгоны и долгое время ассоциировался в таких сказках со злом и несчастьем. Некоторые комментаторы предположили, что изменение яркости звезды (которое можно наблюдать невооруженным глазом) могло способствовать ее неприятной репутации, поскольку древние считали такое изменение своего рода зловещим «подмигиванием».

Диаметры затменных двойных звезд

Теперь вернемся к основной теме нашего рассказа, чтобы обсудить, как все это можно использовать для измерения размеров звезд. Техника включает в себя построение кривой блеска затменной двойной звезды, графика, показывающего, как яркость меняется со временем. Давайте рассмотрим гипотетическую двойную систему, в которой звезды сильно различаются по размеру, как показано на рисунке \(\PageIndex{2}\). Чтобы упростить жизнь, предположим, что орбита просматривается точно с ребра.

Хотя в такой системе мы не можем видеть две звезды по отдельности, кривая блеска может сказать нам, что происходит. Когда меньшая звезда только начинает проходить позади большей звезды (точка, которую мы называем первым контактом ), яркость начинает падать. Затмение становится полным (меньшая звезда полностью скрыта) в точке, называемой вторым контактом . В конце полного затмения ( третье контакт ) , начинает появляться меньшая звезда. Когда меньшая звезда достигает последний контакт , затмение полностью закончилось.

Чтобы увидеть, как это позволяет нам измерять диаметры, внимательно посмотрите на рисунок \(\PageIndex{2}\). За время между первым и вторым контактами меньшая звезда переместилась на расстояние, равное ее собственному диаметру. За время от первого до третьего контакта меньшая звезда переместилась на расстояние, равное диаметру большей звезды. Если в спектре двойной видны спектральные линии обеих звезд, то скорость меньшей звезды относительно большей можно измерить по доплеровскому смещению. Но знание скорости, с которой движется меньшая звезда, и времени, затраченного на преодоление некоторого расстояния, может определить размах этого расстояния — в данном случае диаметры звезд. Скорость, умноженная на интервал времени от первого до второго контакта, дает диаметр меньшей звезды. Умножаем скорость на время между первым и третьим контактами, чтобы получить диаметр большей звезды.

Рисунок \(\PageIndex{2}\) Кривая блеска затменно-реберной двойной системы. Здесь мы видим кривую блеска гипотетической затменной двойной звезды, орбиту которой мы видим точно с ребра, на которой две звезды полностью затмевают друг друга. По временным интервалам между контактами можно оценить диаметры двух звезд.

В действительности ситуация с затменно-двойными звездами часто немного сложнее: орбиты, как правило, не видны точно с ребра, и свет от каждой звезды может быть лишь частично перекрыт другой. Кроме того, орбиты двойных звезд, как и орбиты планет, представляют собой эллипсы, а не окружности. Однако все эти эффекты можно разобрать при очень тщательных измерениях кривой блеска. 92 \nonumber\]

Затем светимость (\(L\)) звезды определяется как площадь ее поверхности в квадратных метрах, умноженная на поток энергии:

\[L=(A \times F)\]

Ранее мы определили массы двух звезд в двойной системе Сириуса. Сириус излучает в 8200 раз больше энергии, чем его более слабая звезда-компаньон, хотя обе звезды имеют почти одинаковую температуру. Чрезвычайно большая разница в светимости связана с разницей в радиусе, поскольку температуры и, следовательно, потоки энергии для двух звезд почти одинаковы. Для определения относительных размеров двух звезд возьмем отношение соответствующих светимостей: 92_{\text{companion}}} \end{array} \nonumber\]

Таким образом, относительные размеры двух звезд можно найти, взяв квадратный корень из относительной светимости. Поскольку \(\sqrt{8200} = 91\), радиус Сириуса в 91 раз больше, чем радиус его слабого компаньона.

Показанный здесь метод определения радиуса требует, чтобы обе звезды были видны, что не всегда так.

Диаметры звезд

Результаты многих измерений размеров звезд за прошедшие годы показали, что большинство ближайших звезд имеют размер примерно с Солнце, а их типичный диаметр составляет миллион километров или около того. Слабые звезды, как и следовало ожидать, обычно меньше, чем более яркие звезды. Однако есть несколько драматических исключений из этого простого обобщения.

Некоторые очень яркие звезды, в том числе красные (указывающие на относительно низкую температуру поверхности), оказываются поистине огромными. Эти звезды достаточно уместно называются звездами-гигантами или звездами-сверхгигантами. Примером может служить Бетельгейзе, вторая по яркости звезда в созвездии Ориона и одна из дюжины самых ярких звезд на нашем небе. Примечательно, что его диаметр превышает 10 а.е. (1,5 миллиардов километров!), достаточно большой, чтобы заполнить всю внутреннюю Солнечную систему почти так же далеко, как Юпитер. В книге «Звезды от юности до старости» мы подробно рассмотрим эволюционный процесс, который приводит к образованию таких звезд-гигантов и сверхгигантов.

Посмотрите это видео со сравнением размеров звезд, чтобы увидеть поразительное наглядное представление о размерах звезд и планет, а также о диапазоне размеров звезд.

Сводка

Диаметры звезд можно определить, измерив время, которое требуется объекту (Луне, планете или звезде-компаньону), чтобы пройти перед ним и заблокировать его свет.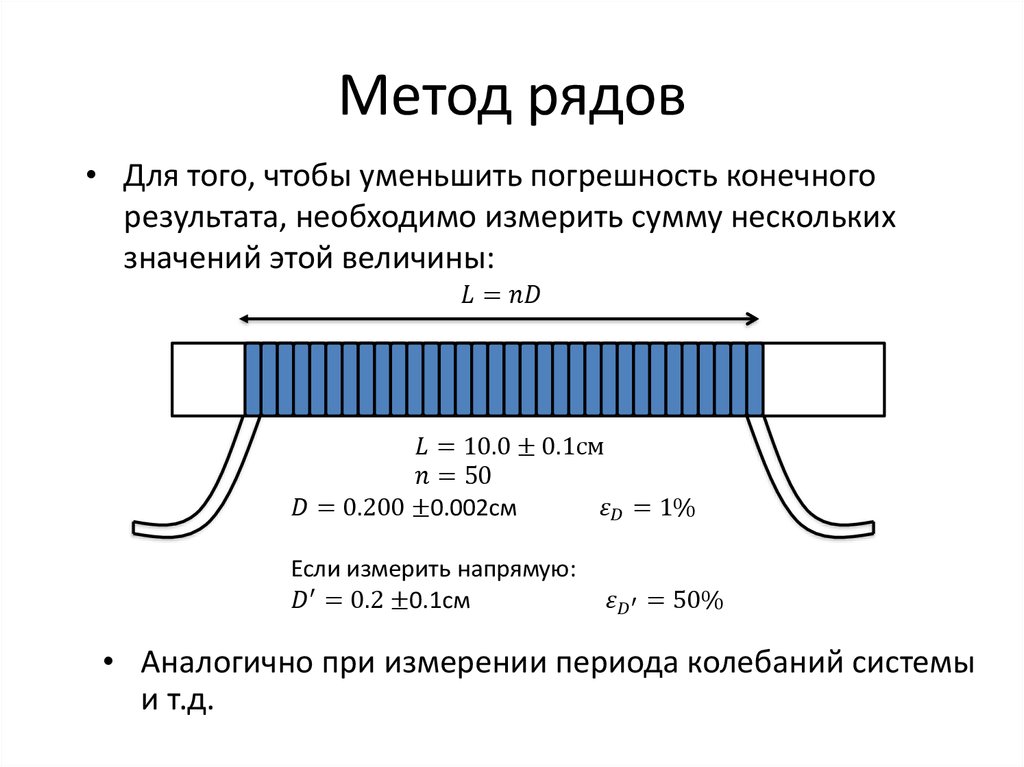 Диаметры членов затменных двойных систем (где звезды проходят друг перед другом) можно определить путем анализа их орбитальных движений.

Footnotes

³ Поклонники комиксов и фильмов о Бэтмене узнают, что это имя было дано главному злодею в сериале.

Глоссарий

затменно-двойная система

двойная звезда, у которой плоскость вращения двух звезд почти обращена к нашему лучу зрения, так что свет одной звезды периодически ослабляется другой, проходящей перед ней

---

Эта страница под названием 18.3: Diameters of Stars распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Метки

   1. затменно-двойная система
   2. источник@https://openstax.

      No related posts.