Формула a в квадрате b в квадрате: Сколько будет а плюс б в квадрате

Содержание

Формулы сокращенного умножения.

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности.

Вы сейчас находитесь в каталоге: Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности.

Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности. «>

Формулы сокращенного умножения. Разность квадратов, сумма кубов и разность кубов и разность четвертых степеней. Квадрат суммы и квадрат разности и куб суммы и куб разности.
Разность квадратов	a²-b² = (a-b)(a+b)
Квадрат суммы	(a+b)² = a²+2ab+b²
Квадрат разности	(a-b)² = a²-2ab+b²
Куб суммы	(a+b)³= a³+3a²b+3ab²+b³
Куб разности	(a-b)³ = a³-3a²b+3ab²-b³
Сумма кубов	a³+b³ = (a+b)(a²-ab+b²)
Разность кубов	a³-b³ = (a-b)(a²+ab+b²)
Разность четвертых степеней	a⁴-b⁴ = (a²-b²)(a²+b²)=(a-b)(a+b)(a²+b²)

Справочно, только для тех кто хочет больше представлять тему: Бином Ньютона.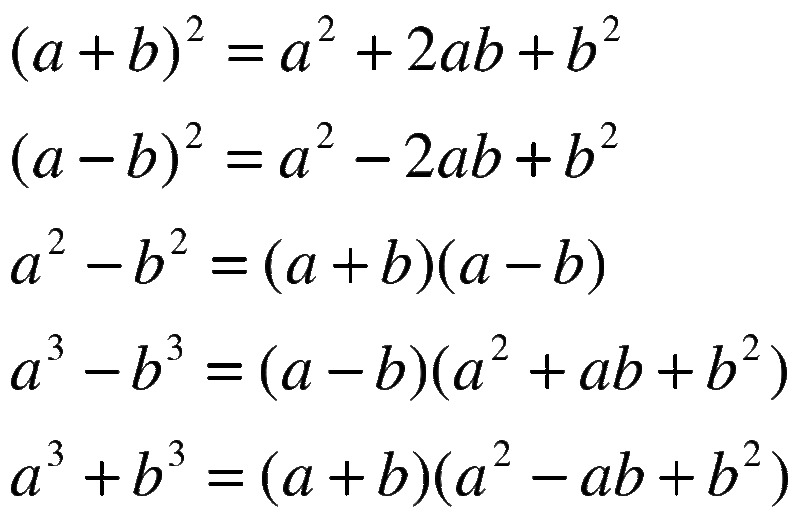 2-12x = 153 $

-60x+225-12x = 153

-72x = 153-225

-72x = -72

x = 1

2 формула может быть выражена как:
a ² + b ² = (a +b) ² — 2ab
Кроме того, + 2ab
где, a, b = произвольные числа.
Пусть a и b — два числа, квадраты a и b равны a ² и b ² . Сумма квадратов a и b равна a ² + b ² . Мы могли бы получить формулу, используя известное алгебраическое тождество (a+b) 92 Формула
Пример 1: Используя формулу суммы квадратов, найдите значение 5 ² + 6 ² ?
Решение:
Чтобы найти: значение 5 ² + 6 ²
Дано: а = 5, b = 6
Используя формулу суммы квадратов,
а ² + б ² = (а + б) ² — 2аб
5 ² + 6 ² = (5 + 6) ² − 2(5)(6)
= 121 — 2(30)
= 121 − 60
= 61
Ответ: значение 5
2 + 6 ² IS 61.
Пример 2: Убедитесь, что значение x ² + y ² is (x + y) ² — 2xy по формуле ² + b ².
Решение: Для проверки x ² + y ² = (x + y) ² — 2xy
Воспользуемся формулой a ² + b ²
. а = х, б = у
По формуле (a + b) ² разложим исходные члены.
(а + б) ² = а ² + б ² + 2аб
Подставим значения a и b вместо x и y
(x + y) ² = x ² + y ² + 2xy
Вычитая 2xy с обеих сторон,
x ² + y ² = (x + y) ² — 2xy
Ответ: Следовательно проверено

формула. Подтвердите свои ответы.
Решение:
10 ² + 20 ² = 100 + 400 = 500
Используя формулу а ² + b ² = (a +b) ² -2ab, получаем 10 ² + 20 ² = (10 + 20 × 2 ^{2 ^{)
= 900 — 400
= 500
Таким образом проверено.
Часто задаваемые вопросы по
² + b ² Формула Что такое расширение
² + b ² Формула? a ² + b ² формула известна как формула суммы квадратов, она читается как квадрат плюс b квадрат. Его расширение выражается как а ² + b ² = (a + b) ² -2ab.
Что такое a
² + b ² Формула в алгебре? Формула a ² + b ² является одним из важных алгебраических тождеств. Он представлен a ² + b ² и читается как квадрат плюс b квадрат. Формула (a ² + b ²) выражается как a ² + b ² = (a +b) ² -2ab.
Как упростить числа, используя формулу a
² + b ²? Давайте разберемся в использовании формулы a ² + b ² a ² + b ² на следующем примере.
Пример: Найти значение 20 ² + 30 ² по формуле a ² + b ² .
Чтобы найти: 20 ² + 30 ²
Предположим, что a = 20 и b = 30,
Мы подставим их в формулу суммы квадратов, то есть a ² + b ²
а ² + б ² = (а +б) ² -2аб
20 ² +30 ² = (20+30) ² — 2(20)(30)
= 2500 — 1200 = 1300 92 как власть или нет и в виде ² + б ² . Запишите формулу суммы квадратов a ² + b ² = (a +b) ² -2ab
Подставьте значения a и b в сумму квадратов формулы a ² + b ² и упростите.
Теорема Пифагора
Теорема Пифагора была названа в честь известного греческого математика Пифагора. Это важная формула, которая гласит следующее: a ² + b ² = c ²
Глядя на рисунок выше, сделали ли вы следующее важное замечание? Это может помочь нам понять, почему формула работает.

В красном квадрате 2 треугольника
В синем квадрате тоже 2 треугольника
В черном квадрате 4 таких же треугольника
Следовательно, площадь красного квадрата + площадь синего квадрата = площадь черного квадрата
Пусть a = длина стороны красного квадрата
Пусть b = длина стороны синего квадрата
Пусть c = длина стороны черного квадрата
Следовательно, a ² + б ² = в ²
Вообще говоря, в любом прямоугольном треугольнике пусть с будет длина самой длинной стороны (называемой гипотенузой), а пусть а и b будут длинами двух других сторон (называемых катетами).
Теорема утверждает, что квадрат длины гипотенузы равен длине стороны a в квадрате плюс длина стороны b в квадрате.
Записывается в виде уравнения, c ² = a ² + b ²
Таким образом, по двум сторонам можно найти третью сторону по формуле.

Мы проиллюстрируем это примерами, но прежде чем продолжить, вы должны знать, как находить квадратный корень числа и как решать уравнения с помощью вычитания.
Примеры использования теоремы Пифагора
Упражнение №1
Пусть a = 3 и b = 4. Найдите c или наибольшую сторону
c ² = A ² + B ²
C ² = 3 ² + 4 ²
C ² = 9 + 16
C ² = 25
C = √ 25
Знак (√) означает квадратный корень
c = 5
Упражнение №2
Пусть c = 10 и a = 8. Найдите b или другую сторону.
c ² = a ² + b ²
10 ² = 8 ² + b ²
100 = 64 + B ²
100 — 64 = 64 — 64 + B ² (минус 64 с обеих сторон до изолята B ²)
36 = 0 + B ²
) 36 = B ²
B = √36 = 6
Упражнение № 3
Пусть C = 13 и B = 5. Найдите
C ² = A ² + B ²
13 ² = ² + 5 ²
169 = ² + 25
169 — 25 = A ² + 25-25
144 = A ² + 0
144 = A ²
a = √144 = 12
Взять питагоре ниже, чтобы увидеть, насколько хорошо вы поняли этот урок.

Купить полную электронную книгу по геометрическим формулам. Все геометрические формулы объясняются хорошо подобранными текстовыми задачами, чтобы вы могли освоить геометрию.
Типы треугольников
03, 22 декабря 12:47
Научитесь определять 6 типов треугольников по их сторонам или углам и еще 7 типов по сторонам и углам.
Подробнее
График прямоугольников и усов
18, 22 ноября 08:20
Легко научитесь строить график прямоугольников и усов для набора данных, используя средние и экстремальные значения.
No related posts.}}