Синус 2 угла: Формулы двойного аргумента (базовый уровень) — урок. Алгебра, 10 класс.

Синус и косинус двойного угла.

Дата проведения:.

Тема урока: синус и косинус двойного угла.

Тип урока: изучение нового материала.

Цели урока:

1)образовательные: формируют познавательную активность и мотивацию изучения математики; умения сравнивать, обобщать изучаемые факты; выделяют и формулируют познавательную цель, структурируют знания.

2)развивающие: развивать эмоции учащихся путем привлечения наглядности; развивать умение грамотно излагать свои мысли, обосновывать свои действия.

3)воспитательная:  воспитать интерес к уроку

Литература: алгебра и начала математического анализа А.Н.Колмогоров

 

                                                                 Ход урока

 

1)Организационный момент (1 мин.)

2)Повторение (5 мин.)

а) Ребус (2мин

)

3) Новая тема

Теперь запишем все формулы двойного угла

 в виде списка.

Заметим, что формулы синуса и косинуса двойного угла справедливы для любого угла . Формула тангенса двойного угла имеет место для любых , при которых определен  (то есть, при , где z – любое целое число). В свою очередь формула котангенса двойного угла справедлива для любых , при которых имеет место  (то есть, при ).

Формулы двойного угла доказываются достаточно просто – они следуют из формул сложения.

 

4.Закрепление

Задание №1  Дано: сosα = -, π .

Вычислить: sin 2 α.

Решение.

1. sin 2α =2 sin α cosα; π , 3 четверть, sinα sin² α + cos² α = 1 следует, что sin² α = 1- cos² α,

sin α =, sin α = — .

 

sin 2α =2 sin α cosα = 2^. Sin 2α= .

Ответ: sin 2α= .

Задание№2    Дано: sin α = — .

Вычислите: сos 2α.

Решение.

cos 2α = cos² α – sin² α, из основного тригонометрического тождества sin² α + cos² α = 1 следует, что

cos² α = 1-sin² α = 1 — .

cos 2α = cos² α – sin² α =

cos 2α =.    Ответ: cos 2α =.

Задание№3       2) cos² 15⁰ – sin² 15⁰ = cos 2^. 15⁰ = cos 30⁰= .

4) (cos 15⁰ + sin 15⁰)² = cos² 15⁰ +2 sin 15⁰ cos15⁰ + sin² 15⁰=

= 1 + 2 sin 15⁰ cos15⁰ =1 + sin 30⁰=1 + = .

.

Вариант 1.

а) 2sin π/8 cos π/8;  Вычислите cos 2α, sin 2α, если sin α = 0,6, Ответы: 1 вариант:1) а) ; б) .

Вариант 2.

1. Вычислите:

а) 2sin π/12 cos π/12; Вычислите sin 2α, cos 2α, если cos α = 0,8 и 3π/2 π.

1. Ответы: 2 вариант: 1) а) ; б) .

 

 

 

 

 

Просмотр содержимого документа
«Синус и косинус двойного угла. »

Дата проведения:.

Тема урока: синус и косинус двойного угла.

Тип урока: изучение нового материала.

Цели урока:

1)образовательные: формируют познавательную активность и мотивацию изучения математики; умения сравнивать, обобщать изучаемые факты; выделяют и формулируют познавательную цель, структурируют знания.

2)развивающие: развивать эмоции учащихся путем привлечения наглядности; развивать умение грамотно излагать свои мысли, обосновывать свои действия.

3)воспитательная: воспитать интерес к уроку

Литература: алгебра и начала математического анализа А.Н.Колмогоров

Ход урока

1)Организационный момент (1 мин.)

2)Повторение (5 мин.)

а) Ребус (2мин

)

3) Новая тема

Теперь запишем все формулы двойного угла в виде списка.

Заметим, что формулы синуса и косинуса двойного угла справедливы для любого угла 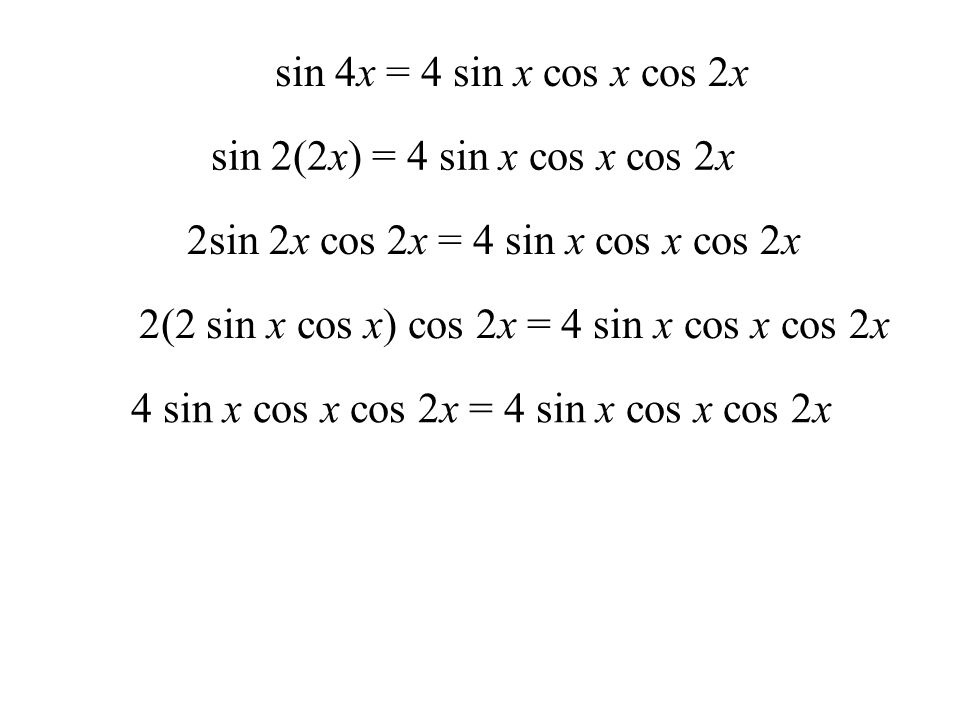 . Формула тангенса двойного угла имеет место для любых  , при которых определен   (то есть, при  , где z – любое целое число). В свою очередь формула котангенса двойного угла справедлива для любых  , при которых имеет место   (то есть, при  ).

Формулы двойного угла доказываются достаточно просто – они следуют из формул сложения.

4.Закрепление

Задание №1 Дано: сosα = — , π .

Вычислить: sin 2 α.

Решение.

1. sin 2α =2 sin α cosα; π , 3 четверть, sinα sin² α + cos² α = 1 следует, что sin² α = 1- cos² α,

sin α = , sin α = —  .

sin 2α =2 sin α cosα = 2^. Sin 2α=  .

Ответ: sin 2α=  .

Задание№2 Дано: sin α = —  .

Вычислите: сos 2α.

Решение.

cos 2α = cos² α – sin² α, из основного тригонометрического тождества sin² α + cos² α = 1 следует, что

cos² α = 1-sin² α = 1 —  .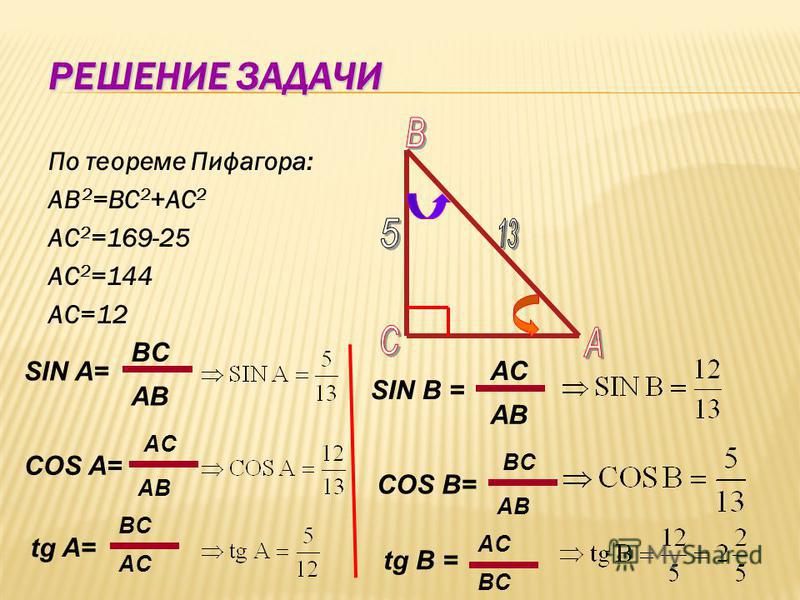

cos 2α = cos² α – sin² α =

cos 2α = . Ответ: cos 2α = .

Задание№3 2) cos² 15⁰ – sin² 15⁰ = cos 2^. 15⁰ = cos 30⁰=  .

4) (cos 15⁰ + sin 15⁰)² = cos² 15⁰ +2 sin 15⁰ cos15⁰ + sin² 15⁰=

= 1 + 2 sin 15⁰ cos15⁰ =1 + sin 30⁰=1 +  =  .

.

Вариант 1.

а) 2sin π/8 cos π/8; Вычислите cos 2α, sin 2α, если sin α = 0,6, Ответы: 1 вариант:1) а) ; б) .

Вариант 2.

1. Вычислите:

а) 2sin π/12 cos π/12; Вычислите sin 2α, cos 2α, если cos α = 0,8 и 3π/2 π.

1. Ответы: 2 вариант: 1) а) ; б) .

5.Итог урока

Вопросы по теме урока. Оценивание. д/задание

Правило синусов — GCSE по математике

Введение

Что такое правило синусов?

Как я могу использовать правило синусов?

Как найти недостающую сторону или недостающий угол треугольника с помощью правила синусов

Рабочий лист правила синусов

Распространенные заблуждения

Похожие уроки

Практикуйте вопросы по правилу синусов

Правило синусов GCSE вопросы

Контрольный список обучения

Следующие уроки

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Теперь доступны еженедельные онлайн-уроки повторения математики GCSE

Узнать больше

Введение

Что такое правило синусов?

Как я могу использовать правило синусов?

Как найти недостающую сторону или недостающий угол треугольника с помощью правила синусов

Рабочий лист правила синусов

Распространенные заблуждения

Похожие уроки

Практикуйте вопросы по правилу синусов

Правило синусов GCSE вопросы

Контрольный список обучения

Следующие уроки

Все еще застряли?

Здесь мы узнаем о правиле синусов , в том числе о том, как использовать правило синусов для нахождения недостающих сторон и углов в треугольниках.

Существуют также рабочие листы правила синусоиды, основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое правило синусов?

Правило синусов (или закон синусов) представляет собой отношение между величиной угла в треугольнике и противолежащей стороной.

Мы можем использовать правило синусов для определения недостающего угла или стороны в треугольнике, когда у нас есть информация об угле и стороне, противоположной ему, а также о другом угле и стороне, противоположной ему.

Это правило синусов:

\[\frac{a}{\sin (A)}=\frac{b}{\sin (B)}=\frac{c}{\sin (C)} \]

Несмотря на то, что в треугольнике есть три соотношения между тремя углами и их противоположными сторонами, нам нужно использовать только два из них для правила синусов.

Это будет выглядеть примерно так:

\[\frac{a}{\sin (A)}=\frac{b}{\sin (B)}\]

Что такое правило синусов

Как я могу использовать правило синусов?

Мы можем использовать правило синусов, чтобы найти недостающие стороны и углы, когда у нас есть информация о паре углов и их противоположных сторонах.

1 Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.

Заглавные буквы A, B, C используются для обозначения вершин (углов) треугольника, а строчные буквы a, b, c используются для обозначения сторон треугольника.

Противоположный угол — это та же буква, что и противоположная сторона.

Неважно, какие стороны а, b и с, но заглавная буква для вершины должно стоять напротив той же буквы сбоку, чтобы синусоидальное отношение работало.

2 Сформулируйте правило синусов, затем подставьте данные значения в уравнение.

Теперь, когда мы знаем, какие стороны и углы у нас есть, нам нужно подставить эту информацию в правило синусов. Затем мы можем решить это уравнение, чтобы найти недостающую сторону или угол.

Поскольку они вычисляются немного по-другому, мы можем изменить правило синусов, чтобы оно соответствовало той части треугольника, которую мы пытаемся найти. Вот две версии.

Чтобы найти недостающий угол:

\frac{\sin (A)}{a}=\frac{\sin (B)}{b}

Чтобы найти недостающую сторону:

\frac{a} {\sin(A)}=\frac{b}{\sin(B)}

Одно уравнение является перестановкой другого.

Основные советы:

Когда мы находим отсутствующий угол, мы помещаем углов поверх (sin A, sin B, sin C)

Когда мы находим отсутствующую сторону , мы кладем стороны сверху (a, b, c)

3 Решите уравнение.

Как только все подставлено в правило синусов, мы можем решить уравнение для вычисления неизвестной стороны или угла.

Как найти недостающую сторону или недостающий угол треугольника с помощью правила синусов

Чтобы найти недостающую сторону треугольника с помощью правила синусов:

1. Обозначьте каждый угол (A, B, C) и каждая сторона (a, b, c) треугольника.
2. Сформулируйте правило синусов, затем подставьте данные значения в уравнение.
3. Решите уравнение.

Объясните, как найти недостающую сторону или недостающую сторону треугольника с помощью правила синусов

Рабочий лист по правилу синусов

Получите бесплатный рабочий лист по правилу синусов, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Икс

Рабочий лист по правилу синусов

Получите бесплатный рабочий лист по правилу синусов, содержащий более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.

СКАЧАТЬ БЕСПЛАТНО

Примеры правила синусов (недостающая сторона)

Пример 1: нахождение недостающей стороны треугольника

Вычислите длину AB. Запишите свой ответ с точностью до двух знаков после запятой.

1. Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника .

2 Сформулируйте правило синусов, затем подставьте данные значения в уравнение.

Здесь нам известна сторона а, и мы хотим найти длину с, поэтому мы можем сказать:

\[\begin{выровнено} \frac{a}{\sin (A)}&=\frac{c}{\sin (C)}\\\\ \frac{6}{\sin (55)}&=\frac{c}{\sin (73)} \end{выровнено} \]

3 Решите уравнение.

\начало{массив}{л} \\\frac{6}{\sin (55)}=\frac{c}{\sin (73)}\\\\ c=\frac{6}{\sin (55)}\times\sin(73)\\\\ c=\frac{6\sin(73)}{\sin(55)}\\\\ c=7.00\quad(2d.p.) \end{array}

Здесь длина AB = 7,00 см (2 д.п.).

Пример 2: найти недостающую сторону треугольника

Вычислить длину BC. Запишите свой ответ с точностью до двух знаков после запятой.

Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.

Сформулируйте правило синусов, затем подставьте данные значения в уравнение.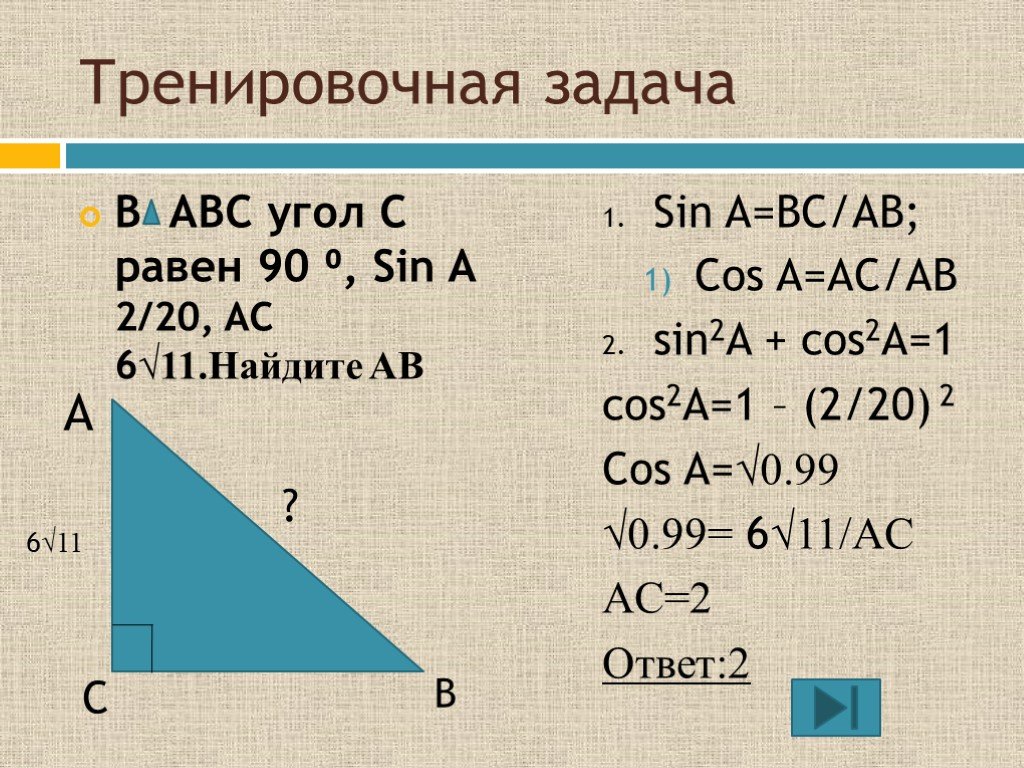

Здесь мы знаем сторону c и хотим найти длину a, поэтому мы можем указать:

\begin{align} \\\frac{a}{\sin (A)}&=\frac{c}{\sin (C)}\\ \\\frac{a}{\sin (41)}&=\frac{3.4}{\sin (27)}\\ \end{align}

Решите уравнение.

\начало{массив}{л} \frac{a}{\sin (41)}=\frac{3.4}{\sin (27)}\\ \\a=\frac{3.4}{\sin (27)}\times\sin(41)\\ \\a=\frac{3.4\sin(41)}{\sin(27)}\\ \\a=4.91\quad(2d.p.) \end{array}

Здесь длина BC = 4,91 см (2 д.п.).

Пример 3: нахождение недостающей стороны треугольника

Вычислите длину AC. Запишите свой ответ с точностью до двух знаков после запятой.

Маркируйте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.

Сформулируйте правило синусов, затем подставьте данные значения в уравнение.

Здесь мы знаем сторону a и хотим найти длину стороны b, поэтому мы можем указать:

\begin{align} \\\frac{a}{\sin (A)}&=\frac{b}{\sin (B)}\\ \\\frac{10. 8}{\sin (81)}&=\frac{b}{\sin (48)}\\ \end{align}

Решите уравнение.

\начало{массив}{л} \\\frac{10.8}{\sin (81)}=\frac{b}{\sin (48)}\\ \\b=\frac{10.8}{\sin (81)}\times\sin(48)\\ \\b=\frac{10.8\sin(48)}{\sin(81)}\\ \\b=8.13\quad(2d.p.) \конец{массив}

Здесь длина AC = 8,13 см (2 д.п.).

Примеры правила синусов (недостающий угол)

Пример 4: нахождение недостающего угла треугольника

Вычислите величину недостающего угла θ. Запишите свой ответ с точностью до одного десятичного знака.

Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника

Запишите полученные значения в правило синуса уравнение 9{\circ} (2d.p.).\]

Пример 5: нахождение недостающего угла треугольника

Вычислите величину недостающего угла θ. Запишите свой ответ с точностью до одного десятичного знака.

Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.

Сформулируйте правило синусов, затем подставьте данные значения в уравнение.

Здесь нам известен угол при B, и мы хотим найти угол при C, поэтому мы можем сказать: 9{\ circ} \ quad (1 д.п.) \end{array}

Здесь длина AB = 61,6º (1 д.п.).

Пример 6: нахождение недостающего угла треугольника

Вычислите величину недостающего угла θ.

Обозначьте каждый угол (A, B, C) и каждую сторону (a, b, c) треугольника.

Сформулируйте правило синусов, затем подставьте данные значения в уравнение. 9{\ circ} \ четырехъядерный \end{array}

Здесь длина AB = 60º.

Распространенные заблуждения

• Неправильная маркировка треугольника

Это может вызвать сквозную ошибку при подстановке значений в уравнение.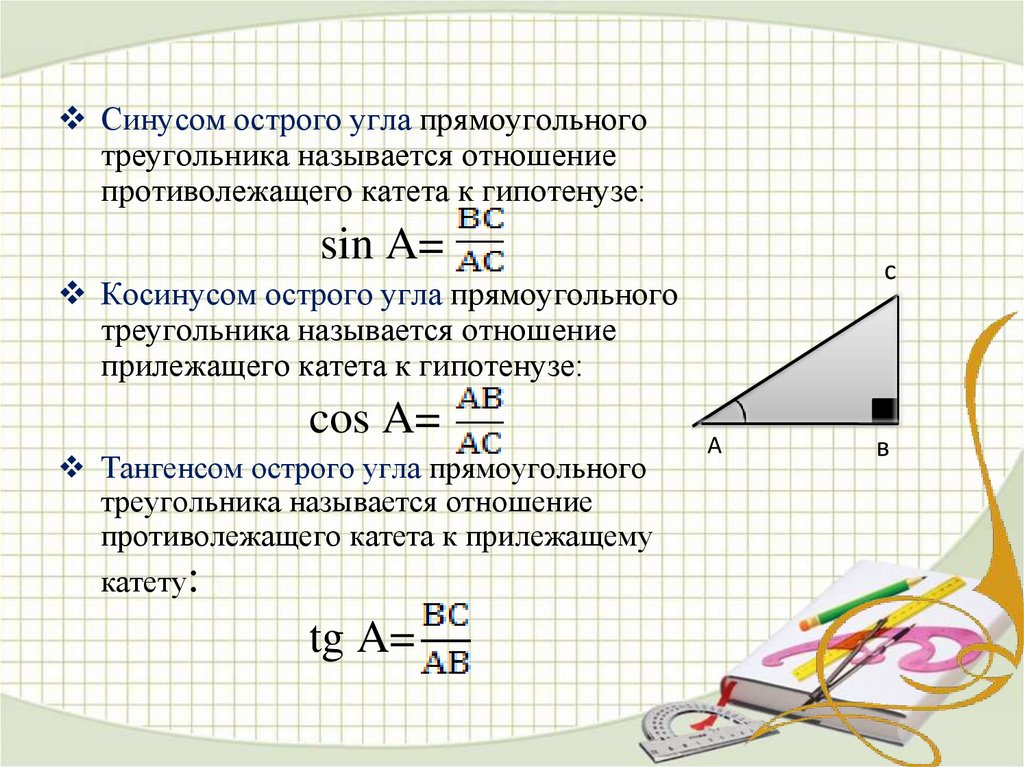 Например, в этом треугольнике неправильно обозначена сторона рядом с углом.

Это повлияет на формулу уравнения синусов, так как она будет выглядеть так, а не так, как в примере 5.

• Путают, когда используют функцию синуса и обратного синуса

При поиске стороны используйте функцию синуса. При нахождении недостающего угла нужно использовать функцию обратного синуса.

• Использование правила синусов для нахождения недостающей стороны, если значение двух углов в треугольнике неизвестно

другой. Если мы находим недостающую сторону, нам нужно знать два угла и одну из противоположных сторон, мы можем использовать эту информацию, чтобы найти сторону, противоположную другому углу.

• Слишком раннее округление десятичной дроби

Это может привести к потере меток точности. Всегда используйте как можно больше знаков после запятой в расчетах, а затем округляйте решение.

• Использование неправильной настройки для формулы правила синусов

Не должно быть слишком сложно изменить формулу после замены значений, однако небольшие ошибки повлияют на ваше решение.

• Отмена функций синуса

Например, при расчете значения a в примере 2 возникает следующая ошибка расчета.

\начало{массив}{л} \\\frac{a}{\sin (41)}=\frac{3.4}{\sin (27)}\\ \\a=\frac{3.4}{\sin (27)}\times\sin(41)\\ \\a=\frac{3.4\sin(41)}{\sin(27)}\\ \\a=\frac{3.4\times41}{27}\\ \\a=5.16\quad(2dp) \end{array}

Это неверно, потому что синус — это функция, поэтому мы не можем этого сделать.

• Помните о неоднозначном случае правила синусов

Из-за характера функции синуса может быть несколько ответов на вопрос.
Возьмем, к примеру, sin(60). Это дает то же решение, что и sin(120) (дополнительную информацию см. в разделе Тригонометрические графики).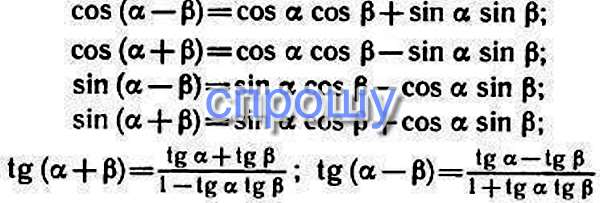

Калькулятор запрограммирован на возврат первого значения угла, но вы должны знать, что для тупого угла может существовать другое решение.

Чтобы проверить, выдал ли калькулятор нужное вам решение, можно выполнить 3 простые проверки.

1. Sin(θ) = 1. Этот случай имеет только одно решение, θ = 90º (прямоугольный треугольник).
2. Сумма углов больше 180º. Получится невозможный треугольник.
3. Угол напротив более длинной стороны должен быть больше. Сравните значения сторон треугольника a, b и c с их противоположными углами A, B и C. Большая сторона всегда будет находиться напротив большего угла.

Практические вопросы по правилу синусов

6,29 см

4,95 см

6,07 см

6,11 см

 

 

 

\начать{массив}{л} \frac{a}{\sin(A)}=\frac{c}{\sin(C)}\\\\ \frac{a}{\sin(48)}=\frac{5.5}{\sin(42)}\\\\ a=\frac{5.5}{\sin(42)} \times \sin(48)\\\\ а=6,11 \mathrm{~см} \конец{массив}

88,02 мм

34,37 мм

99,69 мм

88,21 мм

 

3  

3 

3

3

3 \начать{массив}{л} \frac{b}{\sin(B)}=\frac{c}{\sin(C)}\\\\ \frac{55}{\sin(32)}=\frac{c}{\sin(58)}\\\\ a=\frac{55}{\sin(32)} \times \sin(58)\\\\ а=88,02 \mathrm{~мм} \конец{массив} 9{\ круг}.

{\circ} \end{выровнено}

(1)

2. Определите величину угла BCD.

 

 

(5 баллов)

Показать ответ

\frac{BD}{\sin(77)}=\frac{14}{\sin(51)}

(1)

 

\begin{выровнено} BD&=\frac{14}{\sin(51)} \times \sin(77)\\\\ BD&= 17,553\mathrm{см} \end{выровнено}

(1)

 

\frac{sin(\theta)}{17,55}=\frac{sin(82)}{30} 9{\ круг} \конец{массив}

(1)

 

\frac{AB}{\sin(92)}=\frac{17}{\sin(46)}

(1)

 

AB=\frac{17}{\sin(46)} \times \sin(92)

(1)

 

АВ=23,6 см

(1)

Контрольный список для обучения

Теперь вы научились:

• знать и применять правило синусов для нахождения неизвестных длин и углов

Все еще застряли?

Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.

Узнайте больше о нашей программе повторения GCSE по математике.

Мы используем необходимые и необязательные файлы cookie для улучшения работы нашего веб-сайта. Пожалуйста, ознакомьтесь с нашей Политикой в ​​отношении файлов cookie, чтобы узнать, как мы используем файлы cookie и как управлять или изменять ваши настройки файлов cookie. Принять

Формула правила синусов — GeeksforGeeks

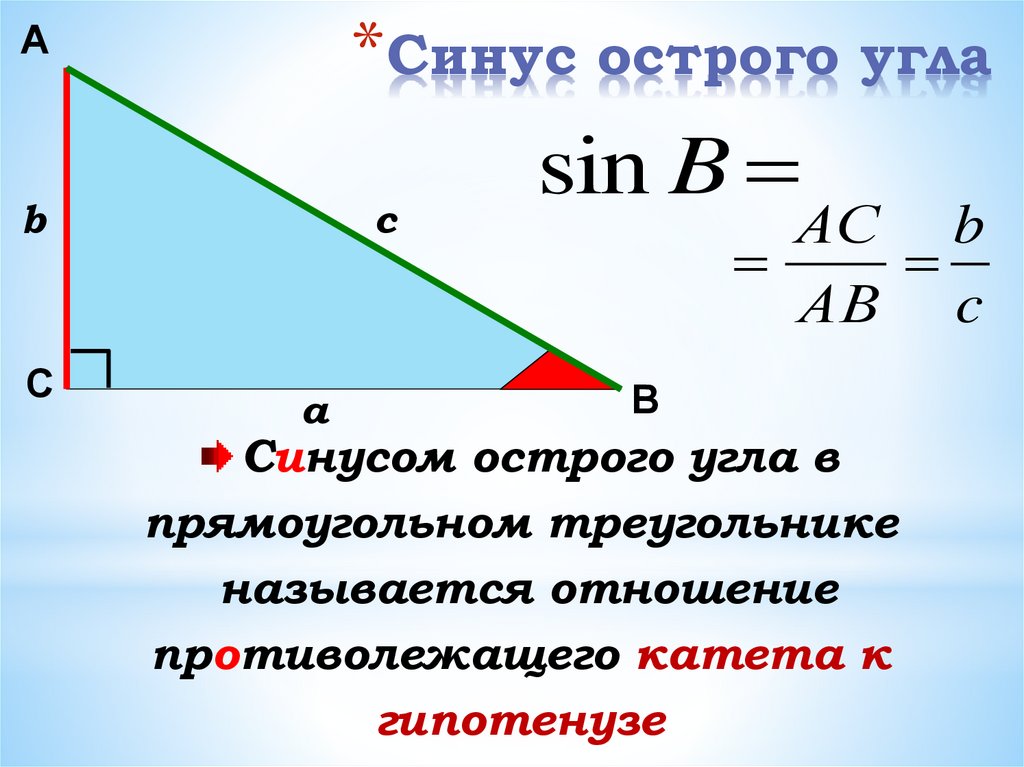
Тригонометрия — важный раздел математики, изучающий соотношение между длинами сторон и углами прямоугольного треугольника. Слово тригонометрия происходит от греческих слов, где «три» означает «три», «гон» означает «стороны», а «метрон» означает «мера». Синус, косинус, тангенс, котангенс, косеканс и секанс — это шесть тригонометрических отношений. Где тригонометрическое отношение изображается как отношение между сторонами треугольника. Теперь формулы тригонометрического отношения даны как,

• синус θ = противолежащая сторона/гипотенуза
• косинус θ = прилежащая сторона/гипотенуза
• тангенс θ = противолежащая сторона/гипотенуза
• косеканс θ = 1/синус θ = гипотенуза/противоположная сторона
• 7
• 7
θ = гипотенуза/прилежащая сторона
• котангенс θ = 1/тангенс θ = прилежащая сторона/противоположная сторона

Правило синусов или закон синусов стороны и углы треугольника (непрямоугольный треугольник).

Пусть a, b и c будут длинами трех сторон треугольника ABC и A, B и C относительно их противоположных углов. Теперь выражение для правила синусов дается как,

  sin A/a = sin B/b = sin C/c  (или) a/sin A = b/sin B = c/sin C

Применение 

С помощью формулы правила синуса мы можем найти длину стороны треугольника, угол треугольника, а также площадь треугольника.

Доказательство

В треугольнике ABC стороны треугольника равны AB = c, BC = a и AC = b.

 

Проведем перпендикуляр BD, перпендикулярный AC. Теперь у нас есть два прямоугольных треугольника ADC и BDC.

BD = h ₁ — высота треугольника ABC.

В тре 1) и (2).

Получаем, sin A/sin C = a/c ⇒ a/sin A = c/sin C ⇢ (3)

Аналогичным образом проведем перпендикуляр AE, перпендикулярный BC. Теперь AEB и BEC — прямоугольные треугольники, разделенные h _2.

В тре 4) и (5),

sin B/sin C = b/c ⇒ b/sin B = c/sin C ⇢ (6)

Теперь, приравнивая уравнения (3) и (6), получаем ,

a/sin A = b/sin B = c/sin C (или) sin A/a = sin B/b = sin C/c

Примеры задач

Задача 1. Найти оставшиеся длины треугольника XYZ, когда ∠X = 30°, ∠Y = 45° и x = 5 см.

Решение:

Учитывая данные, ∠X = 30°, ∠Y = 45° и x = 5 см

 

Мы знаем, что сумма трех углов треугольника равна 180°

. , ∠X + ∠Y + ∠Z = 1

30° + 45° + ∠Z = 180°   ⇒  75° + ∠Z = 180°

∠Z = 105°

Теперь по закону синусов, x / sin X = y/ sin Y = z/ sin Z

x/sin X = y/ sin Y ⇒ 5/ sin 30° = y/ sin 45°

⇒ x/(1/2) = y/( 1/√2) ⇒ 10 =√2y ⇒ y = 7,07 см

Аналогично, x/sin X = z/sin Z ⇒ 5/sin 30° = z/sin 105°  [sin 105° = (√6 + √2)/4 = 0,965]

⇒ 5/(1/2 ) = z/(0,965) ⇒ z = 9,65 см

Задача 2. Найти ∠P и ∠Q и длину третьей стороны при ∠R = 36° и p = 2,5 см и r = 7 см ?

Решение:

Дано, ∠R = 36°, p = 2,5 см и r = 7 см = r/sin R

⇒ 2,5/sin P = q/sin Q = 7/sin 36°

⇒ 2,5/sin P = 7/sin 36° [sin 36° = 0,5878]

⇒ sin P = 0,20992 ⇒ P = sin 9089 -1 (0,20992)

⇒ тийс = 12,12 °

⇒ мы имеем, секрет + ↑к. Q = 131,88 °

⇒ q/sin 131,88 ° = 7/sin 36 °

⇒ Q/0,7445 = 7/0,5878 ⇒ Q = 8,866 CM (приблизительно)

. = 131,88° и q = 8,866 см

Задача 3: Найдите отношение сторон треугольника ABC, когда ∠A = 15°, ∠B = 45° и ∠C = 120°?

Решение:

Дано: ∠A = 15°, ∠B = 45° и ∠C = 120° c/ sin C ⇒  a : b : c = sin A : sin B : sin C

⇒ a : b : c = sin 15° : sin 45° : sin 120°

sin 15° = (√3 – 1)/2√2 = 0,2588 (приблизительное значение)

sin 45° = 1/√2 = 0,7071  (приблизительное значение)

sin 120° = √3/2 = 0,866  (приблизительное значение)

Отсюда отношение трех сторон треугольника ABC равно a : b : c = 0,2588 : 0,7071 : 0,866

Задача : Найдите площадь треугольника ABC, если BC = 10 см, AB = 12 см и ∠B = 30°?

Решение:

Дано, BC = a = 10 см, AB = c = 12 см и ∠B = 30° высота) = ½ (а) (ч) ⇢ (1)

Из рисунка sin B = высота/c

h = c sin B ⇢ (2)

Теперь подставим уравнение (2) в (1),

Площадь треугольника ABC = ½ (a)(c) sin B = ½ (10) (12) sin 30° [sin 30° = ½]

⇒ Площадь = ½ (120) ½ = 30 см ²

Следовательно, площадь треугольник ABC равен 30 см ² .

No related posts.