Формула а в квадрате минус в: Минус а минус в в квадрате

Содержание

Алгебра. Учебник для 6-8 классов

Барсуков А.Н. Алгебра. Учебник для 6-8 классов. 11-е изд., стер. — М.: Просвещение, 1966. — 296 с.

Учебник для средних общеобразовательных школ СССР в 50-60-е годы.

Шестое издание „Алгебры» А.Н. Барсукова переработано и приведено в соответствие с новой программой. Переработка учебника и изложение вопросов, вновь включенных в программу восьмилетней школы, выполнены С.И. Новоселовым.

Главу „Счётная (логарифмическая) линейка* и о возвышении в квадрат и куб, извлечении квадратного и кубического корней при помощи счётной линейки написал учитель математики школы № 315 Москвы И. Б. Вейцман. Одиннадцатое издание печатается с десятого без изменений.

§ 2. Алгебраические выражения.
§ 3. Допустимые значения букв.
§ 4. Порядок действий.
§ 5. Основные законы сложения и умножения.
§ 6. Краткие исторические сведения.
ГЛАВА ВТОРАЯ. РАЦИОНАЛЬНЫЕ ЧИСЛА.
§ 7. Положительные и отрицательные числа.
§ 8. Числовая ось.
§ 9. Противоположные числа.
§ 10. Абсолютная величина числа.
§ 11. Сравнение рациональных чисел.
§ 12. Сложение рациональных чисел.
§ 13. Сложение нескольких чисел.
§ 14. Законы сложения.
§ 15. Вычитание рациональных чисел.
§ 16. Алгебраическая сумма.
§ 17. Умножение.
§ 18. Умножение нескольких чисел.
§ 19. Законы умножения.
§ 20. Деление.
§ 21. Свойства деления.
§ 22. Возведение в степень.
§ 23. Порядок выполнения действий.
§ 24. Уравнения.
§ 25. Решение задач с помощью уравнений.
§ 26. Графики.
§ 27. Краткие исторические сведения. (Из истории отрицательных чисел.)

ГЛАВА ТРЕТЬЯ. ДЕЙСТВИЯ НАД ЦЕЛЫМИ АЛГЕБРАИЧЕСКИМИ ВЫРАЖЕНИЯМИ.

§ 28. Одночлен и многочлен.
§ 29. Тождества и тождественные преобразования.
§ 30. Коэффициент.
§ 31. Расположенные многочлены.
§ 32. Приведение подобных членов.
§ 33. Сложение одночленов и многочленов.
§ 34. Противоположные многочлены.
§ 35. Вычитание одночленов и многочленов
§ 36. Умножение одночленов.
§ 37. Умножение многочлена на одночлен.
§ 38. Умножение многочленов.
§ 39. Умножение расположенных многочленов.
§ 40. Возведение одночленов в степень.
§ 41. Формулы сокращённого умножения.
§ 42. Общие замечания о делении целых алгебраических выражений.
§ 43. Деление одночленов.
§ 44. Деление многочлена на одночлен
§ 45. Примеры решения уравнений.
ГЛАВА ЧЕТВЁРТАЯ. УРАВНЕНИЯ ПЕРВОЙ СТЕПЕНИ С ОДНИМ НЕИЗВЕСТНЫМ.
§ 47. Равносильные уравнения.
§ 48. Два основных свойства уравнений.
§ 49. Уравнения, содержащие неизвестное в обеих частях.
§ 50. Уравнение первой степени с одним неизвестным.
§ 51. Общие указания к решению уравнений.

§ 52. Решение задач с помощью уравнений.
§ 53. Краткие исторические сведения. (Из истории уравнений.)
ГЛАВА ПЯТАЯ. РАЗЛОЖЕНИЕ МНОГОЧЛЕНОВ НА МНОЖИТЕЛИ.
§ 54. Понятие о разложении на множители.
§ 55. Вынесение за скобки общего множителя.
§ 56. Способ группировки.
§ 57. Применение формул сокращённого умножения.
§ 58. Применение нескольких способов.
§ 59. Деление многочленов при помощи разложения на множители.
ГЛАВА ШЕСТАЯ. АЛГЕБРАИЧЕСКИЕ ДРОБИ.
§ 60. Понятие об алгебраической дроби.
§ 61. Основное свойство дроби и сокращение дробей.
§ 62. Перемена знака у членов дроби.
§ 63. Целая отрицательная и нулевая степени числа.

§ 64. Приведение дробей к общему знаменателю.
§ 65. Сложение дробей.
§ 66. Вычитание дробей.
§ 67. Умножение дробей.
§ 68. Деление дробей.
§ 69. Возведение дроби в натуральную степень.
§ 70. Дробные уравнения.
§ 71. Примеры решения уравнений с буквенными коэффициентами.
ГЛАВА СЕДЬМАЯ.

КООРДИНАТЫ И ПРОСТЕЙШИЕ ГРАФИКИ.
§ 72. Координаты точки на плоскости.
§ 73. Прямо пропорциональная зависимость.
§ 74. График прямо пропорциональной зависимости.
§ 75. Линейная зависимость.
§ 76. Обратно пропорциональная зависимость.
ГЛАВА ВОСЬМАЯ. СИСТЕМА УРАВНЕНИЙ ПЕРВОЙ СТЕПЕНИ С ДВУМЯ НЕИЗВЕСТНЫМИ.
§ 77. Уравнение первой степени с двумя неизвестными.
§ 78. Система двух уравнений первой степени с двумя неизвестными.
§ 79. Равносильные системы.
§ 80. Решение систем уравнений.
§ 81. Графическое решение системы двух уравнений.
§ 82. Решение задач.
§ 83. Уравнение с тремя неизвестными.
§ 84. Система трёх уравнений с тремя неизвестными.
ГЛАВА ДЕВЯТАЯ. СЧЁТНАЯ (ЛОГАРИФМИЧЕСКАЯ) ЛИНЕЙКА.
§ 85. Равномерные и неравномерные шкалы.
§ 86. Устройство счётной (логарифмической) линейки.
§ 87. Основная шкала.
§ 88. Умножение и деление с помощью счётной линейки.
ГЛАВА ДЕСЯТАЯ. КВАДРАТНЫЙ КОРЕНЬ.
§ 89. Построение графика зависимости y = x^2
§ 90.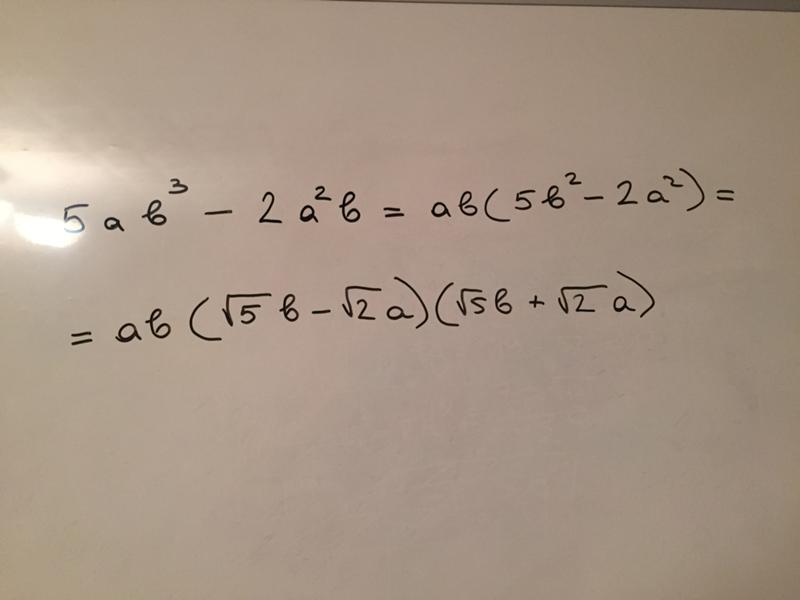

(1/3)
§ 130. Примеры графического решения уравнений и систем уравнений.

Чему равен квадрат разности: формула, доказательство, примеры

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Квадрат разности: формула и примеры

В данной публикации мы рассмотрим одну из формул сокращенного умножения – квадрат разности. Также разберем примеры решения задач для закрепления изложенного материала.

Формула квадрата разности
Доказательство формулы
Примеры задач

Формула квадрата разности

Квадрат разности a и b равняется квадрату уменьшаемого (a) минус удвоенное произведение уменьшаемого и вычитаемого (a и b) плюс квадрат вычитаемого (b).

(a – b)² = a² – 2ab + b²

Данное выражение равносильно и в обратную сторону:

a² – 2ab + b² = (a – b)²

Доказательство формулы

Так как возведение в квадрат – это умножение числа/выражения на само себя, давайте представим нашу формулу в виде перемножения двух одинаковых скобок:
(a-b)(a-b).

Остается согласно арифметическим правилам убрать скобки, тем самым, разложив произведение на множители:
(a-b)(a-b) = a² – ab – ba + b² = a² – 2ab + b².

Примеры задач

Задание
Разложите на множители квадрат разности: (4x – 2y⁴)².

Решение
Применив формулу сокращенного умножения получаем:
(4x – 2y⁴)² = (4x)² – 2 ⋅ 4x ⋅ 2y⁴ + (2y⁴)² = 16x² – 16xy⁴ + 4y⁸

Примечание:
Знание формулы, также, позволяет производить быстрые вычисления в уме:

77² = (80 – 3)² = 80² – 2 ⋅ 80 ⋅ 3 + 3² = 6400 – 480 + 9 = 5929.
48² = (50 – 2)² = 50² – 2 ⋅ 50 ⋅ 2 + 2² = 2500 – 200 + 4 = 2304.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

факторизация и решение квадратного уравнения, уравнений физики

vi(t)+1/2{(a)t в квадрате)

Электрический ток18 формула

43 формула

A	B
a в квадрате (минус) b в квадрате =	(a+b)(a-b)
a в квадрате (плюс) 3a1 1 1 ab (плюс) в квадрате б) в квадрате
a в кубе (плюс) b в кубе =	(a+b)(a в квадрате — ab + b в квадрате)
a в кубе b (минус) ab =	ab(a+1) )(а-1)
a в квадрате (минус) 2ab (плюс) b в квадрате =	(a-b) в квадрате
a в кубе (минус) b в кубе =	(a-b)(a в квадрате + ab + b в квадрате)
		решение ax в квадрате (плюс) bx + c= 0	x= -b (плюс или минус) знак квадратного корня b в квадрате (минус) 4ac (деленное на) 2a
квадратное уравнение	ax в квадрате (плюс) bx (плюс) c = 0
Формула плотности	D=m/v
формула расстояния	d=vt
формула ускорения	a=vf-vi/t (vf=конечная скорость, vi=начальная скорость, t=время)
формула скорости4
формула силы	F=ma (m=масса, a=ускорение)
формула силы тяжести	Fg=G(масса объекта1)(масса объекта 2), деленная на d в квадрате
d в квадрате силы тяжести формула означает	separation distance
momentum formula	p=mv
Work formula	W=Fd
Work formula is what type of problem	gravitational potential energy problem
Power formula	P=Вт/т
формула мощности — это тип задачи	электричество (ватты)
Формула кинетической энергии	K. E.=1/2(m)(скорость в квадрате)
Формула электрической силы	Fe=k(Q электрического заряда 1)(Q электрического заряда 2), деленное на d в квадрате
Формула разности электрических потенциалов	V=W/Q
I=Q/t
Формула электрической энергии	Вт=Vlt (l=ток)
Мощность в формуле электрического тока	P=Vl (l=тепловой ток)
H=cm(форма треугольника)T (c=удельная теплоемкость)
(форма треугольника)T	изменение температуры по Цельсию
Суммарная сила — это закон Ньютона	901 2-й закон движения
3-й закон Ньютона	для каждого действия существует равная противоположная реакция
1-й закон Ньютона	равномерно движущийся объект стремится оставаться в движении, если к нему не приложена внешняя сила
Второй закон Ньютона:	Сила вызывает изменение скорости (ускорения) объекта закон Ньютона	это второй закон движения по Ньютону
Гравитационная постоянная	6,6726(10 в степени минус 11)(раз) Н минус м в квадрате разделить на кг в квадрате (м=расстояние)
Coulomb’s Constant	K = 9 (раз) от 10 до 9-й мощности (время) N-M квадрат, разделенные на C Squared
Joules
N в физических уравнениях означает	Сила какого-либо вида (электрическая,
кинетическая энергия это энергия в чем	движение

Разность квадратов | Великолепная математика и естественные науки Wiki

Сандип Бхардвадж, 敬全钟, Сэм Рив, и

способствовал

Содержимое

Личность
Примеры проблем
Дальнейшее расширение 92 = (5-2) \умножить на (5+2) = 3\умножить на 7. \ _\square52−22=(5−2)×(5+2)=3×7. □
Вычислить 299×301299\умножить на 301299×301.
Вы можете найти ответ на эту задачу с помощью калькулятора, но у нас есть более приятный способ. Мы можем применить разность тождества двух квадратов.
Сначала мы можем подумать об использовании метода длинного умножения, но это отнимает время и, конечно, скучно. Обратите внимание, что 299=300−1299=300-1299=300−1 и 301=300+1301=300+1301=300+1, поэтому 92 \, ?992−982?

Примечание. Попробуйте без калькулятора.
20142014×20142014−20142013×20142015=?\large \color{#3D99F6}{2014}\color{#3D99F6}{2014} \times \color{#3D99F6}{2014}\color{#3D99F6}{2014 } — \color{#3D99F6}{2014}\color{#D61F06}{2013} \times \color{#3D99F6}{2014}\color{фуксия}{2015} = ? 20142014×20142014−20142013×20142015=?
Не пользуйтесь калькулятором!
1. Поскольку два фактора отличаются на 2b2b2b, коэффициенты всегда будут иметь одинаковую четность. То есть, если a-ba-ba-b четно, то a+ba+ba+b также должно быть четно, поэтому произведение делится на четыре. Или ни одно из них не делится на 2, поэтому произведение нечетное. Это означает, что числа, кратные 2, но не кратные 4, не могут быть выражены как разность 2 квадратов. 9\text{th}(n−1)-й член равен 1, поэтому конечный продукт равен n+12n\frac{n+1}{2n}2nn+1. □_\квадрат□
Упростить (5+6+7)(5+6−7)(5−6+7)(−5+6+7).\left(\sqrt5+\sqrt6+\sqrt7\right)\left(\sqrt5+\sqrt6 -\sqrt7\right)\left(\sqrt5-\sqrt6+\sqrt7\right)\left(-\sqrt5+\sqrt6+\sqrt7\right).(5+6+7)(5+6− 7)(5−6+7)(–5+6+7).
Мы можем расширить его, но это требует много времени и чревато ошибками. Пусть личность решит эту проблему. У нас есть 92\\&=5+6+2\sqrt{30}-7\\&=4+2\sqrt{30}.\end{выровнено}(5+6+7)(5+6 −7)=(5+6)2−(7)2=5+6+230−7=4+230.
Аналогично, произведение двух последних членов равно
.
(5−6+7)(−5+6+7)=(7+(5−6))(7−(5−6))=−4+230. \begin{выровнено} \big(\sqrt5-\sqrt6+\sqrt7\big)\big(-\sqrt5+\sqrt6+\sqrt7\big) &= \left(\sqrt7+\big(\sqrt5-\sqrt6\big)\right)\left( \sqrt7-\big(\sqrt5-\sqrt6\big)\справа) \\ &=-4+2\sqrt{30}. \end{выровнено} (5−6+7)(−5+6+7)= (7+(5−6))(7−(5−6))=−4 +230. 9{2} — (123456788 х 123456790).1234567892−(123456788×123456790).
Если вы используете калькулятор, точность которого недостаточно высока, чтобы ответить на этот вопрос, то вы ответите на эту задачу неправильно.
25 125 625 5
Если
x=4(5+1)(54+1)(58+1)(516+1),x=\frac{4}{\big(\sqrt{5}+1\big )\big(\sqrt[4]{5}+1\big)\big(\sqrt[8]{5}+1\big)\big(\sqrt[16]{5}+1\big)} ,x=(5+1)(45+1)(85+1)(165+1)4, 9{\ color {# 624F41} y} & = & \ large { \ frac 5 3} \\ \\ \\ \ big {\ color {# 624F41} x} — {\ color {# 624F41} y} & = & \ large \, ? \end{align} 2x−2y4x−4yx−y===135?
Детали и предположения:
- xxx и yyy — действительные числа.
  No related posts.