Перевести 4 5 в десятичную дробь: Переведите дробь 4/5 в десятичную !

Содержание

Mathway | Популярные задачи

1	Найти объем	сфера (5)	
2	Найти площадь	окружность (5)	
3	Найти площадь поверхности	сфера (5)	
4	Найти площадь	окружность (7)	
5	Найти площадь	окружность (2)	
6	Найти площадь	окружность (4)	
7	Найти площадь	окружность (6)	
8	Найти объем	сфера (4)	
9	Найти площадь	окружность (3)	
10	Вычислить	(5/4(424333-10220^2))^(1/2)
11	Разложить на простые множители	741
12	Найти объем	сфера (3)	
13	Вычислить	3 квадратный корень из 8*3 квадратный корень из 10
14	Найти площадь	окружность (10)	
15	Найти площадь	окружность (8)	
16	Найти площадь поверхности	сфера (6)	
17	Разложить на простые множители	1162
18	Найти площадь	окружность (1)	
19	Найти длину окружности	окружность (5)	
20	Найти объем	сфера (2)	
21	Найти объем	сфера (6)	
22	Найти площадь поверхности	сфера (4)	
23	Найти объем	сфера (7)	
24	Вычислить	квадратный корень из -121
25	Разложить на простые множители	513
26	Вычислить	квадратный корень из 3/16* квадратный корень из 3/9
27	Найти объем	прямоугольный параллелепипед (2)(2)(2)	
28	Найти длину окружности	окружность (6)	
29	Найти длину окружности	окружность (3)	
30	Найти площадь поверхности	сфера (2)	
31	Вычислить	2 1/2÷22000000
32	Найти объем	прямоугольный параллелепипед (5)(5)(5)	
33	Найти объем	прямоугольный параллелепипед (10)(10)(10)	
34	Найти длину окружности	окружность (4)	
35	Перевести в процентное соотношение	1. 2-4*-1+2
45	Разложить на простые множители	228
46	Вычислить	0+0
47	Найти площадь	окружность (9)	
48	Найти длину окружности	окружность (8)	
49	Найти длину окружности	окружность (7)	
50	Найти объем	сфера (10)	
51	Найти площадь поверхности	сфера (10)	
52	Найти площадь поверхности	сфера (7)	
53	Определить, простое число или составное	5
54	Перевести в процентное соотношение	3/9
55	Найти возможные множители	8
56	Вычислить	(-2)^3*(-2)^9
57	Вычислить	35÷0. 2
60	Преобразовать в упрощенную дробь	2 1/4
61	Найти площадь поверхности	сфера (12)	
62	Найти объем	сфера (1)	
63	Найти длину окружности	окружность (2)	
64	Найти объем	прямоугольный параллелепипед (12)(12)(12)	
65	Сложение	2+2=
66	Найти площадь поверхности	прямоугольный параллелепипед (3)(3)(3)	
67	Вычислить	корень пятой степени из 6* корень шестой степени из 7
68	Вычислить	7/40+17/50
69	Разложить на простые множители	1617
70	Вычислить	27-( квадратный корень из 89)/32
71	Вычислить	9÷4
72	Вычислить	2+ квадратный корень из 21
73	Вычислить	-2^2-9^2
74	Вычислить	1-(1-15/16)
75	Преобразовать в упрощенную дробь	8
76	Оценка	656-521
77	Вычислить	3 1/2
78	Вычислить	-5^-2
79	Вычислить	4-(6)/-5
80	Вычислить	3-3*6+2
81	Найти площадь поверхности	прямоугольный параллелепипед (5)(5)(5)	
82	Найти площадь поверхности	сфера (8)	
83	Найти площадь	окружность (14)	
84	Преобразовать в десятичную форму	11/5
85	Вычислить	3 квадратный корень из 12*3 квадратный корень из 6
86	Вычислить	(11/-7)^4
87	Вычислить	(4/3)^-2
88	Вычислить	1/239
89	Вычислить	12/4-17/-4
90	Вычислить	2/11+17/19
91	Вычислить	3/5+3/10
92	Вычислить	4/5*3/8
93	Вычислить	6/(2(2+1))
94	Упростить	квадратный корень из 144
95	Преобразовать в упрощенную дробь	725%
96	Преобразовать в упрощенную дробь	6 1/4
97	Вычислить	7/10-2/5
98	Вычислить	6÷3
99	Вычислить	5+4
100	Вычислить	квадратный корень из 12- квадратный корень из 192

Что такое десятичные дроби .

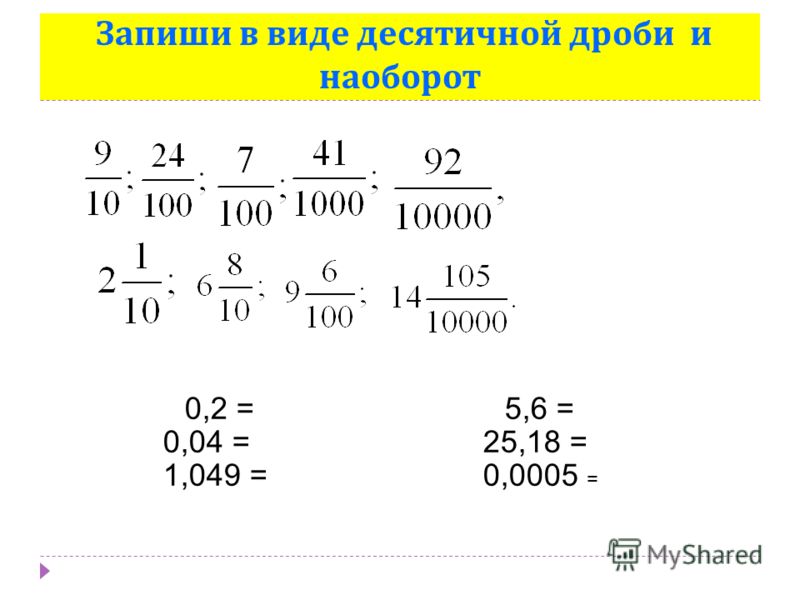знакомство с термином .

Десятичные дроби

Мы уже говорили, что дроби бывают обыкновенные и десятичные. На данный момент мы немного изучили обыкновенные дроби. Мы узнали, что обыкновенные дроби бывают правильные и неправильные. Также мы узнали, что обыкновенные дроби можно сокращать, складывать, вычитать умножать и делить. И ещё мы узнали, что бывают так называемые смешанные числа, которые состоят из целой и дробной части.

Мы ещё не до конца изучили обыкновенные дроби. Есть немало тонкостей и деталей, о которых следует поговорить, но уже сегодня мы начнём изучать десятичные дроби, поскольку обыкновенные и десятичные дроби достаточно часто приходится сочетать. То есть при решении задач приходиться работать с обоими видов дробей.

Этот урок возможно покажется сложным и непонятным. Это вполне нормально. Такого рода уроки требуют, чтобы их именно изучали, а не просматривали поверхностно.

Содержание урока

Выражение величин в дробном виде
Перевод смешанных чисел в десятичные дроби
Перевод обыкновенных дробей в десятичные дроби
Перевод неправильных дробей в десятичную дробь
Перевод десятичной дроби в смешанное число
Перевод десятичной дроби в обыкновенную дробь

Выражение величин в дробном виде

Иногда удобно бывает показать что-либо в дробном виде. Например, одна десятая часть дециметра записывается так:

Это выражение означает, что один дециметр был разделён на десять равных частей, и от этих десяти частей была взята одна часть. А одна часть из десяти в данном случае равна одному сантиметру:

Рассмотрим следующий пример. Пусть требуется показать 6 см и ещё 3 мм в сантиметрах в дробном виде.

Итак, 6 целых сантиметров у нас уже есть:

Но осталось еще 3 миллиметра. Как показать эти 3 миллиметра, при этом в сантиметрах? На помощь приходят дроби. Один сантиметр это десять миллиметров. Три миллиметра это три части из десяти. А три части из десяти записываются как см

Выражение см означает, что один сантиметр был разделён на десять равных частей, и от этих десяти частей взяли три части.

В результате имеем шесть целых сантиметров и три десятых сантиметра:

Цифра 6 показывает число целых сантиметров, а дробь — число дробных. Эта дробь читается как «шесть целых и три десятых сантиметра».

Дроби, в знаменателе которых присутствуют числа 10, 100, 1000 можно записывать без знаменателя. Сначала пишут цéлую часть, а потом числитель дробной части. Целая часть отделяется от числителя дробной части запятой.

Например, запишем без знаменателя. Сначала записываем целую часть. Целая часть это 6

Целая часть записана. Сразу же после написания целой части ставим запятую:

И теперь записываем числитель дробной части. В смешанном числе числитель дробной части это число 3. Записываем после запятой тройку:

6,3

Любое число, которое представляется в таком виде, называется десятичной дробью.

Поэтому показать 6 см и ещё 3 мм в сантиметрах можно с помощью десятичной дроби:

6,3 см

Выглядеть это будет следующим образом:

На самом деле десятичные дроби это те же самые обыкновенные дроби и смешанные числа. Особенность таких дробей заключается в том, что в знаменателе их дробной части содержатся числа 10, 100, 1000 или 10000.

Как и смешанное число, десятичная дробь имеет цéлую часть и дробную. Например, в смешанном числе целая часть это 6, а дробная часть это .

В десятичной дроби 6,3 целая часть это число 6, а дробная часть это числитель дроби , то есть число 3.

Бывает и так, что обыкновенные дроби в знаменателе которых числа 10, 100, 1000 даны без целой части. Например, дробь дана без целой части. Чтобы записать такую дробь как десятичную, сначала записывают 0, затем ставят запятую и записывают числитель дробной части. Дробь без знаменателя будет записана следующим образом:

0,5

Читается как «ноль целых, пять десятых».

Перевод смешанных чисел в десятичные дроби

Когда мы записываем смешанные числа без знаменателя, мы тем самым перевóдим их в десятичные дроби. При переводе обыкновенных дробей в десятичные дроби нужно знать несколько моментов, о которых мы сейчас поговорим.

После того как записана целая часть, обязательно нужно посчитать количество нулей в знаменателе дробной части, поскольку количество нулей дробной части и количество цифр после запятой в десятичной дроби должно быть одинаковым. Что это значит? Рассмотрим следующий пример: перевести смешанное число в десятичную дробь.

Сначала записываем целую часть и ставим запятую:

И можно бы сразу записать числитель дробной части и десятичная дробь готова, но обязательно нужно посчитать сколько нулей содержится в знаменателе дробной части.

Итак, посчитаем количество нулей в дробной части смешанного числа . Видим, что в знаменателе дробной части один ноль. Значит в десятичной дроби после запятой будет одна цифра и это цифра будет числитель дробной части смешанного числа , то есть число 2

3,2

Таким образом, смешанное число при переводе в десятичную дробь обращается в 3,2. Эта десятичная дробь читается так:

«Три целых, две десятых»

«Десятых» потому что в дробной части смешанного числа содержится число 10.

Пример 2. Перевести смешанное число в десятичную дробь.

Записываем цéлую часть и ставим запятую:

И можно бы сразу записать числитель дробной части и получить десятичную дробь 5,3 но правило говорит, что после запятой должно быть столько цифр сколько нулей в знаменателе дробной части смешанного числа . А мы видим, что в знаменателе дробной части два нуля. Значит в нашей десятичной дроби после запятой должно быть две цифры, а не одна.

В таких случаях числитель дробной части нужно немного видоизменить: добавить ноль перед числителем, то есть перед числом 3

Теперь можно довести дело до конца. Записываем после запятой числитель дробной части:

5,03

Видим, что количество цифр после запятой и количество нулей в знаменателе дробной части смешанного числа одинаково.

Десятичная дробь 5,03 читается так:

«Пять целых, три сотых»

«Сотых» потому что в знаменателе дробной части смешанного числа содержится число 100.

Пример 3. Перевести смешанное число в десятичную дробь.

Из предыдущих примеров мы узнали, что для успешного перевода смешанного числа в десятичную дробь, количество цифр в числителе дробной части и количество нулей в знаменателе дробной части должно быть одинаковым.

Перед переводом смешанного числа в десятичную дробь, его дробную часть нужно немного видоизменить, а именно сделать так, чтобы количество цифр в числителе дробной части и количество нулей в знаменателе дробной части было одинаковым.

В первую очередь смóтрим на количество нулей в знаменателе дробной части. Видим, что там три нуля:

Наша задача организовать в числителе дробной части три цифры. Одна цифра у нас уже есть — это цифра 2. Осталось добавить ещё две цифры. Ими будут два нуля. Добавим их перед цифрой 2. В результате количество нулей в знаменателе и количество цифр в числителе станет одинаковым:

Теперь можно заняться переводом этого смешанного числа в десятичную дробь. Записываем сначала цéлую часть и ставим запятую:

и сразу записываем числитель дробной части

3,002

Десятичная дробь 3,002 читается так:

«Три целых, две тысячных»

«Тысячных» потому что в знаменателе дробной части смешанного числа содержится число 1000.

Перевод обыкновенных дробей в десятичные дроби

Обыкновенные дроби, у которых в знаменателе числа 10, 100, 1000 или 10000, тоже можно перевести в десятичные дроби. Поскольку у обыкновенной дроби целая часть отсутствует, сначала записывают 0, затем ставят запятую и записывают числитель дробной части.

Здесь также количество нулей в знаменателе и количество цифр в числителе должно быть одинаковым. Поэтому следует быть внимательным.

Пример 1. Перевести обыкновенную дробь в десятичную дробь.

Целая часть отсутствует, значит сначала записываем 0 и ставим запятую:

Теперь смóтрим на количество нулей в знаменателе. Видим, что там один ноль. И в числителе одна цифра. Значит можно спокойно продолжить десятичную дробь, записав после запятой цифру 5

0,5

В полученной десятичной дроби 0,5 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.

Десятичная дробь 0,5 читается так:

«Ноль целых, пять десятых»

Пример 2. Перевести обыкновенную дробь в десятичную дробь.

Целая часть отсутствует. Записываем сначала 0 и стáвим запятую:

Теперь смóтрим на количество нулей в знаменателе. Видим, что там два нуля. А в числителе только одна цифра. Чтобы сделать количество цифр и количество нулей одинаковым, добавим в числителе перед цифрой 2 один ноль. Тогда дробь примет вид . Теперь количество нулей в знаменателе и количество цифр в числителе одинаково. Значит можно продолжить десятичную дробь:

0,02

В полученной десятичной дроби 0,02 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.

Десятичная дробь 0,02 читается так:

«Ноль целых, две сотых».

Пример 3. Перевести обыкновенную дробь в десятичную дробь.

Записываем 0 и стáвим запятую:

Теперь посчитаем количество нулей в знаменателе дроби . Видим, что там пять нулей, а в числителе только одна цифра. Чтобы сделать количество нулей в знаменателе и количество цифр в числителе одинаковым, нужно в числителе перед цифрой 5 дописать четыре нуля:

Теперь можно продолжить десятичную дробь. Записываем после запятой числитель дроби

0,00005

В полученной десятичной дроби 0,00005 количество цифр после запятой и количество нулей в знаменателе дроби одинаково. Значит дробь переведена правильно.

Десятичная дробь 0,00005 читается так:

«Ноль целых, пять стотысячных».

Перевод неправильных дробей в десятичную дробь

Неправильная дробь это дробь, у которой числитель больше знаменателя.

Бывают неправильные дроби, у которых в знаменателе содержатся числа 10, 100, 1000 или 10000. Такие дроби можно переводить в десятичные. Но перед переводом в десятичную дробь, у таких дробей необходимо выделять цéлую часть.

Пример 1. Перевести неправильную дробь в десятичную.

Дробь является неправильной. Чтобы перевести такую дробь в десятичную, нужно в первую очередь выделить у нее цéлую часть. Вспоминаем, как выделять целую часть у неправильных дробей. Если забыли, советуем вернуться к этой теме и хорошенько изучить её.

Итак, выделим целую часть в неправильной дроби . Напомним, что дробь означает деление — в данном случае деление числа 112 на число 10. Деление нужно выполнить с остатком:

Посмóтрим на этот рисунок и соберём новое смешанное число, подобно детскому конструктору. Частное 11 будет целой частью, остаток 2 — числителем дробной части, делитель 10 — знаменателем дробной части:

Мы получили смешанное число . Его и переведём в десятичную дробь. А как переводить такие числа в десятичные дроби мы уже знаем. Сначала записываем целую часть и ставим запятую:

11,

Теперь посчитаем количество нулей в знаменателе дробной части. Видим, что там один ноль. И в числителе дробной части одна цифра. Значит количество нулей в знаменателе дробной части и количество цифр в числителе дробной части одинаково. Это даёт нам возможность сразу записать после запятой числитель дробной части:

11,2

Значит, неправильная дробь при переводе в десятичную обращается в 11,2

Десятичная дробь 11,2 читается так:

«Одиннадцать целых, две десятых».

Пример 2. Перевести неправильную дробь в десятичную дробь.

Это неправильная дробь, поскольку числитель больше знаменателя. Но её можно перевести в десятичную дробь, поскольку в знаменателе содержится число 100.

В первую очередь выделим целую часть этой дроби. Для этого разделим уголком 450 на 100:

Соберём новое смешанное число — получим . Теперь переведём его в десятичную дробь. Записываем целую часть и ставим запятую:

Теперь посчитаем количество нулей в знаменателе дробной части и количество цифр в числителе дробной части. Видим, что количество нулей в знаменателе и количество цифр в числителе одинаково. Это даёт нам возможность сразу записать числитель дробной части после запятой:

4,50

Значит неправильная дробь при переводе в десятичную обращается в 4,50

При решении задач, если в конце десятичной дроби оказываются нули, их можно отбросить. Давайте и мы отбросим ноль в нашем ответе. Тогда мы получим 4,5

Это одна из интересных особенностей десятичных дробей. Она заключается в том, что нули которые стоят в конце дроби, не придают этой дроби никакого веса. Другими словами, десятичные дроби 4,50 и 4,5 равны и между ними можно поставить знак равенства:

4,50 = 4,5

Возникает вопрос «а почему так происходит?» Ведь на вид 4,50 и 4,5 разные дроби. Весь секрет кроется в основном свойстве дроби, котором мы изучали ранее. Мы попробуем доказать, почему равны десятичные дроби 4,50 и 4,5, но после изучения следующей темы, которая называется «перевод десятичной дроби в смешанное число».

Перевод десятичной дроби в смешанное число

Любая десятичная дробь может быть обратно переведена в смешанное число. Для этого достаточно уметь читать десятичные дроби.

Например, переведём 6,3 в смешанное число. 6,3 это шесть целых и три десятых. Записываем сначала шесть целых:

и рядом три десятых:

Пример 2. Перевести десятичную дробь 3,002 в смешанное число

3,002 это три целых и две тысячных. Записываем сначала три целых

и рядом записываем две тысячных:

Пример 3. Перевести десятичную дробь 4,50 в смешанное число

4,50 это четыре целых и пятьдесят сотых. Записываем четыре целых

и рядом пятьдесят сотых:

Кстати, давайте вспомним последний пример из предыдущей темы. Мы сказали, что десятичные дроби 4,50 и 4,5 равны. Также мы сказали, что ноль можно отбросить. Докажем, что десятичные 4,50 и 4,5 равны. Для этого переведем обе десятичные дроби в смешанные числа.

После перевода в смешанное число десятичная дробь 4,50 обращается в , а десятичная дробь 4,5 обращается в

Имеем два смешанных числа и . Переведём эти смешанные числа в неправильные дроби:

Теперь имеем две дроби и . Теперь вспоминаем основное свойство дроби, которое говорит о том, что при умножении (или делении) числителя и знаменателя дроби на одно и то же число, значение дроби не меняется.

Давайте разделим числитель и знаменатель первой дроби на число 10

Получили , а это есть вторая дробь. Значит и равны между собой и равны одному и тому же значению:

Попробуйте на калькуляторе разделить сначала 450 на 100, а затем 45 на 10. Забавная штука получится.

Перевод десятичной дроби в обыкновенную дробь

Любая десятичная дробь может быть обратно переведена в обыкновенную дробь. Для этого опять же достаточно уметь читать десятичные дроби. Например, переведём 0,3 в обыкновенную дробь. 0,3 это ноль целых и три десятых. Записываем сначала ноль целых:

и рядом три десятых 0 . Ноль по традиции не записывают, поэтому окончательный ответ будет не 0 , а просто .

Пример 2. Перевести десятичную дробь 0,02 в обыкновенную дробь.

0,02 это ноль целых и две сотых. Ноль не записываем, поэтому сразу записываем две сотых

Пример 3. Перевести 0,00005 в обыкновенную дробь

0,00005 это ноль целых и пять сто тысячных. Ноль не записываем, поэтому сразу записываем пять сто тысячных

Пример 4. Перевести 3,5 в обыкновенную дробь

Сначала переведём данную десятичную дробь в смешанное число:

Теперь смешанное число переведём в неправильную (обыкновенную) дробь:

Пример 5. Перевести 1,25 в обыкновенную дробь

Сначала переведём данную десятичную дробь в смешанное число:

Теперь смешанное число переведём в неправильную (обыкновенную) дробь:

4/5 в виде десятичной дроби | Преобразование 4/5 в десятичное число

Преобразование дроби в десятичный формат очень простое и легкое дело. В этой статье мы покажем вам, как именно преобразовать дробь 4/5 в десятичную, и приведем множество примеров, которые помогут вам.

Ищете дроби в десятичных таблицах? Нажмите здесь, чтобы увидеть все наши бесплатные дроби в десятичных таблицах.

Два основных способа представления дроби в виде десятичной дроби:

С калькулятором!
Использование длинного деления.

Очевидно, что самый простой способ — использовать калькулятор. Это быстро и легко. Чтобы представить дробь в виде десятичной дроби, нужно разделить верхнее число дроби (числитель) на нижнее число (знаменатель), и в результате получится десятичная дробь.

Давайте рассмотрим быстрый пример, используя дробь 45 и преобразуя ее в десятичную с помощью калькулятора.

4 &дел; 5 = 0,8

Как видите, одним быстрым вычислением мы преобразовали дробь 45 в ее десятичное выражение, 0,8.

Если у вас нет калькулятора, вы можете представить дробь как десятичную, используя вместо этого старое доброе длинное деление.

  0,800
5 4.000
-0
  40
-40/>   00
  -0/>    000
   -0/>     0000
     0000
      0000
     -0 0/>

(Примечание: в этой статье мы всегда вычисляем до 3 знаков после запятой)

При методе длинного деления целое число вверху является ответом, а число внизу — остатком:

Остаток: 0

Существуют и другие методы преобразования дробей в десятичную версию, но очень маловероятно, что вы когда-либо будете использовать что-то, кроме простого калькулятора или метода деления в длинных числах.

Зачем преобразовывать 4/5 в десятичную дробь?

Нам часто нужно преобразовать дробь, например 4/5, в десятичную, потому что это позволяет представить дробь в понятной форме.

В повседневной жизни вы обнаружите, что работаете с десятичными дробями гораздо чаще, чем с дробями, и это учит ваш мозг понимать десятичные числа.

Итак, если вам нужно выполнить какие-либо обычные арифметические действия, такие как сложение, вычитание, деление или умножение, преобразование 4/5 в десятичную дробь — хороший способ выполнить эти вычисления.

Еще одним преимуществом отображения 4/5 в виде десятичной дроби является возможность сравнения. Очень легко сравнить два десятичных числа и увидеть, какое из них больше, а какое меньше, но когда у вас есть дроби с разными числителями и знаменателями, это не всегда сразу понятно при сравнении.

Тем не менее, и дроби, и десятичные числа имеют место в математике, потому что дроби легко умножать, с ними проще выражать большие десятичные числа, и важно научиться и понимать, как преобразовывать как дробь в десятичную, так и десятичную в дробь.

Практика преобразования дробей в десятичные числа

Как и большинство математических задач, преобразование дробей в десятичные будет становиться для вас намного проще, чем больше вы будете практиковаться в решении задач, и чем больше вы будете практиковаться, тем больше вы поймете.

Независимо от того, являетесь ли вы учеником, родителем или учителем, вы можете создавать свои собственные рабочие листы преобразования дробей в десятичные числа, используя наш генератор рабочих листов дробей в десятичные числа. Этот совершенно бесплатный инструмент позволит вам создавать полностью рандомизированные, дифференцированные задачи с дробями на десятичные числа, которые помогут вам в изучении и понимании дробей.

Преобразование дробей в десятичные числа на примерах

Если вы хотите продолжить изучение того, как преобразовывать дроби в десятичные, взгляните на быстрые вычисления и случайные вычисления на боковой панели справа от этой записи в блоге.

Мы перечислили некоторые из наиболее распространенных дробей в разделе быстрого расчета, а также подборку совершенно случайных дробей, чтобы помочь вам решить ряд проблем.

Каждая статья шаг за шагом покажет вам, как преобразовать дробь в десятичную, и поможет учащимся действительно изучить и понять этот процесс.

Преобразование другой дроби в десятичное число

Введите дробь в поля ниже и нажмите «Рассчитать», чтобы преобразовать дробь в десятичную.

Пожалуйста, используйте инструмент ниже, чтобы вернуться на эту страницу или цитировать/ссылаться на нас во всем, для чего вы используете информацию. Ваша поддержка помогает нам продолжать предоставлять контент!

Преобразование 4 5/8 в десятичную форму

4 5/8 равно 4,625 в десятичной форме. Используйте наш калькулятор преобразования дробей в десятичные, чтобы преобразовать любую дробь в десятичную и узнать, является ли она завершающей или повторяющейся (повторяющейся) десятичной дробью.

Калькулятор / конвертер дробей в десятичные дроби

Введите дробное число:

Пример: 1/2, 2 1/2, 5/3 и т. д. Обратите внимание, что 2 1/2 означает два с половиной = 2 + 1/2 = 2,5

Ответ:

Пошаговое решение:

См. также:

Калькулятор дробей
Калькулятор десятичной дроби
Калькулятор доли в процентах
Фракции Simplifier/Reducer
Калькулятор эквивалентных дробей

Таблица преобразования: дробь в десятичные дюймы и эквивалент в миллиметрах

Чтобы преобразовать дроби в десятичные дроби и миллиметры и наоборот, используйте эту формулу:

1 дюйм = 25,4 мм точно, поэтому . ..

Чтобы преобразовать из дюймов в миллиметры умножьте значение в дюймах на 25,4.

Чтобы преобразовать миллиметры в дюймы, разделите значение в миллиметрах на 25,4.

Проще всего это сделать с помощью приведенной ниже таблицы. Как?

Пример 1

Преобразование 1 1/32 дюйма в миллиметры:

Найдите 1 1/32 и прочитайте справа под столбцом мм! Вы найдете 26,1938. форма).

778 13/648 8.7625798 13/648. 70088 5/16888888888888,5406778 5/168 5/168 5/168 5/168 5/168 5/168 5/168 5/168 5/168 5/168 5/168 5/168 5/168 5/168 5/1688 5.5406 5.

5406 5.5406.0088 21/64

fraction	decimal	mm
1/64	0.0156	0.3969
1/32	0.0313	0.7938
3/64	0.0469	1.1906
1/16	0.0625	1.5875
5/64	0.0781	1.9844
3/32	0.0938	2.3813
7/64	0.1094	2.7781
1/8	0.1250	3. 1750
9/64	0.1406	3.5719
5/32	0.1563	3.9688
11/64	0,1719	4,3656
3/16	0,1875	4,7625
			9.7625.0088 7/32	0.2188	5.5563
15/64	0.2344	5.9531
1/4	0.2500	6.3500
17/64	0.2656	6.7469
9/32	0,2813	7,1438
19/64	0,2969	7,5406
0.3281	8.3344
11/32	0.3438	8.7313
23/64	0.3594	9.1281
3/8	0.3750	9.5250
25/64	0.3906	9.9219
13/32	0.4063	10.3188
27/64	0.4219	10.7156
7/16	0.4375	11.1125
29/64	0.4531	11.5094
15/32	0.4688	11.9063
31/64	0.4844	12.3031
1/2	0.5000	12.7000
33/64	0.5156	13.0969
17/32	0.5313	13.4938
35/64	0. 5469	13.8906
9/16	0.5625	14.2875
37/64	0.5781	14.6844
19/32	0.5938	15.0813
39/64	0.6094	15.4781
5/8	0.6250	15.8750
41/64	0.6406	16.2719
21/32	0.6563	16.6688
43/64	0.6719	17.0656
11/16	0.6875	17.4625
45/64	0.7031	17.8594
23/32	0.7188	18.2563
47/64	0.7344	18.6531
3/4	0.7500	19.0500
49/64	0.7656	19.4469
25/32	0. 7813	19.8438
51/64	0.7969	20.2406
13/16	0.8125	20.6375
53/64	0.8281	21.0344
27/32	0.8438	21.4313
55/64	0.8594	21.8281
7/8	0.8750	22.2250
57/64	0.8906	22.6219
29/32	0.9063	23.0188
59 /64	0.9219	23.4156
15/16	0.9375	23.8125
61/64	0.9531	24.2094
31/32	0.9688	24.6063
63/64	0.9844	25.0031
1	1.0000	25.4000

fraction	decimal	mm
1 1/64	1. 0156	25.7969
1 1/32	1.0313	26.1938
1 3/64	1.0469	26.5906
1 1/16	1.0625	26.9875
1 5/64	1.0781	27.3844
1 3/32	1.0938	27.7813
1 7/64	1.1094	28.1781
1 1/8	1.1250	28.5750
1 9/64	1.1406	28.9719
1 5/32	1.1563	29.3688
1 11/64	1.1719	29.7656
1 3/16	1.1875	30.1625
1 13/64	1.2031	30.5594
1 7/32	1.2188	30.9563
1 15/64	1.2344	31. 3531
1 1/4	1.2500	31.7500
1 17/64	1.2656	32.1469
1 9/32	1.2813	32.5438
1 19/64	1.2969	32.9406
1 5/16	1.3125	33.3375
1 21/64	1.3281	33.7344
1 11/32	1.3438	34.1313
1 23/64	1.3594	34.5281
1 3/8	1.3750	34.9250
1 25/64	1.3906	35.3219
1 13/32	1.4063	35.7188
1 27/64	1.4219	36.1156
1 7/16	1.4375	36.5125
1 29/64	1.4531	36.9094
1 15/32	1. 4688	37.3063
1 31/64	1.4844	37.7031
1 1/2	1.5000	38.1000
1 33/64	1.5156	38.4969
1 17/32	1.5313	38.8938
1 35/64	1.5469	39.2906
1 9/16	1.5625	39.6875
1 37/64	1.5781	40.0844
1 19/32	1.5938	40.4813
1 39/64	1.6094	40.8781
1 5/8	1.6250	41.2750
1 41/64	1.6406	41.6719
1 21/32	1.6563	42.0688
1 43/64	1.6719	42.4656
1 11/16	1. 6875	42.8625
1 45/64	1.7031	43.2594
1 23/32	1.7188	43.6563
1 47/64	1.7344	44.0531
1 3/4	1.7500	44.4500
1 49/64	1.7656	44.8469
1 25/32	1.7813	45.2438
1 51/64	1.7969	45.6406
1 13/16	1.8125	46.0375
1 53/64	1.8281	46.4344
1 27/32	1.8438	46.8313
1 55/64	1.8594	47.2281
1 7/8	1.8750	47.6250
1 57/64	1.8906	48.0219
1 29/32	1. 9063	48.4188
1 59/64	1.9219	48.8156
1 15/16	1.9375	49.2125
1 61/64	1.9531	49.6094
1 31/32	1.9688	50.0063
1 63/64	1.9844	50.4031
2	2.0000	50.8000

fraction	decimal	mm
2 1/64	2.0156	51.1969
2 1/ 32	2.0313	51.5938
2 3/64	2.0469	51.9906
2 1/16	2.0625	52.3875
2 5/64	2.0781	52.7844
2 3/32	2.0938	53.1813
2 7/64	2. 1094	53.5781
2 1/8	2.1250	53.9750
2 9/64	2.1406	54.3719
2 5/32	2.1563	54.7688
2 11/64	2.1719	55.1656
2 3/16	2.1875	55.5625
2 13/64	2.2031	55.9594
2 7/32	2.2188	56.3563
2 15 /64	2.2344	56.7531
2 1/4	2.2500	57.1500
2 17/64	2.2656	57.5469
2 9/32	2.2813	57.9438
2 19/64	2.2969	58.3406
2 5/16	2.3125	58.7375
2 21/64	2.3281	59. 1344
2 11/32	2.3438	59.5313
2 23/64	2.3594	59.9281
2 3/8	2.3750	60.3250
2 25/64	2.3906	60.7219
2 13/32	2.4063	61.1188
2 27/64	2.4219	61.5156
2 7/16	2.4375	61.9125
2 29/64	2.4531	62.3094
2 15/32	2.4688	62.7063
2 31/64	2.4844	63.1031
2 1/2	2.5000	63.5000
2 33/64	2.5156	63.8969
2 17/32	2.5313	64.2938
2 35/64	2.5469	64. 6906
2 9/16	2.5625	65.0875
2 37/64	2.5781	65.4844
2 19/32	2.5938	65.8813
2 39/64	2.6094	66.2781
2 5/8	2.6250	66.6750
2 41/64	2.6406	67.0719
2 21/32	2.6563	67.4688
2 43/64	2.6719	67.8656
2 11/16	2.6875	68.2625
2 45/64	2.7031	68.6594
2 23/32	2.7188	69.0563
2 47/64	2.7344	69.4531
2 3/4	2.7500	69.8500
2 49/64	2.7656	70. 2469
2 25/32	2.7813	70.6438
2 51/64	2.7969	71.0406
2 13/16	2.8125	71.4375
2 53/64	2.8281	71.8344
2 27/32	2.8438	72.2313
2 55/64	2,8594	72,6281
2 7/8	2,8750	73,0250
2 57/649393
2 57/64
2 57/64
./32	2.9063	73.8188
2 59/64	2.9219	74.2156
2 15/16	2.9375	74.6125
2 61/64	2.9531	75.0094
2 31/32	2.9688	75.4063
2 63/64	2.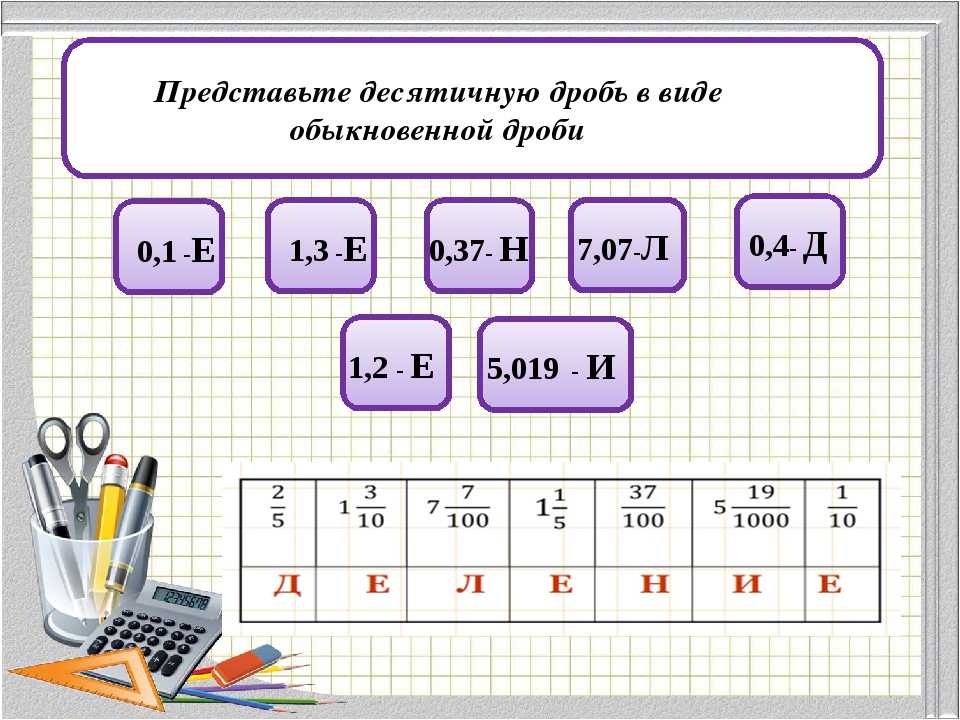 9844	75.8031
3	3.0000	76.2000

Калькулятор десятичной дроби

Пожалуйста, перейдите на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.

Фракция выборки до десятичных расчетов

3 77/15 до десятичного десятичного деть.
1/877 до десятичной
1 13/21 до десятичной
с 1 27/56 до десятичного десятичного детья
4 3/4 до десятичного десятичного детью
2 11/16 до десятичного деть. 3 13/16 до десятичной дроби
1/78 до десятичной дроби

Отказ от ответственности

Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.