Формула арифметической прогрессии и геометрической: Арифметическая и геометрическая прогрессии — урок. Основной государственный экзамен 9 класс, Математика.

Содержание

Арифметическая и геометрическая прогрессии

Арифметическая и геометрическая прогрессия не будет для Вас сложной темой после просмотра следующих примеров. Внимательно ознакомьтесь с ответами среднего уровня сложности и выберите для себя самое необходимое. Если приведенные примеры для Вас тяжелые, прочитайте для начала простые примеры на арифметическую и геометрическую прогрессию (1 уровень).

Группа Б (уровень 2)

Пример 1. В арифметической прогрессии а₈=12,4; a₂₃=4,7. Вычислить сумму а₁₄+a₁₇.
Решение: Представим 14 член прогрессии через 8 и 17 через 23. В виде формул они будут запись
a₁₄=а₈+6d;
a₁₇=a₂₃-6d.
Находим искомую сумму членов прогрессии
a₁₄+a₁₇=a₈+6d+a₂₃-6d=a₈+a₂₃;
a₁₄+a₁₇=12,4+4,7=17,1.
Ответ: сумма равна 17,1.

Пример 2. 2+6*2=24.
Из второго уравнения, учитывая значение первого члена, находим шаг прогрессии
d=24-2a₁=24-2*9=6.
По общей формуле вычисляем 6 член арифметической прогрессии
a₆=a₁+5d=9+5*6=39.
Ответ: a₆=39.

Пример 4. Сумма п первых членов арифметической прогрессии выражается формулой S_n=n²+5n. Вычислить a₁₀.
Решение: Задача идентичное предыдущей, только на этот раз попробуем решить по другой методике. Используем сумму арифметической прогрессии в виде

Подставим в эту формулу заданную зависимость суммы и приравняем коэффициенты при одинаковых степенях n

Это и есть важная формула, из которой находим первый член прогрессии и разность (шаг)

d=2; a₁=5+d/2=6.
Вычисляем 10 член прогрессии
a₁₀=a₁+9d=6+9*2=24.
Ответ: a₁₀=24.

Пример 5. Вычислить сумму всех четных натуральных чисел до 100 включительно.
Решение: Первый элемент последовательности равен a₁=2, последний равен 100. От 1 до 10 имеем 5 четных чисел. В сотни всего 10 десятков то есть 10*5 четных чисел. Если рассуждать по-другому, то половина элементов до 100 четные, половина — нечетные.
100/2=50 – количество четных чисел.
Разница прогрессии равна 2.
Далее подставляем известные значения в формулу и вычисляем

Сумма четных чисел до 100 равна 2550.
Ответ: S₅₀=2550.

Пример 6. Вычислить сумму всех двузначных чисел.
Решение: Номер члена прогрессии будет равен его значению
a₁=1;… a₉₉=99.
Разница прогрессии равна единице d=1. Находим сумму арифметической прогрессии по формуле

Сумма равна 4950.
Ответ: S₉₉=4950.

Пример 7. В арифметической прогрессии а₂+a₁₁=10, а₅+a₆=13. Вычислить разницу прогрессии.
Решение: Аглоритм решения подобных примеров следующий: Выражаем члены прогрессии через один, имеющий наименьший порядковый номер
a₁₁=a₂+9d;
a₅=a₂+3d;
a₆=a₂+4d.
Подставляем ету запись в сумму членов прогрессии
a₂+a₂+9d=2*a₂+9d=10;
a₂+3d+a₂+4d=2*a₂+7d=13.
Есть два уравнения с двумя неизвестными. Для отыскания разницы прогрессии от первого уравнения вычитаем второе
9d-7d=2d=10-13;
2d=-3; d=-1,5.
Ответ: d=-1,5.

Пример 8. В арифметической прогрессии а₂+a₁₁=10, а₅+a₆=13. Вычислить a₁.
Решение: Задача аналогична предыдущей. Выражаем, для удобства, все члены суммы через 1 номер
a₂=a₁+d; a₁₁=a₁+10d;
a₅=a₁+4d; a₆=a₁+5d.
Подставляем в формулы и составляем уравнение
a₁+d+a₁+10d=2*a₁+11d=10;
a₁+4d+a₁+5d=2*a₁+9d=13.
От первого уравнения вычтем второе и найдем шаг прогрессии
11d-9d=2d=10-13=-3.
2d=-3; d=-1,5.
Зная шаг прогрессии, первый ее элемент находим из уравнения
2*a₁+9*(-1,5)=13; 2*a₁=13+13,5=26,5;
a₁=26,5/2=13,25.
Ответ: a₁=13,25.

Пример 9. Вычислить сумму всех двузначных натуральных чисел которые при делении на 3 дают в остатка 2.
Решение: Сначала запишем общую формулу члена прогрессии для данной задачи. Учитывая условие получим зависимость
a[n]=3*n+2.
Первое двузначное число, которое удовлетворяет условию это 11.
a[3]=3*3+2=11.
Последнее число равно 98 и оно соответствует 32 номеру прогрессии
a[32]=3*32+2=98.
Дальше есть выбор из двух вариантов — искать частичную сумму прогрессии или от полной суммы вычесть первых два элемента. Поступим по второй схеме
a₁=3+2=5; a₂=3*2+2=8;

От найденной суммы вычитаем первые два элемента прогрессии
S=1648-5-8=1635.
Ответ: S=1635.

Пример 10. Вычислить сумму всех двузначных натуральных чисел которые при делении на 4 дают в остатка 1.
Решение: Выпишем общую формулу члена прогрессии
a[n]=4*n+1.
Всегда поступайте таким образом для описания прогрессии.
Первое нужное число равно 13. Его легко получить взяв несколько членов прогрессии – 5; 9;13; …
С последним номером немного больше поисков, но можно установить, что это будет 97.
a[3]=13; a[24]=97.
Шаг прогрессии составляет d=4.
Находим сумму двузначных натуральных чисел

Получили в сумме 1210.
Ответ: S=1210.

Пример 11. Вычислить сумму всех нечетных натуральных чисел от 13до 81 включительно.
Решение: Запишем формулу нечетных чисел.
a[n]=2*n+1, n=0; 1; …
Сделаем замену в прогрессии так, чтобы элемент под первым номером был равен 13.
a[n]=2*n+1=13.
Отсюда n=6. Значит новая прогрессия выходит с предыдущей добавлением к индексу n+1=6; n=5.
b[n]=2(n+5)+1.
Найдем под каким номером в прогрессии идет число 81.
2*(n+5)+1=81;
n+5=(81-1)/2=40; n=35.
Итак b[35]=81.
Находим сумму первых 35 членов прогрессии

Следовательно, искомая сумма равна 1645.
Второй метод заключается в нахождении суммы прогрессии a[n] с определенного ее номера. Для этого нужно знать формулу, которую порой нет возможности на контрольных или тестах выводить из формулы суммы прогрессии

Если Вы ее знаете, то в этом случае нужную найти сумму от 6 до 40 члена прогрессии a[n]

И на «закуску» третий способ, который заключается в вычитании из полной суммы прогрессии суммы ее первых членов.

На этом вычисления примера завершены.
Ответ: S=1645.

Пример 12. В арифметической прогрессии а₁₈=12,3; a₃₂=2,8. Вычислить а₂₁+a₂₉.
Решение: Если Вы внимательно просмотрели ответы в предыдущих примерах то знаете как поступить в этом задании. Сначала выражаем 21 и 29 член прогрессии через 18 и 32.
a₂₁=a₁₈+(21-18)d=a₁₈+3d;
a₂₉=a₃₂+(29-32)d=a₃₂-3d.
Легко видеть, что при суммировании разница прогрессии пропадает
a₂₁+a₂₉=a₁₈+a₃₂=12,3+2,8=15,1.
Ответ: сумма равна 15,1.

Пример 13. Сумма п первых членов арифметической прогрессии выражается формулой S_n=13n²+5n. Вычислить разницу прогрессии.
Решение: Подобная задача рассматривали под номером 3, 4. Запишем общую формулу суммы прогрессии и приравняем к заданной

Приравняем коэффициенты при квадрате номера прогрессии

Разница прогрессии равна 26
Ответ: d=26.

Пример 14 Сумма п первых членов арифметической прогрессии выражается формулой S_n=3n²+8n. Вычислить разницу прогрессии.
Решение: Здесь не будем Вас утомлять и по аналогии с предыдущим примером запишем, что коэффициент при квадрате индекса равен половине разницы прогрессии
d/2=3; d=3*2=6.
Видим, наскоько просто найти разницу прогрессии.
Ответ: d=6.

Пример 15. В геометрической прогрессии b_m-n=7,2; b_m=9,6. Вычислить b_m+n
Решение: На вид задания на геометрическую прогрессию сложное.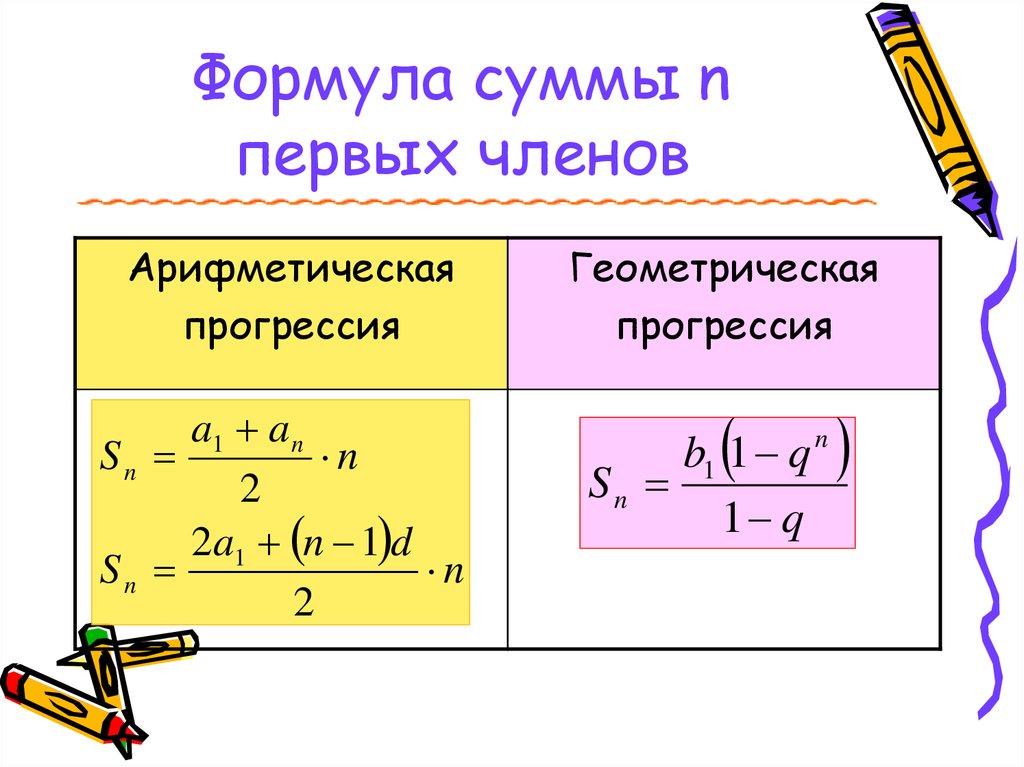 n.

Выполним соответствующие расчеты
b[m-n]=4,2*4,2/6,3=2,8.
Ответ: b[m-n]=2,8.

Пример 17. В арифметической прогрессии а_т+п=1,4; а_т-п=92,8. Вычислить а_т.
Решение: Неизвестный член арифметической прогрессии равен среднему арифметическому соседних элементов. Поскольку а_т+п и а_т-п есть равноудалены елементами прогрессии от а_т , то его находим по формуле

a[m]=(92,8+1,4)/2=47,1.
Ответ a[m]=47,1.

Пример 18. В арифметической прогрессии а_т =8,75; а_т+п=13,8. Вычислить a[m-n]

Решение: Выразим следующие члены прогрессии через предыдущие
a[m+n]=a[m]+n*d;
a[m]=a[m-n]+ n*d.
С первой формулы находим произведение n*d и подставляем во вторую
n*d= a[m+n]-a[m];
a[m-n]=a[m]-n*d=2*a[m]-a[m+n].
Подставим значение в формулу и найдем нужный элемент прогрессии
a[m-n]= 2*8,75-13,8=3,7.
Ответ: a[m-n]=3,7.

Пример 19. В геометрической прогрессии b₂1*b₇=62,7. Вычислить b₁₉ если b₉=5,5.
Решение: Задача одна из сложных среди всех которые рассмотренные здесь, однако на практике решить возможно. Запишем все старшие члены геометрической прогрессии через b₇

Запишем произведение 21 и 7 члена геометрической прогрессии и расписано b₉

Чтобы получить выражение для 19 члена прогрессии нужно произведение b₂₁*b₇ разделить на b₉

С опытом Вы увидите, что в подобных примерах остается делить одни значения на вторые или умножать, примеры где нужно тянуть корни или подносить к степени в геометрических прогрессиях встречаются крайне редко.
Вычисляем b₁₉
b[19]=62,7/5,5=11,4.
Ответ: b[19]=11,4.

Пример 20. Вычислить сумму первых двадцати членов арифметической прогрессии (а_n) если а₆ +а₉+а₁₂+ а₁₅ = 20 .
Решение: Выглядит на первый взгляд непонятно, как с такой записи получить сумму. Однако, если вспомнить формулу суммы арифметической прогрессии, то все что там фигурирует — это первый и последний член суммы, а также их количество. Таким образом следует представить сумму заданных членов прогрессии через первый и последний элемент. Уверяю Вас, что разница прогрессии в расчетах упростится и заданное условие не что иное, как удвоенная сумма первого и 20 члена прогрессии. В этом Вы сейчас наглядно убедитесь. Расписываем первые два слагаемые суммы через a [1], а остальные через a[20].
a[6]=a[1]+5d;
a[9]=a[1]+8d;
a[12]=a[20]-8[d];
a[15]=a[20]-5d.
Просуммировав их всех получим
a[6]+a[9]+a[12]+a[15]=2*a₁+2*a[20].
Формула суммы 20 членов арифметической прогрессии имеет вид

Числитель дроби и является заданной суммой, разделенной на 2 Поэтому сразу выполняем вычисления
S[20]=20/2/2*20=100.
Ответ: S[20]=100.

Пример 21. Сумма первого и пятого членов арифметической прогрессии равна 28,а произведение четвертого и третьего членов 280. Вычислить сумму первых десяти членов прогрессии.
Решение: В этом задании и подобных нужно составлять систему уравнений. Для этого запишем сначала условие задания в виде
a[1]+a[5]=28; a[3]*a[4]=28.
Поскольку 3 член прогрессии является равноудален от 1 и 5, то их среднее арифметическое и будет 3 членом прогрессии
a[3]=(a[1]+a[5])/2=28/2=14.
Произведение распишем через 3 член прогрессии
a[3]*a[4]=a[3]*(a[3]+d)=280;
14*(14+d)=280.
Отсюда находим разницу прогрессии
14+d=280/14=20;
d=20-14=6.
Вычислим 1 и 10 член арифметической прогрессии
a[1]=a[3]-2d=14-2*6=2;
a[10]=a[3]+7d=14+7*2=28.
Есть все необходимые елементы для вычисления суммы прогрессии
S[10]=(2+28)*10/2=150.
Ответ: S[10]=150.

Пример 22. Знайты четыре числа которые образуют геометрическую прогрессию в которой третий член больше первого на 9, а второй больше четвертого на 18. В ответе записать их сумму.
Решение: Запишем условие задачи в виде
b[3]-b[1]=9; b[2]-b[4]=18.
Распишем члены геометрической прогрессии через 1 элемент

Поделив второе уравнения на первое получим знаменатель прогрессии

Из первого уравнения находим 1 член геометрической прогрессии

Все остальные члены прогрессии получаем умножением предыдущего номера на знаменатель.
b[2]=b[1]*q=3*(-2)=-6;
b[3]=b[2]*q=-6*(-2)=12;
b[4]=12*(-2)=-24.
Осталось вычислить сумму членов геометрической прогрессии
S=3-6+12-24=-15.
Ответ: S=-15.

Пример 23. Знаменатель геометрической прогрессии 1/3, третий член геометрической прогрессии 1/9, а сумма всех членов геометрической прогрессии 13/9. Найти количество членов геометрической прогрессии.
Решение: Сумма членов геометрической прогрессии находим по формуле

Найдем первый член прогрессии через 3 и знаменатель.

Подставим значение в формулу суммы и найдем количество суммируемых членов

Итак, получили 3 члена геометрической прогрессии.
Ответ: n=3.

Пример 24. Дано две арифметические прогрессии. Первый и пятый члены первой прогрессии соответственно равны 7 и -5. Первый член второй прогрессии равна 0, а последний 7/2. Вычислить сумму членов второй прогрессии если известно,что третьи члены обеих прогрессий равны между собой.
Решение: Запишем условие примера
a[1]=7;a[5]=-5;
b[1]=0; b[n]=7/2;
a[3]=b[3]; S[n]-?
Найдем 3 член первой прогрессии через среднее арифметическое соседних
a[3]=(a[1]+a[5])/2=(7-5)/2=1.
Учитывая что
b[3]=a[3]=1,
найдем шаг второй прогрессии.
b[3]=b[1]+2*d;
1=0+2*d; d=1/2=0,5.
Найдем номер последнего члена второй прогрессии
b[n]=0+(n-1)d=7/2=3,5;
n-1=3,5/d=3,5/0,5=7;
n=7+1=8.
Вычислим сумму восьми членов прогрессии
S[8]=(0+3,5)*8/2=3,5*4=14.
Ответ: S[8]=14.

После такой практиктики я думаю Вы знаете как находить сумму арифметической и геометрической прогрессии. Если нет ознакомьтесь с примерами изначально (это была шутка).

Похожие материалы:

Арифметическая прогрессия. Формула суммы
Геометрическая прогрессия. Формула суммы
Простые примеры на прогрессию
Арифметическая и геометрическая прогрессии. Простые примеры
Арифметическая и геометрическая прогрессии. Сложные примеры

Если примеры были полезны Вам — посоветуйте их друзьям.

9 класс Урок-презентация «Арифметическая и геометрическая прогрессии» | Презентация к уроку по алгебре (9 класс) по теме:

Урок-презентация по математике в 9 классе по теме: «Арифметическая и геометрическая прогрессии»

Учитель 1 квалификационной категории Церетели Н.К.

Цели урока:

Дидактическая:

— систематизировать знания по изучаемой теме,

— применять теоретический материал при решении задач,

— формировать умение выбирать наиболее рациональные способы решения,

Развивающая:

— развивать логическое мышление,

— продолжить работу по развитию математической речи,

Воспитательная:

— формировать эстетические навыки при оформлении записей,

— формировать у учащихся самостоятельность мышления и интерес к изучению предмета.

Оборудование:

Компьютеры, проектор, презентация: «Арифметическая и геометрическая прогрессии».

Ход урока:

Организационный момент: (слайд 2-5)

Число, классная работа, тема урока.

Изучена данная тема,
Пройдена теории схема,
Вы много новых формул узнали,
Задачи с прогрессией решали.
И вот в последний урок
Нас поведет
Красивый лозунг
“ПРОГРЕССИО — ВПЕРЕД”

Цель нашего урока повторить и закрепить умения и навыки использования основных формул прогрессии при решении задач. Осмыслить и сравнить формулы арифметической и геометрической прогрессии.

Актуализация знаний учащихся: (слайд 6,7)

Что называется числовой последовательностью?

Что называется арифметической прогрессией?

Что называется геометрической прогрессией?

( два ученика записывают формулы на доске )

Сравните арифметическую и геометрическую прогрессии.

Математический диктант: (слайд 12-16)

Какая последовательность?

1) 2; 5; 8; 11;14; 17;…

2) 3; 9; 27; 81; 243;…

3) 1; 6; 11; 20; 25;…

4) –4; –8; –16; –32; …

5) 5; 25; 35; 45; 55;…

6) –2; –4; – 6; – 8; …

Истинно или ложно каждое высказывание?

1. В арифметической прогрессии

2,4; 2,6;… разность равна 2.

2. В геометрической прогрессии

0,3; 0,9;… третий член равен 2,7

3. 11-ый член арифметической прогрессии, у

которой равен 0,2

4. Сумма 5 первых членов геометрической прогрессии,

у которой b =1, q = -2 равна 11.

5. Последовательность чисел, кратных 5,

является геометрической прогрессией.

6. Последовательность степеней числа 3

является арифметической прогрессией.

Проверка ответов.

( один ученик зачитывает ответы, разбор по презентации)

Самостоятельная работа: (слайд 18-26)

1 уровень

(задания по коррекции знаний ученики решают за компьютером, затем проверяют ответы по готовым решениям)

1) Дано: (а n ) арифметическая прогрессия

а1 = 5 d = 3

Найти: а6 ; а10.

2) Дано: (b n ) геометрическая прогрессия

b1= 5 q = 3

Найти: b3 ; b5.

3) Дано: (а n ) арифметическая прогрессия

а4 = 11 d = 2

Найти: а1 .

4) Дано: (b n ) геометрическая прогрессия

b4= 40 q = 2

Найти: b1.

5) Дано: (а n ) арифметическая прогрессия

а4=12,5; а6=17,5

Найти: а5

6) Дано: (b n ) геометрическая прогрессия

b4=12,5; b6=17,5

Найти: b5

2 уровень

(класс решает самостоятельную работу на 15 минут)

1)Дано: (а n ), а1 = – 3, а2 = 4. Найти: а16 – ?

2)Дано: (b n ) , b 12 = – 32, b 13 = – 16. Найти: q – ?

3)Дано: (а n ), а21 = – 44, а22 = – 42.Найти: d — ?

4)Дано: (b n ) , bп > 0, b2 = 4, b4 = 9.Найти: b3 – ?

5)Дано: (а n ), а1 = 28, а21 = 4. Найти: d — ?

6) Дано: (b n ) , q = 2. Найти: b5 – ?

7) Дано: (а n ), а7 = 16, а9 = 30.Найти: а8 –?

3 уровень

(задания по сборнику «Тематические тесты ГИА-9», под редакцией

Лысенко Ф. Ф.)

Проверка ответов

Решение заданий ГИА. (слайд 27)

( разбор задач на доске )

1) Пятый член арифметической прогрессии равен 8,4, а ее десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.

2) Число –3,8 является восьмым членом арифметической прогрессии (ап), а число –11 является ее двенадцатым членом. Является ли членом этой прогрессии число ап =-30,8?

3) Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.

4) В геометрической прогрессии b12 = 315 и b14 =317. Найдите b1.

Применение арифметической и геометрической прогрессии при решении текстовых задач. (слайд 28,29)

Курс воздушных ванн начинают с 15 минут в первый увеличивают время этой процедуры в каждый следующий день на 10 минут. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы максимальная продолжительность была 1 час 45 минут.
Ребенок заболеет ветрянкой, если в его организме окажется не менее 27000 вирусов ветряной оспы. Если заранее не сделана прививка от ветрянки, то каждый день число попавших в организм вирусов утраивается. Если в течении 6 дней после попадания инфекции болезнь не наступает, организм начинает вырабатывать антитела, прекращающие размножение вирусов. Какое минимальное количество вирусов должно попасть в организм, чтобы ребенок, которому не сделали прививку, заболел.

Итог урока:

Анализ и оценка успешности достижения целей урока.

Анализ адекватности самооценки.

Выставление оценок.

Намечается перспектива последующей работы.

Домашнее задание: (слайд 31)

сборник №1247,1253,1313,1324

Урок сегодня завершён,

Но каждый должен знать:

Познание, упорство, труд

К прогрессу в жизни

приведут.

Применение AP и GP: Знайте разницу

Автор ШВЕТА Б. Р.
Последнее изменение 25-01-2023

Применение A.P. и G.P.: Арифметическая прогрессия (AP) представляет собой набор терминов, в которых различия между каждым термином одинаковы. Каждый последующий член геометрической прогрессии (ГП) получается путем умножения обыкновенного отношения на предыдущий член. Используя базовые знания о применении А.П. и О.П., мы можем понимать и применять их в повседневной жизни и находить решения многих проблем более простым способом.

Математика — один из самых важных, но страшных предметов для многих учащихся. Однако при правильном учебном плане и регулярной практике вы можете освоить этот предмет. Maths NCERT Solutions будет самым полезным ресурсом в вашем путешествии. С помощью этих решений вы сможете решить все важные вопросы и получить высокие баллы на экзамене. Кроме того, основные понятия и основы математики будут очищены. Вам также следует скачать NCERT Books for Maths, чтобы решать вопросы по тексту и упражнениям.

{{\text{th}}}}\), вы можете получить члены последовательности. 9{2} \ldots\), где $a$ — первый член, а $r$ — знаменатель последовательности. Для обыкновенного отношения возможны как отрицательные, так и положительные числа.

Геометрическая прогрессия (ГП)

Каждый последующий член геометрической прогрессии получается путем умножения обыкновенного отношения на предыдущий член.

Пример: $6, 12, 24, 48,…$

Геометрическая прогрессия (G.P) Формула

Обыкновенное отношение геометрической прогрессии $r=\frac{a_{2 }}{а_{1}}$ 9{n}-1\right)}{r-1}\)

Сумма бесконечной геометрической формулы $S_{\infty}=\frac{a}{1-r}$, где $r<1 $.

Применение арифметической прогрессии

Некоторые примеры применения арифметической прогрессии в реальной жизни: любая последовательность. Они могут предсказать, когда прибудет следующее такси, если движение идет с постоянной скоростью.

A.P. используется в шаблонах, подобных пирамидам, где все постоянно меняется, и во многих других приложениях.

Проверка счетов в Интернете является основным применением ежедневных арифметических операций. С учетом риска кражи личных данных и онлайн-банкинга в таких обстоятельствах необходимы общие знания фундаментальной математики.

Когда вы берете такси, вы можете испытать реальное применение арифметической прогрессии. С вас будет взиматься первоначальная стоимость, а затем плата за милю или километр после того, как вы сядете в такси. На этой диаграмме изображена арифметическая последовательность, в которой с вас будет взиматься фиксированная (постоянная) ставка плюс начальная ставка за каждый пройденный километр.

Применение геометрической прогрессии

Ниже перечислены некоторые примеры применения геометрической прогрессии в реальной жизни:

Конечная геометрическая последовательность является примером отскока мяча. Высота мяча уменьшается наполовину каждый раз, когда он отскакивает. Если в следующий раз мяч отскочит с высоты $4$ фута, самым высоким отскоком будет $2$ фута, затем $1$, затем $6$ дюймов и так далее, пока не мяч перестает прыгать.
Геометрическая прогрессия обычно используется для расчета заработанных процентов.
Геометрическая прогрессия обычно используется для расчета суммы на нашем сберегательном счете.
Геометрическая прогрессия помогает рассчитать размер экспоненциального роста популяции, например, бактерий в чашке Петри.
Математики постоянно применяют геометрические ряды. Они важны в физике, технике, биологии, экономике, информатике, теории массового обслуживания и финансах, а также во многих других областях.

Примеры применения А.П. и Г.П. .

Пример применения A.P.

Применение арифметической прогрессии

Арифметическая прогрессия представляет собой набор терминов, в которых различия между каждым термином одинаковы.

Из приведенного выше примера мы можем записать арифметическую прогрессию как

$1, 3, 5, 7, 9, 11,…$

Пример применения G.P.:

Геометрическая прогрессия – это набор значений, в котором каждый новый член (за исключением первого) вычисляется путем умножения предыдущего члена на постоянный коэффициент $(r)$.

Например, предположим, что один человек болел гриппом и не смог прикрыть рот, когда к нему пришли два человека, пока он лежал в постели. Они уходят, и болезнь поражает их на следующий день. Представьте, что каждый друг передает вирус двум друзьям на следующий день с помощью одной и той же капельки. Если эта закономерность сохранится и каждый заболевший заразит еще двух человек, мы сможем оценить количество инфицированных.

Пример геометрической прогрессии

Из приведенного выше примера мы можем записать геометрическую прогрессию как 9{\text {th}}\) член данного GP равен $\frac{1}{224}$.

Q.2. Найдите сумму первых $12$ членов АП: $8, 3,–2,…$
Ответ: Данных АП: $8,3, -2, \ldots$
Здесь $a=8$, общая разность $d=3-8=-5$ и $n=12$
Мы знаем,
Сумма $n\ ) членов арифметической прогрессии \(S_{n}=\frac{n}{2}[2 a+(n-1) d]$
$S_{12}=\frac{12}{2}[ 2(8)+(12-1)(-5)]$
$S_{12}=\frac{12}{2}[16+11(-5)]$ 9{{\text{th}}}}\) срок?
Ответ: Из заданного $a=3, l=17, S_{n}=150, a_{n}=$ ?
$S_{n}=\frac{n}{2}[a+l]$
$\Rightarrow 150=\frac{n}{2}[3+17]$
$\Rightarrow 150=\frac{n}{2}[20]$
$\Rightarrow 150=10 n$
$\Rightarrow n=\frac{150}{10}$
$\Rightarrow n= 15$
Теперь $a_{15}=a+(n-1) d$
$\Longrightarrow 17=3+14 d$
$\Longrightarrow 14 d=14$
$\ Стрелка вправо d=\frac{14}{14}=1$
Итак, $a_{4}=a+3 d$
$a_{4}=3+3(1)$ 9{{\text{th}}}}\) срок.
Ответ: Дано: $S_{n}=1050, n=14$ и $a=10$
Мы знаем, что сумма $n$ членов арифметической прогрессии $S_{n}=\frac{n}{2}[2 a+(n-1) d]$
$\Rightarrow 1050=\frac{14}{2}[2(10)+(14) -1) d]$
$\Стрелка вправо 1050=7[20+13 d]$
$\Стрелка вправо \frac{1050}{7}=20+13 d$
$\Стрелка вправо 150- 20=13 d$
$\Стрелка вправо 13 d=130$
$\Стрелка вправо d=\frac{130}{13}$
$\Стрелка вправо d=10$ 9{{\text{й}}}}\) год.

Резюме

Арифметическую прогрессию можно применять в реальной жизни, если понять конкретную схему, в том числе A.P., используемую при прямолинейной амортизации. Геометрические последовательности имеют множество применений в повседневной жизни, но одним из наиболее распространенных является вычисление процентов. Эта статья включает определение, формулы, примеры и приложения А.П. и Г.П.

Эта статья «Применение А.П. и Г.П.» очень помогает в понимании реальных приложений А.П. и Г.П.

Часто задаваемые вопросы по применению A.P. и G.P.

Q.1: Каковы приложения арифметической прогрессии?
Ответ: Некоторые приложения арифметической прогрессии перечислены ниже.
1. A.P. используется при линейном расчете амортизации
2. A.P. используется, когда кто-то ждет такси. AP используется для прогнозирования любой последовательности. Они могут предсказать, когда прибудет следующее такси, если движение идет с постоянной скоростью.
3. A.P. используется в пирамидоподобных паттернах, где вещи постоянно меняются, и во многих других приложениях.
4. Использование A.P. для проверки счетов в Интернете является основным применением ежедневной арифметики.

Q.2: Каково применение геометрической последовательности в реальной жизни?
Ответ: Геометрические последовательности имеют широкое применение в повседневной жизни, но расчет процентов является одним из наиболее распространенных применений. Член ряда вычисляется путем умножения начального значения последовательности на коэффициент, возведенный в степень, меньшую, чем номер члена.

Q.3: Что такое AP и GP? Приведи пример .
Ответ: Арифметическая прогрессия — это набор членов, в которых различия между каждым членом одинаковы.
Каждое слагаемое, кроме первого, получается добавлением заданного целого числа к предыдущему слагаемому в арифметической прогрессии.
Пример: $1, 3, 5, 7, 9,…$
Геометрическая прогрессия — это последовательность, в которой каждый член имеет фиксированное отношение, известное как обыкновенное отношение. Г.П. обозначает геометрическую прогрессию. 9n} – 1} \right)}}{{r – 1}}\)

Мы надеемся, что эта статья «Применение AP и GP» окажется для вас полезной. В случае возникновения каких-либо вопросов, вы можете связаться с нами в разделе комментариев, и мы постараемся их решить.

Арифметические и геометрические последовательности – Последовательности и закономерности – Матигон

В 1682 году астроном Эдмон Галлей наблюдал необычное явление: светящийся белый объект с длинным хвостом, который двигался по ночному небу. Это была комета , маленькая ледяная скала, которая летела в космосе, оставляя за собой след из пыли и льда.

Галлей вспомнил, что другие астрономы наблюдали подобные кометы намного раньше: одна в 1530 году, а другая в 1606 году. Обратите внимание, что разрыв между двумя последовательными наблюдениями одинаков в обоих случаях: годы.

Изображение кометы Галлея,
, сделанное в 1986 году на острове Пасхи. Он обращается вокруг Солнца и проходит мимо Земли примерно каждые 76 лет. Он также предсказал, когда комета будет видна в следующий раз:

1530, 1606 +76, 1682 +76 , 1758 +76 , +76 , +76 , +76 ,

, на самом деле, не является временем, а не временной интернет, а не времена — это время +76 ,

. лет: может варьироваться на один-два года, так как орбита кометы прерывается другими планетами. Сегодня мы знаем, что комета Галлея наблюдалась древними астрономами еще в 240 году до нашей эры!

Изображения кометы Галлея во времени: вавилонская табличка (164 г. до н. э.), средневековый гобелен (1070-е гг.), научный журнал (1910) и советская марка (1986 г.).

Другая группа ученых исследует поведение прыгающего теннисного мяча. Они сбросили мяч с высоты 10 метров и замерили его положение во времени. При каждом отскоке мяч теряет часть своей первоначальной высоты:

Ученые заметили, что после каждого отскока мяч теряет 20% своей высоты. Другими словами, максимальная высота каждого отскока составляет 80% от предыдущего. Это позволило им предсказать высоту каждого следующего отскока:

10, 8 × 0,8, × 0,8 , × 0,8, 4,096 × 0,8, 3,277 × 0,8, 2,621 × 0,8, 2,097 × 0,8, …

Определения

Если вы сравните обе эти задачи, вы можете заметить, что много общего: последовательность кометы Галлея одинакова между последовательными терминами, в то время как последовательность отскоков теннисного мяча имеет то же самое между последовательными терминами.

Последовательности с этими свойствами имеют специальное имя:

Арифметическая последовательность имеет константу разница d между последовательными терминами.

К каждому члену прибавляется или вычитается одно и то же число, чтобы получить следующий.

Геометрическая последовательность имеет постоянное отношение r между последовательными элементами.

Каждое слагаемое умножается или делится на одно и то же число, чтобы получить следующее.

Вот несколько разных последовательностей. Сможете ли вы определить, какие из них являются арифметическими, геометрическими или ни тем, ни другим, и каковы значения числа 9?0154 д и р есть?

2, 4, 8, 16, 32, 64, …

есть , с отношением .

2, 5, 8, 11, 14, 17, …

есть , с отличием .

17, 13, 9, 5, 1, –3, …

есть , с отличием .

2, 4, 7, 11, 16, 22, …

есть .

40, 20, 10, 5, 2,5, 1,25, …

есть , с соотношением .

Чтобы определить арифметическую или геометрическую прогрессию, мы должны знать не только общую разность или отношение, но и начальное значение (называемое а). Здесь вы можете создавать свои собственные последовательности и отображать их значения на графике, изменяя значения a, д и р . Можете ли вы найти какие-либо закономерности?

Арифметическая последовательность

a = ${a}, d = ${d}

${арифметика(a,d,0)}, ${арифметика(a,d,1)}, ${ арифметика(a,d,2)}, ${арифметика(a,d,3)}, ${арифметика(a,d,4)}, ${арифметика(a,d,5)}, …

Геометрическая Последовательность

a = ${b}, r = ${r}

${геометрическая(b,r,0)}, ${геометрическая(b,r,1)}, ${геометрическая(b ,r,2)}, ${геометрический(b,r,3)}, ${геометрический(b,r,4)}, ${геометрический(b,r,5)}, …

Обратите внимание, что все арифметических последовательностей выглядят очень похоже: если разница положительна, то они стабильно , а если разность отрицательна, они стабильно .

Геометрические последовательности, с другой стороны, могут вести себя совершенно по-разному в зависимости от значений a и r :

Если , члены будут , вплоть до бесконечности. Математики говорят, что последовательность расходится с .

Если , условия будут всегда . Мы говорим, что последовательность сходится .

Если , члены будут чередоваться между положительными и отрицательными, в то время как их становится больше.

Вы узнаете больше о конвергенции и дивергенции в последнем разделе этого курса.

Рекурсивные и явные формулы

В предыдущем разделе вы узнали, что рекурсивная формула сообщает вам значение каждого члена как функцию предыдущих членов. Вот рекурсивные формулы для арифметических и геометрических последовательностей:

xn=

Одна из проблем с рекурсивными формулами заключается в том, что, например, чтобы найти 100-й член, мы сначала должны вычислить предыдущие 99 членов, а это может занять много времени. Вместо этого мы можем попытаться найти явную формулу , которая напрямую сообщает нам значение n -го члена.

Для арифметических последовательностей мы должны добавлять d на каждом шаге:

x1=a

x2=a+d

x3=a+d+d

8 x1=

x5=

В n -м члене мы добавляем копии d , так что общая формула

xn=a+d×n−1.

Для геометрических последовательностей мы должны умножать r на каждом шаге:

x1=a

x2=a×r

x3=a×r×r

90=09 60 x4=

81 В n -м члене мы умножаем копии r , поэтому общая формула

xn=a×rn−1.

Вот сводка всех определений и формул, которые вы видели до сих пор:

Арифметическая последовательность имеет первый член a и общую разность d между последовательными членами.

Рекурсивная формула : xn=xn−1+d

Явная формула : xn=a+d×n−1

Геометрическая последовательность имеет первый член a и обыкновенное отношение r между последовательными членами.

Рекурсивная формула : xn=xn−1×r

Явная формула : xn=a×rn−1

Теперь давайте посмотрим на несколько примеров, где все это можно использовать!

Заплати вперед

Вот короткий отрывок из фильма Заплати вперед , где 12-летний Тревор объясняет свою идею сделать мир лучше:

Суть идеи Тревора в том, что если каждый «платит вперед», то один человек может оказать огромное влияние на мир:

Обратите внимание, как количество людей на каждом шаге образует , с обыкновенным отношением :

1, 3 × 3, 9 × 3, × 3, × 3, × 3, …

Используя явную формулу для геометрических последовательностей, мы можно вычислить, сколько новых людей затронуто на любом этапе:

xn =

Число людей увеличивается невероятно быстро. На 10-м шаге вы достигли бы 19 683 новых, а после 22 шагов вы достигли бы большего количества людей, чем в настоящее время живет на Земле.