Арифметическая прогрессия на примерах
Арифметической прогрессией называют последовательность чисел (членов прогрессии )
в которой каждый последующий член отличается от предыдущего на сталое слагаемое, которое еще называют шагом или разницей прогрессии.
Таким образом, задавая шаг прогрессии и ее первый член можно найти любой ее элемент по формуле
1) Каждый член арифметической прогрессии, начиная со второго номера является средним арифметическим от предыдущего и следующего члена прогрессии
Обратное утверждение также верно. Если среднее арифметическое соседних нечетных (четных) членов прогрессии равно члену, который стоит между ними, то данная последовательность чисел является арифметической прогрессией . По этим утверждением очень просто проверить любую последовательность.
Также по свойству арифметической прогрессии, приведенную выше формулу можно обобщить до следующей
В этом легко убедиться, если расписать слагаемые справа от знака равенства
Ее часто применяют на практике для упрощения вычислений в задачах.
2) Сумма n первых членов арифметической прогрессии вычисляется по формуле
Запомните хорошо формулу суммы арифметической прогрессии, она незаменима при вычислениях и довольно часто встречается в простых жизненных ситуациях.
3) Если нужно найти не всю сумму, а часть последовательности начиная с k-го ее члена, то в Вам пригодится следующая формула суммы
4) Практический интерес представляет отыскание суммы n членов арифметической прогрессии начиная с k-го номера . Для этого используйте формулу
На этом теоретический материал заканчивается и переходим к решению распространенных на практике задач.
Пример 1. Найти сороковой член арифметической прогрессии 4;7;…
Решение:
Согласно условию имеем
Определим шаг прогрессии
По известной формуле находим сороковой член прогрессии
Пример2. Арифметическая прогрессия задана третьим и седьмым ее членом . Найти первый член прогрессии и сумму десяти.
Решение:
Распишем заданные элементы прогрессии по формулам
От второго уравнения вычтем первое, в результате найдем шаг прогрессии
Найденное значение подставляем в любое из уравнений для отыскания первого члена арифметической прогрессии
Вычисляем сумму первых десяти членов прогрессии
Не применяя сложных вычислений ми нашли все искомые величины.
Пример 3. Арифметическую прогрессию задано знаменателем и одним из ее членов . Найти первый член прогрессии, сумму 50 ее членов начиная с 50 и сумму 100 первых.
Решение:
Запишем формулу сотого элемента прогрессии
и найдем первый
На основе первого находим 50 член прогрессии
Находим сумму части прогрессии
и сумму первых 100
Сумма прогрессии равна 250.
Пример 4.
Найти число членов арифметической прогрессии, если:
а3-а1=8, а2+а4=14, Sn=111.
Решение:
Запишем уравнения через первый член и шаг прогрессии и определим их
Полученные значения подставляем в формулу суммы для определения количества членов в сумме
Выполняем упрощения
и решаем квадратное уравнение
Из найденных двух значений условии задачи подходит только число 8 . Таким образом сумма первых восьми членов прогрессии составляет 111.
Таким образом сумма первых восьми членов прогрессии составляет 111.
Пример 5.
Решить уравнение
1+3+5+…+х=307.
Решение: Данное уравнение является суммой арифметической прогрессии. Выпишем первый ее член и найдем разницу прогрессии
Найденные величины подставим в формулу суммы прогрессии для отыскания числа слагаемых
Как и в предыдущем задании, выполним упрощения и решим квадратное уравнение
Выбираем более логичное из двух значений . Имеем, что сумма 18 членов прогрессии с заданными величинами а1=1, d=2 равна Sn=307.
На этом знакомство с арифметической прогрессией только начинается. В книгах вы найдете много подобных задач, методика решений которых не была рассмотрена . Приведенного материала должно хватить Вам с головой, чтобы разобраться и решить задачи самостоятельно. Если же нет то обращайтесь и мы Вам поможем с вычислениями.
Похожие материалы:
Арифметическая прогрессия – Определение, Примеры, Формулы 9 класс
Определение числовой последовательности
Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.
Последовательности можно задавать разными способами:
- Словесно — когда правило последовательности объясняется словами:
«Последовательность простых чисел: 4, 6, 10, 19, 21, 33…»
- Аналитически — когда указана формула ее n-го члена: yn = f(n).
Последовательность yn = C называют постоянной или стационарной.
- Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.
Арифметическая прогрессия — (an), задана таким соотношением:
a1 = a, an+1= an + d.Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: a
Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
- Графически — когда график последовательности состоит из точек с абсциссами
1, 2, 3, 4. ..
..
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.
Свойства числовых последовательностей:
- Последовательность {yn} называют возрастающей, если каждый ее член кроме первого больше предыдущего:
y1 < y2 < y3 < … < yn < yn+1 < …
- Последовательность {yn} называют убывающей, если каждый ее член кроме первого меньше предыдущего:
y1 > y2
> y3 > … > yn > yn+1 > …Возрастающие и убывающие последовательности называют монотонными последовательностями.
- Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: yn = yn+T.
 Число T — длина периода.
Число T — длина периода.
Разобраться во всех правилах и быстро щелкать задачки помогут внимательные учителя детской школы Skysmart. Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой, увлекательные математические комиксы и даже онлайн-доска, на которой можно чертить вместе с учителем.
Запишите вашего ребенка на бесплатный вводный урок математики: покажем, как все устроено и вдохновим на учебу.
Запишем числа, которые первые пришли в голову: 7, 19, 0, -1, 2, -11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.
Пример числовой последовательности выглядит так:
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.
N-ный член алгебраической последовательности — это число с порядковым номером n.
Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1, a2,…, a10…, an
.N-ый член последовательности можно задать формулой. Например:
- Формула an = 3n — 5 задает последовательность: −2, 1, 4, 7, 10…
- Формула an = 1 : (n + 2) задает последовательность: 13, 14, 15, 16…
Определение арифметической прогрессии
Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.
Рассмотрим основные определения и как найти арифметическую прогрессию.
Арифметическая прогрессия — это числовая последовательность a1, a2,. .., an,… для которой для каждого натурального n выполняется равенство: .., an,… для которой для каждого натурального n выполняется равенство:an+1= an + d, где d — это разность арифметической прогрессии. |
Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.
Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:
Если известны первый член a1 и n-ый член прогрессии, разность можно найти так:
Арифметическая прогрессия бывает трех видов:
- Возрастающая — арифметическая прогрессия, у которой положительная разность, то есть d > 0.
Пример: последовательность чисел 11, 14, 17, 20, 23… — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.
- Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть d < 0.

Пример: последовательность чисел 50, 48, 46, 44, 43… — это убывающая арифметическая прогрессия, так как ее разность d = –2 < 0.
- Стационарная — арифметическая прогрессия, у которой разность равна нулю, то есть d = 0.
Пример: последовательность чисел 23, 23, 23, 23, 23… — это стационарная арифметическая прогрессия, так как ее разность d = 0.
Свойство арифметической прогрессии
Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.
Рассмотрим пример арифметической прогрессии.
Дано: арифметическая прогрессия (an), где a1 = 0 и d = 2.
Найти: первые пять членов прогрессии и десятый член прогрессии.
Решение арифметической прогрессии:
- Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:
a2 = a1 + d = 0 + 2 = 2;
a
3 = a2 + d = 2 + 2 = 4;a4 = a3 + d = 4 + 2 = 6;
a5 = a4 + d = 6 + 2 = 8.

- Используем общую формулу an = a1 + d * (n — 1).
По условиям задачи n = 10, подставляем в формулу:
a10 = a1 + 2 * (10 — 1) = 0 + 2⋅9 = 18.
Формулы арифметической прогрессии
В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:
- Рекуррентной формулой:
- Формулой n-го члена: an = a1+ d · (n — 1).
- Формулой вида an = kn + b, где k и b — числа, n — число членов последовательности.
Сумма первых n членов арифметической прогрессии (аn) обозначается Sn:
Формулы нахождения суммы n членов арифметической прогрессии:
Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:
Формула n-го члена арифметической прогрессии
Из определения арифметической прогрессии следует, что равенство истинно:
Поэтому:
и т. д.
д.
Значит,
Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.
Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.
Формулу an = a1 + d * (n — 1) называют формулой n-го члена арифметической прогрессии.
Доказательство формулы n-го члена арифметической прогрессии
Формулу n-го члена арифметической прогрессии можно доказать при помощи метода математической индукции.
Пусть дано:
Нужно доказать:
Как доказываем:
- Формула верна при n = 1.
Действительно,
- Предположим, что формула верна при n = k, то есть
- Докажем, что формула верна и при n = k + 1, то есть
- Из условия и предположения получаем:
Согласно принципу математической индукции формула верна для любого натурального числа.
Геометрическая прогрессия
Геометрическая прогрессия — это последовательность (bn), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.
Если последовательность (bn) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:
| bn+1 = bn * q, где q — знаменатель геометрической прогрессии |
Если в геометрической прогрессии (bn) известен первый член b1 и знаменатель q, то можно найти любой член прогрессии:
- b2 = b 1 * q;
- b3 = b2 * q = b1 * q * q = b1 * q²;
- b4 = b1 * q³;
- и т. д.
Общий член геометрической прогрессии bn можно вычислить при помощи формулы:
bn = b1 * qn−1, где n — порядковый номер члена прогрессии, b1 — первый член последовательности, q — знаменатель.
Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.
Пример 2. 3, -3, 3, -3,… — геометрическая прогрессия b = 3, q = -1.
3, -3, 3, -3,… — геометрическая прогрессия b = 3, q = -1.
Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.
Приходите тренироваться: весело, современно и с результатом. В детской школе Skysmart знают, как подружить ребенка с самой коварной темой по математике и повысить оценки в школе.
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Определение 1. Числовую последовательность
a1 , a2 , … an , …
называют арифметической прогрессией, если справедливы равенства
a2 – a1 = a3 – a2 = a4 – a3 =
= … = an – an – 1 =…
Определение 2. Если последовательность чисел
a1 , a2 , … an , …
является арифметической прогрессией, то число d, определенное формулой
d = a2 – a1 = a3 – a2 =
= a4 – a3 = … =
= an – an – 1 =… ,
называют разностью этой арифметической прогрессии.
Из определений 1 и 2 вытекает, что для того, чтобы задать арифметическую прогрессию, нужно знать два числа, например, первый член арифметической прогрессии a1 и разность арифметической прогрессии d. Если числа a1 и d известны, то все остальные члены прогрессии можно найти по формулам:
| (1) |
По этой причине многие задачи на арифметическую прогрессию удобно решать при помощи составления системы уравнений для определения чисел a1 и d .
Из формул (1) вытекает общая формула
| an = a 1 + d ( n – 1), n = 1, 2, 3, … | (2) |
позволяющая по любому номеру n вычислить член арифметической прогрессии an , зная первый член и разность прогрессии. Эта формула носит название формулы общего члена арифметической прогрессии.
Эта формула носит название формулы общего члена арифметической прогрессии.
Из формулы (2) вытекает утверждение, называемое характеристическим свойством арифметической прогрессии. Это свойство формулируется так: — «Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому своих соседних членов». Таким образом, характеристическое свойство арифметической прогрессии утверждает, что при справедливо равенство
Из формулы (2) также вытекают следующие соотношения:
a1 + an = a2 + an – 1 =
= a3 + an – 2 = … ,
которые используются, в частности, при выводе формулы для суммы первых n членов арифметической прогрессии, и при решении различных примеров и задач.
Если для суммы первых n членов арифметической прогрессии ввести обозначение
Sn = a1 + a2 + … + an ,
n = 1, 2, 3, … ,
то будет справедливо равенство
которое называется формулой для суммы первых n членов арифметической прогрессии.
С примерами решений различных задач по теме «Арифметическая прогрессия» можно ознакомиться в нашем учебном пособии «Арифметическая и геометрическая прогрессии».
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Урок 34. формула суммы первых n членов арифметической прогрессии — Алгебра — 9 класс
Напомним, что арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d. Число d называют разностью арифметической прогрессии.
Зная первый член и разность, можно найти любой член арифметической прогрессии по его номеру. Это позволяет сделать формула n-го члена.
Мы выяснили, что последовательность является арифметической прогрессией тогда и только тогда, когда каждый член, начиная со второго, равен среднему арифметическому предыдущего и последующего членов.
 Это свойство арифметической прогрессии называется её характеристическим свойством.
Это свойство арифметической прогрессии называется её характеристическим свойством. Более того, любой член арифметической прогрессии, равен не только среднему арифметическому своих непосредственных соседей, но и среднему арифметическому членов прогрессии, находящихся от него на одинаковом расстоянии. Например, 10-й член арифметической прогрессии равен среднему арифметическому 9-го и 11-го членов, а также 8-го и 12-го, 7-го и 13-го, … 1-го и 19-го.
Обозначим сумму первых n членов арифметической прогрессии как эс энное и запишем эту сумму дважды.
Первый раз – в порядке возрастания номеров членов, во втором случае в порядке убывания.
Сумма каждой пары членов прогрессии, расположенных друг под другом, равна сумме первого и n-го её членов.
Число таких пар равно n. Поэтому, складывая почленно равенства 1 и 2, получаем…
Разделим обе части полученного равенства на 2 и получим формулу суммы n первых членов арифметической прогрессии
Вернёмся к задаче, которую мы решали в начале урока.
 Найдём сумму всех трёхзначных числе, кратных восьми.
Найдём сумму всех трёхзначных числе, кратных восьми.Заметим, что эти числа образуют арифметическую прогрессию с разностью 8.
Первый член – наименьшее трёхзначное число, кратное восьми, 104.
Как известно, на 8 делится число 1000, но оно четырёхзначное. Отнимая от тысячи восемь, получим наибольшее трёхзначное число, кратное восьми, — число 992. Это n-й член данной арифметической прогрессии.
По формуле n-го члена найдём число n – номер этого члена.
Таким образом, сумма всех кратных восьми трёхзначных чисел равна сумме первых 112-ти членов данной арифметической прогрессии.
Конечно, последнее действие придётся выполнить в столбик, но это единственное трудоёмкое вычисление при сложении 112-ти трёхзначных чисел.
По полученной формуле можно находить сумму n первых членов арифметической прогрессии, если известны её первый и n-й члены и количество членов. Но далеко не всегда нам известен n -й член.
Воспользуемся формулой n – го члена арифметической прогрессии и выведем ещё одну формулу суммы – через первый член и разность арифметической прогрессии
Найдём сумму первых 97-ми чисел натурального ряда, кратных 11-ти.

Заметим, что эти числа образуют арифметическую прогрессию с первым членом 11 и разностью 11.
Сумма первых 97-ми чисел натурального ряда, кратных 11-ти, равна сумме первых 97-ми членов этой арифметической прогрессии.
Сумма первых 20-ти членов арифметической прогрессии равна –2040, её первый член равен 2,5. Найдём её разность.
Запишем формулу суммы n первых членов арифметической прогрессии, подставим в неё известные величины, решим полученное уравнение.
Разность арифметической прогрессии равна –11.
Формула суммы n первых членов арифметической прогрессии
Цели: формирование знаний о возможных
вариантах формул для вычисления суммы n первых
членов арифметической прогрессии; развитие
умений сравнивать, сопоставлять, обобщать,
выявлять закономерности; воспитание
уважительного отношения к труду как умственному,
так и физическому; показ тесной связи математики
с физикой, расширение кругозора обучающихся.
Ход урока
1. Фронтальный опрос – подготовка к восприятию нового материала.Что называется числовой последовательностью? Приведите примеры числовых последовательностей.
Какие бывают последовательности? (классификация: конечная, бесконечная, возрастающая, убывающая). Приведите примеры таких последовательностей.
Перечислите способы задания последовательностей. В чём их отличие? Какой из способов наиболее удобен и широко применим и почему?
2. Устная работа.Задание №1.
Дана числовая последовательность (Сn): 17,
14, 11, 8, 5, 2. Дайте полную характеристику этой
последовательности (конечная, убывающая,…).
Выясните, является ли она арифметической
прогрессией и объясните почему? (Да, так как по
определению арифметической прогрессии каждый
член данной последовательности, начиная со
второго, равен предшествующему члену, сложенному
с одним и тем же числом -3. Это число – разность
арифметической прогрессии.). Задайте эту
последовательность тремя способами:
Это число – разность
арифметической прогрессии.). Задайте эту
последовательность тремя способами:
- Рекуррентный: С1=17, Сn+1= Сn–3 – рекуррентная формула.
- Аналитический: Сn=С1–3(n – 1) – формула n – го члена.
- Описательный: пользуясь определением арифметической прогрессии.
Задача. (См. приложение 1, слайд №2) Садовнику нужно изготовить лестницу для сбора яблок из 13 ступеней так, чтобы длина каждой следующей ступени была меньше предыдущей на 2 см. Какой длины брусок нужно взять садовнику для этих перекладин, если первая снизу длиной 50 см?
На слайде №3 демонстрируется садовая лестница.
Создана проблемная ситуация. Обучающиеся
понимают, что для ответа на вопрос задачи
необходимо найти сумму 13-ти слагаемых, а сначала
сами слагаемые: 50, 48, 46, 44, … – последовательность,
которая является арифметической прогрессией по
определению. Это долго и нерационально. Поэтому
надо бы вывести формулу для вычисления суммы n
первых членов арифметической прогрессии.
Это долго и нерационально. Поэтому
надо бы вывести формулу для вычисления суммы n
первых членов арифметической прогрессии.
Записываем в тетрадях тему урока: Формула суммы n первых членов арифметической прогрессии.
Каждую ступеньку можно обозначить как члены арифметической прогрессии: а1, а2,…, а13.
Появляется вторая лестница (слайд №4) и обучающиеся замечают некоторую закономерность: а+а=а+а=…=а+а
Всего 13 пар слагаемых, сумма пар одинакова.
Используя это свойство, найдём сумму длин ступенек 2 лестниц
S = (а+ а)13 и поделим на 2.
494 см = 4 м 94 см
Ответ: садовнику понадобится брусок длиной 4м 94 см.
Таким образом, задача решена и для любого числа n получена формула
Её удобно использовать, если известны а1 и
аn. А если известны а1 и d, то лучше
зная, что аn = а+ d(n – 1), получить другую формулу
(это могут сделать сами обучающиеся).
А если известны а1 и d, то лучше
зная, что аn = а+ d(n – 1), получить другую формулу
(это могут сделать сами обучающиеся).
Sn=
Sn=
Можно пойти другим путём и оставить вывод второй формулы до решения задачи №1. Тогда перед обучающимися снова будет стоять проблема, и они воочию убедятся в необходимости получения и применения новой формулы. Также полезно предложить обучающимся для использования в решении задач следующие формулы:
5. Первичное осмысление нового материала.Задание №2.
Вычислите длину необходимого садовнику бруска, используя 2-ую формулу.
Вывод: что необходимо знать для вычисления суммы n первых членов арифметической прогрессии?
6. Закрепление изученного материала.№369(б).
Задача №1.
Тело в первую секунду прошло 15 м, а в каждую
следующую на 2 м больше, чем в предыдущую.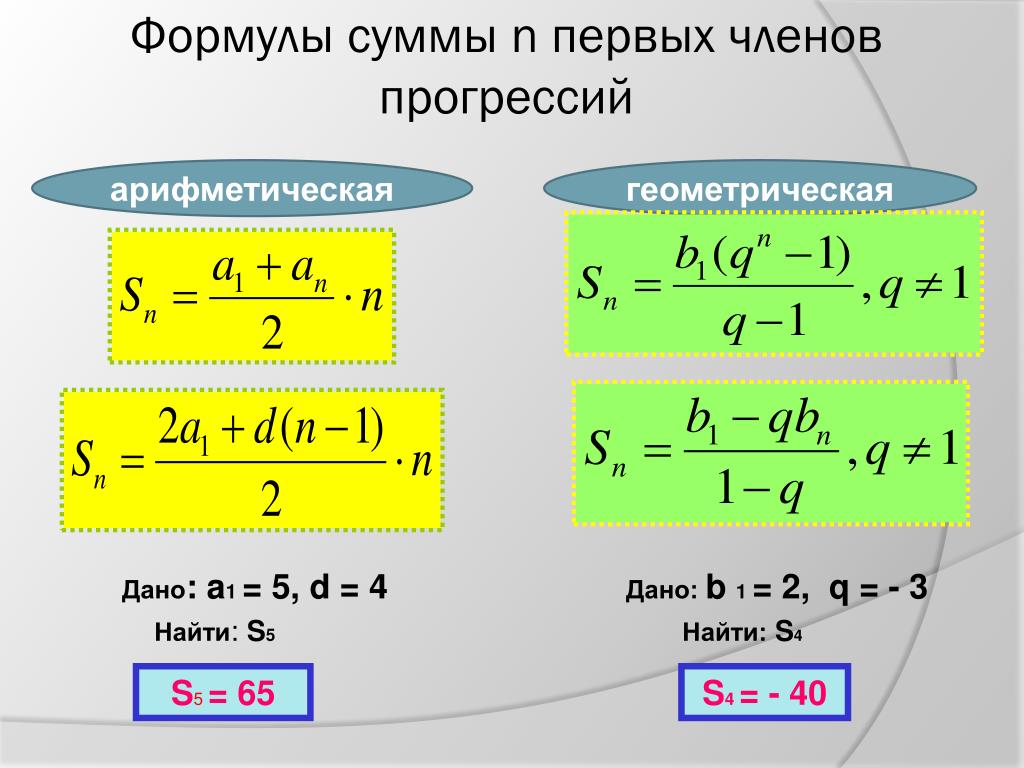 Какой
путь прошло тело за 20 с?
Какой
путь прошло тело за 20 с?
Прочитав задачу, обучающиеся понимают, что необходимо вычислить сумму n первых членов арифметической прогрессии, в которой a1 = 15, d = 2, n =20. Решение оформляется следующим образом.
Решение: выбираем удобную формулу и записываем её общий вид:
Sn=
S20 = = (30 + 2= 680
Ответ: 680 м – путь тела за 20 с.
Задача №2.
Тело падает с башни, высота которой 26 м. Первую секунду оно проходит 2 м, а за каждую следующую секунду – на 3 м больше, чем за предыдущую. Сколько секунд пройдёт до падения тела?
Анализируя условие задачи можно задать
9-тиклассникам вопрос из области физики. Почему
тело во время падения за каждую последующую
секунду проходит путь больше, чем за предыдущую?
Так как они уже знакомы с равноускоренным
движением и причиной падения тел на Землю, то
могут дать полный ответ на поставленный вопрос.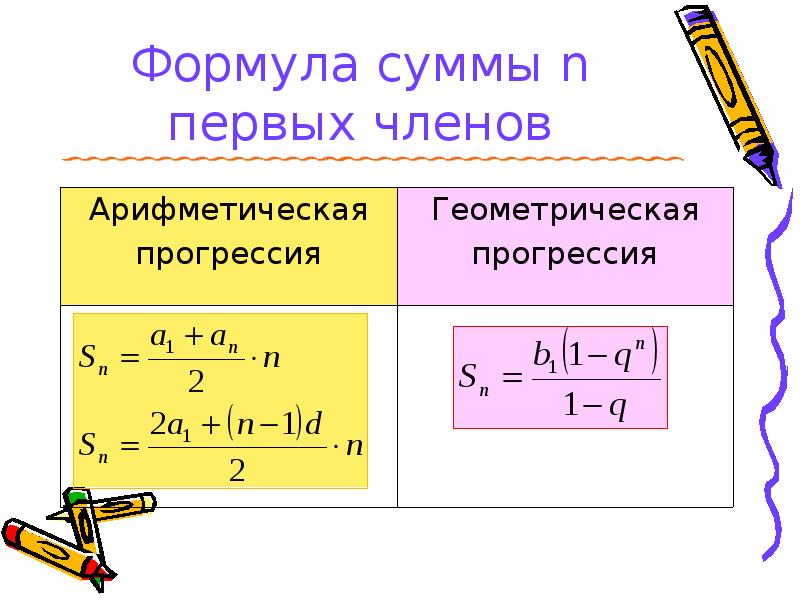 Для активизации внимания обучающихся полезно
показать слайд №5, на котором изображена
Пизанская башня, можно сказать и несколько слов о
ней, дать возможность сделать короткое сообщение
кому-то из обучающихся (прямо на уроке спросить,
что им известно о ней?).
Для активизации внимания обучающихся полезно
показать слайд №5, на котором изображена
Пизанская башня, можно сказать и несколько слов о
ней, дать возможность сделать короткое сообщение
кому-то из обучающихся (прямо на уроке спросить,
что им известно о ней?).
Решение: Sn =
26 =
52 = (4 + 3n – 3)n
52 = 3n2 + n
3n2 + n – 52 = 0
D = 625 = 252 >0 =>2 корня
n1,2 =
n1 = 4, n2 = – 4
Число секунд не может быть отрицательным числом, значит n = 4.
Ответ: тело упадёт через 4 с.
Задача №3. Том Сойер красил забор длиной 105 м, причем день за днем количество выкрашенного за день уменьшалось на одну и ту же величину. За сколько дней был выкрашен забор, если за первые три дня Том выкрасил 36 м забора, а за последние три дня – 27 м?
Решение:
Ответ: 10 дней.
а) а1 и аn; б) а1 и d?
8. Домашнее задание:п.15-17
№371а, №373 – объяснить алгоритм выполнения
№386 – на повторение свойств степени.
Презентация
Арифметическая прогрессия (ЕГЭ — 2021)
На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.
Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.
Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.
Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется \( \displaystyle 6\) блочных кирпичей.
Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?
В данном случае прогрессия выглядит следующим образом:
\( \displaystyle 6;\text{ }5;\text{ }4;\text{ }3;\text{ }2;\ 1\).
Разность арифметической прогрессии \( \displaystyle ~=\text{ }d\text{ }=\text{ }-1\).
Количество членов арифметической прогрессии \( \displaystyle=6\).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).
Разность арифметической прогрессии \( \displaystyle ~=\text{ }d\text{ }=\text{ }-1\).
Количество членов арифметической прогрессии \( \displaystyle=6\).
Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).
Способ 1.
\( \begin{array}{l}{{S}_{n}}=\frac{\left( {{a}_{1}}+{{a}_{n}} \right)\cdot n}{2}\\~~{{S}_{6}}=\frac{\left( 6+1 \right)\cdot 6}{2}=\frac{7\cdot 6}{2}=21\\~\end{array}\)
Способ 2.
\( \displaystyle {{S}_{n}}=\frac{2{{a}_{1}}+d\left( n-1 \right)}{2}\cdot n\)
\( {{S}_{n}}=\frac{2\cdot 6+1\left( 6-1 \right)}{2}\cdot 6=\frac{12+5\cdot 6}{2}=\frac{7\cdot 6}{2}=\frac{42}{2}=21\)
А теперь можно и на мониторе посчитать: сравни полученные значения с тем количеством блоков, которое есть в нашей пирамиде.
Сошлось?
Молодец, ты освоил сумму \( \displaystyle n\)-ных членов арифметической прогрессии.
Конечно, из \( \displaystyle 6\) блоков в основании пирамиду не построишь, а вот из \( \displaystyle 60\)?
Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.
Справился?
Верный ответ – \( \displaystyle 1830\) блоков:
\( \begin{array}{l}{{S}_{n}}=\frac{\left( {{a}_{1}}+{{a}_{n}} \right)\cdot n}{2}\\{{S}_{60}}=\frac{\left( 60+1 \right)\cdot 60}{2}=\frac{61\cdot 60}{2}=61\cdot 30=1830.\end{array}\)
Информатика — Арифметическая прогрессия
1. Определения.
Определение. Арифметическая прогрессия – это такая последовательность
a1, …, an,
что для всех n > 1 разность an,- an-1 постоянна и равна одному и тому же числу d. Это число d называется знаменателем прогрессии.
Таким образом,
a2 = a1+d;
a3 = a2+d = a1+d + d = a1+2d;
a4 = a3+d = a1+2d + d = a1+3d;
….
an = an-1+d = a1+(n-2)*d + d = a1+(n-1)*d;
Замечание. Иногда арифметической прогрессией называют бесконечную последовательность, у которой разность между соседними числами постоянна. Тогда конечную последовательность a1, …, anназывают начальным участком арифметической прогрессии.
2. Сумма арифметической прогрессии
Задача. Дана арифметическая прогрессия a1, …, an; знаменатель прогрессии равен d. Найти сумму
S = a1+ …+ an
Решение.
Имеем:
S = a1+ …+ an (1)
Запишем слагаемые в сумме в обратном порядке:
S = an+ …+ a1 (2)
Сложим (1) и (2) и сгруппируем в правой части слагаемые, которые стоят друг под другом:
2S = (a1+ an ) + (a2+ an-1 ) + (a3+ an-2 ) +…+ (an+ a1 ) (3)
Докажем, что все слагаемые в правой части равенства (3) равны. Действительно, k—е слагаемое имеет вид:
Действительно, k—е слагаемое имеет вид:
ak+ an+1-k ; k = 1, … , n
Воспользуемся формулой (см. раздел 1)
ak = a1+(k-1)*d (4)
Тогда
an+1-k = a1+((n+1-k)-1)*d = a1+(n-k)*d (5)
Складываем (4) и (5). Получим:
ak+ an+1-k = a1+(k-1)*d + a1+(n-k)*d = 2*a1+(n-1)*d (6)
Итак, в правой части формулы (3) есть n слагаемых и каждое из них равно
2*a1+(n-1)*d = a1+ an (7)
Поэтому из (3) и (7) получаем:
2S = n* (2*a1+(n-1)*d) = n*(a1+ an)
Отсюда получаем две формулы для суммы арифметической прогрессии.
Формула 1.
S = n* (2*a1+(n-1)*d)/2 = n* a1+n*(n-1)*d/2
Формула 2.
S = n*(a1+ an)/2
3. Пример: сумма n первых натуральных чисел.
Рассмотрим последовательность 1, …, n .Это – арифметическая прогрессия со знаменателем 1. Поэтому по Формуле 2 для суммы 1 + …+ n получаем:
1 + …+ n = n*(n+1)/2
Формула 1, естественно, даст тот же результат. 🙂
Сумма первых n членов арифметической последовательности
Предположим, что последовательность номеров
арифметика
(то есть увеличивается или уменьшается на постоянную величину для каждого члена), и вы хотите найти сумму первых
п
термины.
Обозначим эту частичную сумму через S п . потом
S
п
знак равно
п
(
а
1
+
а
п
)
2
,
где
п
это количество терминов,
а
1
это первый член и
а
п
это последний срок.
Сумма первых п члены арифметической последовательности называются арифметический ряд .
Пример 1:
Найдите сумму первых 20 члены арифметического ряда, если а 1 знак равно 5 а также а 20 знак равно 62 .
S 20 знак равно 20 ( 5 + 62 ) 2 S 20 знак равно 670
Пример 2:
Найдите сумму первых
40
термины арифметики последовательность
2
,
5
,
8
,
11
,
⋯
.
Сначала найдите 40 th срок:
а 40 знак равно а 1 + ( п — 1 ) d знак равно 2 + 39 ( 3 ) знак равно 119
Затем найдите сумму:
S п знак равно п ( а 1 + а п ) 2 S 40 знак равно 40 ( 2 + 119 ) 2 знак равно 2420
Пример 3:
Найдите сумму:
∑ k знак равно 1 50 ( 3 k + 2 )
Первая находка а 1 а также а 50 :
а 1 знак равно 3 ( 1 ) + 2 знак равно 5 а 50 знак равно 3 ( 50 ) + 2 знак равно 152
Затем найдите сумму:
S k знак равно k ( а 1 + а k ) 2 S 50 знак равно 50 ( 5 + 152 ) 2 знак равно 3925
Смотрите также: сигма-обозначение ряда а также n-й член арифметической последовательности
Сумма N условий AP | Решенные примеры | Алгебра
Содержание
Мы в Cuemath считаем, что математика — это жизненный навык. Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Студенты могут изучить огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.
Наши эксперты по математике сосредотачиваются на том, «почему» стоит за «что». Студенты могут изучить огромное количество интерактивных листов, наглядных пособий, симуляторов, практических тестов и многого другого, чтобы глубже понять концепцию.
Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня! и поучаствуйте в онлайн-классе Cuemath LIVE вместе со своим ребенком.
ВведениеВ 19 годах в Германии преподавали математику для 10 класса.
Учитель попросила своих учеников просуммировать все числа от \ (1 \) до \ (100 \).
Студенты пытались подсчитать сумму всех этих чисел.
Один мальчик выкрикнул ответ \ (5050 \), в то время как другие ученики все еще находились на начальных этапах подсчета суммы.
Этим мальчиком был великий немецкий математик Карл Фридрих Гаусс.
Как он так быстро пришел к сумме?
Ну, он заметил, что члены, равноотстоящие от начала и до конца ряда, имеют постоянную сумму, равную \ (101 \).
Мы видим, что в последовательности \ (1,2,3 ,.{th} \) срок, \ (a_n \) известен:
\ [S_n = \ frac {n} {2} [a_1 + a_n] \]
Как получить эти формулы?
Мы будем использовать ту же логику, которую использовал выше Карл Фридрих Гаусс.
Рассмотрим арифметическую прогрессию с \ (n \) членами:
\ [a, a + d, a + 2d, … (a + (n-2) d), (a + (n-1) d) \]
Сумма \ (n \) членов этой прогрессии составляет:
\ [S_n = a + (a + d) + \ ldots + (a + (n-2) d) + (a + (n-1) d) \, \, \, \, \, \, \ rightarrow (1) \]
Путем изменения порядка членов этого уравнения:
\ [S_n = (a + (n-1) d) + (a + (n-2) d) + \ ldots + (a + d) + a \, \, \, \, \, \, \ rightarrow (2 ) \]
Мы видим, что сумма соответствующих членов уравнения (1) и уравнения (2) дает ту же сумму, которая равна \ (2a + (n-1) d \).
Мы знаем, что в указанном выше AP есть полностью \ (n \) терминов.
Итак, сложив (1) и (2), мы получаем:
\ [\ begin {align}
2S_n & = n (2a + (n-1) d) \\ [0,3 см]
S_n & = \ frac {n} {2} (2a + (n-1) d)
\ end {align} \]
Вышеупомянутая сумма уравнения арифметической прогрессии может быть записана как:
\ [\ begin {align}
S_n & = \ frac {n} {2} (2a + (n-1) d) \\ [0,3 см]
S_n & = \ frac {n} {2} (a + a + (n-1) d) \\ [0.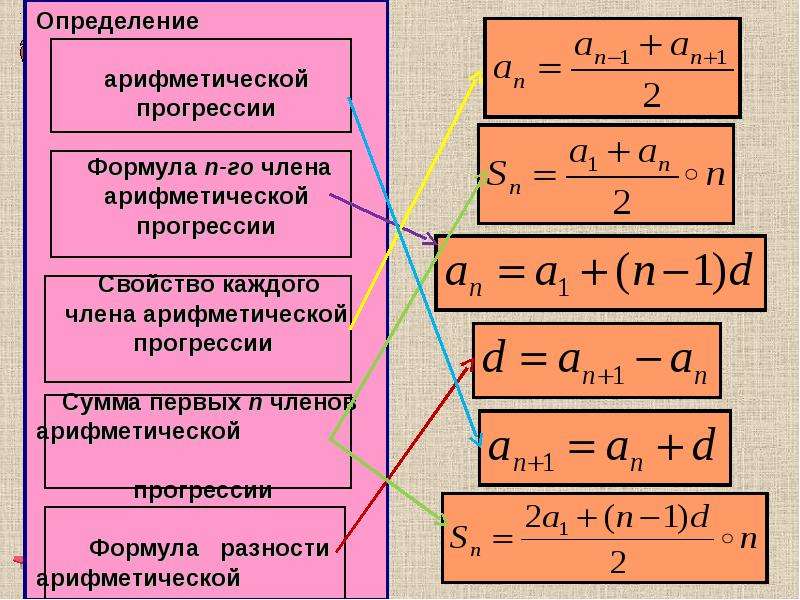 3см]
3см]
S_n & = \ frac {n} {2} (a_1 + a_n) [\ потому что a_n = a + (n-1) d \ text {и} a = a_1]
\ end {align} \]
Таким образом, сумма уравнений арифметической прогрессии равна:
| \ (\ begin {align} S_n & = \ frac {n} {2} (2a + (n-1) d) \\ [0,3 см] S_n & = \ frac {n} {2} (a_1 + a_n) \ end {align} \) |
Давайте взглянем на следующую блок-схему, чтобы получить представление о формуле, которая должна использоваться для нахождения суммы арифметической прогрессии в соответствии с доступной нам информацией.
CLUEless по математике? Узнайте, как учителя CUEMATH объяснят вашему ребенку Sum of n терминов AP , используя интерактивные модели и рабочие листы, чтобы им больше никогда не пришлось запоминать что-либо по математике!
Изучите интерактивные и персонализированные онлайн-классы Cuemath, чтобы сделать своего ребенка экспертом по математике. Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!
Забронируйте БЕСПЛАТНОЕ пробное занятие сегодня!
Сумма AP натуральных чисел
AP натуральных чисел:
\ [1,2,3 ,…, п, … \]
Найдем сумму \ (n \) членов AP натуральных чисел.
Это будет:
\ [1 + 2 + 3 + … + n \]
Мы можем найти сумму двумя способами, используя две приведенные выше формулы.
Метод 1Здесь,
Первый член — \ (a = 1 \).
Общая разница: \ (d = 1 \).
Количество терминов \ (n \).
Подставьте все эти значения в первую сумму формулы AP:
\ [\ begin {align}
S_n & = \ frac {n} {2} (2a + (n-1) d) \\ [0.3см]
S_n & = \ frac {n} {2} (2 (1) + (n-1) 1) \\ [0,3 см]
S_n & = \ frac {n} {2} (2 + n-1) \\ [0,3 см]
S_n & = \ frac {n (n + 1)} {2}
\ end {align} \]
Здесь,
Первый член — \ (a_1 = 1 \).
n-й член вышеуказанного AP равен \ (a_n = n \).
Подставьте все эти значения во вторую сумму формулы AP:
\ [\ begin {align}
S_n & = \ frac {n} {2} (a_1 + a_n) \\ [0,3 см]
S_n & = \ frac {n} {2} (1 + n) \\ [0.3см]
S_n & = \ frac {n (n + 1)} {2}
\ end {align} \]
Таким образом, из описанных выше методов сумма AP натуральных чисел равна:
| Сумма AP натуральных чисел \ (= \ dfrac {n (n + 1)} {2} \) |
Сумма бесконечных AP
Рассмотрим пример суммы бесконечной AP.
\ [2+ 5 + 8 + … \]
Здесь первый член \ (a = 2 \).
Общая разница: \ (d = 3 \).
Количество терминов: \ (n = \ infty \).
Подставьте все эти значения в формулу суммы AP:
\ [\ begin {align}
S_n & = \ frac {n} {2} (2a + (n-1) d) \\ [0,3 см]
S_n & = \ frac {\ infty} {2} (2 (2) + (\ infty-1) 3) \\ [0,3 см]
S_n & = \ infty
\ end {align} \]
Мы обнаружили, что сумма бесконечных AP равна \ (\ infty \), когда
\ (d> 0 \).
Таким же образом сумма бесконечных AP равна \ (- \ infty \), когда
\ (d <0 \).
Таким образом,
| \ (\ text {Сумма бесконечных чисел} A P = \ left \ {\ begin {array} {ll} \ infty, & \ text {if} \ quad d> 0 \ [0,3 см] — \ infty, & \ text {if} \ quad d <0 \ end {array} \ right. \) |
Важные примечания
- Сумма арифметической прогрессии, первый член которой равен \ (a \), а общая разница равна \ (d \), может быть вычислена по одной из следующих формул:
\ [\ begin {align}
S_n & = \ frac {n} {2} (2a + (n-1) d) \\ [0.3см]
S_n & = \ frac {n} {2} (a_1 + a_n)
\ end {align} \] Сумма AP натуральных чисел \ (n \) равна:
\ [\ Dfrac {n (n + 1)} {2} \]Сумма бесконечных AP:
\ [\ left \ {\ begin {array} {ll}
\ infty, & \ text {if} \ quad d> 0 \ [0,3 см]
— \ infty, & \ text {if} \ quad d <0
\ end {array} \ right.
\]
Мы можем узнать сумму AP, используя следующий «Калькулятор суммы AP», введя первый член, общую разницу и количество членов.
Помогите своему ребенку набрать больше баллов с помощью запатентованного БЕСПЛАТНОГО диагностического теста Cuemath. Получите доступ к подробным отчетам, индивидуальным планам обучения и БЕСПЛАТНОЙ консультации. Попытайтесь проверить сейчас.
Решенные примеры
Вычислите следующую сумму:
\ [S = \ underbrace {190 + 167 + 144 + 121 + \ ldots} _ {20 \ text {terms}} \]
Решение:
Нам неизвестен последний член в этой последовательности, поэтому мы будем использовать первую формулу для вычисления этой суммы, которая составляет:
\ [S = \ frac {n} {2} (2a + (n-1) d) \]
Здесь имеем:
\ [a = 190, \ quad d = -23, \ quad n = 20 \]
Подставляя все эти значения в формулу выше,
\ [\ begin {align} S & = \ frac {20} {2} (2 (190) + (20-1) (- 23)) \\ [0. 3см]
3см]
& = 10 (380-437) \\ [0,3 см]
& = 10 (-57) \\ [0,3 см]
& = — 570
\ end {align} \]
Рассмотрим следующую точку доступа:
\ [24,21,18, \ ldots \]
Сколько членов этой AP нужно учесть, чтобы их сумма была \ (78 \)?
Решение:
Обозначим количество членов, дающих сумму \ (78 \), как \ (n \).
У нас:
\ [a = 24, d = -3, \ quad S = 78 \]
Подставляя все эти значения в первую формулу суммы AP,
\ [\ begin {align}
S = & \ frac {n} {2} (2 a + (n-1) d) \\ [0.{2} -17 n + 52 = 0 \\ [0,3 см]
\ Rightarrow & (n-4) (n-13) = 0 \\ [0,3 см]
\ Rightarrow & n = 4, \, \, 13
\ end {align}
\]
| \ (\ следовательно \ begin {align} \ text {Сумма 4-х членов} & = 78 \\ \ text {Сумма 13 членов} & = 78 \\ \ end {align} \) |
Учитывая \ (a = 5 \), \ (d = 3 \) и \ (a_n = 50 \), найдите значение \ (S_n \). {th} \) член AP, мы используем следующую формулу, чтобы найти сумму:
{th} \) член AP, мы используем следующую формулу, чтобы найти сумму:
\ [\ begin {align} S_n & = \ frac {n} {2} (a_1 + a_n) \\ [0,3 см] S_n & = \ frac {16} {2} (5 + 50) \\ [0,3 см ] S_n & = 8 (55) \\ [0,3 см] S_n & = 440 \ end {align} \]
Сложные вопросы
- Найдите сумму \ (7 + 10 \ frac {1} {2} +14+ \ ldots + 84 \).
- Найдите сумму \ (\ frac {1} {15}, \ frac {1} {12}, \ frac {1} {10}, \ ldots, \ text {to} 13 \ text {terms.} \)
- Сколько членов АП \ (9,17,25, \ ldots \).нужно взять, чтобы получить сумму \ (636 \)?
Образцы материалов олимпиады по математике
IMO (Международная олимпиада по математике) — это конкурсный экзамен по математике, который ежегодно проводится для школьников. Он побуждает детей развивать свои навыки решения математических задач с точки зрения соревнований.
Вы можете БЕСПЛАТНО скачать образцы работ по оценкам ниже:
Чтобы узнать больше об олимпиаде по математике щелкните здесь
Часто задаваемые вопросы (FAQ)
1. Какова сумма арифметической последовательности?
Сумма арифметической последовательности — это «сумма первых \ (n \) членов» последовательности, и ее можно найти с помощью одной из следующих формул:
\ [\ begin {align}
S_n & = \ frac {n} {2} (2a + (n-1) d) \\ [0.{th} \) срок
\ (S_n \) = сумма первых \ (n \) членов.
2. Какова сумма n членов AP?
Сумма арифметической последовательности — это «сумма первых \ (n \) членов» последовательности, и ее можно найти с помощью одной из следующих формул:
\ [\ begin {align}
S_n & = \ frac {n} {2} (2a + (n-1) d) \\ [0,3 см]
S_n & = \ frac {n} {2} (a_1 + a_n)
\ end {align} \]
Здесь,
\ (a = a_1 \) = первый член
\ (d \) = общая разница
\ (n \) = количество терминов
\ (a_n = n ^ {th} \) срок
\ (S_n \) = сумма первых \ (n \) членов. {th} \) срок
{th} \) срок
\ (S_n \) = сумма первых \ (n \) членов.{n} -1 \ right)} {r-1} \]
Здесь
\ (a \) = первый член
\ (r \) = обыкновенное отношение
\ (n \) = количество терминов
\ (S_n \) = сумма первых \ (n \) членов.
4. Какова формула \ (S_n \)?
Мы используем несколько формул при нахождении суммы ряда, представленного как \ (S_n \).
- Если серия AP, то мы используем следующие формулы, чтобы найти сумму.
\ [\ begin {align}
S_n & = \ frac {n} {2} (2a + (n-1) d) \\ [0.{n} -1 \ right)} {r-1} \]
Здесь
\ (a \) = первый член
\ (r \) = обыкновенное отношение
\ (n \) = количество терминов
\ (S_n \) = сумма первых \ (n \) членов.
Арифметических последовательностей и серии
Арифметические последовательности
Арифметическая последовательность: последовательность чисел, в которой каждое последующее число является суммой предыдущего числа и некоторой константы d . , Или арифметическая прогрессия, используемая при обращении к арифметической последовательности., представляет собой последовательность чисел, в которой каждое последующее число является суммой предыдущего числа и некоторой константы d .
, Или арифметическая прогрессия, используемая при обращении к арифметической последовательности., представляет собой последовательность чисел, в которой каждое последующее число является суммой предыдущего числа и некоторой константы d .
an = an − 1 + d Арифметическая последовательность
И поскольку an − an − 1 = d, константа d называется общей разностью Константа d , которая получается вычитанием любых двух последовательных членов арифметической последовательности; an − an − 1 = d .. Например, последовательность положительных нечетных целых чисел является арифметической последовательностью,
1,3,5,7,9,…
Здесь a1 = 1, а разница между любыми двумя последовательными членами равна 2.Мы можем построить общий член an = an − 1 + 2, где,
a1 = 1a2 = a1 + 2 = 1 + 2 = 3a3 = a2 + 2 = 3 + 2 = 5a4 = a3 + 2 = 5 + 2 = 7a5 = a4 + 2 = 7 + 2 = 9 ⋮
В общем, учитывая первый член a1 арифметической последовательности и его общую разницу d , мы можем написать следующее:
a2 = a1 + da3 = a2 + d = (a1 + d) + d = a1 + 2da4 = a3 + d = (a1 + 2d) + d = a1 + 3da5 = a4 + d = (a1 + 3d) + d = a1 + 4d ⋮
Отсюда мы видим, что любая арифметическая последовательность может быть записана в терминах ее первого элемента, общей разности и индекса следующим образом:
an = a1 + (n − 1) d Арифметическая последовательность
Фактически, любой общий член, линейный в n , определяет арифметическую последовательность.
Пример 1
Найдите уравнение для общего члена данной арифметической последовательности и используйте его, чтобы вычислить его 100 -й член : 7,10,13,16,19,…
Решение:
Начните с поиска общей разницы,
d = 10-7 = 3
Обратите внимание, что разница между любыми двумя последовательными членами равна 3. Последовательность действительно является арифметической прогрессией, где a1 = 7 и d = 3.
an = a1 + (n − 1) d = 7 + (n − 1) ⋅3 = 7 + 3n − 3 = 3n + 4
Следовательно, мы можем написать общий член an = 3n + 4. Уделите минуту, чтобы убедиться, что это уравнение описывает заданную последовательность. Используйте это уравнение, чтобы найти член 100 th :
а100 = 3 (100) + 4 = 304
Ответ: an = 3n + 4; а100 = 304
Общая разница арифметической последовательности может быть отрицательной.
Пример 2
Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 75 -го члена: 6,4,2,0, −2,…
Решение:
Начните с поиска общей разницы,
d = 4−6 = −2
Затем найдите формулу для общего члена, здесь a1 = 6 и d = −2.
an = a1 + (n − 1) d = 6 + (n − 1) ⋅ (−2) = 6−2n + 2 = 8−2n
Следовательно, an = 8−2n и член 75 th можно рассчитать следующим образом:
a75 = 8−2 (75) = 8−150 = −142
Ответ: an = 8−2n; а100 = -142
Термины между данными членами арифметической последовательности называются средними арифметическими. Термины между данными членами арифметической последовательности.
Пример 3
Найдите все члены арифметической последовательности между a1 = −8 и a7 = 10. Другими словами, найдите все средние арифметические значения между 1 и 7 членами.
Другими словами, найдите все средние арифметические значения между 1 и 7 членами.
Решение:
Начните с поиска общей разницы d . В этом случае нам дается первый и седьмой член:
an = a1 + (n − 1) d Используйте n = 7. a7 = a1 + (7−1) da7 = a1 + 6d
Подставляем a1 = −8 и a7 = 10 в приведенное выше уравнение, а затем решаем общую разность d .
10 = −8 + 6d18 = 6d3 = d
Затем используйте первый член a1 = −8 и общую разность d = 3, чтобы найти уравнение для n -го члена последовательности.
an = −8 + (n − 1) ⋅3 = −8 + 3n − 3 = −11 + 3n
При an = 3n − 11, где n — положительное целое число, найдите пропущенные члены.
a1 = 3 (1) −11 = 3−11 = −8a2 = 3 (2) −11 = 6−11 = −5a3 = 3 (3) −11 = 9−11 = −2a4 = 3 (4) — 11 = 12−11 = 1a5 = 3 (5) −11 = 15−11 = 4a6 = 3 (6) −11 = 18−11 = 7} среднее арифметическое a7 = 3 (7) −11 = 21−11 = 10
Ответ: −5, −2, 1, 4, 7
В некоторых случаях первый член арифметической последовательности может не указываться.
Пример 4
Найдите общий член арифметической последовательности, где a3 = −1 и a10 = 48.
Решение:
Чтобы определить формулу для общего члена, нам нужны a1 и d. Линейная система с этими переменными может быть сформирована с использованием данной информации и an = a1 + (n − 1) d:
{a3 = a1 + (3−1) da10 = a1 + (10−1) d⇒ {−1 = a1 + 2d48 = a1 + 9d Используйте a3 = −1. Используйте a10 = 48.
Исключите a1, умножив первое уравнение на -1, и прибавьте результат ко второму уравнению.
{−1 = a1 + 2d48 = a1 + 9d ⇒ × (−1) + {1 = −a1−2d48 = a1 + 9d¯ 49 = 7d7 = d
Подставляем d = 7 в −1 = a1 + 2d, чтобы найти a1.
−1 = a1 + 2 (7) −1 = a1 + 14−15 = a1
Затем используйте первый член a1 = −15 и общую разность d = 7, чтобы найти формулу для общего члена.
an = a1 + (n − 1) d = −15 + (n − 1) ⋅7 = −15 + 7n − 7 = −22 + 7n
Ответ: an = 7n − 22
Попробуй! Найдите уравнение для общего члена данной арифметической последовательности и используйте его для вычисления его 100 -го члена : 32,2,52,3,72,…
Ответ: an = 12n + 1; а100 = 51
Арифметическая серия
Арифметический ряд Сумма членов арифметической последовательности. представляет собой сумму членов арифметической последовательности. Например, сумма первых 5 членов последовательности, определенной как an = 2n − 1, выглядит следующим образом:
представляет собой сумму членов арифметической последовательности. Например, сумма первых 5 членов последовательности, определенной как an = 2n − 1, выглядит следующим образом:
S5 = Σn = 15 (2n − 1) = [2 (1) −1] + [2 (2) −1] + [2 (3) −1] + [2 (4) −1] + [2 (5) −1] = 1 + 3 + 5 + 7 + 9 = 25
Добавлением 5 положительных нечетных целых чисел, как мы сделали выше, можно управлять. Однако рассмотрите возможность добавления первых 100 положительных нечетных целых чисел. Это было бы очень утомительно. Поэтому затем мы разработаем формулу, которую можно использовать для вычисления суммы первых n членов, обозначенных Sn, любой арифметической последовательности.В целом
Sn = a1 + (a1 + d) + (a1 + 2d) +… + an
Записывая эту серию в обратном порядке, мы имеем,
Sn = an + (an − d) + (an − 2d) +… + a1
И сложив эти два уравнения вместе, члены, включающие d , прибавляют к нулю, и мы получаем n множителя a1 + an:
2Sn = (a1 + an) + (a1 + an) +… + (an + a1) 2Sn = n (a1 + an)
Деление обеих сторон на 2 приводит к формуле для n -й частичной суммы арифметической последовательности Сумма первых n членов арифметической последовательности, заданной формулой: Sn = n (a1 + an) 2. :
:
Sn = n (a1 + an) 2
Используйте эту формулу для вычисления суммы первых 100 членов последовательности, определенной как an = 2n − 1. Здесь a1 = 1 и a100 = 199.
S100 = 100 (a1 + a100) 2 = 100 (1 + 199) 2 = 10 000
Пример 5
Найдите сумму первых 50 членов заданной последовательности: 4, 9, 14, 19, 24,…
Решение:
Определите, есть ли общее различие между данными терминами.
d = 9−4 = 5
Обратите внимание, что разница между любыми двумя последовательными членами равна 5. Последовательность действительно является арифметической прогрессией, и мы можем написать
an = a1 + (n − 1) d = 4 + (n − 1) ⋅5 = 4 + 5n − 5 = 5n − 1
Следовательно, общий член an = 5n − 1. Чтобы вычислить частичную сумму 50 этой последовательности, нам понадобятся члены 1 и 50 :
а1 = 4а50 = 5 (50) -1 = 249
Затем используйте формулу, чтобы определить частичную сумму 50 -й заданной арифметической последовательности.
Sn = n (a1 + an) 2S50 = 50. (A1 + a50) 2 = 50 (4 + 249) 2 = 25 (253) = 6,325
Ответ: S50 = 6,325
Пример 6
Вычислить: Σn = 135 (10−4n).
Решение:
В этом случае нас просят найти сумму первых 35 членов арифметической последовательности с общим членом an = 10−4n. Используйте это, чтобы определить 1 -й и 35 -й член.
a1 = 10−4 (1) = 6a35 = 10−4 (35) = — 130
Затем используйте формулу для определения частичной суммы 35 -й .
Sn = n (a1 + an) 2S35 = 35⋅ (a1 + a35) 2 = 35 [6 + (- 130)] 2 = 35 (−124) 2 = −2,170
Ответ: −2,170
Пример 7
Первый ряд сидений в амфитеатре под открытым небом содержит 26 сидячих мест, второй ряд — 28 сидений, третий ряд — 30 сидячих мест и так далее. Если рядов 18, какова общая вместимость театра?
Если рядов 18, какова общая вместимость театра?
Рисунок 9.2
Римский театр (Википедия)
Решение:
Начните с поиска формулы, которая дает количество мест в любом ряду.Здесь количество мест в каждом ряду образует последовательность:
26,28,30,…
Обратите внимание, что разница между любыми двумя последовательными членами равна 2. Последовательность представляет собой арифметическую прогрессию, где a1 = 26 и d = 2.
an = a1 + (n − 1) d = 26 + (n − 1) ⋅2 = 26 + 2n − 2 = 2n + 24
Таким образом, количество мест в каждом ряду равно an = 2n + 24. Чтобы рассчитать общую вместимость 18 рядов, нам нужно вычислить частичную сумму 18 -го .Для этого нам понадобятся 1 st и 18 th термины:
а1 = 26а18 = 2 (18) + 24 = 60
Используйте это, чтобы вычислить частичную сумму 18 -й следующим образом:
Sn = n (a1 + an) 2S18 = 18⋅ (a1 + a18) 2 = 18 (26 + 60) 2 = 9 (86) = 774
Ответ: Всего 774 места.
Попробуй! Найдите сумму первых 60 членов заданной последовательности: 5, 0, −5, −10, −15,…
Ответ: S60 = −8,550
Основные выводы
- Арифметическая последовательность — это последовательность, в которой разница d между последовательными членами является постоянной.
- Общий член арифметической последовательности может быть записан в терминах его первого члена a1, общей разности d и индекса n следующим образом: an = a1 + (n − 1) d.
- Арифметический ряд — это сумма членов арифметической последовательности.
- Частичная сумма n арифметической последовательности может быть вычислена с использованием первого и последнего членов следующим образом: Sn = n (a1 + an) 2.
Тематические упражнения
−3, −7, −11, −15, −19,…
−6, −14, −22, −30, −38,…
−5, −10, −15, −20, −25,…
−13, 23, 53, 83, 113,…
13, 0, −13, −23, −1,…
14, −12, −54, −2, −114,…
0.
 8, 2, 3.2, 4.4, 5.6,…
8, 2, 3.2, 4.4, 5.6,…4,4, 7,5, 10,6, 13,7, 16,8,…
Найдите положительное нечетное целое число 50 -го .
Найдите положительное четное число 50 -го .
Найдите 40 -й член в последовательности, состоящей из всех остальных положительных нечетных целых чисел: 1, 5, 9, 13,…
Найдите 40 -й член в последовательности, состоящей из всех остальных положительных четных чисел: 2, 6, 10, 14,…
Какое число представляет собой член 355 в арифметической последовательности −15, −5, 5, 15, 25,…?
Какое число является членом −172 в арифметической последовательности 4, −4, −12, −20, −28,…?
Учитывая арифметическую последовательность, определяемую рекуррентным соотношением an = an − 1 + 5, где a1 = 2 и n> 1, найдите уравнение, которое дает общий член в терминах a1 и общей разности d .

Учитывая арифметическую последовательность, определяемую рекуррентным соотношением an = an − 1−9, где a1 = 4 и n> 1, найдите уравнение, которое дает общий член в терминах a1 и общей разности d .
a4 = −2310 и a21 = −252
Часть A: Арифметические последовательности
Запишите первые 5 членов арифметической последовательности, учитывая их первый член и общую разницу. Найдите формулу для его общего члена.
Найдите формулу для его общего члена.
Учитывая арифметическую последовательность, найдите формулу для общего члена и используйте ее, чтобы определить 100 -й член .
Учитывая члены арифметической последовательности, найдите формулу для общего члена.
Найдите все средние арифметические значения между заданными членами.
∑n = 1160 (3n)
∑n = 1121 (−2n)
∑n = 1250 (4n − 3)
∑n = 1120 (2n + 12)
∑n = 170 (19−8n)
∑n = 1220 (5 − п)
∑n = 160 (52−12n)
∑n = 151 (38n + 14)
∑n = 1120 (1.
 5n − 2,6)
5n − 2,6)∑n = 1175 (-0,2n-1,6)
Найдите сумму первых 200 натуральных чисел.
Найдите сумму первых 400 натуральных чисел.
Сумма первых 50 положительных нечетных целых чисел.

Сумма первых 200 положительных нечетных целых чисел.
Сумма первых 50 положительных четных целых чисел.
Сумма первых 200 положительных четных целых чисел.
Сумма первых k положительных нечетных целых чисел.
Сумма первых k положительных четных целых чисел.
Первый ряд в малом театре состоит из 8 мест.
 После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?
После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?Первый ряд сидений в амфитеатре под открытым небом содержит 42 сиденья, второй ряд — 44 сиденья, третий ряд — 46 сидячих мест и так далее.Если рядов 22, какова общая вместимость театра?
Если в треугольной стопке кирпичей 37 кирпичей в нижнем ряду, 34 кирпича во втором ряду и так далее, с одним кирпичом наверху. Сколько кирпичей в стопке?
В каждом последующем ряду треугольной стопки кирпичей на один кирпич меньше, пока наверху не останется только один кирпич.Сколько рядов в стеке, если всего кирпичей 210?
10-летний договор о заработной плате предлагает 65 000 долларов в первый год с повышением на 3200 долларов каждый дополнительный год.
 Определите общую сумму обязательств по заработной плате за 10-летний период.
Определите общую сумму обязательств по заработной плате за 10-летний период.Башня с часами бьет в колокол количество раз, указанное в часах.В час дня он ударяет один раз, в два часа — дважды и так далее. Сколько раз за день башня с часами бьет в колокол?
Часть B: Арифметическая серия
Рассчитайте указанную сумму по формуле для общего члена.
Оценить.
Общий член для последовательности положительных нечетных целых чисел задается как an = 2n − 1, а общий член для последовательности положительных четных целых чисел задается как an = 2n. Найдите следующее.
Является ли последовательность Фибоначчи арифметической последовательностью? Объяснять.
Используйте формулу для n -й частичной суммы арифметической последовательности Sn = n (a1 + an) 2 и формулу для общего члена an = a1 + (n − 1) d, чтобы получить новую формулу для n -я частичная сумма Sn = n2 [2a1 + (n − 1) d].
 При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.
При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.Обсудите методы расчета сумм, в которых индекс не начинается с 1. Например, Σn = 1535 (3n + 4) = 1,659.
Известная история повествует о плохом поведении Карла Фридриха Гаусса в школе.В наказание учитель поручил ему сложить первые 100 целых чисел. Легенда гласит, что молодой Гаусс правильно ответил в считанные секунды. Каков ответ и как, по-вашему, он смог так быстро найти сумму?
Часть C: Обсуждение
ответов
5, 8, 11, 14, 17; ан = 3n + 2
15, 10, 5, 0, −5; ан = 20−5н
12, 32, 52, 72, 92; an = n − 12
1, 12, 0, −12, −1; ан = 32−12н
1.
 8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2
8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2ан = 1.
 2n − 0,4; а100 = 119,6
2n − 0,4; а100 = 119,6
7.
 2 — Арифметические последовательности 7.2 — Арифметические последовательности
2 — Арифметические последовательности 7.2 — Арифметические последовательностиАрифметическая последовательность — это последовательность, в которой разница между последовательными сроки постоянны.
Общая разница
Поскольку это различие является общим для всех следующих друг за другом пар терминов, оно называется общая разница. Обозначается d. Если разница в последовательных термины непостоянны, то последовательность не арифметическая. Общая разница можно найти путем вычитания двух последовательных членов последовательности.
Формула общей разности арифметической последовательности: d = a n + 1 — а п
Общие условия
Арифметическая последовательность — это линейная функция. Вместо y = mx + b мы пишем a n = dn + c где d — общая разность, а c — константа (не первый член последовательность, однако).
Рекурсивное определение, поскольку каждый термин находится путем добавления общей разницы. к предыдущему члену k + 1 = a k + d.
к предыдущему члену k + 1 = a k + d.
Для любого термина в последовательности мы добавили разницу на один раз меньше, чем номер срока. Например, для первого члена мы не добавили разница вообще (0 раз). Для второго члена мы добавили разницу однажды. Для третьего члена мы добавили разницу в два раза.
Формула для общего члена арифметической последовательности: a n = а 1 + (п-1) г
Частичная сумма арифметической последовательности
Серия — это сумма последовательности.Мы хотим найти частичный номер n th сумма или сумма первых n членов последовательности. Обозначим частичный номер n -й . Сумма в виде S n .
Рассмотрим арифметический ряд S 5 = 2 + 5 + 8 + 11 + 14. Там это простой способ вычислить сумму арифметического ряда.
Ю 5 = 2 + 5 + 8 + 11 + 14
Ключ в том, чтобы изменить порядок терминов. Сложение коммутативно, поэтому изменение
заказ не меняет сумму.
Ю 5 = 14 + 11 + 8 + 5 + 2
Теперь сложите эти два уравнения вместе.
2 * S 5 = (2 + 14) + (5 + 11) + (8 + 8) + (11 + 5) + (14 + 2)
Обратите внимание, что каждая из этих сумм справа равна 16. Вместо записи 16 (сумма первого и последнего слагаемых) пять раз, мы можем записать это как 5 * 16 или 5 * (2 + 14)
2 * S 5 = 5 * (2 + 14)
Наконец, разделите все на 2, чтобы получить сумму, а не удвоенную сумму
S 5 = 5/2 * (2 + 14)
Я специально не упрощал 2 + 14, чтобы вы могли видеть, где числа родом из.Эта сумма будет 5/2 * (16) = 5 (8) = 40.
Теперь, если мы попытаемся выяснить, откуда берутся различные части этой формулы
откуда мы можем сделать предположение о формуле для частичной суммы n th .
5 — потому что было пять членов, n. 16 — это сумма первого и
последние условия, a 1 + a n . 2 потому что мы добавили сумму
дважды и останется 2. Таким образом, сумма первых n членов арифметического
последовательность: S n = n / 2 * (a 1 + a n )
Таким образом, сумма первых n членов арифметического
последовательность: S n = n / 2 * (a 1 + a n )
Есть еще одна формула, которая иногда используется для частичного n th сумма арифметической последовательности.Он получается подстановкой формулы для общий термин в приведенной выше формуле и упрощение. Предпочтительный метод найти термин n th , а затем просто вставить этот номер в формулу.
S n = n / 2 * (2a 1 + (n-1) d)
ПримерНайдите сумму от k = 3 до 17 из (3k-2).
Первый член находится заменой k = 3 на 3k-2, чтобы получить 7. Последний член член 3 (17) -2 = 49.Всего 17 — 3 + 1 = 15 терминов. Итак, сумма составляет 15 / 2 * (7 + 49) = 15/2 * 56 = 420.
Обратите внимание, что там 15 терминов. Когда нижняя граница суммирования
равно 1, то вычислить количество терминов не составляет особого труда. Тем не мение,
когда нижний предел — любое другое число, это, кажется, вызывает у людей затруднения.
Никто не станет спорить, что если перейти от 1 к 10, получится 10 чисел. Тем не мение,
разница между 10 и 1 составляет всего 9. Итак, когда вы находите число
терминов это верхний предел минус нижний предел плюс один.
Тем не мение,
когда нижний предел — любое другое число, это, кажется, вызывает у людей затруднения.
Никто не станет спорить, что если перейти от 1 к 10, получится 10 чисел. Тем не мение,
разница между 10 и 1 составляет всего 9. Итак, когда вы находите число
терминов это верхний предел минус нижний предел плюс один.
сумма арифметической прогрессии
Сумма арифметической прогрессии обозначается $ S_ {n} $. Это не что иное, как сумма n членов A.P. с первым термином «a» и общей разницей «d».Формула для суммы n членов AP:
$ S_ {n} = \ frac {n} {2} [2a + (n-1) d] $
$ S_ {n} = \ frac {n} { 2} [a + l] $, где l = последний член = a + (n -1) d
Доказательство: Пусть $ a_ {1}, a_ {2}, a_ {3}, …, a_ {n} $ — точка доступа с первым элементом как «a» и общим отличием как «d».
$ а_ {1} $ = а; $ a_ {2} $ = а + г; $ a_ {3} $ = a + 2d; … $ a_ {n} $ = a + (n -1) d
$ S_ {n} = a_ {1} + a_ {2} + a_ {3} + … + a_ {n-1} + a_ {n} $
⇒ $ S_ {n} $ = a + (a + d) + (a + 2d) +… + [a + (n-2) d] + [a + (n -1) d ] —— (i)
Запишите приведенное выше уравнение в обратном порядке:
$ S_ {n} $ = [a + (n -1) d] + [a + (n-2) d] + … + (A + 2d) + (a + d) + a —— (ii)
Теперь сложите два уравнения,
2 $ S_ {n} $ = [2a + (n -1) d] + [2a + (n-1) d] +… + [2a + (n-1) d]
[2a + (n-1) d] повторяет ‘n’ раз
∴ 2 $ S_ {n} $ = n [2a + (n -1) d]
$ S_ {n} = \ frac {n} {2} $ [2a + (n -1) d]
Поскольку последний член l = a + (n — 1 ) d
∴ $ S_ {n} = \ frac {n} {2} $ [a + a + (n -1) d]
$ S_ {n} = \ frac {n} {2} $ [a + l]
Примечание: В приведенной выше формуле 4 неизвестных величины. Итак, если даны какие-либо три, мы можем найти четвертый.
Итак, если даны какие-либо три, мы можем найти четвертый.
Если дана сумма $ S_ {n} $ n элементов последовательности, то n-й член $ a_ {n} $ последовательности может быть определен с помощью следующей формулы.
$ a_ {n} = S_ {n} — S_ {n — 1} $
Решенные примеры по сумме арифметической прогрессии
1) 50,46,42,… 10 членов.Решение: 50,46,42,… 10 членов
Формула для нахождения суммы:
$ S_ {n} = \ frac {n} {2} $ [2a + (n -1) d]
Количество термины = n = 10; Первый член = а = 50; Общая разница = d = 46 — 50 = -4
Поместите все заданные значения в формулу, которую мы получим,
$ S_ {10} = \ frac {10} {2} [2 \ times $ 50 + (10 -1) (-4)]
$ S_ {10} $ = 5 [100 + (9) (- 4)]
$ S_ {10} $ = 5 [100 + (-36)]
$ S_ {10} $ = 5 (64)
$ S_ {10} $ = 320
2) 3, $ \ frac {9} {2} $, 6, $ \ frac {15} {2} $,… 25 членов.
Решение: 3, $ \ frac {9} {2} $, 6, $ \ frac {15} {2} $,… 25 членов.
Формула для вычисления суммы:
$ S_ {n} = \ frac {n} {2} $ [2a + (n -1) d]
Количество членов = n = 25; Первый член = а = 3; Общая разница = d =, $ \ frac {9} {2} $ — 3 = $ \ frac {3} {2} $
Поместите все заданные значения в полученную формулу,
$ S_ {25} = \ frac {25} {2} [2 \ times 3 + (25 -1) \ frac {3} {2} $]
$ S_ {25} $ = 12,5 [6 + (24) (1,5)]
$ S_ { 25} $ = 12,5 [6 + 36]
$ S_ {25} $ = 12,5 (42)
$ S_ {25} $ = 525
3) В A. {2}} {2} + \ frac {13} {2} \ times24 $.
{2}} {2} + \ frac {13} {2} \ times24 $.
$ S_ {24} $ = 1080
Как мы знаем,
$ a_ {n} = S_ {n} — S_ {n -1} $
$ a_ {25} = S_ {25} — S_ {24 } $
$ a_ {25} $ = 1100 — 1080 = 80
∴ 25-й семестр равен 80.
От суммы арифметической прогрессии к дому
Covid-19 привел мир к феноменальному переходу .
Электронное обучение — это будущее уже сегодня.
Оставайтесь дома, оставайтесь в безопасности и продолжайте учиться !!!
Covid-19 повлиял на физическое взаимодействие между людьми.
Не позволяйте этому влиять на ваше обучение.
Доказательство формулы арифметического суммирования
Purplemath
Сумма S n первых n членов арифметического ряда определяется как:
На интуитивном уровне формула суммы конечного арифметического ряда говорит, что сумма всего ряда представляет собой среднее значение первого и последнего значений, умноженное на количество добавляемых значений.
MathHelp.com
Это имеет смысл, особенно если визуально представить суммирование как сумму площадей столбцов, изображенных ниже:
Поскольку столбцы растут на фиксированную величину на каждом шаге, вы можете, по сути, «усреднить» столбцы, чтобы получить общую площадь:
(Приведенный выше рисунок анимирован на «живой» странице.)
Хотя картинки помогают понять, что происходит, они ничего не доказывают в математическом смысле. Чтобы правильно доказать эту формулу, потребуется немного больше работы. Будем действовать по индукции:
Чтобы правильно доказать эту формулу, потребуется немного больше работы. Будем действовать по индукции:
Докажите, что формула для n -й частичной суммы арифметического ряда верна для всех значений n ≥ 2.
Доказательство: Пусть n = 2.Тогда имеем:
Для n = k , предположим следующее:
Пусть n = k + 1. Тогда имеем:
По характеру арифметических последовательностей имеем:
a k = a k +1 — d
a k +1 = a 1 + kd
Тогда, подставив вышеуказанное в выражение n = k + 1, мы получим:
Следовательно, результат верен для n = k + 1, и формула доказана для всех n ≥ 2.Q.E.D.
Вернуться к уроку
URL: https://www.purplemath.com/modules/series6.htm
Формула суммыдля каждого арифметического ряда с заданными первым и последним членами — Mathlibra
Арифметическая прогрессия (AP или AP)
Напомним некоторые формулы и свойства, изученные ранее.
Последовательность a 1 , a 2 , a 3 ,…, a n называется арифметической последовательностью или арифметической прогрессией, если a
61 ( n n n ) = a n + d , n ∈N, где a 1 называется первым членом, а постоянный член d называется общей разностью A.С.
Рассмотрим A.P. (в его стандартной форме) с первым членом a и общей разностью d , то есть a , a + d , a +2 d ,….
Тогда n -й член (общий термин) A.P. равен a n = a + ( n -1) d .
Мы можем проверить следующие простые свойства A.P .:
(i) Если к каждому члену A добавляется константа.P., результирующая последовательность также является AP
(ii) Если константа вычитается из каждого члена AP, результирующая последовательность также является AP
(iii) Если каждый член AP умножается на константу, то результирующая последовательность также является AP
(iv) Если каждый член AP делится на ненулевую константу, то результирующая последовательность также является AP
Здесь мы будем использовать следующие обозначения для арифметической прогрессии:
a = первый член, ℓ = последний член, d = общая разница, n = количество членов. S n = сумма n членов AP
Пусть a , a + d , a +2 d , a + ( n -1) d быть AP Тогда ℓ = a + ( n -1) d
Мы также можем написать: S n = ½ n ( a + ℓ )
Формула для суммы n Условия AP
Пусть
Записывая выражение в обратном порядке, получаем
S n = ( a + ( n -1) d ) + ( a + ( n -2) d ) +… + ( a +2 d ) + ( a + d ) + a … (2)
Складывая (1) и (2) по вертикали, получаем
2 S n = [2 a + ( n -1) d ] + [2 a + ( n — 1) d ] +… + [2 a + ( n -1) d ]… ( n выражений)
⇒ S n = ½ n [2 a + ( n -1) d ]
Альтернативная форма формулы суммы
S n = ½ n [ a + a + ( n -1) d ]
⇒ S n = ½ n [ a + ℓ ]
где ℓ = a + ( n -1) d — последний член AP
(Доказательство 1).Первый и последний члены AP равны , и ℓ соответственно. Покажите, что сумма n -го члена от начала и n -го члена образуют конец ( a + ℓ ).
Решение:
В данной AP первый член = a и последний член = ℓ .
Пусть общая разница будет d .
Тогда n -й член от начала равен
Аналогично, n -й член от конца задается как
a n = ℓ — ( n -1) d … (2)
Складывая (1) и (2), получаем
a + ( n -1) d + { ℓ — ( n -1) d }
= a + ( n -1) d + ℓ — ( n -1) d
= a + ℓ
Следовательно, сумма n -го члена от начала и n -го члена от конца ( a + ℓ ).
(Доказательство 2). Если p -й член AP равен q , а его q -й член равен p , тогда покажите, что его ( p + q ) -й член равен нулю.
Решение:
В данной AP пусть первый член будет a , а общая разница будет d .
Тогда a n = a + ( n -1) d
a q = a + ( q -1) d = p … (ii)
Вычитая (i) из (ii), мы получаем
( q — p ) d = ( p — q )
d = -1
Положив d = -1 в (i), мы получим
a = ( p + q -1)
Таким образом, a = ( p + q -1) и d = -1 Теперь, a ( p + q ) = a + ( p + q -1) d
= ( p + q -1) + ( p + q -1) (- 1)
= (p + q-1) — ( p + q -1) = 0
Следовательно, ( p + q ) -й член равен 0 (нулю).
Пример 1. Найдите сумму каждого из следующих арифметических рядов:
(i) 7 + 10½ + 14 + ⋯ +84
(ii) 34 + 32 + 30 + ⋯ +10
(iii) (-5) + (-8) + (- 11) + ⋯ + (- 230)
Решение:
(i) Данный арифметический ряд равен 7 + 10½ + 14 + ⋯ +84.
Здесь a = 7, d = 10½-7 = 3½ и ℓ = 84.
Пусть данная серия содержит n термина. Тогда a n = 84.
7+ ( n -1) ∙ 3½ = 84… (× 2)
14+ ( n -1) ∙ 7 = 168
n -1 = (168-14) ÷ 7
n -1 = 22
n = 23
S n = ½ n [ a + ℓ ]
∴ Требуемая сумма S 23 = ½ ∙ 23 ∙ (7 + 84)
= ½ ∙ 23 ∙ 91
= ½ ∙ 2030
= 1046½
(ii) Данный арифметический ряд равен 34 + 32 + 30 + ⋯ +10.
Здесь a = 34, d = 32-34 = -2 и ℓ = 10.
Пусть данный ряд содержит n члена. Тогда a n = 10.
34+ ( n -1) ⋅ (-2) = 10
-2 n +36 = 10
-2 n = 10-36 = -26
n = 13.
S n = ½ n [ a + ℓ ]
∴ Требуемая сумма S 13 = ½ ∙ 13 ∙ (34 + 10)
= ½ ∙ 13 ∙ 44
= ½ ∙ 286
(iii) Данный арифметический ряд равен (-5) + (- 8) + (- 11) + ⋯ + (- 230).
Здесь a = -5, d = -8 — (- 5) = — 8 + 5 = -3 и ℓ = 230.
Пусть данный ряд содержит n члена. Тогда a n = -230.
-5+ ( n -1) ⋅ (-3) = — 230
-3 n -2 = -230
-3 n = -230 + 2 = -228
n = 76
S n = ½ n [ a + ℓ ]
∴ Требуемая сумма S 76 = ½ ∙ 76 ∙ (-5-230)
= 38 ∙ (-235)
= -8930
Найдите сумму каждого арифметического ряда от Ex2 до Ex11.
Ex2. 4 + 8 + 12 +… + 200
Решение:
12-8 = 4
Общая разница составляет 4.
a 1 = 4, a n = 200, d = 4
a n = a 1 + ( n — 1) d
200 = 4 + ( n -1) 4
4 n = 200
n = 50
Найдите сумму ряда.
S n = ½⋅ n ⋅ ( a 1 + a n )
S 50 = ½⋅50⋅ (4 + 200)
= 5100
= 5100
Ответ:
5100
Ex3.-18 + (- 15) + (- 12) +… + 66
Решение:
-12 — (- 15) = 3
Общая разница составляет 3.
a 1 = -18, a n = 66
Найдите значение n .
a n = a 1 + ( n -1) d
66 = -18 + ( n -1) 3
3 n = 87
n = 29
Найдите сумму.
S n = ½ n ( a 1 + a n )
S 29 = ½⋅29⋅ (-18 + 66)
= 696
Ответ: 696
Ex4.-24 + (- 18) + (- 12) +… + 72
Решение:
-12 — (- 18) = 6
Общая разница составляет 6.
a 1 = -24, a n = 72
Найдите значение n .
a n = a 1 + ( n -1) d
72 = -24 + ( n -1) 6
6 n = 102
n = 17
Найдите сумму.
S n = ½ n ( a 1 + a n )
S 17 = ½⋅17⋅ (-24 + 72)
= 408
Ответ: 408
Ex5. a 1 = 12, a n = 188, d = 4
Решение:
188 = 12 + ( n -1) 4
4 n = 180
n = 45
Найдите сумму ряда.
S n = ½⋅ n ⋅ ( a 1 + a n )
S 45 = ½⋅45⋅ (12 + 188)
= 4500 Ответ:
4500
Ex6. a n = 145, d = 5, n = 21
Решение:
a 1 = 45
Найдите сумму ряда.
S n = ½⋅ n ⋅ ( a 1 + a n )
S 21 = ½⋅21⋅ (45 + 145)
= 1995 9000 Ответ:
1995 г.
Ex7.первые 50 натуральных чисел
Решение:
= ½⋅50⋅51
= 1275
Ответ: 1275
Ex8. первые 100 нечетных натуральных чисел
Решение: Здесь a 1 = 1, a 100 = 199 и n = 100
Найдите сумму.
S 100 = ½⋅100⋅ (1 + 199)
= 10,000
= 10,000
Ответ: 10 000
Ex9.первые 200 нечетных натуральных чисел
Решение:
Здесь a 1 = 1 и a 200 = 399.
Найдите сумму.
S 200 = ½⋅200⋅ (1 + 399000)
= 40,000
= 40,000 Ответ: 40 000
Ex10. первые 100 четных натуральных чисел
Решение: Здесь a 1 = 2 и a 100 = 200.
Найдите сумму.
S 100 = ½⋅100⋅ (2 + 200)
= 10,100 Ответ: 10 100
Ex11. первые 300 четных натуральных чисел
Решение:
Здесь a 1 = 2, a 300 = 300 и n = 300.
Найдите сумму.
S 300 = ½⋅300⋅ (2 + 600)
= 90,300 Ответ: 90 300
Ex12.Определите сумму ряда: 19 + 22 + 25 +… + 121
решение:
a n = 3 n + 16 = 121 = ℓ
3 n = 105
n = 35
S n = ½ n ( a + ℓ )
S 35 (19½ 35 +121) = 35⋅½⋅140 = 35⋅70 = 2450
Ex13. Найдите сумму ряда 1 + 3,5 + 6 + 8,5 +… + 101.
Решение:
Это арифметический ряд, потому что разница между членами является постоянной величиной, 2.5. Мы также знаем, что первый член равен 1, а последний член — 101. Но мы не знаем, сколько членов в ряду. Таким образом, нам нужно будет использовать формулу для последнего члена арифметической прогрессии,
чтобы дать нам 101 = 1 + ( n -1) × 2,5.
Теперь это просто уравнение для n , количества членов в ряду, и мы можем его решить. Если мы вычтем 1 из каждой стороны, мы получим
100 = ( n -1) × 2.5
а затем разделив обе стороны на 2,5, мы получим
40 = n -1
так что n = 41. Теперь мы можем использовать формулу для суммы арифметической прогрессии в версии, использующей ℓ , чтобы получить
S n = ½ n ( a + ℓ )
S 41 = ½ × 41 × (1 + 101)
= ½ × 41 × 102
= 41 × 51
2091
Ex14. Найдите сумму -6 + 1 + 8 + 15 +… + 141.
решение:
Ряд является арифметическим с u 1 = -6, d = 7 и u n = 141.Сначала нам нужно найти n .
-6 + 7 ( n -1) = 141
7 ( n -1) = 147
n -1 = 21
n = 22
Используя S n = ½ n ( u 1 + u n )
S 22 = ½⋅22⋅ (-6 + 141)
= 11⋅135 = 1485
Ex15. Найдите количество членов AP -12, -9, -6,…, 21.
Если к каждому члену этой AP добавляется 1, то получается сумма всех членов AP, полученная таким образом.
Решение:
Дано AP -12, -9, -6,…, 21.
Здесь a = -12, d = -9 — (- 12) = — 9 + 12 = 3 и ℓ = 21.
Предположим, что в AP имеется n термина.
[ a n = a + ( n -1) d ]
-12+ ( n -1) ⋅3 = 21
3 n -15 = 21
3 n = 21 + 15 = 36
n = 12.
Таким образом, в AP 12 терминов.
Если к каждому члену AP добавляется 1, то полученная таким образом новая AP будет -11, -8, -5,…, 22.
Здесь первый член a = -11, последний член ℓ = 22 и n = 12.
Получите сумму террн этой AP.
S n = ½ n ( a + ℓ )
∴ S 12 = ½⋅12⋅ (-11 + 22)
= 6⋅11 = 66
Следовательно, необходимая сумма — 66.
Ex16. Сумма первых 20 нечетных натуральных чисел равна
(a) 100 (b) 210 (c) 400 (d) 420
Решение:
Первые 20 нечетных натуральных чисел — это 1, 3, 5,…, 39.
Эти номера указаны в AP.
Здесь a = 1, ℓ = 39 и n = 20.
∴ Сумма первых 20 нечетных чисел
S 20 = ½⋅20⋅ (1 + 19)
= 10⋅40
= 400.
Ответ: (c) 400
Ex17. Найдите сумму всех нечетных чисел от 0 до 50.
Решение:
Все нечетные числа от 0 до 50 равны 1, 3, 5, 7,…, 49.
Это AP, в которой a = 1, d = (3-1) = 2 и ℓ = 49.
Пусть количество терминов будет n .
Тогда a n = 49
1+ ( n -1) ⋅2 = 49
2 n = 50
n = 25
∴ Требуемая сумма = ½ n ( a + ℓ )
= ½⋅25⋅ (1 + 49)
= 25⋅½⋅50
= 25⋅25 = 625
Следовательно, необходимая сумма — 625.
Пр. 18: Нахождение суммы ряда арифметических операций
Найдите сумму всех нечетных чисел от 51 до 99 включительно.
Решение:
Сначала используйте a 1 = 51, a n = 99, чтобы найти n :
99 = 51 + ( n -1) 2
n = 25
Теперь найдите S 25 .
S n = ½ n ( a 1 + a n )
S 25 = ½⋅25⋅ (51 + 99)
= 1875
Ex19.Найдите сумму всех целых чисел от 100 до 1000, которые делятся на 9.
Решение: первое целое число, большее 100 и делимое на 9, равно 108, а целое число, которое меньше 1000 и делится на 9, равно 999. Таким образом, мы должны найти сумму ряда.
Здесь t = a = 108, d = 9 и ℓ = 999
Пусть n будет общим числом членов в ряду n . Тогда
999 = 108 + 9 ( n -1)… (÷ 9)
111 = 12 + ( n -1)
n = 100
Следовательно, требуемая сумма
S n = ½ n ( a + ℓ )
= ½⋅100⋅ (108 + 999)
= 50 (1107) = 55350.
Давайте прочитаем числа в сообщениях, которые делятся на целое число или кратны ему в арифметической последовательности
. Вопрос 1. (5 + 13 + 21 +… + 181) =?
(а) 2476 (б) 2337 (в) 2219 (г) 2139
Решение:
Здесь a = 5, d = (13-5) = 8 и ℓ = 181.
Пусть количество термов будет n . Тогда a n = 181
a + ( n -1) d = 181
5+ ( n -1) ⋅8 = 181
8 n = 184
n = 23
∴ Требуемая сумма = ½ n ( a + ℓ )
= 23⋅½⋅ (5 + 181) = 23⋅93 = 2139.
Следовательно, необходимая сумма составляет 2139.
Ответ: (г) 2139
Q2. В местном театре 30 мест в первом ряду и всего 50 рядов. Каждый последующий ряд содержит по два дополнительных сиденья. Сколько мест в театре?
решение:
Мне нужно знать, сколько мест в 50-м ряду. Я найду формулу, чтобы начать работу.
a 1 = 2 (1) + x
30 = 2 + x
28 = x
формула для последовательности: a n = 2 n +28.
Расчет количества мест в 50-м ряду: a 50 = 2 (50) + 28 = 128.
Мне нужно сложить эти числа, чтобы получить ответ: 30 + 32 + 34 +… .. + 128.
Я буду использовать формулу S n = ½ ( a 1 + a n )
S 50 = ½⋅50⋅ (30 + 128) = 25 (158) = 3950
Ответ: Всего 3950 мест.
Q3. Открытый амфитеатр рассчитан на 40 мест в первом ряду, 41 место во втором ряду, 42 места в третьем ряду.Картина продолжается. В амфитеатре 70 рядов.
Сколько мест в амфитеатре?
раствор:
Мне нужно знать, сколько мест в 70-м ряду. Я найду формулу, чтобы начать работу.
a n = 1 n + x
a 1 = 1 (1) + x
40 = 1 + x
39 = x
Формула для последовательности: a n = n +39.
Расчет количества мест в 70-м ряду: a 70 = 70 + 39 = 109.
Мне нужно сложить эти числа, чтобы получить ответ: 40 + 41 + 42 +… .. + 109.
Я буду использовать формулу S n = ½ ( a 1 + a n ).
S 70 = ½⋅70⋅ (40 + 109) = 35 (149) = 5215
Ответ: Всего 5215 мест.
Q4. Первый и последний члены AP — 17 и 350 соответственно. Если общая разница — 9, сколько членов и какова их сумма?
Решение:
Предположим, что в AP имеется n термина.
Здесь a = 17, d = 9 и ℓ = 350.
[ a n = a + ( n -1) d ]
17+ ( n -1) ⋅9 = 350
9 n + 8 = 350
9 n = 350-8 = 342
n = 38.
Таким образом, в P.
S n = ½ n ( a + ℓ )
S 38 = ½⋅38⋅ (17 + 350)
= 19⋅367
= 6973
Следовательно, необходимая сумма — 6973.
Q5. (Конкурсы) Призы в еженедельных радиоконкурсах начинались с 150 долларов и увеличивались на 50 долларов за каждую неделю, пока длился конкурс. Если конкурс длился одиннадцать недель, сколько всего было присуждено?
Решение:
Дано, a 1 = 150, d = 50 и n = 11.
Найдите значение a 11 .
a 11 = a 1 000 + (11-1) d d d = 150 + 10⋅50
= 650
Найдите сумму.
S n = ½⋅ n ⋅ ( a 1 + a n )
= 11⋅½⋅ (150 + 650)
= 4400
Денежный приз за одиннадцатинедельный конкурс составил 4400 долларов.
Ответ: 4400 долларов
Q6. (Драма) У Лауры будет драматический спектакль через 12 дней. Она планирует репетировать свои реплики каждую ночь. В первый вечер она репетирует свои реплики 2 раза. На следующий вечер она репетирует свои реплики 4 раза. На третью ночь она репетирует свои реплики 6 раз. На одиннадцатый вечер, сколько раз она репетировала свои реплики?
Решение:
Арифметическая последовательность, которая представляет ситуацию: 2, 4, 6,….
Замените 2 на a 1 , 2 на d и 11 на n в формуле для n -го члена и найдите a 11 .
a 11 = 2 + (11-1) 2
= 2 + 20
= 22
Подставьте 2 вместо a 1 , 22 вместо a n , 11 вместо n в формуле суммы
S n = ½ n ( a 1 + a n )
= 11⋅½⋅ (2 + 22)
= 11⋅12
= 132
Ответ: 132 .

 ..
.. Число T — длина периода.
Число T — длина периода.


 8, 2, 3.2, 4.4, 5.6,…
8, 2, 3.2, 4.4, 5.6,…
 5n − 2,6)
5n − 2,6)
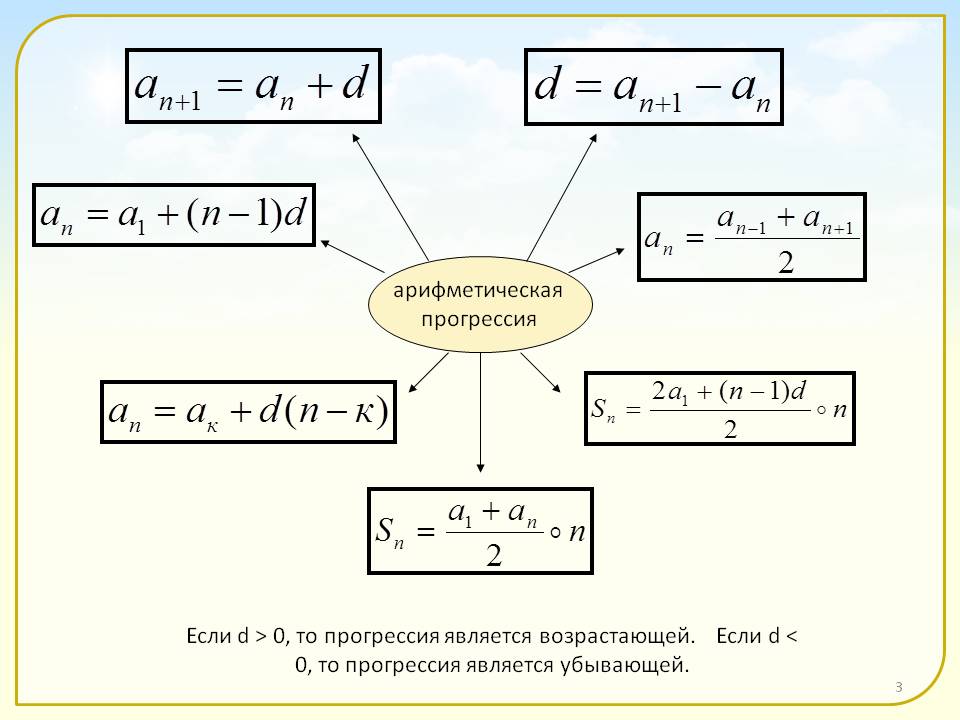 После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре?
После этого в каждом ряду будет на 3 места больше, чем в предыдущем. Если рядов 12, сколько всего мест в театре? Определите общую сумму обязательств по заработной плате за 10-летний период.
Определите общую сумму обязательств по заработной плате за 10-летний период. При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере.
При каких обстоятельствах эта формула была бы полезной? Объясните на собственном примере. 8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2
8, 2,4, 3, 3,6, 4,2; ан = 0,6n + 1,2 2n − 0,4; а100 = 119,6
2n − 0,4; а100 = 119,6