Что такое окружность | Треугольники
Как и треугольники, окружность является одной из основных геометрических фигур. Что же такое окружность?
Определение.
точка О — центр окружности
Окружность — это фигура, которая состоит из всех точек плоскости, расположенных на одинаковом расстоянии от данной точки.
Эта точка называется центром окружности.
OA — радиус окружности
Отрезок, соединяющий центр окружности с любой ее точкой, называется радиусом окружности.
Радиус обычно обозначают R или r.
Расстояние от центра окружности до любой ее точки равно длине радиуса: OA=R.
MK, FK — хорды окружности
Отрезок, соединяющий любые две точки окружности, называется хордой окружности.
BC — диаметр окружности
Хорда, проходящая через центр, называется
Центр окружности является серединой любого диаметра.
Диаметр окружности обычно обозначают d: BC=d.
Диаметр является наибольшей из всех хорд окружности.
Диаметр окружности в два раза больше длины ее радиуса: d=2R.
Любые две точки окружности делят ее на две части. Каждая из таких частей называется дуга окружности.
Если назвать дугу окружности двумя буквами — CD — непонятно, о какой из частей идет речь.
Добавив к названию дуги третью букву, определяем дугу однозначным образом:
дуга CFD или дуга CHD.
www.treugolniki.ru
ОКРУЖНОСТЬ — это… Что такое ОКРУЖНОСТЬ?
Окружность — и её центр Окружность геометрическое место всех точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное неотрицательное расстояние, называемое её радиусом. Содержание … Википедия
окружность — кольцо, эпицикл, кривая, местность, околоток, окрестность, деферент, круг, округа Словарь русских синонимов. окружность 1. см. круг. 2. см. окрестность … Словарь синонимов
ОКРУЖНОСТЬ — замкнутая плоская кривая, все точки которой одинаково удалены от ее центра O. (рис.). Расстояние R каждой точки окружности до ее центра называется радиусом. Прямая АВ, соединяющая любые две точки окружности, называется ее хордой, хорда CD,… … Большой Энциклопедический словарь
ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, расстояние, измеряемое по краю плоской геометрической фигуры, именуемой кругом, для которого это расстояние определяется как 2pr, где r радиус. Изредка этот термин применяют также к другим фигурам … Научно-технический энциклопедический словарь
ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, окружности, жен. 1. Замкнутая кривая, все точки которой равно удалены от точки, называемой центром; замкнутая кривая, ограничивающая плоскость круга (мат.). 2. Линия измерения кругообразных поверхностей и предметов. Яма метров десяти… … Толковый словарь Ушакова
ОКРУЖНОСТЬ — ОКРУЖНОСТЬ, и, жен. 1. В математике: замкнутая на плоскости кривая, все точки к рой равно удалены от центра. 2. Линия измерения округлых, кругообразных поверхностей и предметов. О. водоёма. Воронка пяти метров в окружности. 3. Окружающая… … Толковый словарь Ожегова
Окружность — кривая линия, все точки которой находятся на одинаковомрасстоянии от одной внутренней точки, называемой центром. Прямые,проведенный из центра к точкам О., называются paдиуcaми. Прямая,проходящая чрез две точки О. и ограниченная этими точками,… … Энциклопедия Брокгауза и Ефрона
окружность — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN round … Справочник технического переводчика
ОКРУЖНОСТЬ — замкнутая плоская кривая, все точки которой находятся на одинаковом расстоянии от некоторой точки О, лежащей в плоскости этой кривой и называемой её центром. Расстояние от любой точки окружности до её центра измеряется отрезком, называемым… … Большая политехническая энциклопедия
окружность — и; ж. 1. Матем. Замкнутая на плоскости кривая, все точки которой равно удалены от центра. 2. Линия измерения округлых, кругообразных поверхностей и предметов. О. озера. Воронка трёх метров в окружности. 3. Устар. Окружающая местность, округа. ◁ В … Энциклопедический словарь
dic.academic.ru
Окружность
Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром. Центр окружности является серединой любого диаметра.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Длина единичной полуокружности обозначается через π.
Сумма градусных мер двух дуг окружности с общими концами равна 360º.
Часть плоскости, ограниченная окружностью, называется кругом.
Круговой сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора .
Две окружности, имеющие общий центр, называются концентрическими.
Две окружности, пересекающиеся под прямым углом, называются ортогональными.
Взаимное расположение прямой и окружности
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d ), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку. Такая прямая называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.
- Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .
Центральные и вписанные углы
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Теорема о вписанном угле
Вписанный угол измеряется половиной дуги, на которую он опирается.
- Следствие 1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны. - Следствие 2.
Вписанный угол, опирающийся на полуокружность — прямой.
Теорема о произведении отрезков пересекающихся хорд.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Основные формулы
- Длина окружности:
- Длина дуги окружности:
- Длина дуги окружности:
где α — градусная мера длины дуги окружности)
- Площадь круга:
- Площадь кругового сектора:
Уравнение окружности
- В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C (xо;yо) имеет вид:
- Уравнение окружности радиуса r с центром в начале координат имеет вид:
Другие заметки по алгебре и геометрии
edu.glavsprav.ru
Все свойства окружности
Геометрия. Планиметрия
Окружность и её свойства
к содержанию справочника
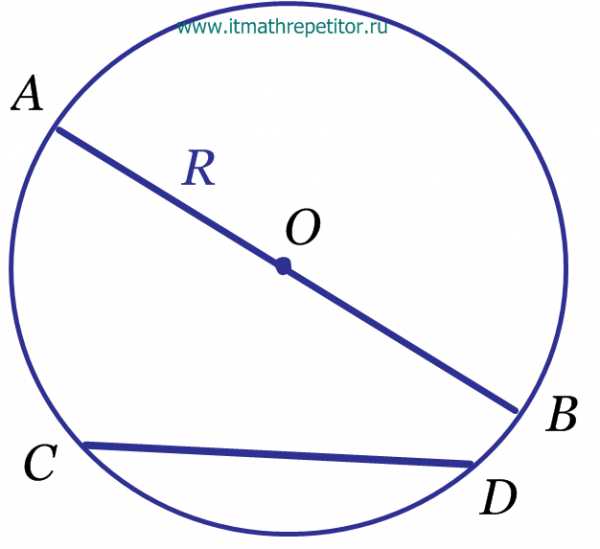
- Длина окружности и площадь круга
(длина окружности)
(площадь круга)
(диаметр)
(радиус окружности)
(хорда окружности)
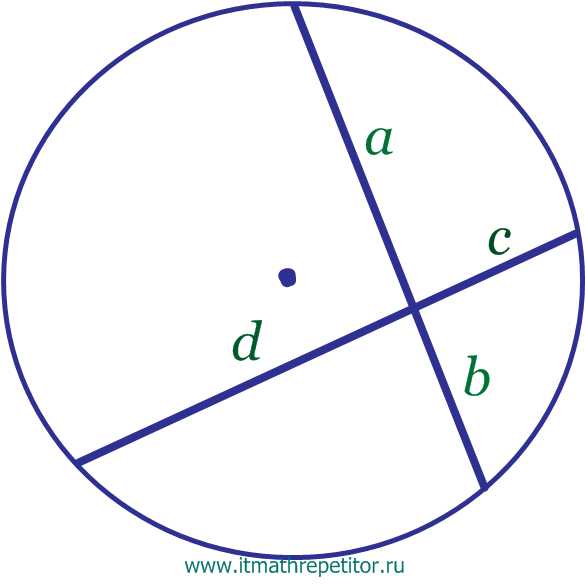
- Свойство хорд
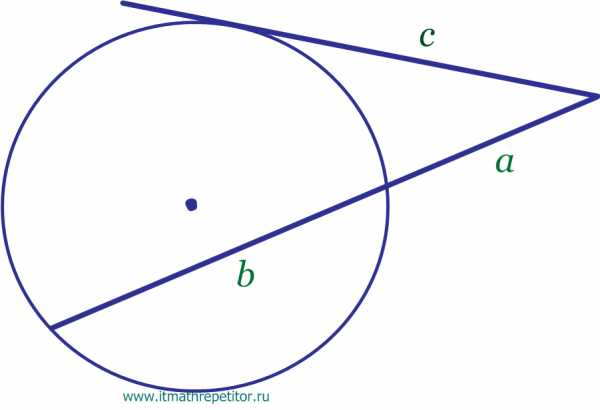
- Свойство касательной и секущей
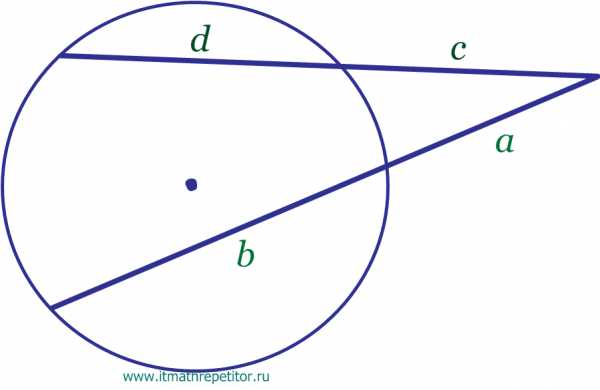
- Свойство секущих
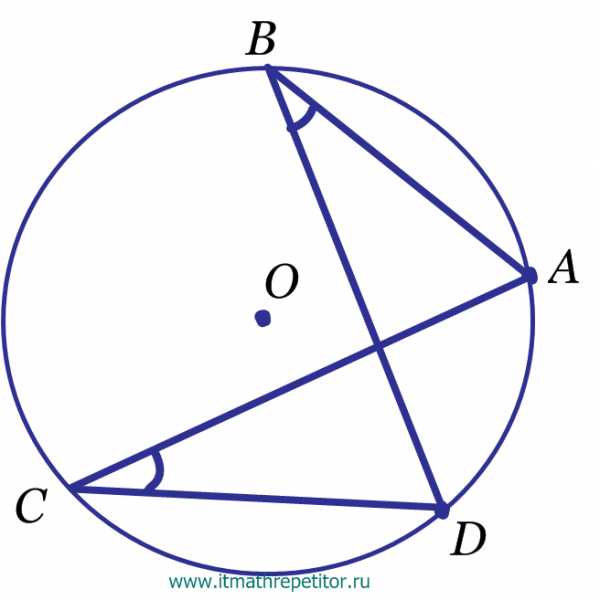
- Свойство вписанных углов, опирающихся на одну дугу
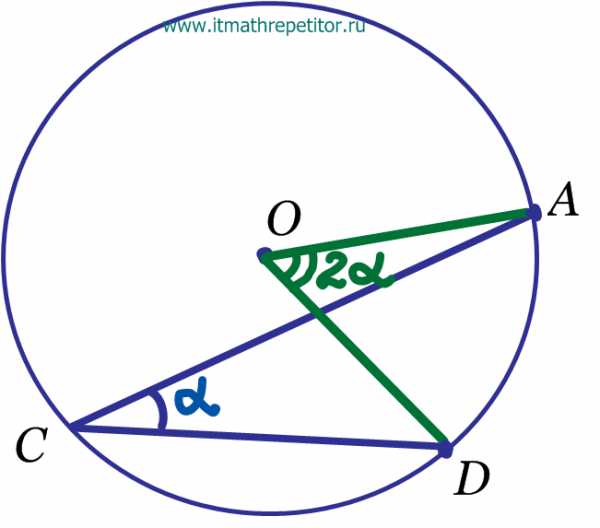
Вписанные углы, опирающиеся на одну дугу, равны - Свойство вписанного и центрального углов, опирающихся на одну дугу
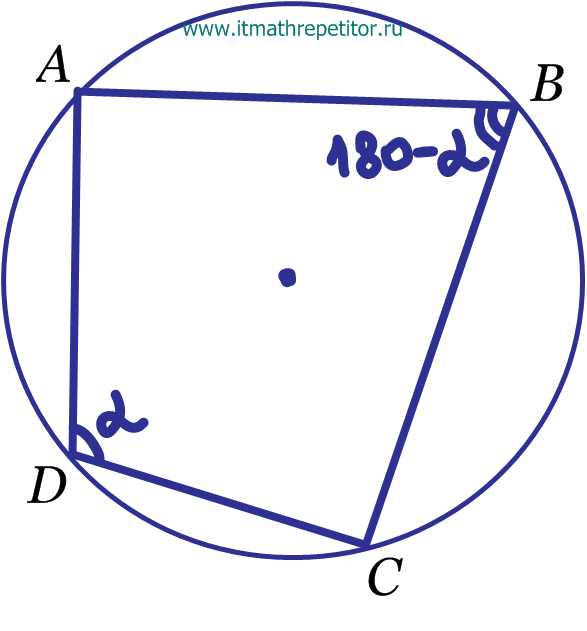
Вписанный угол в два раза меньше центрального угла, опирающегося на ту же дугу - Четырехугольник, вписанный в окружность
Сумма противолежащих углов вписанного четырехугольника равна 180о
Если сумма двух противолежащих углов четырехугольника равна 180о, то около этого четырехугольника можно описать окружность
смотрите еще Свойства произвольного треугольника
Метки окружность. Смотреть запись.
www.itmathrepetitor.ru
Свойства окружности, с примерами
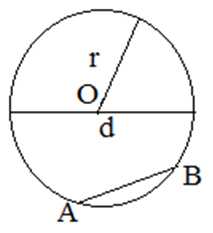
Отрезок , соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром () окружности.
Прямая, имеющая с окружностью одну общую точку, называется касательной. Прямая, имеющая с окружностью две общие точки, называется секущей.
Окружность можно описать вокруг многоугольника и вписать в многоугольник.
Центральный угол окружности – это угол, вершина которого лежит в центре окружности.
Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее.
Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
Точка касания двух окружностей лежит на прямой, проходящей через их центры.
Длина окружности вычисляется по формуле
Из всех замкнутых кривых данной длины окружность ограничивает область максимальной площади.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Формула определения длины окружности
Окружность
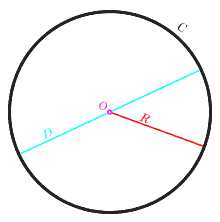Окружность (C), её центр (O), радиус (R) и диаметр (D)Окру́жность — замкнутая плоская кривая, которая состоит из всех точек на плоскости, равноудалённых от заданной точки[1]. Эта точка называется центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом; радиусом называется также и длина этого отрезка. Внутренность окружности называется кругом; в зависимости от подхода, круг может включать граничные точки (то есть окружность) или не включать их.
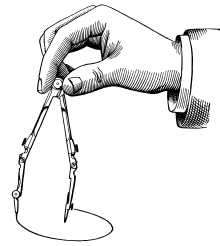Построение окружности с помощью циркуляПрактическое построение окружности производится с помощью циркуля. Окружность нулевого радиуса (вырожденная окружность) является точкой, далее этот случай исключается из рассмотрения, если не оговорено иное.
Окружность называется единичной, если её радиус равен единице. Единичная окружность является одним из основных объектов тригонометрии.
Далее всюду буква R {\displaystyle R} обозначает радиус окружности.
Хорды, дуги и касательные
Окружность разбивает свою плоскость на две части[2] — конечную внутреннюю (круг) и бесконечную внешнюю, состоящую из точек плоскости, удалённых от центра более чем на R {\displaystyle R} .
Прямая, пересекающая окружность в двух различных точках, называется секущей. Отрезок секущей, расположенный внутри окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром; тот же термин используется для его длины. Диаметр вдвое больше радиуса: D = 2 R , {\displaystyle D=2R,} он делит окружность и круг на две равные части и поэтому является их осью симметрии. Диаметр больше любой другой хорды[3].
Хорда разбивает круг на две части, называемые сегментами круга. Два различных радиуса тоже разбивают круг на две части, называемые секторами круга (см. рисунки)[3].
Любые две не совпадающие точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. Дуга называется полуокружностью, если отрезок, соединяющий её концы, является диаметром.
Для заданной окружности имеют место следующие свойства[3].
- Хорды, равноотстоящие от центра, равны. Обратно, если две хорды равны по длине, то они одинаково удалены от центра.
- Равным хордам соответствуют равные дуги, и наоборот.
- При пересечении двух хорд произведение отрезков, на которые точка пересечения делит одну из них, равно произведению отрезков другой.
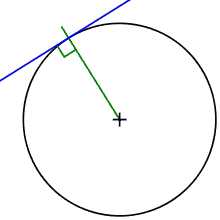Касательная к окружностиПрямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Касательная к окружности всегда перпендикулярна её радиусу (и диаметру), проведенному в точке касания. То есть радиус является одновременно и нормалью к окружности[4].
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Углы
-
Вписанный угол θ равен половине величины центрального угла 2θ, опирающегося на ту же самую дугу (розового цвета)
-
К расчёту длины дуги и хорды
Центральный угол — угол с вершиной в центре окружности. Централь
zna4enie.ru
Ответе плиз. Что такое определение? Дайте определение окружности, что такое центр , радиус , хорда и диаметр окружности
ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.
Всё есть в учебнике «Геометрия 7-9».
НАТАЛЬЯ СУЧКА
ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.
Окружностью называется геометрическое место точек равноудаленных от данной точки (центра окружности) на заданное расстояние (радиус окружности) Радиус — отрезок, соединяющий центр окружности с любой её точкой. Кругом называется геометрическое место точек удаленных от данной точки (центра круга) неболее чем на заданное расстояние (радиус круга) Секущая — это прямая, имеющая с окружностью две общие точки (на рисунке 1 показана секущая l ). Отрезок секущей, лежащий внутри окружности, называется хордой (на рисунке 1 показана хорда АВ). Итак, Хордой называется отрезок соединяющий две произвольные (несовпадающие) точки окружности. Части, на которые хорда разбивает круг , называются сегментами. В случае, когда хорда совпадает с диаметром, эти сегменты превращаются в полукруги. Диаметром называют хорду, проходящую через центр окружности. Сектором круга называют часть круга, ограниченная двумя его радиусами и дугой окружности, соединяющей концы этих радиусов
в учебнике написано
ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.
ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.
ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.
ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.
Определение — объяснение понятия, опирающееся на начальные понятия (например, понятие «точка») или на определенные ранее. Окружность — это геометрическое место точек плоскости, равноудаленных от одной точки плоскости. Центр окружности — точка плоскости, равноудаленная от всех точек окружности. Радиус окружности — равные отрезки, соединяющие центр с точками окружности. Хорда — отрезок, соединяющий любые две точки окружности. Диаметр окружности — хорда, проходящая через центр.
ОКРУЖНОСТЬ — геометрическое место точек, равноудалённых от одной точки, называемой ЦЕНТРОМ. РАДИУС — равные отрезки, соединяющие центр окружности с точками окружности. ХОРДА — отрезок прямой, проходящей через две точки окружности, лежащий внутри окружности. ДИАМЕТР — хорда, проходящая через центр окружности.
touch.otvet.mail.ru