Формула частоты колебаний пружинного маятника в физике
Формула частоты колебаний пружинного маятника в физикеЧастота колебаний
Определение
Частота колебаний ($\nu$) является одним из параметров, которые характеризуют колебания Это величина обратная периоду колебаний ($T$):
\[\nu =\frac{1}{T}\left(1\right).\]
Таким образом, частотой колебаний называют физическую величину, равную числу повторений колебаний за единицу времени.
\[\nu =\frac{N}{\Delta t}\left(2\right),\]
где $N$ — число полных колебательных движений; $\Delta t$ — время, за которые произошли данные колебания.
Циклическая частота колебаний (${\omega }_0$) связана с частотой $\nu $ формулой:
\[\nu =\frac{{\omega }_0}{2\pi }\left(3\right).\]
Единицей измерения частоты в Международной системе единиц (СИ) является герц или обратная секунда:
\[\left[\nu \right]=с^{-1}=Гц.
2_0=\frac{k}{m}$ — циклическая частота колебаний пружинного маятника. Решение уравнения (4) это функция синуса или косинуса вида:
\[x=A{\cos \left({\omega }_0t+\varphi \right)=A{\sin \left({\omega }_0t+{\varphi }_1\right)\ }\ }\left(5\right),\]
где ${\omega }_0=\sqrt{\frac{k}{m}}>0$- циклическая частота колебаний пружинного маятника, $A$ — амплитуда колебаний; ${(\omega }_0t+\varphi )$ — фаза колебаний; $\varphi $ и ${\varphi }_1$ — начальные фазы колебаний.
Частота колебаний пружинного маятника
Из формулы (3) и ${\omega }_0=\sqrt{\frac{k}{m}}$, следует, что частота колебаний пружинного маятника равна:
\[\nu =\frac{1}{2\pi }\sqrt{\frac{k}{m}}\ \left(6\right).\]
Формула (6) справедлива в случае, если:
- пружина в маятнике считается невесомой;
- груз, прикрепленный к пружине, является абсолютно твердым телом;
- крутильные колебания отсутствуют.
Выражение (6) показывает, что частота колебаний пружинного маятника увеличивается с уменьшением массы груза и увеличением коэффициента упругости пружины.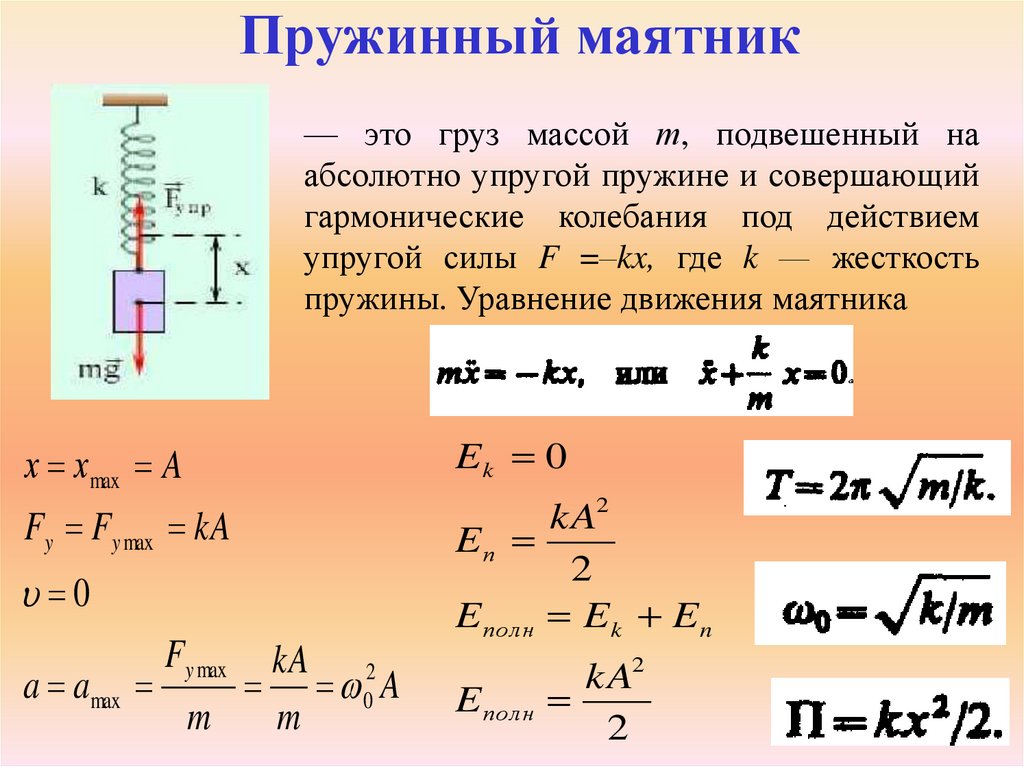
{-3}}=200\ \left(Гц\right).\]
Циклическая частота связана с частотой $\nu $ как:
\[{\omega }_0=2\pi \nu \ \left(1.2\right).\]
Вычислим циклическую частоту:
\[{\omega }_0=2\pi \cdot 200\approx 1256\ \left(\frac{рад}{с}\right).\]
Ответ. $1)\ \nu =200$ Гц. 2) ${\omega }_0=1256\ \frac{рад}{с}$
Пример 2
Задание. Массу груза, висящего на упругой пружине (рис.2), увеличивают на величину $\Delta m$, при этом частота уменьшается в $n$ раз. Какова масса первого груза?
Решение. Будем считать, что грузы на пружине совершают свободные гармонические колебания, тогда за основу решения задачи примем формулу:
\[\nu =\frac{1}{2\pi }\sqrt{\frac{k}{m}}\ \left(2.1\right).\]
Для первого груза частота будет равна:
\[{\nu }_1=\frac{1}{2\pi }\sqrt{\frac{k}{m}}\ \left(2.
2-1}$
Читать дальше: формула частоты.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
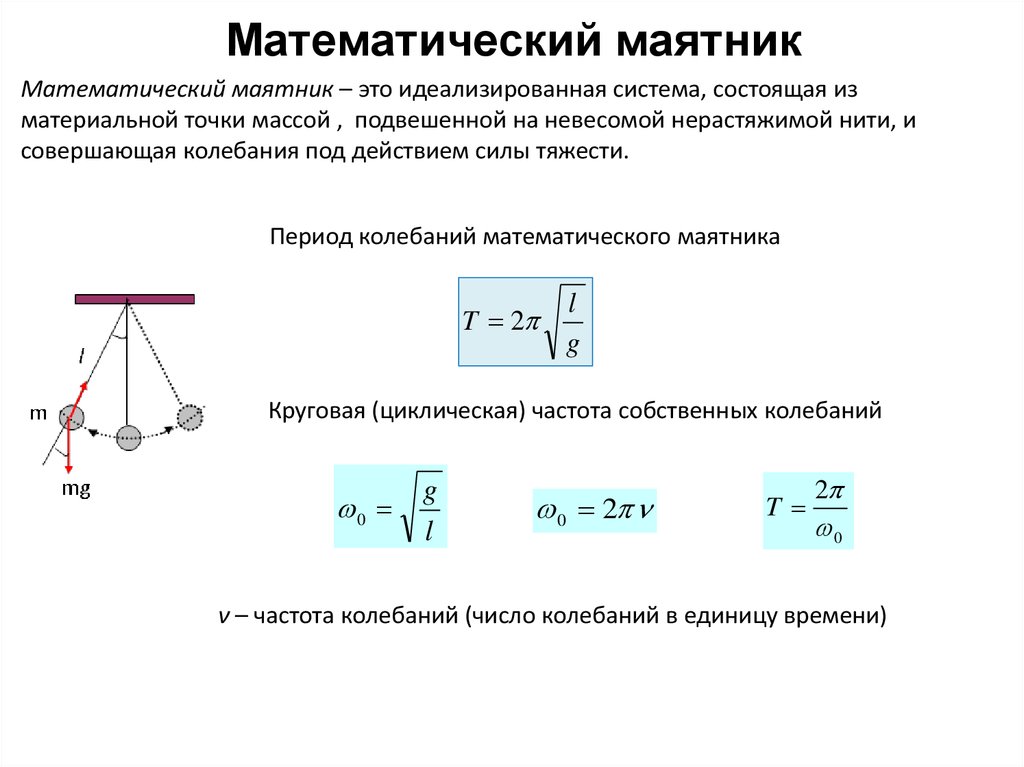
Математический маятник. Частота колебаний математического маятника (формула).
Математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити, и совершавшая колебания в вертикальной плоскости под действием силы тяжести. Если отклонить маятник от положения равновесия, то сила тяжести и сила упругости будут направлены под углом. Равнодействующая сила уже не будет равна нулю. Под воздействием этой силы маятник устремится к положению равновесия, но по инерции движение продолжится и маятник отклоняется в другую сторону. Равнодействующая сила его снова возвращает.
Частота
математического маятника —
Чем больше период колебаний математического
маятника, тем меньше частота.
Важно где происходят колебания! На Луне и на Земле один и тот же математический маятник при одинаковых начальных условиях колебаться будет по-разному. Так как ускорение свободного падения на Луне отличается от ускорения свободного падения на Земле.
Линейная скорость материальной точки, линейное ускорение материальной точки, единицы измерения. Сложение скоростей.
линейная скорость — это производная от пройденного пути по времени.
Отдельные точки вращающегося тела имеют различные линейные скорости (метр/сек). Скорость каждой точки, будучи направлена по касательной к соответствующей окружности, непрерывно изменяет свое направление. Величина скорости определяется скоростью вращения тела и расстоянием R рассматриваемой точки от оси вращения. Пусть за малый промежуток времени тело повернулось на угол Точка, находящаяся на расстоянии R от оси проходит при этом путь, равный :
Линейная скорость точки по определению:
линейное
ускорение — это производная от скорости по времени.
Формула линейного ускорения:
a = dv/dt = d2s/dt2, где s – путь,пройденный телом.
Сложение скоростей — с помощью данного закона определяется скорость движения тела относительно неподвижной системы отсчёта. Она равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости самой подвижной системы отсчета относительно неподвижной системы
Для того, чтоб было более понятно, как работает закон сложения скоростей, рассмотрим такой пример. Вагон движется со скоростью 50 км\ч (это будет ), в вагоне идет человек со скоростью 3 км\ч (это будет ), найти скорость человека относительно Земли.
У данной задачи будет два решения. Если человек будет идти по направлению движения вагона, то скорость человека относительно Земли будет 53 км\ч.
А если человек будет идти против движения вагона, то скорость человека относительно Земли будет 47 км\ч.
В Формуле мы использовали :
— Конечная скорость тела
— Скорость тел в различных инерциальных системах отчета
Свободные колебания.
Пружинный маятник. Частота колебаний пружинного маятника (формула).
Пружинный маятник. Частота колебаний пружинного маятника (формула).Колебания называются свободными (или собственными), если они совершаются за счет первоначальной сообщенной энергии при последующем отсутствии внешних воздействий на колебательную систему (систему, совершающую колебания).
Пружинный маятник — это груз массой т, подвешенный на абсолютно упругой пружине и совершающий гармонические колебания под действием упругой силы F = –kx, где k — жесткость пружины.
Частота пружинного маятника — Чем больше период колебаний пружинного маятника, тем меньше частота
— Частота Пружинного маятника, — Период колебаний маятника
— Масса груза, или масса маятника, — Жесткость пружины
Угловая скорость, частота вращения, период вращения (определение, единицы измерения, связь между величинами). Связь между линейной и угловой скоростями.
Угловая
скорость численно равна углу поворота
радиуса за единицу времени.
Период и частота
Период вращения T — это время, за которое тело совершает один оборот.
Частота вращение — это количество оборотов за одну секунду.
Частота и период взаимосвязаны соотношением
Связь с угловой скоростью
Линейная скорость точки. Направление вектора линейной скорости всегда совпадает с касательной к окружности Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так:
Так как , то
Условия возникновения затухающих колебаний (соотношение между собственной частотой и коэффициентом затухания). Амплитуда затухающих колебаний (формула).
Соотношение: β — коэффициент затухания. Этот коэффициент
характеризует скорость затухания
колебаний, При наличии сил сопротивления
энергия колеблющейся системы будет
постепенно убывать, колебания будут
затухать.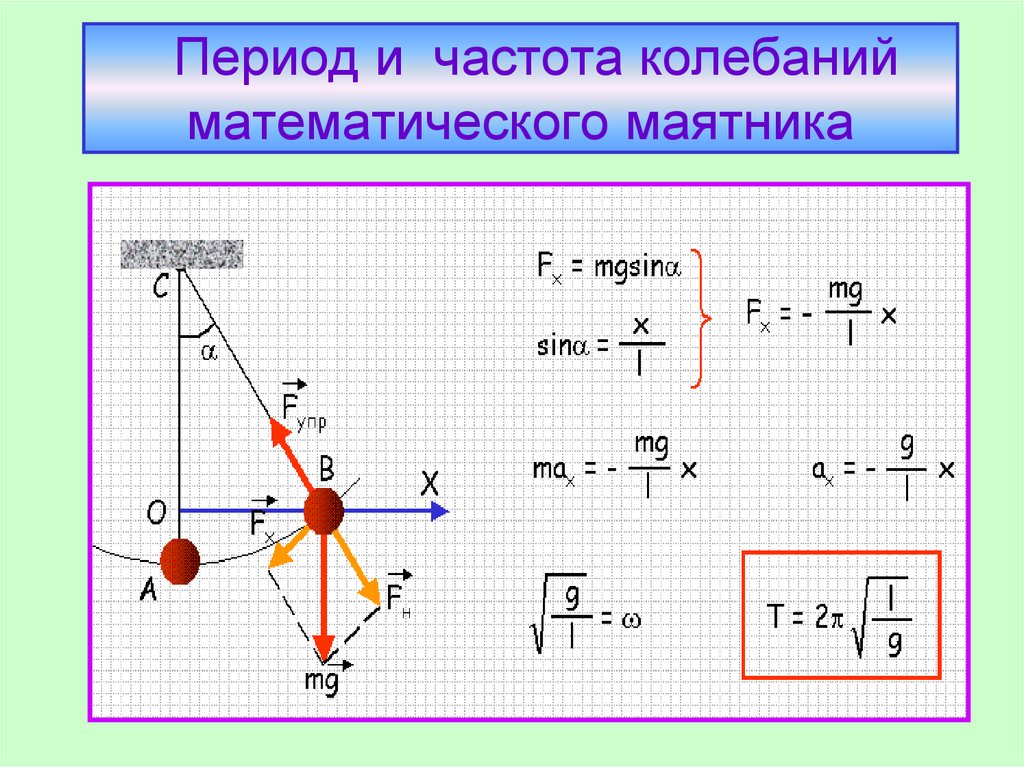
Амплитуда колебаний — это максимальное расстояние, на которое удаляется колеблющееся тело от своего положения равновесия. Амплитуда затухающих колебаний изменяется по закону , где А0 – начальная амплитуда. Зависимость амплитуды показана на рис. 8.3.
Рис. 8.3. График затухающих колебаний
Механическая работа (определение, единицы измерения). Мощность силы (определение, единицы измерения).
Механическая рабоат — то скалярная физическая величина, которая характеризует процесс перемещения тела под действием силы и равна произведению модуля силы F на модуль перемещения S и на косинус угла между ними
Если тело под действием силы совершает перемещение , работа А этой силы равна скалярному произведению силы на вектор перемещения. Работа силы есть скалярная величинаА=
А=
мощность силы — скалярная физическая величина N, равная отношению работы А, совершаемой силой, к промежутку времени , в течение которого она совершается:
Работа
силы, совершаемая в единицу времени,
называется мощностью.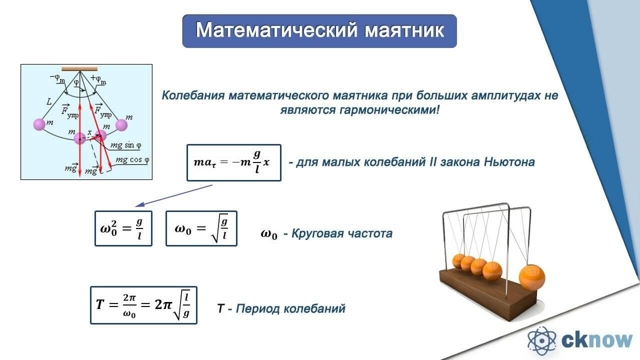
Мощность N это
физическая величина, равная отношению
работы A к
промежутку времени t,
в течение которого совершена эта
работа:
В Международной системе (СИ) единица мощности называется ватт (Вт). Ватт равен мощности силы, совершающей работу в 1 Дж за время 1 с.
Если тело движется прямолинейно и на него действует постоянная сила, то она совершает работу . Поэтому мощность этой силы
Уравнения для простого маятника Рона Куртуса
SfC Home > Physics > Mechanics >
Рон Куртус
Уравнения для простого маятника показывают, как найти частоту и период движения.
Простой маятник состоит из точечной массы, подвешенной на нити или проволоке с незначительной массой. Если груз маятника или груз потянуть на относительно небольшой угол от вертикали и отпустить, он будет качаться вперед и назад с постоянным периодом и частотой. Эти требования позволяют уравнениям быть относительно простыми и называются простое гармоническое движение .
Если грузик больше, проволока имеет массу или угол больше, то такой маятник называется физическим маятником со сложными уравнениями движения.
Хотя демпфирующие эффекты от сопротивления воздуха и трения являются фактором, им можно пренебречь для основных уравнений, касающихся частоты или периода маятника.
Возможные вопросы:
- Каковы факторы и параметры движения маятника?
- Какие уравнения для частоты и периода?
- Каковы уравнения для длины струны маятника?
Этот урок ответит на эти вопросы. Полезный инструмент: Преобразование единиц измерения
Факторы и параметры
Основным фактором, включаемым в уравнения для расчета частоты простого маятника, является длина стержня или проволоки при условии, что начальный угол или амплитуда качания малы. Масса или вес боба не влияет на частоту простого маятника, но ускорение под действием силы тяжести является фактором.
Примечание : Это означает, что частота и период будут отличаться на Луне и на Земле.
Зная длину маятника, можно определить его частоту. Или, если вы хотите конкретную частоту, вы можете определить необходимую длину.
Факторы и параметры простого маятника
( См. Демонстрация маятника, чтобы увидеть маятник в движении )
Уравнение периода
Период движения маятника — это время, необходимое для его раскачивания вперед и назад, измеряемое в секундах. Уравнение для периода простого маятника, начинающегося с малого угла α (альфа):
Т = 2π√(л/г)
где
- T — период в секундах (с)
- π — это греческая буква пи и приблизительно равна 3,14 .
- √ — это квадратный корень из числа, заключенного в скобки .
- L длина стержня или проволоки в метрах или футах
- g ускорение свободного падения (9,8 м/с² или 32 фута/с² на Земле)
Таким образом, если L = 2 метра:
T = 2 * 3,14 * √(2/9,8) = 6,28 * √(0,204) = 6,28 * 0,4517
T = 2,837 секунды или немного округлить до T = 2,8 с.
Частотное уравнение
Частота маятника — это количество колебаний маятника вперед и назад в секунду, измеряемое в герцах.
Частота f является обратной величиной периода T :
f = 1/T
f = 1/[2π√(л/г)]
Уравнение также можно изменить следующим образом:
f = [√(г/л)]/2π
Таким образом, если L = 2 метра,
f = [√(9,8/2)]/2*3,14
f = [√(4,9)]/6,28 = 2,21/6,28 = 0,353 Гц.
Длина провода
Можно найти длину стержня или провода для заданной частоты или периода.
Частота
Решить уравнение для L :
f = [√(г/л)]/2π
2πf = √(г/л)
Возведение в квадрат обеих частей уравнения:
4π 2 f 2 = г/л
Найти L :
L = г/(4π 2 f 2 )
Например, длина маятника с частотой 1 Гц (1 цикл в секунду) составляет около 0,25 метра.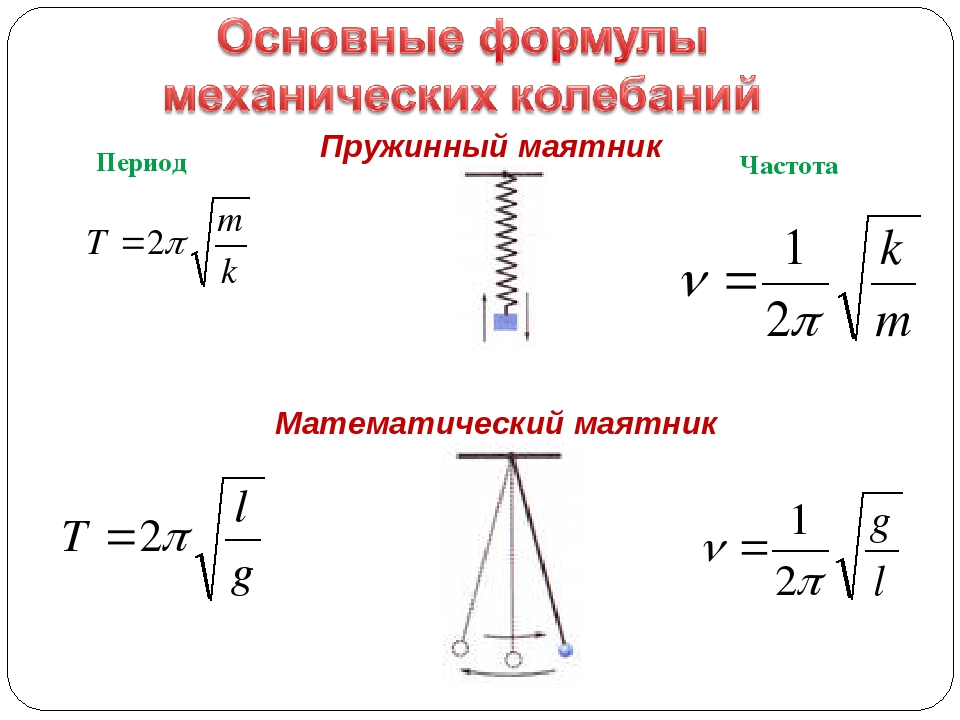
Период
Аналогично, длина провода за данный период составляет:
Т = 2π√(л/г)
Квадрат с обеих сторон:
T 2 = 4π 2 (л/г)
Найти L :
L = gT 2 /4π 2
Резюме
Если вес маятника или груз простого маятника потянуть на относительно небольшой угол и отпустить, он будет качаться вперед и назад с постоянной частотой. Эти требования позволяют уравнениям быть относительно простыми и называются простое гармоническое движение .
Если демпфирующие эффекты от сопротивления воздуха и трения пренебрежимо малы, можно рассчитать уравнения, касающиеся частоты и периода колебаний маятника, а также длины струны.
Уравнение периода: T = 2π√(л/г)
Частотное уравнение: f = [√(г/л)]/2π
Уравнения длины: L = g/(4π 2 f 2 ) и L = gT 2 /4π 2
Почувствуйте себя хорошо, выполнив свои самые лучшие
Ресурсы и ссылки
Рон Куртус.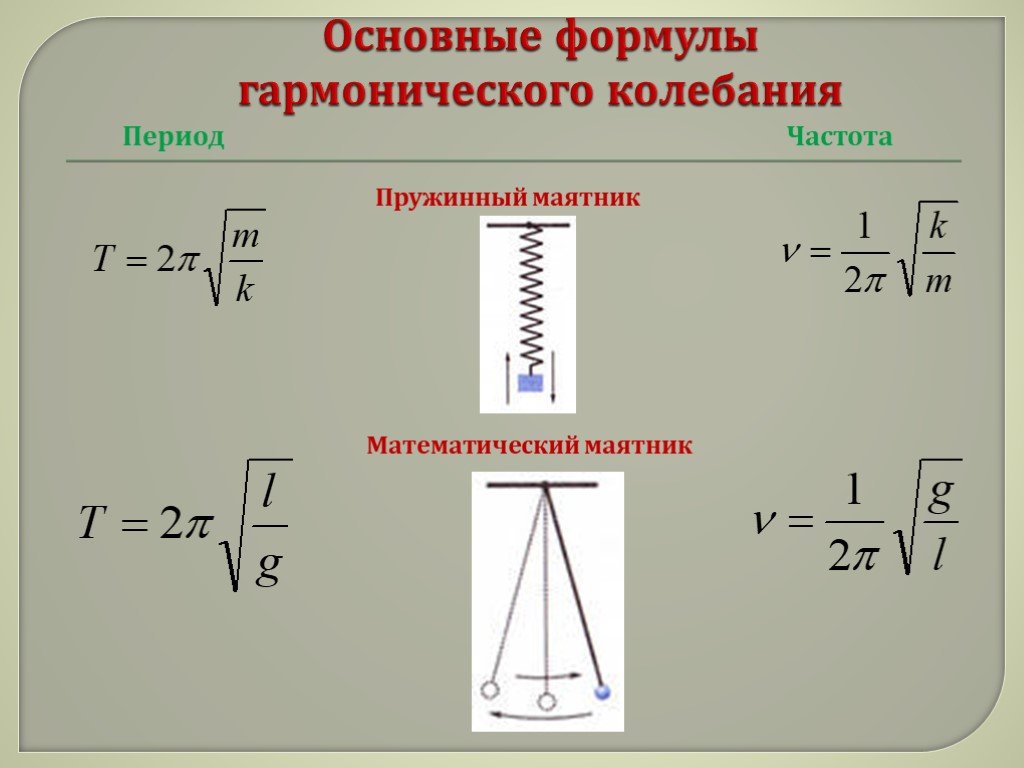
Книги
(Примечание: Школа чемпионов может получать комиссионные за покупку книг)
Книги с самым высоким рейтингом на Pendulums
Книги с самым высоким рейтингом по периодическому движению
Книги с самым высоким рейтингом по физике движения
Поделиться этой страницей или другие услуги:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
pendulum_equations.htm
Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.
Copyright © Ограничения
Где ты сейчас?
Школа Чемпионов
Темы по физике
Уравнения для простого маятника
Маятник
Маятник Простой маятник — это маятник, который можно рассматривать как точечную массу, подвешенную к нити или стержню незначительной массы.
Шон Кэрролл рассказывает об открытии Галилеем того факта, что при малых амплитудах период и частота не зависят от амплитуды. «В 1581 году молодой Галилео Галилей, как сообщается, сделал прорывное открытие, когда скучал во время церковной службы в Пизе. ветра, например) и медленнее, когда он не двигался так далеко. | Index Periodic motion concepts Carroll | |||||
| Вернуться |
Это резонансная система с одной резонансной частотой. При малых амплитудах период такого маятника может быть аппроксимирован выражением: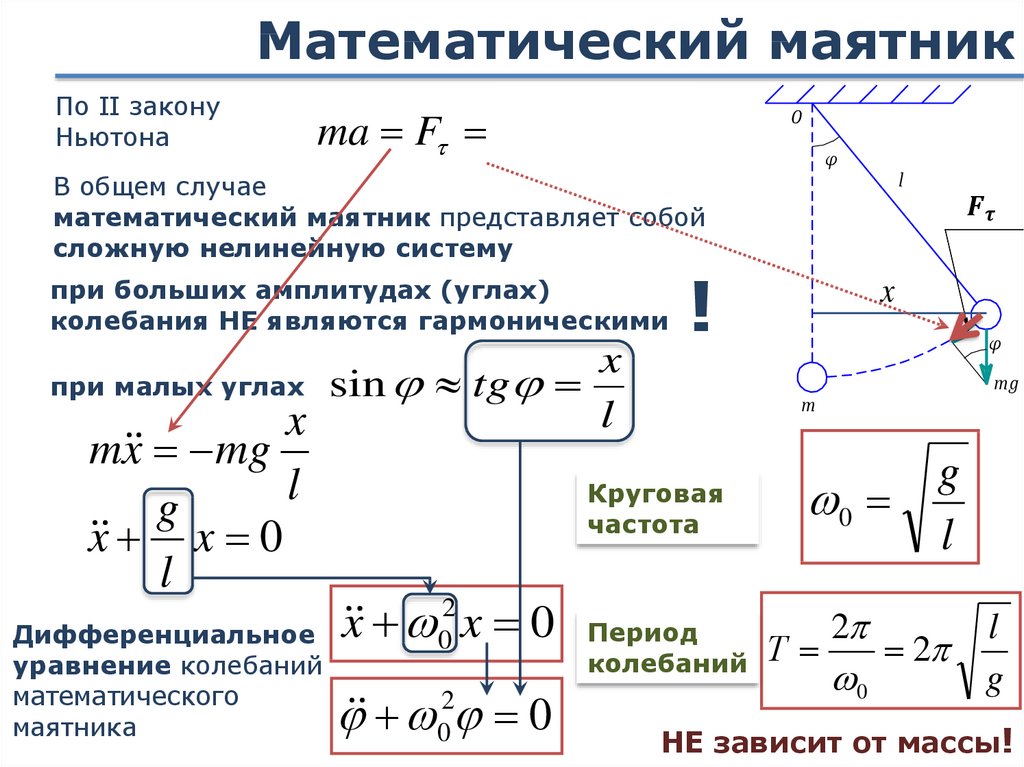
Заинтригованный, Галилей решил измерить, сколько времени требуется для каждого колебания, используя единственное приблизительно периодическое событие, к которому он имел доступ: биение его Он обнаружил кое-что интересное: количество ударов сердца между качаниями люстры было примерно одинаковым, независимо от того, были ли качания широкими или узкими. влияют на частоту этих колебаний».Движение простого маятника подобно простому гармоническому движению в том смысле, что уравнение для углового смещения имеет вид
| Индекс Концепции периодического движения | |||||||||||||
| Вернуться |
Точечная масса, висящая на безмассовой нити, представляет собой идеализированный пример простого маятника. При смещении из точки равновесия восстанавливающая сила, возвращающая его в центр, определяется выражением:
|
