Определения, формулы с примерами и ответы на часто задаваемые вопросы
Термины длина, высота, наклонная высота, площадь поверхности и т. д. используются для определения форм. «Диаметр» — одна из таких характеристик, описывающих форму круга. В геометрии любой отрезок прямой линии, который проходит через центр окружности и имеет конечные точки, находящиеся на окружности, называется диаметром. Самая длинная хорда окружности — другое ее название. Диаметр сферы можно определить любым из двух способов. Это важное круговое измерение. На самом деле, это одна из характеристик, которая отличает круги. Диаметр — это измерение длины окружности, проведенной от края к краю через его центр.
Диаметр круга
Окружность круга, измеренная от края до края, включает всю его длину от центра до центра. Вот эта длина и есть все. Буква «d» обозначает диаметр окружности.
Радиус круга равен удвоенному диаметру круга. Внутри круга несколько диаметров. Диаметр круга — это расстояние, на котором две точки, расположенные на его периферии, соединяются линией, проходящей через центр круга.
Каждый круг содержит четыре основные характеристики. Вот они:
Радиус — это отрезок, проходящий от центра до любой точки на окружности. Его знак в формулах — «r».
Диаметр — это линия, которая начинается в одной точке периметра окружности, проходит через ее центр и заканчивается в точке окружности, диаметрально противоположной начальной точке. Его символ «д».
Длина окружности – это ее длина от края до края. С — его символ.
Площадь: вся окружность круга. Его обозначение A.
Шаги: Создайте диаметр круга.
Чтобы создать «хорду», проведите линию через круг.
Создайте диаметр окружности, создав биссектрису хорды.
Чтобы найти центр окружности, создайте биссектрису этого диаметра.
Связь между радиусом и диаметром
Радиус окружности — это расстояние, которое проходит точка на окружности окружности от ее центра.
Диаметр окружности — это прямая линия, проходящая через ее центр и заканчивающаяся на окружности.
Следовательно, радиус равен половине диаметра.
Диаметр = 2(Радиус)
\(Диаметр = 2\x r \)
Формула диаметра круга
Диаметр круга вычисляется по формуле диаметра. Формулу диаметра можно использовать для определения расстояния между двумя краями круга.
Диаметр круга с использованием длины окружности
Формулу диаметра можно просто вывести из длины окружности.
Для вычисления длины окружности используется следующая формула: \pi } \)
Например:
Длина окружности 38 метров, поэтому определите ее диаметр.
Решение:
Окружность = 38 метров
\( C = \pi d \)
38 = \( \pi d \)
\( \Стрелка вправо \frac{22}{7}\times d\) = 38
\( \Стрелка вправо d = \frac{38\times 7}{22 } \)= 12
Диаметр круга с использованием радиуса
Радиус круга — это расстояние по линии, проведенной от его центра к одному из его концов, тогда как его диаметр равен удвоенному этому расстоянию.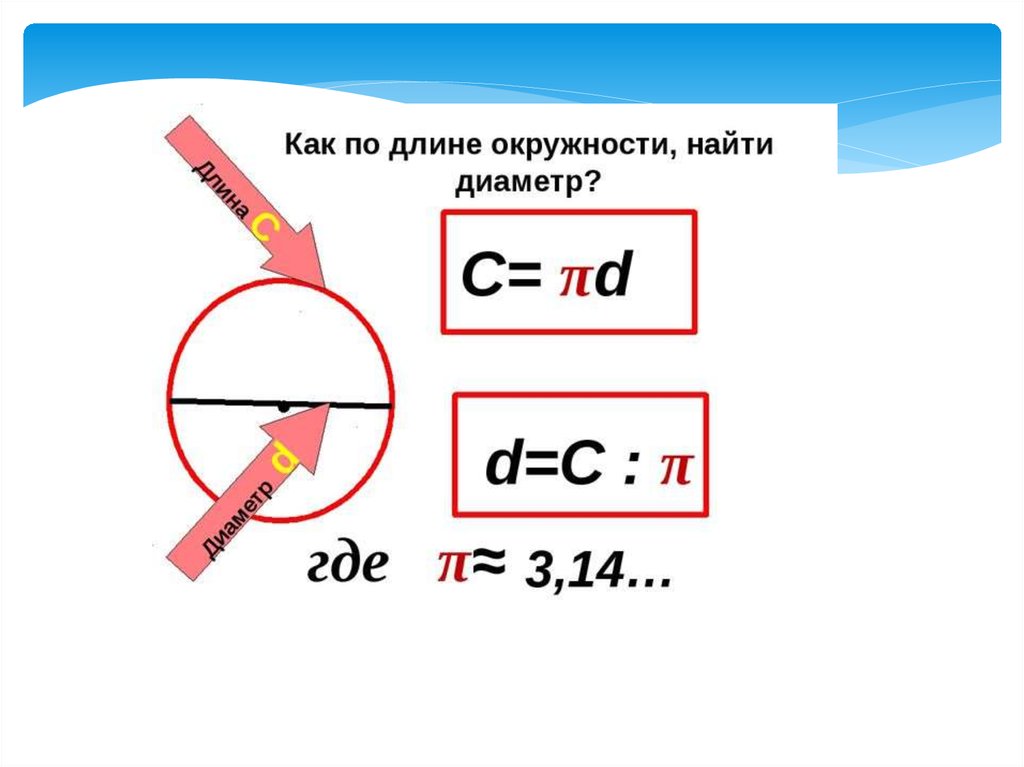
Используя эту концепцию, формула диаметра будет следующей0003
Например:
Джой нарисовала круг радиусом 7 единиц. Каков диаметр круга?
Решение:
Радиус окружности = 7 ед.
Формула диаметра с использованием площади круга
Используя формулу площади круга, мы можем вычислить диаметр круга, то есть 9{2}
Извлекаются квадратные корни с обеих сторон.
11 = r
Диаметр (d) = 2r
\(d = 2\times 11 \)
Диаметр круга равен 22 см
Задача: 2 Если диаметр круга равен 38 единицам, Вы можете рассчитать его радиус?
Решение:
Диаметр = 38 единиц
Радиус, разделенный на два, дает диаметр. Это означает, что радиус равен диаметру, деленному на два.
\( Диаметр = 2\х Радиус \)
\( r = \frac{d}{2} \)
\( r = \frac{38}{2} \)
= 19
радиус окружности 19 единиц
Вы хотите хорошо сдать экзамены по математике? Тогда вы находитесь в правильном месте.
Платформа Testbook предлагает еженедельную подготовку к тестам, живые занятия и серию экзаменов. Подготовьте умную и высокорейтинговую стратегию к экзамену, скачав приложение Testbook прямо сейчас.
Часто задаваемые вопросы о диаметре
В.1 Как рассчитать диаметр?
Ответ 1 Используя эту формулу, мы можем вычислить диаметр\( d = 2\x r \)
Q.2 Диаметр – это длина или ширина?
Ответ 2 Диаметр – это длина.
Q.3 Сколько диаметров в круге?
Ответ 3 Один диаметр в круге.
Q.4 Может ли круг иметь 2 диаметра?
Ответ 4 Нет, каждый круг нарисован с одним диаметром.
В.5 Как найти радиус по диаметру?
Ответ 5 С помощью следующей формулы мы можем вычислить радиус круга\( r =\frac{d}{2} \)
Q.6 Как найти длину окружности с диаметр?
Ответ 6 \( C = \pi d \) с помощью этой формулы мы можем вычислить длину окружности.
Q.7 Является ли диаметр самой длинной хордой окружности?
Ответ 7 Да, самая длинная хорда круга, диаметр, соединяет два места на его окружности в центре.
Скачать публикацию в формате PDF| Radicand & its Difference with Radical and Index with Examples |
| Perimeter of Hexagon: Formula, Method, and Solved Examples |
| Properties of Cylinder: Types, Formulas, Curvature, Цилиндр как призма и геометрическое место линий с примерами. |
| Как найти периметр сектора с помощью формулы и примеров |
| Стандартная форма: формулы, типы и примеры решения |
Цилиндрическое зубчатое колесо Терминология и формулы
Что такое Spur Gear?
Цилиндрическое зубчатое колесо — один из самых простых и распространенных типов цилиндрических зубчатых колес. Цилиндрические шестерни имеют прямые зубья, которые идут параллельно валу.
Эти шестерни просты в изготовлении и могут использоваться в различных областях. Эти приложения включают увеличение или уменьшение скорости, увеличение крутящего момента и повышение точности систем позиционирования.
В этом блоге мы дадим определение терминологии цилиндрических зубчатых колес и предоставим формулы для определения значений этих терминов.
Цилиндрические зубчатые колеса – термины, определения и расчеты
Следующие термины относятся к цилиндрическим зубчатым колесам:
- Приложение : Высота зуба над делительной окружностью.
- Люфт : Зазор между двумя сопряженными зубьями отдельных шестерен.
- Базовая окружность : Теоретическая окружность, используемая для создания эвольвентной кривой при создании профилей зубьев. 903:30
- Межосевое расстояние : Расстояние между центральными валами двух шестерен.
- Хордальное дополнение : расстояние между хордой, проходящей через точки, где
- делительная окружность пересекает профиль зуба и вершину зуба.
- Толщина хорды : Толщина зуба, измеренная вдоль хорды, проходящей через точки, где делительная окружность пересекает профиль зуба.
- Круговой шаг : Измерение длины дуги делительной окружности от одной точки на зубе до той же точки на соседнем зубе. 903:30
- Толщина окружности : Толщина зуба на делительной окружности.
- Зазор : пространство между малым диаметром одной шестерни и большим диаметром сопрягаемой шестерни.
- Дедендум : Глубина зуба между делительной окружностью и малым диаметром.
- Диаметральный шаг : Количество зубьев на дюйм делительного диаметра.
- Скругление : Малый радиус, соединяющий профиль зуба с корневой окружностью. 903:30
- Внешний диаметр : Главный диаметр шестерни.
- Шестерня : Шестерня меньшего размера в любой зацепленной паре.
- Окружность тангажа : Окружность, радиус которой равен расстоянию от центра шестерни до точки тангажа. Здесь измеряется скорость шестерни.
- Делительный диаметр : Диаметр делительной окружности.
- Точка тангажа : Точка касания окружностей тангажа пары сопряженных шестерен.
- Угол давления : Угол между линией действия и линией, перпендикулярной линии центров.
- Корневая (или дедендумная) окружность : Меньший диаметр зуба.
- Коэффициент скорости : Отношение оборотов входной шестерни к оборотам выходной шестерни в течение заданного периода времени.
- Полная глубина : Высота зуба от большого диаметра до малого диаметра шестерни.
- Рабочая глубина : Глубина, на которую зуб входит в пространство между зубьями сопряженной шестерни.
Формулы для определения некоторых из этих терминов включают:
| Приложение | 1,0 ÷ диаметральный шаг |
| Зазор | 0,157 ÷ диаметральный шаг |
| Диаметральный шаг | Количество зубьев ÷ средний диаметр |
| Количество зубьев | Делительный диаметр * диаметральный шаг |
| Внешний диаметр | (Количество зубьев + 2) ÷ диаметральный шаг |
| Делительный диаметр | Количество зубьев ÷ диаметральный шаг |
| Толщина зуба | 1,5708 ÷ диаметральный шаг |
| Вся глубина | 2,157 ÷ диаметральный шаг |
| Рабочая глубина | 2 ÷ диаметральный шаг |
Обзор прямозубых зубчатых колес
Реверс-инжиниринг цилиндрических зубчатых колес
Нас часто спрашивают, как реконструировать прямозубые зубчатые колеса, и есть ли у нас возможности для этого.
Ответ: да, мы можем реконструировать образцы клиентов. Мы используем координатно-измерительную машину (КИМ) в сочетании со специализированным программным обеспечением для зубчатых колес, чтобы определить точные параметры данного цилиндрического зубчатого колеса.
Несмотря на то, что можно реконструировать прямозубую шестерню, используя простые измерительные инструменты и немного математических расчетов, этот метод можно использовать только для стандартных шестерен. Часто зубчатое колесо изготавливается на заказ для конкретного применения, и некоторые размеры или допуски будут изменены. Поэтому для определения истинных параметров зубчатого колеса необходимо использовать КИМ или специальное устройство для проверки зубчатых колес. Информацию об этом процессе см. в нашем руководстве по обратному инжинирингу цилиндрических зубчатых колес.
Производство необходимого снаряжения в Grob
В компании Grob мы можем изготовить холоднокатаные прямозубые зубчатые колеса, точно соответствующие спецификациям вашего проекта.