Разность и сумма векторов примеры: Сложение и вычитание векторов

Содержание

Алгебра свободных и скользящих векторов

Меркин Д.Р. Алгебра свободных и скользящих векторов. М: изд-во «Физматгиз», 1962 — 165 с.

В книге дается подробное изложение алгебры свободных и скользящих векторов. Содержание первой главы соответствует в основном программе по векторной алгебре курса высшей математики втузов. Во второй главе рассматривается теория преобразования системы скользящих векторов и приведения их к простейшему виду. Эта теория имеет важное значение в различных вопросах физики и техники; она может рассматриваться также, как вводная глава винтового исчисления.

В книге большое внимание уделено примерам и разъяснению некоторых деталей и особенностей векторного исчисления, весьма важных в приложениях.

Книга может служить учебным пособием для студентов и преподавателей втузов и университетов. Она рассчитана также на инженеров, желающих повысить свою теоретическую подготовку.

ПРЕДИСЛОВИЕ
ВВЕДЕНИЕ
ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА
2. Определение вектора.
3. Классификация векторов.
4. Равенство векторов.
5. Перенос вектора.
6. Нуль-вектор.
7. Компланарность и коллинеарность векторов.
8. Прямопротивоположные векторы.
§ 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ
2. Сумма векторов.
3. Свойства суммы векторов.
4. Правила параллелограмма и параллелепипеда.
5. Разность двух векторов.
6. Свойства модуля суммы векторов.
§ 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО
2. Свойства произведения.
3. Деление вектора на число.
4. Единичные векторы.
5. Орт оси.
6. Коллинеарность двух векторов.
§ 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ
3. Разложение вектора по трем другим векторам.

4. Разложение вектора по ортам базиса.
§ 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ
2. Условие коллинеарности двух векторов.
3. Условие компланарности трех векторов.
4. Линейная зависимость четырех векторов.
§ 6. ПРОЕКЦИИ ВЕКТОРА
2. Свойства составляющих вектора.
3. Проекция вектора на ось.
4. Свойства проекций.
5. Угол между векторами.
6. Вычисление проекций вектора.
7. Теорема о проекции сумммы векторов.
8. Псевдоскаляры.
§ 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА
2. Естественный способ задания свободного вектора.
3. Задание свободного вектора с помощью его проекций (координатный метод).
4. Связь между естественным и координатным способами задания вектора.
5. Задание несвободного вектора.
6. Задание скользящего вектора.
7. Некоторые приложения.
§ 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ
2. Свойства скалярного произведения.
3. Выражение скалярного произведения через проекции векторов.
4. Векторные уравнения геометрических мест.

5. Уравнение плоскости.
7. Изменение проекций вектора при преобразовании координат.
8. Другое определение вектора.
§ 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
2. Примеры из физики.
3. Способ Н. Е. Жуковского построения векторного произведения.
4. Свойства векторного произведения.
5. Разложение вектора-произведения по координатным ортам.
6. Условие коллинеарности двух векторов.
7. Тождество Лагранжа.
8. Полярные и аксиальные векторы.
§ 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
2. Двойное векторное произведение.
3. Разложение вектора по трем другим векторам.
4. Скалярное произведение двух векторных произведений.
5. Векторное произведение двух векторных произведений.
6. Произведение двух смешанных произведений.

7. Взаимные реперы.
§ 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ
2. Уравнение прямой, проходящей через две заданные точки.
3. Плюкерово уравнение прямой в пространстве.
4. Прямая как пересечение двух плоскостей.
§ 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ
ГЛАВА II.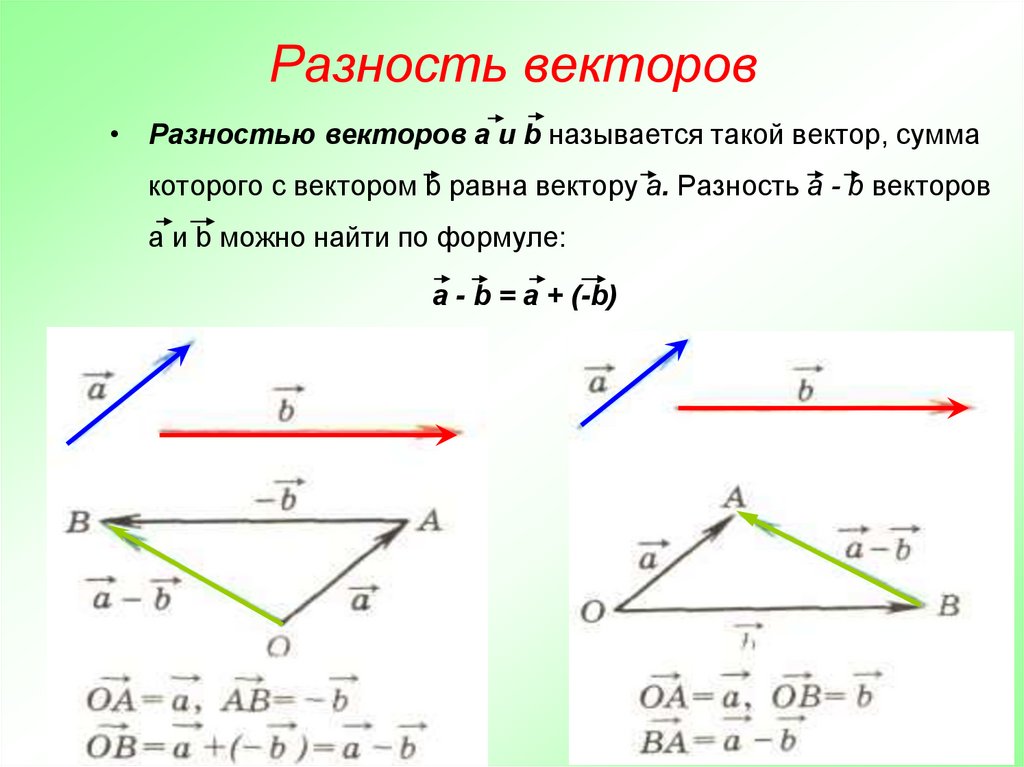

АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ
§ 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА
2. Момент вектора относительно точки.
3. Проекции момента.
4. Момент вектора относительно оси.
5. Задание скользящего вектора его проекциями и моментами относительно координатных осей.
§ 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ
2. Главный вектор системы векторов.
3. Главный момент системы векторов.
4. Система двух равнопротивоположных векторов.
5. Первая теорема Вариньона.
6. Изменение главного момента с изменением полюса.
7. Инварианты системы векторов.
8. Минимальный момент и центральная ось системы.
9. Распределение главных моментов в пространстве.
10. Понятие о винте.
11. Винт системы векторов.
§ 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ
2. Основные определения и аксиомы.
§ 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
§ 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ
2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение).

§ 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ
2. Условия эквивалентности двух систем скользящих векторов.
3. Преобразование эквивалентных систем.
§ 19. ТЕОРИЯ ПАР
1. Пара векторов и ее момент.
2. Свойства пар.
3. Винт
§ 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ
2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение).

3. Приведение системы скользящих векторов к вектору и паре.
4. Пример из кинематики.
5. Приведение системы скользящих векторов к винту.
6. Примеры.
7. Уравнения равновесия векторов.
8. Вторая теорема Вариньона.
§ 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ
2. Плоская система скользящих векторов.
3. Система параллельных скользящих векторов.
4. Центр системы параллельных векторов.

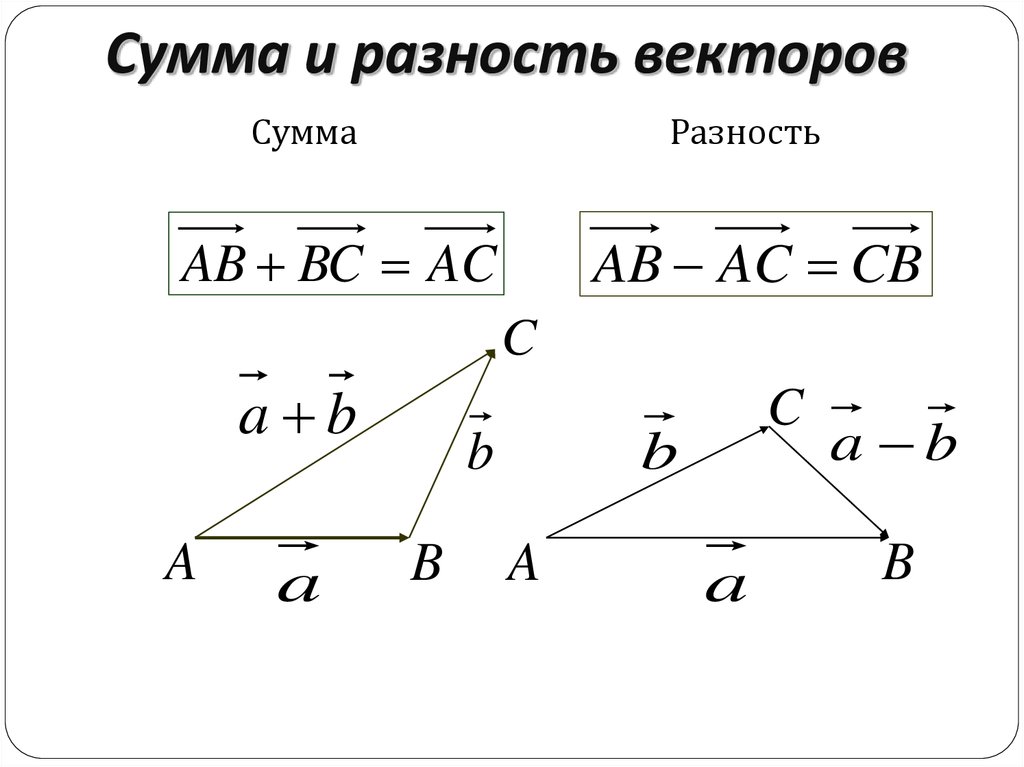
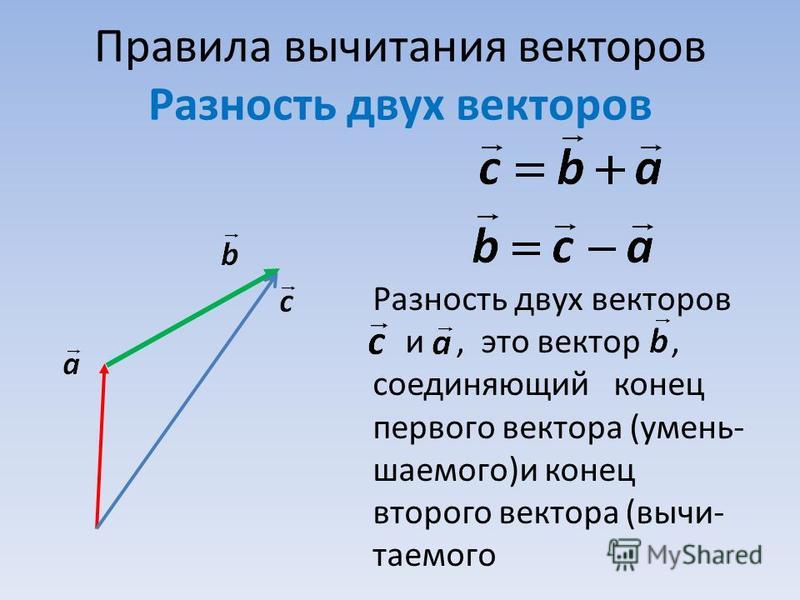
Разность векторов

Разностью x-y векторов x и y называется вектор z такой, что z+y=x.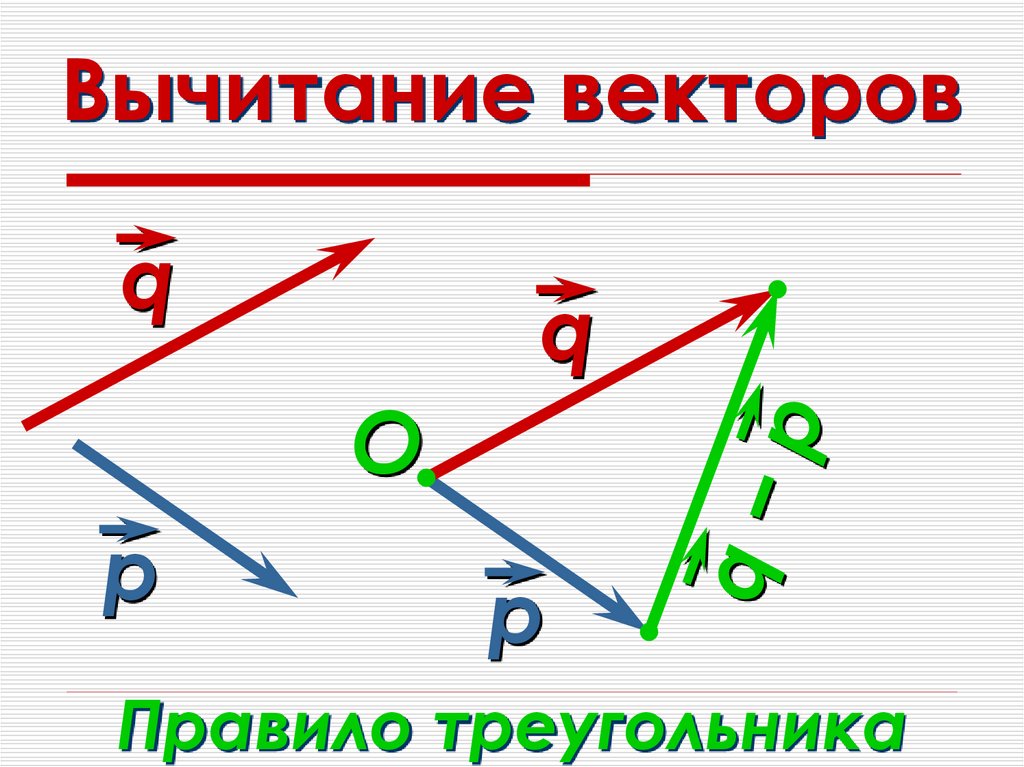

Вариант 1. Начальные точки всех векторов совпадают с началом координат.

Построим разность векторов и .

Для построения разницы векторов z=x-y, нужно сложить вектор x

с противоположным к y вектором y’. Противоположный вектор y’ строится просто:

Вектор y’ является противоположным к вектору y, так как y+y’=0, где 0 — нулевой вектор соответствующего размера. Далее выполняется сложение векторов x и y’:

Из выражения (1) видно что для построения разницы векторов достаточно вычислить разницы соответствующих координатов векторов x и y.

Рис. 1

На рисунке Рис. 1 в двухмерном пространстве представлен разность векторов x=(10,3) и y=(2,4).

Вычислим z=x-y=(10-3,3-4)=(7,-1). Сравним полученный результат с геометрической интерпретацией. Действительно, после построения вектора y’ и параллельного перемещения начальной точки вектора y’ на конечную точку вектора x, получим вектор y», а после сложения векторов x

и y», получим вектор z.

Вариант 2. Начальные точки векторов произвольные.

В этом случае процесс вычисления разницы векторов не так очевиден. Для построения разницы векторов z=x-y, нужно сложить вектор x с противоположным к y вектором y’. Здесь в качестве противоположного к вектору y можно взять тот же вектор y и поменять направление вектора, изменив начальный и коненый точки местами. Можно также взять вектор y’, который симметричен с y относительно начала координат. Если начальный и конечный точки вектора y и , то начальный и конечный точки противоположного вектора y’ будут и соответственно. Таким образом для вычисления разницы векторов x и y, вычисляем сумму векторов x и y’ (подробно см. в разделе сложение векторов).

Рис. 2

На рисунке Рис. 2 в двухмерном пространстве представлен разность векторов

x=AB и y=CD, где A(1,0), B(11,3), C(1,2), D(3,6).

Для вычисления вектора z=x-y, построен противоположный к вектору y вектор y’:

Далее нужно сложить векторы x и y’. Вектор y’ перемещается параллельно так, чтобы точка C’ совпала с точкой B. Для этого вычисляются разницы координатов точек B и С:

Получаем:

Для перемещения точки D’ на точку E, сделаем следующее преобразование координат точки D’

: В результате получим вектор z=AE, A(1,0), E(9, -1), который является разницей векторов x=AB и y=CD.

Интерпретация оси ЭКГ • LITFL • Основы библиотеки ЭКГ

Сердечная ось представляет собой сумму векторов деполяризации, генерируемых отдельными кардиомиоцитами.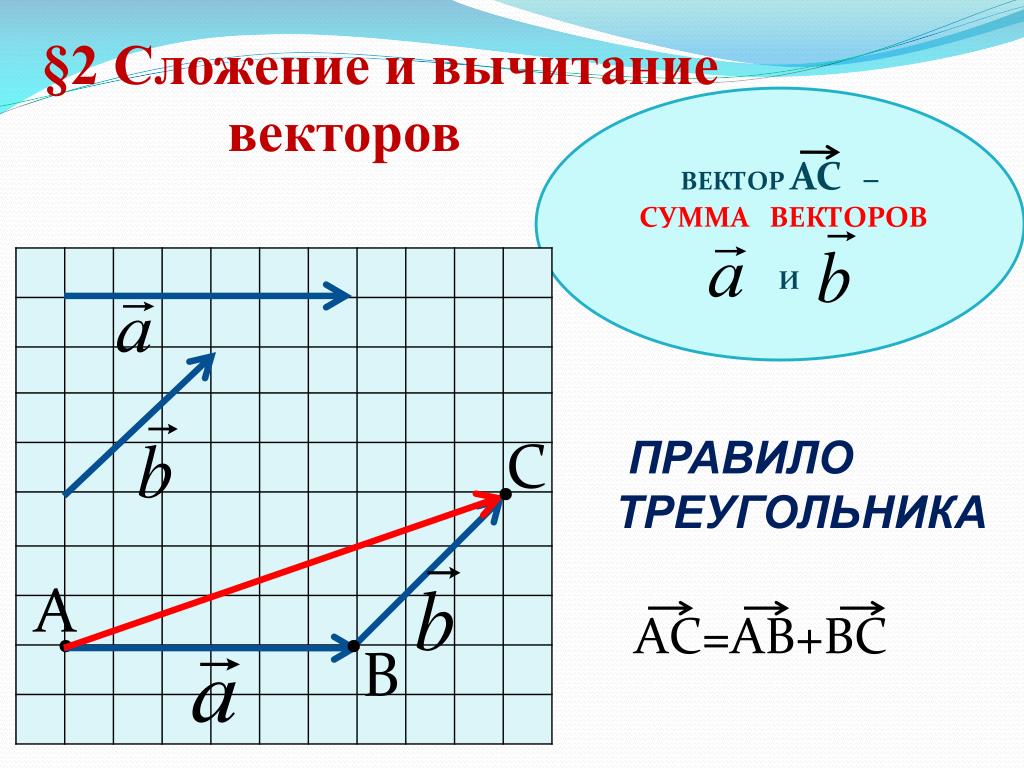 Клинически это отражается осью желудочков, и интерпретация зависит от определения взаимосвязи между осью QRS и отведениями от конечностей на ЭКГ (ниже на диаграмме)

Поскольку в нормальных условиях левый желудочек составляет большую часть сердечной мышцы, нормальная сердечная ось направлен вниз и немного влево:

Нормальная ось = ось QRS между -30° и +90°.

Аномальное отклонение оси, указывающее на лежащую в основе патологию, демонстрируется:

Отклонение оси влево = ось QRS менее -30°.
Отклонение оси вправо = ось QRS больше +90°.
Экстремальное отклонение оси = ось QRS между -90° и 180° (также известная как «северо-западная ось»).

Обратите внимание, что при интерпретации педиатрической ЭКГ ось сердца лежит в диапазоне от +30 до +190 градусов при рождении и движется влево с возрастом .

CardiacAxis.com

Методы интерпретации оси ЭКГ

Существует несколько дополнительных подходов к оценке оси QRS, которые обобщены ниже: (Отведение I, Отведение II и aVF)

Изоэлектрический анализ отведений

Super SAM the Axis Man

Метод 1 – Метод квадранта

Наиболее эффективный способ оценки оси — посмотреть на ОТВЕДЕНИЕ I и ОТВЕДЕНИЕ aVF .

Изучите комплекс QRS в каждом отведении и определите, является ли он положительным, изоэлектрическим (эквифазным) или отрицательным: Положительный QRS в отведении aVF аналогично выравнивает ось с отведением aVF.

Объединение обеих цветных областей – квадрант перекрытия определяет ось. Итак, если отведение I и aVF равны оба положительный , ось находится в диапазоне от 0° до +90° (т. е. нормальная ось).

Теперь оцените AXIS, используя отведение I и aVF – метод квадрантов:

AXIS: QRS положительное отведение I – QRS отрицательное отведение aVFAXIS: QRS отрицательное отведение I – QRS положительное отведение aVFAXIS: QRS отрицательное отведение I – QRS отрицательное отведение aVF
Сводная таблица:
Примечание: **Возможный LAD можно дополнительно оценить с помощью Lead II , как подробно описано в методе 2 ниже…
Метод 2: анализ трех отведений – (отведение I, отведение II и aVF)
Далее мы добавляем отведения II к анализу отведения I и aVF.
A положительный комплекс QRS в отведении I направляет ось примерно в том же направлении, что и отведение I.
Затем мы можем объединить обе цветные области, и область перекрытия определяет ось. Итак, если отведения I и II равны оба положительный , ось находится в диапазоне от -30° до +90° (т. е. нормальная ось).
Комбинированная оценка отведений I, отведений II и aVF позволяет быстро и точно оценить QRS. Добавление отведения II может помочь определить патологическую ПМЖВ по нормальной оси/физиологической ПМЖВ
0012
Теперь оцените AXIS с помощью анализа трех отведений:
Положительное отведение QRS I – Эквифазное отведение QRS II – Отрицательное отведение QRS aVFQRS Положительное отведение I – Отрицательное отведение QRS II – Отрицательное отведение QRS aVFQRS Отрицательное отведение I – Положительное отведение QRS II – Положительное отведение QRS aVFQRS Отрицательное отведение I – Отрицательное отведение QRS II – Отрицательное отведение QRS aVF
Сводная таблица:
Метод 3 – Изоэлектрическое отведение
Этот метод позволяет более точно оценить ось QRS, используя диаграмму оси ниже.
Ключевые принципы
Если QRS ПОЛОЖИТЕЛЬНЫЙ в любом заданном отведении, ось указывает в примерно то же направление , что и в этом отведении.
Если комплекс QRS ОТРИЦАТЕЛЬНЫЙ в любом заданном отведении, ось указывает в приблизительно направлении, противоположном этому отведению.
Если QRS ISOELECTRIC (равнофазный) в любом заданном отведении ( положительное отклонение = отрицательное отклонение ), ось находится в 90° к этому отведению.
Шаг 1: Найдите изоэлектрический электрод. Изоэлектрическое (равнофазное) отведение — это лобное отведение с нулевой амплитудой . Это может быть:
Двухфазный комплекс QRS, где высота зубца R = глубине зубца Q или S.
Комплекс QRS с плоской линией без видимых особенностей.
Шаг 2: Найдите положительные выводы.
Найдите отведения с самыми высокими зубцами R (или самыми высокими отношениями R/S)
Шаг 3: Рассчитайте ось QRS.
Ось QRS находится на 90° изоэлектрического отведения, указывая в направлении положительных отведений.
Поначалу эту концепцию может быть трудно понять, и лучше всего ее можно проиллюстрировать несколькими примерами. Пример 10004
aVF = ПОЛОЖИТЕЛЬНЫЙ
Это помещает ось в квадрант между 0° и +90°, т.е. нормальная ось
положительные и отрицательные прогибы (нет необходимости точно измерять это).
Из приведенной выше диаграммы видно, что aVL расположен на -30° .
Ось комплекса QRS должна находиться в пределах ± 90° от отведения aVL либо на +60°, либо на -120°
При положительных отведениях I (0), II (+60) и aVF (+90) мы знаем, что ось должна лежать где-то между 0 и +90°.
Это ставит ось QRS на +60 ° — , т. Е. Обычная ось
Пример 2 Ответ — Метод квадранта
Head I = отрицательный
Lead II = affice Equivide
999999999999999999999999999999
9999999999
99
9999999999
99999999
9999999 aVF = POSITIVE
Это помещает ось в квадрант между +90° и +180°, т.е. RAD .
Ответ – Метод изоэлектрического отведения
Отведение II (+60°) – это изоэлектрическое отведение .
Ось комплекса QRS должна находиться в пределах ± 90° от отведения II либо на +150°, либо на -30°.
Правые отведения III (+120°) и aVF (+90°) положительные, а aVL (-30°) отрицательные.
Это переводит ось QRS на +150°.
Это пример отклонения ЭОС вправо вследствие гипертрофии правого желудочка.
Пример 3 Ответ — Метод квадранта
LEAND I = Положительный
LEAND II = Equiphasic
СВЕДЕНИЯ AVF = Отрицательный
Это ставит опор в квадрате. 90°, т.е. нормальный или LAD.
Отведение II не является ни положительным, ни отрицательным (изоэлектрическим), что указывает на физиологическую ПМЖВ.
Ответ – Метод изоэлектрического отведения
Отведение II (+60°) является изоэлектрическим .
Ось комплекса QRS должна находиться в пределах ± 90° от отведения II либо на +150°, либо на -30°.
Более левые отведения I (0°) и aVL (-30°) являются положительными, а отведение III (+120°) — отрицательным.
Это подтверждает, что ось находится на -30°.
Это пример пограничного отклонения осевой оси влево из-за нижнего ИМ.
Пример 4 Ответ – Квадрантный метод
Отведение I = ОТРИЦАТЕЛЬНЫЙ
Отведение II = ОТРИЦАТЕЛЬНОЕ
Отведение aVF = ОТРИЦАТЕЛЬНОЕ
Это помещает ось в верхний правый квадрант, между -90° и 180°, т. е. крайнее отклонение оси .
Примечание. Наличие положительного QRS в aVR с отрицательным QRS в нескольких отведениях является еще одним признаком наличия экстремального отклонения оси.
Ответ – Метод изоэлектрического отведения
Наиболее изоэлектрическим отведением является aVL (-30°).
Ось QRS должна быть на ± 90° от aVL на +60° или -120°.
Отведение aVR (-150°) положительное, отведение II (+60°) отрицательное.
Устанавливает ось на -120°.
Это пример крайнего отклонения оси из-за желудочковой тахикардии.
Пример 5 Раскройте ответ
Отведение I = изоэлектрическое.
Отведение aVF = положительное.
Это самая простая ось, которую вам когда-либо приходилось вычислять. Он должен быть под прямым углом к отведению I и в направлении aVF, что делает его ровно +9.0°!
Это называется «вертикальной осью» и наблюдается у пациентов с эмфиземой, у которых обычно сердце расположено вертикально.
Причины отклонения оси
Отклонение оси вправо
Гипертрофия правого желудочка
Острая деформация правого желудочка, например. из-за легочной эмболии
Боковой ИМпST
Хроническое заболевание легких, например. ХОБЛ
Гиперкалиемия
Блокада натриевых каналов, напр. Отравление ТСА
Wolff-Parkinson-White Syndrome
Dextrocardia
Эктопия желудочков
Secundum ASD-RSR ‘Pattern
Нормальная педиатрическая ECG
Левый сзади. Ушибленная диагностика
.
Отклонение оси левого желудочка
Гипертрофия левого желудочка
Блокада левой ножки пучка Гиса
Нижний инфаркт миокарда
Желудочковая стимуляция/эктопия
Wolff-Parkinson-White Syndrome
Primem ASD-RSR ‘Pattern
Левый передний фарсикулярный блок-Диагностика исключения
Горизонтально ориентированные сердца-Краткое пациент с приклеиком
Экстремальная оси.
9009 Вент
Экстрему , AIVR, желудочковая эктопия
Гиперкалиемия
Тяжелая гипертрофия правого желудочка
Дополнительная литература
вести.
Определение оси мастеринга: Часть 1 EMS 12 ВЫДЕЛА
Определение оси мастеринга: Часть 2 EMS 12 ВЫДЕЛА
Определение оси мастеринга: Часть 3 EMS 12 Ведущий
. EMS 12 отведений
Определение основной оси: часть 5 EMS 12 отведений
Определение основной оси: часть 6 EMS 12 отведений
Дополнительная литература
Онлайн
Висбауэр Ф., Кюн П. Мастерство ЭКГ: онлайн-курс «Желтый пояс» — станьте экспертом по ЭКГ. Медмастери
Wiesbauer F, Kühn P. Онлайн-курс «Голубой пояс» по ЭКГ: научитесь диагностировать любые проблемы с ритмом. Медмастери
Равшани А. Клиническая интерпретация ЭКГ Волны ЭКГ
Смит SW. Блог доктора Смита об ЭКГ.
Учебники
Mattu A, Tabas JA, Brady WJ. Электрокардиография в неотложной, неотложной и интенсивной терапии. 2д, 2019
Brady WJ, Lipinski MJ et al. Электрокардиограмма в клинической медицине. 1e, 2020
Straus DG, Schocken DD. Практическая электрокардиография Marriott 13e, 2021
Хэмптон Дж. Практическая ЭКГ 7e, 2019
Грауэр К. Карманный мозг ЭКГ (расширенный) 6e, 2014
Брэди В.Дж., Трувит Д.Д. Критические решения в неотложной и неотложной помощи Электрокардиография 1e, 2009
Surawicz B, Knilans T. Chou Электрокардиография в клинической практике: взрослые и дети 6e, 2008
Mattu A, Brady W. ЭКГ для врача скорой помощи, часть I 1e, 2003 г. и часть II
Chan TC. ЭКГ в неотложной медицине и неотложной помощи 1e, 2004
Smith SW. ЭКГ при остром ИМ. 2002 [PDF]
Цитируйте эту статью как: Майк Кадоган и Роберт Баттнер, «Интерпретация оси ЭКГ», В: LITFL — Life in the FastLane , по состоянию на 10 февраля 2023 г.
No related posts.