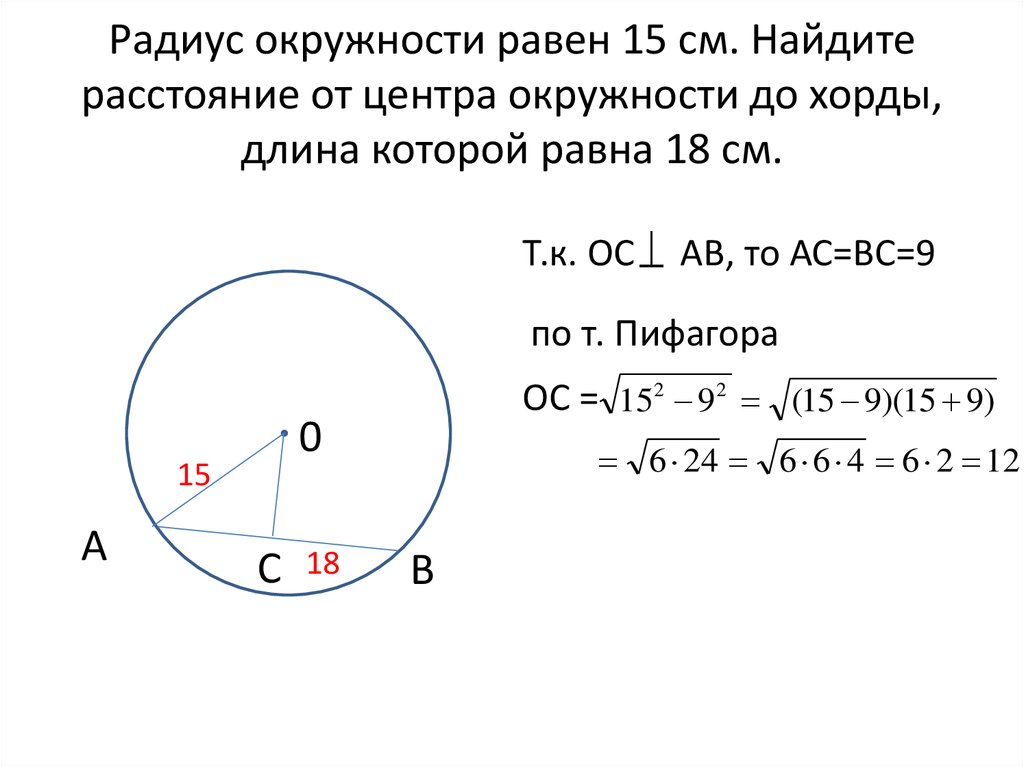
Длина хорды: основные понятия
Бывают случаи в жизни, когда знания, полученные во время школьного обучения, очень полезны. Хотя во время учебы эти сведения казались скучными и ненужными. Например, как можно использовать информацию о том, как находится длина хорды? Можно предположить, что для специальностей, не связанных с точными науками, такие знания малопригодны. Однако можно привести много примеров (от конструирования новогоднего костюма до сложного устройства аэроплана), когда навыки решения задач по геометрии являются нелишними.
Понятие «хорда»
Данное слово означает «струна» в переводе с языка родины Гомера. Оно было введено математиками древнего периода. Хордой обозначают в разделе элементарной геометрии часть прямой линии, которая объединяет две любые точки какой-либо кривой (окружности, параболы или эллипса). Другими словами, данный связующий геометрический элемент находится на прямой, пересекающей заданную кривую в нескольких точках. В случае окружности длина хорды заключена между двумя точками этой фигуры.
Часть плоскости, ограниченная прямой, пересекающей окружность, и ее дугой называют сегментом. Можно отметить, что с приближением к центру длина хорды увеличивается. Часть окружности, находящуюся между двумя точками пересечения данной прямой, называют дугой. Ее мерой измерения является центральный угол. Вершина данной геометрической фигуры находится в середине круга, а стороны упираются в точки пересечения хорды с окружностью.
Свойства и формулы
Длина хорды окружности может быть вычислена по следующим условным выражениям:
L =D×Sinβ или L=D×Sin(1/2α), где β – угол при вершине вписанного треугольника;
D – диаметр окружности;
α – центральный угол.
Можно выделить некоторые свойства данного отрезка, а также других фигур, связанных с ним. Эти моменты приведены в следующем списке:
- Любые хорды, находящиеся на одинаковом расстоянии от центра, имеют равные длины, при этом обратное утверждение также верно.
- Все углы, которые вписаны в окружность и опираются на общий отрезок, который объединяет две точки (при этом их вершины находятся в одной стороне от данного элемента), являются идентичными по величине.

- Самая большая хорда является диаметром.
- Сумма любых двух углов, если они опираются на данный отрезок, но при этом их вершины лежат в разных сторонах относительно него, составляет 180о.
- Большая хорда — по сравнению с аналогичным, но меньшим элементом — лежит ближе к середине данной геометрической фигуры.
- Все углы, которые вписаны и опираются на диаметр, равны 90˚.
Другие вычисления
Чтобы найти длину дуги окружности, которая заключена между концами хорды, можно использовать формулу Гюйгенса. Для этого необходимо провести такие действия:
- Обозначим искомую величину р, а хорда, ограничивающая данную часть окружности, будет иметь название АВ.
- Найдем середину отрезка АВ и к ней поставим перпендикуляр. Можно отметить, что диаметр окружности, проведенный через центр хорды, образует с ней прямой угол. Верно и обратное утверждение. При этом точку, где диаметр, проходя через середину хорды, соприкасается с окружностью, обозначим М.

- Тогда отрезки АМ и ВМ можно назвать соответственно, как l и L.
- Длина дуги может быть вычислена по следующей формуле: р≈2l+1/3(2l-L). Можно отметить, что относительная погрешность данного выражения при возрастании угла увеличивается. Так, при 60˚ она составляет 0,5%, а для дуги, равной 45˚, эта величина уменьшается до 0,02%.
Длина хорды может использоваться в различных сферах. Например, при расчетах и конструировании фланцевых соединений, которые широко распространены в технике. Также можно увидеть вычисление этой величины в баллистике для определения расстояния полета пули и так далее.
Хорда окружности: онлайн-калькулятор, формулы и примеры
Окружность – это фигура на плоскости, все точки которой равноудалены от центра окружности. Окружность
– самая простая фигура, которую можно провести на местности, для этого достаточно колышка для
обозначения центра окружности и веревки с чертилкой. Чтобы вычертить окружность на листе бумаги,
достаточно циркуля.
Хорда – это отрезок, соединяющий 2 любые точки окружности. Самой длинной хордой является диаметр, или согласно другому определению, диаметр – это хорда, проходящая через центр окружности. Нередко появляется практическая необходимость рассчитать длину хорды по известному радиусу окружности и одному из 2 углов, определяющих положение хорды (центральному или вписанному). В окружности центральный угол – это угол, вершина которого располагается в центре окружности, а вписанный угол – это угол, вершина которого лежит на окружности. Или же, вписанный угол — это угол, образованный двумя пересекающимися на окружности хордами.
- Длина хорды через радиус и угол между радиусами
- Длина хорды через вписанный угол и радиус
Через радиус и угол между радиусами
Если известен радиус и угол между радиусами, то формула будет следующая:
L = 2R * sin α/2
где R – радиус окружности, α – центральный угол между радиусами, опирающийся на хорду.
Радиус (R):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Пример. Решим практическую задачу: на местности строится из кирпича сооружение, в плане имеющее форму неполной окружности с радиусом 3 м, со стороны входа стянутой хордой, на которую опирается центральный угол в 36°. Найти длину хорды, что требуется для построения на местности без откладывания угла, а также проверки, достаточно ли в прямой стенке места для входа и устройства двери. L = 2R * sin α/2 = 2 * 3 * sin 36°/2 = 6 * 0,309 = 1,854 (м).
Через вписанный угол и радиус
Если известен вписанный угол и радиус, то формула по нахождению длины хорды следующая:
L = 2R * sin α
где R — радиус, sin α — вписанный угол
Радиус (R):
ммсмдмм
Угол (α):
градусырадианыsin
Цифр после запятой:
012345678910Результат в: ммсмдмм
Удивительно простой вид этой формулы основан на теореме о вписанном угле, согласно которой вписанный
угол равен половине центрального угла, опирающегося на ту же дугу (а соответственно на ту же хорду),
тем самым данная формула выводится из предыдущей.
Пример. В качестве примера, рассчитаем длину хорды в окружности радиусом 10 м, на которую опирается вписанный угол 30°. L = 2R * sin α = 2 * 10 * sin 30° = 20 * 0,5 = 10 (м). Длина хорды оказалась равной радиусу, т.е. представляет собой одну сторону вписанного в окружность шестиугольника.
Таким образом, расчет длины хорды позволяет построить на местности или бумаге любой правильный многоугольник без необходимости откладывания углов, центральных или вписанных. Уже в эпоху первобытного строя люди знали о свойствах окружности, и пользовались ими для своих целей. Одно из самых известных сооружений той поры – Стоунхендж в Англии, предположительно являвшийся астрономической обсерваторией. Следовательно, уже тогда появилась необходимость выдерживать строго центральные и вписанные углы.
геометрия — Найдите длину окружности по хорде и длине остальной части окружности
Задавать вопрос
спросил
Изменено 6 лет, 1 месяц назад
Просмотрено 7к раз
$\begingroup$
Если вы знаете длину хорды в окружности, а также длину окружности за вычетом отрезка, отсекаемого хордой, можете ли вы найти длину окружности?
Например, учитывая рисунок ниже, предположим, что мы знаем $d$, длину синей дуги, а также $b$, длину красной хорды.
Используя информацию о дуге, мы можем получить уравнение с двумя неизвестными, r и $\theta$.
Из уравнения хорды мы можем получить другое уравнение относительно r и $\sin\theta$.
Следующим шагом является объединение этих двух (предполагаемых независимыми) одновременных уравнений в одно путем исключения r (или $\theta$).
Для первого результирующее комбинированное уравнение будет иметь множитель в виде $\dfrac {\sin \theta}{2\pi — \theta}$ (более или менее). Это уравнение относится к типу, называемому трансцендентным уравнением, которое не может быть решено обычным математическим методом. Мы можем получить только приблизительный ответ, используя численные методы. Исключение $\theta$ приведет к еще одному трансцендентному уравнению.
$\endgroup$
$\begingroup$
Если внутренний угол хорды равен $\psi$, то длина хорды равна
$$ S = 2 r \sin \left( \frac{\psi}{2} \right) $$
Также оставшаяся окружность равна $$K = (2\pi-\psi) r$$
Из этих двух уравнений вас просят найти $r$ и $\psi$. К сожалению, аналитических решений нет, потому что, если вы разделите два уравнения, вы получите
К сожалению, аналитических решений нет, потому что, если вы разделите два уравнения, вы получите
$$ \frac{S}{K} = \frac{2 \sin \left( \frac{\psi}{2} \right) }{2\пи — \пси} $$
Получив численное решение, вы получите радиус из $$r = \frac{K}{2\pi-\psi}$$
Приложение I
Если угол действительно мал $\psi \ rightarrow 0$, тогда у вас есть $$\psi \приблизительно \frac{2\pi S}{K+S}$$
или
$$\psi \приблизительно \pi \left( \sqrt{\left( \ frac{4 S}{K}+1\right)}-1 \right) $$
$\endgroup$
2
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Как рассчитать длину хорды
••• robinlaw/iStock/GettyImages
Обновлено 3 ноября 2020 г.
Автор Chris Deziel
Хорда — это отрезок, соединяющий любые две точки на окружности. Диаметр круга, отрезок линии, проходящий через центр, также является его самой длинной хордой. Вы можете рассчитать длину хорды по длине радиуса и углу, образованному линиями, соединяющими центр окружности с двумя концами хорды. Вы также можете рассчитать длину хорды, если знаете как радиус, так и длину правой биссектрисы, то есть расстояние от центра окружности до центра хорды.
TL;DR (слишком длинно, не читал)
Вы можете рассчитать длину хорды окружности, если знаете радиус и одну из двух других переменных. Одной переменной является длина перпендикулярной линии от хорды до центра окружности. Другой — это угол, образованный двумя радиусными линиями, которые касаются точек пересечения хорды и окружности окружности.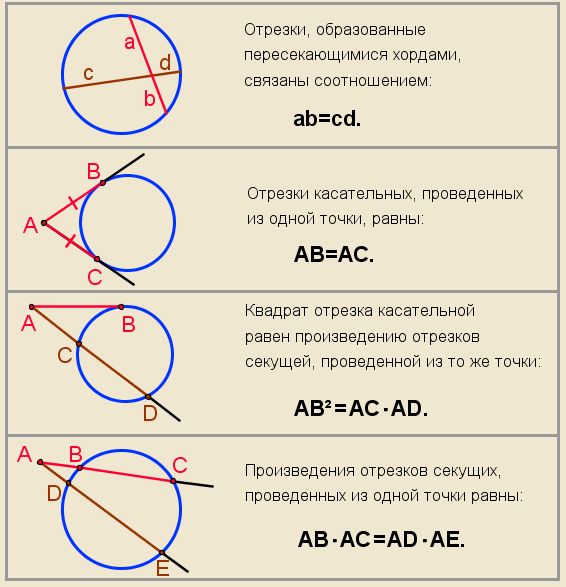
Основная стратегия расчета длины хорды
Тригонометрическая процедура расчета длины хорды начинается с продолжения линий радиуса до каждой точки, в которой хорда пересекает окружность. Это создает треугольник с одной вершиной в центре круга и вершиной в каждой из точек пересечения. Если вы продолжите перпендикулярную линию от хорды к центру круга, она разделит пополам угол этой вершины и создаст два прямоугольных треугольника по обе стороны от хорды. Если весь угол равен θ (тета), угол по обе стороны от линии бисекции равен θ /2.
Теперь вы можете составить уравнение, связывающее длину хорды ( c ) с радиусом ( r ) и углом между двумя линиями радиуса ( θ ). Поскольку половина хорды ( c /2) образует противоположную прямую в прямоугольном треугольнике, а r образует гипотенузу, верно следующее:
\sin \bigg(\frac{ θ}{2}\bigg) = \frac{c/2}{r}
Решение для c :
c = \text{ длина хорды }= \sin \bigg(\frac{θ}{2}\bigg)
Если вы знаете радиус окружности и можете измерить угол θ , у вас есть все необходимое для расчета длины хорды.