|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Интересное: Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны… Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего. Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
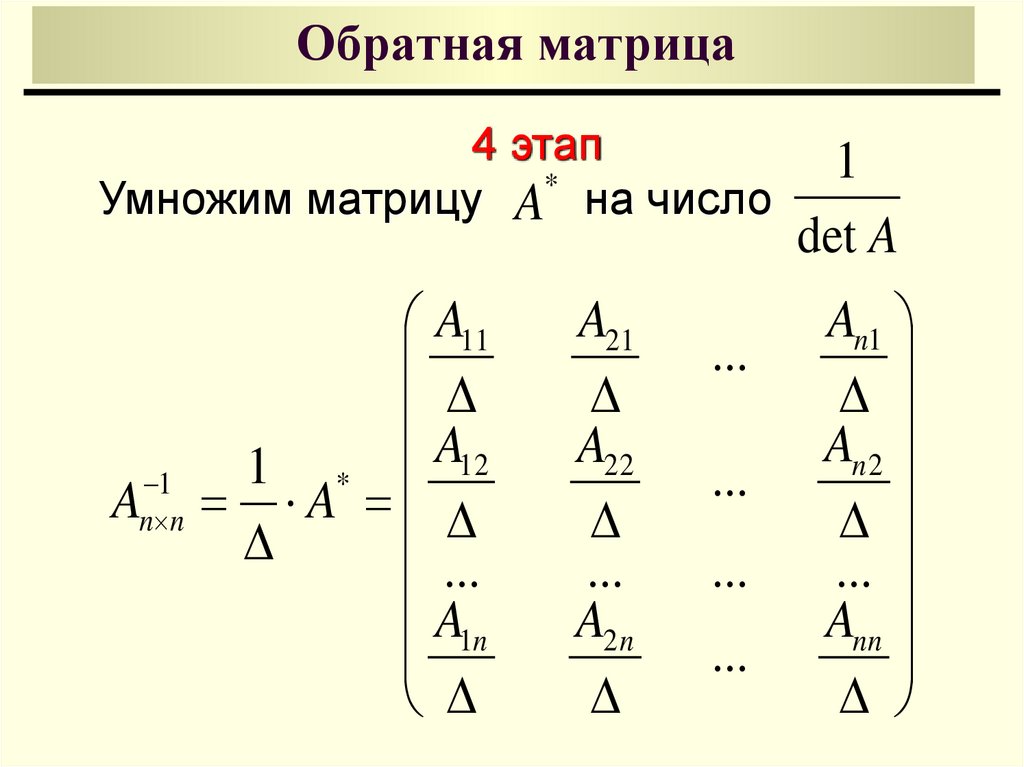
⇐ ПредыдущаяСтр 2 из 2 Матрица называется обратной матрице А, если выполняется условие , где Е – единичная матрица того же порядка, что и матрица А. Квадратная матрица, определитель которой равен нулю, называется вырожденной. Союзная матрица: , где – алгебраическое дополнение элемента ij данной матрицы. Условие существования обратной матрицы. Лемма: Если А – квадратная матрица n-ого порядка, – союзная к ней матрица, то , где Е – единичная матрица n-ого порядка. Доказательство: Рассмотрим произведение матрицы А и При вычислении элементов матрицы произведения, стоящих на главной диагонали, будет получаться сумма произведений элементов i-ой строки матрицы А на их алгебраическое дополнение, а это равно определителю. Для получения остальных элементов матрицы надо находить сумму произведений элементов i-ой строки на алгебраическое дополнение элементов j-ой строки, а это согласно 10-ому свойству определителей равно нулю. Теорема 1, о существовании обратной матрицы. Для того, чтобы существовала матрица , обратная матрице А, необходимо и достаточно, чтобы матрица А была невырожденной. Доказательство. Необходимость. Пусть матрица А имеет обратную матрицу , тогда . По 9-ому свойству определителей . Так как |E|=1, то , следовательно матрица A – невырожденная. Достаточность. Пусть матрица А – невырожденная, то есть . Докажем, что существует такая матрица , которая является обратной к матрице А и докажем, что такой матрицей является , где – союзная матрица к A. Согласно лемме Формула обратной матрицы: Теорема 2, о единственности обратной матрицы. Для невырожденной матрицы существует единственная обратная матрица. Доказательство. Пусть существуют матрицы и обратные невырожденной матрице А, тогда (слева). 10. Ранг матрицы и его свойства. Рассмотрим матрицу . Выделим в ней k строк и k столбцов, где , необязательно рядом. Рангом матрицы А называется наибольший из порядков миноров данной матрицы, отличных от нуля. Обозначается r, r(A), rang. Из определения следует: 1. Ранг матрицы не превосходит меньший из ее размеров, то есть . 2. , тогда и только тогда, когда все элементы матрицы равны нулю, то есть матрица – нулевая. 3. Для квадратной матрицы n-ого порядка r=n тогда и только тогда, когда матрица А – невырожденная. Свойства ранга матрицы: 1. При транспонировании ранг матрицы не меняется. 2. Ранг матрицы, полученный из данной вычеркиванием какого-либо ряда, равен рангу данной матрицы или меньше его на единицу. 3. Ранг матрицы, полученный из данной приписыванием к ней ряда, элементами которого являются произвольные числа, равен рангу исходной матрицы или больше его на единицу. 4. Если вычеркнуть из матрицы или прибавить к ней нулевой ряд, то ранг матрицы не меняется. 5. Ранг матрицы не изменяется при элементарных преобразованиях матрицы.
11. (только практика) Способы вычисления ранга. 1 способ, по определению. 2 способ, с помощью приведению к виду трапеции. Ранг равен количеству ненулевых строк. 3 способ. Максимальное число линейно независимых строк/столбцов матрицы равно рангу матрицы. 12.Сформулировать элементарные преобразования матриц. Определение эквивалентных матриц. Элементарные преобразования матрицы: 1. Отбрасывание нулевого ряда. 2. Умножение всех элементов матрица на число неравное нулю. 3. Перестановка местами двух параллельных рядов матрицы. 4. Прибавление к каждому элементу одного ряда соответствующих элементов параллельного ряда, умноженных на одно и то же число. Две матрицы называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. 14.Определение системы линейных уравнений (в том числе, что значит решить систему, какие системы называются совместными, определенными и эквивалентными). Системой линейных уравнений, содержащей m уравнений и n неизвестных, называется система вида: , где числа – коэффициенты при неизвестных, – свободные члены, – неизвестные или переменные. Решением системы уравнений называется упорядоченная система чисел при подстановке которой все уравнения системы обращаются в верное равенство. Решить систему – значит выяснить, совместна ли она или несовместна. Если система совместна – найти все ее решения. Система уравнений называется совместной, если она имеет хотя бы одно решение и не совместной, если она не имеет решений. Совместная система называется определенной, если она имеет единственное решение и неопределенной, если она имеет более одного решения. Системы уравнений называют эквивалентными (равносильными), если они имеют одно и то же множество решений. Элементарные преобразования систем: 1. Умножение некоторого уравнения системы на число, отличное от нуля. 2. Прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число. 3. Перестановка местами двух уравнений системы или слагаемых в уравнениях. 4. Вычеркивание нулевого уравнения. 5. Удаление уравнений, являющимися линейными комбинациями других уравнений системы. Матрица, состоящая из коэффициентов при неизвестных называется основной матрицей системы. – матрица неизвестных; – матрица свободных членов; – матричная форма записи системы.
13.Определение базисного минора матрицы. Сформулировать теорему о базисном миноре. Следствия из данной теоремы. Базисным минором матрицы называют отличный от нуля ее минор, порядок которого равен рангу матрицы. Строки и столбцы, на пересечении которых стоят элементы базисного минора, называют базисными. Теорема о базисном миноре: 1. Любая строка/столбец матрицы является линейной комбинацией базисных строк/столбцов. 2. Базисные строки/столбцы линейно независимы. Из теоремы следует: Максимальное число линейно независимых строк/столбцов матрицы равно рангу матрицы. 15.(только практика) Решение системы матричным способом. Метод обратной матрицы. Применим только для случая, когда число уравнений равно числу неизвестных. Основная матрица системы – квадратная порядка n. Определитель этой матрицы называется определителем системы. Если определитель системы отличен от нуля, то матрица А – невырожденная и существует обратная матрица . , то есть решение системы существует. Если определитель системы = 0, то система не имеет решения. 16.(только практика) Решение системы методом Крамера. Применим только для случая, когда число уравнений равно числу неизвестных. , где ∆ — определитель основной матрицы; – определитель, полученный из определителя ∆ заменой i-ого столбца столбцом свободных членов матрицы b.
17.(только практика) Решение системы методом Гаусса. Применим для решения систем общего вида, содержащих m уравнений и n неизвестных. Метод Гаусса – метод последовательного исключения переменных. Заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе трапециевидного или треугольного вида (прямой ход), из которого последовательно, начиная с последних по номеру переменных находятся все остальные переменные (обратный ход). Прямой ход. 1. Составить расширенную матрицу системы. (Расширенная матрица системы получается из основной матрицы приписыванием столбца свободных членов). 2. С помощью элементарных преобразований строк расширенной матрицы приводим ее к трапециевидному или треугольному виду. 3. Если число ненулевых строк преобразованной матрицы равно числу ненулевых строк части матрицы, стоящей слева от вертикальной черты, то система совместна. Обратный ход. 1. Если преобразованная матрица приведена к треугольному виду, то система имеет единственное решение, начиная с последнего ее уравнения последовательно находят значения всех ее неизвестных. 2. Если преобразованная система имеет трапециевидный вид, то система имеет бесконечное множество решений. В этом случае неизвестные называют свободными и формируют правые части уравнений, оставим в левых частях слагаемые, содержащие базисные переменные. Количество базисных переменных равно количеству ненулевых строк трапециевидной матрицы (равно рангу матрицы).
Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства. Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
Обратная матрица 3×3
Чтобы найти обратную матрицу 3×3, нам сначала нужно вычислить определитель матрицы. Определитель — это значение, которое можно вычислить для любой квадратной матрицы. Обозначается символом |A|.
Чтобы вычислить определитель матрицы 3×3, мы используем следующую формулу:
|А| = a11(a22a33 – a23a32) – a12(a21a33 – a23a31) + a13(a21a32 – a22a31)
, где A – наша матрица 3×3, а aij представляет элемент в i-й строке и j-м столбце.
Теперь, когда у нас есть определитель, мы можем вычислить обратную матрицу 3×3, используя следующую формулу:
A-1 = 1/|A| * [a33(-a12 + a13) – a32(a11 – a13) + a31(-a11 + a12)]
[-(a23*-a12 + a22*a13) + (a21*-a13 + a23*a11)]
[ a22(-a31 + ia32) – ia21(w30 – w32)]
где A-1 — наша обратная матрица, 1/|A| известен как адъюгат или кофактор и используется для умножения каждого из них.
Что является обратной матрицей 3×3?
В математике обратной матрицей называется матрица, которая при умножении на исходную матрицу дает единичную матрицу. Обратная матрица 3×3 — это матрица, которая при умножении на исходную матрицу 3×3 дает единичную матрицу 3×3.
Обратную матрицу можно найти с помощью нескольких различных методов, включая метод сопряженных уравнений, метод Гаусса-Жордана и метод определителя. Обратные матрицы важны в математике, потому что их можно использовать для решения систем линейных уравнений.
Обратная матрица 3×3 определяется как:
Обратная = 1/det(A) * adj(A)
, где det(A) — определитель A, а adj(A) — сопряженная A.
Чтобы найти обратную матрицу 3×3 с помощью метода определителя, сначала вычислите определитель матрицы. Определитель находится путем произведения диагональных элементов и вычитания произведения недиагональных элементов. Например, если у нас есть следующая матрица 3×3:
A = [1 2 3] B = [-1 0 1] C = [0 -2 4] 9-1 = 1/det(A) * adj(A)
, где det(A) — определитель A, а adj(A) — сопряженная матрица A.
Обратная матрица 3×3, в частности, полезен при решении систем линейных уравнений. Чтобы найти обратную матрицу 3 × 3, мы должны сначала вычислить определитель и сопряженную матрицу данной матрицы. Для вычисления определителя используем следующую формулу:
det(A) = a11*a22*a33 + a12*a23*a31 + a13*a21*a32 – a13*a22*a31 – a12*a21*a33 – a11* а23*а32 9(i+j)*Mji
, где Ci — элемент i,j в матрице кофакторов, а Mji — элемент j,i в исходной (транспонированной) матрице.
Сопряженный к матрице 3×3
Предполагая, что A обратим, сопряженный к A определяется как
Adj(A) = (1/det(A))*transpose(cof(A))
Где transpose(cof(A)) — матрица кофакторов матрицы A. Кофактор матрицы 3×3 определяется следующим образом:
Учитывая матрицу
[ a b c ]
[ d e f ]
[ g h i ]
Матрица кофакторов определяется как
[ det(e,f,h,i) -det(b,c,h,i) det(b,c,e,f) ]
[ -det(d, f,g,i) det(a,c,g,i) -det(a,c,d.f) ]
[ det(d. e.g.h) -det(abg.h) det(-a,-b,-e,-f )]
e.g.h) -det(abg.h) det(-a,-b,-e,-f )]
Определитель матрицы 3×3
Чтобы вычислить обратную матрицу 3×3, нам сначала нужно вычислить определитель матрицы. Определитель — это значение, которое можно вычислить для любой квадратной матрицы. Это единственное число, которое представляет общую структуру матрицы.
Для вычисления определителя матрицы 3×3 воспользуемся следующей формулой:
det(A) = a11(a22a33 – a23a32) – a12(a21a33 – a23a31) + a13(a21a32 – a22a31)
где A — наша матрица 3×3, а aij представляет элемент в i-й строке и j-м столбце.
Например, допустим, у нас есть следующая матрица 3×3:
A = [1 2 3] [4 5 6] [7 8 9]
Затем мы можем вычислить ее определитель, используя приведенную выше формулу:
дет(А) = 1*(5*9 – 6*8) – 2*(4*9– 6*7) + 3*(4*8 – 5*7) дет(А) = 1*45 – 2*54 + 3*56 дет(А) = 45 – 108 + 168 дет(А) = 105
Формула, обратная матрице 3×3
Чтобы найти обратную матрицу 3×3, необходимо сначала вычислить определитель матрицы. Определитель — это значение, которое представляет величину и направление вектора. Он рассчитывается путем скалярного произведения трех векторов, составляющих матрицу.
Определитель — это значение, которое представляет величину и направление вектора. Он рассчитывается путем скалярного произведения трех векторов, составляющих матрицу.
После того, как вы вычислили определитель, вы можете найти обратную матрицу, используя следующую формулу:
inverse(A) = 1/det(A) * adj(A)
, где A — матрица 3×3, а adj(A) — сопряженная матрица матрицы A.
Сопряженная матрица находится по формуле транспонировать матрицу кофакторов. Матрица кофакторов представляет собой матрицу 3 × 3, которая содержит значения, используемые для вычисления определителя. Чтобы найти матрицу кофакторов, вы берете каждый элемент по очереди и умножаете его на соответствующий кофактор.
Нахождение обратной матрицы 3×3 с использованием операций со строками
Чтобы найти обратную матрицу 3 × 3 с помощью операций со строками, нам нужно использовать определитель и сопряжение матрицы. Определитель — это скалярное значение, которое можно вычислить из элементов квадратной матрицы. Обозначается как |А| или дет(А). Для матрицы 3×3 мы можем вычислить определитель по следующей формуле:
Обозначается как |А| или дет(А). Для матрицы 3×3 мы можем вычислить определитель по следующей формуле:
|A| = a11(a22a33 – a23a32) – a12(a21a33 – a23a31) + a13(a21a32 – a22a31)
Кофактор элемента квадратной матрицы – это определитель подматрицы, образованной удалением строки и столбца, содержащего этот элемент. Сопряженная матрица, обозначаемая как adj(A), является транспонированной матрицей кофакторов. Другими словами, это получается путем транспонирования каждой матрицы кофакторов Cij.
Например, для следующей матрицы 3×3 A:
A = 1 2 3 4 5 6 7 8 9
имеем:
|A| = 1(5 9 – 6 8) – 2(4 9 – 6 7) + 3(4 8 – 5 7) = 1*54-2*48+3*47 = 36-96+141 = 81
Решение системы уравнений 3×3 с использованием обратной операции
Систему линейных уравнений можно решить с помощью операции матричной обратной операции. В этом сообщении блога мы покажем вам, как решить систему уравнений 3 × 3 с использованием обратных матриц.
Для начала нам нужно определить, что такое обратная матрица. Обратная матрица — это квадратная матрица, которая при умножении на исходную матрицу дает единичную матрицу. Единичная матрица — это особая матрица, в которой 1 на главной диагонали и 0 на всех остальных.
Обратная матрица — это квадратная матрица, которая при умножении на исходную матрицу дает единичную матрицу. Единичная матрица — это особая матрица, в которой 1 на главной диагонали и 0 на всех остальных.
Теперь, когда мы знаем, что такое обратная матрица, мы можем использовать ее для решения нашей системы уравнений 3×3. Для этого нам нужно умножить обе части нашего уравнения на обратную матрицу коэффициентов. Это аннулирует матрицу коэффициентов в левой части, оставив нам только вектор наших решений в правой части.
Затем мы можем решить для каждой переменной в нашем векторе решения путем деления на соответствующий элемент в инвертированной матрице коэффициентов. Получив решения, мы можем снова подключить их к исходному уравнению, чтобы убедиться, что они верны.
В этом сообщении блога мы показали, как решить систему уравнений 3×3 с использованием обратных матриц. Мы надеемся, что вы нашли это полезным!
Обратная матрица 3×3 Примеры
Когда мы говорим об обратной матрице, мы говорим о матрице, которая при умножении на исходную матрицу дает единичную матрицу. Другими словами, это матрица, которая отменяет работу исходной матрицы.
Другими словами, это матрица, которая отменяет работу исходной матрицы.
Чтобы найти обратную матрицу 3×3, нам нужно использовать следующую формулу: 9-1 = 1/det(A) * adj(A)
Где det(A) — определитель A, а adj(A) — сопряженный A.
Определитель — это значение, которое можно вычислить для любого квадратная матрица. По сути, это способ измерить, насколько «обратима» матрица. Если определитель равен 0, то у матрицы нет обратной, потому что она необратима.
Адъюгат матрицы также известен как матрица кофакторов. Чтобы вычислить его, мы берем транспонированную матрицу кофакторов A. Матрица кофакторов — это просто миноры A, деленные на соответствующий элемент в определителе. Итак, если у нас есть:
А = [а б в; г д е; g h i]
тогда:
|b c| |е ф| |ч я| 1/det(A)*[[d -g] [i -h] [-f g] [a -c] [-i b] [
Заключение
В этой статье мы рассмотрели обратную Матрица 3×3 и что это значит. Мы также видели несколько примеров того, как вычислить обратную матрицу. Помните, что обратная матрица определена только для квадратных матриц (матриц с одинаковым количеством строк и столбцов). Итак, если вы когда-нибудь застряли, пытаясь вычислить обратную матрицу, убедитесь, что она квадратная, прежде чем продолжить.
Помните, что обратная матрица определена только для квадратных матриц (матриц с одинаковым количеством строк и столбцов). Итак, если вы когда-нибудь застряли, пытаясь вычислить обратную матрицу, убедитесь, что она квадратная, прежде чем продолжить.
Линейная алгебра: поиск обратной матрицы с помощью Python | Чао Де-Ю | январь 2023 г.
Часть 3. Подробное пошаговое руководство по нахождению обратной матрицы с использованием элементарных операций со строками и определителей матрицы
Фото Раймонда Клавинса на Unsplashоперации. В этой статье мы подробно рассмотрим два разных метода получения обратной матрицы с помощью элементарных операций со строками и с использованием определителей матрицы.
Обратная -матрица аналогична -обратному числу таким образом, что -кратное умножение числа на его обратное дает 1 , а -умножение матрицы на обратную дает -единичную матрицу4 .
 Однако, чтобы найти обратную матрицу, матрица должна быть квадратной с одинаковым количеством строк и столбцов. Существует два основных метода нахождения обратной матрицы:
Однако, чтобы найти обратную матрицу, матрица должна быть квадратной с одинаковым количеством строк и столбцов. Существует два основных метода нахождения обратной матрицы:
Вспомнил 3 типа операций со строками, используемых для решения линейных систем: замена, изменение масштаба и поворот. Эти операции можно записать на элементарные матрицы . А левое умножение с расширенной матрицей линейной системы представляет собой элементарных операции со строками .
Пример расширенной матрицы линейной системы. (Изображение автора)Замена матрицы : поменять местами строки i и j единичной матрицы.
Поменять местами строку 1 и строку 2 матрицы A. (Изображение автора)Масштабирование матрицы : если операция k раз уравнение i, поместите число k в позицию (строка = i, столбец = i) тождества матрица.
Строка 1 умножается на константу 3. (Изображение автора) Сводная матрица : если кратное уравнение i добавляется к уравнению j, поместите число k в позицию (строка = j, столбец = i) тождества матрица.
Теперь мы можем использовать элементарные матрицы с по и найти обратную матрицу .
- Если A обратимо, то Eₖ…E₂E₁A = I
- Умножьте обе части на A в обратном порядке, получится:
- Последовательность операций с элементарными строками может свести A к I, и та же последовательность операций с элементарными строками превращает I в обратную матрицу A.
- Если A является обратимой матрицей , то для каждого вектор-столбца b система уравнений, Ax = b имеет ровно одно решение .
Пример нахождения инверсии A с использованием операций со строками:
Нахождение инверсии A с использованием операций со строками. (Изображение автора) Нахождение обратного с помощью элементарных матриц. (Изображение автора)Определитель и инверсия матрицы 2 x 2
Определитель матрицы, det(A) или |A|, является полезным значением для квадратной матрицы. Для матрицы A 2 на 2, приведенной ниже, det(A) = ad — bc , и A обратима, если det(A) ≠ 0. Для матрицы 2 x 2 обратная матрица определяется как:
Для матрицы A 2 на 2, приведенной ниже, det(A) = ad — bc , и A обратима, если det(A) ≠ 0. Для матрицы 2 x 2 обратная матрица определяется как:
Однако, чтобы вычислить определитель матрицы размером больше 2 x 2, нам нужно получить ее миноры и кофакторы.
Миноры и кофакторы
Для квадратной матрицы A минор записи aᵢⱼ, Mᵢⱼ, определяется как определитель подматрицы, образованной удалением i-й строки и j-го столбца из матрицы A и кофактора записи aᵢⱼ, Cᵢⱼ, выглядит следующим образом:
Уравнение кофакторов из миноров. (Изображение автора)Иллюстрация того, как получить миноры и кофакторы из квадратной матрицы A. (Изображение автора)Расширение кофактора для получения определителя матрицы
Определитель квадратной матрицы можно вычислить путем умножения элементов в любом строку или столбцы соответствующими кофакторами и сложением полученных продуктов:
Наконец, обратная матрица может быть вычислена путем умножения транспонированной матрицы кофакторов на 1/детерминант .




 Из элементов, стоящих на пересечении выделенных строк и столбцов составить определитель k-ого порядка. Все такие определители называются минорами матрицы (не путать с минорами элементов!!!).
Из элементов, стоящих на пересечении выделенных строк и столбцов составить определитель k-ого порядка. Все такие определители называются минорами матрицы (не путать с минорами элементов!!!).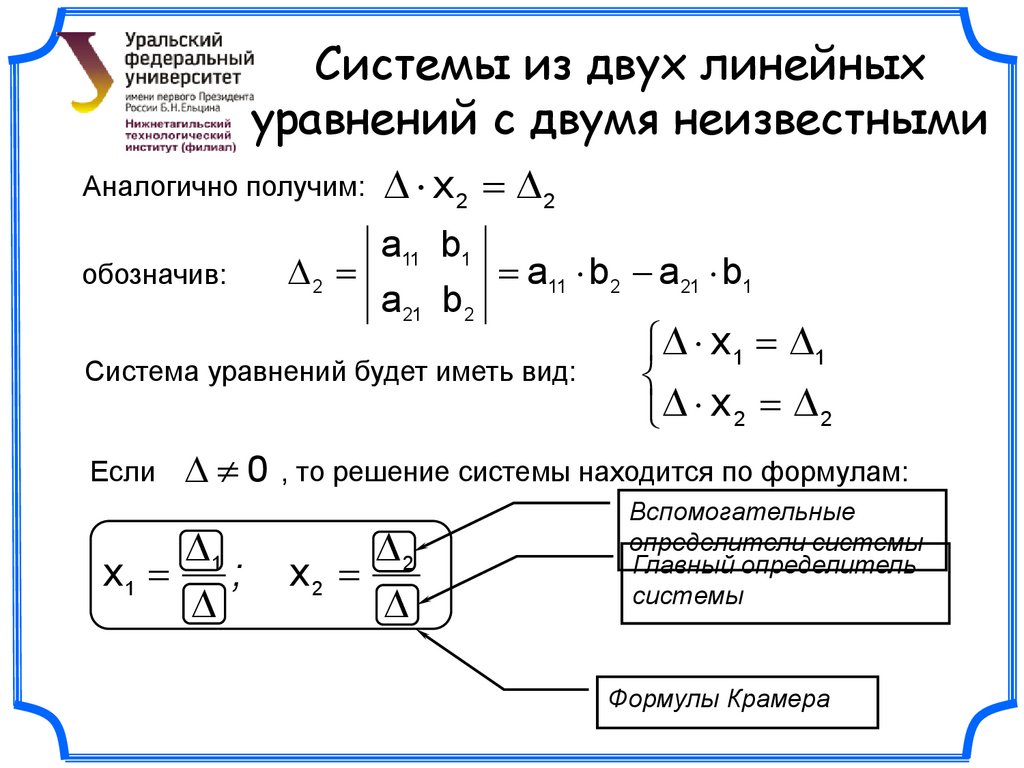
 Обозначаются .
Обозначаются .


 В противном случае она несовместна.
В противном случае она несовместна. ..
..