6 способов найти площадь трапеции
27 марта 2020 Ликбез Образование
Выбирайте формулу в зависимости от известных величин.
1. Как найти площадь трапеции через основания и высоту
Посчитайте сумму оснований трапеции.
Умножьте результат на высоту и поделите на два.
Иллюстрация: Лайфхакер- S – искомая площадь трапеции.
- a и b – основания трапеции (её параллельные стороны).
- h – высота трапеции.
2. Как вычислить площадь трапеции через высоту и среднюю линию
Просто умножьте высоту трапеции на среднюю линию.
Иллюстрация: Лайфхакер- S – искомая площадь трапеции.
- m – средняя линия трапеции (отрезок, соединяющий середины боковых сторон).
- h – высота трапеции.
3. Как найти площадь трапеции через диагонали и угол между ними
Умножьте одну диагональ на другую, а затем — на синус любого угла между ними.
Поделите результат на два.
Иллюстрация: Лайфхакер- S – искомая площадь трапеции.

- x и y – диагонали трапеции.
- α – любой угол между диагоналями.
4. Как найти площадь трапеции через четыре стороны
Отнимите от большего основания меньшее.
Найдите квадрат полученного числа.
Прибавьте к результату квадрат одной боковой стороны и отнимите квадрат второй.
Поделите полученное число на удвоенную разность оснований.
Найдите квадрат результата и отнимите его от квадрата боковой стороны.
Найдите корень из полученного числа.
Умножьте результат на половину от суммы оснований.
Иллюстрация: Лайфхакер- S – искомая площадь трапеции.
- a, b – основания трапеции.
- c, d – боковые стороны.
5. Как вычислить площадь равнобедренной трапеции через четыре стороны
Отнимите от большего основания трапеции меньшее и поделите результат на два.
Найдите квадрат полученного числа и отнимите его от квадрата боковой стороны.
Найдите корень из результата.
Умножьте полученное число на сумму оснований и поделите на два.
- S — искомая площадь трапеции.
- a, b — основания трапеции.
- c, d — боковые стороны (напомним, в равнобедренной трапеции они равны).
6. Как найти площадь равнобедренной трапеции через радиус вписанной окружности и угол
Найдите квадрат радиуса и умножьте его на четыре.
Поделите результат на синус известного угла.
Иллюстрация: Лайфхакер- r — радиус вписанной окружности.
- α — любой угол трапеции.
Читайте также 📐✏️🎓
- 8 способов найти длину окружности
- 8 способов найти периметр треугольника
- 7 способов найти площадь прямоугольника
- Как перевести обычную дробь в десятичную
- Как освоить устный счёт школьникам и взрослым
Площадь равнобедренной трапеции через.
 Как найти площадь трапеции
Как найти площадь трапецииПрактика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции. Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними:
Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними:
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α.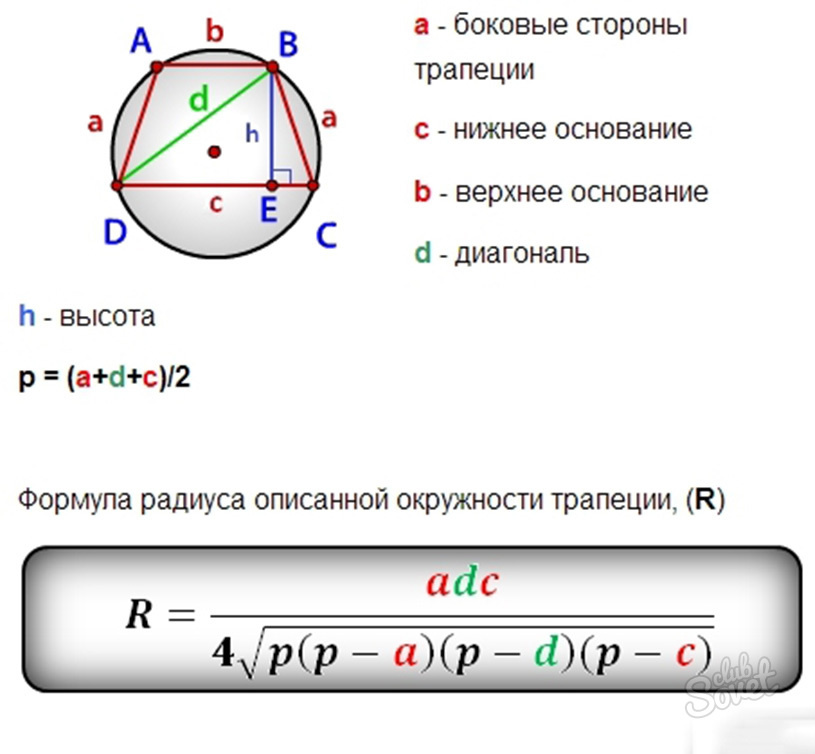
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα . Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение:
Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение: Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Раздел содержит задачи по геометрии (раздел планиметрия) о трапециях. Если Вы не нашли решения задачи — пишите об этом на форуме. Курс наверняка будет дополнен.
Трапеция. Определение, формулы и свойства
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого ровно одна пара противолежащих сторон параллельна.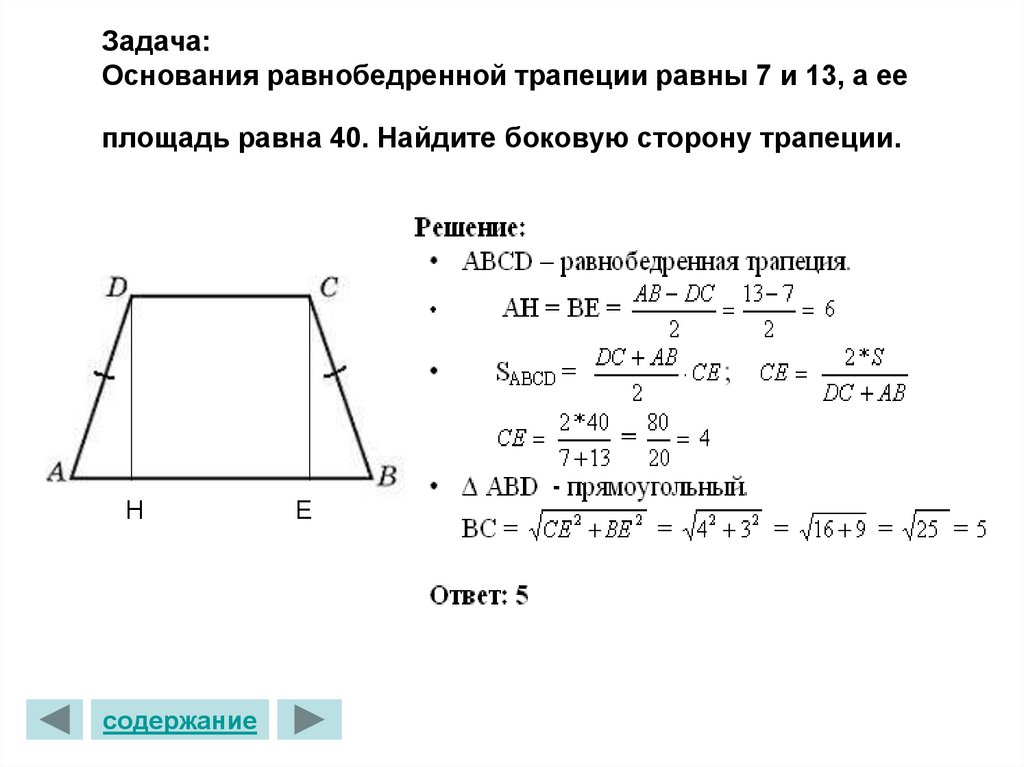
Трапеция — четырёхугольник, у которого пара противолежащих сторон параллельна.
Примечание. В этом случае параллелограмм является частным случаем трапеции.
Параллельные противоположные стороны называются основаниями трапеции, а две другие — боковыми сторонами.
Трапеции бывают:
— разносторонние ;
— равнобокие ;
— прямоугольные
.
Красным и коричневым цветами обозначены боковые стороны, зеленым и синим — основания трапеции.
A — равнобокая (равнобедренная, равнобочная) трапеция
B — прямоугольная трапеция
C — разносторонняя трапеция
У разносторонней трапеции все стороны разной длины, а основания параллельны.
У боковые стороны равны, а основания параллельны.
У основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям.
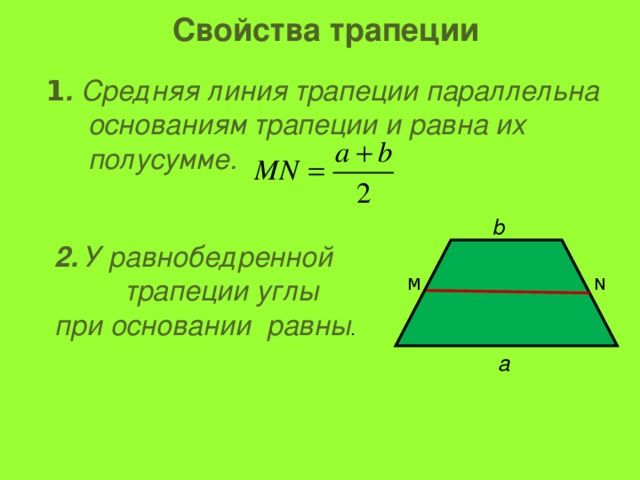
Свойства трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме
- Отрезок, соединяющий середины диагоналей , равен половине разности оснований и лежит на средней линии.
 Его длина
Его длина - Параллельные прямые, пересекающие стороны любого угла трапеции, отсекают от сторон угла пропорциональные отрезки (см. Теорему Фалеса)
- Точка пересечения диагоналей трапеции , точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой (см. также свойства четырехугольника)
- Треугольники, лежащие на основаниях трапеции, вершины которых являются точкой пересечения ее диагоналей являются подобными. Соотношение площадей таких треугольников равно квадрату соотношения оснований трапеции
- Треугольники, лежащие на боковых сторонах трапеции, вершины которых являются точкой пересечения ее диагоналей являются равновеликими (равными по площади)
- В трапецию можно вписать окружность , если сумма длин оснований трапеции равна сумме длин её боковых сторон. Средняя линия в этом случае равна сумме боковых сторон, делённой на 2 (так как средняя линия трапеции равна полусумме оснований)
- Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам и равен удвоенному произведению оснований, деленному на их сумму 2ab / (a +b) (Формула Буракова)
Углы трапеции
Углы трапеции бывают острые, прямые и тупые .
Прямыми бывают только два угла.
У прямоугольной трапеции два угла прямые , а два других – острый и тупой. У других видов трапеций бывают: два острых угла и два тупых.
Тупые углы трапеции принадлежат меньшему по длине основанию, а острые – большему основанию.
Любую трапецию можно рассматривать как усеченный треугольник , у которого линия сечения параллельна основанию треугольника.
Важно . Обратите внимание, что таким способом (дополнительным построением трапеции до треугольника) могут решаться некоторые задачи про трапецию и доказываются некоторые теоремы.
Как найти стороны и диагонали трапеции
Нахождение сторон и диагоналей трапеции делают с помощью формул, которые приведены ниже:
В указанных формулах применяются обозначения, как на рисунке.
a — меньшее из оснований трапеции
b — большее из оснований трапеции
c,d — боковые стороны
h 1 h 2 — диагонали
Сумма квадратов диагоналей трапеции равна удвоенному произведению оснований трапеции плюс сумма квадратов боковых сторон (Формула 2)
Практика прошлогодних ЕГЭ и ГИА показывает, что задачи по геометрии вызывают сложности у многих школьников. Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
Вы легко справитесь с ними, если заучите все нужные формулы и попрактикуетесь в решении задач.
В этой статье вы увидите формулы нахождения площади трапеции, а также примеры задач с решениями. Такие же могут попасться вам в КИМах на аттестационных экзаменах или на олимпиадах. Поэтому отнеситесь к ним внимательно.
Что нужно знать про трапецию?
Для начала вспомним, что трапецией называется четырехугольник, у которого две противоположные стороны, их еще называют основаниями, параллельны, а две другие – нет.
В трапеции также может быть опущена высота (перпендикуляр к основанию). Проведена средняя линия – это прямая, которая параллельна основаниям и равна половине их суммы. А также диагонали, которые могут пересекаться, образуя острые и тупые углы. Или, в отдельных случаях, под прямым углом. Кроме того, если трапеция равнобедренная, в нее можно вписать окружность. И описать окружность около нее.
Формулы площади трапеции
Для начала рассмотрим стандартные формулы нахождения площади трапеции.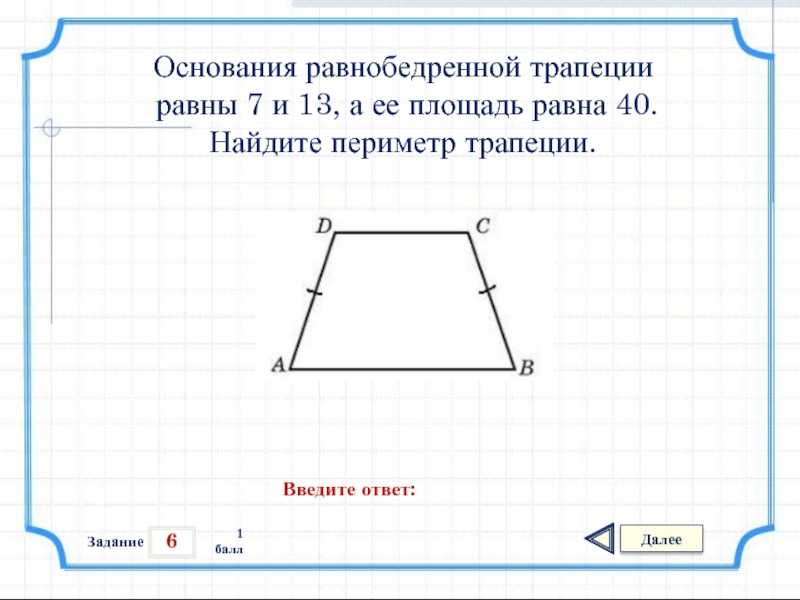 Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Способы вычислить площадь равнобедренной и криволинейной трапеций рассмотрим ниже.
Итак, представьте, что у вас есть трапеция с основаниями a и b, в которой к большему основанию опущена высота h. Вычислить площадь фигуры в таком случае проще простого. Надо всего лишь разделить на два сумму длин оснований и умножить то, что получится, на высоту: S = 1/2(a + b)*h .
Возьмем другой случай: предположим, в трапеции, кроме высоты, проведена средняя линия m. Нам известна формула нахождения длины средней линии: m = 1/2(a + b). Поэтому с полным правом можем упростить формулу площади трапеции до следующего вида: S = m* h . Другими словами, чтобы найти площадь трапеции, надо умножить среднюю линию на высоту.
Рассмотрим еще один вариант: в трапеции проведены диагонали d 1 и d 2 , которые пересекаются не под прямым углом α. Чтобы вычислить площадь такой трапеции, вам нужно разделить на два произведение диагоналей и умножить то, что получится, на sin угла между ними: S= 1/2d 1 d 2 *sinα .
Теперь рассмотрим формулу для нахождения площади трапеции, если о ней неизвестно ничего, кроме длин всех ее сторон: a, b, c и d. Это громоздкая и сложная формула, но вам будет полезно запомнить на всякий случай и ее: S = 1/2(a + b) * √c 2 – ((1/2(b – a)) * ((b – a) 2 + c 2 – d 2)) 2 .
Кстати, приведенные выше примеры верны и для того случая, когда вам потребуется формула площади прямоугольной трапеции. Эта трапеция, боковая сторона которой примыкает к основаниям под прямым углом.
Равнобедренная трапеция
Трапеция, боковые стороны которой равны, называется равнобедренной. Мы рассмотрим несколько вариантов формулы площади равнобедренной трапеции.
Первый вариант: для случая, когда внутрь равнобедренной трапеции вписана окружность с радиусом r, а боковая сторона и большее основание образуют острый угол α. Окружность может быть вписана в трапецию при условии, что сумма длин ее оснований равна сумме длин боковых сторон.
Площадь равнобедренной трапеции вычисляется так: умножьте квадрат радиуса вписанной окружности на четыре и разделите все это на sinα: S = 4r 2 /sinα .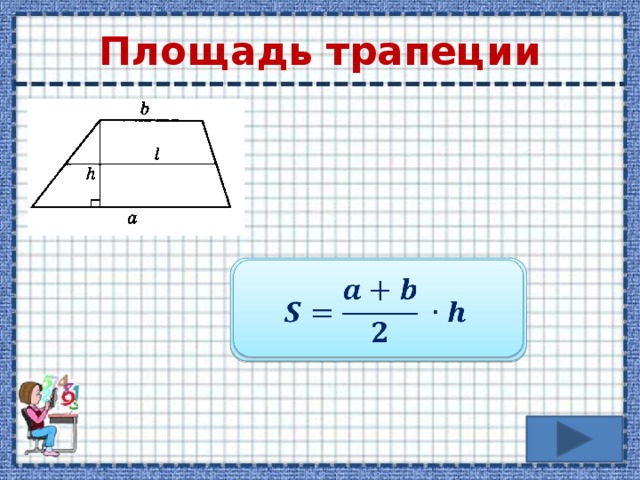 Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Еще одна формула площади является частным случаем для того варианта, когда угол между большим основанием и боковой стороной равен 30 0: S = 8r 2 .
Второй вариант: на этот раз возьмем равнобедренную трапецию, в которой вдобавок проведены диагонали d 1 и d 2 , а также высота h. Если диагонали трапеции взаимно перпендикулярны, высота составляет половину суммы оснований: h = 1/2(a + b). Зная это, легко преобразовать уже знакомую вам формулу площади трапеции в такой вид: S = h 2 .
Формула площади криволинейной трапеции
Начнем с того, что разберемся: что такое криволинейная трапеция. Представьте себе ось координат и график непрерывной и неотрицательной функции f, которая не меняет знака в пределах заданного отрезка на оси x. Криволинейную трапецию образуют график функции у = f(x) – вверху, ось х – внизу (отрезок ), а по бокам – прямые, проведенные между точками a и b и графиком функции.
Вычислить площадь такой нестандартной фигуры нельзя приведенными выше способами. Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Тут нужно применить математический анализ и использовать интеграл. А именно: формулу Ньютона-Лейбница – S = ∫ b a f(x)dx = F(x)│ b a = F(b) – F(a) . В этой формуле F – первообразная нашей функции на выбранном отрезке . И площадь криволинейной трапеции соответствует приращению первообразной на заданном отрезке.
Примеры задач
Чтобы все эти формулы лучше улеглись в голове, вот вам несколько примеров задач на нахождение площади трапеции. Лучше всего будет, если вы сперва попробуете решить задачи сами, и только потом сверите полученный ответ с готовым решением.
Задача №1: Дана трапеция. Ее большее основание – 11 см, меньшее – 4см. В трапеции проведены диагонали, одна длиной 12 см, вторая – 9 см.
Решение: Постройте трапецию АМРС. Проведите прямую РХ через вершину Р так, чтобы она оказалась параллельной диагонали МС и пересекла прямую АС в точке Х. Получится треугольник АРХ.
Мы рассмотрим две полученных в результате этих манипуляций фигуры: треугольник АРХ и параллелограмм СМРХ.
Благодаря параллелограмму мы узнаем, что РХ = МС = 12 см и СХ = МР = 4см. Откуда можем вычислить сторону АХ треугольника АРХ: АХ = АС + СХ = 11 + 4 = 15 см.
Мы также можем доказать, что треугольник АРХ – прямоугольный (для этого примените теорему Пифагора – АХ 2 = АР 2 + РХ 2). И высчитать его площадь: S APX = 1/2(AP * PX) = 1/2(9 * 12) = 54 см 2 .
Дальше вам потребуется доказать, что треугольники АМР и РСХ являются равновеликими. Основанием послужит равенство сторон МР и СХ (уже доказанное выше). А также высоты, которые вы опустите на эти стороны – они равны высоте трапеции АМРС.
Все это позволит вам утверждать, что S AMPC = S APX = 54 см 2 .
Задача №2: Дана трапеция КРМС. На ее боковых сторонах расположены точки О и Е, при этом ОЕ и КС параллельны. Также известно, что площади трапеций ОРМЕ и ОКСЕ находятся в соотношении 1:5. РМ = а и КС = b. Требуется найти ОЕ.
Решение:
Проведите через точку М прямую, параллельную РК, и точку ее пересечения с ОЕ обозначьте Т. А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
А – точка пересечения прямой, проведенной через точку Е параллельно РК, с основанием КС.
Введем еще одно обозначение – ОЕ = х. А также высоту h 1 для треугольника ТМЕ и высоту h 2 для треугольника АЕС (вы можете самостоятельно доказать подобие этих треугольников).
Будем считать, что b > а. Площади трапеций ОРМЕ и ОКСЕ относятся как 1:5, что дает нам право составить такое уравнение: (х + а) * h 1 = 1/5(b + х) * h 2 . Преобразуем и получим: h 1 / h 2 = 1/5 * ((b + х)/(х + а)).
Раз треугольники ТМЕ и АЕС подобные, имеем h 1 / h 2 = (х – а)/(b – х). Объединим обе записи и получим: (х – а)/(b – х) = 1/5 * ((b + х)/(х + а)) ↔ 5(х – а)(х + а) = (b + х)(b – х) ↔ 5(х 2 – а 2) = (b 2 – х 2) ↔ 6х 2 = b 2 + 5а 2 ↔ х = √(5а 2 + b 2)/6.
Таким образом, ОЕ = х = √(5а 2 + b 2)/6.
Заключение
Геометрия не самая легкая из наук, но вы наверняка сможете справиться с экзаменационными заданиями. Достаточно проявить немного усидчивости при подготовке. И, конечно, запомнить все нужные формулы.
Мы постарались собрать в одном месте все формулы вычисления площади трапеции, чтобы вы могли воспользоваться ими, когда будете готовиться к экзаменам и повторять материал.
Обязательно расскажите про эту статью одноклассникам и друзьям в социальных сетях. Пускай хороших оценок за ЕГЭ и ГИА будет больше!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Площадь трапеции. Приветствую вас! В этой публикации мы рассмотрим указанную формулу. Почему она именно такая и как её понять. Если будет понимание, то и учить её вам нет необходимости. Если же вы просто хотите посмотреть эту формулу и при чём срочно, то сразу можете прокрутить страницу вниз))
Теперь подробно и по порядку.
Трапеция это четырёхугольник, две стороны этого четырёхугольника параллельны, две другие нет. Те, что не параллельны – это основания трапеции. Две другие называются боковыми сторонами.
Если боковые стороны равны, то трапеция называется равнобедренной.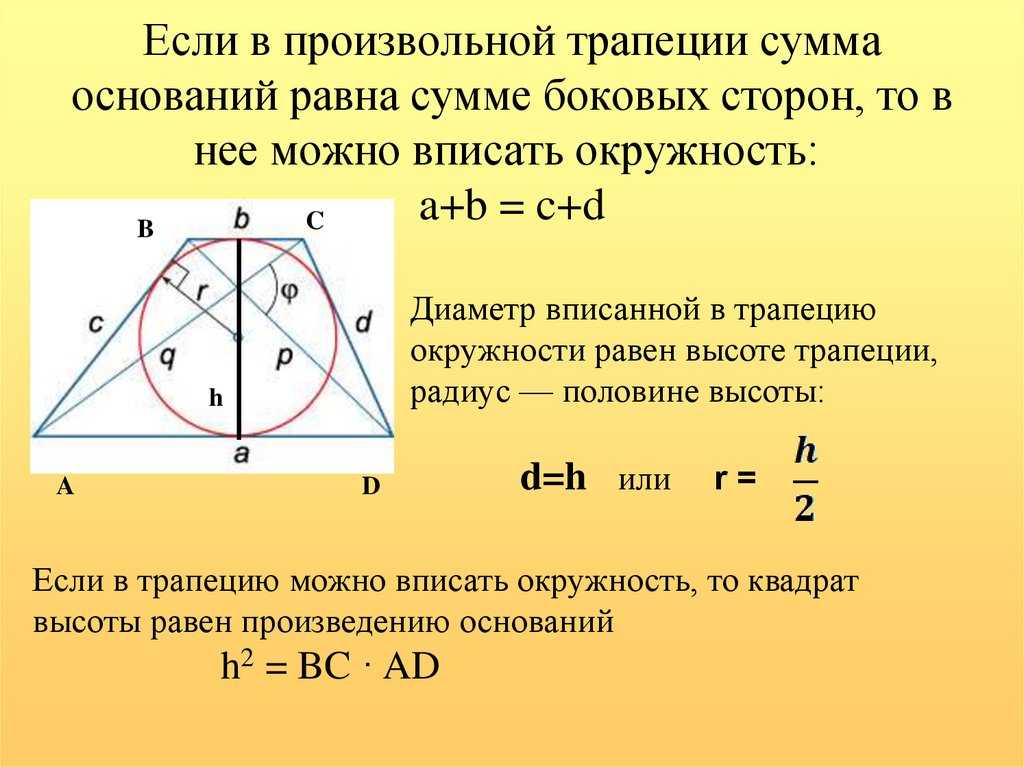 Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
Если одна из боковых сторон перпендикулярна основаниям, то такая трапеция называется прямоугольной.
В классическом виде трапецию изображают следующим образом – большее основание находится внизу, соответственно меньшее вверху. Но никто не запрещает изображать её и наоборот. Вот эскизы:
Следующее важное понятие.
Средняя линия трапеции это отрезок, который соединяет середины боковых сторон. Средняя линия параллельна основаниям трапеции и равна их полусумме.
Теперь давайте вникнем глубже. Почему именно так?
Рассмотрим трапецию с основаниями a и b и со средней линией l , и выполним некоторые дополнительные построения: через основания проведём прямые, а через концы средней линии перпендикуляры до пересечения с основаниями:
*Буквенные обозначения вершин и других точек не введены умышленно, чтобы избежать лишних обозначений.
Посмотрите, треугольники 1 и 2 равны по второму признаку равенства треугольников, треугольники 3 и 4 тоже самое. Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Из равенства треугольников следует равенство элементов, а именно катетов (они обозначены соответственно синим и красным цветом).
Теперь внимание! Если мы мысленно «отрежем» от нижнего основания синий и красный отрезок, то у нас останется отрезок (это сторона прямоугольника) равный средней линии. Далее, если мы «приклеим» отрезанные синий и красный отрезок к верхнему основанию трапеции, то у нас получится также отрезок (это тоже сторона прямоугольника) равный средней линии трапеции.
Уловили? Получается, что сумма оснований будет равна двум средним линиям трапеции:
Посмотреть ещё одно объяснение
Сделаем следующее – построим прямую проходящую через нижнее основание трапеции и прямую, которая пройдёт через точки А и В:
Получим треугольники 1 и 2, они равны по стороне и прилегающим к ней углам (второй признак равенства треугольников). Это означает что полученный отрезок (на эскизе он обозначен синим) равен верхнему основанию трапеции.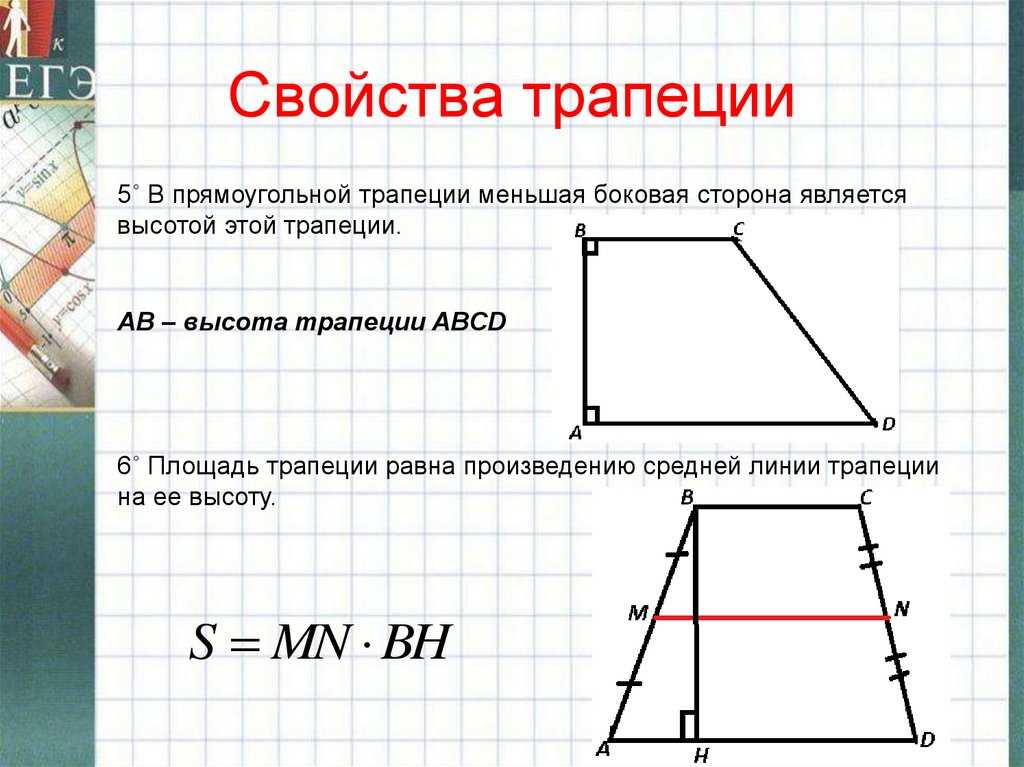
Теперь рассмотрим треугольник:
*Средняя линия данной трапеции и средняя линия треугольника совпадают.
Известно, что треугольника равна половине параллельного ей основания, то есть:
Хорошо, разобрались. Теперь о площади трапеции.
Площадь трапеции формула:
Говорят: площадь трапеции равна произведению полусуммы её оснований и высоты.
То есть, получается, что она равна произведению средней линии и высоты:
Вы, наверное, уже заметили, что это очевидно. Геометрически это можно выразить так: если мы мысленно отрежем от трапеции треугольники 2 и 4 и положим их соответственно на треугольники 1 и 3:
То у нас получится прямоугольник по площади равный площади нашей трапеции. Площадь этого прямоугольника будет равна произведению средней линии и высоты, то есть можем записать:
Но дело тут не в записи, конечно, а в понимании.
Скачать (посмотреть) материал статьи в формате *pdf
На этом всё. Успеха вам!
Успеха вам!
С уважением, Александр.
Что такое равнобедренная трапеция? Это геометрическая фигура, противолежащие не параллельные стороны которой равны. Существует несколько различных формул для нахождения площади трапеции с различными условиями, которые даны в задачах. То есть площадь найти можно, если дана высота, стороны, углы, диагонали и т.д. Также нельзя не упомянуть, что для равнобедренных трапеций существует некоторые “исключение”, благодаря которым поиск площади и сама формула значительно упрощается. Ниже описаны подробные решения каждого случая с примерами.
Необходимые свойства для нахождения площади равнобедренной трапеции
Мы уже выяснили, что геометрическая фигура, имеющая противолежащие не параллельные, но равные стороны – это трапеция, причем, равнобедренная. Существуют специальные случаи, когда трапеция считается равнобедренной.
- Это условия равенства углов. Итак, обязательный пункт: углы при основании (возьмем рисунок ниже) должны быть равны.
 В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD - Второе важное правило – в подобной трапеции диагонали должны быть равны. Следовательно, АС = ВD.
- Третий аспект: противоположные углы трапеции в сумме должны давать 180 градусов. Это значит, что угол ABC + угол CDA = 180 градусов. С углами BCD и BAD аналогично.
- В-четвертых, если трапеция допускает описание вокруг нее окружности – то она равнобедренная.
Как найти площадь равнобедренной трапеции – формулы и их описание
- S = (a+b)h/2 – это самая распространенная формула для нахождения площади, где а – нижнее основание, b – верхнее основание, а h – это высота.
- Если высота неизвестна, то искать ее можно по подобной формуле: h = с*sin(x), где с это либо AB, либо CD. sin(x) – это синус угла при любом основании, то есть угол DAB = угол CDA = x. В конечном итоге формула принимает вот такой вид: S = (a+b)*с*sin(x)/2.
- Высота также может находиться по этой формуле:
- Итоговая формула имеет такой вид:
- Площадь равнобедренной трапеции можно найти и через среднюю линию и высоту.
 Формула такова: S = mh .
Формула такова: S = mh .
Рассмотрим условие, когда в трапецию будет вписана окружность.
В случае, изображенном на картинке,
QN = D = H – диаметр окружности и одновременно высота трапеции;
LO, ON, OQ = R – радиусы окружности;
DC = a – верхнее основание;
AB = b – нижнее основание;
DAB, ABC, BCD, CDA – альфа, бета – углы оснований трапеции.
Подобный случай допускает нахождение площади по таким формулам:
- Теперь попробуем найти площадь через диагонали и углы между ними.
На рисунке обозначим AC, DB – диагонали – d. Углы COB, DOB – альфа; DOC, AOB – бета. Формула площади равнобедренной трапеции через диагонали и угол между ними, (S ) такова:
Площадь трапеций: формула, типы и уравнение
Вы можете встретить трапеции, когда видите тачку в саду или когда проходите по мосту и смотрите на его фермы. Эти геометрические формы важны в приложениях архитектуры и строительства. Возможно, вы уже знакомы с тем, как вычислять площадь треугольников, что будет полезно для этой статьи, когда мы рассмотрим формулу площади трапеции и несколько примеров ее использования.
Возможно, вы уже знакомы с тем, как вычислять площадь треугольников, что будет полезно для этой статьи, когда мы рассмотрим формулу площади трапеции и несколько примеров ее использования.
Начнем с того, что вспомним, что такое трапеция.
Трапеция Определение
Трапеция — это четырехугольник (четырехсторонняя плоская фигура), который имеет ровно одну пару параллельных сторон.
Следующая фигура представляет собой трапецию.
Иллюстрация трапеции
На приведенном выше рисунке параллельных сторон (в данном случае \(\overline{AD}\) и \(\overline{BC}\)) называются основаниями трапеции. . непараллельных сторон (\(\overline{AB}\) и \(\overline{DC}\)) называются 92\) и т. д.
Формула площади трапеции
Рассмотрим следующую трапецию:
Трапеция с основаниями a и b и высотой h
Площадь трапеции определяется по формуле:
\[\text{Площадь} = \frac{1}{2} h (a + b)\]
где:
\(h \Rightarrow\) высота трапеции (перпендикулярное расстояние между основаниями) ,
\(a, b \Rightarrow\) длины оснований.
Как мы получили эту формулу, спросите вы? Давайте покажем вам.
Напомним, что площадь треугольника определяется по формуле:
\[\text{Площадь} = \frac{1}{2} \text{основание} \cdot \text{высота}\]
Мы можем разделить эту трапецию на два треугольника по любой из диагоналей. Возьмем диагональ \(\overline{BD}\) и разделим трапецию на треугольники \(\triangle{BAD}\) и \(\triangle{BCD}\).
Трапеция, разделенная на \(\треугольник{BAD}\) и \(\треугольник{BCD}\) диагональю \(\overline{BD}\)
Тогда мы можем сказать, что
\[\begin{align}\text{Площадь трапеции ABCD} & = \text{Площадь } \triangle{BAD} + \text{Площадь } \triangle{BCD} \\ \\& = \frac{1}{2} b \cdot h + \frac{1}{2} a \cdot h \\ \\& = \frac{1}{2} h (a + b )\end{align}\]
Представьте себе параллелограмм, у которого обе пары противоположных сторон параллельны. Вы можете применить приведенную выше формулу, чтобы вывести формулу площади параллелограмма.
\[\begin{align}\text{Area} & = \frac{1}{2} h (a + b) \\ \\& = \frac{1}{2} h (b + b) \qquad \text{Противоположные стороны параллелограмма имеют одинаковую длину} \\ \\& = \frac{1}{2} h (2b) \\ \\& = b \cdot h\end{align}\]
Это формула площади параллелограмма.
Примеры площади трапеции
Теперь давайте рассмотрим некоторые примеры, связанные с площадью трапеции.
Трапеция имеет длины оснований \(10\ см\) и \(15\ см\). Перпендикулярное расстояние между основаниями равно \(8\см\). Найдите площадь трапеции.
Решение
Чтобы решить эту задачу, нам просто нужно подставить значения длин оснований и высоты в площадь формулы трапеции. 92\).
Теперь давайте рассмотрим пример с использованием координатной плоскости.
Найдите площадь следующей трапеции.
Трапеция на координатной плоскости
Решение
В этом случае, чтобы найти площадь вышеуказанной трапеции, нужно найти длину оснований и высоту трапеции.
Эти значения не даны, но мы можем использовать координатную плоскость для их расчета.
Нам нужно рассчитать расстояние между каждой из точек, как мы можем это сделать?
Расстояние между точками \(B(6, 2)\) и \(C(9, 2)\) можно рассчитать, найдя абсолютное значение разницы между их координатами x, используя \(|x_2 — х_1|\). То же самое относится и к расстоянию между точками \(A(2, 7)\) и \(D(10, 7)\).
То же самое относится и к расстоянию между точками \(A(2, 7)\) и \(D(10, 7)\).
Расстояние между точками \(B(6, 2)\) и \(E(6, 7)\) можно рассчитать, найдя абсолютное значение разницы между их координатами y, используя \(|y_2 — у_1|\).
\[\begin{align}a &= \overline{BC} = |x_2 — x_1| = |92\) имеет основания длин \(3\m\) и \(4\m\). Найдите расстояние между параллельными сторонами.
Решение
Расстояние между параллельными сторонами равно высоте трапеции. Итак, давайте подставим значения, которые у нас есть, в формулу площади трапеции, а затем найдем \(h\).
\[\begin{align}\text{Area} & = \frac{1}{2} h (a + b) \\ \\35 & = \frac{1}{2} \cdot h (3 + 4) \\ \\35 & = \frac{7 \cdot h}{2} \\ \\h & = \frac{35 \cdot 2}{7} \\ \\& = \frac{70} {7} \\ \\& = 10\ m\end{align}\]
Высота трапеции \(10\ м\).
Площадь трапеции без известной высоты
Если вам дана трапеция с длинами всех ее оснований и катетов, но не указана высота, то вам нужно сначала вычислить ее высоту, чтобы иметь возможность найти площадь трапеция. Давайте посмотрим на пример, чтобы показать вам, что делать в этом случае.
Давайте посмотрим на пример, чтобы показать вам, что делать в этом случае.
Найдите площадь следующей трапеции.
Пример трапеции без высоты
Обратите внимание, что стороны трапеции имеют одинаковую длину \(6\ м\), следовательно, это равнобедренная трапеция , и мы можем вычислить ее высоту следующим образом.
Высота трапеции по Пифагору
Обратите внимание, что у нас есть прямоугольный треугольник с каждой стороны. Основания каждого треугольника рассчитывались путем нахождения разницы между \(18\) и \(10\), а затем деления результата на \(2\).
\[18 — 10 = \frac{8}{2} = 4\ m\]
Теперь мы можем вычислить высоту, используя теорему Пифагора , которая утверждает, что в прямоугольном треугольнике 92\).
Площадь трапеции при заданных диагоналях
Другой интересный сценарий, когда вам нужно вычислить площадь трапеции, когда заданы только длины ее диагоналей и угол между ними.
Рассмотрим трапецию с длинами диагоналей \(d_1\) и \(d_2\) и углом \(\alpha\) между ними.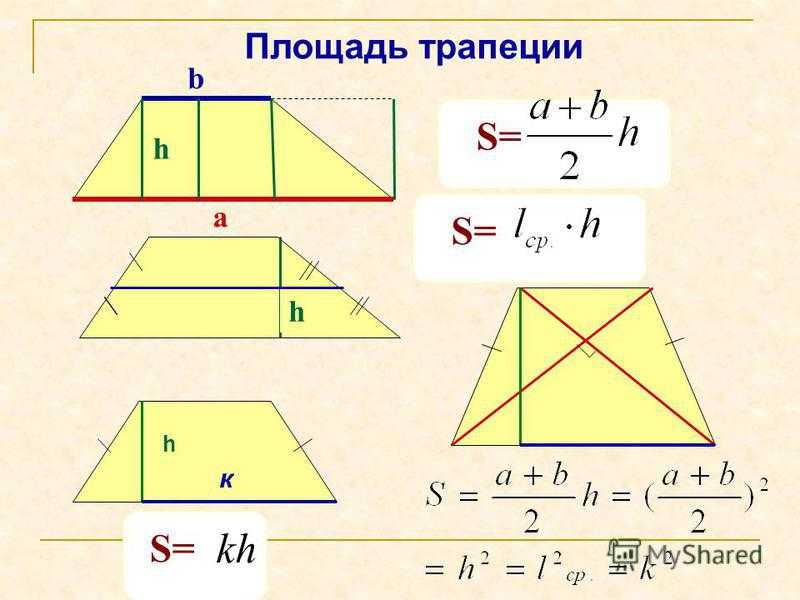
Трапеция с диагоналями \(d_1\) и \(d_2\)
В этом случае площадь трапеции определяется как
\[\text{Площадь} = \frac{1}{2} d_1 \ cdot d_2 \cdot sin(\alpha)\] 92\).
Площадь трапеций — основные выводы
- Трапеция — это четырехугольник, у которого ровно одна пара параллельных сторон.
- Площадь трапеции определяется пространством, заключенным в ее границах, как занятое в двумерной плоскости.
- Площадь трапеции находится по формуле: \(\text{Площадь} = \frac{1}{2} h (a + b)\).
- Если вам дана трапеция с длинами всех ее оснований и катетов, но не указана высота, вам нужно сначала вычислить ее высоту, используя теорему Пифагора, чтобы иметь возможность найти площадь трапеции.
- Когда вам нужно вычислить площадь трапеции, когда даны только длины ее диагоналей и угол между ними, вы можете использовать формулу: \(\text{Площадь} = \frac{1}{2} d_1 \cdot d_2 \cdot sin(\alpha)\).
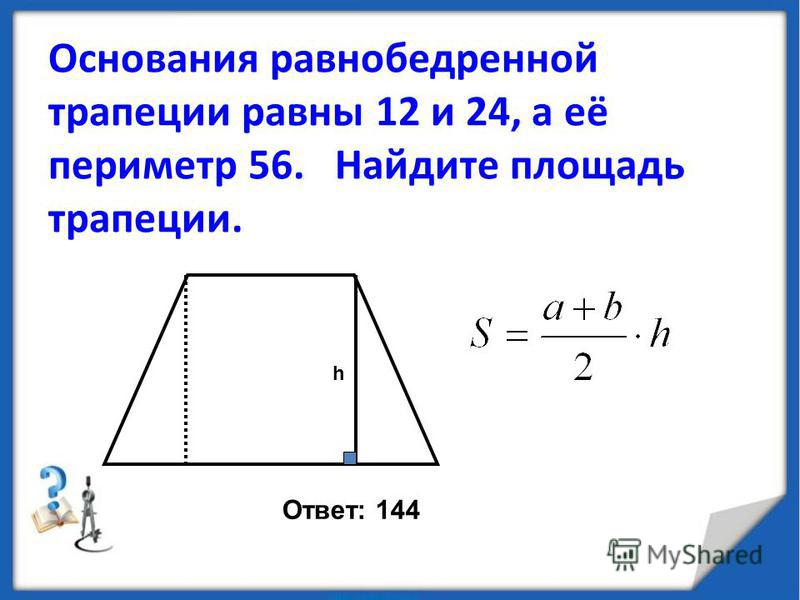
5. его высота равна 8, а его периметр равен 48.
 найдите площадь РЕШЕНИЕ: пожалуйста, помогите мне ответить на этот вопрос как можно скорее.
меры последовательных сторон равнобедренной трапеции равны 4:5:10:5. его высота равна 8, а его периметр равен 48. найдите площадь
найдите площадь РЕШЕНИЕ: пожалуйста, помогите мне ответить на этот вопрос как можно скорее.
меры последовательных сторон равнобедренной трапеции равны 4:5:10:5. его высота равна 8, а его периметр равен 48. найдите площадьАлгебра -> Настраиваемые средства решения задач Word -> Геометрия -> РЕШЕНИЕ: пожалуйста, помогите мне ответить на этот вопрос как можно скорее. меры последовательных сторон равнобедренной трапеции равны 4:5:10:5. его высота равна 8, а его периметр равен 48. найдите площадь Войти
|
|


 Его длина
Его длина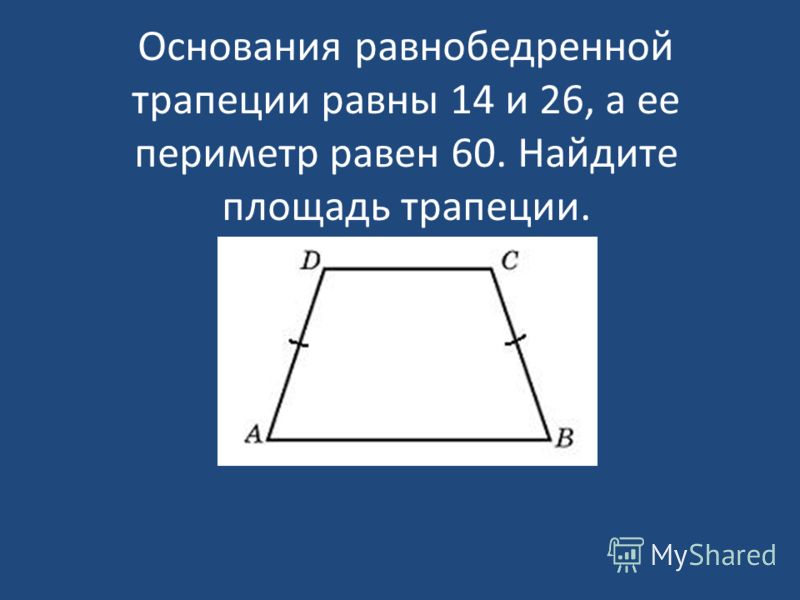 В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD
В нашем случае угол ВАD = углу CDA, a угол ABC = углу BCD Формула такова: S = mh .
Формула такова: S = mh .