приведение матрицы к треугольному виду : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
| ArniLand |
| ||
12/09/10 |
| ||
| |||
| maxmatem |
| ||
15/08/09 |
| ||
| |||
| Null |
| |||
12/08/10 |
| |||
| ||||
| maxmatem |
| ||
15/08/09 |
| ||
| |||
| ArniLand |
| ||
12/09/10 |
| ||
| |||
| mkot |
| ||
18/10/08 |
| ||
|
| |||
| ArniLand |
| ||
12/09/10 |
| ||
| |||
| mihailm |
| ||
19/05/10 |
| ||
| |||
| ArniLand |
| ||
12/09/10 |
| ||
| |||
| mihailm |
| ||
19/05/10 |
| ||
| |||
| gris |
| |||
13/08/08 |
| |||
| ||||
| ArniLand |
| ||
12/09/10 |
| ||
| |||
| mihailm |
| ||
19/05/10 |
| ||
| |||
| ArniLand |
| ||
12/09/10 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 14 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Матрица определители метод накопления нулей.
 Понижение порядка определителя
Понижение порядка определителяЗадание. Вычислить определитель , разложив его по элементам какой-то строки или какого-то столбца.
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй — пять третьих и от четвертой — три третьих строки, получаем:
Полученный определитель разложим по элементам первого столбца:
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
Ответ.
12. Слау 3 порядка
1. Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение
элементов в первом определителе, которые
соединены прямыми, берется со знаком
«плюс»; аналогично, для второго
определителя — соответствующие
произведения берутся со знаком «минус»,
т. е.
е.
2. Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
3. Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Задание. Разложив по первой строке, вычислить определитель
Решение.
Ответ.
4.Приведение определителя к треугольному виду
С помощью элементарных
преобразований над строками или столбцами
определитель приводится к треугольному
виду и тогда его значение, согласно свойствам
определителя, равно произведению
элементов стоящих на главной диагонали.
Пример
Задание. Вычислить определитель приведением его к треугольному виду.
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Определение1. 7 . Минором элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, в которых стоит выбранный элемент.
Обозначение: выбранный элемент определителя, его минор.
Пример. Для
Определение1. 8. Алгебраическим дополнением элемента определителя называется его минор, если сумма индексов данного элемента i+j есть число четное, или число, противоположное минору, если i+j нечетно, т.е.
Рассмотрим еще один способ вычисления определителей третьего порядка – так называемое разложение по строке или столбцу. Для этого докажем следующую теорему:
Для этого докажем следующую теорему:
Теорема 1.1 . Определитель равен сумме произведений элементов любой его строки или столбца на их алгебраические дополнения, т.е.
где i=1,2,3.
Доказательство.
Докажем теорему для первой строки определителя, так как для любой другой строки или столбца можно провести аналогичные рассуждения и получить тот же результат.
Найдем алгебраические дополнения к элементам первой строки:
Таким образом, для вычисления определителя достаточно найти алгебраические дополнения к элементам какой-либо строки или столбца и вычислить сумму их произведений на соответствующие элементы определителя.
Пример. Вычислим определитель с помощью разложения по первому столбцу. Заметим, что при этом искать не требуется, так как следовательно, и Найдем и Следовательно,
Определители более высоких порядков .
Определение1. 9 . Определитель n-го порядка
есть сумма n! членов каждый из которых соответствует одному из n! упорядоченных множеств полученных r попарными перестановками элементов из множества 1,2,…,n.
Замечание 1. Свойства определителей 3-го порядка справедливы и для определителей n-го порядка.
Замечание 2. На практике определители высоких порядков вычисляют с помощью разложения по строке или столбцу. Это позволяет понизить порядок вычисляемых определителей и в конечном счете свести задачу к нахождению определителей 3-го порядка.
Пример. Вычислим определитель 4-го порядка с помощью разложения по 2-му столбцу. Для этого найдем и :
Следовательно,
Теоре́ма Лапла́са — одна из теорем линейной алгебры. Названа в честь французского математика Пьера-Симона Лапласа (1749 — 1827), которому приписывают формулирование этой теоремы в 1772 году , хотя частный случай этой теоремы о разложении определителя по строке (столбцу) был известен ещё Лейбницу.
олнение минора определяется следующим образом:
Справедливо следующее утверждение.
Число миноров, по которым берётся сумма в теореме Лапласа, равно числу способов выбрать столбцов из , то есть биномиальному коэффициенту .
Так как строки и столбцы матрицы равносильны относительно свойств определителя, теорему Лапласа можно сформулировать и для столбцов матрицы.
Разложение определителя по строке (столбцу) (Следствие 1)
Широко известен частный случай теоремы Лапласа — разложение определителя по строке или столбцу. Он позволяет представить определитель квадратной матрицы в виде суммы произведений элементов любой её строки или столбца на их алгебраические дополнения.
Пусть — квадратная матрица размера . Пусть также задан некоторый номер строки либо номер столбца матрицы . Тогда определитель может быть вычислен по следующим формулам.
Для определителя четвёртого и более высоких порядков обычно применяются иные методы вычисления, нежели использование готовых формул как для вычисления определителей второго и третьего порядков . Один из методов вычисления определителей высших порядков — использование следствия из теоремы Лапласа (саму теорему можно посмотреть, например, в книге А.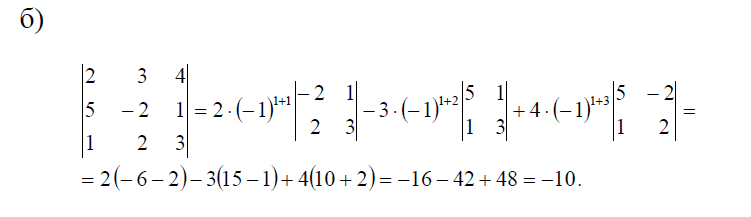 Г. Куроша «Курс высшей алгебры»). Это следствие позволяет разложить определитель по элементам некоторой строки или столбца. При этом вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка. Именно поэтому такое преобразование именуют понижением порядка определителя. Например, вычисление определителя четвёртого порядка сводится к нахождению четырёх определителей третьего порядка.
Г. Куроша «Курс высшей алгебры»). Это следствие позволяет разложить определитель по элементам некоторой строки или столбца. При этом вычисление определителя n-го порядка сводится к вычислению n определителей (n-1)-го порядка. Именно поэтому такое преобразование именуют понижением порядка определителя. Например, вычисление определителя четвёртого порядка сводится к нахождению четырёх определителей третьего порядка.
Допустим, нам задана квадратная матрица n-го порядка, т.е. $A=\left(\begin{array} {cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \\ \end{array} \right)$. Вычислить определитель этой матрицы можно, разложив его по строке или по столбцу.
Зафиксируем некоторую строку, номер которой равен $i$. Тогда определитель матрицы $A_{n\times n}$ можно разложить по выбранной i-й строке, используя следующую формулу:
\begin{equation} \Delta A=\sum\limits_{j=1}^{n}a_{ij}A_{ij}=a_{i1}A_{i1}+a_{i2}A_{i2}+\ldots+a_{in}A_{in} \end{equation}
$A_{ij}$ обозначает алгебраическое дополнение элемента $a_{ij}$. {n}a_{ij}A_{ij}=a_{1j}A_{1j}+a_{2j}A_{2j}+\ldots+a_{nj}A_{nj}
\end{equation}
{n}a_{ij}A_{ij}=a_{1j}A_{1j}+a_{2j}A_{2j}+\ldots+a_{nj}A_{nj}
\end{equation}
Правила, выраженные формулами (1) и (2), можно сформулировать так: определитель равен сумме произведений элементов некоей строки или столбца на алгебраические дополнения этих элементов. Для наглядности рассмотрим определитель четвёртого порядка, записанный в общем виде:
$$\Delta=\left| \begin{array} {cccc} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \\ \end{array} \right|$$
Выберем произвольный столбец в этом определителе. Возьмём, к примеру, столбец под номером 4. Запишем формулу для разложения определителя по выбранному четвёртому столбцу:
Аналогично, выбирая, к примеру, третью строку, получим разложение по этой строке:
Пример №1
Вычислить определитель матрицы $A=\left(\begin{array} {ccc} 5 & -4 & 3 \\ 7 & 2 & -1 \\ 9 & 0 & 4 \end{array} \right)$, используя разложение по первой строке и второму столбцу. 4\cdot \left| \begin{array} {cc} 7 & 2 \\ 9 & 0 \end{array} \right|=7\cdot 0-2\cdot 9=-18.
\end{aligned}
4\cdot \left| \begin{array} {cc} 7 & 2 \\ 9 & 0 \end{array} \right|=7\cdot 0-2\cdot 9=-18.
\end{aligned}
Как мы нашли алгебраические дополнения? показать\скрыть
Подставляя все найденные значения в записанную выше формулу, получим:
$$ \Delta A= a_{11}\cdot A_{11}+a_{12}\cdot A_{12}+a_{13}\cdot A_{13}=5\cdot{8}+(-4)\cdot(-37)+3\cdot(-18)=134. $$
Как видите, процесс нахождения определителя третьего порядка мы свели к вычислению значений трёх определителей второго порядка. Иными словами, мы понизили порядок исходного определителя.
Обычно в таких простых случаях не расписывают решение подробно, отдельно находя алгебраические дополнения, а уж затем подставляя их в формулу для вычисления определителя. Чаще всего просто продолжают запись общей формулы, — до тех пор, пока не будет получен ответ. Именно так мы станем раскладывать определитель по второму столбцу.
Итак, приступим к разложению определителя по второму столбцу. Вспомогательных вычислений производить не будем, — просто продолжим формулу до получения ответа. Обратите внимание, что во втором столбце один элемент равен нулю, т.е. $a_{32}=0$. Это говорит о том, что слагаемое $a_{32}\cdot A_{32}=0\cdot A_{23}=0$. Используя формулу для разложения по второму столбцу, получим:
Обратите внимание, что во втором столбце один элемент равен нулю, т.е. $a_{32}=0$. Это говорит о том, что слагаемое $a_{32}\cdot A_{32}=0\cdot A_{23}=0$. Используя формулу для разложения по второму столбцу, получим:
$$ \Delta A= a_{12}\cdot A_{12}+a_{22}\cdot A_{22}+a_{32}\cdot A_{32}=-4\cdot (-1)\cdot \left| \begin{array} {cc} 7 & -1 \\ 9 & 4 \end{array} \right|+2\cdot \left| \begin{array} {cc} 5 & 3 \\ 9 & 4 \end{array} \right|=4\cdot 37+2\cdot (-7)=134. $$
Ответ получен. Естественно, что результат разложения по второму столбцу совпал с результатом разложения по первой строке, ибо мы раскладывали один и тот же определитель. Заметьте, что при разложении по второму столбцу мы делали меньше вычислений, так как один элемент второго столбца был равен нулю. Именно исходя из таких соображений для разложения стараются выбирать тот столбец или строку, которые содержат побольше нулей.
Ответ : $\Delta A=134$.
Пример №2
Вычислить определитель матрицы $A=\left(\begin{array} {cccc}
-1 & 3 & 2 & -3\\
4 & -2 & 5 & 1\\
-5 & 0 & -4 & 0\\
9 & 7 & 8 & -7 \end{array} \right)$, используя разложение по выбранной строке или столбцу. 6\cdot \left| \begin{array} {ccc} -1 & 3 & -3 \\ 4 & -2 & 1 \\ 9 & 7 & -7 \end{array} \right|=-5\cdot 10-4\cdot (-34)=86.
$$
6\cdot \left| \begin{array} {ccc} -1 & 3 & -3 \\ 4 & -2 & 1 \\ 9 & 7 & -7 \end{array} \right|=-5\cdot 10-4\cdot (-34)=86.
$$
Ответ : $\Delta A=86$.
Лекция 2. определители
Определители второго порядка
Определители третьего порядка
Алгебраические дополнения и миноры
Разложение определителя по строке или столбцу
Свойства определителей
Обратная матрица
Свойства обратной матрицы
1. Определители второго порядка
Понятие определителя вводится только для квадратной матрицы .
Определитель – это число, которое считается по определенным правилам. Порядок определителя – это порядок квадратной матрицы. Если для задания матриц использовались круглые скобки, то в теории определителей используют прямые скобки.
Каждой
квадратной матрице поставим в соответствие
некоторое число, которое будем называть определителем
матрицы, и
укажем правило его вычисления. Обозначения:
Обозначения:
.
Пример
1.
.
2. Определители третьего порядка
В каждом произведении нет чисел из одного столбца или одной строки.
Приведем схему для запоминания порядка получения слагаемых в определителе.
Произведение чисел на одной диагонали берется со знаком «+» (это главная диагональ матрицы), а на другой – с противоположным знаком.
Пример 2 .
3. Алгебраические дополнения и миноры
Для вычисления определителей порядка больше третьего применяют другие способы вычисления.
Пример
3. Минор
определителя
есть.
.
Полезно
запомнить, что
и
.
Пример 4. В примере 3алгебраическое дополнение
4. Разложение определителя по строке или столбцу
Вычисление
определителя
-го
порядка можно свести к вычислению
определителей порядка
,
используя следующие формулы.
Это
число равно сумме произведений элементов любой -й строки на их алгебраические
дополнения .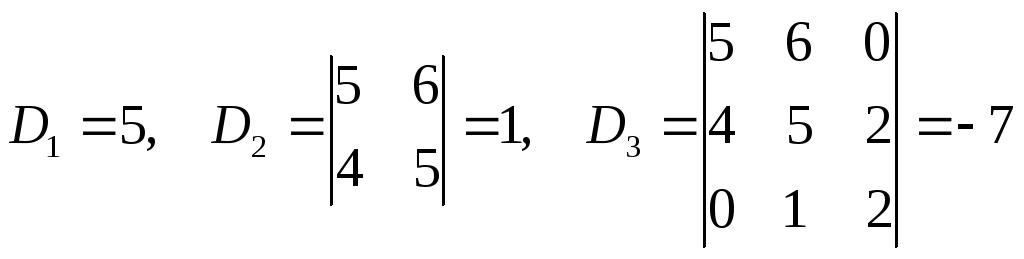
Пример
5 . Вычислить
определитель третьего порядка
разложением по первой строке.
Решение
Это число равно сумме произведений элементов любого -го столбца на их алгебраические дополнения.
Независимо от способа разложения всегда получается один и тот же ответ.
5. Свойства определителей
1. При
транспонировании квадратной матрицы ее определитель не меняется:
.
Вывод. Свойства определителей, сформулированных для строк, справедливы и для столбцов.
2. При
перестановке двух строк (столбцов) определитель меняет знак на
противоположный. Например,
.
3. Определитель равен нулю , если:
а)
он имеет нулевую строку (столбец)
;
б)
он имеет пропорциональные (одинаковые)
строки (столбец)
.
4. Общий
множитель в строке (столбце) можно выносить за знак определителя.
Например,
.
5. Определитель не изменяется , если к элементам какой-либо строки прибавить (вычесть) соответствующие элементы другой строки, умноженные на любое число.
Например,
.
6. Если в определителе каждый элемент строки есть сумма двух слагаемых, то этот определитель равен сумме двух определителей:
.
7. Определитель произведения двух квадратных матриц одного и того же порядка равен произведению определителей этих матриц:
.
8. Определитель квадратной матрицы треугольного вида равен произведению элементов, стоящих на главной диагонали:
.
6. Обратная матрица
Вместо операции деления матриц вводится понятие обратной матрицы.
Обозначается
обратная матрица
, то
есть
.
Очевидна
аналогия с числами: для числа 2 число ½
есть обратное, так как
.
Именно поэтому матрица, обратная к А,
обозначается
.
Теорема
«Необходимое и достаточное условие
существования обратной матрицы». Для
того чтобы квадратная матрица
имела обратную матрицу
,
необходимо и достаточно, чтобы определитель
матрицыбыл не равен нулю.
Правило
нахождения обратной матрицы
0) Смотрим, является ли матрица квадратной. Если нет, то обратной матрицы не существует; если квадратная, то переходим к пункту 1.
1) Вычисляем определитель матрицы
:
если он не равен нулю, то обратная матрица
существует:
;
если
равен нулю, то обратной матрицы нет.
2) Для каждого элемента матрицы вычисляем его алгебраическое дополнение.
3) Составляем матрицу из алгебраических
дополнений, которая затем транспонируем:
.
4) Каждый элемент матрицы
делим на определитель:
Получаем матрицу, обратную данной.
7. Нахождение обратной матрицы для матриц второго порядка
Пример
6. Дана матрица
. Найти обратную матрицу.
Найти обратную матрицу.
Решение .
Проверка. Убедимся, что найдена действительно
обратная матрица. Найдем произведение
матриц
и
.
8. Свойства обратной матрицы
1.
,
где А и В – невырожденные квадратные матрицы одинакового порядка.
2.
.
3.
.
4.
.
Контрольные вопросы
Что называется определителем второго порядка?
Как вычислить определитель третьего порядка?
Как вычислить определитель 3 порядка по правилу треугольников?
Что называется алгебраическим дополнением элемента определителя? Приведите примеры для определителей 2 и 3 порядков.
Напишите разложения определителя третьего порядка по элементам произвольной строки и произвольного столбца.
Пусть имеется квадратная матрица A размером n x n .
Определение. Определителем называется алгебраическая сумма всевозможных произведений элементов, взятых по одному из каждого столбца и каждой строки матрицы A . Если в каждом таком произведении (члене определителя) множители расположены в порядке следования столбцов (т.е. вторые индексы элементов a ij в произведении расположены в порядке возрастания), то со знаком (+) берутся те произведения, у которых перестановка первых индексов чётная, а со знаком (-) – те, у которых она нечетная.
Если в каждом таком произведении (члене определителя) множители расположены в порядке следования столбцов (т.е. вторые индексы элементов a ij в произведении расположены в порядке возрастания), то со знаком (+) берутся те произведения, у которых перестановка первых индексов чётная, а со знаком (-) – те, у которых она нечетная.
.
Здесь — число инверсий в перестановке индексов i 1 , i 2 , …, i n .
Методы нахождения определителей
- Определитель матрицы разложением по строкам и столбцам через миноры.
- Определитель методом приведения к треугольному виду (методом Гаусса)
Свойство определителей
- При транспонировании матрицы её определитель не меняется.
- Если поменять местами две строки или два столбца определителя, то определитель изменит знак, а по абсолютной величине не изменится.
- Пусть C = AB где A и B квадратные матрицы. Тогда detC = detA ∙ detB .
- Определитель с двумя одинаковыми строками или с двумя одинаковыми столбцами равен 0.
 Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю.
Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю. - Определитель с двумя пропорциональными строками или столбцами равен 0.
- Определитель треугольной матрицы равен произведению диагональных элементов. Определитель диагональной матрицы равен произведению элементов стоящих на главной диагонали.
- Если все элементы строки (столбца) умножить на одно и то же число, то определитель умножится на это число.
- Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы) кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
- Теорема Якоби: Если к элементам некоторого столбца определителя прибавить соответствующие элементы другого столбца, умноженные на произвольный множитель λ, то величина определителя не изменится.
- транспонировать матрицу;
- прибавить к какой-либо строке другую строку, умноженную на любое число.

Задание 1 . Вычислить определитель, разлагая его по строке или столбцу.
Решение :xml :xls
Пример 1 :xml :xls
Задание 2 . Вычислить определитель двумя способами: а) по правилу «треугольников»; б) разложением по строке.
Решение .
а) Слагаемые, входящие в со знаком «минус», строятся таким же образом относительно побочной диагонали.
| = |
б) Запишем матрицу в виде:
| A = |
|
Главный определитель:
∆ = 2 (0 0-2 4)-(-1 (2 0-2 1))+(-2 (2 4-0 1)) = -34
Задание 3 . Укажите, чему равен определитель квадратной матрицы A четвертого порядка, если ее ранг r(A)=1.
Укажите, чему равен определитель квадратной матрицы A четвертого порядка, если ее ранг r(A)=1.
Ответ: det(A) = 0.
Определители и обратные
Определители и обратные
I. Домашнее задание
II. Определители:
Рассмотрите возможность уменьшения строки стандартной матрицы 2×2
Предположим, что а не равно нулю.
| и | б |
| с | д |
1/а Р 1 -> R 1
| 1 | б/у |
| с | д |
R 2 — cR 1 -> R 2
| 1 | б/у |
| 0 | д — кб/а |
Теперь обратите внимание, что мы не можем сделать нижний правый угол равным 1, если
г — сб/а = 0 или
да — св = 0 или
объявление — н. э. = 0
э. = 0
Определение: Назовем ad — bc определителем матрицы 2 на 2.
| и | б |
| с | д |
он говорит нам, когда можно сократить матрицу и найти решение к линейной системе
Пример: определитель матрицы
| 3 | 1 |
| 5 | 2 |
3(2) — 1(5) = 6 — 5 = 1
III. Определители трех на три матрицы
Определим определитель треугольной матрицы
| и | д | и |
| 0 | б | ф |
| 0 | 0 | в |
как det = abc
Обратите внимание, что если мы умножаем строку на константу k, то новый определитель
в k раз больше старого.
Теорема: Влияние трех основных операций над строками на определитель таков:
1) Умножение строки на константу умножает определитель по этой константе.
2) Перестановка двух строк меняет знак определителя.
3) Замена одной строки этой строкой + умножение другой строки не имеет влияние на определитель.
Чтобы найти определитель матрицы, мы используем операции, чтобы сделать матрицу треугольной, а затем работать в обратном порядке.
Пример:
| 2 | 6 | 10 |
| 2 | 4 | -3 |
| 0 | 4 | 2 |
1/2 R 1 <-> R 1 (Умножает определитель на 1/2)
| 1 | 3 | 5 |
| 2 | 4 | -3 |
| 0 | 4 | 2 |
R 2 — 2R 1 -> R 2 Не влияет
на определитель. Обратите внимание, что нам не нужно обнулять верхний
средний номер. Нам нужно только обнулить нижние левые числа.
Обратите внимание, что нам не нужно обнулять верхний
средний номер. Нам нужно только обнулить нижние левые числа.
| 1 | 3 | 5 |
| 0 | -2 | -13 |
| 0 | 4 | 2 |
R 3 + 2R 2 -> R 3 Не влияет на определитель. Обратите внимание, что нам не нужно делать среднее число 1.
| 1 | 3 | 5 |
| 0 | -2 | -13 |
| 0 | 0 | -24 |
Определитель этой матрицы равен 48. Поскольку эта матрица имеет 1/2, определитель определитель исходной матрицы имеет определитель 48(2) = 96.
IV. Инверсии
Мы называем квадратную матрицу I со всеми единицами по диагонали и нулями
везде еще тож матрица. Обладает уникальным свойством
что если A — квадратная матрица с теми же размерами, то
Обладает уникальным свойством
что если A — квадратная матрица с теми же размерами, то
АИ = ИА = А
Определение
Если A — квадратная матрица, то обратная A -1 матрицы A — это единственная матрица такая, что
АА -1 = А -1 А = I
Пример:
Пусть А =
| 2 | 5 |
| 1 | 3 |
тогда
А -1 =
| 3 | -5 |
| -1 | 2 |
Если у нас будет время, мы проверим это.
Теорема: матрица, обратная матрице, существует тогда и только тогда, когда определитель отличен от нуля.
Чтобы найти обратную матрицу, мы пишем новую расширенную матрицу с
тождество справа. Затем полностью убавляем ряд, получившийся
матрица справа будет обратной матрицей.
Пример:
| 2 | -1 |
| 1 | -1 |
Прежде всего заметим, что определитель этой матрицы равен -2 + 1 = -1, следовательно, инверсия существует. Теперь мы устанавливаем расширенную матрицу как
| 2 | -1 | 1 | 0 |
| 1 | -1 | 0 | 1 |
Р 1 <-> Р 2
| 1 | -1 | 0 | 1 |
| 2 | -1 | 1 | 0 |
R 2 — 2R 1 -> R 2
| 1 | -1 | 0 | 1 |
| 0 | 1 | 1 | -2 |
Р 1 + Р 2 -> Р 1
| 1 | 0 | 1 | -1 |
| 0 | 1 | 1 | -2 |
Обратите внимание, что левая часть теперь является идентификатором. Правая рука
сторона обратная. Следовательно
Правая рука
сторона обратная. Следовательно
А -1 =
| 1 | -1 |
| 1 | -2 |
V. Решение уравнений с использованием матриц
Пример:
Предположим, у нас есть система
2х — у = 3
х — у = 4
Тогда мы можем записать это в матричной форме
Ах = б
куда
А =
| 2 | -1 |
| 1 | -1 |
х =
а также
б =
Мы можем умножить обе части на A -1 :
А -1 А х = А -1 б
или х = А -1 б.
Раньше,
А -1 =
| 1 | -1 |
| 1 | -2 |
Следовательно, наше решение
или х = -1 и у = 5
VI. Легкий путь
Легкий путь
Мы узнаем, как использовать калькулятор TI 85, чтобы найти обратные и детерминанты
Экономичный подход к гибкому выбору опорных точек для оценки определителя и обратной матрицы
- Список журналов
- PLoS один
- PMC38
PLoS Один. 2014; 9(2): e87219.
Опубликовано в Интернете 3 февраля 2014 г. doi: 10.1371/journal.pone.0087219
, 1 , * , 1 , 1 , 2 и 3
Херардо Адессо, редактор
Информация об авторе Примечания к статье Информация об авторских правах и лицензиях Отказ от ответственности
В этой статье представлены новые простые подходы к вычислению определителя и обратной матрицы. Выбор точки опоры был произвольным, поэтому они уменьшают ошибку при решении плохо обусловленной системы. Вычисление определителя матрицы стало более эффективным за счет экономии ненужного хранилища данных, а также за счет уменьшения порядка матрицы на каждой итерации, в то время как словарная запись [1] была включена для вычисления обратной матрицы, что избавляет от ненужных вычислений. Эти алгоритмы очень ориентированы на классную комнату, просты в использовании и реализуются учащимися. Воспользовавшись гибкостью выбора опорной точки, можно легко избежать развития фракций в большинстве случаев. В отличие от метода обращения матриц [2] и [3], представленные алгоритмы исключают использование перестановок и обратных перестановок.
Выбор точки опоры был произвольным, поэтому они уменьшают ошибку при решении плохо обусловленной системы. Вычисление определителя матрицы стало более эффективным за счет экономии ненужного хранилища данных, а также за счет уменьшения порядка матрицы на каждой итерации, в то время как словарная запись [1] была включена для вычисления обратной матрицы, что избавляет от ненужных вычислений. Эти алгоритмы очень ориентированы на классную комнату, просты в использовании и реализуются учащимися. Воспользовавшись гибкостью выбора опорной точки, можно легко избежать развития фракций в большинстве случаев. В отличие от метода обращения матриц [2] и [3], представленные алгоритмы исключают использование перестановок и обратных перестановок.
Термин «детерминант» изначально связан с системой линейных уравнений. Это дает нам предвидение характера решения данной системы линейных уравнений.
Маклорен [4] опубликовал первый результат об определителе и системе, который был обобщен Крамером [5] для систем. Позже Лаплас предложил известное разложение Лапласа для вычисления определителя, но тогда он использовал термин «результант» вместо определителя. Впервые термин определитель в современном контексте был сделан Коши [6]. В 1866 г. Доджсон представил другой метод нахождения определителя систем, который он назвал «методом конденсации» [7]. Для более крупных систем наиболее предпочтительным методом оценки определителя до сих пор является метод Гаусса [8]. Он решает проблему путем преобразования матрицы коэффициентов в эквивалентную верхнюю/нижнюю треугольную форму. Произведение опорных элементов дает определитель.
Позже Лаплас предложил известное разложение Лапласа для вычисления определителя, но тогда он использовал термин «результант» вместо определителя. Впервые термин определитель в современном контексте был сделан Коши [6]. В 1866 г. Доджсон представил другой метод нахождения определителя систем, который он назвал «методом конденсации» [7]. Для более крупных систем наиболее предпочтительным методом оценки определителя до сих пор является метод Гаусса [8]. Он решает проблему путем преобразования матрицы коэффициентов в эквивалентную верхнюю/нижнюю треугольную форму. Произведение опорных элементов дает определитель.
Существование обратной матрицы также зависит от ее определителя. Метод нахождения обратного по методу Гаусса обсуждается далее в этой статье. Ахмед и Хан [2], а также Хан, Шах и Ахмад [3] предложили алгоритмы вычисления обратной матрицы, которые представляют собой упрощенные формы метода Гаусса и также требуют перестановок и обратных перестановок. В этой статье мы представили два новых алгоритма, связанных с вычислением определителя и обратной матрицы. Первый из представленных алгоритмов оценивает определитель и является более эффективным, чем метод Гаусса, поскольку он уменьшает порядок матрицы на каждой итерации, тем самым экономя ненужные вычисления. Во втором алгоритме мы представили еще один простой способ вычисления обратной матрицы путем построения словаря данной системы и, таким образом, исключения необходимости перестановок и обратных перестановок.
Первый из представленных алгоритмов оценивает определитель и является более эффективным, чем метод Гаусса, поскольку он уменьшает порядок матрицы на каждой итерации, тем самым экономя ненужные вычисления. Во втором алгоритме мы представили еще один простой способ вычисления обратной матрицы путем построения словаря данной системы и, таким образом, исключения необходимости перестановок и обратных перестановок.
Определитель квадратной матрицы A , обозначаемый det ( A ), в основном представляет собой вещественную функцию. Из-за его полезной связи с матрицей A и решением системы уравнений вида A x = b , при изучении матриц становится необходимым знание определителей. Оценка детерминанта через его кофакторное расширение (также известное как расширение Лапласа) известно матрицами более низкого порядка.
Позвольте быть второстепенным элементом, который является определителем подматрицы, полученной после удаления строки и столбца A .
Если столбец A выбран для расширения кофактора, то
где — кофактор входа такой, что .
Аналогичным образом разложение кофактора по строке будет
Для матрицы порядка n оценка определителя с помощью приведенного выше разложения кофактора требует вычисления n определителя матриц порядка ( n −1). Поэтому его можно легко реализовать для нахождения определителя матрицы 2-го или 3-го порядка, но для более высоких порядков это становится утомительной работой. Чтобы уменьшить вычислительные усилия, обычно для оценки определителя включаются следующие три основные операции над строками матриц [9], метод известен как оценка определителя путем сокращения строк (также известный как метод Гаусса).
Элементарные операции со строками
Пусть A быть матрицей, могут быть применены следующие элементарные операции над строками
Умножение строки на ненулевую константу.
Поменяйте местами два ряда.

Добавить кратность одной строки к другой строке.
Влияние операций со строками на значение определителя: [9]
Пусть A будет матрицей, тогда
0651 A умножается на скаляр k, тогда det( B ) = k det( A ).
Если B является матрицей, которая получается при перестановке двух строк или двух столбцов матрицы A , то det( B ) = −det( A ).
Если B является матрицей, полученной при добавлении числа, кратного одной строке числа A , к другой строке или при добавлении числа, кратного одному столбцу, к другому столбцу, то det( B ) = det( A ).
Лемма: [9]
Если A является треугольной матрицей (верхней треугольной, нижней треугольной или диагональной), то det( A ) является произведением элементов на главной диагонали матрицы; то есть, .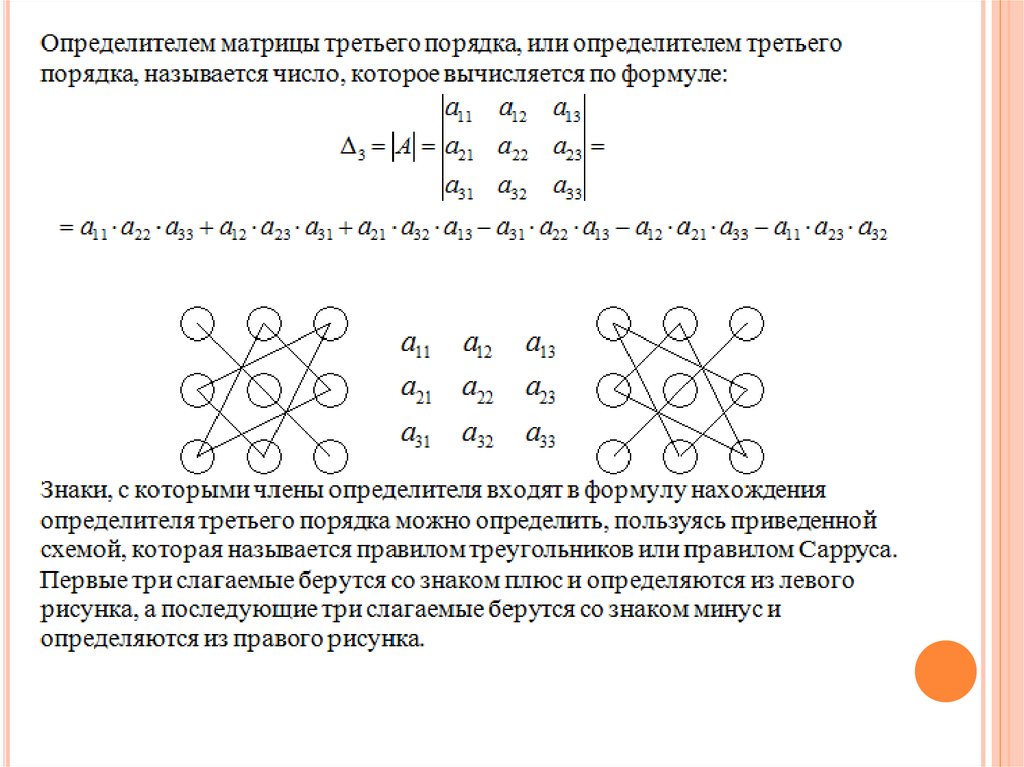
Вычисление определителя путем редукции строк
Суть метода заключается в приведении заданной матрицы к ее верхнему/нижнему треугольному виду путем применения элементарных операций над строками. Затем определитель можно вычислить, включив свойства, определенные выше в «Эффект операций со строками» и лемму.
Пример
Подход сокращения строк может включать все элементарные операции строк, как показано в приведенном выше примере. Здесь мы определяем операцию (скажем, операцию поворота для оценки определителя), которая состоит из ( n −1) приложений только операции со строками (с) и может использоваться для оценки определителей, минуя операции со строками (а). и (б).
Например, рассмотрим следующую матрицу:
Выбор ненулевого опорного элемента, расположенного в произвольном месте ( i, j ), скажем , и выполняя операцию со строками (c), чтобы сделать оставшиеся элементы столбца равными нулю, мы получаем
Здесь мы видим, что основная строка остается неизменной, а элемент матрицы, , где и равны элементы, соответствующие опорному элементу в опорном столбце и опорной строке соответственно.
Расширение кофактора по столбцу даст
Вышеприведенная процедура приводит к вычислению определителя матрицы пониженного порядка ( n -1). Повторение описанной выше процедуры в конечном итоге даст определитель. Для матрицы должно быть n ненулевых опорных элемента. Произведение соответствующих опорных элементов дает значение определителя. Однако, если на любом шаге не существует ненулевого центра, мы можем сделать вывод, что определитель данной матрицы равен 0.
Задача 1
Найти определитель матрицы A = порядка .
Алгоритм 1
Шаг 1: Набор d : = 1,
Шаг 2: набор P : = {1,2,3,……, n }
Шаг 3: Выберите любой p P такой, что L : = { k : , k Р }.
Шаг 4: Если L = , то d = 0 и перейти к шагу 7
В противном случае p П , к л и
Шаг 5: Уменьшить порядок A , удалив строку и столбец A . Также установите n : = n −1
Также установите n : = n −1
Шаг 6: . Если перейти к шагу 2.
Шаг 7: det ( A ) = d . Выход.
Пример
Итерация 1:
P : = {1,2,3,4}, здесь берем p = 1 так, L : = {1,2,3,4}. Принимая к = 1
Итерация 2:
P : = {1,2,3}, здесь берем p = 1, значит, L : = {2,3}. Принимая к = 2
Итерация 3:
P : = {1,2}, здесь берем p = 1, значит, L : = {1,2}. Принимая к = 1
Итерация 4:
P : = {1}, здесь берем p = 1, значит, L : = {1}. Принимая к = 1
Следовательно, определитель данной матрицы равен 12.
Сравнение с методом сокращения строк
Приведенный выше пример иллюстрирует эффективность алгоритма с точки зрения памяти и количества вычисляемых элементов. Если матрица 4-го порядка решается методом редукции строк, количество вычисленных элементов будет равно 12, 6 и 2 на первой, второй и третьей итерациях соответственно. Однако мы вычислили 9, 4 и 1 элемент в соответствующих итерациях. Таким образом, общее количество вычислений элементов, необходимых для метода сокращения строк, равно 20, но нашему методу требуется только 14 вычислений элементов. Также на каждой итерации размер матрицы уменьшался. Метод редукции строк должен хранить 16 элементов для каждой итерации, следовательно, в целом метод требует хранения 48 элементов в памяти, в то время как наш алгоритм хранит 16+9.+4+1 = 30 элементов, что является заметным сокращением требований к хранению.
Если матрица 4-го порядка решается методом редукции строк, количество вычисленных элементов будет равно 12, 6 и 2 на первой, второй и третьей итерациях соответственно. Однако мы вычислили 9, 4 и 1 элемент в соответствующих итерациях. Таким образом, общее количество вычислений элементов, необходимых для метода сокращения строк, равно 20, но нашему методу требуется только 14 вычислений элементов. Также на каждой итерации размер матрицы уменьшался. Метод редукции строк должен хранить 16 элементов для каждой итерации, следовательно, в целом метод требует хранения 48 элементов в памяти, в то время как наш алгоритм хранит 16+9.+4+1 = 30 элементов, что является заметным сокращением требований к хранению.
Сравнение числа элементов, вычисленных и сохраненных для оценки определителя различных порядков путем редукции строк и нашего алгоритма, показано на .
Таблица 1
Сравнение метода сокращения строк с алгоритмом 1 для вычисления определителя матрицы.
| Порядок | Метод сокращения строк | Алгоритм 1 | ||
No. of Element Computations of Element Computations | Storage Requirements (no. of elements) | No. of Element Computations | Storage Requirements (no. of elements) | |
| 2 | 2 | 8 | 1 | 5 |
| 4 | 20 | 48 | 14 | 30 |
| 5 | 40 | 125 | 30 | 55 |
| 7 | 112 | 343 | 94 | 140 |
| 10 | 330 | 1000 | 285 | 385 |
| 12 | 572 | 1728 | 506 | 650 |
Открыть в отдельном окне
Рассмотрим матрицу порядка n .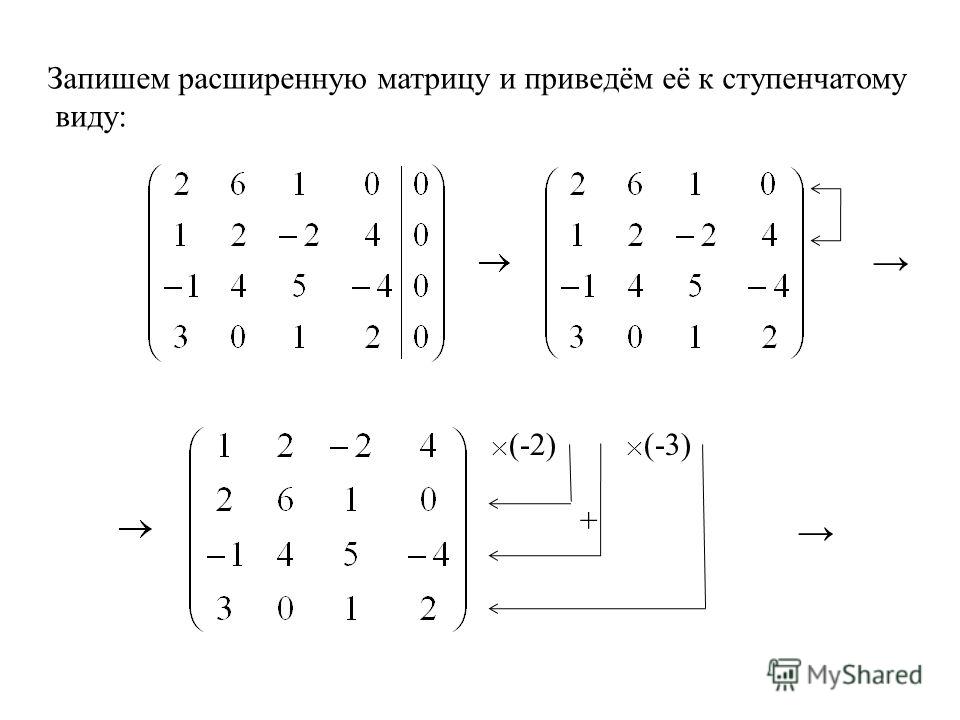 Чтобы вычислить обратную матрицу, скажем, B , нужно решить следующую n система уравнений, для
Чтобы вычислить обратную матрицу, скажем, B , нужно решить следующую n система уравнений, для
Решения приведенной выше системы:
Из системы (1) :
Из системы (2) :
Из системы ( n ) :
Тогда матрица называется обратной матрицы A .
Эту процедуру можно компактно представить, представив вышеописанную систему в расширенной форме,
(1)
, где и I — единичная матрица порядка n .
Если A обратима, применяя последовательные элементарные операции над строками метода Гаусса, получаем,
Теперь снова рассмотрим уравнение (1) в расширенной форме,
Обычно для решения вышеуказанной системы используется следующая расширенная матрица,
Здесь мы используя концепцию словарной записи, разработанную в [1]. Теперь базовыми переменными являются переменные, коэффициенты которых имеют вид любого столбца единичной матрицы, а базисом является совокупность всех базовых переменных. Мы можем видеть эту основу для приведенной выше матрицы и можем рассматривать ее как неоснову текущей матрицы. Цель состоит в том, чтобы преобразовать базовые переменные в небазовые переменные и наоборот с помощью операций поворота. Используя концепцию словаря, определенную в [1], мы можем удалить основные столбцы из матрицы и построить следующую словарную форму с базой B и неосновные N : (Обратите внимание, что основные переменные показаны в крайнем левом столбце, а неосновные переменные — в верхней строке словаря).
Мы можем видеть эту основу для приведенной выше матрицы и можем рассматривать ее как неоснову текущей матрицы. Цель состоит в том, чтобы преобразовать базовые переменные в небазовые переменные и наоборот с помощью операций поворота. Используя концепцию словаря, определенную в [1], мы можем удалить основные столбцы из матрицы и построить следующую словарную форму с базой B и неосновные N : (Обратите внимание, что основные переменные показаны в крайнем левом столбце, а неосновные переменные — в верхней строке словаря).
Pivot operation for evaluating inverse
The following pivot operations [1] may be applied to enter x i into basis B and y j into non-basis N ,
Разделить сводную строку на опорный элемент и опорный столбец на отрицательное значение опорного элемента (кроме опорного элемента).
Остальные ( n −1) 2 элементов определяются по формуле, определенной в новом методе определителя.

Поверните шарнирный элемент возвратно-поступательным движением.
Если количество опорных элементов равно порядку матрицы, результирующая матрица дает обратную, в противном случае можно сделать вывод, что обратной не существует.
Задача 2
Найдите обратную матрицу A = порядка .
Алгоритм 2
Шаг 1: Установить H : = {1,2,3,……, n }, B : = и N : = , . Построить словарь матрицы A , т.е. D ( A ).
Шаг 2: Набор P : = { p :}
Шаг 3: Если P = , перейдите к шагу 6.
В противном случае L : = { k : , x k N }
Шаг 4: Если L = , то обратное не существует. Выход
Иначе по любому
Шаг 5: а также . Обновите D ( A ) и перейдите к шагу 2.
Обновите D ( A ) и перейдите к шагу 2.
Шаг 6: Инв ( A ) = Выход.
Пример
Здесь N : = {}, B : = {}
Итерация 1:
H : = {1,2,3,4}, P : = {1,2,3,4}, принимая p = 1 получаем L : = {1,2,3,4}. Принимая к = 1
N : = {}, B : = {}
Итерация 2:
P : = {2,3,4}, взяв p = 2, получим L : = {3,4}. Принимая к = 3
N : = {}, B : = {}
Итерация 3:
P : = {3,4}, взяв p = 3, получим L : = {2,4}. Принимая к = 2
N : = {}, B : = {}
Итерация 4:
P : = {4}, взяв p = 4, получим L : = {4}. Принимая к = 4
Принимая к = 4
N : = {}, B : = {}
Теперь расположим элементы по индексам переменных в B и N .
Например Здесь H : = {1,2,3,4}, Так и , подразумевает . Также и подразумевает . Аналогично размещая остальные элементы получаем
Сравнение с методом Гаусса
Приведенный выше пример иллюстрирует эффективность алгоритма с точки зрения памяти и количества вычисляемых элементов. Если матрица порядка 4 решается методом Гаусса, количество вычисляемых элементов будет равно 20 на каждой итерации. Однако наш метод требует вычисления 16 элементов на каждой итерации. Таким образом, общее количество вычислений элементов, необходимых для метода Гаусса, составляет 80, с другой стороны, для нашего метода это 64. Кроме того, метод Гаусса должен хранить 32 элемента для каждой итерации, поэтому в целом метод Гаусса требует хранения 128 элементов. в памяти, в то время как наш алгоритм, напротив, хранит 64 элемента, что является заметным сокращением требований к памяти.
Сравнение количества элементов, вычисленных и сохраненных для оценки обратной по методу Гаусса и нашему алгоритму, показано на .
Таблица 2
Сравнение метода Гаусса с алгоритмом 2 для вычисления обратной матрицы.
| Порядок | Метод Гаусса | Алгоритм 2 | ||
| Количество элементов Расчеты 2 ( | элементов) | Элементы0942 No. of Element Computations | Storage Requirements (no. of elements) | |
| 2 | 12 | 8 | 8 | 4 |
| 4 | 80 | 32 | 64 | 16 |
| 5 | 150 | 50 | 125 | 25 |
| 7 | 392 | 98 | 343 | 49 |
| 10 | 1100 | 200 | 1000 | 100 |
| 12 | 1872 | 288 | 1728 | 144 |
Open in a separate window
Matrix determinant and inverse have applications in various таких областях, как математика, экономика, физика, биология и т. д. Решение различных моделей, таких как рост населения, требует использования определителя матрицы и обратной. Матрица, обратная и определитель, также используются в криптографии [10]. Линейные преобразования (поворот, отражение, перемещение и т. д.) предполагают вычисление обратной матрицы. Матрица, обратная и определитель, также используются в исследовании операций при решении линейных программ, пересмотренном симплекс-методе и цепях Маркова. Определители третьего порядка используются для нахождения площадей треугольников и проверки коллинеарности точек. Метод наименьших квадратов данных требует оценки обратной матрицы [11]. p -мерный объем параллелепипеда в определяется вычислением определителя [12].
д. Решение различных моделей, таких как рост населения, требует использования определителя матрицы и обратной. Матрица, обратная и определитель, также используются в криптографии [10]. Линейные преобразования (поворот, отражение, перемещение и т. д.) предполагают вычисление обратной матрицы. Матрица, обратная и определитель, также используются в исследовании операций при решении линейных программ, пересмотренном симплекс-методе и цепях Маркова. Определители третьего порядка используются для нахождения площадей треугольников и проверки коллинеарности точек. Метод наименьших квадратов данных требует оценки обратной матрицы [11]. p -мерный объем параллелепипеда в определяется вычислением определителя [12].
В этой статье представлены простые алгоритмы вычисления определителя и обратной матрицы. Поскольку порядок данной матрицы уменьшался на каждом шаге при вычислении ее определителя, алгоритм уменьшает требования к памяти (как показано в примере). Вычисление обратного было выполнено с использованием словарных обозначений, что позволяет избежать использования перестановок и упрощает обучение в классе. Плохо обусловленная система также может быть обработана, так как выбор точек опоры остается произвольным, что повышает числовую точность системы.
Плохо обусловленная система также может быть обработана, так как выбор точек опоры остается произвольным, что повышает числовую точность системы.
У авторов нет поддержки или финансирования для отчета.
1. Хватал В. (1983) Линейное программирование. Соединенные Штаты Америки: W.H. Фримен и компания. [Google Scholar]
2. Ахмад Ф., Хан Х. (2010) Эффективный и простой алгоритм обращения матриц. Международный журнал распространения технологий 20–27. [Google Scholar]
3. Хан Х., Шах И.А., Ахмад Ф. (2010) Эффективный и универсальный алгоритм обращения матриц. Международный журнал распространения технологий 36–41. [Академия Google]
4. Маклорен С. (1748 г.) Трактат по алгебре. Лондон: А. Миллар и Дж. Норс. [Google Scholar]
5. Крамер Г. (1750) Введение в анализ алгебраических кривых. [Google Scholar]
6. Огюстен К.Л. (1815) Memoire sur les fonctions qui ne peuvent obtenir que deux valeurs égales et des signes contraires par suite des transpositions operées entre les variable qu’elles renferment.

 Мне не понятно как привести матрицу к треугольному виду. Читал в учебнике «А.С. Бортаковский, А.В. Пантелеев. Линейная алгебра в примерах и задачах», но не могу понять алгоритм приведения матрицы к треугольному виду. Решать за меня разумеется не нужно, прошу пояснить данный метод, или еще лучше скинуть ссылку на какую нибудь теорию с хорошим примером такого преобразования. Матрица выглядит следующим образом:
Мне не понятно как привести матрицу к треугольному виду. Читал в учебнике «А.С. Бортаковский, А.В. Пантелеев. Линейная алгебра в примерах и задачах», но не могу понять алгоритм приведения матрицы к треугольному виду. Решать за меня разумеется не нужно, прошу пояснить данный метод, или еще лучше скинуть ссылку на какую нибудь теорию с хорошим примером такого преобразования. Матрица выглядит следующим образом: 09.2010, 16:23
09.2010, 16:23  09.2010, 16:33
09.2010, 16:33  09.2010, 16:34
09.2010, 16:34 

 Вычтите из второй строки определителя первую умноженную на 7/4
Вычтите из второй строки определителя первую умноженную на 7/4 Выглядит не сложно. Буду для проверки отписываться.
Выглядит не сложно. Буду для проверки отписываться.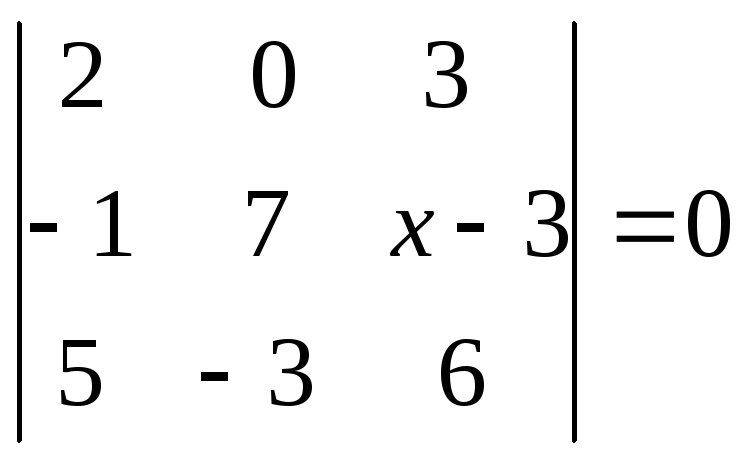 Выглядит не сложно. Буду для проверки отписываться.
Выглядит не сложно. Буду для проверки отписываться. 09.2010, 17:55
09.2010, 17:55  09.2010, 18:24
09.2010, 18:24 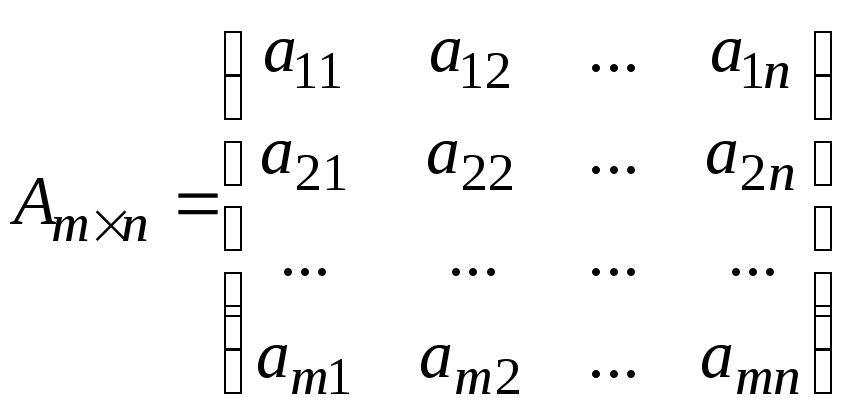 09.2010, 18:39
09.2010, 18:39  09.2010, 19:30
09.2010, 19:30  Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю.
Если все элементы некоторой строки или столбца равны нулю, то и сам определитель равен нулю.

