Формула коэффициент подобия треугольников: Подобные треугольники — урок. Геометрия, 8 класс.

Геометрия. Урок 7. Практические задачи по геометрии

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

• Подобные треугольники

Понятие подобных треугольников
Отношение периметров
Отношение площадей
Первый признак подобия
Второй признак подобия
Третий признак подобия

• Задачи про часы и стрелки

• Задачи про колесо со спицами

• Задачи про лестницу со ступеньками

• Задачи на нахождение длин и площадей

• Примеры решений заданий из ОГЭ

 

Два треугольника называются подобными, если углы одного треугольника соответственно равны углам другого треугольника, а стороны одного треугольника соответственно пропорциональны сторонам другого треугольника.

Подобие треугольников обозначается значком «∼». Запишем подобие двух треугольников:

△ABC∼△A1B1C1

Соответственные стороны двух подобных треугольников – это стороны, которые лежат напротив равных углов.

 

 

Пары равных углов:

∠A и ∠A1

∠B и ∠B1

∠C и ∠C1

Пары соответственных сторон:

BC и B1C1

AC и A1C1

AB и A1B1

Представьте себе, что на смартфоне или планшете вы открыли изображение треугольника. Вы захотели получше его рассмотреть и увеличили изображение. Сам треугольник увеличился, но его пропорции сохранились (он не сплюснулся, не вытянулся, просто стал больше). Вот такие два треугольника: исходный и увеличенный будут подобными. Масштаб увеличенной картинки изменился в k. Это число k будет являться коэффициентом подобия этих треугольников.

Коэффициент подобия k это число, равное отношению соответственных сторон подобных треугольников.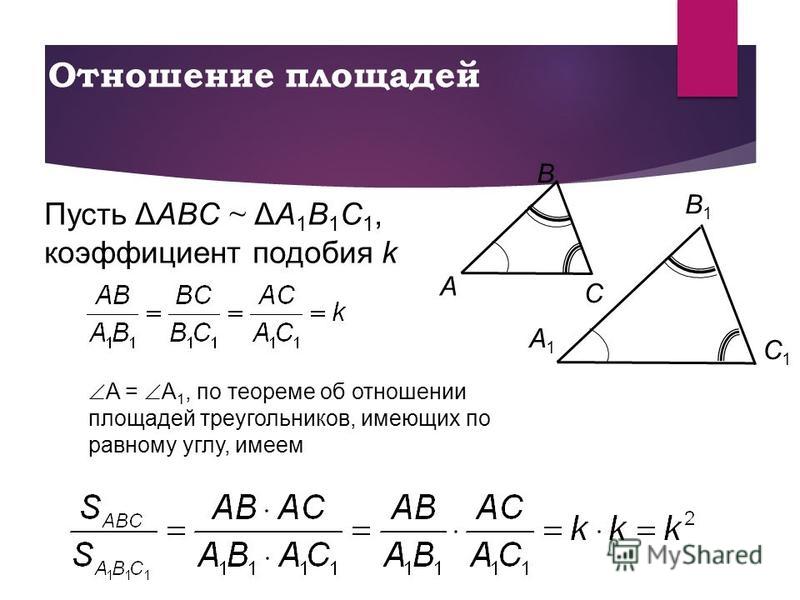

 

 

k=A1B1AB=A1C1AC=B1C1BC

• Если стороны большего треугольника относить к сторонам меньшего треугольника, то коэффициент подобия k>1.

• Если стороны меньшего треугольника относить к сторонам большего треугольника, то коэффициент подобия k<1.

 

Отношение периметров подобных треугольников равно коэффициенту подобия.

P△A1B1C1P△ABC=k

 

Отношение площадей подобных треугольников равно квадрату коэффициента подобия.

S△A1B1C1S△ABC=k2

 

Первый признак подобия треугольников (по двум углам)

Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.

 

 

∠A=∠A1∠B=∠B1|⇒△ABC∼△A1B1C1

 

Второй признак подобия треугольников (по двум сторонам и углу между ними)

Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.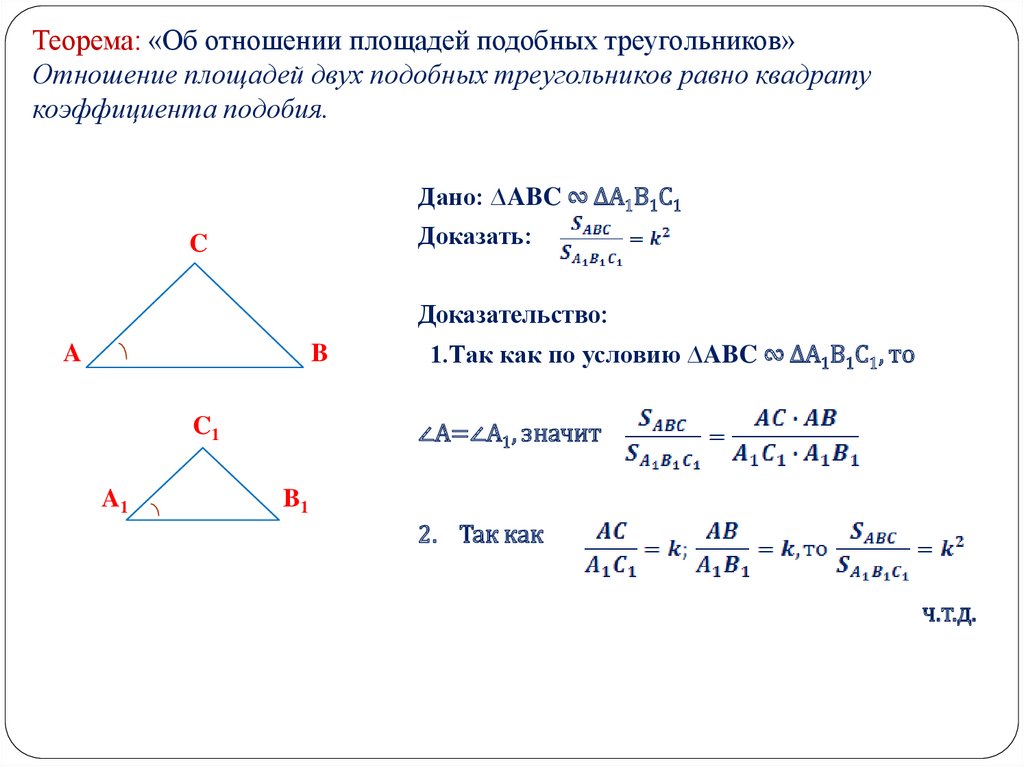

 

 

∠A=∠A1A1B1AB=A1C1AC=k|⇒△ABC∼△A1B1C1

 

Третий признак подобия треугольников (по трём сторонам)

Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

 

 

A1B1AB=A1C1AC=B1C1BC=k⇒△ABC∼△A1B1C1

 

В задании 17 ОГЭ встречаются задачи, в которых необходимо найти угол между часовой и минутной стрелкой. Давайте разберёмся, как их решать.

Часовой циферблат – это окружность.

Градусная мера всей окружности равна 360°.

Стрелки – стороны центральных углов.

На окружности 60 маленьких делений и 12 больших.

Каждое маленькое деление отсекает от окружности дугу, градусная мера которой равна 360°60=6°.

Каждое большое деление отсекает от окружности дугу, градусная мера которой равна 360°12=30°.

Можно рассуждать, что одна большая дуга содержит пять маленьких, то есть её градусная мера равна 6°⋅5=30°.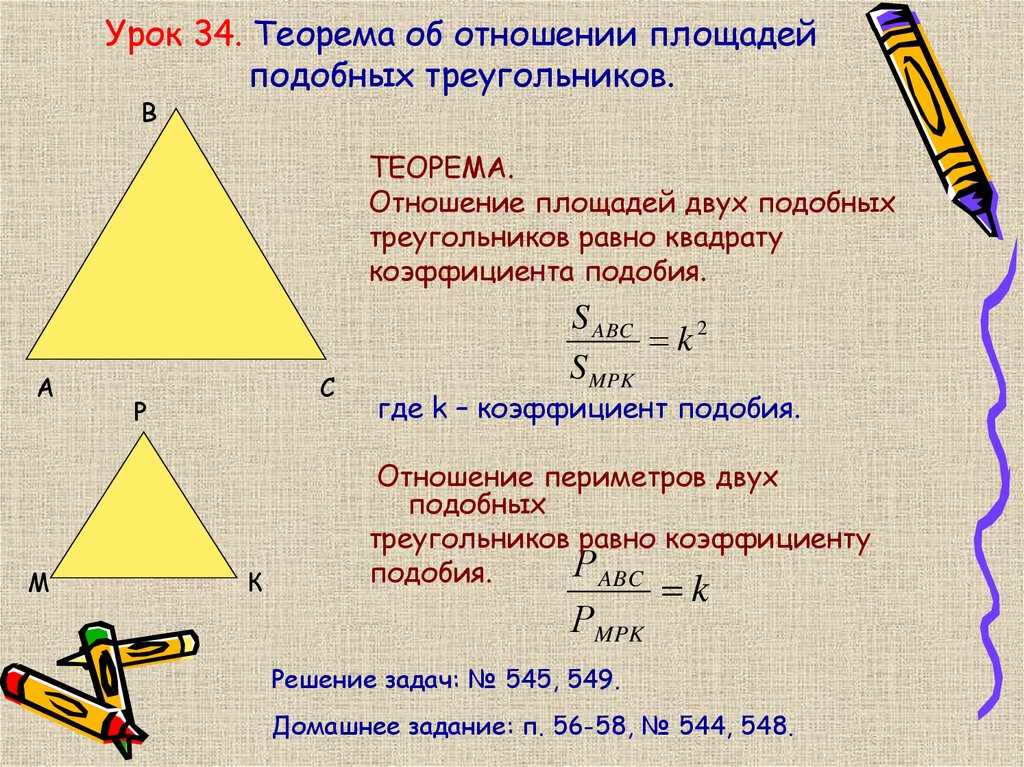

 

 

В задании 17 ОГЭ встречаются задачи, в которых дано колесо со спицами и требуется определить либо угол между соседними спицами (если дано количество спиц), либо количество спиц (если дан угол между соседними спицами). Будем разбираться, как такие задачи решать.

Пусть у нас есть колесо, в котором n спиц. Тогда эти спицы образуют n равных центральных углов α.

 

 

Формула, которая связывает количество спиц и угол между двумя соседними:

α⋅n=360°

 

В задаче данного типа дана лестница, состоящая из n ступенек. Каждая ступенька характеризуется своей высотой (вертикальный отрезок) и длиной (горизонтальный отрезок). Сама лестница характеризуется своей длиной (отрезок AC), высотой (отрезок BC) и отрезком AB.

 

 

Высота всей лестницы – количество ступенек, умноженное на высоту одной ступеньки. Длина всей лестницы – количество ступенек, умноженное на длину одной ступеньки. Для нахождения длины лестницы необходимо применить теорему Пифагора.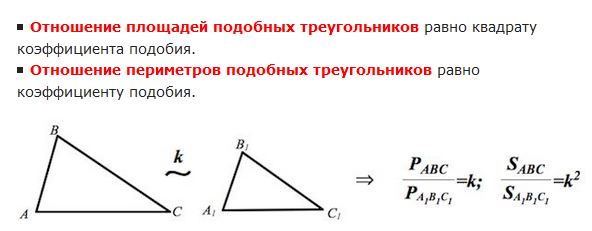

 

Теоретический и практический материал по нахождению площадей треугольников и четырехугольников можно найти в уроках 3 и 4 модуля геометрия.

Перейти по ссылкам:

• Площадь треугольника

• Площадь равностороннего треугольника

• Площадь прямоугольного треугольника

• Площадь параллелограмма

• Площадь ромба

• Площадь прямоугольника

• Площадь квадрата

• Площадь трапеции

 

3). В подобных треугольниках:

а). периметры подобных треугольников относятся как коэффициент подобия

б). площади подобных треугольников относятся как коэффициент подобия в квадрате.

B

N

A

C M P

Δ ABC Δ MNP

3.

Формулы площадей треугольника

1). Равносторонний треугольник

S =a – сторона треугольника

h = h – высота треугольника

2). Прямоугольный треугольник

S = a b a, b – катеты треугольника

3). Разносторонний треугольник

S = a h a

– сторона треугольника

h – высота, проведенная к этой стороне

S = a b sin ά a, b – стороны треугольника

ά — угол между этими сторонами

S = a, b, c – стороны треугольника

p – полупериметр; p = (a + b + c)

S = a, b, c – стороны треугольника

R – радиус описанной окружности

S =

P r P –периметр треугольника

r – радиус вписанной окружности

4.

Решение треугольников.

1). Теорема синусов:

Стороны треугольника пропорциональны синусам противолежащих углов.

Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу описанной окружности.

2). Теорема косинусов:

Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

5. Прямоугольные треугольники.

1). Решение прямоугольного треугольника

2). Опорные прямоугольные треугольники

3). Признаки равенства прямоугольных треугольников

Два прямоугольных треугольника равны, если у них равны:

а). катет и гипотенуза

б).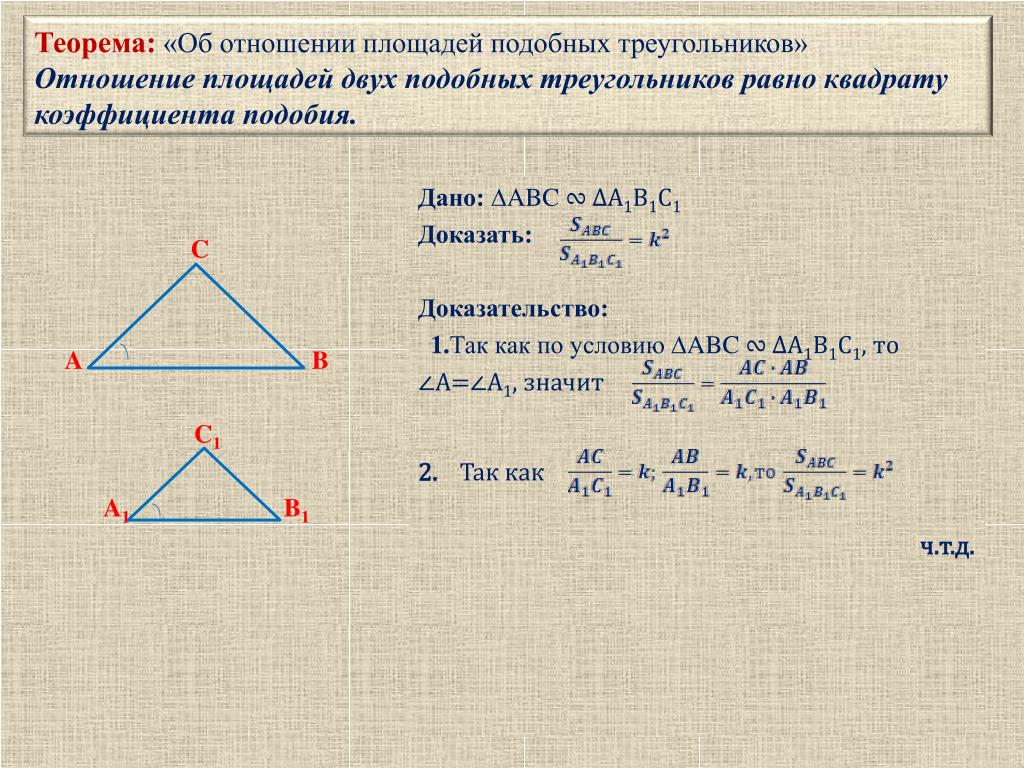 гипотенуза и острый угол

4). Соотношение в прямоугольном треугольнике

6. Описанные и вписанные треугольники

1). Положения центра окружности.

а). Центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.

Радиус вписанной окружности – перпендикуляр, опущенный из этой точки на сторону треугольника.

б). Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.

Радиус описанной окружности –отрезок, соединяющий центр окружности с вершиной треугольника

в). В равностороннем треугольнике центр вписанной и описанной окружностей совпадают .

Подобие прямоугольного треугольника

Мы открыты — звоните сейчас!

Позвоните сейчас, чтобы записаться на обучение

(888) 736-0920

HotmathMath Домашнее задание. Делай быстрее, учись лучше.

Сходство острого угла

Если один из острых углов прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то Сходство угол-угол треугольники подобны.

На рисунке , так как оба угла прямые и .

Так, .

Сходство ног

Если длины соответствующих катетов двух прямоугольных треугольников пропорциональны, то по Сторона-угол-боковое сходство треугольники подобны.

На рисунке .

Так, .

Сходство гипотенузы-ножки

Если длины гипотенуза и катет прямоугольного треугольника пропорциональны соответствующим частям другого прямоугольного треугольника, то эти треугольники подобны. (Вы можете доказать это, используя Теорема Пифагора чтобы показать, что третья пара сторон также пропорциональна. )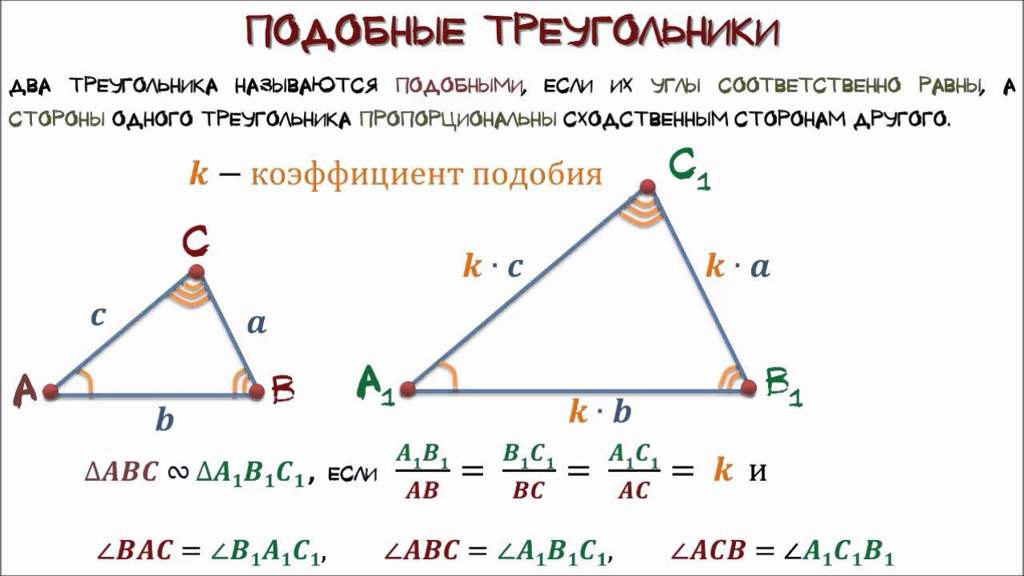

На рисунке .

Так, .

Объединив сходство катетов и гипотенус-контрастов, мы можем сказать, что если любые две стороны прямоугольного треугольника пропорциональны соответствующим сторонам другого прямоугольного треугольника, то эти треугольники подобны.

Предметы рядом со мной

• Серия 26 Курсы и классы
• IBEW — Международное братство электротехников Подготовка к экзаменам
• Статистические курсы для выпускников
• FAA — подготовка к экзамену Федерального авиационного управления
• CPCE — подготовка советника к комплексному экзамену, подготовка к экзамену
• Репетиторы по всемирной истории в средней школе
• Репетиторы по домашним заданиям в детском саду
• Репетиторы по всемирной истории в старшей школе Китайский язык 3 преподавателя
• Преподаватели стратиграфии
• Облако CCNA — курсы и классы Cisco Certified Network Associate-Cloud
• Репетиторы по символической логике
• CAPM — сертифицированный специалист по подготовке к экзаменам по управлению проектами
• CLEP Курсы и классы по математике для колледжей
• Репетиторы по геммологии
• Репетиторы по Joomla
• Репетиторы по голосу
• Репетиторы по физике для колледжа Under-1 Prep5 900

Популярные города

• Репетиторство в Солт-Лейк-Сити
• Репетиторство в Шарлотте
• Репетиторство в Сан-Антонио
• Репетиторство в Луисвилле
• Nashville Tutoring
• Tampa Tutoring
• Cincinnati Tutoring
• Madison Tutoring
• Pittsburgh Tutoring
• Austin Tutoring

Popular Subjects

• SAT Tutors in Denver
• Biology Tutors in New York City
• Statistics Tutors in Miami
• Репетиторы статистики в Вашингтоне, округ Колумбия
• Репетиторы испанского языка в Фениксе
• Репетиторы информатики в Фениксе
• Репетиторы GMAT в Атланте
• Репетиторы испанского языка в Атланте
• Репетиторы ISEE в Далласе, Форт-Уэрт
• Репетиторы алгебры в районе залива Сан-Франциско

Загрузите наши бесплатные приложения для обучения и книги для подготовки к экзаменам

Подобные прямоугольные треугольники

Два треугольника подобны соответствующие им углы равны.

Пример:

На схеме, показанной выше,

ΔABC ∼ ΔXYZ

Напомним, что соответствующие длины сторон подобных треугольников пропорциональны.

Теорема

Если высота проведена к гипотенузе прямоугольного треугольника, то два образовавшихся треугольника подобны исходному треугольнику и друг другу.

На приведенной выше диаграмме

ΔCBD ∼ ΔABC

ΔACD ∼ ΔABC

ΔCBD ∼ ΔACD

высота CD проведена к гипотенузе AB.

Доказать:

ΔCBD ∼ ΔABC, ΔACD ∼ ΔABC, ΔCBD ∼ ΔACD

Доказательство :

Первое доказательство того, что ΔCBD ∼ ΔABC. В каждом треугольнике есть прямой угол, и каждый включает ∠B. Треугольники подобны в соответствии с постулатом подобия АА.

Мы можем использовать аналогичные рассуждения, чтобы показать, что ΔACD ∼ ΔABC.

Чтобы показать, что ΔCBD ∼ ΔACD, начните с демонстрации того, что ∠ACD ≅ ∠B, поскольку они оба дополняют ∠DCB. Затем вы можете использовать постулат подобия АА.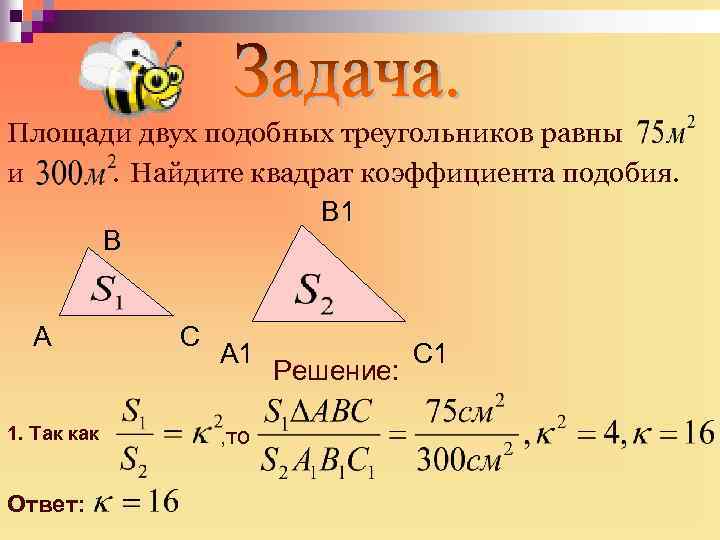

Использование среднего геометрического для решения задач

В правом ΔABC, показанном выше, высота CD проведена к гипотенузе, образуя два меньших прямоугольных треугольника, которые подобны ΔABC. Из приведенной выше теоремы мы знаем, что ΔCBD ∼ ΔACD ∼ ΔABC.

Обратите внимание, что CD — это более длинная часть ΔCBD, а более короткая — ΔACD. Когда мы пишем пропорцию, сравнивающую длины катетов ΔCBD и ΔACD, мы видим, что CD — это среднее геометрическое BD и AD.

Стороны CB и AC также встречаются более чем в одном треугольнике. Длины их сторон также являются средними геометрическими, как показано ниже в пропорциях:

Эти результаты выражены в теоремах ниже.

Теоремы о среднем геометрическом

Теорема 1 :

В прямоугольном треугольнике высота от прямого угла до гипотенузы делит гипотенузу на два сегмента.

На правом ΔABC, показанном выше, длина высоты CD представляет собой среднее геометрическое длин двух сегментов.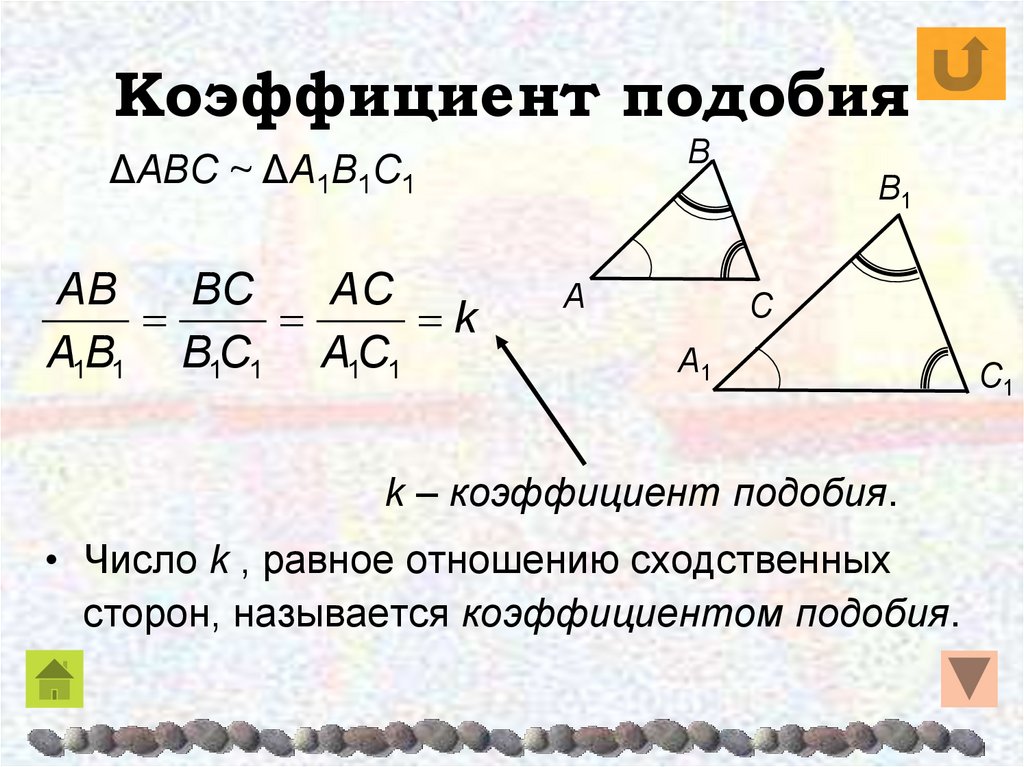 АД и БД.

То есть

BD/CD = CD/AD

CD ²  = AD ⋅ BD

CD = √(AD ⋅ BD)

Теорема 2 :

900, Прямой угол к гипотенузе делит гипотенузу на два отрезка.

Длина каждого катета прямоугольного треугольника равна среднему геометрическому длин гипотенузы и отрезка гипотенузы, примыкающего к катету.

В правом ΔABC, показанном выше,

CB = √ (ab ⋅ db)

ac = √ (ab ⋅ ad)

Нахождение высоты крыши

Пример:

A ROOча имеет аттров. поперечное сечение прямоугольного треугольника. На схеме показаны примерные размеры этого сечения.

а. Найдите подобные треугольники.

б. Найдите высоту h крыши.

Решение (a) :

Мы можем счесть полезным нарисовать три подобных прямоугольных треугольника так, чтобы соответствующие углы и стороны имели одинаковую ориентацию. Отметьте равные углы.

Обратите внимание, что некоторые стороны встречаются более чем в одном треугольнике.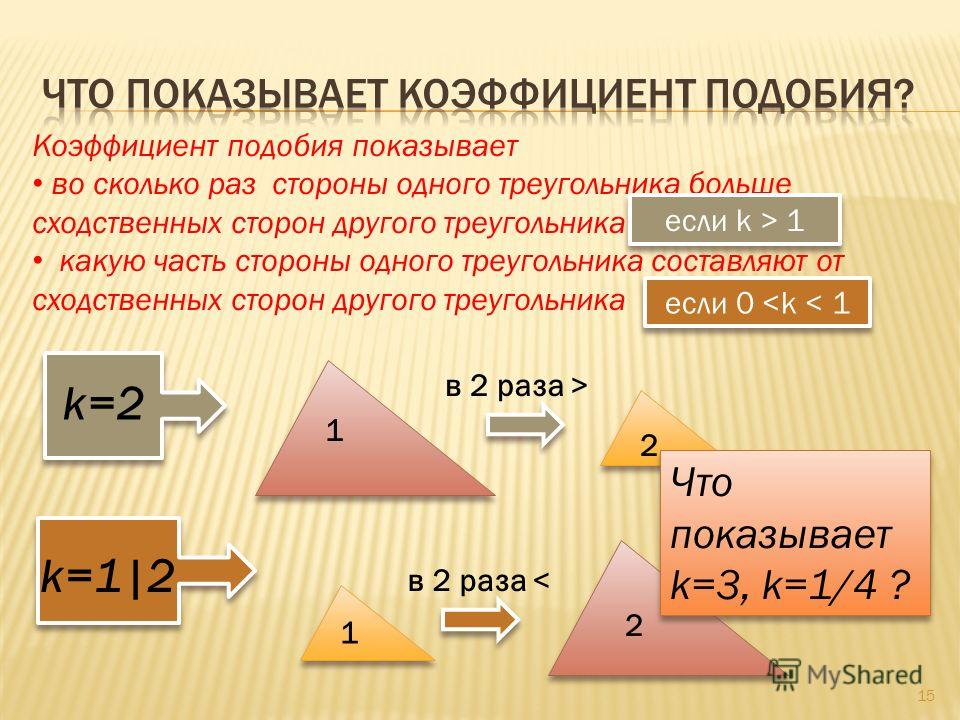

Например, BC — это гипотенуза в ΔBCA и более короткий катет в ΔBDC.

На приведенной выше диаграмме

ΔBCA ∼ ΔCDA ∼ ΔBDC

Решение (b) :

Используйте тот факт, что ΔBCA ∼ ΔBDC, чтобы написать пропорцию.

Соответствующие длины сторон пропорциональны:

CA/DC = BC/BD

Замена.

h/5,5 = 3,1/6,3

Применить свойство перекрестного произведения.

6,3h = 3,1 (5,5)

Решите для h.

h ≈ 2,7

Отсюда высота крыши около 2,7 метра.

Использование среднего геометрического

Пример 1:

Найдите значение x на диаграмме, показанной ниже.

Решение:

Применить теорему о среднем геометрическом 1.

x/3 = 6/x

Применить свойство векторного произведения.

x ²  = 18

Найдите x.

х = √18

х = √(3 ⋅ 3 ⋅ 2)

x = 3√2

Пример 2:

Найдите значение y на диаграмме, показанной ниже.

Решение:

Применить теорему о среднем геометрическом 2.